Abstract
Introduction:
Direct reactions are crucial tools for accessing properties of the atomic nucleus. Fundamental and exotic phenomena such as collective modes, pairing, weakbinding effects and evolution of single-particles energies can be investigated in peripheral collisions between a heavy nucleus and a light target. The necessity of using inverse kinematics to reveal how these structural properties change with isospin imbalance renders direct reactions a challenging technique when using the missing mass method.
Methods:
In this scenario, Active Target Time Projection Chambers (AT-TPC) have demonstrated an outstanding performance in enabling these types of reactions even under conditions of very low beam intensities. The AT-TPC of the Facility for Rare Isotope Beams (FRIB) is a next generation multipurpose Active Target. When operated inside a solenoidal magnet, direct reactions benefit from the measurement of the magnetic rigidity that enables particle identification and the determination of the excitation energy with high resolution without the need of auxiliary detectors. Additionally, the AT-TPC can be coupled to a magnetic spectrometer improving even further its spectroscopic investigation capability.
Results:
In this contribution, we discuss inelastic scattering and transfer reaction data obtained via the AT-TPC and compare them to theory. In particular, we present the results for the 14C(p,p′) and 12Be (p,d)11Be reactions.
Discussion:
For 14C, we compare the experimental excitation energy of the first 1– excited state with coupled-cluster calculationsbased on nuclear interactions from chiral effective field theory and with available shell-model predictions. For 12Be, we determine the theoretical spectroscopic factors of the 12Be (p,d)11Be transfer reaction in the shell modeland compare them to the experimental excitation spectrum from a qualitative standpoint.
1 Introduction
Direct reactions, such as scattering, nucleon transfer and removal, are among the most powerful tools for extracting spectroscopic information about nuclear structure through charged-particle spectroscopy [1]. These reactions are very selective and can provide insights into both single-particle and collective nuclear excitations. A wide range of phenomena can be uncovered, including migration of nuclear magic numbers, modifications in single-particle structures, pairing modes and strengths, and the emergence of collective features in complex nuclei [2]. Direct reactions also play a key role in modeling nuclear processes relevant to explosive nucleosynthesis [3] and testing fundamental symmetries [4]. At large isospin imbalance, such phenomena may evolve along isotopic and isotonic chains revealing properties usually not found near the valley of stability. In this context, the nucleon-nucleon interaction and the interplay between collectivity and single-particle structure are essential to the nuclear shell model, a cornerstone of nuclear structure theory. In light of this, the conventional magic numbers may vanish. At the limits of stability where these phenomena predominantly occur, weak-bindings effects become more significant and are manifested through specific near-threshold resonances that highlight the role of the coupling to the continuum, formation of halos (skins) and weakening of the spin-orbit splittings.
The choice of an specific reaction is crucial when probing both single-particle and collective phenomena. Single-nucleon transfer reactions have been used preferentially to access experimental information on the location and occupation of nuclear levels because of its selectivity. Moreover, the cross section yields direct information on the overlap between the initial- and final-state wave functions as well as on the angular momentum and spin-parity of the states of interest. The process is described by a simple picture of a transferred particle/hole orbiting around the core. The normalization factor between the experimental cross section and the calculated single-particle cross section, known as spectroscopic factor, reveals the single-particle strengths of the populated levels, indicating the configuration mixing in the wave function. Both neutron and proton transfer reactions have been extensively used to study the evolution of single-particles energies and to reveal effective interactions between nucleons [5]. On the other hand, two-particle transfer reactions, particularly those involving neutrons, have been one of the essential tools for investigating the ubiquitous pairing in its many forms, naturally leading to the exploration of particle-particle correlations and its role on halo and Borromean systems. Accessing nuclear spectroscopic information can also be achieved using elastic and inelastic scattering with light targets/projectiles such as proton, deuteron or particles, although with much reduced selectivity. In addition to fundamental spectroscopy studies, inelastic scattering has been extensively employed to probe many forms of nuclear collectivity, for example, to extract the contribution of protons and neutrons to electric and magnetic transitions by considering their deformation lengths through the cross sections [6–8], to infer about cluster structures characterized by large monopole transitions [9, 10] and pygmy and giant resonances and electromagnetic responses of different natures [11–13]. Traditionally, Coulomb excitation (Coulex) has been the preferred reaction mechanism as electromagnetic probe. However, as mentioned before, hadronic probes provide insight into the contribution of the neutron motion to the collective matrix elements as well as the isoscalar and isovector components of the nucleus electromagnetic response. The Coulex and nuclear contributions to the reaction mechanism are highly dependent on the energy of the beam and the angle of measurement. Hadronic probes such as proton inelastic scattering are dominated by excitation through virtual photon exchange at zero degrees which opens a doorway to perform Coulex experiments under more favorable conditions [14, 15].
In the emerging era of next-generation radioactive ion-beam facilities, direct reactions will play a crucial role in the study of the nuclear structure at the edge of stability. Most experimental efforts are focused on advancing radioactive beam production and detection systems in tandem. Due to the limited production of the most exotic isotopes, experimental apparatuses that provide high detection efficiency are required to explore the limits of the landscape. Active Target Time Projection Chambers are particularly suited for direct reactions, in particular for low-intensity beams and for the multiple detection of low-energy particles [16–18]. Coupling Active Targets to a solenoid magnet enhances its sensitivity dramatically and its resolution thanks to the measurement of the particle magnetic rigidity [19]. These devices are known as solenoidal spectrometers, with the Helical Orbit Spectrometer (HELIOS) being the first and a pioneer in this field [20], followed by Solaris Sol [21] and the Isolde Solenoidal Spectrometer (ISS) [22]. In this work we discuss the performance of the Active Target Time Projection Chamber (AT-TPC) of the Facility for Rare Isotope Beams (FRIB) for experiments with radioactive beams. We will present results from two experiments performed with the AT-TPC coupled to the HELIOS magnet using low-intensity 14C and 12Be radioactive beams on a proton target. First, we focus on 14C proton inelastic scattering data, allowing for the extraction of low-energy excited states. In particular, the obtained value for the excitation energy of the first state is compared to the results of ab initio calculations [23, 24] from coupled-cluster theory [25] based on chiral effective field theory interactions [26–28]. Second, we consider the 12Be (p,d)11Be transfer reaction and provide predictions for the corresponding spectroscopic factors employing the shell model.
2 Materials and methods
The experiments were performed at Argonne National Laboratory using the combination of AT-TPC and the HELIOS magnet. The AT-TPC is a cylindrical Active Target of 1 m length and 25 cm of radius. The sensor consists of a dual micropattern gas detector (MPGD) featuring a 10,240 channel micromegas [29] pad plane and a multilayer thick gas electron multiplier M-THGEM [30] (See Figure 1). The use of the M-THGEM provides the sufficient gain to operate the detector with pure elemental gases such as hydrogen, deuterium or helium. The pad plane is read out by the General Electronics for TPCs, a dedicated data acquisition system capable of recording the drift time of ionization electrons with frequencies from 1 to 100 MHz [31]. The dynamic range can be adjusted from 120 fC to 10 pC, well suited for active target experiments where the injected beam may produce a much larger ionization than the scattered particle.
FIGURE 1

Left panel: Micromegas pad plane. Right panel: M-THGEM installed on top of the micromegas.
The HELIOS magnet is a decommissioned Magnetic Resonance Imaging (MRI) magnet that features constant radial and axial fields within the volume of the detector up to 2.85 T and a 0.9 m bore [20]. The magnet was adapted to deploy the AT-TPC and to couple it to the Argonne In-Flight Radioactive Ion Separator (RAISOR) beamline, as shown in Figure 2. The downstream end of the AT-TPC was coupled to a pair of silicon detectors and a LYSO crystal scintillator to detect the beam particle in coincidence with the scattered target and to evaluate the isomer content in the 12Be beam. A small ion chamber (2.54 cm diameter and 5 cm of length) was installed upstream of the AT-TPC to identify the incoming particles and also to serve as time reference for the data acquisition. The ion chamber windows were made of 12 m of Poly [p-phenylene terephthalamide) (PPTA) and was filled with 50 torr of tetrafluoromethane ].
FIGURE 2

Left panel: Downstream end of the AT-TPC and the GET electronics installed. Right panel: Upstream end of the AT-TPC coupled to RAISOR through an ion chamber.
The analysis of the AT-TPC data is a complex procedure involving the reconstruction of three-dimensional point clouds that capture the interaction of reaction products with the target gas as recorded by the pad plane. The convergence of the data analysis is tested using two distinct analysis frameworks, ATTPCROOTv2 and Spyral, which employ different tracking algorithms based on a linear quadratic estimator (Kalman filter) [19, 32] and a interpolator-based non-linear least squares fitter [33], respectively. The results presented in this paper are derived from the Spyral framework, with validation performed using both approaches. Spyral superior excitation energy resolution and improved efficiency for detecting short particle tracks. A more detailed description of the AT-TPC working principle and its associated data analysis can be found in Refs Bradt et al. [34]; Bazin et al. [18]; Ayyad et al. [17,19] and in the documentation of the data analysis frameworks [35].
3 Results
3.1 Proton inelastic scattering of 14C
The low-energy spectrum of 14C was determined by proton inelastic scattering using a14C beam of about 12.4 MeV and an intensity of about 2,000 pps for about 25 h of beam time. The AT-TPC was filled with 300 torr of pure hydrogen gas under static pressure. The beam energy after the AT-TPC window (also 12 m of PPTA) was about 12.4 MeV. The magnetic field was set to 2.85 T. The trajectory of the reaction products was determined on a event-by-event basis, enabling the inference of the angle and the magnetic rigidity through the track point cloud. The magnetic rigidity and the energy loss are used to identify the reaction products, as shown in the left panel of Figure 3. The most intense band on this plot corresponds to scattered protons.
FIGURE 3
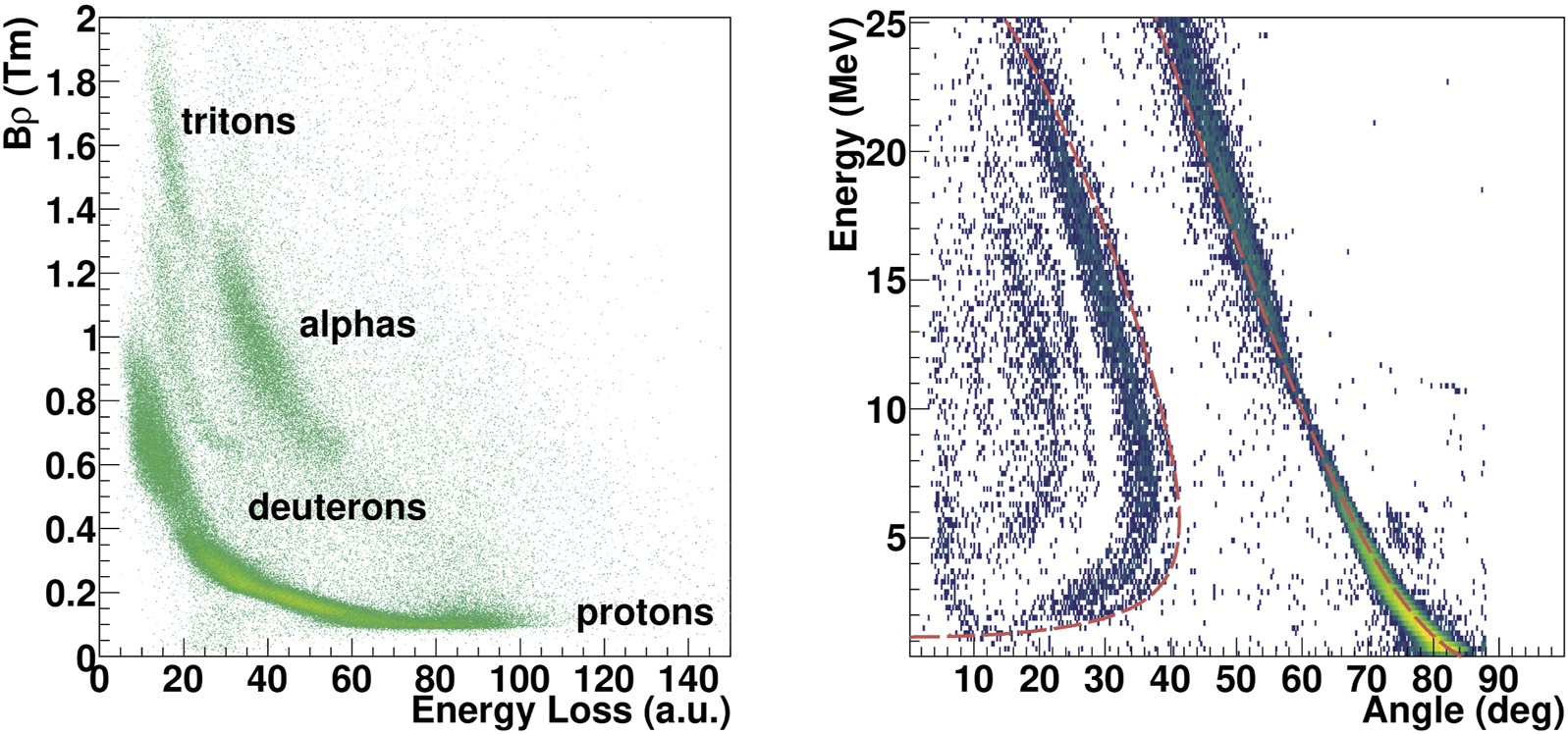
Left panel: Energy loss as a function of the magnetic rigidity of the reaction products. Right panel: Kinematics of the 14C + p reaction.
The excitation energy spectrum of 14C has been obtained after selecting the protons in the identification matrix and correcting for the energy loss of the beam in the detector. The characteristic kinematic lines of 14C excited states are shown in the right panel of Figure 3. The dashed lines refer to the calculated kinematics at the center of the detector for the ground state and the first excited state. The magnetic rigidity vastly increases the dynamic range of the detector as can be seen in the proton energy range covered in this reaction. It is important to highlight that at high proton energies there is a systematic deviation of the data with respect to the calculated kinematics. This discrepancy is likely caused by the electric field edge effects at the outer radius of the detector volume, which impact the reconstruction of high-rigidity particles.
The excitation energy spectrum of 14C is shown in the upper left panel of Figure 4. Besides the ground state, we are able to resolve the first excited state (6.091 MeV, ) and the at 8.317 MeV. The group of states at around 7 MeV has been identified as 6.728 MeV , 7.012 and 7.341 MeV , in agreement with Ref. Lozowski [36]. The values of the energy levels were extracted from the Nuclear Structure and Decay Data (NuDat) database [37]. The experimental resolution in this case, determined from a gaussian fit to the ground state peak, is 150 keV (standard deviation), with an accuracy of 30 keV [19]. The apparent peak at about 9 MeV is attributed to an excited state in 14N above the proton emission threshold, which is populated through the (p,n) charge-exchange reaction. Such events are identified by momentum conservation since the efficiency for the detection of neutrons in the AT-TPC is very low, although not negligible working as a proton target. The angular distribution associated to the state, shown in the upper right panel of Figure 4, was directly deduced from to in CM. In this angular domain, the peak is well isolated from the neighboring states. The angular distribution was corrected for acceptance and reconstruction efficiency effects. This correction utilized a comprehensive simulation that accounted for both the geometry and response of the AT-TPC. The simulated angular distribution, shown in the lower panel of Figure 4, was obtained generating events by sampling from a flat distribution between and in center of mass (CM). The gradual loss of efficiency between and can be attributed to the limited acceptance imposed by the pad plane’s hole for particles emitted at forward angles. At angles above , the energy loss of the protons becomes insufficient to ensure 100 of trigger efficiency. It is evident from the region of the distribution where the efficiency exceeds one that a fraction of misreconstructed events is not rejected but instead assigned incorrect angles or energies.
FIGURE 4

Upper left panel: Excitation energy spectrum obtained for the 14C + p reaction. Upper right panel: Angular distribution of the 6.091 MeV state of 14C including statistical error bars. Lower panel: Detection efficiency determined through simulations that accounted for both the detector acceptance and the track reconstruction process.
3.2 Neutron pick up on 12Be
Among the intricate structures of neutron-rich beryllium isotopes, 12Be stands as a candidate to observe a halo-like structure built on an excited state of a nucleus [38]. Its structure can be understood as the coupling between a valence neutron and a11Be core. Therefore, one could expect the possibility of observing an excited state on 12Be with a strong overlap to the 11Be ground state, a paradigmatic neutron halo nucleus. The bound structure of 12Be favors this hypothesis because the state is located around 400 keV below the neutron emission threshold ( = 3.170 MeV), a common feature of weakly-bound systems with a large spatial distribution. We designed an experiment to investigate an enhanced transition l = 1 from the isomeric state in 12Be as a possible signature of a halo structure in an excited state via inelastic scattering as primary probe. To validate the detection method, the setup was commissioned to detect the scattered proton in coincidence with the beam-like 12Be isomer. Concurrently, we measured cross sections for the 12Be (p,d) transfer reaction, which provides valuable information on the 12Be-10Ben overlap. In this work, we present results on the latter reaction.
The experiment was conducted using a low-intensity 12Be beam of about 150 pps at 12 MeV. The AT-TPC was filled with 600 torr of pure hydrogen gas. The data analysis was performed in the same fashion as discussed for the proton inelastic scattering on 14C.
The kinematics for the 12Be (p,d)11Be reaction and the 11Be excitation energy spectrum are shown in the left and right panels or Figure 5, respectively. Within our experimental resolution of 200 keV (standard deviation) and an accuracy of about 20 keV, we observe the population of several states of 11Be with established : ground state, 0.320 MeV (1/), 1.78 MeV (5/), 2.65 MeV (3/) and a doublet consisting of the 3.89 (3/ or 5/) and 3.96 MeV (3/). Although the ground and first excited states are unresolved, we can infer quantitative information on the population strength by considering the corresponding angular distributions. Extracting spectroscopic information with such a low-intensity beam clearly demonstrates the outstanding capabilities of Active Targets for experiments with radioactive beams. A detailed analysis of the angular distributions will be addressed in a separate publication to allow for a more thorough exploration.
FIGURE 5
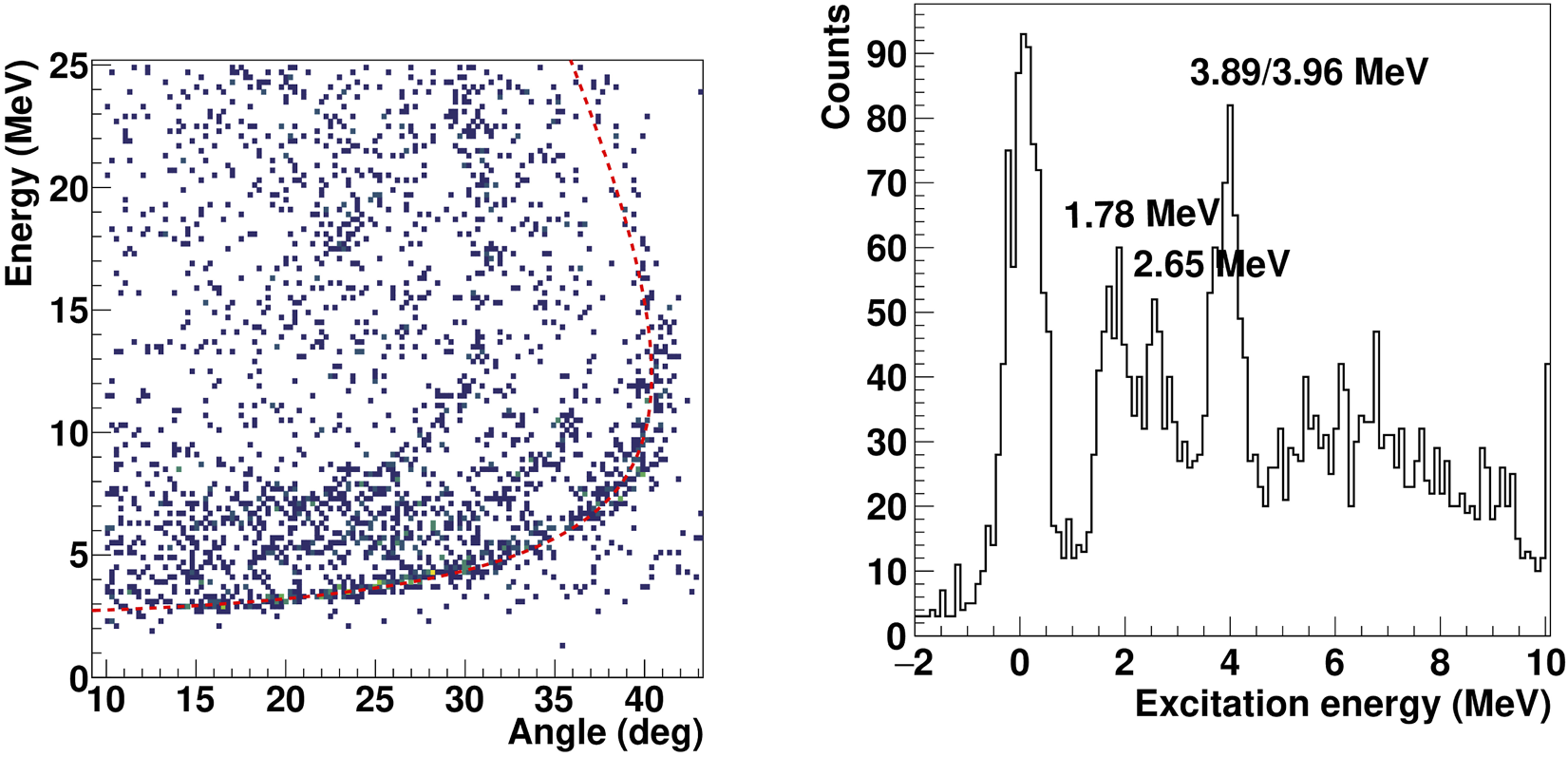
Left panel: Kinematics of the 12Be (p,d) reaction. Right panel: 11Be excitation energy spectrum obtained via 12Be (p,d).
4 Comparison with theory
4.1 Low-energy spectrum of 14C
The low-energy spectrum obtained for 14C via proton inelastic scattering can be compared to ab initio calculations employing nuclear interactions from chiral effective field theory. To solve the quantum many-body problem, we employ the coupled-cluster (CC) approach, where one starts from a mean-field solution and parametrizes the nuclear ground state wavefunction as (Equation 1)Here, is the so-called cluster operator, which can be expanded as a sum of -particle--hole excitations: . In this framework, excited states can be accessed employing the equation-of-motion coupled-cluster (EOM-CC) method [39]. In EOM-CC, the target state is computed via the ansatz (Equation 2)where also the EOM excitation operator can be written in terms of a particle-hole expansion. In CC theory, both the cluster operator and the EOM operator are truncated due to computational limitations. Coupled-cluster singles and doubles (CCSD), where and are truncated at the 2p-2h level, is the most frequently used approximation. Adding linear 3p-3h excitations in the so-called CCSDT-1 approximation [40] leads to increased precision.
As an example, we focus here on the first state in the spectrum of 14C and compare it to the experimental spectrum obtained with the AT-TPC. To this aim, we employ the chiral (394) and (450) interactions [41]. These nuclear force models, given at next-to-next-to-next-to-leading order in the chiral expansion, contain the isobar as an explicit degree of freedom and they have been successfully employed in several applications [42, 43]. We performed CC calculations starting from a Hartree-Fock Slater determinant including up to 15 major harmonic oscillator shells, and we studied convergence by varying the harmonic oscillator frequency between 12 and 16 MeV.
Our results for the excitation energy of the first state are shown in Table 1. Theoretical uncertainties account for the residual dependence on the model space parameters, and for the truncation of the coupled-cluster expansion according to the strategy employed in Simonis et al. [44]; Acharya et al. [45]. We observe that our predictions lie higher than the experimental determination at around 6.1 MeV. However, it is worth pointing out that the addition of linear 3p-3h excitation reduces the excitation energy of an amount varying between and on the basis of the interaction, moving theory in the direction of the experimental result. A complete analysis of model uncertainties, including the effect of the chiral EFT truncation and of different optimization protocols for the low-energy constants, is left for future work.
TABLE 1
| Interaction | Excitation energy [MeV] |
|---|---|
| (394) | 7.7 (0.7) |
| (450) | 7.9 (0.9) |
Excitation energies of the first excited state of14C in the CCSDT-1 approximation.
The experimental results on the first excited state of 14C can also be compared to available shell-model calculations. In Ref. Yuan et al. [46], the first excited state of 14C is calculated with three different shell-model interactions (YSOX [46], SFO [47], WBP [48]) optimized for the -shell region. The latter predict excitation energies ranging from 5.5 to 6 MeV, in close proximity to the experimental data.
Future experimental campaigns will exploit the AT-TPC to study electromagnetic responses up to the giant dipole resonance region. Electromagnetic strength data could be compared to calculations combining CC theory with the Lorentz Integral Transform technique [49] in the so-called LIT-CC method [50, 51]. This approach allows for an ab initio desciption of electromagnetic reaction observables in nuclei at and in the vicinity of closed-shells [44, 52, 53]. It is based on the calculation of an integral transform with Lorentzian kernel of the response. Considering small values of the Lorentzian width, we can construct a discretized strength function, where continuum excited states of the nucleus are represented by bound pseudo-states. As an example, let us focus on the E1 strength function of 14C, shown in Figure 6. At low energy, below 8 MeV, we distinguish the first excited state under analysis in this work. Its transition strength amounts to around of the one observed for states at excitation energies above 15 MeV.
FIGURE 6
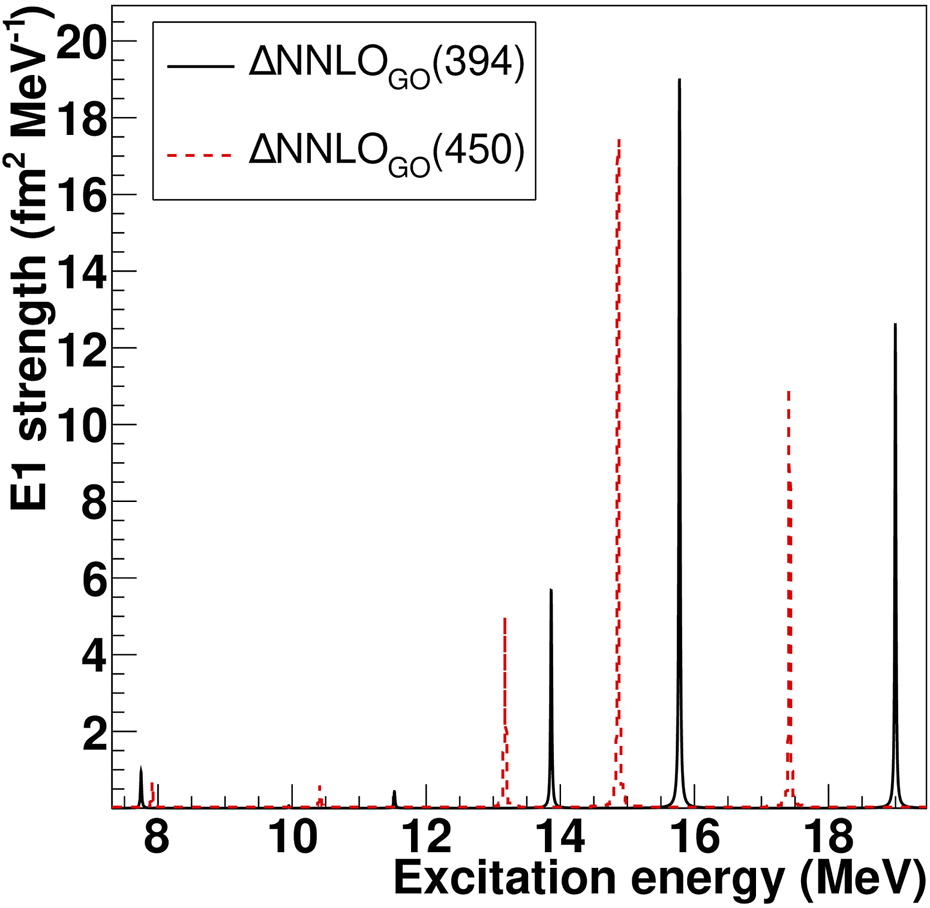
Discretized dipole response functions for the two different chiral forces in the CCSDT-1 approximation. The curves have been obtained using a model space size of 15 major oscillator shells and a harmonic oscillator frequency of 12 MeV.
4.2 Shell model calculations for 11Be
We have studied the structure of 11Be from a qualitative point of view from the spectrum obtained in the transfer measurement. We have applied shell model calculations, with the YSOX interaction [46] to calculate the spectroscopic factors of the 12BeBe reaction. This interaction works in a full model space, including excitations, and it can give good description of the energy, quadrupole and spin properties of the psd-shell nuclei. The calculated spectroscopic factors are compared to the experimental results shown in Figure 7. The spectroscopic factors represent the neutron occupancy of the , , and orbitals. It can be seen that the ground state and the first two excited states are populated, showing that the shell model is predicting a very strong configuration mixing in the ground state of 12Be due to the breakdown of magic number. This is in agreement with the experimental spectrum, except that the ground and the first excited states are not well isolated. However, it is expected that their individual contributions can be determined by the angular distribution, owing to their very different shapes. The higher excited states are populated due to the removal strength from the orbital. Significantly, the energy of the state deviates from the experimental results because the effective energy of the interaction is not optimized for nuclei far from the stability, and the continuum coupling effect was not accounted for. The experimental results presented in this work show strong agreement with previous findings from knock-out [54] and transfer [55] experiments, although a comprehensive discussion will be provided in a forthcoming publication.
FIGURE 7

Theoretical spectroscopic factors for the 12BeBe reaction obtained from shell model calculations. Black and red bars refer to positive and negative parity states, respectively.
5 Conclusion
In this work, we have showcased the use of solenoidal spectrometers in active target mode for direct reactions through the measurement of proton inelastic scattering on 14C and the neutron transfer reaction 12BeBe in inverse kinematics, both using the AT-TPC. This detection scheme enables the measurement of these reactions with beam intensities as low as 100 pps and with adequate resolution. The combination of target thickness and magnetic rigidity results in a broad dynamic range covered by the detector. These capabilities are reflected in the data we have obtained in these measurements. The low-lying E1 strength of 14C was employed to benchmark ab initio calculations including interactions from chiral effective field theory. The comparison between theory and experiment, although limited in excitation energy range, paves the way to investigate the E1 strength up to high-excitation energies. The measurement of the full electromagnetic response at very forward angles can be realized using the AT-TPC coupled to a magnetic spectrometer (see Refs. [19, 56]). Such an experimental program has been already initiated at FRIB with the measurement of the E1 response of 11Li via proton inelastic scattering at forward angles. We have also performed shell model calculations, using the YSOX interaction, to clarify the structure of 11Be obtaining a good agreement with the experimental results, from a qualitative standpoint. Obtaining relevant spectroscopic information in such conditions opens a wide range of opportunities for conducting transfer reaction experiments with the most exotic species currently producible.
Statements
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
YA: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. DB: onceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, riting–original draft, Writing–review and editing. FB: Formal Analysis, Investigation, Methodology, Software, Validation, Writing–original draft, Writing–review and editing. JC: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Resources, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. XL: Formal Analysis, Investigation, Methodology, Writing–review and editing. AA: Methodology, Software, Validation, Writing–review and editing. MA: Writing–review and editing. SB-N: Writing–review and editing. KB: Writing–review and editing. CC: Writing–review and editing. TF: Writing–review and editing. VG: Writing–review and editing. AH-S: Writing–review and editing. CH: Writing–review and editing. HJ: Writing–review and editing. TK: Writing–review and editing. HK: Writing–review and editing. JL-G: Writing–review and editing, Formal Analysis. JL-F: Writing–review and editing. AM: Writing–review and editing. GM: Formal Analysis, Software, Writing–review and editing, Data curation, Investigation, Methodology, Visualization. CM-G: Writing–review and editing. AM-R: Writing–review and editing, Formal Analysis, Software. WM: Writing–review and editing. BO: Writing–review and editing. ZR: Writing–review and editing. DR: Writing–review and editing. JR: Writing–review and editing. SS: Writing–review and editing. CS: Writing–review and editing. MS: Writing–review and editing, Formal Analysis, Software. TT: Writing–review and editing. IT: Writing–review and editing. NT: Software, Writing–review and editing. NW: Writing–review and editing. JZ: Software, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work has received financial support from the Xunta de Galicia (CIGUS Network of Research Centres) and the European Union; from the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, under Contract Number DE-AC02-06CH11357 (Argonne), DE-SC0020451 (FRIB). SOLARIS is funded by the DOE Office of Science under the FRIB Cooperative Agreement DE-SC0000661. Y.A. is supported by grant RYC2019-028438-I and PID2021-125995NA-I00 funded by MCIN/AEI/10.13039/501100011033 and by the Regional Government of Galicia under the program “Proyectos de excelencia” Grant No. ED431F 2022/13. SB is supported by Grant RYC2020-030669 and PID2022-142557NA-I00 funded by MCIN/AEI/10.13039/501100011033. FB’s work is supported by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, under the FRIB Theory Alliance award DE-SC0013617, and Office of Advanced Scientific Computing Research and Office of Nuclear Physics, Scientific Discovery through Advanced Computing (SciDAC) program (SciDAC-5 NUCLEI). This research used resources of the Oak Ridge Leadership Computing Facility located at Oak Ridge National Laboratory, which is supported by the Office of Science of the Department of Energy under contract No. DE-AC05-00OR22725. Computer time was provided by the Innovative and Novel Computational Impact on Theory and Experiment (INCITE) program.
Acknowledgments
FB would like to thank Gaute Hagen for access to the spherical coupled-cluster code and Thomas Papenbrock for helpful discussions.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1.
Hansen P Tostevin J . Direct reactions with exotic nuclei. Annu Rev Nucl Part Sci (2003) 53:219–61. 10.1146/annurev.nucl.53.041002.110406
2.
Wimmer K . Nucleon transfer reactions with radioactive beams. J Phys G: Nucl Part Phys (2018) 45:033002. 10.1088/1361-6471/aaa2bf
3.
Bardayan DW . Transfer reactions in nuclear astrophysics. J Phys G: Nucl Part Phys (2016) 43:043001. 10.1088/0954-3899/43/4/043001
4.
Leach KG Garrett PE Ball GC Bender PC Bildstein V Brown BA et al Searching for 0+ states in 50Cr: implications for the superallowed β decay of 50Mn. Phys Rev C (2016) 94:011304. 10.1103/PhysRevC.94.011304
5.
Schiffer JP True WW . The effective interaction between nucleons deduced from nuclear spectra. Rev Mod Phys (1976) 48:191–217. 10.1103/RevModPhys.48.191
6.
Chen J Kay BP Tang TL Tolstukhin IA Hoffman CR Li H et al Probing the quadrupole transition strength of 15C via deuteron inelastic scattering. Phys Rev C (2022) 106:064312. 10.1103/PhysRevC.106.064312
7.
Jiang Y Lou JL Ye YL Liu Y Tan ZW Liu W et al Quadrupole deformation of 16C studied by proton and deuteron inelastic scattering. Phys Rev C (2020) 101:024601. 10.1103/PhysRevC.101.024601
8.
Corsi A Boissinot S Obertelli A Doornenbal P Dupuis M Lechaftois F et al Neutron-driven collectivity in light tin isotopes: proton inelastic scattering from 104sn. Phys Lett B (2015) 743:451–5. 10.1016/j.physletb.2015.03.018
9.
Yang ZH Ye YL Li ZH Lou JL Wang JS Jiang DX et al Observation of enhanced monopole strength and clustering in 12Be. Phys Rev Lett (2014) 112:162501. 10.1103/PhysRevLett.112.162501
10.
Kawabata T Akimune H Fujita H Fujita Y Fujiwara M Hara K et al 2α +t cluster structure in 11b. Phys Lett B (2007) 646:6–11. 10.1016/j.physletb.2006.11.079
11.
Harakeh MN van der Borg K Ishimatsu T Morsch HP van der Woude A Bertrand FE (1977). Direct evidence for a new giant resonance at 80 mev in the lead region. Phys Rev Lett38, 676–9. 10.1103/PhysRevLett.38.676
12.
Morsch HP Rogge M Turek P Mayer-Böricke C . New giant resonances in 172-mev α scattering from 208Pb. Phys Rev Lett (1980) 45:337–40. 10.1103/PhysRevLett.45.337
13.
Kanungo R Sanetullaev A Tanaka J Ishimoto S Hagen G Myo T et al Evidence of soft dipole resonance in 11Li with isoscalar character. Phys Rev Lett (2015) 114:192502. 10.1103/PhysRevLett.114.192502
14.
Tamii A Poltoratska I von Neumann-Cosel P Fujita Y Adachi T Bertulani CA et al Complete electric dipole response and the neutron skin in 208Pb. Phys Rev Lett (2011) 107:062502. 10.1103/PhysRevLett.107.062502
15.
Tamii A Kobayashi N . Studies on electromagnetic dipole responses of atomic nuclei at rcnp. AAPPS Bull (2024) 34:7. 10.1007/s43673-023-00108-0
16.
Beceiro-Novo S Ahn T Bazin D Mittig W . Active targets for the study of nuclei far from stability. Prog Part Nucl Phys (2015) 84:124–65. 10.1016/j.ppnp.2015.06.003
17.
Ayyad Y Bazin D Beceiro-Novo S Cortesi M Mittig W . Physics and technology of time projection chambers as active targets. The Eur Phys J A (2018) 54:181. 10.1140/epja/i2018-12557-7
18.
Bazin D Ahn T Ayyad Y Beceiro-Novo S Macchiavelli A Mittig W et al Low energy nuclear physics with active targets and time projection chambers. Prog Part Nucl Phys (2020) 114:103790. 10.1016/j.ppnp.2020.103790
19.
Ayyad Y Anthony AK Bazin D Chen J McCann GW Mittig W et al Kinematics reconstruction in solenoidal spectrometers operated in active target mode. The Eur Phys J A (2023) 59:294. 10.1140/epja/s10050-023-01205-2
20.
Lighthall J Back B Baker S Freeman S Lee H Kay B et al Commissioning of the helios spectrometer. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2010) 622:97–106. 10.1016/j.nima.2010.06.220
21.
SOLARIS SOL. A solenoidal spectrometer apparatus for reaction studies white paper. Tech Rep (2018).
22.
Tang TL Kay BP Hoffman CR Schiffer JP Sharp DK Gaffney LP et al First exploration of neutron shell structure below lead and beyond n = 126. Phys Rev Lett (2020) 124:062502. 10.1103/PhysRevLett.124.062502
23.
Ekström A Forssén C Hagen G Jansen GR Jiang W Papenbrock T . What is ab initio in nuclear theory?Front Phys (2023) 11. 10.3389/fphy.2023.1129094
24.
Hergert H . A guided tour of ab initio nuclear many-body theory. Front Phys (2020) 8. 10.3389/fphy.2020.00379
25.
Hagen G Papenbrock T Hjorth-Jensen M Dean DJ . Coupled-cluster computations of atomic nuclei. Rep Prog Phys (2014) 77:096302. 10.1088/0034-4885/77/9/096302
26.
Epelbaum E Hammer H-W Meißner U-G . Modern theory of nuclear forces. Rev Mod Phys (2009) 81:1773–825. 10.1103/RevModPhys.81.1773
27.
Machleidt R Entem D . Chiral effective field theory and nuclear forces. Phys Rep (2011) 503:1–75. 10.1016/j.physrep.2011.02.001
28.
Hammer H-W König S van Kolck U . Nuclear effective field theory: status and perspectives. Rev Mod Phys (2020) 92:025004. 10.1103/RevModPhys.92.025004
29.
Giomataris Y Rebourgeard P Robert J Charpak G . Micromegas: a high-granularity position-sensitive gaseous detector for high particle-flux environments. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (1996) 376:29–35. 10.1016/0168-9002(96)00175-1
30.
Cortesi M Rost S Mittig W Ayyad-Limonge Y Bazin D Yurkon J et al Multi-layer thick gas electron multiplier (M-THGEM): a new MPGD structure for high-gain operation at low-pressure. Rev Scientific Instr (2017) 88:013303. 10.1063/1.4974333
31.
Pollacco E Grinyer G Abu-Nimeh F Ahn T Anvar S Arokiaraj A et al Get: a generic electronics system for tpcs and nuclear physics instrumentation. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2018) 887:81–93. 10.1016/j.nima.2018.01.020
32.
Anthony A Ayyad Y . ACeulemans, freund17, lisacarpenter, cnhunt, Héctor AT-TPC collaboration. At-tpc document Alvarez Pol, Juan Zamora, Nabin Rijal, Alicia Muñoz Ramos, bolaizol, AriAtari, Ruchi-GADGETII, Simon, Wieskejo, & diazcort. (2023). ATTPCROOT (v0.4.0-beta). Zenodo. 10.5281/zenodo.10027879
33.
[Dataset] McCann G . Attpc/spyral: v0.16.0rc0. Turinath (2024). 10.5281/zenodo.14165743
34.
Bradt J Bazin D Abu-Nimeh F Ahn T Ayyad Y Beceiro Novo S et al Commissioning of the active-target time projection chamber. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2017) 875:65–79. 10.1016/j.nima.2017.09.013
35.
AT-TPC collaboration. At-tpc documentation (2024). Available online at: https://attpc.github.io/. Accessed January 15, 2025
36.
Lozowski W . Three diverse target preparations: 14c (12 mg/cm2), 71ga24mg (12 mg/cm271ga, 3 mg/cm224mg), and 66,67zn (1.8–14.9 mg/cm2). Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (1989) 282:54–61. 10.1016/0168-9002(89)90108-3
37.
National Nuclear Data Center, Brookhaven National Laboratory. (2008, March 18). NuDat (Nuclear Structure and Decay Data). Available online at: https://www.nndc.bnl.gov/nudat3/. Accessed March 11, 2025
38.
Potel G Idini A Barranco F Vigezzi E Broglia RA . Nuclear field theory predictions for 11li and 12be: shedding light on the origin of pairing in nuclei. Phys At Nuclei (2014) 77:941–68. 10.1134/S106377881407014X
39.
Stanton JF Bartlett RJ . The equation of motion coupled-cluster method. a systematic biorthogonal approach to molecular excitation energies, transition probabilities, and excited state properties. The J Chem Phys (1993) 98:7029–39. 10.1063/1.464746
40.
Watts JD Gauss J Bartlett RJ . Coupled-cluster methods with noniterative triple excitations for restricted open-shell Hartree–Fock and other general single determinant reference functions. energies and analytical gradients. The J Chem Phys (1993) 98:8718–33. 10.1063/1.464480
41.
Jiang WG Ekström A Forssén C Hagen G Jansen GR Papenbrock T . Accurate bulk properties of nuclei from a = 2 to ∞ from potentials with Δ isobars. Phys Rev C (2020) 102:054301. 10.1103/PhysRevC.102.054301
42.
Hu B Jiang W Miyagi T Sun Z Ekström A Forssén C et al Ab initio predictions link the neutron skin of 208pb to nuclear forces. Nat Phys (2022) 18:1196–200. 10.1038/s41567-022-01715-8
43.
Sun ZH Ekström A Forssén C Hagen G Jansen GR Papenbrock T (2025). Multiscale Physics of Atomic Nuclei from First Principles. Phys. Rev. X. 15(1) 011028. 10.1103/PhysRevX.15.011028
44.
Simonis J Bacca S Hagen G . First principles electromagnetic responses in medium-mass nuclei - recent progress from coupled-cluster theory. Eur Phys J (2019) A 55:241. 10.1140/epja/i2019-12825-0
45.
Acharya B Bacca S Bonaiti F Li Muli SS Sobczyk JE . Uncertainty quantification in electromagnetic observables of nuclei. Front Phys (2023) 10:1066035. 10.3389/fphy.2022.1066035
46.
Yuan C Suzuki T Otsuka T Xu F Tsunoda N . Shell-model study of boron, carbon, nitrogen, and oxygen isotopes with a monopole-based universal interaction. Phys Rev C (2012) 85:064324. 10.1103/PhysRevC.85.064324
47.
Suzuki T Fujimoto R Otsuka T . Gamow-teller transitions and magnetic properties of nuclei and shell evolution. Phys Rev C (2003) 67:044302. 10.1103/PhysRevC.67.044302
48.
Warburton EK Brown BA . Effective interactions for the 0p1s0d nuclear shell-model space. Phys Rev C (1992) 46:923–44. 10.1103/PhysRevC.46.923
49.
Efros VD Leidemann W Orlandini G Barnea N . The lorentz integral transform (lit) method and its applications to perturbation-induced reactions. J Phys G: Nucl Part Phys (2007) 34:R459–528. 10.1088/0954-3899/34/12/R02
50.
Bacca S Barnea N Hagen G Orlandini G Papenbrock T . First principles description of the giant dipole resonance in 16O. Phys Rev Lett (2013) 111:122502. 10.1103/PhysRevLett.111.122502
51.
Bacca S Barnea N Hagen G Miorelli M Orlandini G Papenbrock T . Giant and pigmy dipole resonances in 4He, 16,22O, and 40Ca from chiral nucleon-nucleon interactions. Phys Rev C (2014) 90:064619. 10.1103/PhysRevC.90.064619
52.
Bonaiti F Bacca S Hagen G Jansen GR . Electromagnetic observables of open-shell nuclei from coupled-cluster theory. Phys Rev C (2024) 110:044306. 10.1103/PhysRevC.110.044306
53.
Marino F. Bonaiti F. Bacca S. Hagen G. Jansen G. Tichai A. (2024). Recent advances in coupled cluster computations of open-shell atomic nuclei. Available online at: https://arxiv.org/abs/2410.19511
54.
Navin A Anthony DW Aumann T Baumann T Bazin D Blumenfeld Y et al Direct evidence for the breakdown of the N = 8 shell closure in12be. Phys Rev Lett (2000) 85:266–9. 10.1103/PhysRevLett.85.266
55.
Pain SD Catford WN Orr NA Angélique JC Ashwood NI Bouchat V et al Structure of 12Be: intruder d-wave strength at n = 8. Phys Rev Lett (2006) 96:032502. 10.1103/PhysRevLett.96.032502
56.
Giraud S Zamora JC Zegers RGT Bazin D Ayyad Y Bacca S et al β + gamow-teller strengths from unstable 14O via the (d,2He) reaction in inverse kinematics. Phys Rev Lett (2023) 130:232301. 10.1103/PhysRevLett.130.232301
Summary
Keywords
direct reactions, transfer, inelastic scattering, active target, time projection chamber, solenoidal spectrometer
Citation
Ayyad Y, Bazin D, Bonaiti F, Chen J, Li X, Anthony A, Avila M, Beceiro-Novo S, Bhatt K, Cabo C, Furuno T, Guimarães V, Hall-Smith A, Hunt C, Jayatissa H, Kawabata T, Kumi H, López-González JM, Lois-Fuentes J, Macchiavelli A, McCann G, Müller-Gatermann C, Muñoz-Ramos A, Mittig W, Olaizola B, Rahman Z, Regueira D, Rufino J, Sakajo S, Santamaria C, Serikow MZ, Tang T, Tolstukhin I, Turi N, Watwood N and Zamora J (2025) Direct reactions with the AT-TPC. Front. Phys. 13:1539148. doi: 10.3389/fphy.2025.1539148
Received
03 December 2024
Accepted
28 February 2025
Published
24 March 2025
Volume
13 - 2025
Edited by
Alan Wuosmaa, University of Connecticut, United States
Reviewed by
Grigory Nigmatkulov, University of Illinois Chicago, United States
Julian Kahlbow, Berkeley Lab (DOE), United States
Updates
Copyright
© 2025 Ayyad, Bazin, Bonaiti, Chen, Li, Anthony, Avila, Beceiro-Novo, Bhatt, Cabo, Furuno, Guimarães, Hall-Smith, Hunt, Jayatissa, Kawabata, Kumi, López-González, Lois-Fuentes, Macchiavelli, McCann, Müller-Gatermann, Muñoz-Ramos, Mittig, Olaizola, Rahman, Regueira, Rufino, Sakajo, Santamaria, Serikow, Tang, Tolstukhin, Turi, Watwood and Zamora.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yassid Ayyad, yassid.ayyad@usc.es
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.