Abstract
Bell inequality violation has been widely tested by using the bipartite entangled pure states and properly encoding the local observables in various experimental platforms, and the detector-, local-, and random loopholes have already been closed. A natural question is, how to deliver the Bell inequality violation by properly encoding the local observables? Here, we show that the Bell inequality violation is directly related to the coherence degree, which is controllable by encoding the different local observables into the entangled state. With the usual space-like correlation detections, we show that the coherence degree can be measured and thus the Bell nonlocality can be tested. The feasibility of the proposal is demonstrated by a numerical experiment typically with the cavity quantum electrodynamic system, in which the coherence degrees of the locally encoded bipartite entangled state can be conveniently measured by the spectral detection of the driven cavity. The present work might provide a feasible approach to verify the Gisin theorem, i.e., Bell inequality can be violated for any bipartite entangled pure state, once the local observables are properly encoded into the entangled state for keeping the desirable coherence.
1 Introduction
It is well known that, the quantum entanglement is contradictory to the localization and reality in classical theory [1–4]. Bell provides a mathematical criterion called later as the Bell inequality [5–7] to test the existence of the nonlocal correlations between the distant particles. Until now, the violation of such inequality has been experimentally verified by using entangled states in various systems, and also the detector-, local-, and random loopholes have been closed [8–12]. Therefore, using the nonlocal correlations to implement quantum information processing, typically such as quantum communication [13, 14], quantum computation [15], and quantum metrology [16, 17], etc., have been paid much attention.
Basically, Gisin had proved that the Bell inequality can be violated for any entangled pure bipartite state, if it is encoded properly by the local observables [18, 19]. This implies that the violation of the Bell inequality not only depends on the existence of the bipartite entanglement, but is also related to the local encodes of the bipartite entangled state. Furthermore, Horodecki et.al. gave the necessary and sufficient conditions of the Bell inequality violation for the entangled mixed states Horodecki et al. [20], and thus entanglement and Bell nonlocality are practically different quantum resources [21]. However, the inherent physical mechanism for the violation of the Bell inequality seems still unclear. Recently, Liang et.al., showed that [22]; [23, 24] the violation of the Bell inequality originated from the nonlocality of the bipartite quantum state, i.e., the non-diagonal part of the corresponding density matrix. Given the density matrix with only the non-diagonal elements does not exist, as should be satisfied for any practical quantum state, here we investigate the relationship between the quantum coherence and the Bell inequality violation, as coherence degree is measurable [25]. Basically, quantum coherence can be quantified by such as fidelity, trace distance, relative entropy, and norm, etc. [26–29]. In this paper, we use the -norm to quantify quantum coherence, which can be measured by the proposed spectral detection.
The paper is organized as follows: In Sec. 2, beginning with a brief review of the basic concepts of quantum locality, nonlocality, and their relationships between the Bell inequality violations, we propose a quantum coherence condition for the Bell inequality violation. This argument is assisted with that from Gisin theorem Gisin [18], i.e., Bell inequality can be violated for any bipartite entangled pure state once the local observable encodes satisfy certain conditions. In Sec. 3, we provide a numerical experiment to test Bell inequality involved coherence measurements with a cavity QED system, wherein the coherence measurements are implemented by probing the spectral of the driven cavity. Finally, in Sec. 4, we summarize our work.
2 Quantum coherence, nonlocality, and bell inequality violation
The well-known Bell inequality for the experimental tests can be expressed as the following CHSH form [7].where is the CHSH function, which can be calculated by measuring the values of the correlation function for the local observables: . Gisin’s theorem states that, for any bipartite entangled pure state, the Bell-CHSH inequality Equation 1 can be violated by properly selecting the local observables [18, 19]. Indeed, by properly encoding the local observables into the generated entangled states, the violation of the Bell inequality has been tested experimentally (see, e.g., [30–34]). The question is how to properly select the local observables for the experimental violation of such an inequality.
2.1 The relationship between the nonlocality and the violation of bell inequality
Following Liang et al. [22–24], the local- and nonlocal features of a quantum system can be described by the diagonal part and the non-diagonal one of the relevant density matrix, respectively. For example, for the system in the pure statewith the density matrix:where (with and being the arbitrary -number) and , its locality and nonlocality refer to.andrespectively. Certainly, any quantum state is not a pure nonlocal, as its density matrix should satisfy the basic condition: , and thus, the diagonal elements should be included.
To test the Bell inequality Equation 1 with the entangled pure state Equation 2, the local observables should be encoded into the state Equation 2 typically by performing the following single-qubit Hadamard-like gate operation [35]:
Obviously, after the above operations, the density matrix of the entangled pure state becomeswherewithandwithrespectively. Above, , , .
Theoretically, the correlation between the bipartite in the state can be calculated by the expected value of the operator [35], i.e.,
One can easily check that , which means that the locality of the original entangled pure state does not contribute to the correlation between the entangled bipartite, and thus only the nonlocality of the entangled state determines the bipartite correlation, i.e.,
Obviously, the bipartite correlation originated from the nonlocality of the bipartite entangled state, as argued previously in Ref. [22, 23]. Of course, the correlation function and thus the value of the CHSH function is dependent on not only the nonlocality of the entangled state but also the local observables encoded into such an entangled state. For the arbitrarily given entangled parameters in the state , e.g., , Figure 1 shows how the local observable encodings: , influence the value of the CHSH function thus the violation of the CHSH-Bell inequality (1). It is seen from Figures 1A–F that, for a given bipartite entangled pure state, the inequality is violated within the range of the white dotted lines, once the local observables are encoded properly. Specifically, the Bell inequality can be maximally violated, i.e., , if the local observables are encoded as . Furthermore, it is shown in Figure 2 that, for arbitrarily selected local observable encodings, typically such as , one can always find the corresponding bipartite entangled pure state to demonstrate the Bell inequality violation. Following the Gisin [18, 19], Bell inequality can be violated with any bipartite entangled pure state, once the local observables are encoded properly. Therefore, the bipartite entanglement is the necessary but not the sufficient condition for the Bell inequality violation. Specifically, we verified the argument in Ref. [22, 23] that the Bell inequality violation is due to the nonlocality of the bipartite entangled pure state, and its locality does not contribute to the nonlocal correlation between the bipartite.
FIGURE 1
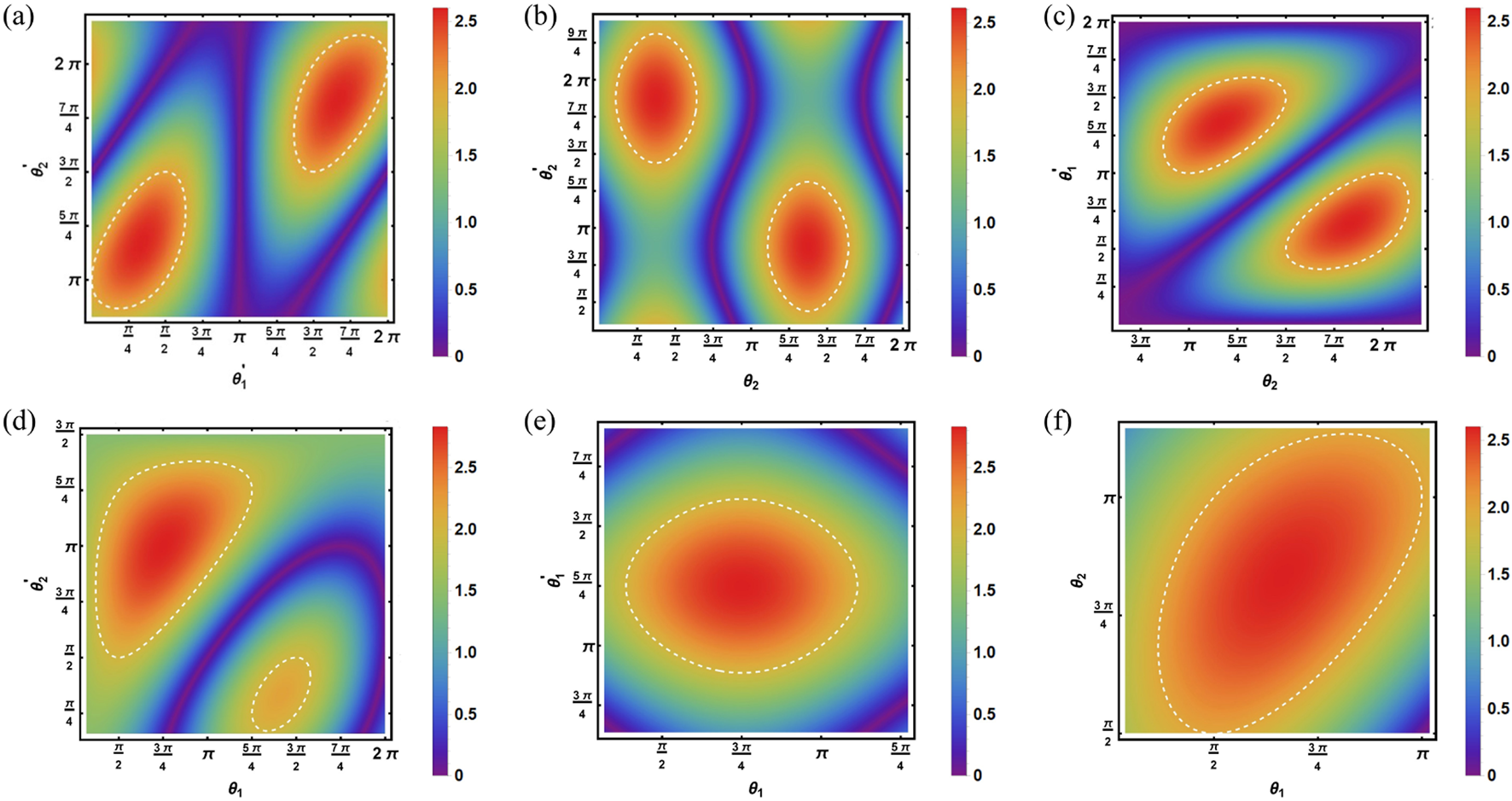
Testing the Bell inequality for a given bipartite entangled pure state (with ) for the different local observable encodings; (A), and are variables, (B), and are variables, (C), and are variables, (D), and are variables, (E), and are variables, and (F), and are variables. Here, the inequality is violated within the range of the white dotted lines.
FIGURE 2
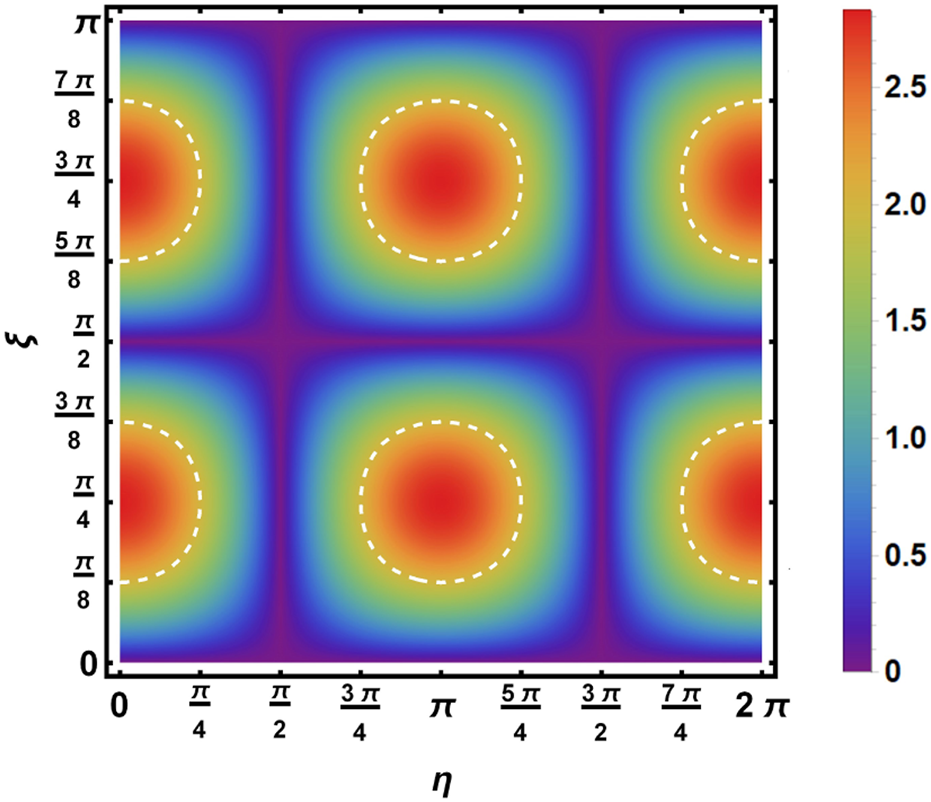
The value of the CHSH function versus the entangled parameters and in the bipartite entangled pure states , wherein the local observable are encoded as: , and . The inequality is violated within the range of the white dotted lines.
Given the nonlocality of the entangled pure state is described by a non-physical density matrix without diagonal elements, below we discuss the relationship between the coherence, rather than the nonlocality, of the bipartite entangled pure state and the Bell inequality violation by properly local observable encodings.
2.2 Coherence condition for the bell inequality violation
As demonstrated above, the nonlocality of the quantum state cannot be existed alone, as the density matrix for any experimental quantum state must be satisfied the condition: . Physically, quantum coherence originates from the superposition of quantum states [25], and a series of approaches have been proposed to measure the coherence of quantum state, typically such as fidelity, trace distance, relative entropy, and norm, etc. [27]. Without loss of the generality, we simply use the norm [26]:to quantify the quantum coherence of the quantum state described by the density matrix . Specifically, for the bipartite entangled pure state Equation 2, we have . Of course, for the maximal mixed state, whose density matrix contains only the diagonal elements, the degree of the coherence should be zero, i.e., . While, for the maximally entangled Bell-state, i.e., the state Equation 2 with , we have , which is the maximal coherence.
Certainly, the degree of quantum coherence of a pure quantum system can be engineered by the unitary quantum operation. For example, for the entangled pure state Equation 2 with the density matrix , the norm reads . However, after the Hadamard-like operations for the local observable encodings, the state is changed as with the coherence being changed accordingly asObviously, from Equation 12 we getTherefore, the coherence of the state originated from the state (2) by local observable encodings is measured by experimental measurement of the correlation function . Consequently, by substituting Equation 16 into Equation 1, the CHSH inequality Equation 1 can be written as the following form:which is determined by the coherence of the quantum states with different local observable encodings.
Figure 3 shows that the relationship between the coherence of the state Equation 7 and Bell inequality violation for the given local observable encoding: , and for the different entangled pure state Equation 2. It is seen that, within the range of the white dotted lines, the Bell inequality is violated, i.e., . The results are consistent with those tested by performing the correlation measurements shown in Figure 2. Therefore, by the measurements of coherence, instead of the nonlocal correlation, of the entangled pure state with the local observable encodings, the test of the Bell inequality is also feasible.
FIGURE 3
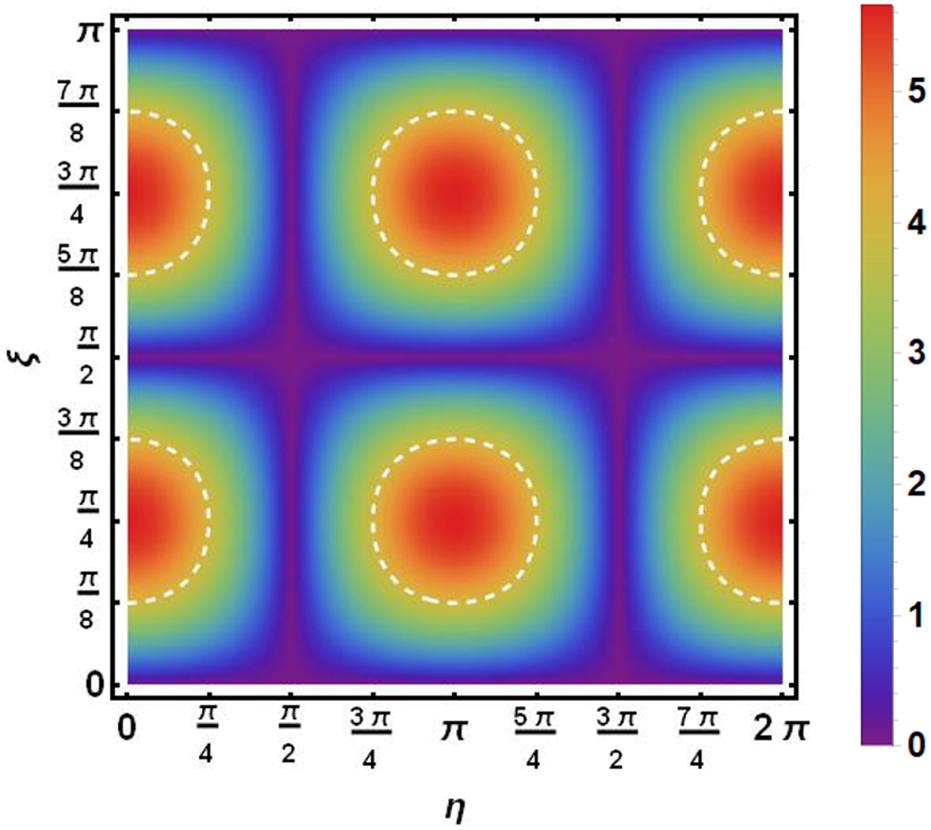
The CHSH function defined by quantum coherence versus the entangled parameters and of the bipartite entangled pure states , which is locally encoded as: , and . It is seen that the regime for the Bell inequality violation is the same as that shown in Figure 2.
3 Numerical experiments to test the bell inequality by coherence detections
In what follows, we numerically simulate the violation of CHSH-Bell inequality Equation 17 by measuring the coherence of an arbitrarily given entangled pure state with the different local observable encodings. The experimental configuration considered here is shown in Figure 4, wherein a two-qubit entangled pure state is prepared, and its coherence for different local observable encodings is measured by probing the spectra of the driven cavity, which is coupled to the two qubits dispersively.
FIGURE 4
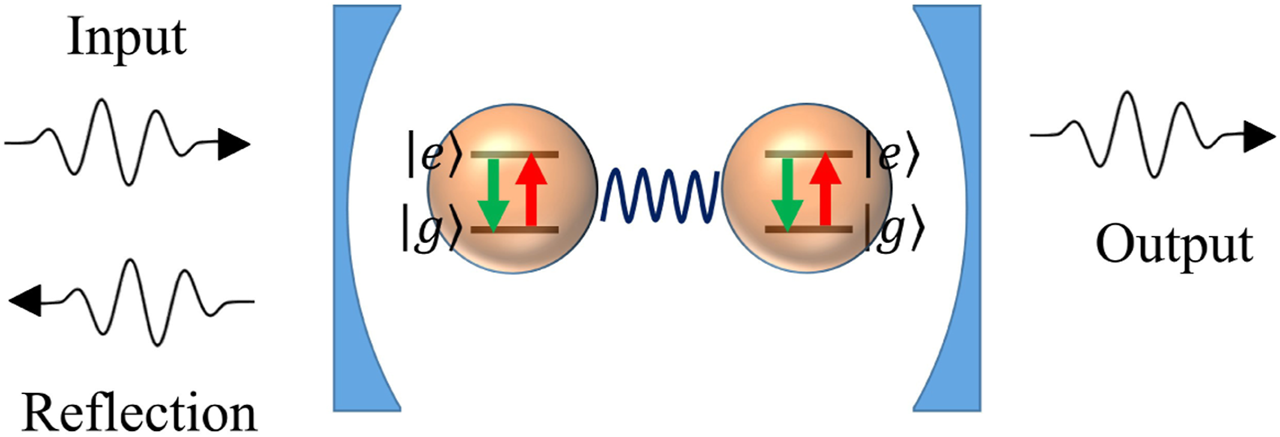
A cavity QED system for the numerical experiments of Bell inequality test. Here, the two-qubit state can be non-destructively detected by the transmitted spectral measurements of the driven cavity, which is dispersively coupled to the qubits [44–47].
3.1 A spectral method to implement the correlation detections of arbitrary two-qubit states
The system of two qubits being dispersively coupled to a driven cavity can be described by the Hamiltonian [36–40].here, and are respectively frequency and dissipation of the cavity, is the coupling strength between the th qubit (with the transition frequency ) and the cavity, are the generation and annihilation operators of the left/right traveling wave photons, respectively. is the coupling strength between the cavity and the left/right traveling wave photons, and is the detuning between the cavity and the th qubit.
Suppose that the system satisfies the dispersive condition: , and thus any interaction between the qubits can be safely neglected [39]. As a consequence, with the standard input-output theory, the transmitted amplitude of the driven cavity can be obtained as [40, 41].with the phase shiftAbove, is the effective interaction strength between the left/right traveling wave photons and the cavity, and and represent the output field operator and the input field one, respectively.
Specifically, for a given two-qubit quantum pure state: , Figure 5 shows the transmitted spectra of the driven cavity, wherein the peaks are located at , and , respectively. Here, is the frequency of the empty cavity, (with ) is the center frequency of the transmitted peak corresponding to the state of the qubits. Interestingly Huang et al. [37], we found that the relative height of the peak marking the state is equivalent to its superposed probability in the state .
FIGURE 5
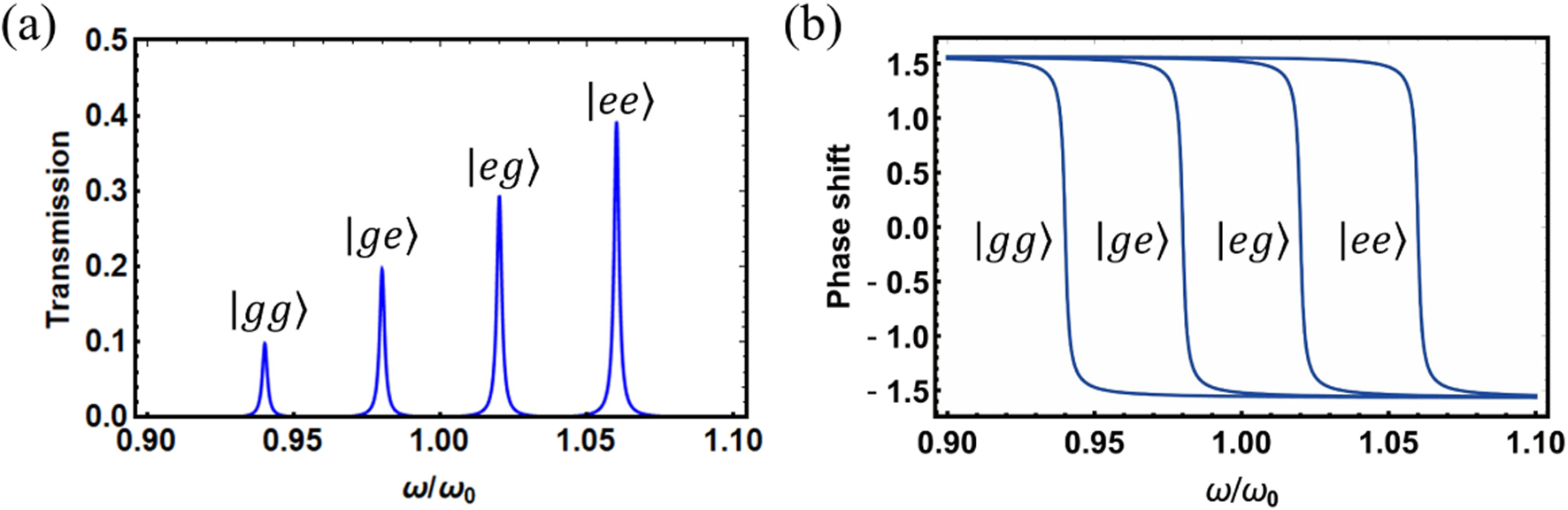
The steady-state transmission spectra (A) and phase shift spectrum (B) of the driven cavity with the two-qubit superposed state: . The relevant parameters are set as: , , , .
3.2 Testing bell inequality by the simulated coherence measurements
One can see easily from Equation 15 that, the value of coherence for the bipartite entangled pure state Equation 7, delivered by encoding the local observables into the original entangled pure state Equation 2, is related to the parameter . Theoretically, this parameter can be obtained by the observed relative heights of the transmitted peaks, i. e.,
Therefore, by arbitrarily measuring one of the diagonal elements (i.e., with ) of the density matrix Equation 7, the value of can be obtained.
Immediately, with the numerical experiments demonstrated above, all the diagonal elements of the density matrix Equation 7 can be obtained by observing the transmitted peaks of the driven cavity coupled dispersively to the two qubits, which are prepared in the state . As motioned previously, the relative height of the peak marking the two-qubit state is related to the diagonal element , i.e.,
However, due to the practically existing measurement errors, the value of the -parameter obtained by observing the different peaks might be different. As a consequence, the value of the CHSH function defined in Equation 17 can be measured as with , , and is the standard deviation of the measured value of .
For example, by using the transmitted spectra shown in Figure 6 for the given quantum state Equation 2 with and the corresponding local observable encodings, the values of the parameter listed in Table 1 can be obtained. Consequently, the CHSH functions defined by quantum coherence can be calculated, , which indicates that the inequality Equation 17 is not violated. Similarly, by using the transmitted spectra shown in Figure 7 for the given quantum state Equation 2 with and the same local observable encodings, the values of parameter can also be gotten, see Table 2. As a consequence, the CHSH functions , defined by quantum coherence, can be calculated as , showing that the inequality Equation 17 is now violated.
FIGURE 6
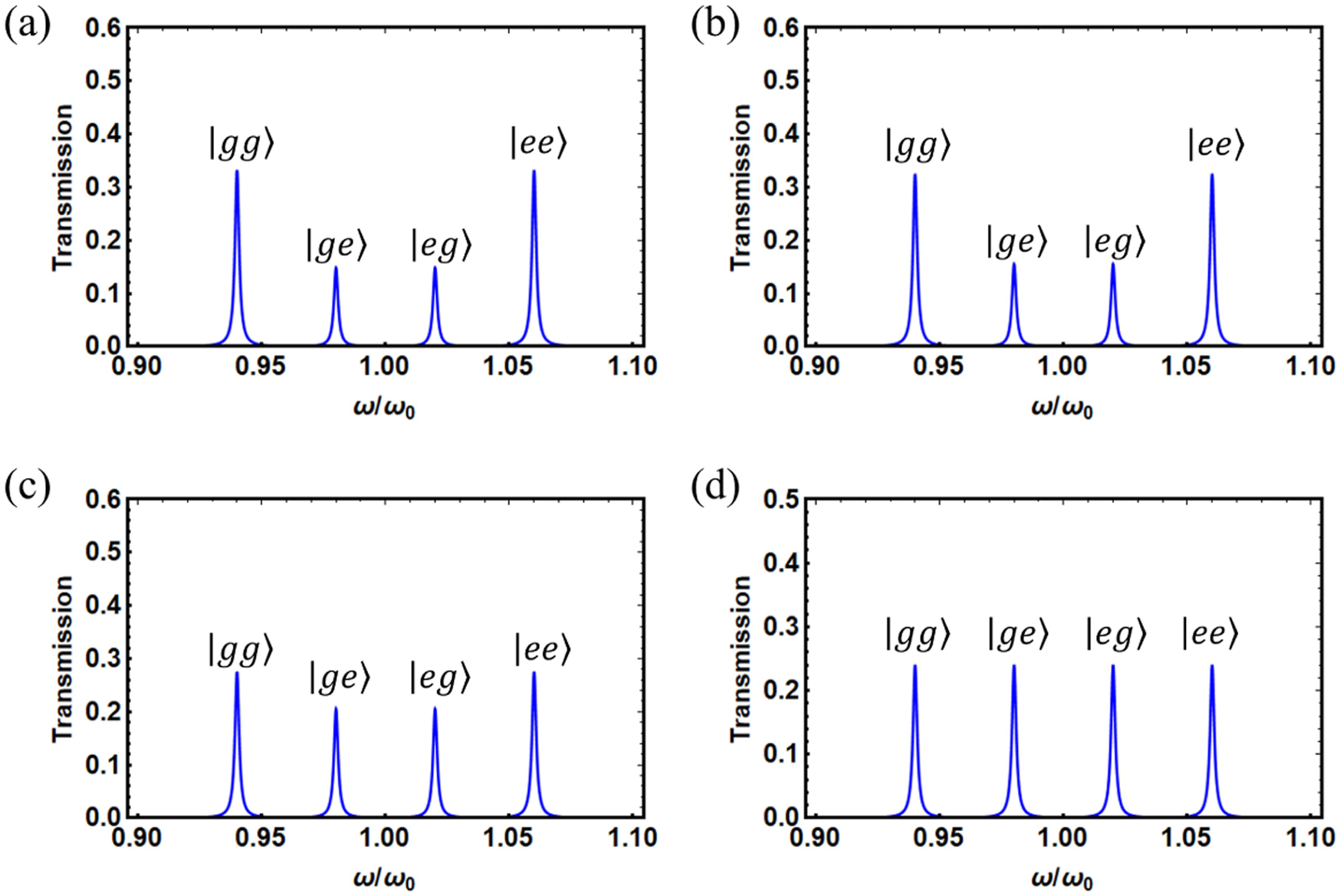
The steady-state transmission spectrums of the driving cavity versus the driving frequency when the local observables are encoded on the quantum state Equation 2 (with , ). Here, the local observables corresponding to (A–D) are , , , respectively. The other parameters are the same as in Figure 5.
TABLE 1
| 0.3389 | 0.3317 | 0.2809 | 0.2451 | ||
| 0.3556 | 0.3268 | 0.1236 | −0.0196 | 1.5716 | |
| 0.1513 | 0.1584 | 0.2092 | 0.2451 | ||
| 0.3948 | 0.3664 | 0.1632 | 0.0196 | 1.8088 | |
| 0.1513 | 0.1584 | 0.2092 | 0.2451 | ||
| 0.3948 | 0.3664 | 0.1632 | 0.0196 | 1.8088 | |
| 0.3389 | 0.3317 | 0.2809 | 0.2451 | ||
| 0.3556 | 0.3268 | 0.1236 | −0.0196 | 1.5716 |
The relative heights of the peaks, the -parameters, and the CHSH functions defined by quantum coherence, corresponding to the states in the Figures 6A–D, respectively.
FIGURE 7
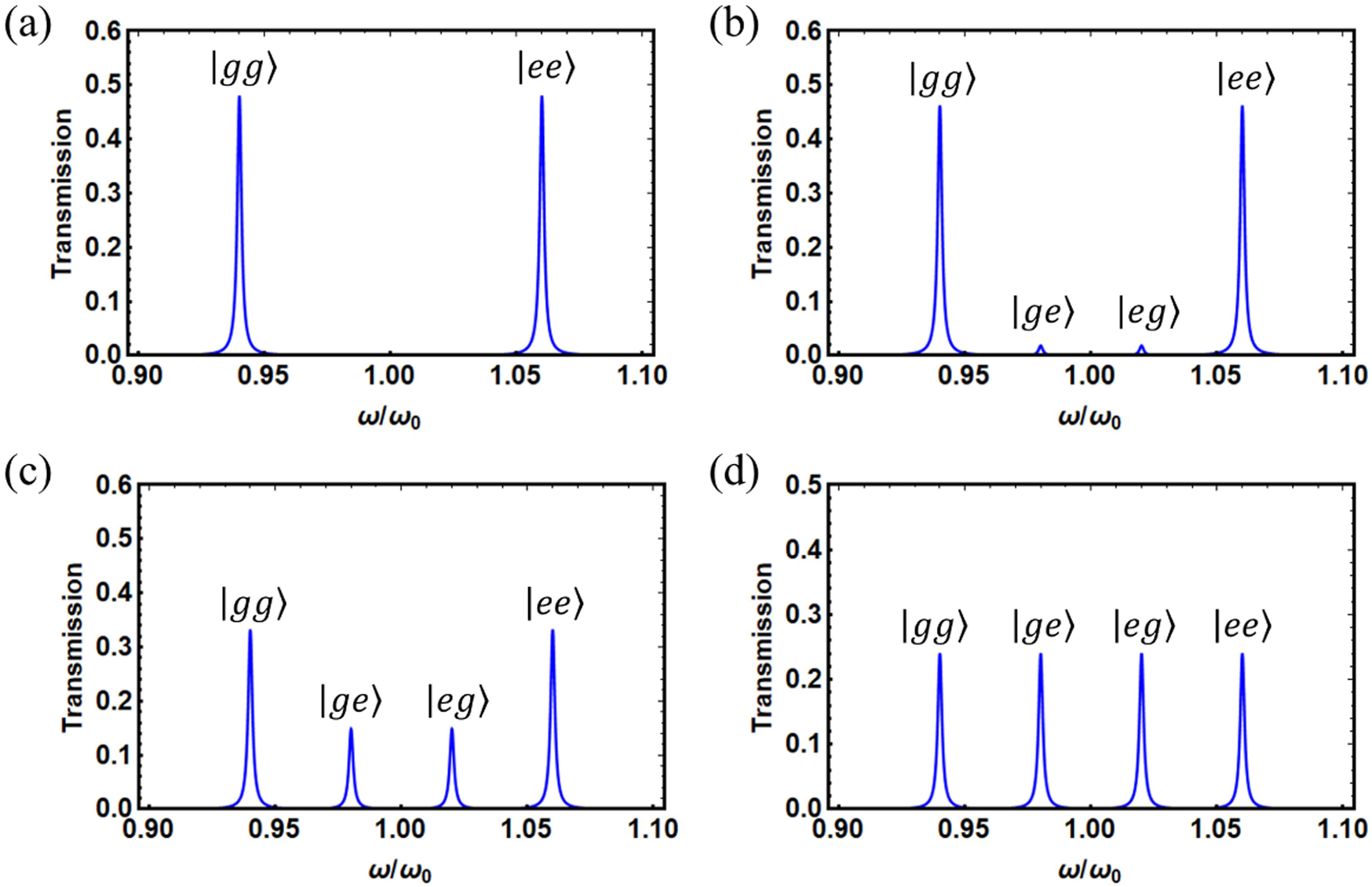
The steady-state transmission spectrums of the driving cavity versus the driving frequency when the local observables are encoded on the quantum state Equation 2. Wherein (A–D) shows the steady-state transmission spectrum of the quantum state Equation 2 with the superposition parameters of . Here, the local observables corresponding to (A–D) are , , , respectively. Other parameters are the same as in Figure 5.
TABLE 2
| 0.4901 | 0.4715 | 0.3389 | 0.2451 | ||
| 0.9604 | 0.886 | 0.3556 | −0.0196 | 4.3643 | |
| 0 | 0.0187 | 0.1513 | 0.2451 | ||
| 1 | 0.9252 | 0.3948 | 0.0196 | 4.6001 | |
| 0 | 0.0187 | 0.1513 | 0.2451 | ||
| 1 | 0.9252 | 0.3948 | 0.0196 | 4.6001 | |
| 0.4901 | 0.4715 | 0.3389 | 0.2451 | ||
| 0.9604 | 0.886 | 0.3556 | −0.0196 | 4.3643 |
The relative heights of the peaks, the -parameters, and the CHSH functions defined by quantum coherence, corresponding to the states in the Figures 7A–D, respectively.
To check if only the nonlocality of the bipartite entangled pure state contributes to the Bell inequality violation, we now consider the contribution from the locality of the state Equation 2, which is described by the local density matrix Equation 4. The steady-state transmission spectra related to such a density matrix are shown in Figure 8. The observed values of the -parameter and thus the calculated CHSH functions are listed in Table 3. It is seen clearly that , which indicates that the locality of the bipartite entangled pure state does not contribute to the violation of the Bell inequality Equation 17, whatever the local observable encodings of the entangled state.
FIGURE 8
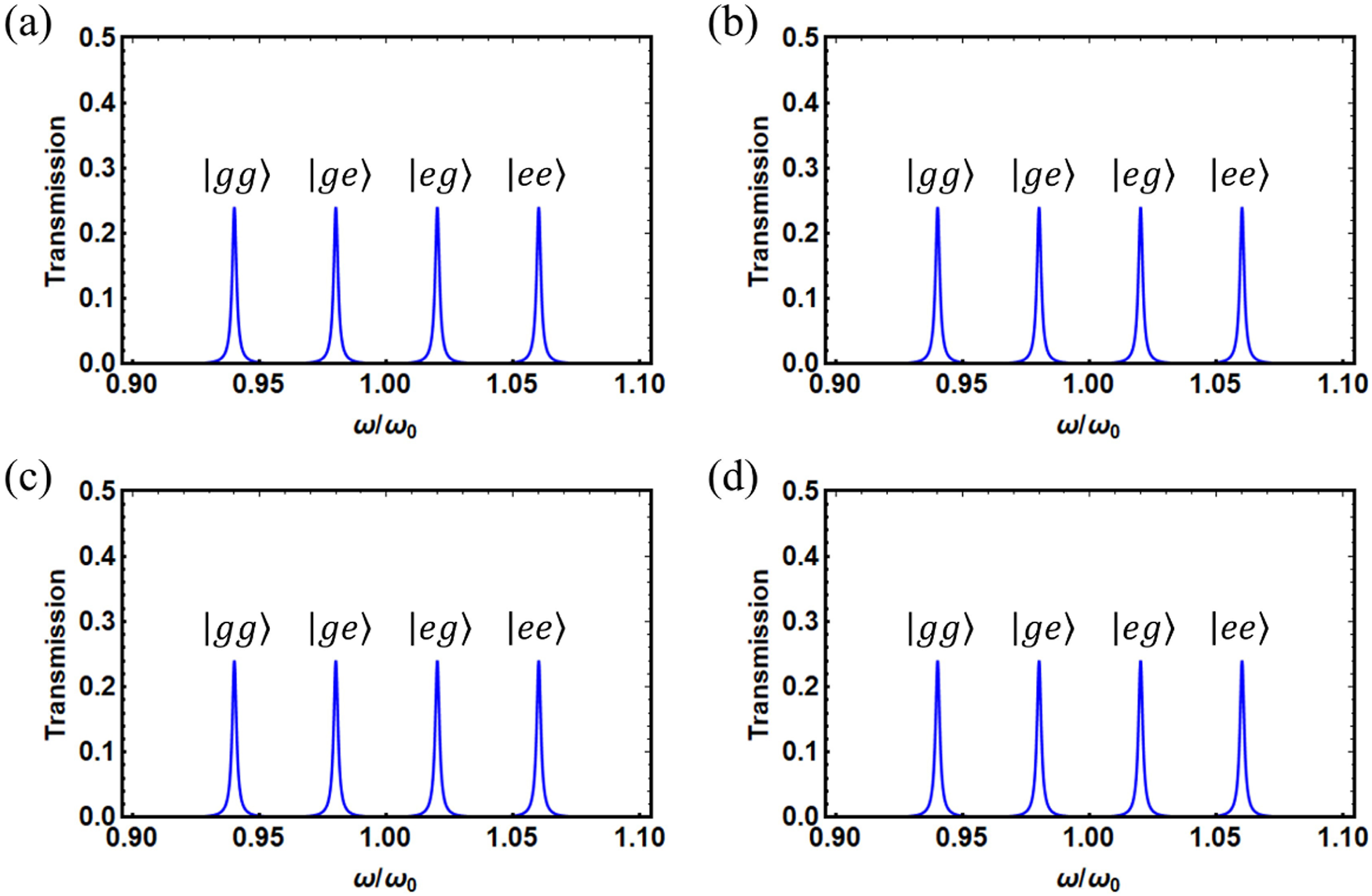
The steady-state transmission spectrums of the driving cavity versus the driving frequency when the local observables are encoded on the local quantum state Equation 4. The local observables corresponding to (A–D) are , and , and the other parameters are the same as in Figure 5.
TABLE 3
| 0.2451 | 0.2451 | 0.2451 | 0.2451 | ||
| −0.0049 | −0.0049 | −0.0049 | −0.0049 | 0.0399 | |
| 0.2451 | 0.2451 | 0.2451 | 0.2451 | ||
| 0.0049 | 0.0049 | 0.0049 | 0.0049 | 0.0399 | |
| 0.2451 | 0.2451 | 0.2451 | 0.2451 | ||
| 0.0049 | 0.0049 | 0.0049 | 0.0049 | 0.0399 | |
| 0.2451 | 0.2451 | 0.2451 | 0.2451 | ||
| −0.0049 | −0.0049 | −0.0049 | −0.0049 | 0.0399 |
The relative heights of the peaks, the -parameters, and the CHSH functions defined by quantum coherence, corresponding to the states in the Figures 8A–D, respectively.
The above discussions with the relevant numerical experiments showed clearly that the Bell inequality violation can be tested by measuring the coherence of the bipartite entangled pure state encoded by the proper local observable encodings. Physically, the coherence of the quantum pure state is related to the non-diagonal elements of the physical density matrix and thus can be experimentally measured. Test the Bell inequality Equation 17 provides a feasible approach to verify the arguments given in Refs. [22] on the relationship between the Bell inequality violation and nonlocality of the entangled pure state.
3.3 Numerical experiments to verify the equivalence between the inequalities Equation 1 and Equation 17
Usually, Bell’s theorem is verified by testing the violation of the inequality Equation 1 by performing the local space-like measurements. For a generic bipartite entangled pure state with the local observable encodings: and :where is the superposed probability amplitude of the two-qubit states , the nonlocal correlation function can be theoretically calculated as [35, 42].here, represents the probability of the two qubits being at the same (different) logic states, i.e., with . Experimentally, the correlation function Equation 24 can be determined by performing the local space-like measurements on the bipartite. With the obtained correlation functions for different local observable encodings and sequentially, the CHSH-Bell function can be obtained and then the inequality Equation 1 can be tested.
With the numerical experiments proposed above, the probabilities for the different local observable encodings can also be determined by observing the relative height of the peak in the spectra marking the state . As a consequence, the correlation function :can be obtained by reading out the parameters (with ) from the relevant spectra. Specifically, from the observed relative heights of the peaks shown in Figures 6A–D and thus the CHSH function in Equation 1, defined by the correlation functions, can be calculated as . Thus, the Bell inequality Equation 1 is not violated for the entangled pure state Equation 2 (in which ) encoded by the local observable encodings: . Similarly, from the spectra shown in Figures 7A–D the relative heights of the transmitted peaks and also the CHSH function is obtained as for the entangled pure state Equation 2 (in which ) with the same local observable encodings. Therefore, the inequalities Equation 1 and Equation 17 are formally equivalent for Bell inequality tests.
Certainly, we can also check that the Bell inequality violation just originated from the nonlocality of the entangled pure state Equation 2, and its locality does not contribute practically to the nonlocal bipartite correlations and thus the Bell inequality violation. Again, with the transmitted spectra shown in Figure 8 for the two-qubit being prepared in the state , one can easily find that the values of all the correlation functions are zero, i.e., . This indicates that the locality, described by the density matrix in Equation 4, does not contribute to the nonlocal correlations of the bipartite, although it can still be locally encoded as . Therefore, nonlocal correlations of the bipartite originated from the nonlocality, described by the density matrix of the entangled pure state Equation 2, once the local observables are encoded properly. Given the nonlocal density matrix is not physical, and thus we perform alternatively the numerical experiments to check if the Bell inequality violation, i.e., Equation 17, by performing the coherence measurements demonstrated in the above subsection.
4 Conclusion
In summary, based on the Gisin theorem and the basic idea proposed in Ref. [22], we confirm the relationship between the Bell inequality violation and the nonlocality of the bipartite entangled pure state, which can be encoded by different local observables. Given any quantum state is not the pure nonlocal, as its density matrix should satisfy the basic condition: , we treat the nonlocality of the entangled pure state by its coherence rather than the non-physics density matrix without any diagonal elements, and deliver a new Bell inequality with the quantum coherence measurements, instead of the correlation function measurements. To confirm the validity of the proposal, we demonstrated the relevant numerical experiments with a cavity QED system, by which any elements of the density matrix of quantum state, encoded by arbitrarily chosen local observables, can be non-destructively measured via spectral measurements. As a consequence, both the local correlation function and the quantum coherence can be determined for the Bell inequality tests. Formally, instead of the usual Bell nonlocality tests by measuring the local correlation functions, here the Bell inequality violation is tested by the coherence measurements.
Note that Bell inequality has been tested by a series of cavity QED experiments. For example, with the cavity QED with the superconducting qubits (with the distance being about 3.1 mm), the Bell inequality violation had been confirmed by the correlation detections with the durations being about 30ns [30]. Furthermore, such an experiment has been generalized to that, wherein the distance of two qubits are lengthened to be 78 cm, and the duration of the correlation detections of the qubits is shortened to be about 20ns [43]. The result showed again that, the Bell inequality is really violated. Therefore, the application of the cavity QED systems to test Bell inequality by coherence degree measurements should be feasible, at least theoretically. It is expected that, the present proposal could be tested experimentally in future and also generalized to the cases with either the multiple entangled pure states or the entangled mixture states.
Statements
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
SH: Conceptualization, Data curation, Formal Analysis, Methodology, Software, Visualization, Writing–original draft, Writing–review and editing. YL: Methodology, Software, Writing–review and editing. JL: Conceptualization, Methodology, Writing–review and editing. LW: Conceptualization, Funding acquisition, Methodology, Validation, Writing–original draft, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was partially supported in part by the National Key Research and Development Program of China under Grant No. 2021YFA0718803, the National Natural Science Foundation of China under Grant No. 11974290, and the Fundamental Research Funds for the Central Universities under Grant No. 2682024CX048.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1.
EinsteinAPodolskyBRosenN. Can quantum-mechanical description of physical reality be considered complete?Phys Rev (1935) 47:777–80. 10.1103/PhysRev.47.777
2.
HorodeckiRHorodeckiPHorodeckiMHorodeckiK. Quantum entanglement. Rev Mod Phys (2009) 81:865–942. 10.1103/RevModPhys.81.865
3.
PaneruDCohenEFicklerRBoydRWKarimiE. Entanglement: quantum or classical?Rep Prog Phys (2020) 83:064001. 10.1088/1361-6633/ab85b9
4.
AntonZ. Quantum entanglement: a fundamental concept finding its applications. Phys Scr (1998) 1998:203. 10.1238/Physica.Topical.076a00203
5.
BellJS. On the einstein podolsky rosen paradox. Phys Physique Fizika (1964) 1:195–200. 10.1103/PhysicsPhysiqueFizika.1.195
6.
ClauserJFHorneMAShimonyAAholtR. Proposed experiment to test local hidden-variable theories. Phys Rev Lett (1970) 23:880–4. 10.1103/PhysRevLett.23.880
7.
BrunnerNCavalcantiDPironioSScaraniVWehnerS. Bell nonlocality. Rev Mod Phys (2014) 86:419–78. 10.1103/RevModPhys.86.419
8.
BarendsRKellyJMegrantAVeitiaASankDJeffreyEet alLoophole-free bell inequality violation using electron spins separated by 1.3 kilometres. Nature (2015) 526:682–6. 10.1038/nature15759
9.
GiustinaMVersteeghMAMWengerowskySHandsteinerJHochrainerAPhelanKet alSignificant-loophole-free test of bell’s theorem with entangled photons. Phys Rev Lett (2015) 115:250401. 10.1103/PhysRevLett.115.250401
10.
ShalmLKMeyer-ScottEChristensenBGBierhorstPWayneMAStevensMJet alStrong loophole-free test of local realism. Phys Rev Lett (2015) 115:250402. 10.1103/PhysRevLett.115.250402
11.
HandsteinerJFriedmanASRauchDGallicchioJLiuBHospHet alCosmic bell test: measurement settings from milky way stars. Phys Rev Lett (2017) 118:060401. 10.1103/PhysRevLett.118.060401
12.
AbellánCAcínAAlarcónAAlibartOAndersenCKAndreoliFet alChallenging local realism with human choices. Nature (2018) 557:212–6. 10.1038/s41586-018-0085-3
13.
ChenYAZhangQChenT-YCaiW-QLiaoS-KZhangJet alAn integrated space-to-ground quantum communication network over 4,600 kilometres. Nature (2021) 589:214–9. 10.1038/s41586-020-03093-8
14.
WuJLongGLHayashiM. Quantum secure direct communication with private dense coding using a general preshared quantum state. Phys Rev Appl (2022) 17:064011. 10.1103/PhysRevApplied.17.064011
15.
HuangHLWuDFanDZhuX. Superconducting quantum computing: a review. Sci China Inf Sci (2020) 63:180501. 10.1007/s11432-020-2881-9
16.
DegenCLReinhardFCappellaroP. Quantum sensing. Rev Mod Phys (2017) 89:035002. 10.1103/RevModPhys.89.035002
17.
LongXHeW-TZhangN-NTangKLinZLiuHet alEntanglement-enhanced quantum metrology in colored noise by quantum zeno effect. Phys Rev Lett (2022) 129:070502. 10.1103/PhysRevLett.129.070502
18.
GisinN. Bell’s inequality holds for all non-product states. Phys Lett A (1991) 154:201–2. 10.1016/0375-9601(91)90805-I
19.
ChenJLWuCFKwekLCOhCH. Gisin’s theorem for three qubits. Phys Rev Lett (2004) 93:140407. 10.1103/PhysRevLett.93.140407
20.
HorodeckiRHorodeckiPHorodeckiM. Violating Bell inequality by mixed states: necessary and sufficient condition. Phys Lett A (1995) 200:340–4. 10.1016/0375-9601(95)00214-N
21.
BrunnerNGisinNScaraniV. Entanglement and non-locality are different resources. New J Phys (2005) 7:88. 10.1088/1367-2630/7/1/088
22.
GuYLiWDHaoXLLiangJQWeiLF. Generalized bell-like inequality and maximum violation for multiparticle entangled Schrödinger cat states of spin s. Phys Rev A (2022) 105:052212. 10.1103/PhysRevA.105.052212
23.
BaiXMGaoCPLiJQLiuNLiangJQ. Entanglement dynamics for two spins in an optical cavity-field interaction induced decoherence and coherence revival. Opt Express (2017) 25:17051. 10.1364/OE.25.017051
24.
BaiXYBaiXMLiuNLiJQLiangJQ. The measurement-induced nonlocality of two spins in a single-model cavity system. Quan Inf. Process. (2021) 20:364. 10.1007/s11128-021-03315-6
25.
StreltsovAAdessoGPlenioMB. Colloquium: quantum coherence as a resource. Rev Mod Phys (2017) 89:041003. 10.1103/RevModPhys.89.041003
26.
BaumgratzTCramerMPlenioMB. Quantifying coherence. Phys Rev Lett (2014) 113:140401. 10.1103/PhysRevLett.113.140401
27.
HuMLHuXWangJPengYZhangYRFanH. Quantum coherence and geometric quantum discord. Phys Rep (2018) 762-764:1–100. 10.1016/j.physrep.2018.07.004
28.
BlaisAGrimsmoALGirvinSMWallraffA. Circuit quantum electrodynamics. Rev Mod Phys (2021) 93:025005. 10.1103/RevModPhys.93.025005
29.
WendinG. Quantum information processing with superconducting circuits: a review. Rep Prog Phys (2017) 80:106001. 10.1088/1361-6633/aa7e1a
30.
AnsmannHMarkusWBialczakRCHofheinzMLuceroENeeleyMet alViolation of bell’s inequality in josephson phase qubits. Nature (2009) 461:504–6. 10.1038/nature08363
31.
NeeleyMBialczakRCLenanderMLuceroEMariantoniMO’ConnellADet alGeneration of three-qubit entangled states using superconducting phase qubits. Nature (2010) 467:570–3. 10.1038/nature09418
32.
DiCarloLReedMDSunLJohnsonBRChowJMGambettaJMet alPreparation and measurement of three-qubit entanglement in a superconducting circuit. Nature (2010) 467:574–8. 10.1038/nature09416
33.
OmranALevineHKeeslingASemeghiniGWangTTEbadiSet alGeneration and manipulation of Schrödinger cat states in rydberg atom arrays. Science (2019) 365:570–4. 10.1126/science.aax9743
34.
LuMVilleJ-LCohenJPetrescuASchrepplerSChenLet alMultipartite entanglement in rabi-driven superconducting qubits. PRX Quan (2022) 3:040322. 10.1103/PRXQuantum.3.040322
35.
WeiLFLiuYXNoriF. Testing bell’s inequality in a constantly coupled josephson circuit by effective single-qubit operations. Phys Rev B (2005) 72:104516. 10.1103/PhysRevB.72.104516
36.
BlaisAGambettaJWallraffASchusterDIGirvinSMDevoretMHet alQuantum-information processing with circuit quantum electrodynamics. Phys Rev A (2007) 75:032329. 10.1103/PhysRevA.75.032329
37.
HuangJSOhCHWeiLF. Testing tripartite mermin inequalities by spectral joint measurements of qubits. Phys Rev A (2011) 83:062108. 10.1103/PhysRevA.83.062108
38.
FilippSMaurerPLeekPJBaurMBianchettiRFinkJMet alTwo-qubit state tomography using a joint dispersive readout. Phys Rev Lett (2009) 102:200402. 10.1103/PhysRevLett.102.200402
39.
GuoWWangYWeiLF. Controllable photon bunching by atomic superpositions in a driven cavity. Phys Rev A (2016) 93:043809. 10.1103/PhysRevA.93.043809
40.
HeSLiYWeiLF. Group delay controls of the photons transmitting through two cavities coupled by an artificial atomic ensemble: controllable electromagnetically induced transparency-like effects. Opt Express (2022) 30:721. 10.1364/OE.440027
41.
GardinerCWCollettMJ. Input and output in damped quantum systems: quantum stochastic differential equations and the master equation. Phys Rev A (1985) 31:3761–74. 10.1103/PhysRevA.31.3761
42.
YuanHWeiLFHuangJSVedralV. Quantum nonlocality test by spectral joint measurements of qubits in driven cavity. Europhys Lett (2012) 100:10007. 10.1209/0295-5075/100/10007
43.
ZhongYPChangHSSatzingerKJChouMHBienfaitAConnerCRet alViolating bell’s inequality with remotely connected superconducting qubits. Nat Phys (2019) 15:741–4. 10.1038/s41567-019-0507-7
44.
MajerJChowJMGambettaJMKochJJohnsonBRSchreierJAet alCoupling superconducting qubits via a cavity bus. Nature (2007) 449:443–7. 10.1038/nature06184
45.
ChowJMDiCarloLGambettaJMNunnenkampABishopLSFrunzioLet alDetecting highly entangled states with a joint qubit readout. Phys Rev A (2010) 81:062325. 10.1103/PhysRevA.81.062325
46.
YuanHWeiLF. Testing hardy’s ladder proof of nonlocality by joint measurements of qubits. Quan Inf. Process. (2013) 12:3341–52. 10.1007/s11128-013-0602-0
47.
XuPYangXCMeiFXueZY. Controllable high-fidelity quantum state transfer and entanglement generation in circuit qed. Sci Rep (2016) 6:18695. 10.1038/srep18695
Summary
Keywords
quantum coherence, quantum entanglement, bell inequality, spectral detection, coherence degree
Citation
He S, Li Y, Liang JQ and Wei LF (2025) Quantum coherence and the bell inequality violation: a numerical experiment with the cavity QEDs. Front. Phys. 13:1541888. doi: 10.3389/fphy.2025.1541888
Received
08 December 2024
Accepted
27 January 2025
Published
28 February 2025
Volume
13 - 2025
Edited by
Nilakantha Meher, SRM University, India
Reviewed by
Liqiang Liu, Hunan University, China
Mohammed Ateto, South Valley University, Egypt
Updates
Copyright
© 2025 He, Li, Liang and Wei.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: L. F. Wei, lfwei@swjtu.edu.cn
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.