The effect of pump laser pulse chirp on the properties of generated nonlinear Thomson scattering radiation

In order to explore better electron radiation properties, we introduce laser pulses with different chirps and different pulse widths to drive electrons to produce relativistic nonlinear Thomson scattering. We numerically simulate electron radiation.The relativistic electron dynamics and resulting Thomson scattering spectra are calculated using a nonlinear model, incorporating the electronic response function under chirped conditions. We found that under the influence of chirp, the laser pulse width produces a regular change in the radiation properties of excited electrons. The peak radiation pulse increases and then decreases with increasing pulse width, while the FWHM decreases with increasing pulse width, Almost 10³ orders of magnitude larger in chirped condition than in no-chirp condition, and the radiation characteristics of negative chirp are Almost an order of magnitude less than positive chirp for the same pulse width and the same absolute value of chirp parameter. In addition, we verify that the electronic response function still holds under chirp conditions, and we are surprised to find that the electronic response function can also be used to measure the gain of chirp on the radiated power, which provides a brand new perspective for the deep understanding of the role of chirp. This work suggests potential applications in high-field physics and compact radiation source design, where chirp engineering could enhance performance.

1 Introduction

Since the first demonstration of laser acceleration of electrons in 1962 [1], laser particle acceleration has received much attention from the laser physics community, and along with the emergence and development of chirp amplification technology [2–4], there has been a major breakthrough in laser physics, the use of ultra-short and ultra-intense lasers has become another possibility for the acceleration of charged particles, and the interaction between electrons and lasers is one of its important applications. The interaction of electrons with lasers to produce X-ray radiation sources is one of its important applications [5, 6], the X-rays so produced have a wide range of applications in fields such as medicine [7–9], materials science [10–12], astrophysics [13], and nuclear physics [14].

Past work has shown that the radiation properties of stationary electrons vary according to the parameters of the laser pulse. The parameters of nonlinear Thomson scattering including pulse width [15–17], beamwidth radius [18], laser intensity [19] etc., Have been well investigated and this lays the foundation for the introduction of chirped laser pulses. Khachatryan et al. [20] reported for the first time that the chirped laser pulses can lead to a nonzero net energy gain for the electrons, which further validates the feasibility of our introduction of chirped laser pulses for better electron radiation properties.

There have been many attempts in laser physics to start with chirped laser pulses. Tong Xu et al. [21] discussed the effect of the energy chirp of an accelerated electron beam on the spectral bandwidth of the final radiation. Szabolcs Hack et al. [22] proposed a possibility of separating out an attosecond pulse at the energy of $\mu J$ using chirped laser pulses driving electrons. Amol R. Holkundkar et al. [23] found that the frequency and intensity of electron Thomson scattering emitted radiation is significantly enhanced under the introduction of negative chirp conditions Sharma, V. et al. Investigated the effect of different Gaussian profiles on the energy gain of electrons in the acceleration of the laser wake field [24]. Liu et al. [30] realized a wavelength-tunable chirped pulse amplification system based on thulium-doped fiber.

The model of stationary electrons with circularly polarised chirped laser pulses studied in this paper (Figure 1) is established in the framework of classical nonlinear Thomson scattering, where the chirped laser pulses have phase-varying properties, and therefore adjusting the pulse width of the chirped laser pulses amplifies the action time with its phase-varying properties, which in turn has a large impact on the electrodynamic and radiative properties of the electrons. In addition, we verify the relationship between the electron radiated power and the electron motion in the chirp case, and furthermore point out the numerical solution of the chirp for the measure of the radiated power gain. Finally, we propose a theoretical method to produce optical pulses of 10-1zs level under chirp conditions.

Figure 1

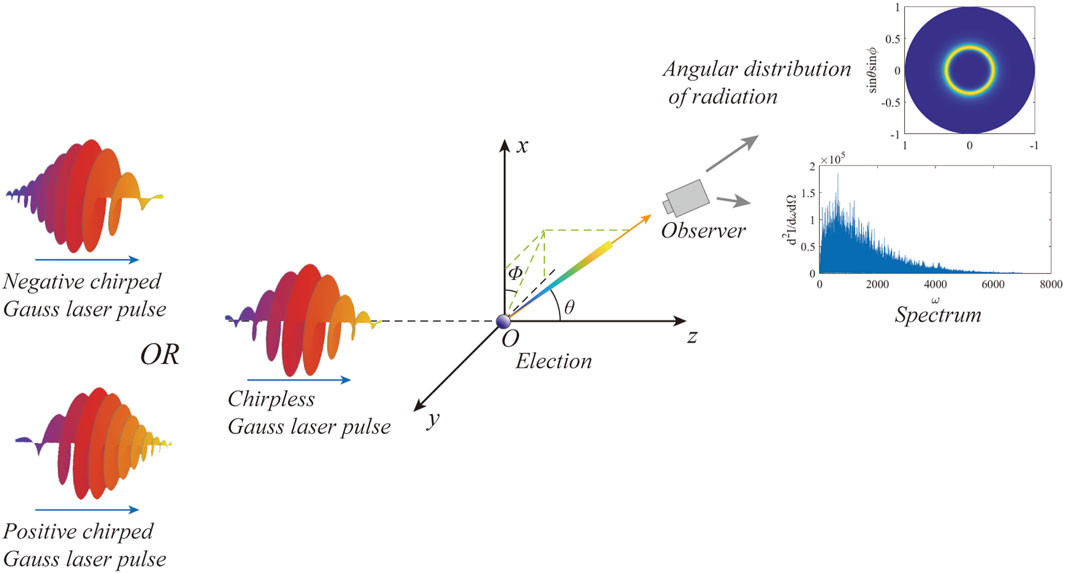
Figure 1. Geometric schematic of relativistic nonlinear Thomson forward scattering of stationary electrons driven by Gaussian circularly polarised intense laser pulses with three chirped modulations (positive chirp, negative chirp, and zero chirp).

2 Theory and formula

Firstly, it is stated that the wavelength of the chirped laser pulse used in this paper is chosen as λ₀ = 1μm . It is evident that all the formulas involved in the following have been normalised in time and space coordinates by ω₀^-1 and k₀^-1, respectively. With ω₀ = 2πc/λ0 being the circular frequency of the incident laser, k₀ = 2π/λ0 being the wave number of the laser in vacuum, and c being the speed of light.

In a 3D coordinate system, the phase of a circularly polarised focused chirped laser pulse φ can be expressed as

$\psi ={\psi }_0+{\psi }_P+{\psi }_R-{\psi }_G+c_0{r}^2(1)$

Where r = z-ct , is an auxiliary quantity characterising the coherence of space and time, and c0 is the chirp parameter of the laser pulse. From Equation 1, it can be seen that the chirp characteristic mainly affects the phase of the laser, which in turn affects the electron trajectory, and further affects the radiation characteristics of high-energy electrons. ψR is the phase associated with the curvature of the wavefront. ψG is the Guoy phase associated with the additional displacement generated by the propagation of the Gaussian beam from $-\infty$ to $+\infty$, and ${\psi }_0$is the initial phase of the laser pulse. They can be described respectively by the following equations:

${\psi }_R=k\left({\mathrm{x}}^2+{\mathrm{y}}^2\right)/2R\left(z\right)(2)$

${\psi }_G={\tan }^{-1}\left(z/z_r\right)(3)$

Where $R\left(z\right)=z\left(1+{\mathrm{z}}_f^2/z^2\right)$ is the radius of curvature of the beam front, while $z_r=\pi b_0^2/\lambda$ corresponds to the Rayleigh distance of the laser, and b₀ is the radius of the beam waist of the laser.

In this paper, by solving the near-axis approximate solution of the Helmholtz equation, the circularly polarised chirped laser field can be represented as [25, 26]:

$A_r=\frac{{a_{0}b}_0}{b}·\mathit{exp}\left(-\frac{r^2}{L^2}\right)\exp \left(-\frac{{\rho }^2}{b^2}\right)(4)$

Where ρ² = x²+y² , $b=b_0{\left(1+z^2/z_r^2\right)}^{1/2}$ , denote the spot radius of the laser at the corresponding z coordinates, and $a_0=0.85\times {10}^{-9}{\lambda }_0\sqrt{I}$ is the peak laser amplitude normalised by $m{c}^2/e$ . For tightly focused laser pulses, the accurate fifth-order expression for the laser divergence angle ε = b_0/z_r is essential for the accuracy of the relativistic laser field expression. Therefore, a circularly polarised Gaussian laser pulse can be expressed by the following electric and magnetic field components:

$\begin{array}{ll}\hfill E_x& ={\mathrm{A}}_r\left\{S_0+{\epsilon }^2\left[{\alpha }^2{S}_2-\frac{r^4{S}_3}{4}\right]\right.\hfill \\ \hfill & +{\epsilon }^4\left[\frac{S_2}{8}-\frac{r_2{S}_3}{4}-\frac{r^2\left(r^2-16{\alpha }^2\right)S_4}{16}-\frac{r^4\left(r^2+2{\alpha }^2\right)S_5}{8}+\frac{r^8{S}_6}{32}\right]\hfill \\ \hfill & \left.+{\epsilon }^2{C}_2+{\epsilon }^4\left[r^2{C}_4-\frac{r^4{C}_5}{4}\right]\right\}\hfill \end{array}(5)$

$\begin{array}{ll}\hfill E_y& ={\mathrm{A}}_r\left\{C_0+{\epsilon }^2\left[{\beta }^2{C}_2-\frac{r^4{C}_3}{4}\right]\right.\hfill \\ \hfill & +{\epsilon }^4\left[\frac{C_2}{8}-\frac{r^2{C}_3}{4}-\frac{r^2\left(r^2-16{\beta }^2\right)C_4}{16}-\frac{r^{4}9r^2+2{\beta }^2)C_5}{8}+\frac{r^8{C}_6}{32}\right]\hfill \\ \hfill & \left.+{\epsilon }^2{S}_2+{\epsilon }^4\left[r^2{S}_4-\frac{r^4{S}_5}{4}\right]\right\}\hfill \end{array}(6)$

$\begin{array}{ll}\hfill E_z& =A_r\alpha \left\{\epsilon C_1+{\epsilon }^3\left[-\frac{C_2}{2}+r^2{C}_3-\frac{r^4{C}_4}{4}\right]\right.\hfill \\ \hfill & \left.+{\epsilon }^5\left[-\frac{3C_3}{8}-\frac{3r^2{C}_4}{8}+\frac{17r^4{C}_5}{16}-\frac{3r^6{C}_5}{16}-\frac{3r^6{C}_6}{8}+\frac{r^8{C}_7}{32}\right]\right\}\hfill \\ \hfill & -A_r\beta \left\{\epsilon S_1+{\epsilon }^3\left[-\frac{S_2}{2}+r^2{S}_3-\frac{r^4{S}_4}{4}\right]\right.\hfill \\ \hfill & \left.+{\epsilon }^5\left[-\frac{3S_3}{8}-\frac{3r^2{S}_4}{8}+\frac{17r^2{S}_5}{16}-\frac{3r^6{S}_5}{16}-\frac{3r^6{S}_6}{8}+\frac{r^8{S}_7}{32}\right]\right\}\hfill \end{array}(7)$

$B_x={\mathrm{A}}_r\left\{C_0+{\epsilon }^2\left[\frac{r^2{C}_2}{2}-\frac{r^4{C}_3}{4}\right]+{\epsilon }^4\left[-\frac{C_2}{8}+\frac{r^2{C}_3}{4}+\frac{5r^4{C}_4}{16}-\frac{r^6{C}_5}{4}+\frac{r^8{C}_6}{32}\right]\right\}(8)$

$B_y={\mathrm{A}}_r\left\{S_0+{\epsilon }^2\left[\frac{r^2{S}_2}{2}-\frac{r^4{S}_3}{4}\right]+{\epsilon }^4\left[-\frac{S_2}{8}+\frac{r^2{S}_3}{4}+\frac{5r^4{S}_4}{16}-\frac{r^6{S}_5}{4}+\frac{r^8{S}_6}{32}\right]\right\}(9)$

$\begin{array}{ll}\hfill B_z& =A_r\beta \left\{\epsilon C_1+{\epsilon }^3\left[\frac{C_2}{2}+\frac{r^2{C}_3}{2}-\frac{r^4{C}_4}{4}\right]\right.\left.+{\epsilon }^5\left[\frac{3C_3}{8}\frac{3r^2{C}_4}{8}+\frac{3r_4{C}_5}{16}-\frac{r^6{C}_6}{4}+\frac{r^8{C}_7}{32}\right]\right\}\hfill \\ \hfill & -A_r\alpha \left\{\epsilon S_1+{\epsilon }^3\left[\frac{S_2}{2}+\frac{r^2{S}_3}{2}-\frac{r^4{S}_4}{4}\right]\right\}\hfill \end{array}(10)$

Where $\alpha =x/b_0$ , $\beta =y/b_0$ , $\xi =\rho /b_0$ , $S_n$ and $C_n$ describing the phase are shown below:

$\left\{\begin{array}{c}{S}_n={\left(\frac{b_0}{b}\right)}^n\sin \left(\psi +n{\psi }_G\right),n=0,1,2,\dots \\ C_n={\left(\frac{b_0}{b}\right)}^n\cos \left(\psi +n{\psi }_G\right),n=0,1,2,\dots \end{array}\right.(11)$

In a laser field with a Gaussian envelope, the equations of motion for relativistic electrons can be introduced via the Lorentz equation and the Lagrangian function as [27]:

$\left\{\begin{array}{l}\frac{d}{dt}\left(\mathit{p}-\mathit{a}\right)=-{\nabla }_a\left(\frac{\mathit{v}}{c}·\mathit{a}\right)\\ \frac{dK}{dt}=\frac{\mathit{v}}{c}·{\partial }_t\mathit{a}\end{array}\right.(12)$

where, $K=\gamma m_e{c}^2$, $\gamma ={\left(1-v^2/c^2\right)}^{-1/2}$ is the electron energy defined by the Lorentz factor, $c$ is the speed of light, $m_e=9.1\times {10}^{-31}$ is the electron static mass, $\mathit{v}$ is the electron velocity, and $\mathit{p}$ is the electron momentum equal to $K\mathit{v}/c^2$.

In order to realise the spatial and temporal discretisation of the electron motion, we derive the full-time partial differential equations for the acceleration, velocity and energy of the electron moving in the chirped laser field. Accordingly, the full-time, full-space trajectory of the electron can be determined as:

$\left\{\begin{array}{l}\gamma d_t{u}_x=\left(1-u_x^2\right){\partial }_t{a}_x+u_y\left({\partial }_y{a}_x-{\partial }_x{a}_y\right)+u_z\left({\partial }_z{a}_x-{\partial }_x{a}_z\right)-u_x{u}_y{\partial }_t{a}_y-u_x{u}_z{\partial }_t{a}_z\\ \gamma d_t{u}_y=\left(1-u_{\mathrm{y}}^2\right){\partial }_t{a}_y+u_x\left({\partial }_x{a}_y-{\partial }_y{a}_x\right)+u_z\left({\partial }_z{a}_y-{\partial }_y{a}_z\right)-u_x{u}_y{\partial }_t{a}_x-u_y{u}_z{\partial }_t{a}_z\\ \gamma d_t{u}_z=\left(1-u_z^2\right){\partial }_t{a}_z+u_x\left({\partial }_x{a}_z-{\partial }_z{a}_x\right)+u_y\left({\partial }_y{a}_z-{\partial }_z{a}_y\right)-u_x{u}_z{\partial }_t{a}_x-u_y{u}_z{\partial }_t{a}_y\\ d_t\gamma =u_x{\partial }_t{a}_x+u_y{\partial }_t{a}_y+u_z{\partial }_t{a}_z\end{array}\right.(13)$

Where $u_x$ , $u_y$ and $u_z$ are the velocity components of the electron in the direction of $x$ , $y$ and $z$ respectively. According to the knowledge of electrodynamics, electrons in relativistic accelerated motion emit electromagnetic radiation. And the radiated power per unit steradian angle of an accelerated electron can be derived from the Poynting vector as follows [28]:

$P{\left(t\right)}_{\mathrm{\Omega }}=\frac{dP\left(t\right)}{d\mathrm{\Omega }}={\left[\frac{{\left|\widehat{\mathit{n}}\times \left[\left(\widehat{\mathit{n}}-\mathit{u}\right)\times d_t\mathit{u}\right]\right|}^2}{{\left(1-\mathit{u}·\widehat{\mathit{n}}\right)}^6}\right]}_{\tau }(14)$

where the radiated power $P{\left(t\right)}_{\mathrm{\Omega }}$ is normalised by $e^2{\omega }_0^2/4\pi c$ , $\widehat{\mathit{n}}$ characterises the direction of radiation, $\tau$ characterises the interaction time of the electrons with the chirped laser pulse, and $t$ observes the point time and the relative delay time, which are related as

$\tau =t+\left(\mathit{R}-\widehat{\mathit{n}}·{\mathbf{x}}_{\mathbf{d}}\right)/c(15)$

Here $\mathit{R}$ is the distance between the observation point and the point of action of the electron and laser pulses. We assume that the observation point is far enough away from the region of action. Therefore, the formula for the radiant energy per unit steradian angle and per unit frequency interval during the interaction between the electron and the laser pulse can be derived from Parseval’s theorem as [25]:

$\frac{d^{2}I}{d\omega d\mathrm{\Omega }}={\left|{\int }_{-\infty }^{+\infty }\frac{\widehat{\mathit{n}}\times \left[\left(\widehat{\mathit{n}}-\mathit{u}\right)\times d_t\mathit{u}\right]}{{\left(1-\mathit{u}·\widehat{\mathit{n}}\right)}^2}{e}^{is\left(t-\widehat{\mathit{n}}·{\mathbf{x}}_{\mathbf{d}}\right)}dt\right|}^2(16)$

Where, $\frac{d^{2}I}{d\omega d\mathrm{\Omega }}$ is normalised by e²/4π² , ω is the radiation frequency, s = ω_sb/ω₀ , ω_sb are the frequencies of the higher harmonics generated by scattering. The full-space, full-time and full-spectrum radiation characteristics of Thomson nonlinear scattering can be obtained by solving the equations.

3 Results and discussion

In this section we study relativistic nonlinear Thomson forward radiation produced by stationary electrons on the drive axis of three Gaussian circularly polarised chirped laser fields. In this case, the initial energy of the electron is $1MeV$, and the incident excitation light pulse propagates along the $+\mathrm{z}$ axis with zero as the angle of incidence and its wavelength ${\lambda }_0=1\mu m$ . The light intensity parameter $a_0=5\left(I=3.45\times {10}^{19}W/{cm}^2\right)$,the beam waist radius $b_0$ is normalised to $5$ ,and the corresponding length is $5\mu m$ . We vary the pulse width from $L=2$ to $L=12$ unit by unit, and select the three chirp parameters $c_0=-0.02$ , $c_0=0$ ,and $c_0=+0.02$ for the cross parameter study. According to Equations 4–16, we can obtain the electron trajectories, spatial radiation, time spectrum and frequency spectrum of nonlinear Thomson scattering under chirped conditions.

3.1 Electrodynamic properties

According to Figure 2, we note that the basic motion trajectories of the electron nonlinear Thomson scattering are the circumferential-like helical motion around the direction of a certain deflection angle along the direction of action of the laser pulse ($+zaxis$) as well as the straight line motion after the end of the helical motion. From Fig. (Ⅱ), we conclude that the effect of pulse width on the electron trajectory lies in the extension of the helical motion of the electrons, which is mainly determined by the nature of the laser pulse itself. As shown in Figure 1, the pulse width characterises the axial length of the laser pulse, or the duration of the laser pulse on the time axis, and the increase or decrease of this variable affects the range of the laser pulse interaction with the electrons in the most intuitive manner, which in turn the spreading of the helical motion.

Figure 2

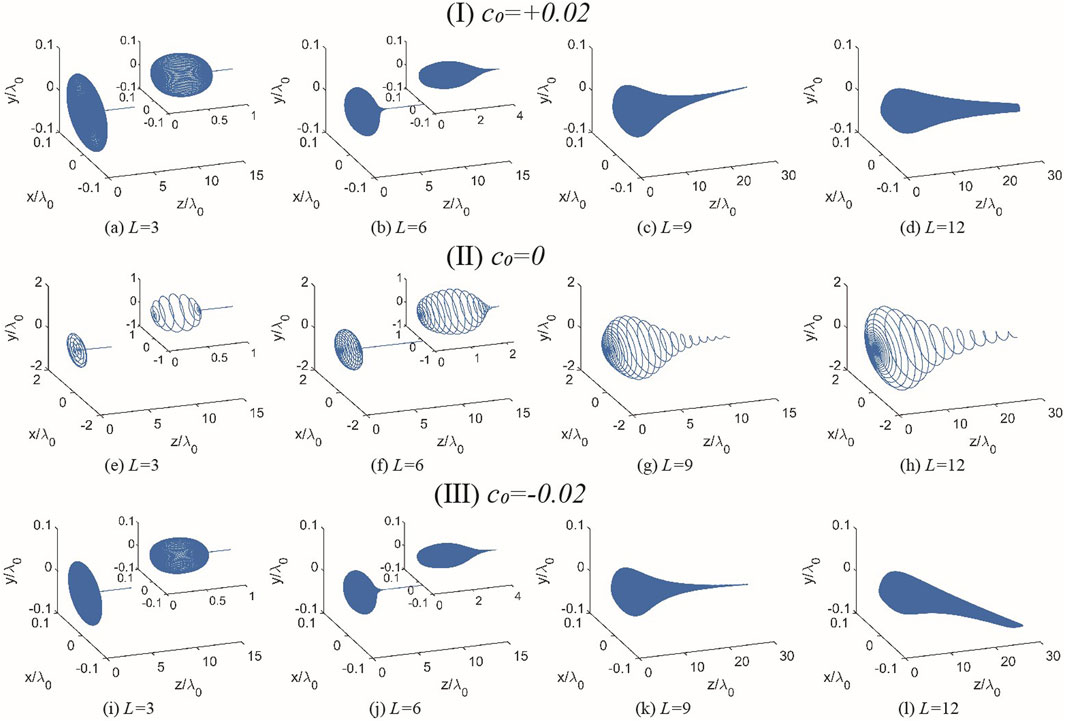
Figure 2. Electron motion trajectories for different pulse widths and different chirp parameter crossover conditions. (I) group includes (a–d), (II) group includes (e–h), and (III) group includes (i–l). (I) group c0=-0.02 , (II) group c0=0, (III) group c0=+0.02, where the x-axis and y-axis coordinate ranges of (I) and (III) groups are contracted to 20 times of that of (II) group for better observation of the features.

Meanwhile, as shown in Figure 2II, the nature of the front and back helix of the laser pulse along the winding direction is different. For ease of presentation, we refer to the electron helical motion from the beginning to the pitch maximum as the front helix and from the maximum pitch to the end of the helical motion as the back helix. In Figures 2e,f, we find that the front helix and the back helix are fundamentally symmetric, and thus the electron trajectory under the action of this smaller pulse width laser pulse exhibits an ellipsoidal shape. In contrast, in Figures 2g,h, the front helix is obviously shorter than the back helix, and the overall structure is spread out at the tail end, evolving from an ellipsoid shape to a teardrop shape. The root of this phenomenon lies in the influence of the pulse width on the two exponential terms of the amplitude of the laser field. For the radial exponential term $\mathit{exp}\left(-\frac{r^2}{L^2}\right)$ containing the pulse width L , the increase of the pulse width L directly leads to the overall increase of the exponential term as well as reduces the decreasing rate of the exponential term; for the longitudinal exponential term $\frac{{a_{0}b}_0}{b}\exp \left(-\frac{{\rho }^2}{b^2}\right)$ , we need to realise that the spot radius b is positively correlated with the z and, in the back helix, the value of z is much greater than that in the front helix, and $\exp \left(-\frac{{\rho }^2}{b^2}\right)$ tends to be close to 1, so that the longitudinal exponential term is mainly shorter than the front helix in the back helix. Therefore, in the back helix, the longitudinal exponential term mainly depends on $\frac{{a_{0}b}_0}{b}$, and it can be concluded that the longitudinal exponential term in the back helix process is decreasing, and the laser action in the back helix part mainly relies on the radial exponential term $\mathit{exp}\left(-\frac{r^2}{L^2}\right)$ , which is specifically embodied in the pitch decrease rate in the back helix part. According to Figures 2g,h, we find that the falling edge of the back helix of the pulse width L = 9 is obviously steeper than that of the back helix of the pulse width L = 12.

Observing Figures 2I,III, we find that the electron motion with the chirped laser pulse follows the basic motion trajectory while generating new features. The most obvious change is the increase in the number of circles during the helical motion, and the feature actually associated with it is the decrease in the pitch of the electron helical motion. Here we can draw the tentative conclusion that the chirped laser pulses act mainly to help the electrons to concentrate more in the winding axis, thus increasing the number of winding circles. This is easy to understand, because the chirp modulation only changes the rate of change of the phase of the laser pulse without affecting the parameters related to the energy carried by the laser pulse, in other words, the chirp modulation ultimately changes the process of excitation of electrons by the laser pulse. The chirped laser field obviously has a higher rate of change in the direction of the time-varying electromagnetic field than that of the general electromagnetic field, and the motion of the electrons is the same as that of the increased density of the winding.

Comparing the subplots in Figure 2 vertically, we find that the chirped laser pulse has almost no effect on the range of electron helical motion determined by the pulse width, but this does not mean that the chirp does not affect the results of the pulse width action. Looking at Figures 2b,f,j, we find that the helical motion paradigm of the electron trajectory under chirp in the enlarged window is about 1λ0 more than that of the unchirped case, and the trailing phenomenon occurs earlier. This phenomenon is due to the fact that the radial distance of the electron motion under chirp $\rho =\sqrt{x^2+y^2}$ decreases by an order of magnitude and the longitudinal exponential term $\exp \left(-\frac{{\rho }^2}{b^2}\right)$ increases in the range towards 1, which means that the closing time of the longitudinal exponential term is delayed, and thus the laser-electron interaction is dependent on the increase in the range of the radial exponential term $\mathit{exp}\left(-\frac{r^2}{L^2}\right)$ , which leads to an increase in the pulse width L which can be shown earlier in chirp action.

Meanwhile, observing Figures 2I,III, we find the difference between positive and negative chirps. In Figures 2d,l, there is an obvious difference in the direction of electron winding, and the difference in the direction of winding is actually the embodiment of the difference in the winding rate, which is also well explained, because there is a difference in the direction of change in the amplitude chirp modulation, the positive chirp is a change in the direction of frequency increase, and the negative chirp is the opposite. In the electron trajectory we are not yet sure of the advantages and disadvantages of which, but to the electronic radiation characteristics, the negative chirp will show its superiority.

3.2 Spatial radiation features of electron radiation

Observing Figure 3II, we conclude that the spatial radiation distribution of electron Thomson scattering is vortex-like distribution, and this vortex-like distribution will produce new structural changes with the change of parameters. Here, we define the bright yellow part on the figure as the peak radiation region. According to Figures 3g–h, with the increase of pulse width, the number of layers of this vortex-like distribution increases, which is specifically reflected in the figure that the peak radiation region becomes obviously thicker. At the same time, we also notice a detail that this increase in the number of vortex layers is from outside to inside. These two details correspond to the changes in the electron motion in Figure 2II, where the change in the radiated power of the inner ring actually corresponds to the change in the back helix--the tail of the back helix spreads out while the number of radiated vortex layers increases. However, we should also realise that the number of turns of the back helix far exceeds the number of turns of the front helix when the pulse width is large, and the gain for the peak radiation region is not proportional, i.e., the peak radiation region is very little affected by the radiation generated by the back helix part, and the peak radiation region is mainly affected by the front helix part.

Figure 3

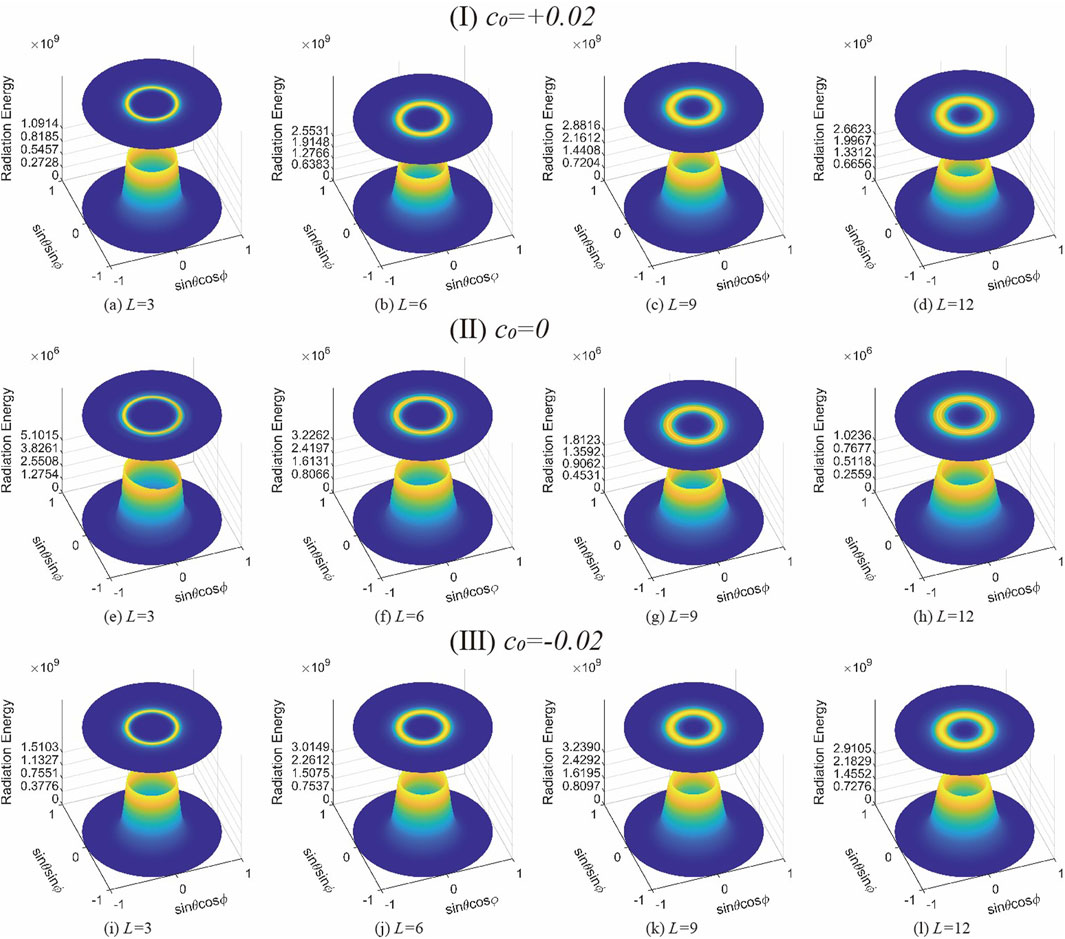
Figure 3. All-angle distribution and projection of electron radiation for different pulse widths and different chirp parameter crossover conditions. (I) group includes (a–d), (II) group includes (e–h), and (III) group includes (i–l). (I) group c0=-0.02, (II) group c0=0 , (III) group c0=+0.02 , where the z-axis is quadratically divided by the respective peak power of radiation.

Under the action of chirped laser pulses, the electron space radiation produces structural changes. Longitudinally comparing Figures 3a–l, we find that the vortex structure of the spatial radiation evolves whether positively or negatively chirped, whereas multiple layers of vortices coupled to each other produce a circular structure with an overall thickening of the peak radiation region. This is also explained in Figure 2, where this circular structure is essentially due to the more concentrated radial displacement of the electron trajectories, resulting in the concentration of the generated radiation into a finite space, which is coupled to each other and evolves into a circular structure. It has been demonstrated above that the peak radiation region is mainly affected by the front helical part, and the number of layers of the overall helical motion of the electrons increases under the effect of chirp, so that the peak radiation region as well as the overall angular range of the radiation increases to a certain extent.

Comparing Figures 3I,III, we note that the difference in the effect of positive and negative chirp on the radiation structure is limited and difficult to observe, but the difference in the numerical value of the radiated power is obvious. It is observed that the peak radiated power of the negative chirp is always greater than that of the positive chirp for the same pulse width, which will be discussed in more detail in Section 3.4.

3.3 Time spectrum of radiation in the maximum direction

As shown in Figure 4b, the time spectrum in the direction of maximum radiated power for nonlinear Thomson scattering from a single stationary electron is a multi-peak structure. We find that the chirp-free time spectrum in the direction of maximum radiated power has only three peaks. In Figures 4a,c, we find that the number of secondary radiation peaks of the time spectrum under the influence of chirp increases by leaps and bounds, and all of these radiation peaks conform to the envelope of a new overall peak. This allows us to invert the chirp-free time spectrum, which should similarly follow this law. The generation of ultra-multiple secondary peaks in the chirp scenario echoes the effect of chirp on the electron trajectory, and fundamentally it is the tight confinement of the region of electron motion under the effect of chirped laser pulses that leads to an increase in the number of radiation pulses received in the direction of the maximum radiated power, resulting in the evolution of the time spectrum into an ultra-dense multi-peak structure.

Figure 4

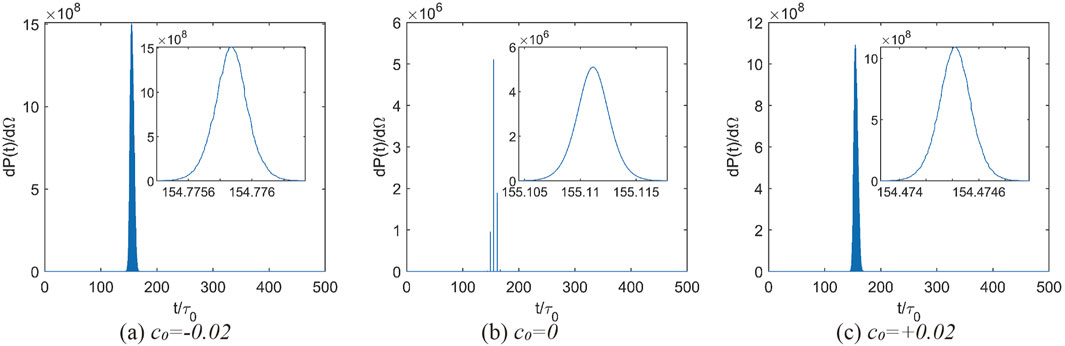
Figure 4. Time spectrum of electron radiation in the maximum direction with different chirp parameters at pulse width L = 3. c₀=−0.02 in (a), c₀=0 in (b), and c₀=+0.02 in (c). Obviously the radiation time spectrum is a multi-peak structure, We refer to the peak where the peak radiated power occurs as the main radiated peak and the others as secondary radiated peaks, while the main radiation peak is shown in the figure window.

However, we are actually more concerned with the radiative properties of the radiative main peak, which are divided into two aspects; the core property is the peak radiated power, while the secondary property is the full width at half maximum (FWHM) of the radiative main peak. For this reason, we focus on the comparison in Section 3.4.

3.4 Two properties of the main radiation peak

Observing Figure 5, we find that the chirped laser pulses completely change the FWHM as well as the peak radiated power variation rule with pulse width. For the FWHM, the two line plots of chirp in Figure 5a show a negative exponential decreasing trend, while the curve of zero chirp shows an increasing trend. Note that the chirp FWHM order of magnitude, which reaches ${10}^{-1}zs$ order of magnitude, is about one order of magnitude lower than the chirp-free FWHM. Also, the FWHM of the negative chirp is always smaller than that of the positive chirp. For example, when $L=3$, ${FWHM}^{-}=0.2334zs<{FWHM}^{+}=0.2812zs<{FWHM}^0=3.3263zs$. We notice that at $L=2$, the positive chirp can match the FWHM of the negative chirp by increasing the pulse width; however, when the pulse width is larger, the FWHM decreases more slowly. And in this case, in order to guarantee the same FWHM as the negative chirp, the pulse width often has to be paid for several times, which is practically uneconomical.

Figure 5

Figure 5. Plot of full width at half maximum (FWHM) and peak radiated power versus pulse width for three chirp cases. (a) shows the relationship between FWHM and pulse width. (b) shows the relationship between peak radiated power and pulse width. Where the half height full width unit is zs and negative chirp c0=−0.02 and positive chirp c0=0.02.

For the peak radiated power, the unchirped curve in Figure 5b shows a decreasing trend, while the two line plots for chirp show an increasing and then decreasing trend. We first note the great advantage of the chirp case, for the gain of peak radiated power, which can reach about ${10}^3$ order of magnitude, and similarly, the negative chirp case always has a larger peak power than the positive chirp. For example,, when $L=3$, ${{\left(\frac{dP}{d\mathrm{\Omega }}\right)}_p}^{-}=1.5103\mathrm{E}+09>{{\left(\frac{dP}{d\mathrm{\Omega }}\right)}_p}^{+}=1.0914\mathrm{E}+09>{\left(\frac{dP}{d\mathrm{\Omega }}\right)}_p^0=5.1015\mathrm{E}+06$ ,where the radiated power $\frac{dP}{d\mathrm{\Omega }}$ is normalised by $e^2{\omega }_0^2/4\pi c$. While noting the saturation point of the chirp curve, we find that the negative chirp has reached its extreme at $L=8\mu m$, while the positive chirp reaches its extreme at $L=9\mu m$. This indicates that the positive chirp requires more reaction time to excite the electrons, and the reaction time required to excite the electrons is different between the two.

The above discussion shows that the variation rule of the peak radiated power and FWHM of the main peak of radiation under the chirp effect with the pulse width is changed. For FWHM, the increase in pulse width directly leads to the increase in the explosive level of secondary radiation peaks, while at the same time, the time range shared by these radiation peaks remains constant, so the FWHM shifts to a negative exponential decreasing trend. For the peak radiated power, we conclude that it is the result of the mutual coupling of the velocity and acceleration of the electron motion, before reaching the maximum value, the electron acceleration is large while the velocity is small, and the increase of the velocity makes the peak radiated power show a rising trend. After crossing the maximum value, the electron velocity is large while the acceleration tends to level off, so the subsequent peak radiated power starts to decrease slowly.

Combining the two graphs in Figure 2, we summarise the following law--for the unchirped laser pulse, the effect of pulse width on radiation is unidirectional, taking $L=2\mu m$ can obtain ultra-short and ultra-intense radiation pulse. For chirped laser pulses, on the other hand, the effect of pulse width on the FWHM is unidirectional. There is an optimal solution of the peak radiated power with respect to the pulse width. The negative chirp outperforms the positive chirp in both characteristics. Based on the principle of priority of core characteristics, we believe that the chirp modulation should be selected as negative chirp modulation and the pulse width $L=8\mu m$ to obtain the higher peak radiated power and lower FWHM。

3.5 Positive correlation of peak radiated power

Yang [29] in his study of laser pulses and electron cross collisions suggested that ${\left(\frac{dP}{d\mathrm{\Omega }}\right)}_{peak}\propto R_e\left(t\right)=\left[{\gamma }^8{\left|d_t{u}_{\perp }\right|}^2\right]\mathit{max}$ holds in the case of laser pulses and electron cross collisions. We are curious to see if this law still holds after the introduction of chirp modulation in order to further understand the process of electron Thomson scattering and the effect of chirp. As shown in Figure 6, we compare the full-time radiation power and the electron response function $R_e\left(t\right)$ is still positively correlated with the full-time radiation power, but also shows the asymmetry between positive and negative chirp,where the negative chirp ${R_e}^{-}\left(t\right)=1.90E+08$ is higher than the positive chirp ${R_e}^{+}\left(t\right)=1.61E+08$ . What is even more encouraging is that the gain of $R_e\left(t\right)$ between the chirp and the zero chirp is the same as that in the full-time radiation power , and there is an ${10}^3$ order of magnitude gain. For example , in the case of the negative chirp, ${Gain}_{Re}=\frac{{R_e}^{-}\left(t\right)}{R_e^0\left(t\right)}=933.72$ , ${Gain}_{peak}=934.40$ , within a certain margin of error, ${Gain}_{Re}\equiv {Gain}_{peak}$ . This means that in future studies we can measure the gain relationship of the chirp by the electron response function $R_e\left(t\right)$.

Figure 6

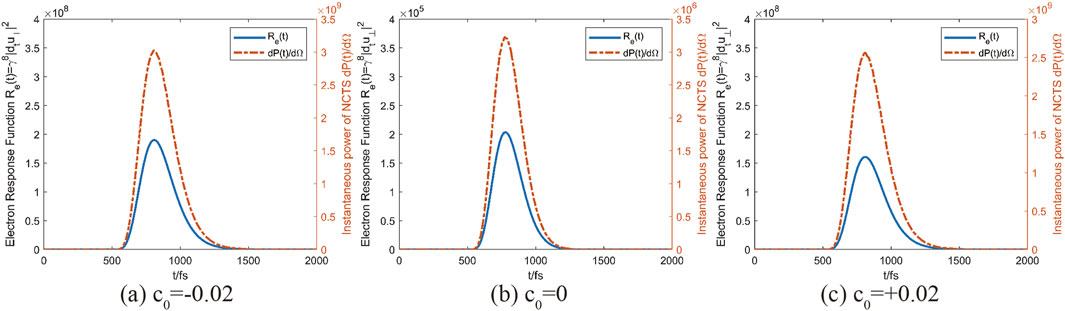
Figure 6. Plot of peak radiated power dP(t)/dΩ against its positive correlation value Re(t) for three chirps. The pulse width L=6 is taken here. c₀=−0.02 in (a), c₀=0 in (b), and c₀=+0.02 in (c).

With the aid of the electron response function $R_e\left(t\right)$ , we may be able to get a glimpse of the role of chirp. In Section 3.1, we find that the radial contraction of the electron trajectory occurs under the chirped laser pulse, where we can conclude that the radial contraction of the electron trajectory is actually a manifestation of the increase of $\left|d_t{u}_{\perp }\right|$ in electron trajectory. The first role of chirp is to increase the rate of change of the radial velocity. $R_e\left(t\right)$ also contains an item ${\gamma }^8$ , $\gamma$ for the whole process of net electron energy gain, which characterises the second effect of chirp, chirp increases the net electron energy gain.

3.6 Spectrum of radiation in the maximum direction

According to Figure 7b, we find that the effect of the pulse width on the spectrum of the chirpless electron radiation is twofold, one of which is to make the spectral spectrum tend to be noisy, which we believe is due to the increase in the number of secondary radiation peaks in the maximal direction caused by the increase in the pulse width, and the other is the overall Doppler redshift of the spectrum with the increase in the pulse width.

Figure 7

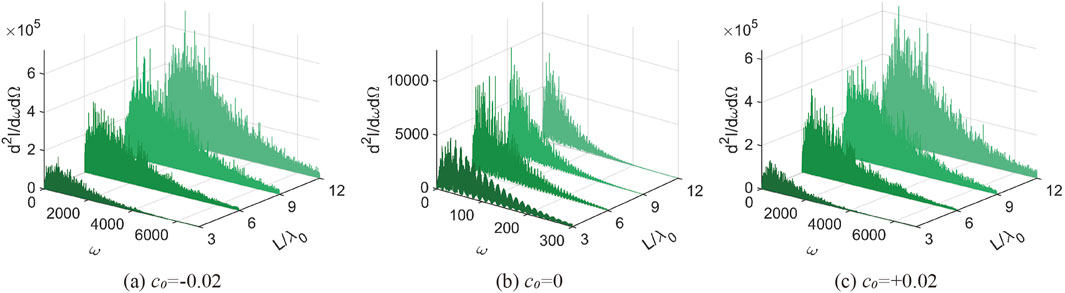
Figure 7. Maximum radiated power distribution of electrons per unit steradian angle and per unit frequency interval for different pulse widths. c₀=−0.02 in (a), c₀=0 in (b), and c₀=+0.02 in (c).

In contrast, in Figures 7a,c, the spectrum is broadened by the chirp effect, while the increase in pulse width causes the spectrum to be Doppler blueshifted. In addition, the overall height of the chirp spectrum spectral lines in the high pulse width case is higher than that of the chirp spectrum spectral lines in the low pulse width case, and it should also be noted that not all the values of the frequency components for low pulse widths are necessarily lower than those of the frequency components for high pulse widths. Overall, the chirp spectrum is richer in frequency components.

4 Summary and conclusions

In summary, we have investigated the nature of tightly focused circularly polarised relativistic nonlinear Thomson scattering in the framework of classical electrodynamics and have gained some insight into the effect of chirp on the radiation properties. The effect of chirp modulation on Thomson scattering arising from the synergistic effect of chirp modulation and laser pulse width is explored through theoretical analyses and numerical studies.

We have investigated the electrodynamic properties of electrons in terms of two directional displacements of the electron helix and two types of helical motions, and summarised the electron radiation properties by means of the electron radiative all-angle distribution, the radiated power time spectrum, the radiated power spectrum, and the electron response function. We find that the peak radiated power increases rapidly and then decreases slowly as the pulse width of the chirped laser pulse increases. The FWHM decreases exponentially, and the spectrum undergoes a Doppler blue shift. Comparing the radiation characteristics under the effect of positive and negative chirped laser pulses, we find that the negative chirp outperforms the positive chirp for the same pulse width. In addition, we find that the positive relationship between the electron response function and the full-time radiation peak, ${\left(\frac{dP}{d\mathrm{\Omega }}\right)}_{peak}\propto R_e\left(t\right)=\left[{\gamma }^8{\left|d_t{u}_{\perp }\right|}^2\right]\mathit{max}$ , still holds under chirped conditions. At the same time, the gain of the electron response function, ${Gain}_{Re}$ , and the gain of the full-time radiation peak, ${Gain}_{peak}$ , are equivalent to each other within a certain error range, which provides a simpler measure for our subsequent theoretical studies.

The results show that a negatively chirped modulated laser pulse at a pulse width of $L=8\mu m$ is more favourable for the production of optical pulses of the order of ${10}^{-1}zs$, subject to the maximum peak radiant power. The combined results show that chirped modulated laser pulses improve all the properties of electron radiation and the worst properties with chirped modulation are far from the best properties without chirped modulation, but the possibility of destruction of radiation properties at finer chirps cannot be excluded.

In this paper, the chirp modulation technique is introduced into nonlinear Thomson scattering, which enriches the research in the field of nonlinear optics and provides theoretical and numerical support for the experimental generation of $zs$ level optical pulses.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

ZW: Writing – original draft, Writing – review and editing. JX: Writing – review and editing. JL: Writing – review and editing. QZ: Writing – review and editing. YT: Writing – review and editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2025.1603637/full#supplementary-material

References

1. Shimoda K. Proposal for an electron accelerator using an optical maser. Appl Opt (1962) 1(1):33–5. doi:10.1364/ao.1.000033

CrossRef Full Text | Google Scholar

2. Maine P, Strickland D, Bado P, Pessot M, Mourou G. Generation of ultrahigh peak power pulses by chirped pulse amplification. IEEE J Quan Electron (1988) 24(2):398–403. doi:10.1109/3.137

CrossRef Full Text | Google Scholar

3. Delfyett PJ, Mandridis D, Piracha MU, Nguyen D, Kim K, Lee S. Chirped pulse laser sources and applications. Prog Quan Electronics (2012) 36(4-6):475–540. doi:10.1016/j.pquantelec.2012.10.001

CrossRef Full Text | Google Scholar

4. Xu JJ, Kong Q, Chen Z, Wang PX, Wang W, Lin D, et al. Vacuum laser acceleration in circularly polarized fields. J Phys D: Appl Phys (2007) 40(8):2464–71. doi:10.1088/0022-3727/40/8/008

CrossRef Full Text | Google Scholar

5. Corde S, Ta Phuoc K, Lambert G, Fitour R, Malka V, Rousse A, et al. Femtosecond x rays from laser-plasma accelerators. Rev Mod Phys (2013) 85(1):1–48. doi:10.1103/revmodphys.85.1

CrossRef Full Text | Google Scholar

6. Kmetec JD, Gordon IIICL, Macklin JJ, Lemoff BE, Brown GS, Harris SE. MeV x-ray generation with a femtosecond laser. Phys Rev Lett (1992) 68(10):1527–30. doi:10.1103/physrevlett.68.1527

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Rawson SD, Maksimcuka J, Withers PJ, Cartmell SH. X-ray computed tomography in life sciences. BMC Biol (2020) 18:21–5. doi:10.1186/s12915-020-0753-2

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Cozzi D, Albanesi M, Cavigli E, Moroni C, Bindi A, Luvarà S, et al. Chest X-ray in new Coronavirus Disease 2019 (COVID-19) infection: findings and correlation with clinical outcome. La radiologia Med (2020) 125:730–7. doi:10.1007/s11547-020-01232-9

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Boutet S, Lomb L, Williams GJ, Barends TR, Aquila A, Doak RB, et al. High-resolution protein structure determination by serial femtosecond crystallography. Science (2012) 337(6092):362–4. doi:10.1126/science.1217737

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Buzzi M, Först M, Mankowsky R, Cavalleri A. Probing dynamics in quantum materials with femtosecond X-rays. Nat Rev Mater (2018) 3(9):299–311. doi:10.1038/s41578-018-0024-9

CrossRef Full Text | Google Scholar

11. Abdel Wahab EA, Shaaban KS, Yousef ES. Enhancement of optical and mechanical properties of sodium silicate glasses using zirconia. Opt Quan Electronics (2020) 52:458–9. doi:10.1007/s11082-020-02575-3

CrossRef Full Text | Google Scholar

12. Hassanien AS, Alamri HR, El Radaf IM. Impact of film thickness on optical properties and optoelectrical parameters of novel CuGaGeSe4 thin films synthesized by electron beam deposition. Opt Quan Electronics (2020) 52(7):335. doi:10.1007/s11082-020-02448-9

CrossRef Full Text | Google Scholar

13. Farinelli R, Fabiani S, Poutanen J, Ursini F, Ferrigno C, Bianchi S, et al. Accretion geometry of the neutron star low mass X-ray binary Cyg X-2 from X-ray polarization measurements. Monthly Notices R Astronomical Soc (2023) 519(3):3681–90. doi:10.1093/mnras/stac3726

CrossRef Full Text | Google Scholar

14. Tabak M, Norreys P, Tikhonchuk VT, Tanaka KA. Alternative ignition schemes in inertial confinement fusion. Nucl Fusion (2014) 54(5):054001. doi:10.1088/0029-5515/54/5/054001

CrossRef Full Text | Google Scholar

15. Li K, Li L, Shu Q, Tian Y, Shi Y, Zhang Z. Spatial characteristics of motion and emission from electron driven by linearly polarized tightly focused laser pulses. Optik. (2019) 183:813–7. doi:10.1016/j.ijleo.2019.02.154

CrossRef Full Text | Google Scholar

16. Zhang X, Chen D, Tian Y. Analysis of the pulse widths on radiation properties from an electron driven by intense elliptically polarized laser. Appl Phys B (2023) 129(8):135. doi:10.1007/s00340-023-08066-z

CrossRef Full Text | Google Scholar

17. Wang Y, Wang C, Li K, Li L, Tian Y. Analysis of spatial radiation and motion features of nonlinear Thomson scattering in circularly polarized laser pulses. Opt Quan Electronics (2021) 53(5):229. doi:10.1007/s11082-021-02870-7

CrossRef Full Text | Google Scholar

18. Yu P, Lin H, Gu Z, Li K, Tian Y. Analysis of the beam waist on spatial emission characteristics from an electron driven by intense linearly polarized laser pulses. Laser Phys (2020) 30(4):045301. doi:10.1088/1555-6611/ab74d4

CrossRef Full Text | Google Scholar

19. Wang C, Wang Y, Li L, Bian Y, Tian Y. Influence of laser intensity on pulse width of nonlinear Thomson scattering in circularly polarized tightly focused laser pulses. In24th Natl Laser Conf and Fifteenth Natl Conf Laser Technology Optoelectronics (2020) 11717:159–67. doi:10.1117/12.2584937

CrossRef Full Text | Google Scholar

20. Khachatryan AG, Van Goor FA, Verschuur JW, Boller KJ. Effect of frequency variation on electromagnetic pulse interaction with charges and plasma. Phys Plasmas (2005) 12(6). doi:10.1063/1.1938167

CrossRef Full Text | Google Scholar

21. Xu T, Chen M, Li FY, Yu LL, Sheng ZM, Zhang J. Spectrum bandwidth narrowing of Thomson scattering X-rays with energy chirped electron beams from laser wakefield acceleration. Appl Phys Lett (2014) 104(1):013903. doi:10.1063/1.4861594

CrossRef Full Text | Google Scholar

22. Hack S, Tóth Z, Varró S, Czirják A. Isolated attosecond pulses of μ j energy via coherent thomson-backscattering, driven by a chirped laser pulse. The Eur Phys J D (2019) 73:1–7. doi:10.1140/epjd/e2019-90535-0

CrossRef Full Text | Google Scholar

23. Holkundkar AR, Harvey C, Marklund M. Thomson scattering in high-intensity chirped laser pulses. Phys Plasmas (2015) 22(10). doi:10.1063/1.4932995

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Sharma V, Kant N, Thakur V. Effect of different Gaussian-like laser profiles on electron energy gain in laser wakefield acceleration. Opt Quan Electronics (2024) 56(1):45. doi:10.1007/s11082-023-05643-6

CrossRef Full Text | Google Scholar

25. Hong X, Wei D, Li Y, Tang R, Sun J, Duan W. Enhanced radiation of nonlinear Thomson backscattering by a tightly focused Gaussian laser pulse and an external magnetic field. Europhysics Lett (2022) 139(1):14001. doi:10.1209/0295-5075/ac7c2f

CrossRef Full Text | Google Scholar

26. Taira Y, Katoh M. Generation of optical vortices by nonlinear inverse Thomson scattering at arbitrary angle interactions. The Astrophysical J (2018) 860(1):45. doi:10.3847/1538-4357/aac211

CrossRef Full Text | Google Scholar

27. He F, Yu W, Lu P, Xu H, Qian L, Shen B, et al. Ponderomotive acceleration of electrons by a tightly focused intense laser beam. Phys Rev E (2003) 68(4):046407. doi:10.1103/physreve.68.046407

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Yariv A. Quantum electronics. 2nd ed. New York: John Wiley and Sons (1975).

Google Scholar

29. Yang Q, Tian Y, Li Y, Wang Y. Generation of atto-zeptosecond X-rays through cross-collision between relativistic electron and tightly focused intense laser pulse. Opt and Laser Technology (2025) 181:111719. doi:10.1016/j.optlastec.2024.111719

CrossRef Full Text | Google Scholar

30. Liu X, Gumenyuk R. Wavelength-tunable chirped pulse amplification system (1720 nm–1800 nm) based on thulium-doped fiber. InPhotonics (2024) 11(5):439. doi:10.3390/photonics11050439

CrossRef Full Text | Google Scholar