1 Introduction
Fractal analysis has become an essential tool in multiple scientific disciplines, including physics, biology, neuroscience, medicine, biomedical engineering, materials science, economics, and environmental sciences, to name a few. The concept was first proposed by Mandelbrot (1983), based on the self-similarity of structures across different scales that are not definable by Euclidean geometry [1–3].
However, despite its widespread application, the precise definition and interpretation of fractal-related concepts remain inconsistent across disciplines [2,4–7]. Terms such as “fractal dimension,” “self-similarity,” “self-affinity,” “roughness,” “scaling laws,” the role of embedding dimension and topological dimension in spatial contexts are frequently applied in contexts where their mathematical rigor is uncertain [8–10]. This has led to a semantic drift in scientific discourse, creating barriers to effective interdisciplinary communication [11,12]. Addressing this, a differentiation between fractal analysis and fractal synthesis has been suggested, where fractal analysis focuses on single-dimension metrics to measure the complexity of an image or time series, whereas fractal synthesis combines local and global dimensions, entropy, and spatial-temporal dynamics to establish a more comprehensive understanding of complex systems. To take this further, this manuscript addresses the technical foundations and methodologies required to reliably interpret fractal descriptions by addressing assumptions of stationarity, selection of scale range, and use of surrogate data testing.
2 Complexity of image and time series data
2.1 Scale and measurement in fractal analysis
Before the advent of fractal analysis, Richardson (1961) explored the relationship between scale and length in coastlines, demonstrating that coastline length increases as measurement scale decreases, following a power-law relationship [13]. The exponent in this relationship quantifies the rate at which length changes with scale, forming the foundation of fractal dimension analysis [3,14]. This early work laid the foundation for modern fractal analysis, which employs techniques such as box-counting, dilation, mass-radius, and the caliper method [5,15–17]. These methods all serve as analytical tools that estimate object size or mass with the measurement scale and collectively form the basis of fractal analysis. The key exponent in these relationships, termed the fractal dimension (DE), characterizes the complexity of an object’s scaling properties. However, there is ongoing debate regarding what constitutes a “dimension” in mathematical and physical sciences. While the Hausdorff dimension is mathematically rigorous, other fractal dimensions, such as Minkowski and Kolmogorov dimensions, are widely used in applied fields despite not meeting strict mathematical definitions [18,19].
Many traditional fractal analysis methods, such as box-counting, assume a well-defined structure within an image or dataset, which does not always translate well to nonlinear and self-affine time-series data. Multifractal detrended fluctuation analysis (MF-DFA) has been introduced to account for these variations but remains sensitive to preprocessing techniques and data resolution, leading to the proposal of diverse multiscaling or multifractal applications [20–30].
A fundamental aspect of fractal analysis when applying DFA or box-counting is the selection of an appropriate scaling range. A shortcoming of DFA is that it assumes stationarity within each detrending window (see below for mathematical treatment). However, this is not always found in physiological time series, which leads to incorrect inferences of fractality. Testing goodness-of-fit and ensuring the correct polynomial detrending order to avoid under- or overfitting provides robust results [31].
2.2 Applications of fractal analysis across scientific fields
Fractal analysis has been employed across a wide spectrum of scientific and technological endeavors as well as in the arts. One of the possibly best-known applications of fractal analysis in the arts was the identification of a fractal-like pattern in the artistic work of Jackson Pollock and the Mandelbrot set [4,32–34]. Differences in different schools of Orthodox iconography and fractal analysis of scribal and ink identification also have a connection to fractal analysis [35,36]. Connected to the arts is the built-up environment [2,37]. From the very large scales to the molecular scale, solar and space physics use fractal approaches to model solar flare distributions, solar wind turbulence, and magnetospheric dynamics. In thermodynamics, fractal analysis deals with the molecular or atomic level [38–40]. From thermodynamics, combustion theory can be understood, where fractals describe flame front irregularities and turbulent eddies [41–44]. In materials science, fractal models describe grain boundary growth and porous structure distributions [45]. Liquid crystal textures exhibit fractal patterns during phase transitions [46]. Statistical physics incorporates fractals to describe anomalous diffusion and scaling in critical phenomena [47]. In geophysics and environmental sciences, fractals appear in models of porous media, glaciology (crevasse networks and ice-sheet roughness), and sedimentary layering [48,49]. Earthquake prediction research uses fractal statistics to characterize fault systems and seismicity patterns [50]. Ocean dynamics, river basin distribution patterns, and tsunami wave modeling leverage fractal structures to capture nonlinear wave propagation and coastline complexity [51,52]. Climate science is another related area of research utilizing fractal analysis principles [53–55]. In finance, fractal analysis is applied to market time series to understand volatility clustering and multifractal structures in asset returns. This rather limited overview of the wide-ranging applications highlights the need for a standardized methodological framework across disciplines. From the previous paragraphs and the citations, it becomes apparent that, for instance, the term “roughness” is quite common to describe surface complexity, yet roughness as discussed later is not a fractal property. The current paper concentrates on physiological processes and morphology related to fractal analysis and argues for a consistent use of definitions.
2.3 Fractal analysis of temporal signals
Beyond spatial applications, fractal analysis has been increasingly applied to physiological time-series data that can be analyzed by several different methods, briefly highlighted in this section [35,56]. Similar to geometric fractals, time-series fractals exhibit scale invariance in their temporal fluctuations, which can be analyzed using a variety of techniques such as detrended fluctuation analysis (DFA), Hurst exponent estimation, wavelet transforms, Higuchi algorithm, diverse entropy-based methods, and symbolic dynamics [30,57–73]. These methods have been linked to understanding neurological function, cardiovascular health, and autonomic regulation which address diverse pathologies including stroke, cardiovascular disease (CVD), mental health disorders, and diabetes, amongst many others.
The Hurst exponent (H) is a classical measure of the persistence or anti-persistence of a time series, including rescaled range (R/S) analysis [74]. It quantifies whether a system exhibits memory effects, where H < 0.5 indicates anti-persistent behavior, H = 0.5 suggests randomness, and H > 0.5 denotes long-range dependence. An often-not-considered aspect of the Hurst exponent is that the traditional Hurst exponent estimation assumes stationarity. This has been addressed by the Hurst-Kolmogorov (HK) method used for estimating the Hurst exponent. The HK method accurately assesses long-range correlations when the measurement time series is short, shows minimal dispersion about the central tendency, and yields a point estimate that does not depend on the length of the measurement time series or its underlying Hurst exponent [75]. Another difficulty in determining the Hurst coefficient is that the computation of H depends on the signal type [31,76]. The signal type can be fractional Gaussian noise () or fractional Brownian motion (), where mathematically is the first derivative of , and is the temporal integral of . is stationary with zero mean and short or long-range correlations, depending on the Hurst exponent has slopes of the power spectral density (PSD) smaller than one (), where is the spectral exponent (slope of power spectral density). Whereas is non-stationary and is self-similar with long-range dependence and increasing variance over time with slope greater than one ( >1) [77]. The power spectral density (PSD) is then defined as:where is frequency and is the scaling exponent, which indicates the complexity of the signal [31,78].
The spectral power exponent is defined through the PSD and indicates how energy or power is distributed across frequencies in a signal and characterizes the scale-invariance and fractal properties in temporal dynamics. indicates signal complexity and is linked to the long-term correlations of the signal. As such defines white noise, which is a completely uncorrelated time series . Pink or noise has correlated fluctuations and is defined as . being greater than 0.5 indicates persistent Brownian motion, whilst less than 0.5 indicates anti-persistent Brownian motion. When , the signal is akin to Brownian motion and exhibits non-stationary time evolution. Brownian motion and stronger persistence, with less local variability, are associated with [77]. From a fractal perspective, reflects the self-affinity of the signal and signals with higher exhibit smoother, more correlated behavior, whereas lower implies higher-frequency fluctuations and greater complexity.
) generalizes classical Brownian motion by introducing memory via the Hurst exponent H∈(0,1), which controls the degree of long-range dependence and smoothness. Mandelbrot and van Ness originally defined this process as:
The process is self-similar with stationary moments, where is the fractional Brownian motion with Hurst exponent ; is the Gamma function, is the standard Wiener process (Brownian motion) and determines the correlation structure. is standard Brownian motion with no memory. indicates persistent behavior and anti-persistent behavior, respectively [31,79]. is a specific process, which is referred to as normal () in the mathematical literature and emphasizes that it is a Gaussian process in the statistical sense. adheres strictly to the Mandelbrot and van Ness (MvN) definition and distinguishes this definition from other generalizations or -like processes. The current paper uses consistently in the MvN sense.
The Hurst coefficient for is calculated with for and with for signals, see [31]. This results in different values for the autocorrelation or the fractal dimension derived from . Here autocorrelation decays as a power law for these processes, depending on :
And the fractal dimension () of the signal is related to by:where smoother signals (with higher H) exhibit lower complexity in their geometric representation. For slopes close to one, the type of signal investigated is uncertain, and, in addition, may be present in any recorded signals.
In recent literature, fractal terminology has evolved to distinguish between various generalizations of that are relevant in the context of non-Brownian, non-Gaussian dynamics observed in empirical signals [80]. Normal fractional Brownian motion () or Gaussian () is now commonly used to refer explicitly to the classical as originally defined by MvN [81,82]. can be further defined as a Gaussian process where the process variance is a non-linear function of time (i.e., sub- or super-linear). By contrast, the term fBm is increasingly applied more broadly to describe processes that exhibit self-similarity and long-range dependence but may not be Gaussian or may not have strictly stationary increments. This includes fractional Lévy motion (), which generalizes to the non-Gaussian, heavy-tailed domain by replacing the Wiener process with an α-stable Lévy process [83–85]. Other terms, such as normalized fractional Lévy noise () and may refer to fractional Brownian-type processes with non-Gaussian features or noise contamination as described above [86,87].
2.3.1 Detrended fluctuation analysis
Similar to the Hurst exponent, detrended fluctuation analysis (DFA) is a widely used method for detecting long-range correlations in non-stationary time series. DFA was introduced by Peng et al. to address the limitations of the classical rescaled range (R/S) developed by Hurst for nonstationary signals [74,88]. For monofractal signals, the scaling exponent α is equivalent to the Hurst exponent [89]. DFA requires integrating the time series to transform the time series into a random walk profile and reveal the underlying trends and fluctuationsWhere k is the index of the cumulative summation step in the integrated signal, . The integrated time series is then divided into non-overlapping segments of length (s), detrending each segment using polynomial fitting and computing RMS
This procedure is repeated for various scales or window sizes, s, and α determined from
DFA quantifies the scaling behavior of a signal by dividing it into segments, detrending each segment, and calculating the root-mean-square fluctuations across multiple time scales. The fractal exponent (α) derived from DFA helps classify signals as uncorrelated (α ≈ 0.5), long-range correlated (0.5 < α < 1), or Brownian motion-like (α ≈ 1.5). However, this method does not distinguish between fractional Lévy and fractional Brownian motion [90]. The former is an important characteristic of physiological time series [91]. is defined via a convolution with Brownian motion:Where is the Wiener process as introduced above. The equation above is a symbolic representation of the MvN conveying the power-law scaling characteristic of rather than being a constructive definition that emphasizes statistical properties like scale invariance:
This is a symbolic representation indicating that the variance of scales with , but does not cover the integral structure and stochastic rigor of the MvN representation.
Conversely, uses a Lévy noise term instead:
and are self-similar stochastic processes with stationary increments but differ in their statistical properties. is a Gaussian process characterized by continuous, non-differentiable paths and finite variance. It exhibits long-range dependence when the Hurst exponent H and its increments follow a normal distribution, leading to light-tailed behavior. In contrast, generalizes by replacing Gaussian noise with Lévy-stable noise, allowing for heavy-tailed, power-law-distributed increments. This substitution introduces discontinuities in the time series and results in infinite variance when the Lévy stability index . While and are self-similar with the scaling relationship
The interpretation of the Hurst exponent differs in depending on the influence of α. The choice between and should therefore depend on whether the data exhibit heavy tails, discontinuities, or rare extreme fluctuations. The distinction between and is important for biosignals and for interpreting for instance heart rate complexity and the choice of HRV analysis features, where assumptions of stationarity and Gaussianity do not hold. Time series features associated with HRV, which for traditional time and frequency domain metrics is assumed to be linear, is usually divided into 5-min windows, which provides a stationary signal and allows frequency domain and fractal spectral dimension analysis [92–96]. However, the difference in practice is that may capture persistent correlations under linear assumptions, while provides a more appropriate framework as heart rate dynamics exhibit abrupt changes, heavy tails, or nonlinear multifractal scaling features [97]. In addition, maintains self-similarity and supports multifractality and modeling of heterogeneous scaling, through its nonlinear dependence on α (tail thickness) and the Hurst exponent (memory) [97]. Wavelet-based methods are better suited for nonlinear, nonstationary time signals and can quantify multifractality from the wavelet coefficients [98].
2.3.2 Wavelet-based fractal analysis
Wavelet-based fractal analysis, particularly the wavelet transform modulus maxima (WTMM) method, extends traditional fractal measures by capturing both time and frequency information. This multifractal analysis detects singularities in a signal by applying the continuous wavelet transform (CWT) and estimates the local scaling properties at different resolutions using the scaling of the modulus maxima of the transform across scales. As WTMM provides high temporal resolution, it is ideal for transient and non-stationary signals. The method is also more robust to noise compared to DFA, but computationally intensive and requires careful selection of the wavelet function [99]. The continuous wavelet transform (CWT) of a signal for a wavelet is given by:Where is the wavelet transform of the signal at scale and position . is the Mother wavelet and its complex conjugate. (1/√a) is then the normalization factor to preserve energy across scales. To analyze multifractality, the partition function is computed over wavelet modulus maxima:Where is the partition function summed over all local maxima of at scale . is the moment order. is the scaling exponent function that characterizes multifractality and maxima(a) with localmaxima positions of at scale . The use of the partition function , when derived from the maxima lines of the wavelet modulus , represents an effective framework for determining multifractality quantitatively, as it directly links scaling behavior across moments to the multifractal spectrum via the scaling exponent [98,100,101].
2.3.3 Higuchi dimension
The Higuchi algorithm quantifies the complexity of a signal by assessing how the curve length changes as a function of the observation scale. The Higuchi method begins by constructing new sub-series from the original signal using a delay parameter , where each sub-series is defined as:
for . For each sub-series, the length is computed by summing the absolute differences between points separated by samples, normalized by a scaling factor to account for the number of terms:
The average length is then calculated across all . The slope of the linear regression of versus provides the Higuchi fractal dimension as:
Although there is often a pronounced linear range in the double logarithmic plot, the fractal range must still be selected. More recent work on time series has suggested a second type of fractal feature, defined as crucial events that are also a function of a power law and derived from converting the time series into a diffusion process [102].
2.3.4 Crucial events and the nature of 1/f noise
A significant development in fractal physiology has been the recognition of crucial events, which disrupt self-similar patterns in time-series data [103–106]. Unlike traditional fractal models, which assume continuous self-similarity, crucial events introduce non-ergodic, intermittent bursts of activity that influence system dynamics [107]. These events play a key role in heart rate variability and neural oscillations, affecting the interpretation of fractal measures in clinical diagnostics [20]. Closely related to crucial events is the concept of noise, a scaling phenomenon observed in numerous biological and cognitive systems [108]. The research on crucial events has now extended the concept of fractal from a Type I noise which originates from stochastic, memoryless fluctuations, characteristic of fractional Brownian motion to Type II noise, arising from self-organized criticality and extended to self-organized temporal criticality, where fluctuations reflect an adaptive, regulatory temporal process [109]. The failure to differentiate between Type I and Type II noise has led to misinterpretations of biological time series, particularly in studies of EEG dynamics and autonomic function [20].
2.3.5 Limitations of fractal analysis and time-series data interpretation
While fractal analysis has proven useful in spatial and morphological studies, its application to time-series data introduces additional complexities. Time-series fractal analysis is commonly used to study physiological signals (EEG, ECG, HRV), financial markets, and ecological trends, but poses challenges, including non-stationarity, as many biological and economic time-series datasets do not exhibit a constant mean or variance over time, making conventional fractal analysis methods unreliable [110–115]. Scaling relationships in time series often show upper and lower bounds, beyond which self-similarity breaks down [75,116,117]. Distinguishing between true self-similarity and random processes (e.g., Type I vs. Type II 1/f noise) remains an active area of research [20,56,118,119]. Many traditional fractal analysis methods, such as box-counting, assume a well-defined structure within an image or dataset, which does not always translate well to nonlinear and self-affine time-series data. Multifractal detrended fluctuation analysis (MF-DFA) has been introduced to account for these variations but remains sensitive to preprocessing techniques and data resolution, leading to the proposal of diverse multiscaling applications such as multiscale Rényi entropy, multiscale diffusion entropy, and DFA [20–30]. DFA is multiscale in the way it is implemented.
2.4 Spatial fractal analysis in 2D and 3D
Fractal geometry is widely used to describe structures of two-dimensional (2D) and three-dimensional (3D) images, which present unique methodological challenges. In 2D fractal analysis, box-counting and perimeter-based techniques are commonly employed to assess the self-similarity of biological forms, plant venation patterns, and coastline structures [13,17,120–122]. In contrast, 3D fractal analysis extends these principles to volumetric datasets, requiring voxel-based segmentation and multi-scale algorithms to quantify complexity in medical imaging, bone morphology, and neural connectivity studies [123–127]. These images are characterized by a lack of infinite length and are not strictly space-filling, though they may optimize coverage through fractal-like growth patterns [128–130]. This distinction is essential to avoid misclassifications or misinterpretation of natural structures as true fractals when they are more accurately described as approximations of fractal behavior and scale invariant rather than self-similar. Recent advances have now included features such as lacunarity as an additional feature describing the space-filling characteristics of objects [17,131–133].
2.5 Distinguishing true and apparent multifractality
Multifractality refers to multiple scaling exponents within a time series, suggesting that different dynamic processes operate at different scales. This phenomenon is widely observed in physiological signals, yet accurately quantifying multifractality remains a major challenge [20,127]. One of the key issues is that preprocessing techniques, such as detrending and filtering, may artificially introduce correlations, leading to overestimating multifractal properties [20,134,135]. Three additional shortcomings are the reduction of the artificial multiscale entropy (MSE) due to the coarse-graining procedure, the fixed cut-off for histogram binning, and the introduction of spurious MSE oscillations due to the suboptimal procedure for the elimination of the fast temporal scales [21,134,136]. Artifacts due to signal distribution, autocorrelation, or nonstationarity need to be addressed to identify true multifractality by including null models or shuffled or phase-randomized surrogate data that highlight whether the multifractal spectrum is retained [137]. True multifractality arises when a stochastic process intrinsically exhibits a spectrum of singularities due to multiplicative cascades or multiscale interactions. It is marked by a nonlinear dependence of the generalized Hurst exponent, or scaling exponent on the moment order , leading to a broad multifractal spectrum . This behavior is robust to surrogate testing, persisting under methods like amplitude adjusted Fourier transform (IAAFT) or phase-randomized surrogates that preserve linear structure but disrupt higher-order dependencies. Apparent multifractality, by contrast, mimics this behavior due to artifacts such as finite-size effects, heavy tails, or nonstationarity. While such signals may exhibit curvature in under MF-DFA or structure-function methods, this effect often vanishes under surrogate testing, indicating the absence of genuine multiscale complexity [138–140].
However, distinguishing true from apparent multifractality does not address another fundamental issue of multifractal analysis, which is associated with how multifractality is interpreted. A striking example of the dichotomy in definitions across disciplines is associated with the fields of economics, finance, and econometrics, where multifractality is often operationalized through the time-varying Hurst exponent, or the Hölder exponent , which is estimated using sliding-window techniques or local detrending procedures. This approach characterizes nonstationarity or regime-switching in market dynamics by tracking local scaling exponents [141,142]. In contrast, physics-based disciplines, including physiology, geophysics, biophysics, and sociophysics, emphasize that multifractality reflects the presence of a spectrum of singularities within a signal or process. This spectrum is then quantified through the multifractal spectrum , implying that the signal possesses a hierarchy of scaling behaviors rather than a single dominant exponent [143–147].
This distinction reflects deep epistemological differences as the econometric approach treats the Hurst exponent as a local, potentially nonstationary parameter, and detached from a strict theoretical model of scale invariance [148,149]. By contrast, in physics, multifractality arises from inherent self-organization and the aggregation of fluctuations across scales, often associated with self-organized criticality (SOC) or self-organized temporal criticality (SOTC) [150]. These frameworks interpret multifractal behavior as a signature of far-from-equilibrium dynamics with embedded memory and complexity [20,151,152]. Thus, complementary interpretations may provide utility in specific applied domains. However, in this work, a multifractal process is described as one that gives rise to a hierarchy of scaling exponents, characterized by a nonlinear relationship between the moment order and the scaling exponent , with the multifractal spectrum derived via Legendre transformation. This interpretation aligns with empirical findings across physiological, linguistic, and sociocultural time series, where complex coordination dynamics and long-range dependencies generate nontrivial scaling spectra.
In addition to the distinction between local Hölder exponent tracking (common in econometrics) and multifractal spectrum analysis (prevalent in physics), another widely used definition of multifractality involves the generalized Hurst exponent , which characterizes the scaling behavior of the order moments of the process. Specifically, for a stochastic process , the structure function
typically scales as . For monofractal processes, is constant across all , indicating uniform scaling. In contrast, a multifractal process exhibits a nonlinear dependence of on , reflecting the presence of multiple scaling regimes and heterogeneous singularities. Multifractal detrended fluctuation analysis (MF-DFA), which estimates empirically from detrended local fluctuations is based on this formalism. The nonlinear shape of the curve or its associated mass exponent function is often used to quantify the degree of multifractality. The corresponding multifractal spectrum can then be obtained by applying the Legendre transformation, where . Thus, the generalized Hurst exponent approach bridges the statistical physics and signal processing perspectives, offering a versatile framework for detecting and characterizing scale-free structures in both stationary and nonstationary signals [140,153,154]. Importantly, this interpretation also connects non-Gaussianity and intermittency where a broader spread or curvature in the function implies the presence of strong fluctuations (bursts or laminar phases) that contribute disproportionately to high-order moments. This makes the generalized Hurst exponent particularly relevant in the analysis of physiological, linguistic, and financial time series, where empirical signals often reveal multifractal characteristics not captured by a single global exponent [98,101].
2.6 Validation strategies and scale selection protocols
Applying fractal and multifractal methods for spatial and time series analysis, validation of the scaling metrics is one of the most important components. Determining the appropriate scale invariance of an object or time series reflects the intrinsic property of the system. Noise, artifacts, and inappropriate preprocessing influence the scale range that is fundamental to characterizing fractality. Linearity of the log-log plot over a minimum of one to 2 decades provides a meaningful result. This is achieved by ensuring scale boundaries are correctly chosen to avoid short-range correlations (e.g., noise) or finite-size effects at long scales. Automated range selection based on R2 optimization or slope stability criteria has been recommended [155–160]. Surrogate analysis can be applied to validate the scaling results, including shuffled time series and phase-randomized Fourier surrogates to preserve linear autocorrelations but remove nonlinear structure. For DFA, comparing the α exponent or multifractal width Δα between the original and surrogate time series provides a means of assessing whether the observed complexity exceeds what may be expected by chance. Sensitivity analysis, such as detrending polynomial order in DFA, embedding dimension, correlation dimension estimation, and q-range determination in multifractal analysis, as well as stationarity testing, further supports the validity of results [24,161–163].
2.7 Practical implementations of fractal analysis in applied domains
Practical implementations or strategies have been proposed to improve the reliability and reproducibility of fractal and multifractal analysis. Associated with the physiological time series analysis, several preprocessing protocols have been developed to ensure stationarity before applying methods that are sensitive to nonstationarity, such as DFA [65,92,164]. Consistency of complexity metrics has been investigated to understand the influence of the underlying mathematical algorithms [165–167]. In geophysics, embedding time windows and applying correlation dimension together with entropy measures for assessing seismic precursors has improved predictability based on fractal analysis [168]. Recent analysis protocols in neuroscience and stock market analysis have emphasized the use of multifractal detrended fluctuation analysis and sliding window applications to identify changes associated with changes in task performance [169–172]. Local stationarity testing, time-varying complexity profiling, and hybrid decomposition-scaling approaches provide more context-sensitive, translatable, and interpretable fractal analysis results across diverse applications.
3 Fractal linguistics and cross-disciplinary communication
Scientific communication ensures that concepts, methodologies, and results are accurately described across disciplines. The interdisciplinary nature of fractal analysis presents a particular challenge in this regard, as the concept of fractals has been adapted across diverse research fields, including mathematics, physics, biology, cognitive science, and artificial intelligence [116,173]. However, despite the apparent universality of fractal theory, its application in non-mathematical disciplines often results in inconsistent terminology and methodological ambiguity. The precise meaning of terms such as fractal dimension (), self-similarity, and scale invariance are often diluted when applied outside their mathematical origins, leading to conceptual drift and misinterpretations [14,116,174].
One of the core difficulties in applying fractal analysis across disciplines is the variability in definitions. For instance, while mathematical fractals exhibit strict self-similarity across scales (e.g., the Mandelbrot set, Koch curve, or Peano curve), natural fractals such as branching trees, neuronal structures, or vascular systems are statistically self-similar or defined as scale-invariant and do not conform to infinite recursion as is the case in mathematical, ideal, theoretical fractals [175–177]. From a computer representation perspective, even theoretical fractals with infinite self-similar scaling will have limitations. Hence, in biomedical applications, fractal-based models employed in image processing, signal analysis, and physiological modeling lack standardization, which has led to conflicting interpretations of what constitutes a fractal object [178,179].
From the above discussion, it becomes clear that there is an inconsistent use of fractal terminology and how analytical methods are applied to determine the fractality of spatial and temporal features across disciplines that have contributed to some extent to a semantic drift, where mathematical rigor is diluted in applied sciences. A lack of precise definitions in fractal-based biomedical research has led to numerous innovations in determining the fractal dimension of scale-invariant images or nonlinear characteristics in time series and confusion in interpreting results. Fractal linguistics, therefore, seeks to establish a standardized lexicon that preserves mathematical accuracy while facilitating interdisciplinary communication.
3.1 The challenge of fractal literacy and communication barriers
Fractal analysis is applied across multiple scientific disciplines, yet its conceptual complexity and specialized language create barriers to effective interdisciplinary communication. As scientific communities form around fractal research, a process of professional socialization occurs, leading to the development of distinct linguistic norms. This specialization, while beneficial within specific domains, contributes to communication gaps between different research communities [
176,
180]. To better understand the diversity of fractal analysis expertise, researchers can be classified into three broad categories:
1. Researchers with expertise in other domains, such as biology, medicine, or social sciences, who have a strong background in mathematics or physics but lack in-depth fractal theory training. These researchers often rely on published methodologies but may struggle with the nuances of fractal interpretation.
2. Experts in fractal and scaling theory, who possess a deep understanding of its mathematical foundations [57,111,144,146,181–186]. This group establishes a unique identity through its specialized discourse, reinforcing its authority in the field.
3. Interdisciplinary bridge-builders, who aim to develop and disseminate tools for fractal analysis in an accessible manner [18,22,116,124,129,187–194]. Ideally, this category consists of members from the second group working to improve knowledge transfer to the first group.
Despite the presence of category Interdisciplinary bridge-builder researchers, a significant gap remains between fractal theory specialists and applied researchers. The core issue lies in the clarity and accessibility of scientific communication. Many fractal specialists are a part of their specific research discourse and find it challenging to translate their knowledge into a more universally understandable format. Consequently, applied researchers with expertise in other domains, and acquiring literacy in fractal methods, often misinterpret or propagate inaccuracies in terminology and methodology. One of the primary risks in this process is that terminology is adopted without a complete understanding of its mathematical implications.
For meaningful interdisciplinary progress, experts in fractal analysis and researchers with expertise in other domains must prioritize clearer dissemination of fractal principles, ensuring that foundational knowledge is communicated effectively. This includes not only publishing in specialized journals but also contributing to open-access resources and interdisciplinary review articles that cater to broader scientific audiences. The section below provides an example.
3.2 The case of diffusion-limited aggregates and fractal misinterpretations
The challenges in fractal research applied to image analysis are exemplified by the case of diffusion-limited aggregates (DLAs), a phenomenon resulting from stochastic growth processes with potential applications in biology, chemistry, and materials science. While physicists have extensively studied DLAs, debate continues over their precise fractal classification [100,195–199]. Key questions that remain unresolved are whether DLAs are strictly self-similar and whether DLAs are multifractal [200,201]. Most publications addressing DLAs are authored by physicists and published in physics journals, reinforcing an insular discourse that limits broader interdisciplinary application. Biological sciences, despite their potential to benefit from fractal modeling, have not embraced fractal analysis to the same extent as physics and engineering. This is largely due to the lack of clear instructional resources that articulate the theoretical underpinnings and applied methodologies in an accessible manner.
4 Addressing the gaps in fractal education and communication
A crucial missing element in fractal research is the documentation of how researchers acquire fluency in fractal theory and its applications. Specialists in the field must articulate how meaning is constructed and communicated in fractal analysis. Standardized educational resources, interdisciplinary training workshops, and accessible computational tools can help bridge the gap between theory and application [
20,
202,
203]. To foster more effective knowledge transfer, future efforts should focus on:
1. Developing interdisciplinary educational frameworks that introduce fractal concepts to non-specialists in an intuitive manner [204,205].
2. Encouraging cross-domain collaboration to refine methodologies and establish consensus on terminology and interpretation [18,19,206].
3. Creating open-access repositories that provide validated computational tools and datasets to ensure methodological reproducibility [35,207].
By improving the clarity, accessibility, and applicability of fractal discourse, the research community can enhance the interdisciplinary impact of fractal analysis across physics, engineering, biology, and cognitive sciences. The next section discusses some of the issues with terminology.
4.1 Refining fractal concepts for interdisciplinary understanding
This section does not aim to provide an exhaustive glossary of fractal terminology but rather to address common misconceptions and clarify foundational concepts. What is a fractal, and how is fractal analysis conducted? Understanding fractals begins with identifying their defining properties.
4.2 Describing fractals and their attributes
A frequently misused term in describing fractals is “roughness”. While commonly used to express irregularity, roughness in fractal linguistics corresponds more accurately to surface complexity and space-filling capacity rather than a simple deviation from a mean value [11,208,209]. In contrast, fractal dimension (DF) quantifies how an object’s size (length, area, or volume) varies with measurement scale [14,124,173,181,209]. Unlike Euclidean shapes, fractals exhibit irregular surfaces at all scales of magnification and lack a characteristic length [3,12,116,210].
To better characterize fractal properties, three attributes are particularly important:
1. Characteristic length–non-fractal objects can be described using simple geometric shapes (e.g., the Earth as a sphere). The presence of a characteristic length implies a smooth surface.
2. Self-similarity/scale invariance–Fractal objects maintain a repeating pattern at different magnifications. The Koch curve exemplifies this principle for a theoretical fractal, lacking a characteristic scale at every iteration. The Koch curve and other mathematically based objects are self-similar to a limit based on the computer screen resolution.
3. Complexity–The fractal dimension, DF, quantifies the extent to which an object fills space. Higher values of DF indicate greater space-filling properties or more complexity.
Self-similarity in fractals implies that increasing magnification does not introduce new structural changes but instead reveals finer details of the same underlying pattern. The degree of scale-invariance in a biological structure can be quantified through fractal analysis, where the gradient of a log-log plot of count number versus scale is proportional to its fractal dimension [156,158,159,211,212].
4.3 Fractal measurement and complexity quantification
The mathematical formulation of fractal measurement follows a power-law relationship where DF is the fractal dimension and N(e) is the number of measurement units at scale e. For the Koch curve, DF ≈ 1.246, indicates a structure more complex than a simple line. A structure with D = 1.2 is less space-filling than one with D = 1.4 [128,213]. A practical challenge in fractal analysis is differentiating between statistical self-similarity (scale-invariance) and true fractality [214,215]. Many biological structures (e.g., lung bronchi, blood vessels, neurons) exhibit statistical self-similarity branching, which may suggest fractal properties, but they are not fractal in the strict mathematical sense [56,177,216–221]. Instead, they are statistically self-similar within a finite range of scales [210]. Furthermore, signals as well as 2D digital images and 3D volumes always have a limited resolution, so that the true fractality can never be determined. A digital image in medicine, for example, rarely has more than 1000 × 1000 pixels. That is one million pixels, but the effective physical range of scales is only three, with 10 × 10, 100 × 100, and 1000 × 1000, or four including the rather questionable scale 1 × 1. Even for very inconvenient images of size 10,000 × 10,000 pixels, the physical range of scales is only increased by 1 decade. Whereas a true or mathematical fractal is self-similar over an infinite range of scales, digital signals and images can only be investigated by the very limited range of three or 4 decades of physically relevant scales.
4.4 Correct classification of the object under investigation
Each object has an intrinsic topological dimension (DT) and is embedded in a space of dimensions, the embedding dimension (DE). From this, it follows that the fractal dimension DF of the object must always be in between these two limits, following DT<=DF<=DE. The topological dimension is defined by the number of directions of neighboring points. For example, a line has only one preceding and one subsequent neighboring point and has therefore DT = 1.
A thin but folded or wrinkled line drawn on a sheet of paper has DT = 1, and also a thin woolen thread folded in 3D has DT = 1, because the neighboring relations do not change. In this example, the sheet of paper is two-dimensional and defines the embedding dimension, which is DE = 2. The woolen thread in 3D space represents an embedding dimension of DE = 3. Despite that, a line is a topological one dimensional, it can have fractal dimensions from 1 up to 2 or from 1 up to 3, depending on the embedding dimension, see Figure 1. In a 2D digital image, the embedding dimension is DE = 2 for binary images and DE = 3 for grey value images. Objects in digital images can be points with DT = 0, lines with DT = 1, or areas with DT = 2. If cells are imaged so small in a medical image that they are represented by points, the fractal dimension can have values from zero up to two. 3D digital volumes increase the possible embedding dimension by one.
FIGURE 1
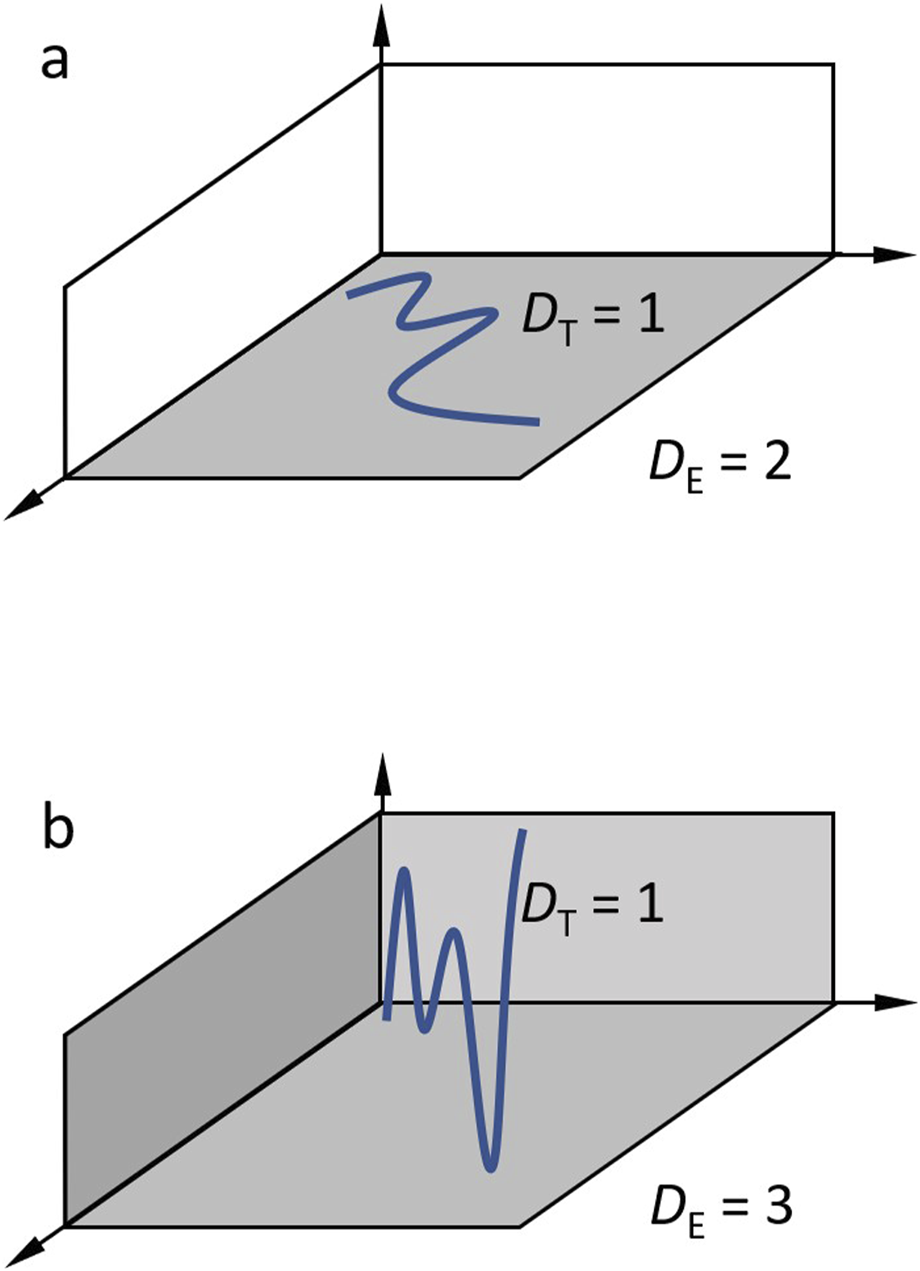
Illustration of topological and embedding dimension. (a) A topological 1D line is embedded in a 2D space. Fractal dimensions of the line can be between one and 2. (b) 3D embedding space. Fractal dimensions can be between 1 and 3.
4.5 Misconceptions and the role of prefractals
A crucial distinction in the fractal analysis is between true fractals and prefractals. Prefractals are approximations of fractals observed at finite iterations rather than infinitely repeating structures [207,222,223]. The Koch snowflake can serve as a useful test image for calibration but is not strictly fractal due to its finite nature when represented as an image due to the resolution limits of the computer [210]. When analyzing biological structures, using Euclidean reference objects (e.g., spheres, cubes) provides a baseline for comparison, but fractal-like forms require specialized methodologies. The challenge in fractal measurement lies in ensuring that the observed scaling relationship remains consistent across magnification levels. Statistical artifacts from image resolution, filtering, or incomplete iterations can lead to misclassification of biological structures as a fractal [131,156,157,224].
4.6 Self-similarity and biological forms
The broad use of the term self-similarity in biological contexts has contributed to confusion. In mathematical fractals, strict self-similarity means that identical patterns occur across all scales. However, biological systems exhibit statistical self-similarity, meaning that their scaling behavior follows probabilistic rather than deterministic patterns. This distinction is critical, as many biological forms including vascular networks and dendritic structures have been incorrectly classified as fractal when they merely exhibit scaling tendencies within a specific range [156]. A biological form should only be classified as fractal if its measured size follows a consistent power-law relationship across all scales, without a characteristic length limit. This is rarely the case in real-world biological systems [156,225]. How this may be addressed follows in the next section.
4.7 Defining surfaces, boundaries, and dimensional analysis
A critical consideration in 2D and 3D fractal analysis is the distinction between a surface, boundary, or perimeter in 2D and 3D structures and the determination and/or fixation of the topological dimension DT [226,227]. A 2D boundary may represent the outermost silhouette of an object, as seen in fractal analyses of particle aggregates, whereas a 3D surface may include internal complexity, requiring different analysis techniques such as volume fractals and porous fractals [5,123,159,228–230]. For instance, silhouette-based fractal analysis of biological aggregates has been employed to quantify sludge morphology, but results can differ depending on whether the boundary or mass is analyzed. Estimates of silhouette boundaries tend to yield lower fractal dimensions compared to sectioned boundaries, highlighting the importance of defining measurement criteria [124,157,231]. Finally, any values of fractal DF smaller than DT are not reliable. And one must be aware of the actual embedding dimension DE, because any values of DF exceeding DE are also not reliable.
5 Operationalizing fractal linguistics: a taxonomy and validation framework
To advance fractal linguistics from a conceptual critique to a practical, cross-disciplinary tool, a comprehensive taxonomy and validation framework designed to identify, classify, and resolve inconsistencies in fractal analysis is required. The proposed framework aims to standardize terminology, standardize methodologies without impeding new developments, and enhance interpretability across diverse fields of research. By providing a structured approach to fractal analysis, the framework promotes clearer communication, improves reproducibility, and enhances the translational potential of fractal measures in applications ranging from biomedical diagnostics to environmental modeling and seismic forecasting. The model framework includes semantic drift identification, methodological variability audit, and interpretation mapping. A prototypical application of the taxonomy is illustrated in Table 1.
TABLE 1
| Term | Original definition | Common misuse | Framework correction |
|---|---|---|---|
| Fractal Dimension | Power-law scaling exponent between object size and measurement scale | Proxy for texture or complexity without scale verification | Requires scale range validation and topological embedding check (DT ≤ DF ≤ DE) |
| Self-similarity | Exact structural invariance across scales | General repetition or irregularity | Specify exact vs. statistical vs. apparent self-similarity |
| Roughness | Surface irregularity is described via standard deviation or amplitude | Equated with the fractal dimension | Disambiguate via lacunarity or the Minkowski cover method |
Prototypical application of the fractal linguistics taxonomy to address semantic drift, methodological variability, and interpretation issues for key fractal terms.
Semantic drift occurs when fractal-related terms diverge from their original mathematical definitions as they are adopted across disciplines. This component of the taxonomy systematically traces and quantifies such divergences to restore terminological precision by identifying the definition of the term as established in mathematical fractal theory, documenting how the term is repurposed in applied disciplines, and developing qualitative or quantitative measures to assess the extent of drift. Practical implementation of semantic drift identification can be achieved through interdisciplinary workshops where domain experts and mathematicians collaboratively review terminology usage. Automated tools, such as natural language processing (NLP) algorithms, can scan literature databases to flag inconsistent definitions, enabling researchers to align their terminology with mathematical foundations. By clarifying terms like fractal dimension or self-similarity, this component addresses the communication gaps between mathematicians, who prioritize rigor, and applied scientists, who often adopt terms heuristically. See Table 2 for examples.
TABLE 2
| Authors | Discipline | Improving operational clarity |
|---|---|---|
| Biomedical HRV | ||
| [60] | Detrended Fluctuation Analysis: Introduced DFA with sound theoretical grounding. Scaling exponent α applied rigorously could have included surrogate tests or local stationarity checks. Higher-order detrending may have provided a more in-depth perspective and explored multifractality more fully | |
| [92] | DFA α1 calculated over very short segments of the time series (<15 s). Improvement requires validating power-law linearity for such short segments from a mathematical perspective | |
| [76] | Contextualized comparison between fGn vs. fBm. Clarifies DFA methodology. Possibly included examples of misclassification and defined preprocessing limits or scaling range guidance more clearly. Leaves room for semantic drift in interpreting α as a complexity measure | |
| [232] | Interpreted DFA scaling exponents in a physiologically broader context and validate more clearly the fundamental assumptions required for fractal interpretation | |
| [167] | DFA α1 applied to short-term HRV segments without validating scaling range or stationarity. α1 is interpreted as a nonlinear feature, reflecting a possible semantic drift due to the inherent methodological restrictions in DFA. | |
| [30] | Postulated requiring extending preprocessing details and possible surrogate data validation | |
| [233] | Addressed parameter sensitivity in Higuchi dimension analysis, warns of noise-induced dimension inflation. Requires reporting on multidecade scaling validation and broader method comparison | |
| Geophysics | ||
| [49] | Presented fractal dimensions and power-law distributions as evidence of fractality. Clearer mathematical or statistical requirements for scale invariance, stationarity, or multifractality could have been included | |
| [168] | Non-stationarity and identifying fractality via log–log plots have included optimal fitting of a regression line. Comment on the use of correlation dimensions estimated from short datasets. Separate the terms chaos and fractality | |
| [234] | Empirical testing has improved the message of the proposed SOC-based model. Uses “fractal” heuristically without computing dimensions or verifying scale invariance | |
| [235] | Required the scaling range needs to be verified when applying power-law and box-counting methods to assert fractality. Assumes stationarity and spatial representativeness. No time-series-based validation | |
| [236] | Reporting estimates of spatial fractal dimensions using box-counting could be improved by testing scale invariance, error estimation, or considering resolution effects, which may lead to misinterpreting fractal characteristics | |
Comparative Heart rate variability and geophysical fractal analysis studies.
Fractal analysis employs a variety of methods, such as box-counting, detrended fluctuation analysis (DFA), wavelet transforms, entropy measures, point processing and Higuchi’s algorithm, each with multiple implementation variants. These variants can lead to divergent outcomes, reducing comparability across studies. The methodological variability audit addresses this challenge through cataloging the specific fractal analysis method used, documenting variations in implementation, and conducting checks of robustness to evaluate how methodological choices affect results [237,238]. Practical implementation of the audit is already available and supported by open-access datasets and repository internet sites such as GitHub, which host computational tools and protocols for fractal analysis. Python or MATLAB libraries (e.g., https://www.mathworks.com/matlabcentral/fileexchange/71770-fractal-analysis-package; https://nolitia.com/; https://tsfel.readthedocs.io/en/latest/) can also provide reference implementations of DFA or box-counting, and include built-in sensitivity analysis modules to quantify the impact of parameter variations [239,240]. Researchers would be encouraged to report method-specific details in publications, adhering to a checklist derived from the audit framework [121,156,157]. This component ensures methodological transparency and reproducibility, which are critical for fields like biomedical engineering, where fractal analysis of heart rate variability (HRV) may use DFA with varying detrending orders. By standardizing reporting, the framework enables meta-analyses and cross-study comparisons, facilitating the development of universal benchmarks for fractal measures in physiological systems [241].
The last section of the framework addresses the interpretation of fractal analysis results, which often relies on implicit assumptions that may not hold across contexts, leading to overgeneralization or misinterpretations [242]. This component maps reported conclusions to their underlying assumptions and realigns them with the proposed framework to ensure validity. To achieve this, it is necessary to identify the reported findings of the study, explicitly articulating assumptions underpinning the interpretation, and adjusting interpretations based on validated assumptions. Practical implementation of interpretation mapping can be integrated into peer-review processes, where reviewers use standardized checklists to evaluate the alignment between claims and assumptions. Computational tools can assist by embedding diagnostic tests into fractal analysis pipelines, which provide researchers with feedback on the validity of their interpretations. This component has the potential to enhance the reliability of fractal-based conclusions in applied domains.
Table 1 demonstrates the application of the taxonomy to three key terms, highlighting their original definitions, common misuses, and proposed corrections. The table serves as a template for researchers to apply the framework to other terms and contexts.
The Supplementary Table 1 provides a more extended Glossary of terms that provides additional definitions, meant as a further guide to applying appropriate fractal terminology. The proposed taxonomy and validation framework enhances cross-disciplinary understanding and practical applications of fractal analysis by addressing semantic drift, methodological variability, and interpretation challenges. It ensures consistent use of terms like fractal dimension and self-similarity, improving communication across fields like biology, neuroscience, and environmental science. For example, it clarifies whether biological structures like vascular networks exhibit statistical or true fractality, ensures transparent documentation in EEG signal analysis, and validates scaling claims for coastal management. The framework aims to standardize reporting, enhance reproducibility, and support reliable applications, such as in biomedical diagnostics for diabetic retinopathy. It can also serve as an information tool, guiding non-specialists through fractal terminology and methods via workshops and resources. Future efforts should focus on developing computational tools, user-friendly software, interdisciplinary consensus guidelines, open-access educational materials, and validated data repositories to promote fractal literacy and reproducibility. This structured approach preserves mathematical rigor while enabling innovative solutions for complex natural and physiological systems.
5.1 Validation across disciplines: HRV and earthquake models
To validate the usefulness of this framework, we conducted a preliminary comparative analysis across two disciplines: biomedical signal processing, including heart rate variability (HRV), and geophysics, specifically earthquake models.
In HRV research, the term “fractal dimension” is often used interchangeably with measures of signal complexity, including Higuchi and Katz dimensions or DFA exponents, often without verifying scale-invariance or embedding dimension assumptions [31,60,111]. In contrast, geophysical models apply fractal statistics to seismic fault distributions and aftershock sequences, frequently assuming long-range correlations and multifractality, yet rarely assess stationarity or artifact influence [49,168,234].
By applying the proposed taxonomy, we reclassified methods and terminology in five key studies from each domain (Table 2). This revealed that in over 60% of HRV studies, reported scaling exponents reflected preprocessing artifacts or misapplication of DFA without proper data stationarity checks. Similarly, in geophysics, inconsistent use of the term “multifractal” emerged due to insufficient analysis of scale windows and spurious correlations introduced through detrending.
A review of the pivotal contributions to the field of fractal analysis, including the authors of Table 2 indicates the expanding interdisciplinary research in applying fractal-based analyses to natural and physiological systems (See also Supplementary Table 2). These studies have laid critical groundwork for modeling complexity, yet there is significant potential to advance fractal analysis methodology, reporting, and understanding of physical and biological systems by operationalizing a standardized framework that enhances clarity and precision. By adopting consistent reporting of scaling ranges, rigorous statistical validation of fractal dimensions, and clear differentiation between multifractality, long-range dependence, and stochastic variability, researchers can improve methodological robustness. Practical steps, such as integrating surrogate testing, resolution sensitivity analysis, and explicit log–log scaling diagnostics, will reinforce the fractal nature of the observed dynamics. Furthermore, refining the semantic precision of terms like “fractal” and “scale-free” by defining them through entropy-based metrics will lead to enhanced cross-disciplinary interpretability. These advancements will have an impact on translational opportunities that drive innovation in fields such as seismic forecasting, biomedical diagnostics, and networked system modeling, while promoting a unified and accessible fractal linguistics framework.
5.2 Key challenges in fractal linguistics
The variability in definitions across diverse fields includes terms like fractal dimension and self-similarity, which are used inconsistently and do not consider scale-invariance, the correct term to describe natural objects. Methodological uncertainty is perhaps the most challenging due to the plethora of computational methods available on the internet and in-house coding, which often generates fractal parameters without clarifying their theoretical foundations. Finally, overgeneralization, which addresses the assumption that all self-similar structures exhibit fractal properties, has resulted in the overuse of fractal models in biology and medicine.
Future research needs to consider prioritizing clearer definitions, interdisciplinary collaboration, and standardized methodologies in fractal-based studies to address these issues [180,202,243]. The current paper addresses some of these issues to fully realize the potential of fractal analysis in modeling complex systems. This requires greater emphasis on fractal analysis descriptions and definitions, especially in biological and clinical sciences. By establishing a linguistics model, which integrates correct descriptions of spatial, temporal, and multifractal approaches, the accuracy and reliability of fractal models can be improved [8,20,225]. The emerging field of fractal linguistics provides a framework for refining terminology, standardizing methodologies, and improving interdisciplinary discourse [11].
6 Conclusion
Fractal analysis is a versatile tool for quantifying the complexity of spatial structures and time series data. However, inconsistent terminology, methodological variability, and interpretation ambiguities reduce the effectiveness of the results and lead to semantic drift and communication barriers across multidisciplinary projects. This paper provides a critical commentary on the evolving usage of fractal and multifractal terminology in the analysis of complex systems and examines how foundational concepts such as fractional Brownian motion (), self-affinity, and multifractality have been adapted, reinterpreted, and occasionally misapplied across disciplines. There is a growing divergence in how terms such as roughness, complexity, and scaling are understood in physics, finance, and biology. The oversimplification of the term roughness, which is a necessary but not sufficient condition for fractality, is often equated directly with the Hurst exponent and ignores the mathematical underpinning associated with scaling phenomena. A signal may be rough (e.g., non-differentiable or noisy) without being self-affine, multifractal, or long-range correlated. Clarifying this distinction is critical to avoid misleading interpretations of results. Multifractality is another ambiguous term if used in diverse contexts. As such, multifractality in econometrics may refer to time-varying Hölder exponents, while in statistical physics it implies a nonlinear spectrum arising from multiplicative cascades. There is also a need to distinguish between true multifractality, characterized by nonlinear moment scaling and a broad multifractal spectrum , and apparent multifractality, which may result from nonstationarity, fat-tailed distributions, or finite-size effects. This distinction is important for correctly describing underlying dynamical mechanisms. Throughout the manuscript, emphasis is placed on correctly applying contemporary descriptors, such as , , and , that extend the original Mandelbrot and van Ness model and incorporate non-Gaussian, nonstationary, and generalized scaling behaviors. Correct use of these terms, which are found now in mathematical and physical sciences, is necessary to prevent terminological drift.
Ultimately, this work contributes to the metatheoretical architecture of fractal analysis. It seeks to foster terminological coherence and epistemological clarity in interdisciplinary research where fractals, scaling, and complexity are described. By tracing the genealogy of key concepts and explicitly differentiating between methods, phenomena, and metaphors, we hope to motivate more rigorous and reflexive applications of fractal models in empirical science. Future work should focus on expanding this framework through transdisciplinary reflection by researchers to use fractal language with both mathematical precision and conceptual transparency. This formalization is critical for improving accuracy and enhancing cross-disciplinary communication.
Statements
Author contributions
HJ: Conceptualization, Writing – original draft, Writing – review and editing. HA: Conceptualization, Writing – original draft, Writing – review and editing.
Funding
The author(s) declare that no financial support was received for the research and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2025.1645620/full#supplementary-material
References
1.
HargittaiI. Remembering Benoit Mandelbrot on his centennial – his fractal geometry changed our view of nature. Struct Chem (2024) 35(5):1657–61. 10.1007/s11224-024-02290-9
2.
ChenY. Fractal modeling and fractal dimension description of urban morphology. Entropy (2020) 22(9):961. 10.3390/e22090961
3.
MandelbrotBB. The fractal geometry of nature. New York: Freeman and Co (1983).
4.
TaylorRSpeharBHagerhallCVan DonkelaarP. Perceptual and physiological responses to Jackson Pollock's fractals. Front Hum Neurosci (2011) 5:60. 10.3389/fnhum.2011.00060
5.
SchroederM. Fractals, chaos, power laws. New York: W. H. Freeman (1991).
6.
FalconerK. Fractal geometry: mathematical foundation and applications. 2 ed.London: John Wiley and Sons (2003).
7.
WenRSinding-LarsenR. Uncertainty in fractal dimension estimated from power spectra and variograms. Math Geol (1997) 29(6):727–53. 10.1007/bf02768900
8.
JelinekHFJonesCLWarfelMD. Is there meaning in fractal analyses?Compl Internat (1998) 6.
9.
VicsekT. Fractal growth phenomena. 2 ed.Singapore: World Scientific (1992).
10.
XueYBogdanP. Reliable multifractal characterization of weighted complex networks: algorithms and implications. Sci Rep (2017) 7(1):7487. 10.1038/s41598-017-07209-5
11.
JelinekHFJonesDWarfelMLucasCDepardieuCAurelG. Understanding fractal analysis? The case of fractal linguistics. ComPlexUs (2006) 9:66–73. 10.1159/000094189
12.
KoroljAWuHTRadisicM. A healthy dose of chaos: using fractal frameworks for engineering higher-fidelity biomedical systems. Biomaterials (2019) 219:119363. 10.1016/j.biomaterials.2019.119363
13.
RichardsonLF. The problem of contiguity: an appendix o statistics of deadly quarrels. In: WrightQLienauCC, editors. Statistics fo deadly quarrels. Pittsburgh: Boxwood Press (1960). p. 139–87.
14.
FalconerK. Fractal geometry: mathematical foundations and applications. John Wiley and Sons (2013).
15.
LandiniG. Fractals in microscopy. J Microsc (2011) 241(1):1–8. 10.1111/j.1365-2818.2010.03454.x
16.
KatzMJGeorgeEB. Fractals and the analysis of growth paths. Bull Math Biol (1985) 47(2):273–86. 10.1007/bf02460036
17.
KarperienALJelinekHF. Box-counting fractal analysis: a primer for the clinician. In: Di IevaA, editor. The fractal geometry of the brain. Cham: Springer International Publishing (2024). p. 15–55.
18.
PeptenatuDAndronacheIAhammerHRadulovicMCostanzaJJelinekHFet alA new fractal index to classify forest disturbance and anthropogenic change. Landsc Ecol (2023) 38:1373–93. 10.1007/s10980-023-01640-y
19.
ChappardDLegrandEHaettichBChalèsGAuvinetBEschardJPet alFractal dimension of trabecular bone: comparison of three histomorphometric computed techniques for measuring the architectural two-dimensional complexity. J Pathol (2001) 195(4):515–21. 10.1002/path.970
20.
JelinekHFTuladharRCulbrethGBoharaGCornforthDWestBJet alDiffusion entropy vs. Multiscale and Rényi entropy to detect progression of autonomic neuropathy. Front Physiol (2021) 11(1759):607324. 10.3389/fphys.2020.607324
21.
ValenciaJFPortaAVallverduMClariaFBaranowskiROrlowska-BaranowskaEet alRefined multiscale entropy: application to 24-h Holter recordings of heart period variability in healthy and aortic stenosis subjects. IEEE Trans Biomed Eng (2009) 56(9):2202–13. 10.1109/tbme.2009.2021986
22.
CornforthDJelinekHFTarvainenM. A comparison of nonlinear measures for the detection of cardiac autonomic neuropathy from heart rate variability. Entropy (2015) 17(3):1425–40. 10.3390/e17031425
23.
TomashinALeonardiGWallotS. Four methods to distinguish between fractal dimensions in time series through recurrence quantification analysis. Entropy (Basel). (2022) 24(9):1314. 10.3390/e24091314
24.
IhlenEAF. Introduction to multifractal detrended fluctuation analysis in matlab. Front Physiol (2012) 3:141. 10.3389/fphys.2012.00141
25.
ShiMShiYLinYQiX. Modified multiscale Renyi distribution entropy for short-term heart rate variability analysis. BMC Med Inform Decis Mak (2024) 24(1):346. 10.1186/s12911-024-02763-1
26.
MiYLinA. Kernel based multiscale partial Renyi transfer entropy and its applications. Commun Nonlinear Sci Numer Simulation (2023) 119:107084. 10.1016/j.cnsns.2023.107084
27.
NasratSAMahmoodiKKhandokerAHGrigoliniPJelinekHF. Multiscale diffusion entropy analysis for the detection of crucial events in cardiac pathology. Annu Int Conf IEEE Eng Med Biol Soc (2023) 2023:1–4. 10.1109/EMBC40787.2023.10340403
28.
FaesLFaesLPortaAJavorkaMNolloGNolloG. Efficient computation of multiscale entropy over short biomedical time series based on linear state-space models. Complex (2017) 2017:–13. 10.1155/2017/1768264
29.
BaumertMJavorkaMSeeckAFaberRSandersPVossA. Multiscale entropy and detrended fluctuation analysis of QT interval and heart rate variability during normal pregnancy. Comput Biol Med (2012) 42(3):347–52. 10.1016/j.compbiomed.2011.03.019
30.
JelinekHFCornforthDJTarvainenMPKhalafK. Investigation of linear and nonlinear properties of a heartbeat time series using multiscale Rényi entropy. Entropy (2019) 21(8):727. 10.3390/e21080727
31.
EkeAHermanPKocsisLKozakLR. Fractal characterization of complexity in temporal physiological signals. Physiol Meas (2002) 23(1):R1–38. 10.1088/0967-3334/23/1/201
32.
RoblesKERobertsMViengkhamCSmithJHRowlandCMoslehiSet alAesthetics and psychological effects of fractal based design. Front Psychol (2021) 12–2021.
33.
BiesAJBlanc-GoldhammerDRBoydstonCRTaylorRPSerenoME. Aesthetic responses to exact fractals driven by physical complexity. Front Hum Neurosci (2016) 10:210. 10.3389/fnhum.2016.00210
34.
DancaM-F. Mandelbrot set as a particular julia set of fractional order, equipotential lines and external rays of Mandelbrot and julia sets of fractional order. Fractal Fractional (2024) 8(1):69. 10.3390/fractalfract8010069
35.
AndronacheILiritzisIJelinekHF. Fractal algorithms and RGB image processing in scribal and ink identification on an 1819 secret initiation manuscript to the Philike Hetaereia. Sci Rep (2023) 13(1):1735. 10.1038/s41598-023-28005-4
36.
PeptenatuDAndronacheIAhammerHTaylorRLiritzisIRadulovicMet alKolmogorov compression complexity may differentiate different schools of Orthodox iconography. Sci Rep (2022) 12(1):10743. 10.1038/s41598-022-12826-w
37.
PatuanoALimaMF. The fractal dimension of Islamic and Persian four-folding gardens. Hum Soc Sci Commun (2021) 8(1):86. 10.1057/s41599-021-00766-1
38.
ManeraM. Perspectives on complexity, chaos and thermodynamics in environmental pathology. Int J Environ Res Public Health (2021) 18(11):5766. 10.3390/ijerph18115766
39.
WatariS. Fractal dimensions of solar activity. Solar Phys (1995) 158(2):365–77. 10.1007/bf00795669
40.
RypdalMRypdalK. Testing hypotheses about sun-climate complexity linking. Phys Rev Lett (2010) 104(12):128501. 10.1103/physrevlett.104.128501
41.
HamppFLindstedtRP. Fractal grid generated turbulence—a bridge to practical combustion applications. In: SakaiYVassilicosC, editors. Fractal flow design: how to design bespoke turbulence and why. Cham: Springer International Publishing (2016). p. 75–102.
42.
BratanovVJenkoFFreyE. New class of turbulence in active fluids. Proc Natl Acad Sci U S A. (2015) 112(49):15048–53. 10.1073/pnas.1509304112
43.
ChhabraABMeneveauCJensenRVSreenivasanKR. Direct determination of the f(alpha) singularity spectrum and its application to fully developed turbulence. Phys Rev A Gen Phys (1989) 40(9):5284–94. 10.1103/physreva.40.5284
44.
SreenivasanKR. Fractals and multifractals in fluid turbulence. Annu Rev Fluid Mech (1991) 23:539–604. 10.1146/annurev.fl.23.010191.002543
45.
HuangNHanSZhangXWangGJiangY. Effects of surface roughness and Reynolds number on the solute transport through three-dimensional rough-walled rock fractures under different flow regimes. Sci Rep (2024) 14(1):22452. 10.1038/s41598-024-73011-9
46.
DierkingI. Fractal growth patterns in liquid crystals. Chem Phys Chem. (2001) 2(1):59–62. 10.1002/1439-7641(20010119)2:1<59::aid-cphc59>3.0.co;2-4
47.
WestBJMudaliarS. Principles entailed by complexity, crucial events, and multifractal dimensionality. Entropy (2025) 27(3):241. 10.3390/e27030241
48.
El-NabulsiRA. A model for ice sheets and glaciers in fractal dimensions. Polar Sci (2025) 44:101171. 10.1016/j.polar.2025.101171
49.
TurcotteDL. Fractals and chaos in geology and geophysics. 2 ed. Cambridge: Cambridge University Press (1997).
50.
Venegas-AravenaPCordaroEGLarozeD. Natural fractals as irreversible disorder: entropy approach from cracks in the semi brittle-ductile lithosphere and generalization. Entropy (2022) 24(10):1337. 10.3390/e24101337
51.
VahabSSankaranA. Multifractal applications in hydro-climatology: a comprehensive review of modern methods. Fractal and Fractional (2025) 9(1):27. 10.3390/fractalfract9010027
52.
Rodriguez-IturbeICaylorKKRinaldoA. Metabolic principles of river basin organization. Proc Natl Acad Sci U S A. (2011) 108(29):11751–5. 10.1073/pnas.1107561108
53.
MaYHeXWuRShenC. Spatial distribution of multi-fractal scaling behaviours of atmospheric XCO(2) concentration time series during 2010-2018 over China. Entropy (2022) 24(6):817. 10.3390/e24060817
54.
YuvalBDM. Studying the time scale dependence of environmental variables predictability using fractal analysis. Environ Sci Technol (2010) 44(12):4629–34. 10.1021/es903495q
55.
KatzRWBrownBG. Extreme events in a changing climate: variability is more important than averages. Climat Change (1992) 21(3):289–302. 10.1007/bf00139728
56.
WestBJ. Complexity synchronization in living matter: a mini review. Front Netw Physiol (2024) 4:1379892. 10.3389/fnetp.2024.1379892
57.
VossASchulzSSchroederRBaumertMCaminalP. Methods derived from nonlinear dynamics for analysing heart rate variability. Phil Trans Roy Soc A: math. Phys Eng Sci. (2009) 367(1887):277–96.
58.
MaoXShangPWangJMaY. Characterizing time series by extended complexity-entropy curves based on Tsallis, Rényi, and power spectral entropy. Chaos (2018) 28(11):113106. 10.1063/1.5038758
59.
GhoshDMarwanNSmallMZhouCHeitzigJKoseskaAet alRecent achievements in nonlinear dynamics, synchronization, and networks. Chaos (2024) 34(10):100401. 10.1063/5.0236801
60.
PengCKHavlinSStanleyHEGoldbergerAL. Quantification of scaling exponents and cross over phenomena in nonstationary heartbeat time series analysis. Chaos (1995) 5(1):82–7.
61.
AshkenazyYIvanovPCHavlinSPengCKYamamotoYGoldbergerALet alDecomposition of heartbeat time series: scaling analysis of the sign sequence. Com Cardiol (2000) 27:139–42.
62.
TeichMCLowenSBJostBMVibe-RheymerK, editors. Heart rate variability: measures and models. New York: IEEE Press (2001).
63.
WehlerDJelinekHFGronauAWesselNKraemerJFKronesRet alReliability of heart-rate-variability features derived from ultra-short ECG recordings and their validity in the assessment of cardiac autonomic neuropathy. Biomed Sig Process Contr (2021) 68:102651. 10.1016/j.bspc.2021.102651
64.
Carricarte NaranjoCMarrasCVisanjiNPCornforthDJSanchez-RodriguezLSchüleBet alShort-term deceleration capacity of heart rate: a sensitive marker of cardiac autonomic dysfunction in idiopathic Parkinson's disease. Clin Auton Res (2021) 31:729–36. 10.1007/s10286-021-00815-4
65.
MarzbanradFKhandokerAHHamblyBDNgETamayoMLuYet alMethodological comparisons of heart rate variability analysis in patients with type 2 diabetes and angiotensin converting enzyme polymorphism. IEEE J Biomed Health Inform (2016) 20(1):55–63. 10.1109/jbhi.2015.2480778
66.
KhandokerAHWeissDNSkinnerJEAnchinJMImamHMJelinekHFet alPD2i heart rate complexity measure can detect cardiac autonomic neuropathy: an alternative test to Ewing battery. In: Computing in cardiology. Hangzhou, China: IEEE Press (2011). p. 525–8.
67.
OidaEMoritaniTYamoriY. Tone-entropy analysis on cardiac recovery after dynamic exercise. J Appl Physiol (1997) 82(6):1794–801. 10.1152/jappl.1997.82.6.1794
68.
PawłowskiRBuszkoKNewtonJLKujawskiSZalewskiP. Heart rate asymmetry analysis during head-up tilt test in healthy men. Front Physiol (2021) 12:657902. 10.3389/fphys.2021.657902
69.
TulppoMPMäkikallioTHSeppänenTAiraksinenJKEHuikuriHV. Heart rate dynamics during accentuated sympathovagal interaction. Am J Physiol Heart Circ Physiol (1998) 274(3):H810–6. 10.1152/ajpheart.1998.274.3.H810
70.
BrennanMKamenPPalaniswamiM. New insights into the relationship between Poincare plot geometry and linear measures of heart rate variability. Istanbul, Turkey: IEEE-EMBS (2001). Available online at: http://www.dtic.mil/cgi-bin/GetTRDoc?AD=ADA411633&Location=U2&doc=GetTRDoc.pdf.
71.
KarmakarCKKhandokerAHGubbiJPalaniswamiM. Modified Ehler's index for improved detection of heart rate asymmetry on Poincaré Plot. Comp Cardiol (2009) 36:169–72.
72.
KarmakarCKKhandokerAGubbiJPalaniswamiM. Complex correlation measure: a novel descriptor for Poincaré plot. Biomed Eng Online (2009) 8(17):17. 10.1186/1475-925x-8-17
73.
KhanMSIJelinekHF. Point of care testing (POCT) in psychopathology using fractal analysis and Hilbert Huang Transform of electroencephalogram (EEG). In: Di IevaA, editor. The fractal geometry of the brain. Cham: Springer International Publishing (2024). p. 693–715. 10.1007/978-3-031-47606-8_35
74.
HurstHE. Long-term storage capacity of reservoirs. Trans Am Soc Civ Eng. (1951) 116:770–99. 10.1061/taceat.0006518
75.
LikensADMangalamMWongAYCharlesACMillsC. Better than DFA? A Bayesian method for estimating the hurst exponent in behavioral sciences. ArXiv (2023):arXiv:2301.11262v1.
76.
EkeAHermánPBassingthwaighteJBRaymondGMPercivalDBCannonMet alPhysiological time series: distinguishing fractal noises from motions. Eur J Physiol. (2000) 439(4):403–15. 10.1007/s004249900135
77.
SchaeferABrachJSPereraSSejdićE. A comparative analysis of spectral exponent estimation techniques for 1/f(β) processes with applications to the analysis of stride interval time series. J Neurosci Meth (2014) 222:118–30. 10.1016/j.jneumeth.2013.10.017
78.
DelignièresDTorreK. Fractal dynamics of human gait: a reassessment of the 1996 data of Hausdorff et al. J Appl Physiol (2009) 106(4):1272–9.
79.
MandelbrotBBvan NessJW. Fractional Brownian motions, fractional noises and applications. Siam Rev (1968) 10:422–37. 10.1137/1010093
80.
SornetteD. Critical phenomena in natural sciences. 2 ed.Heidelberg, Germany: Springer (2006). 10.1007/3-540-33182-4
81.
ben-AvrahamDHavlinS. Diffusion and reactions in fractals and disordered systems. Cambridge: Cambridge University Press (2000).
82.
EvangelistaLRLenziEK. An introduction to anomalous diffusion and relaxation. Cham, Switzerland: Springer (2023).
83.
WestBDeeringW. Fractal physiology for physicists: Lévy statistics. Phys Rep (1994) 246:1–100. 10.1016/0370-1573(94)0005-7
84.
MetzlerRKlafterJ. The random walk's guide to anomalous diffusion: a fractional dynamics approach. Phys Rep (2000) 339(1):1–77. 10.1016/s0370-1573(00)00070-3
85.
LaskinNLambadarisIHarmantzisFCDevetsikiotisM. Fractional Lévy motion and its application to network traffic modeling. Comput Netw (2002) 40(3):363–75.
86.
NezhadhaghighiMGNakhlbandA. Modeling and statistical analysis of non-Gaussian random fields with heavy-tailed distributions. Phys Rev E (2017) 95(4):042114. 10.1103/physreve.95.042114
87.
ChorowskiMGubiecTKutnerR. Fundamental concepts. Anomalous stochastics: a comprehensive guide to multifractals. In: Random walks, and real-world applications. Cham: Springer Nature Switzerland (2025). p. 13–52.
88.
PengCKBuldyrevSVGoldbergerALHavlinSSimonsMStanleyHE. Finite-size effects on long range correlations: implications for the analysis of DNA sequences. Phys Rev E (1993) 47(5):3730–3.
89.
BassingthwaighteJRaymondG. Evaluating rescaled range analysis for time series. Ann Biomed Eng (1994) 22:432–44. 10.1007/bf02368250
90.
RaubitzekSCorpaciLHoferRMallingerK. Scaling exponents of time series data: a machine learning approach. Entropy (2023) 25(12):1671. 10.3390/e25121671
91.
CarpenaPGómez-ExtremeraMBernaola-GalvánPA. On the validity of detrended fluctuation analysis at short scales. Entropy (2021) 24(1):61. 10.3390/e24010061
92.
MaestriRPinnaGDPortaABalocchiRSassiRSignoriniMGet alAssessing nonlinear properties of heart rate variability from short-term recordings: are these measurements reliable?Physiol Meas (2007) 28(9):1067–77. 10.1088/0967-3334/28/9/008
93.
FallahtaftiFWurdemanSRYentesJM. Sampling rate influences the regularity analysis of temporal domain measures of walking more than spatial domain measures. Gait Posture (2021) 88:216–20. 10.1016/j.gaitpost.2021.05.031
94.
RaffaltPCMcCamleyJDentonWYentesJM. Sampling frequency influences sample entropy of kinematics during walking. Med Biol Eng Comput (2019) 57(4):759–64. 10.1007/s11517-018-1920-2
95.
MarmelatVDuncanAMeltzS. Effect of sampling frequency on fractal fluctuations during treadmill walking. PLoS One (2019) 14(11):e0218908. 10.1371/journal.pone.0218908
96.
ZhangHZhouQQChenHHuXQLiWGBaiYet alThe applied principles of EEG analysis methods in neuroscience and clinical neurology. Mil Med Res (2023) 10(1):67. 10.1186/s40779-023-00502-7
97.
WeronABurneckiKMercikSWeronK. Complete description of all self-similar models driven by Lévy stable noise. Phys Rev E Stat Nonlin Soft Matter Phys (2005) 71(1 Pt 2):016113. 10.1103/physreve.71.016113
98.
MuzyJFBacryEArneodoA. Multifractal formalism for fractal signals: the structure-function approach versus the wavelet-transform modulus-maxima method. Physical Review E, Stat Phys, Plasmas, Fluids, Related Interdiscipl Topics (1993) 47(2):875–84. 10.1103/physreve.47.875
99.
GalaskaRMakowiecDDudkowskaAKoprowskiAChlebusKWdowczyk-SzulcJet alComparison of wavelet transform modulus maxima and multifractal detrended fluctuation analysis of heart rate in patients with systolic dysfunction of left ventricle. Ann Noninvasive Electrocardiol (2008) 13(2):155–64. 10.1111/j.1542-474x.2008.00215.x
100.
ArnéodoAArgoulFMuzyJFTabardMBacryE. Beyond classical multifractal analysis using wavelets: uncovering a multiplicative process hidden in the geometrical complexity of diffusion limited aggregates. Fractals (1993) 1(3):629–49.
101.
AuditBBacryEMuzyJFArneodoA. Wavelet-based estimators of scaling behavior. IEEE Trans Inform Theory (2002) 48(11):2938–54. 10.1109/tit.2002.802631
102.
ScafettaNHamiltonPGrigoliniP. The thermodynamics of social processes: the teen birth phenomenon. Fractals (2001) 09(02):193–208. 10.48550/arXiv.cond-mat/0009020
103.
ScafettaNWestBJ. Multiresolution diffusion entropy analysis of time series: an application to births to teenagers in Texas. Chaos, Solitons and Fractals (2004) 20(1):179–85. 10.1016/s0960-0779(03)00442-9
104.
ScafettaNLatoraVGrigoliniP. Lévy scaling: the diffusion entropy analysis applied to DNA sequences. Phys Rev E (2002) 66:031906. 10.1103/physreve.66.031906
105.
ScafettaNGrigoliniP. Scaling detection in time series: diffusion entropy analysis. Phys Rev E Stat Nonlin Soft Matter Phys (2002) 66(3 Pt 2A):036130. 10.1103/physreve.66.036130
106.
AllegriniPBenciVGrigoliniPHamiltonPIgnaccoloMMenconiGet alCompression and diffusion: a joint approach to detect complexity. Chaos, Solitons and Fractals (2003) 15(3):517–35. 10.1016/s0960-0779(02)00136-4
107.
Kelty-StephenDGMangalamM. Multifractal descriptors ergodically characterize non-ergodic multiplicative cascade processes. Physica A (2023) 617:128651. 10.1016/j.physa.2023.128651
108.
GrigoliniPAquinoGBolognaMLukovicMWestBJ. A theory of 1/f noise in human cognition. Physica A (2009) 388:4192–204.
109.
MahmoodiKWestBJGrigoliniP. Self-organized temporal criticality: bottom-up resilience versus top-down vulnerability. Complexity (2018) 2018(1):8139058. 10.1155/2018/8139058
110.
RafieiHAkbarzadeh-TM-R. Understandable time frame-based biosignal processing. Biomedical Signal Processing and Control (2025) 103:107429. 10.1016/j.bspc.2024.107429
111.
WestBJ. Colloquium: fractional calculus view of complexity: a tutorial. Rev Mod Phys. (2014) 86:1169–86. 10.1103/revmodphys.86.1169
112.
ValenzaGCitiLLanatáAScilingoEPBarbieriR. Revealing real-time emotional responses: a personalized assessment based on heartbeat dynamics. Sci Rep (2014) 4:4998. 10.1038/srep04998
113.
LewisGFFurmanSAMcCoolMFPorgesSW. Statistical strategies to quantify respiratory sinus arrhythmia: are commonly used metrics equivalent?Biol Psychol (2012) 89(2):349–64. 10.1016/j.biopsycho.2011.11.009
114.
GoldbergerALPengC-KLipsitzLA. What is physiologic complexity and how does it change with aging and disease?Neurobiol Aging (2002) 23:23–6. 10.1016/s0197-4580(01)00266-4
115.
MansierPClairambaultJCharlotteNMedigueCVerneirenCLePapeGet alLinear and non-linear analyses of heart rate variability: a minireview. Cardiovac Res (1996) 31:371–9. 10.1016/s0008-6363(96)00009-0
116.
GowrisankarABanerjeeS. Framework of fractals in data analysis: theory and interpretation. Eur Phys J Spec Top (2023) 232:965–7. 10.1140/epjs/s11734-023-00890-w
117.
GoldbergerALAmaralLANHausdorffJMIvanovPCPengC-KStanleyHE. Fractal dynamics in physiology: alterations with disease and aging. PNAS (2002) 99(90001):2466–72. 10.1073/pnas.012579499
118.
StoopROrlandoGBufaloMDella RossaF. Exploiting deterministic features in apparently stochastic data. Sci Rep (2022) 12(1):19843. 10.1038/s41598-022-23212-x
119.
WagenmakersEJFarrellSRatcliffR. Estimation and interpretation of 1/fα noise in human cognition. Psychon Bull Rev (2004) 11(4):579–615. 10.3758/bf03196615
120.
JiangWLiuYWangJLiRLiuXZhangJ. Problems of the grid size selection in differential box-counting (DBC) methods and an improvement strategy. Entropy (Basel). (2022) 24(7):977. 10.3390/e24070977
121.
FernandezEJelinekHF. Use of fractal theory in neuroscience: methods, advantages, and potential problems. Methods (2001) 24(4):309–21. 10.1006/meth.2001.1201
122.
SmithJTGMarksWBLangeGDSheriffJWHNealeEA. A fractal analysis of cell images. J Neurosci Methods (1989) 27(2):173–80. 10.1016/0165-0270(89)90100-3
123.
KrohnSFroelingMLeemansAOstwaldDVillosladaPFinkeCet alEvaluation of the 3D fractal dimension as a marker of structural brain complexity in multiple-acquisition MRI. Hum Brain Mapp (2019) 40(11):3299–320. 10.1002/hbm.24599
124.
KarperienALJelinekHF. Morphology and fractal-based classifications of neurons and microglia in two and three dimensions. In: Di IevaA, editor. The fractal geometry of the brain. Cham: Springer International Publishing (2024). p. 149–72.
125.
AhammerHReissMAHackhoferMAndronacheIRadulovicMLabra-SpröhnleFet alComsystanJ: a collection of Fiji/ImageJ2 plugins for nonlinear and complexity analysis in 1D, 2D and 3D. PlosOne (2023) 18(10):e0292217. 10.1371/journal.pone.0292217
126.
DonnanLAPaulMCrowleyLFelesimoKJelinekHF, editors. Complexity and entropy of knee kinematics in a joint reposition test: effect of strapping and kinesiology taping. 2018 Digital Image Computing: techniques and Applications (DICTA). IEEE Press (2018).
127.
CasertaFEldredWDFernandezEHausmanREStanfordLRBulderevSVet alDetermination of fractal dimension of physiologically characterized neurons in two and three dimensions. J Neurosci Meth (1995) 56:133–44. 10.1016/0165-0270(94)00115-w
128.
GrelaJDrogoszZJanarekJOchabJKCifreIGudowska-NowakEet alUsing space-filling curves and fractals to reveal spatial and temporal patterns in neuroimaging data. J Neural Eng (2025) 22(1):016016. 10.1088/1741-2552/ada705
129.
MurrayJD. Use and abuse of fractal theory in neuroscience. J Comp Neurol (1995) 361:369–71. 10.1002/cne.903610302
130.
XuHHAYangXIA. Fractality and the law of the wall. Phys Rev E (2018) 97(5-1):053110. 10.1103/physreve.97.053110
131.
JinYWuYLiHZhaoMPanJ. Definition of fractal topography to essential understanding of scale-invariance. Sci Rep (2017) 7:46672. 10.1038/srep46672
132.
KarperienALJelinekHF. Fractal, multifractal, and lacunarity analysis of microglia in tissue engineering. Front Bioeng Biotechnol (2015) 3(51):51. 10.3389/fbioe.2015.00051
133.
LandiniGMurrayPIMissonGP. Local connected fractal dimensions and lacunarity analyses of 60 degrees fluorescein angiograms. Invest Ophthalmol Vis Sci. (1995) 36:2749–55.
134.
CornforthDTarvainenMJelinekHF. How to calculate renyi entropy from heart rate variability, and why it matters for detecting cardiac autonomic neuropathy. Front Bioeng Biotech (2014) 2:34. 10.3389/fbioe.2014.00034
135.
CostaMGoldbergerALPengC-K. Multiscale entropy analysis of biological signals. Phys Rev E (2005) 71:021906. 10.1103/physreve.71.021906
136.
NasratSPrasadRDimassiZAlefishatEKhandokerAJelinekHF. Multiscaled crucial events complexity analysis of heart rate signals during Tibetan singing bowls meditation. In: Esgco 2024. Zaragoza, Spain: IEEE Press (2024).
137.
TheilerJEubankSLongtinAGaldrikianBDoyne FarmerJ. Testing for nonlinearity in time series: the method of surrogate data. Physica D: Nonlinear Phenomena (1992) 58(1):77–94. 10.1016/0167-2789(92)90102-s
138.
GrechDPamułaG. The local Hurst exponent of the financial time series in the vicinity of crashes on the Polish stock exchange market. Physica A (2008) 387:4299–308. 10.1016/j.physa.2008.02.007
139.
SchreiberTSchmitzA. Improved surrogate data for nonlinearity tests. Phys Rev Lett (1996) 77:635–8. 10.1103/physrevlett.77.635
140.
KantelhardtJWZschiegnerSAKoscielny-BundeEHavlinSBundeAStanleyHE. Multifractal detrended fluctuation analysis of nonstationary time series. Physica A (2002) 316(1):87–114. 10.1016/s0378-4371(02)01383-3
141.
VachaLBarunikJ. Co-movement of energy commodities revisited: evidence from wavelet coherence analysis. Energ Econ (2012) 34(1):241–7. 10.1016/j.eneco.2011.10.007
142.
CalvetLFisherA. Multifractality in asset returns: theory and evidence. Rev Econ Stat (2002) 84(3):381–406. 10.1162/003465302320259420
143.
IvanovPAmaralLANGoldbergerALHavlinSRosenblumMStruzikZRet alMultifractality in human heartbeat dynamics. Nature (1999) 399:461–5. 10.1038/20924
144.
StanleyHEAmaralLANGoldbergerALHavlinSIvanovPCPengCK. Statistical physics and physiology: monofractal and multifractal approaches. Phys A (1999) 270:309–24. 10.1016/s0378-4371(99)00230-7
145.
KantzH. Nonlinear time series analysis — potentials and limitations. Berlin, Heidelberg: Springer Berlin Heidelberg (1996). p. 213–28.
146.
FederJ. Fractals. New York: Plenum Press (1988).
147.
HalseyTCJensenMHKadanoffLPProcacciaIShraimanBI. Fractal measures and their singularities: the characterization of strange sets. Phys Rev A (1986) 33(2):1141–51. 10.1103/physreva.33.1141
148.
Alvarez-RamirezJAlvarezJRodriguezE. Short-term predictability of crude oil markets: a detrended fluctuation analysis approach. Energ Econ (2008) 30(5):2645–56. 10.1016/j.eneco.2008.05.006
149.
SerinaldiF. Use and misuse of some Hurst parameter estimators applied to stationary and non-stationary financial time series. Physica A (2010) 389:2770–81. 10.1016/j.physa.2010.02.044
150.
MahmoodiKWestBJGrigoliniP. Self-organizing complex networks: individual versus global rules. Front Physiol (2017) 8:478. 10.3389/fphys.2017.00478
151.
HakenH. Synergetics: an introduction. 3 ed. Heidelberg: Springer Verlag (1983).
152.
JaegerHMLiuAJ (2010). Far-from-equilibrium physics: an overview. arXiv preprint:10094874.
153.
BarunikJKristoufekL. On Hurst exponent estimation under heavy-tailed distributions. Physica A (2010) 389:3844–55. 10.1016/j.physa.2010.05.025
154.
Di MatteoTAsteTDacorognaMM. Long-term memories of developed and emerging markets: using the scaling analysis to characterize their stage of development. J Banking Finance (2005) 29(4):827–51. 10.1016/j.jbankfin.2004.08.004
155.
SchizasISullivanSKerickSEMahmoodiKBradfordJCBootheDLet al (2024).Complexity synchronization analysis of neurophysiological data: theory and methods. arXiv preprint arXiv:241114602.
156.
JelinekHFElstonGNZietschB. Fractal analysis: pitfalls and revelations in neuroscience. In: LosaGAWeibelERNonnenmacherTF, editors. Fractals in biology and medicine, IV. Lucarno, Switzerland (2005). p. 85–94. Birkäuser Verlag. 10.1007/3-7643-7412-8_8
157.
JelinekHFFernándezE. Neurons and fractals: how reliable and useful are calculations of fractal dimension?J Neurosci Meth (1998) 81:9–18.
158.
DollingerJWRMNonnenmacherTF. Bi-asymptotic fractals: fractals between lower and upper bounds. Journal of Physics A: Math Gen. (1998) 31:3839–47.
159.
RigautJP. An empirical formulation relating boundary lengths to resolution in specimens showing 'non-ideally fractal' dimensions. J Microsc (1984) 133:41–54. 10.1111/j.1365-2818.1984.tb00461.x
160.
CostaLFManoelETMFaucereauFChellyJvan PeltJRamakersG. A shape analysis framework for neuromorphometry. Network: Comput Neural Syst (2002) 13:283–310. 10.1088/0954-898x_13_3_303
161.
ZhaoSJiangYHeWMeiYXieXWanS. Detrended fluctuation analysis based on best-fit polynomial. Front Environ Sci. (2022) 10:1054689. 10.3389/fenvs.2022.1054689
162.
SilvaRPZarpelãoBBCanoAJuniorSB. Time series segmentation based on stationarity analysis to improve new samples prediction. Sensors (2021) 21(21):7333. 10.3390/s21217333
163.
PintoHLazicIAntonacciYPerniceRGuDBaràCet alTesting dynamic correlations and nonlinearity in bivariate time series through information measures and surrogate data analysis. Front Netw Physiol (2024) 4:1385421. 10.3389/fnetp.2024.1385421
164.
SaleemSKhandokerAHAlkhodariMHadjileontiadisLJJelinekHF. A two-step pre-processing tool to remove Gaussian and ectopic noise for heart rate variability analysis. Sci Rep (2022) 12(1):18396. 10.1038/s41598-022-21776-2
165.
GuZZarubinVMartsbergerC. The effectiveness of time domain and nonlinear heart rate variability metrics in ultra-short time series. Physiol Rep (2023) 11(22):e15863. 10.14814/phy2.15863
166.
ShafferFGinsbergJP. An overview of heart rate variability metrics and norms. Front Publ Hlth. (2017) 5:258. 10.3389/fpubh.2017.00258
167.
BrennanMPalaniswamiMKamenP. Do existing methods of Poincaré plot geometry reflect nonlinear features of heart rate variability?IEEE Trans Biomed Eng (2001) 48(11):1342–7.
168.
GoltzC. Fractal and chaotic properties of earthquakes. Berlin: Springer Verlag (1997).
169.
ZhangSFangW. Multifractal behaviors of stock indices and their ability to improve forecasting in a volatility clustering period. Entropy (2021) 23(8):1018. 10.3390/e23081018
170.
de Melo Barros JuniorPRBungeKLSerravalle Reis RodriguesVHFerreiraSMTdos Santos MarinhoEBLima de JesusSJL. Multi-fractal detrended cross-correlation heatmaps for time series analysis. Sci Rep (2022) 12(1):21655. 10.1038/s41598-022-26207-w
171.
NordbeckPCAndradeVSilvaPLKuznetsovNA. DFA as a window into postural dynamics supporting task performance: does choice of step size matter?Front Netw Physiol (2023) 3:1233894. 10.3389/fnetp.2023.1233894
172.
ZuninoLTabakBMFigliolaAPérezDGGaravagliaMRossoOA. A multifractal approach for stock market inefficiency. Physica A: Stat Mechan Applicat (2008) 387(26):6558–66. 10.1016/j.physa.2008.08.028
173.
BarnsleyMF. Fractals everywhere. Academic Press (2014).
174.
GolmankhanehAKWelchKTunçCGasimovYS. Classical mechanics on fractal curves. Eur Phys J Spec Top (2023) 232(7):991–9.
175.
GlennyRWRobertsonHT. Fractal modeling of pulmonary blood flow heterogeneity. J Appl Physiol (1991) 70(3):1024–30. 10.1152/jappl.1991.70.3.1024
176.
WestBJ. The Fractal tapestry of life: a review of fractal physiology. Nonlin Dynam Psychol Life Sci. (2021) 25(3):261–96.
177.
SandauKKurzH. Measuring fractal dimension and complexity - an alternative approach with an application. J Microscop (1997) 186(2):164–76. 10.1046/j.1365-2818.1997.1270685.x
178.
JaquetteJSchweinhartB. Fractal dimension estimation with persistent homology: a comparative study. Commun Nonlinear Sci Numer Simul (2020) 84:105163. 10.1016/j.cnsns.2019.105163
179.
WestBJ. Where medicine went wrong: rediscovering the path to complexity: World Scientific (2006). 352. 10.1142/6175
180.
BassingthwaighteJBLiebovitchLSWestBJ. Fractal physiology. New York: Oxford University Press (1994). p. 364.
181.
MandelbrotBB. Fractals, lacunarity and how it can be tuned and measured. In: NonnenmacherTFLosaGAWeibelER, editors. Fractals in biology and medicine. Boston: Birkhäuser Verlag (1993). p. 21–8.
182.
VicsekMVicsekT. Aggregation models of fractal growth. CWI Quart. (1997) 10(2):153–78.
183.
BoharaGLambertDWestBJGrigoliniP. Crucial events, randomness, and multifractality in heartbeats. Phys Rev E (2017) 96(6-1):062216. 10.1103/physreve.96.062216
184.
StruzikZR. Fractals under the microscope or reaching beyond the dimensional formalism of fractals with the wavelet transform. CWI Quart (1997) 10(2):109–51.
185.
RistanovićDStevanovicBDMiloševićNTGrgurevicMStulicVStulićV. Fractal and nonfractal analysis of cell images: comparison and application to neuronal dendritic arborization. Biol Cybern (2002) 87:278–88. 10.1007/s00422-002-0342-1
186.
BaumertMBrechtelLMLockJVossAAbbottD. Scaling graphs of heart rate time series in athletes demonstrating the VLF, LF and HF regions. Physiol Meas (2006) 27:N35–N9. 10.1088/0967-3334/27/9/n01
187.
MiloševićNTRajkovićNJelinekHF. In: AguilarE, editor. Fractal and multifractal analysis of two dimensional images of the retinopathy of prematurity: morphologic parameters and classification. Nova Publishers (2015).
188.
MastersBR. Fractal analysis of the vascular tree in the human retina. Ann Rev Biomed Eng (2004) 6:427–52. 10.1146/annurev.bioeng.6.040803.140100
189.
KarperienALJelinekHF. ImageJ in computational fractal-based neuroscience: pattern extraction and translational research. In: Di IevaA, editor. The fractal geometry of the brain. Cham: Springer International Publishing (2024). p. 795–814.
190.
JelinekHFElstonGN. Dendritic branching of pyramidal cells in the visual cortex of the nocturanal owl monkey: a fractal analysis. Fractals (2004) 11(4):391–6.
191.
di IevaA, editor. The fractal geometry of the brain. 2 ed.Berlin: Springer Verlag (2024).
192.
AndronacheI. Analysis of forest fragmentation and connectivity using fractal dimension and succolarity. Land (2024) 13(2):138. 10.3390/land13020138
193.
RoblesKERobertsMViengkhamCSmithJHRowlandCMoslehiSet alAesthetics and psychological effects of fractal based design. Front Psychol (2021) 12:699962. 10.3389/fpsyg.2021.699962
194.
CerasaA. Fractals in neuropsychology and cognitive neuroscience. In: Di IevaA, editor. The fractal geometry of the brain. Cham: Springer International Publishing (2024). p. 761–78.
195.
TentiJMHernández GuianceSNIrurzunIM. Fractal dimension of diffusion-limited aggregation clusters grown on spherical surfaces. Phys Rev E (2021) 103(1-1):012138. 10.1103/physreve.103.012138
196.
GrebenkovDSBeliaevD. How anisotropy beats fractality in two-dimensional on-lattice diffusion-limited-aggregation growth. Phys Rev E (2017) 96(4-1):042159. 10.1103/physreve.96.042159
197.
WuHLattuadaMMorbidelliM. Dependence of fractal dimension of DLCA clusters on size of primary particles. Adv Colloid Interface Sci (2013) 195-196:41–9. 10.1016/j.cis.2013.04.001
198.
ProcacciaEBProcacciaI. Dimension of diffusion-limited aggregates grown on a line. Phys Rev E (2021) 103(2):L020101. 10.1103/physreve.103.l020101
199.
GhoshABatabyalRDasGPDevBN. An extended fractal growth regime in the diffusion limited aggregation including edge diffusion. AIP Adv (2016) 6(1):015301. 10.1063/1.4939635
200.
VicsekTFamilyFMeakinP. Multifractal geometry of diffusion-limited aggregates. Europhys Lett (1990) 12(3):217–22. 10.1209/0295-5075/12/3/005
201.
PolimenoMKimCBlanchetteF. Toward a realistic model of diffusion-limited aggregation: rotation, size-dependent diffusivities, and settling. ACS Omega (2022) 7(45):40826–35. 10.1021/acsomega.2c03547
202.
SongJWangBJiangQHaoX. Exploring the role of fractal geometry in engineering image processing based on similarity and symmetry: a review. Symmetry (2024) 16(12):1658. 10.3390/sym16121658
203.
TuladharRBoharaGGrigoliniPWestBJ. Meditation-induced coherence and crucial events. Front Physiol (2018) 9(626):626. 10.3389/fphys.2018.00626
204.
CastilloOMelinP. A new fuzzy fractal control approach of non-linear dynamic systems: the case of controlling the COVID-19 pandemics. Chaos Solitons Fractals (2021) 151:111250. 10.1016/j.chaos.2021.111250
205.
ZuevaMV. Fractality of sensations and the brain health: the theory linking neurodegenerative disorder with distortion of spatial and temporal scale-invariance and fractal complexity of the visible world. Front Aging Neurosci (2015) 7:135. 10.3389/fnagi.2015.00135
206.
WestBJDeeringW. Fractal physiology for physicists: Lévy statistics. Phys Rep (1994) 246(1):1–100. 10.1016/0370-1573(94)00055-7
207.
CzyżaSSzuniewiczKCieślakIBiłozorABajerowskiT. An analysis of the spatial development of European cities based on their geometry and the CORINE land cover (CLC) database. Int J Environ Res Public Health (2023) 20(3):2049. 10.3390/ijerph20032049
208.
GadelmawlaESKouraMMaksoudTElewaISolimanH. Roughness parameters. J Mater Process Technol (2002) 123:133–45. 10.1016/s0924-0136(02)00060-2
209.
ParsonsDFWalshRBCraigVS. Surface forces: surface roughness in theory and experiment. J Chem Phys (2014) 140(16):164701. 10.1063/1.4871412
210.
PeitgenH-OJürgensHSaupeD. Fractals for the classroom. Berlin: Springer-Verlag (1992).
211.
BittnerHRSernetzM, editors. Selfsimilarity within limits: description with the log-logistic function. Lisboa (1990). p. 86.
212.
LosaGRistanovićDRistanovićDZaletelIBeltraminelliS. From fractal geometry to fractal analysis. Appl Math (2016) 216(7):346–54. 10.4236/am.2016.74032
213.
PanicoJSterlingP. Retinal neurons and vessels are not fractal but space-filling. J Comp Neurol (1995) 361:479–90. 10.1002/cne.903610311
214.
SchulzSSchumannABärK-JHaueisenJSeifertGVossA. A new directionality index based on high-resolution joint symbolic dynamics to assess information transfer in multivariate networks. Front Neurosci (2025) 19:1504161. 10.3389/fnins.2025.1504161
215.
LopesR. Multifractal analysis in neuroimaging. In: Di IevaA, editor. The fractal geometry of the brain. Cham: Springer International Publishing (2024). p. 79–93.
216.
NelsonTRWestBJGoldbergerAL. The fractal lung: universal and species-related scaling patterns. Experientia (1990) 46:251–4. 10.1007/bf01951755
217.
MastersBRSernetzMWlczekP. Image analysis of human retinal blood vessels and their characterisation as fractals. ACTA Stereol (1992) 11(Suppl. 1):355–60.
218.
SernetzMJustenMJestczemskiF. Dispersive fractal characterization of kidney arteries by three-dimensional mass-radius analysis. Fractals (1995) 3(4):879–91. 10.1142/s0218348x95000771
219.
CornforthDJelinekHF, editors. Automated classification of dementia subtypes from post-mortem cortex images. AI2005: advances in artificial intelligence. Sydney, Australia: Springer Verlag (2005). conference paper.
220.
HelmbergerMPiennMUrschlerMKullnigPStollbergerRKovacsGet alQuantification of tortuosity and fractal dimension of the lung vessels in pulmonary hypertension patients. Plos One (2014) 9(1):e87515. 10.1371/journal.pone.0087515
221.
JestczemskiFHBSernetzM. Comparison of the surface dimension and the mass dimension of blood vessel systems. Fractals (1996) 4(2):123–32.
222.
KochkarovRKochkarovA. Introduction to the class of prefractal graphs. Mathematics (2022) 10(14):2500. 10.3390/math10142500
223.
ChenY. The solutions to the uncertainty problem of urban fractal dimension calculation. Entropy (2019) 21(5):453. 10.3390/e21050453
224.
CurtinL. Fractal-based morphometrics of glioblastoma. Adv Neurobiol (2024) 36. 545–55. 10.1007/978-3-031-47606-8_28
225.
FernándezEEldredWDAmmermullerJBlockAVon BlohWKolbH. Complexity and scaling properties of amacrine, ganglion, horizontal, and bipoloar cells in the turtle retina. J Comp Neurol (1994) 347:397–408.
226.
Ruiz de MirasJNavasJVillosladaPEstebanFJ. UJA-3DFD: a program to compute the 3D fractal dimension from MRI data. Comput Methods Programs Biomed (2011) 104(3):452–60. 10.1016/j.cmpb.2010.08.015
227.
ZhangLLiuJZDeanDSahgalVYueGH. A three-dimensional fractal analysis method for quantifying white matter structure in human brain. J Neurosci Meth. (2006) 150(2):242–53. 10.1016/j.jneumeth.2005.06.021
228.
GoñiJSpornsOChengHAznárez-SanadoMWangYJosaSet alRobust estimation of fractal measures for characterizing the structural complexity of the human brain: optimization and reproducibility. Neuroimage. (2013) 83:646–57. 10.1016/j.neuroimage.2013.06.072
229.
AhammerHDeVaneyTT. The influence of edge detection algorithms on the estimation of the fractal dimension of binary digital images. Chaos (2004) 14(1):183–8. 10.1063/1.1638947
230.
SendkerFLLoYKHeimerlTBohnSPerssonLJMaisC-Net alEmergence of fractal geometries in the evolution of a metabolic enzyme. Nature (2024) 628(8009):894–900. 10.1038/s41586-024-07287-2
231.
KellerJMCrownoverRMChenRY. Characteristics of natural scenes related to the fractal dimension. IEEE Trans Pattern Anal Mach Intell (1987) 9(5):621–7. 10.1109/tpami.1987.4767956
232.
TurcotteDL, editor. Scale invariance. Fractals and chaos in geology and geophysics, 2. Cambridge: Cambridge University Press (1997). p. 1–5.
233.
MüllerWJungAAhammerH. Advantages and problems of nonlinear methods applied to analyze physiological time signals: human balance control as an example. Sci Rep (2017) 7(1):2464. 10.1038/s41598-017-02665-5
234.
RundleJBTiampoKFKleinWSa MartinsJS. Self-organization in leaky threshold systems: the influence of near-mean field dynamics and its implications for earthquakes, neurobiology, and forecasting. Proc Natl Acad Sci U S A. (2002) 99(Suppl. 1):2514–21. 10.1073/pnas.012581899
235.
KaganYY. Fractal dimension of brittle fracture. J Nonlin Sci (1991) 1(1):1–16. 10.1007/bf01209146
236.
HirataT. Fractal dimension of fault systems in Japan: fractal structure in rock fracture geometry at various scales. Pure Appl Geophys (1989) 131(1):157–70. 10.1007/bf00874485
237.
PekinceAAzlağ PekinceKYasaY. How does the direction of region of interest selection affect the fractal dimension?Oral Radiol (2025) 41(2):180–9. 10.1007/s11282-024-00786-y
238.
HoldenJGRileyMAGaoJTorreK. Fractal analyses: statistical and methodological innovations and best practices. Front Physiol (2013) 4:97. 10.3389/fphys.2013.00097
239.
WeberIOehrnCR. NoLiTiA: an open-source toolbox for non-linear time series analysis. Front Neuroinformat (2022) 16:876012. 10.3389/fninf.2022.876012
240.
SiebertJGroßJSchrothC. A systematic review of packages for time series analysis. Eng Proc (2021) 5(1):22. 10.3390/engproc2021005022
241.
BryceRMSpragueKB. Revisiting detrended fluctuation analysis. Sci Rep (2012) 2:315. 10.1038/srep00315
242.
GlennyRWRobertsonHTYamashiroSBassingthwaighteJB. Applications of fractal analysis to physiology. J Appl Physiol (1985)1991) 70(6):2351–67. 10.1152/jappl.1991.70.6.2351
243.
KusákM. Review article: methods of fractal geometry used in the study of complex geomorphic networks. Geographica (2014) 49:99–110. 10.14712/23361980.2014.19
Summary
Keywords
fractals, chaos, linguistics, time series analysis, image processing
Citation
Jelinek HF and Ahammer H (2025) Operationalizing fractal linguistics: toward a unified framework for cross-disciplinary fractal analysis. Front. Phys. 13:1645620. doi: 10.3389/fphy.2025.1645620
Received
12 June 2025
Accepted
23 July 2025
Published
20 August 2025
Volume
13 - 2025
Edited by
Zbigniew R. Struzik, The University of Tokyo, Japan
Reviewed by
Rami Ahmad El-Nabulsi, Chiang Mai University, Thailand
Ryszard Kutner, University of Warsaw, Poland
Updates
Copyright
© 2025 Jelinek and Ahammer.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Helmut Ahammer, helmut.ahammer@medunigraz.at
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.