The rule for the number of fundamental Peregrine solitons involving multiple rogue wave states in the vector Chen-Lee-Liu nonlinear Schrödinger equation

This study investigates the physical distribution patterns of Peregrine solitons within multi-order rogue wave states and their potential applications in optical systems under the vector Chen-Lee-Liu nonlinear Schrödinger equation framework. Through non-recursive Darboux transformation, we systematically analyze the nonlinear dynamics of vector optical fields during second-harmonic generation, revealing an arithmetic progression in Peregrine soliton evolution across rogue wave orders. For $n$th-order solutions, the fundamental Peregrine soliton count follows an arithmetic sequence with first term $n(n-1)$, last term $n(n+1)$, and common difference $n$, where each rogue wave state comprises fully decoupled Peregrine solitons (e.g., 1/2 for 1st-order, 2/4/6 for 2nd-order, and 6/9/12 for 3rd-order configurations). It is noteworthy that the emergence of nonet rogue wave states (nine Peregrine solitons) in third-order solutions breaks through the conventional even-mode constraint in second-order solutions, opening new avenues for investigating many-body nonlinear interactions in multi-channel photonic devices. These findings provide significant insights into the spatiotemporal localization characteristics of rogue waves in multi-component nonlinear media and their applications in optical sensing and quantum information processing.

1 Introduction

In the last decade, the study of rogue waves has attracted increasing interest in such fields as oceanography [1], fluid dynamics [2, 3], optics and photonics [4–6], acoustics [7], magnetism [8], Bose-Einstein condensation [9, 10], artificial intelligence [11], and topological control [12]. Mathematically, rogue waves can be represented by rational functions localized on the space-time domain [13, 14]. One typical example is the fundamental rational solution of the nonlinear Schrödinger (NLS) equation, termed Peregrine soliton, which was first discovered by Peregrine in 1983 [15]. The most distinctive feature of Peregrine soliton is the bilocalized peak on a finite background. Due to its peculiar spatiotemporal structure, Peregrine soliton is generally recognized as the prototype of rogue waves in reality [16]. Nowadays, Peregrine solitons have been observed in many physical environments, such as water wave tanks [2], optical fibers [17, 18], plasmas [19], and irregular ocean states [20].

In many practical situations, multi-component nonlinear systems with more complex spatiotemporal dynamics rather than scalar integrable models need to be considered [21, 22]. Unlike scalar NLS, the vector Chen-Lee-Liu (CLL) NLS model incorporates some indispensable features. Multi-component coupling between optical fields $u_1$ and $u_2$, essential for modeling polarization-dependent effects in birefringent media [23], and self-steepening, which induces spatiotemporal reshaping critical for ultrashort pulses [24, 25]. These enable phenomena unattainable in scalar models, such as energy-transfer-driven amplitude anomalies and higher-order rogue states. Examples include the formation of anomalous Peregrine solitons involving self-steepening effects in the multi-component systems [26, 27], as well as the formation of Peregrine rogue waves on a background of periodic waves induced by interference [28]. Meanwhile, the dynamics of higher-order Peregrine solitons have also attracted a great deal of research activities [29–31], especially the multiple rogue wave states consisting of multiple Peregrine solitons [32, 33] and the super rogue wave states superimposed by three or six Peregrine solitons [34, 35]. It should be noted that the multiple rogue wave states are different from the super rogue wave states, with the former being composed of a number of well-separated Peregrine solitons. In addition, rogue wave patterns have also been studied in recent years, and these studies are mainly related to the root structure of special polynomials (e.g., Okamoto polynomials or Adler–Moser polynomials), where the distribution of the roots determines the geometry of the patterns [36–39]. These studies have greatly enriched our understanding of the nature of Peregrine solitons.

In our previous research works [40, 41], we explored the omnipresent coexistence as well as Peregrine solitons on periodic backgrounds, using the vector CLL-NLS equation. It is also found that when having the double-root case, the $n$th-order multiple rogue wave states will consist of $n$($n$+1)/2 fundamental Peregrine solitons, as what was found in scalar systems [35, 42, 43]. As for the triple-root case, however, such $n$th-order rogue wave states will exhibit more complex patterns, consisting of at most $n$($n$+1) Peregrine solitons, with at most two and 6 fundamental Peregrine solitons seen for their first- and second-order rogue wave states, which were confirmed in most other vector system [44–46]. One fundamental question naturally arises: as for the third-order rogue wave states, does it satisfy that it consists of at most 12 fundamental Peregrine solitons? If so, what kind of pattern will its fundamental Peregrine solitons show? Will it be similar to the second-order solutions case, with an even number of multiple patterns of rogue wave states?

In this work, we conduct a systematic study of this problem. We obtain up to third-order rogue wave solutions for the vector CLL-NLS system by the nonrecursive Darboux transform (DT) method and analyze the complex patterns of rogue wave states in the triple-root case. In addition, based on the results for the first-, second-, and third-order rogue wave states, the number patterns of the fundamental Peregrine solitons of the $n$th-order rogue wave states are discussed. Our findings may contribute to the possibility of future experimental observations. This paper is structured as follows: first, Section 2 gives an overview of the vector CLL-NLS model and the nonrecursive DT form by which higher-order rogue wave solutions are derived. Then, Section 3 gives a detailed list of the first-, second-, and third-order rogue wave solutions, and discusses the number rule of fundamental Peregrine solitons for rogue wave states. Finally, Section 4 concludes the paper.

2 The vector CLL-NLS model and nonrecursive DT scheme

We consider the vector CLL-NLS model, which controls the mixing of two fundamental-frequency pulses in a second-order nonlinear crystal through the generation process of type II highly phase mismatched second-harmonic [24, 25, 47]. The dimensionless form of the CLL-NLS model is written as

$\begin{array}{cc}\hfill & i{u}_{ız}+\frac{\sigma }{2}{u}_{ıtt}+(|u_1{|}^2+|u_2{|}^2)(u_{ı}+i\gamma u_{ıt})=0,(ı=\mathrm{1,2}),\hfill \end{array}(1)$

where $u_{ı}(z,t)$ are the normalized complex envelopes, with the subscripts denoting the partial derivatives, and $z$ and $t$ being the propagation distance and delay time, respectively. All variables ($z$, $t$, $u_{ı}$) are dimensionless in this study. Physical units can be restored via scaling transformations [23, 48]. The parameter $\sigma$ can be normalized to $+1$ and $-1$ in the case of anomalous and normal dispersion, respectively. The third term of Equation 1 includes the Kerr nonlinear effect, which arises from the intensity-dependent refractive index [23], and the self-steepening effect modulated by the parameter $\gamma$ [48]. It is easy to see that when $\gamma =0$, the above model will regress to the well-known Manakov system, which is widely used in various nonlinear vector systems to model, for example, the propagation of optical pulses in randomly birefringent optical fibers [27], the formation of spatial solitons in planar waveguides [49], and the cross-wave states occurring in the open ocean [50]. As an important generalization of the Manakov system, the vector CLL-NLS model can more accurately describe the dynamical evolution of rogue waves in these different nonlinear media.

Due to complete integrability [51], Equation 1 can be transformed into a $3\times 3$ linear eigenvalue problem

${\mathbf{R}}_t=\mathbf{U}\mathbf{R},{\mathbf{R}}_z=\mathbf{V}\mathbf{R},(2)$

where $\mathbf{R}={[r,s,w]}^{\mathsf{T}}$ is the characteristic function ($\mathsf{T}$ represents transposition, $r$, $s$, and $w$ are functions of $z$, $t$, and the complex spectral parameter $\lambda$). Matrices $\mathbf{U}$ and $\mathbf{V}$ are given by the following equations

$\begin{array}{cc}\hfill \mathbf{U}& =-\frac{i(\lambda -\sigma ){\sigma }_3}{2\sigma \gamma }+\frac{\sqrt{\lambda }}{\sigma }\mathbf{Q}+\frac{i\gamma }{\sigma }\mathbf{K}{\mathbf{Q}}^2,\hfill \\ \hfill \mathbf{V}& =-\frac{i{(\lambda -\sigma )}^2{\sigma }_3}{4\sigma {\gamma }^2}+\frac{i{\gamma }^2}{2\sigma }\mathbf{K}{\mathbf{Q}}^4-\frac{\gamma }{2}\mathbf{K}(\mathbf{Q}{\mathbf{Q}}_t-{\mathbf{Q}}_t\mathbf{Q})\hfill \\ \hfill & +\frac{\sqrt{\lambda }}{2\sigma }\left(\frac{\lambda -\sigma }{\gamma }\mathbf{Q}-i\sqrt{\lambda }{\sigma }_3{\mathbf{Q}}^2+\gamma {\mathbf{Q}}^3+i\sigma {\sigma }_3{\mathbf{Q}}_t\right),\hfill \end{array}(3)$

with

$\mathbf{K}=\left[\begin{array}{ccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right],{\sigma }_3=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -1\hfill \end{array}\right],\mathbf{Q}=\left[\begin{array}{ccc}\hfill 0\hfill & \hfill u_1\hfill & \hfill u_2\hfill \\ \hfill -u_1^{*}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -u_2^{*}\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right].$

The asterisk denotes the complex conjugation operation for any spectral parameter $\lambda$. Equation 1 can be easily derived from the compatibility condition of ${\mathbf{U}}_z-{\mathbf{V}}_t+\mathbf{U}\mathbf{V}-\mathbf{V}\mathbf{U}=0$.

Based on the Lax pair (Equations 2, 3), one can construct a nonrecursive DT [44, 45, 52] by which the $n$th-order rogue wave solutions can be obtained

$\begin{array}{cc}\hfill & u_1^{[n]}=u_{10}\left(1-\frac{i}{|u_{10}|}{\mathbf{Y}}_1{\mathbf{M}}^{-1}{\mathbf{Y}}_2^{†}\right)\left(\frac{\mathrm{d}\mathrm{e}\mathrm{t}(\mathbf{M})}{\mathrm{d}\mathrm{e}\mathrm{t}({\mathbf{M}}^{†})}\right),\hfill \\ \hfill & u_2^{[n]}=u_{20}\left(1-\frac{i}{|u_{20}|}{\mathbf{Y}}_1{\mathbf{M}}^{-1}{\mathbf{Y}}_3^{†}\right)\left(\frac{\mathrm{d}\mathrm{e}\mathrm{t}(\mathbf{M})}{\mathrm{d}\mathrm{e}\mathrm{t}({\mathbf{M}}^{†})}\right).\hfill \end{array}(4)$

Here the sign $†$ indicates the complex conjugate transpose and $\mathrm{d}\mathrm{e}\mathrm{t}$ denotes the determinant of matrices. The non-recursive DT fundamentally differs from recursive approaches. It constructs the $n$th-order solution analytically in one step through the matrix $\mathbf{M}$ and vectors ${\mathbf{Y}}_j$ ($j=\mathrm{1,2,3}$, the same below) avoiding the error-prone iterative dressing of recursive DT. The solution’s degrees of freedom are globally parameterized by 3$n$ complex ${\gamma }_s$ ($s=1,\dots ,3n$), enabling direct control over rogue wave states. $u_{ı0}$ represent the seeding plane-wave solutions

$u_{ı0}=a_{ı}\exp (i{\omega }_{ı}t-i{k}_{ı}z),(5)$

the amplitude $(a_{ı})$, the wavenumber $(k_{ı})$, and the frequency $({\omega }_{ı})$ follow a dispersion relationship

$k_{ı}=(a_1^2+a_2^2){\upsilon }_{ı}+\frac{1}{2}\sigma {\omega }_{ı}^2,{\upsilon }_{ı}=\gamma {\omega }_{ı}-1.(6)$

${\mathbf{Y}}_j$ are $1\times n$ row vectors, defined as

$\left[\begin{array}{c}\hfill {\mathbf{Y}}_1\hfill \\ \hfill {\mathbf{Y}}_2\hfill \\ \hfill {\mathbf{Y}}_3\hfill \end{array}\right]=[{\mathrm{\Phi }}^{(0)},{\mathrm{\Phi }}^{(1)},{\mathrm{\Phi }}^{(2)},\dots ,{\mathrm{\Phi }}^{(n-1)}],(7)$

here ${\mathrm{\Phi }}^{(m)}$ are the series coefficients of the Taylor expansion of the factorized column vector $\mathrm{\Phi }(\lambda )={\mathbf{G}}^{-1}\mathbf{R}(\lambda )$, where the given spectral parameter $\lambda ={\lambda }_0$. $\mathbf{M}$ is an $n\times n$ matrix whose matrix elements $M_{ıj}$ can be obtained by the Taylor expansion of ${\mathrm{\Phi }}^{†}\mathbf{X}\mathrm{\Phi }/(\lambda -{\lambda }^{*})$, and

$\mathbf{G}=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill u_{10}^{*}/a_1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill u_{20}^{*}/a_2\hfill \end{array}\right],\mathbf{X}=\left[\begin{array}{ccc}\hfill \sqrt{{\lambda }^{*}}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \sqrt{\lambda }\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \sqrt{\lambda }\hfill \end{array}\right].(8)$

The key of the above derivation process is to solve the expression for $\mathbf{R}$ and to perform a Taylor expansion of it. Then, by substituting the plane-wave solution (5) into the Lax pair (2), the characteristic function $\mathbf{R}(\lambda )$ can be obtained,

$\mathbf{R}(\lambda )=\mathbf{G}\mathrm{\Phi }(\lambda ),\mathrm{\Phi }(\lambda )={\mathrm{\Gamma }}_1{\mathbf{N}}_1+{\mathrm{\Gamma }}_2{\mathbf{N}}_2+{\mathrm{\Gamma }}_3{\mathbf{N}}_3,(9)$

where ${\mathrm{\Gamma }}_j$ are arbitrary complex constants, and the expressions for ${\mathbf{N}}_j$ are as follows

${\mathbf{N}}_j=\left[\begin{array}{c}\hfill 1\hfill \\ \hfill c_{1j}\hfill \\ \hfill c_{2j}\hfill \end{array}\right]e^{\mathrm{i}{\phi }_j},{\phi }_j={\mu }_{j}t+{\nu }_{j}z,(10)$

with

$\begin{array}{cc}\hfill c_{ıj}& =-\frac{i{a}_{ı}\gamma {\psi }_j}{\sqrt{\lambda }({\psi }_j-2\sigma {\upsilon }_{ı})},{\psi }_j=2{\mu }_j\sigma \gamma -\lambda -\sigma ,\hfill \\ \hfill {\nu }_j& =\frac{2A{\gamma }^2\lambda -{(\lambda -\sigma )}^2}{4\sigma {\gamma }^2}+\frac{i\sqrt{\lambda }}{2}({\omega }_1{a}_1{c}_{1j}+{\omega }_2{a}_2{c}_{2j})\hfill \\ \hfill & +\frac{i\sqrt{\lambda }}{2\gamma \sigma }(A{\gamma }^2-\lambda +\sigma )(a_1{c}_{1j}+a_2{c}_{2j}),\hfill \end{array}(11)$

the parameter ${\mu }_j$ in Equation 10 are the three roots of the cubic equation of $\mu$,

${\left(\mu -\frac{\beta }{2}+\frac{A\gamma }{2\sigma }-\frac{\kappa }{4}\right)}^3-3\varsigma \left(\mu -\frac{\beta }{2}+\frac{A\gamma }{2\sigma }-\frac{\kappa }{4}\right)+2\varrho =0,(12)$

where the coefficients are defined by the following equations

$\varsigma ={\beta }^2+\frac{{\delta }^2}{12}-\frac{\iota }{3\sigma },\varrho ={\beta }^3-\frac{\beta (2\iota +\sigma {\delta }^2)}{4\sigma }+\frac{\delta \varpi }{4\sigma },(13)$

with

$\begin{array}{cc}\hfill & \beta =\frac{A{\gamma }^2+\lambda -\sigma }{3\sigma \gamma }+\frac{\kappa }{6},\iota =a_1^2{\upsilon }_1+a_2^2{\upsilon }_2,\varpi =a_1^2{\upsilon }_1-a_2^2{\upsilon }_2,\hfill \\ \hfill & A=a_1^2+a_2^2,\kappa ={\omega }_1+{\omega }_2,\delta ={\omega }_1-{\omega }_2.\hfill \end{array}(14)$

From Equations 12–14, the spectral parameter $\lambda$ satisfies the following equation

${\varsigma }^3-{\varrho }^2=0,(15)$

and it is easy to see that under the condition (Equation 15), Equation 12 will allow for the double-root ${\mu }_1={\mu }_2={\mu }_0$, or when $\varsigma =\varrho =0$, allow triple-root ${\mu }_1={\mu }_2={\mu }_3={\mu }_0$. Under both conditions, a particular value of ${\lambda }_0$ can be obtained for $\lambda$.

Now, let’s focus on the triple-root case. According to cubic Equation 12 there will be a triple-root

${\mu }_j={\mu }_0=-\frac{\gamma A}{2\sigma }+\frac{\kappa }{4}+\frac{i\sqrt{3}\delta }{4},(16)$

at the point of $A=-\sigma {\delta }^2({\upsilon }_1+{\upsilon }_2)/{\upsilon }_1{\upsilon }_2$, where $\sigma {\upsilon }_{\mathrm{1,2}}<0$.

To simplify the analytic derivation, we split ${\lambda }_0$ into a real part ${\lambda }_r$ and an imaginary part ${\lambda }_m$, i.e., ${\lambda }_0={\lambda }_r+i{\lambda }_m$, in the following form

${\lambda }_r=-A{\gamma }^2-\frac{1}{2}\sigma \gamma \kappa +\sigma ,{\lambda }_m=\frac{3\sqrt{3}}{2}\gamma \delta \sigma .(17)$

When choosing ${\mathrm{\Gamma }}_j$ appropriately, it is easy to check that the factorized eigenfunction $\mathrm{\Phi }(\lambda )$ given by Equation 9 will disappear at $\lambda ={\lambda }_0$. Therefore, the Taylor expansion of $\mathrm{\Phi }(\lambda )$ can be performed at the specific point $\lambda ={\lambda }_0$, thereby obtaining the row vectors ${\mathbf{Y}}_j$ and matrix $\mathbf{M}$. Thus, in the case of triple-root, let $\lambda ={\lambda }_0+\chi {ϵ}^3$ [$\chi ={\lambda }_0-{\lambda }_0^{*}=2i\mathrm{I}\mathrm{m}({\lambda }_0)$]

$\begin{array}{cc}\hfill & {\mathrm{\Gamma }}_1=\frac{1}{3}{\displaystyle \sum _{j=1}^n}\left({\gamma }_{3j-2}-\frac{{\gamma }_{3j-1}{\varphi }_2}{ϵ}+\frac{{\gamma }_{3j}{\varphi }_1}{{ϵ}^2}\right){ϵ}^{3(j-1)},\hfill \\ \hfill & {\mathrm{\Gamma }}_2=\frac{1}{3}{\displaystyle \sum _{j=1}^n}\left({\gamma }_{3j-2}-\frac{{\gamma }_{3j-1}{\varphi }_1}{ϵ}+\frac{{\gamma }_{3j}{\varphi }_2}{{ϵ}^2}\right){ϵ}^{3(j-1)},\hfill \\ \hfill & {\mathrm{\Gamma }}_3=\frac{1}{3}{\displaystyle \sum _{j=1}^n}\left({\gamma }_{3j-2}+\frac{{\gamma }_{3j-1}}{ϵ}-\frac{{\gamma }_{3j}}{{ϵ}^2}\right){ϵ}^{3(j-1)},\hfill \end{array}$

where $ϵ$ is a complex perturbation parameter, ${\gamma }_s$ are $3n$ arbitrary complex constants called structural parameters, ${\varphi }_1=1/2+i\sqrt{3}/2$ and ${\varphi }_2=1/2-i\sqrt{3}/2$, which can be expanded to a power of ${ϵ}^3$ by $\mathrm{\Phi }(\lambda )$,

$\mathrm{\Phi }(\lambda )={\mathrm{\Phi }}^{(0)}+{\mathrm{\Phi }}^{(1)}{ϵ}^3+{\mathrm{\Phi }}^{(2)}{ϵ}^6+\cdot \cdot \cdot +\mathcal{O}({ϵ}^{3n}).(18)$

Here, $\mathcal{O}$ stands for infinitesimals of the same order. Of course, with respect to the case of double-root, it is sufficient to simply replace ${ϵ}^{3n}\to {ϵ}^{2n}$.

Therefore, the matrix elements of $\mathbf{M}$ in Equation 4 are given by the following equation

$\frac{{\mathrm{\Phi }}^{†}\mathbf{X}\mathrm{\Phi }}{\lambda -{\lambda }^{*}}={\displaystyle \sum _{ıj}^n}{M}_{ıj}{ϵ}^{*3(ı-1)}{ϵ}^{3(j-1)}+\mathcal{O}(|ϵ{|}^{6n}).(19)$

From the above derivation procedure, the three one-row matrices ${\mathbf{Y}}_j$ are obtained from Equation 7, and the matrix $\mathit{X}$ is obtained from Equation 8. In this way, we obtain the $n$th-order rogue wave solutions for Equation 4.

The triple-root condition ($\varsigma =\varrho =0$ in Equation 15) induces critical structural changes in the DT: the eigenfunction expansion (Equation 18) requires a cubic perturbation ${ϵ}^3$ (rather than quadratic for double roots), scaling the solution space as ${ϵ}^{3n}$ for $n$th-order solutions. This necessitates the incorporation of 3$n$ complex parameters ${\gamma }_s$ in ${\mathrm{\Gamma }}_j$, effectively tripling the system’s degrees of freedom compared to the double-root case. These expanded parametric capabilities directly enable the matrix $\mathbf{M}$ (Equation 19) to accommodate higher-order polynomial roots, thereby unlocking rogue wave states that can simultaneously host up to $n$($n$+1) fundamental Peregrine solitons. The unique physical manifestation of this phenomenon originates from the nonlinear self-steepening term ($\gamma \ne 0$) in Equation 1, which amplifies the system’s capacity for extreme wave interactions while preserving the mathematical integrity of the triple-root configuration.

3 Complex multiple rogue wave state patterns

When the appropriate ${\mathrm{\Gamma }}_j$ are input, the eigenfunction $\mathrm{\Phi }(\lambda )$ in Equation 9 can be precisely extended to Equation 18. The three expansion terms ${\mathrm{\Phi }}^{(0)}$, ${\mathrm{\Phi }}^{(1)}$, and ${\mathrm{\Phi }}^{(2)}$ can be given by the following equations

${\mathrm{\Phi }}^{(0)}=\mathbf{T}\left[\begin{array}{c}\hfill R_0\hfill \\ \hfill R_1\hfill \\ \hfill R_2\hfill \end{array}\right]e^{i{\phi }_0},{\mathrm{\Phi }}^{(1)}=\mathbf{T}\left[\begin{array}{c}\hfill S_0\hfill \\ \hfill S_1\hfill \\ \hfill S_2\hfill \end{array}\right]e^{i{\phi }_0},{\mathrm{\Phi }}^{(2)}=\mathbf{T}\left[\begin{array}{c}\hfill W_0\hfill \\ \hfill W_1\hfill \\ \hfill W_2\hfill \end{array}\right]e^{i{\phi }_0},(20)$

where $\mathbf{T}=\text{diag}(1,c_{10},c_{20})$(diag means the diagonal matrix), ${\psi }_0=\sigma (\nu -i\sqrt{3}\delta \gamma )(\nu ={\upsilon }_1+{\upsilon }_2)$. ${\phi }_0$, $c_{ı0}$, and ${\nu }_0$ are given by Equations 10, 11 (let $j=0$), respectively. The polynomial representations of $R_{\mathrm{0,1,2}}$, $S_{\mathrm{0,1,2}}$, and $W_{\mathrm{0,1,2}}$ are as follows

$\begin{array}{cc}\hfill R_0& ={\gamma }_1-\frac{i{\gamma }_2}{2}\tau +\frac{i{\gamma }_3}{4}({\tau }^2+2\tau +3i\xi ),\hfill \\ \hfill R_{ı}& =R_0-\frac{\sqrt{3}\delta }{2{\alpha }_{ı}}\left[{\gamma }_2-{\gamma }_3\left(\tau -{\varphi }_{ı}\right)\right],\hfill \\ \hfill S_0& ={\gamma }_1{b}_0+{\gamma }_2{e}_0+{\gamma }_3{h}_0+{\gamma }_4-\frac{i{\gamma }_5}{2}\tau +\frac{i{\gamma }_6}{4}\left({\tau }^2+2\tau +3i\xi \right),\hfill \\ \hfill S_{ı}& =S_0-\frac{\sqrt{3}\delta }{2{\alpha }_{ı}}\left[{\gamma }_1{b}_{ı}+{\gamma }_2{e}_{ı}+{\gamma }_3{h}_{ı}+{\gamma }_5-{\gamma }_6(\tau -{\varphi }_{ı})\right],\hfill \\ \hfill W_0& ={\gamma }_1{l}_0+{\gamma }_2{p}_0+{\gamma }_3{q}_0+{\gamma }_4{b}_0+{\gamma }_5{e}_0+{\gamma }_6{h}_0+{\gamma }_7-\frac{i{\gamma }_8}{2}\tau +\frac{i{\gamma }_9}{4}({\tau }^2+2\tau +3i\xi ),\hfill \\ \hfill W_{ı}& =W_0-\frac{\sqrt{3}\delta }{2{\alpha }_{ı}}\left[{\gamma }_1{l}_{ı}+{\gamma }_2{p}_{ı}+{\gamma }_3{q}_{ı}+{\gamma }_4{b}_{ı}+{\gamma }_5{e}_{ı}+{\gamma }_6{h}_{ı}+{\gamma }_8-{\gamma }_9(\tau -{\varphi }_{ı})\right].\hfill \end{array}(21)$

where

$\begin{array}{cc}\hfill {\alpha }_{ı}& =\frac{{\psi }_0(2\sigma {\upsilon }_{ı}-{\psi }_0)}{4{\upsilon }_{ı}\gamma {\sigma }^2},{\beta }_2=\frac{i(\sqrt{3}\delta -i\kappa )}{8\sigma {\gamma }^2},\hfill \\ \hfill \vartheta & =t-\frac{A\gamma z}{2}+\frac{({\lambda }_0-\sigma )z}{2\gamma }-2{\sigma }^2{\gamma }^{2}z{\beta }_2,\tau =\sqrt{3}\delta \vartheta ,\xi ={\delta }^2\sigma z.\hfill \end{array}(22)$

${\gamma }_s$ are complex structure parameters, the function ϑ and the parameters α_τ, β₂, τ, and ξ are given by Equation 22. According to Equation 21, $R_{\mathrm{0,1,2}}$, $S_{\mathrm{0,1,2}}$, and $W_{\mathrm{0,1,2}}$ have 3, 6, and 9 structure parameters ${\gamma }_s$, corresponding to the first-, second-, and third-order solutions, respectively. The other polynomials $b_{\mathrm{0,1,2}}$, $e_{\mathrm{0,1,2}}$, $h_{\mathrm{0,1,2}}$, $l_{\mathrm{0,1,2}}$, $p_{\mathrm{0,1,2}}$, and $q_{\mathrm{0,1,2}}$ are given in Supplementary Appendix A.

Obviously, the expressions for ${\mathbf{Y}}_j$ and $\mathbf{M}$ can be obtained by substituting Equation 20 into Equations 7, 19, respectively. Then, we can substitute the obtained expressions for ${\mathbf{Y}}_j$ and $\mathbf{M}$ into Equation 4 to obtain up to third-order rogue wave solutions.

3.1 Singlet and doublet rogue wave solutions

Firstly, the first-order rogue wave solutions can be written as

$\begin{array}{cc}\hfill & u_{ı}^{[1]}=u_{ı0}\left[1+\frac{3(1-{\varphi }_{ı}^2){\psi }_0^{*}{R}_0{R}_{ı}^{*}}{2m_{11}}\right]\left(\frac{\sqrt{{\lambda }_0}{m}_{11}}{\sqrt{{\lambda }_0^{*}}{m}_{11}^{*}}\right),\hfill \end{array}(23)$

with

$m_{11}={\lambda }_0^{*}|R_0{|}^2+{\iota }_1|R_1{|}^2+{\iota }_2|R_2{|}^2,{\iota }_{ı}=\frac{a_{ı}^2{\gamma }^2{\psi }_0{\psi }_0^{*}}{({\psi }_0-2\sigma {\upsilon }_{ı})({\psi }_0^{*}-2\sigma {\upsilon }_{ı})}.(24)$

It should be noted that we have translated these solutions on the plane ($z$, $t$) to ensure that their peaks fall on the origin. Thus, at the origin, the ratio of the peak to the average background height of these Peregrine solitons can be estimated by equation $f_{ı}=1+4{\upsilon }_{ı}{\ell }^2/\eta [{(m+{\omega }_{ı})}^2+{\ell }^2],(\eta =\gamma m+1)$ [40]. For the first-order solutions (Equation 23), under the normal dispersion condition ($\sigma =-1$), the background parameters are set as $\gamma =1$, ${\omega }_1=7/4$, ${\omega }_2=5/4$, $a_1=\sqrt{3}/3$, and $a_2=1$. Three structural parameters ${\gamma }_1$-${\gamma }_3$ control nonlinear coupling terms of different orders respectively. When ${\gamma }_2\ne 0$ (${\gamma }_2=1$, ${\gamma }_1={\gamma }_3=0$, Figures 1a,b), the $R_0$ polynomial (Equation 21) dominates the singlet rogue wave structure; when ${\gamma }_1$ and ${\gamma }_3$ are activated in combination (${\gamma }_1=20$, ${\gamma }_1=\mathrm{i}$, and ${\gamma }_3=1$, Figures 1c,d), the quadratic phase modulation of the $S_0$ term (Equation 21) breaks the spatial symmetry and forms a doublet rogue wave mode. This parameter sensitivity arises from the $m_{11}$ polynomial (Equation 24), which manifests itself as ${\gamma }_2$ modulating the amplitude of the single peak, while the ${\gamma }_1/{\gamma }_3$ combination ensures the peak separation. We can observe that under these parameters, the singlet rogue waves in Figures 1a,b exhibit a bright-dark structure, and the peak amplitude of the bright structure exceeds the threefold limit, forming an anomalous Peregrine soliton structure [26, 27]. The doublet rogue wave states in Figures 1c,d consist of two completely separated Peregrine solitons, exhibiting bright-bright and dark-dark structures. This bright-bright configuration also manifests an anomalous Peregrine soliton structure. Unlike scalar NLS rogue waves, this unique amplitude characteristic is attributed to the coupling between field components and the coupling between space and time. Coupling between field components results in energy transfer between the different elements such that the peak amplitude of one wave component is much higher than the threefold background height ($f_1=3.5$), and the peak amplitude of the other wave component decreases ($f_2=0.5$). At the same time, due to the self-steepening ($\gamma$) effect, spatiotemporal coupling will lead to further space-time rearrangement, which will make the Peregrine soliton break through the upper limit of amplitude and exceed the threefold amplitude limit.

Figure 1

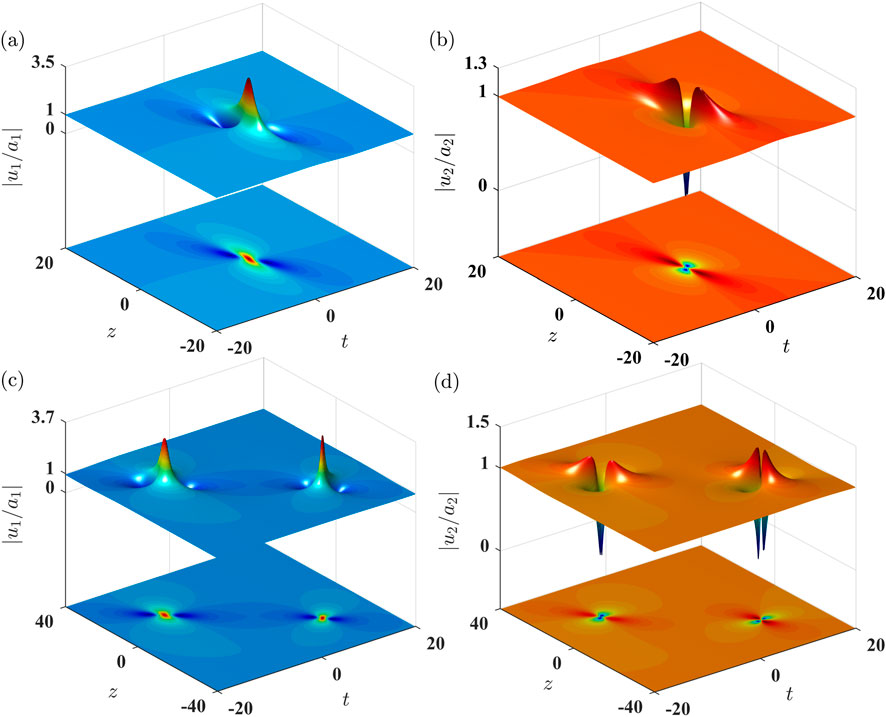
Figure 1. Three-dimensional surface (top) and contour (bottom) plots of the singlet and doublet rogue wave states in the normal dispersion regime ($\sigma =-1$).(a,b) ${\gamma }_2=1$, and ${\gamma }_1={\gamma }_3=0$; (c,d) ${\gamma }_1=20$, ${\gamma }_2=\mathrm{i}$, and ${\gamma }_3=1$. The background parameters are given by $\gamma =1$, ${\omega }_1=7/4$, ${\omega }_2=5/4$, $a_1=\sqrt{3}/3$, and $a_2=1$. Axes in dimensionless units.

This phenomenon results from the nonlinear enhancement of the phase modulation by the self-steepening term, which makes the energy concentrate from the dark component to the bright component. To illustrate this point more clearly, we take the Manakov system ($\gamma =0$, no self-steepening effect) as an example, where the maximum peak amplitudes of the two components obtained are only twice the background height [26, 27]. In the Manakov system, coexistence behavior only occurs in the anomalous dispersion region [44], while the vector CLL-NLS model makes coexistence of different rogue wave solutions occur in a wide range of parameters in the anomalous and normal dispersion regions due to the self-steepening effect, significantly expanding the region in favor of coexistence behavior in the Manakov system [40]. The ubiquitous existence of rogue waves is correlated with two peaks in the Stokes frequency shift region in the modulation instability (MI) spectrum. The ”$\gamma$” influences the shape and characteristics of the MI spectrum indirectly by affecting the dispersion and nonlinear characteristics of the system, thus establishing a relationship with the appearance of rogue waves.

3.2 Doublet, quartet, and sextet rogue wave solutions

Meanwhile, the second-order rogue wave solutions can be written as

$\begin{array}{cc}\hfill & u_{ı}^{[2]}=u_{ı0}\left[1+\frac{3(1-{\varphi }_{ı}^2){\psi }_0^{*}(R_{ı}^{*}X-S_{ı}^{*}Y)}{2W}\right]\left(\frac{{\lambda }_{0}W}{{\lambda }_0^{*}{W}^{*}}\right),\hfill \end{array}(25)$

with

$\begin{array}{cc}\hfill & m_{12}={\lambda }_0^{*}{R}_0^{*}{S}_0+{\iota }_1{R}_1^{*}{S}_1+{\iota }_2{R}_2^{*}{S}_2-\frac{i{\lambda }_m{\lambda }_0^{*}|R_0{|}^2}{{\lambda }_0}-\frac{{\lambda }_r{m}_{11}}{{\lambda }_0},\hfill \\ \hfill & m_{21}={\lambda }_0^{*}{R}_0{S}_0^{*}+{\iota }_1{R}_1{S}_1^{*}+{\iota }_2{R}_2{S}_2^{*}-i{\lambda }_m|R_0{|}^2-m_{11},\hfill \\ \hfill & m_{22}={\lambda }_0^{*}|S_0{|}^2+{\iota }_1|S_1{|}^2+{\iota }_2|S_2{|}^2-i{\lambda }_m(R_0{S}_0^{*}+S_0{R}_0^{*})\hfill \\ \hfill & -m_{12}-\frac{{\lambda }_m^2{R}_0(R_0^{*}+2S_0^{*})}{{\lambda }_0}-\frac{{\lambda }_r{m}_{21}-i{\lambda }_m{m}_{11}}{{\lambda }_0},\hfill \\ \hfill & X=R_0{m}_{22}-S_0{m}_{21},Y=R_0{m}_{12}-S_0{m}_{11},W=m_{11}{m}_{22}-m_{12}{m}_{21}.\hfill \end{array}(26)$

For the second-order solutions, we found that the rogue wave solutions (Equation 25) exhibit doublet, quartet, and sextet rogue wave states only when appropriate structural parameters are selected. Specifically, to obtain such spatiotemporally distributed rogue wave doublets, we should ensure ${\gamma }_1\ne 0$, ${\gamma }_5\ne 0$, and ${\gamma }_2={\gamma }_3=0$; to obtain quartets, ${\gamma }_2\ne 0$ and ${\gamma }_3=0$ should be satisfied; and to generate sextets, ${\gamma }_3\ne 0$ must hold. This can also be verified by examining the highest order of the polynomial $m_{11}{m}_{22}-m_{12}{m}_{21}$ in Equation 26 [46].

Figure 2 shows the doublet, quartet, and sextet rogue wave structures under normal dispersion ($\sigma =-1$) with the same background parameters in Figure 1, but different structural parameters as: (a),(b) ${\gamma }_1=1$, ${\gamma }_5=30$ (doublet rogue wave states); (c),(d) ${\gamma }_1=\mathrm{i}$, ${\gamma }_2=1$, and ${\gamma }_5=300$ (quartet rogue wave states); (e),(f) ${\gamma }_1=5\mathrm{i}$, ${\gamma }_2=2$, ${\gamma }_3=1$, and ${\gamma }_5=400$ (sextet rogue wave states). Unlike the first-order solutions case, the doublet rogue wave states appearing here are obtained from the second-order solutions with more complex six structural parameters. From Figure 2, we can also see that the structures of this even number of multiple rogue wave states consist of two, four, and six fully separated Peregrine solitons, respectively. It is worth noting that each component in these multiple rogue wave states is practically identical, although some may be slightly tilted due to strong interactions among nearby components [41]. This is not surprising, since a pair of complex conjugate ${\lambda }_0$ values are identified from Equation 17, indicating that coexisting rogue wave phenomena do not occur under this special condition.

Figure 2

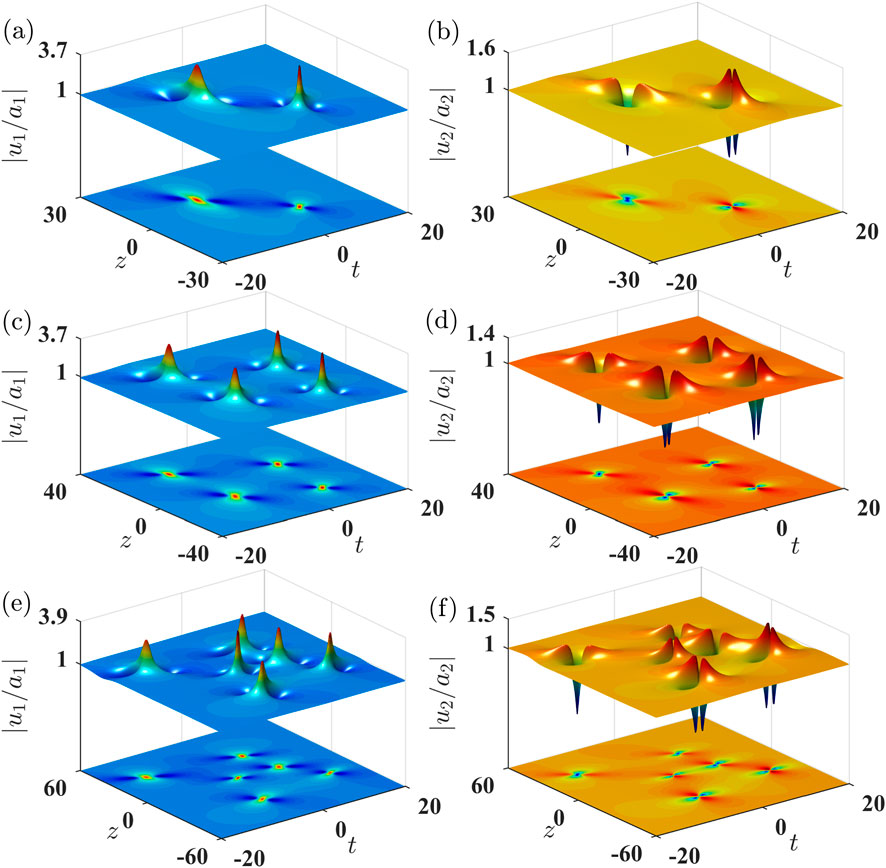
Figure 2. Three-dimensional surface (top) and contour (bottom) plots of the doublet, quartet, and sextet rogue wave structures in the normal dispersion regime ($\sigma =-1$). (a,b) ${\gamma }_1=1$, ${\gamma }_5=30$ (doublets); (c,d) ${\gamma }_1=1$, ${\gamma }_2=1$, and ${\gamma }_5=400$ (quartets); (e,f) ${\gamma }_1=4\mathrm{i}$, ${\gamma }_2=2$, ${\gamma }_3=1$, and ${\gamma }_5=500$ (sextets). Those unspecified parameters ${\gamma }_s$ are set to zero. The other background parameters are kept the same as in Figure 1.

3.3 Sextet, nonet, and dodecatet rogue wave solutions

Furthermore, the third-order rogue wave solutions can be obtained

$\begin{array}{cc}\hfill & u_{ı}^{[3]}=u_{ı0}\left[1+\frac{3(1-{\varphi }_{ı}^2){\psi }_0^{*}(R_{ı}^{*}E+S_{ı}^{*}F+W_{ı}^{*}H)}{2G}\right]\left(\frac{{\lambda }_0\sqrt{{\lambda }_0}G}{{\lambda }_0^{*}\sqrt{{\lambda }_0^{*}}{G}^{*}}\right),\hfill \end{array}(27)$

with

$\begin{array}{cc}\hfill & E=R_0(m_{22}{m}_{33}-m_{23}{m}_{32})-S_0(m_{21}{m}_{33}-m_{23}{m}_{31})+W_0(m_{21}{m}_{32}-m_{22}{m}_{31}),\hfill \\ \hfill & F=R_0(m_{13}{m}_{32}-m_{12}{m}_{33})+S_0(m_{11}{m}_{33}-m_{13}{m}_{31})-W_0(m_{11}{m}_{32}-m_{12}{m}_{31}),\hfill \\ \hfill & H=R_0(m_{12}{m}_{23}-m_{13}{m}_{22})-S_0(m_{11}{m}_{23}-m_{13}{m}_{21})+W_0(m_{11}{m}_{22}-m_{12}{m}_{21}),\hfill \\ \hfill & G=m_{11}(m_{22}{m}_{33}-m_{23}{m}_{32})-m_{12}(m_{21}{m}_{33}-m_{23}{m}_{31})+m_{13}(m_{21}{m}_{32}-m_{22}{m}_{31}).\hfill \end{array}(28)$

where

$\begin{array}{cc}\hfill m_{13}& =\frac{i{\lambda }_m(R_1^{*}{S}_1{\iota }_1+R_2^{*}{S}_2{\iota }_2)}{{\lambda }_0}+\frac{{\lambda }_m^2(|R_1{|}^2{\iota }_1+|R_2{|}^2{\iota }_2)}{2{\lambda }_0^2}\hfill \\ \hfill & +R_0^{*}{W}_0{\lambda }_0^{*}+R_1^{*}{W}_1{\iota }_1+R_2^{*}{W}_2{\iota }_2-m_{12},\hfill \\ \hfill m_{31}& =\frac{{\lambda }_m^2|R_0{|}^2}{2{\lambda }_0^{*}}-i{\lambda }_m{R}_0{S}_0^{*}+R_0{W}_0^{*}{\lambda }_0^{*}+R_1{W}_1^{*}{\iota }_1+R_2{W}_2^{*}{\iota }_2-m_{21},\hfill \\ \hfill m_{23}& =\frac{i{\lambda }_m(|S_1{|}^2{\iota }_1+|S_2{|}^2{\iota }_2)}{{\lambda }_0}+\frac{{\lambda }_m^2(R_1{S}_1^{*}{\iota }_1+R_2{S}_2^{*}{\iota }_2)}{2{\lambda }_0^2}\hfill \\ \hfill & -i{\lambda }_m{R}_0^{*}{W}_0+S_0^{*}{W}_0{\lambda }_0^{*}+S_1^{*}{W}_1{\iota }_1+S_2^{*}{W}_2{\iota }_2-m_{22}-m_{13},\hfill \\ \hfill m_{32}& =\frac{i{\lambda }_m(R_1{W}_1^{*}{\iota }_1+R_2{W}_2^{*}{\iota }_2)}{{\lambda }_0}+\frac{{\lambda }_m^2{R}_0^{*}{S}_0}{2{\lambda }_0^{*}}-i{\lambda }_m|S_0{|}^2\hfill \\ \hfill & +S_0{W}_0^{*}{\lambda }_0^{*}+S_1{W}_1^{*}{\iota }_1+S_2{W}_2^{*}{\iota }_2-m_{22}-m_{31},\hfill \\ \hfill m_{33}& =\frac{i{\lambda }_m(S_1{W}_1^{*}{\iota }_1+S_2{W}_2^{*}{\iota }_2)}{{\lambda }_0}+\frac{{\lambda }_m^2{R}_0^{*}{W}_0}{2{\lambda }_0^{*}}+\frac{{\lambda }_m^2(R_1{W}_1^{*}{\iota }_1+R_2{W}_2^{*}{\iota }_2)}{2{\lambda }_0^2}\hfill \\ \hfill & -i{\lambda }_m{S}_0^{*}{W}_0+|W_0{|}^2{\lambda }_0^{*}+|W_1{|}^2{\iota }_1+|W_2{|}^2{\iota }_2-m_{23}-m_{32}.\hfill \end{array}(29)$

Similar to second-order solutions, for third-order solutions (Equation 27), the spatiotemporal distribution of these rogue waves depends on the selection of nine structural parameters ${\gamma }_s$. Specifically, to obtain this spatiotemporally distributed rogue wave sextets, we should ensure that ${\gamma }_1\ne 0$, ${\gamma }_8\ne 0$, and ${\gamma }_2={\gamma }_3=0$; to obtain nonets, ${\gamma }_2\ne 0$ and ${\gamma }_3=0$ should be satisfied; and to generate the dodecatets, ${\gamma }_3\ne 0$ must be true, while it is necessary to ensure that ${\gamma }_8$ is large enough to ensures the peak separation. This also can be verified by examining the highest order of polynomial $G$ in Equation 28 (combined with Equations 24, 26, 29). Figure 3 shows the structures of multiple rogue wave states with normal dispersion ($\sigma =-1$), and the background parameters are also the same as in Figure 1. We find that for the third-order solutions, there are not an even number of multiple rogue wave states as we expected. Instead, by appropriately selecting the nine structural parameters, sextet rogue wave states (${\gamma }_1=1$, ${\gamma }_8=10000$) form in Figures 3a,b, nonet rogue wave states (${\gamma }_1=3$, ${\gamma }_2=1$, and ${\gamma }_8=20000$) form in Figures 3c,d, and dodecatet rogue wave states (${\gamma }_1=15\mathrm{i}$, ${\gamma }_2=5$, ${\gamma }_3=1$, and ${\gamma }_8=80000$) form in Figures 3e,f, which consist of six, nine, and twelve fully separated Peregrine solitons, respectively. The parameterization capability of non-recursive DT is crucial here. By adjusting ${\gamma }_{1-9}$ in Equation 21, sextet, nonet, and dodecatet states are generated directly (Figure 3), which would require unfeasible nested iterations in a recursive framework. Moreover, the nine Peregrine solitons (non-even modes) emerging in the third-order solution break through the constraint of even-numbered solitons imposed by traditional second-order solutions. We also found that these modes undergo drastic changes once the structural parameters are altered. Furthermore, only when the Peregrine soliton components are well-separated (easily achievable through appropriate parameter selection) do the spatiotemporal distributions exhibit rogue wave structures corresponding to the aforementioned nomenclature [31, 35]. At the same time, we find that the triple-root condition directly implements the observed diversity of rogue wave states. By introducing 3$n$ complex parameters ${\gamma }_s$ that circumvent the even-soliton restriction imposed by double-root systems (where second-order solutions are constrained to 2/4/6 solitons), this condition enables unprecedented odd-numbered configurations like the nonet state (9 solitons) in third-order solutions (Figures 3c,d). The cubic perturbation ${ϵ}^{3n}$ simultaneously generates highly degenerate roots in the determinant det $\mathbf{M}$ (Equation 19), permitting fully decoupled solitons in intricate spatial patterns such as the dodecatet rogue wave states (Figure 3f). Physically, this reflects the role of self-steepening-induced spatiotemporal coupling. The condition $\sigma {\upsilon }_{\mathrm{1,2}}<0$ (Equation 16) and $\gamma \ne 0$ are necessary for triple-roots, linking anomalous amplitude growth (Figure 1) to multi-soliton state formation.

Figure 3

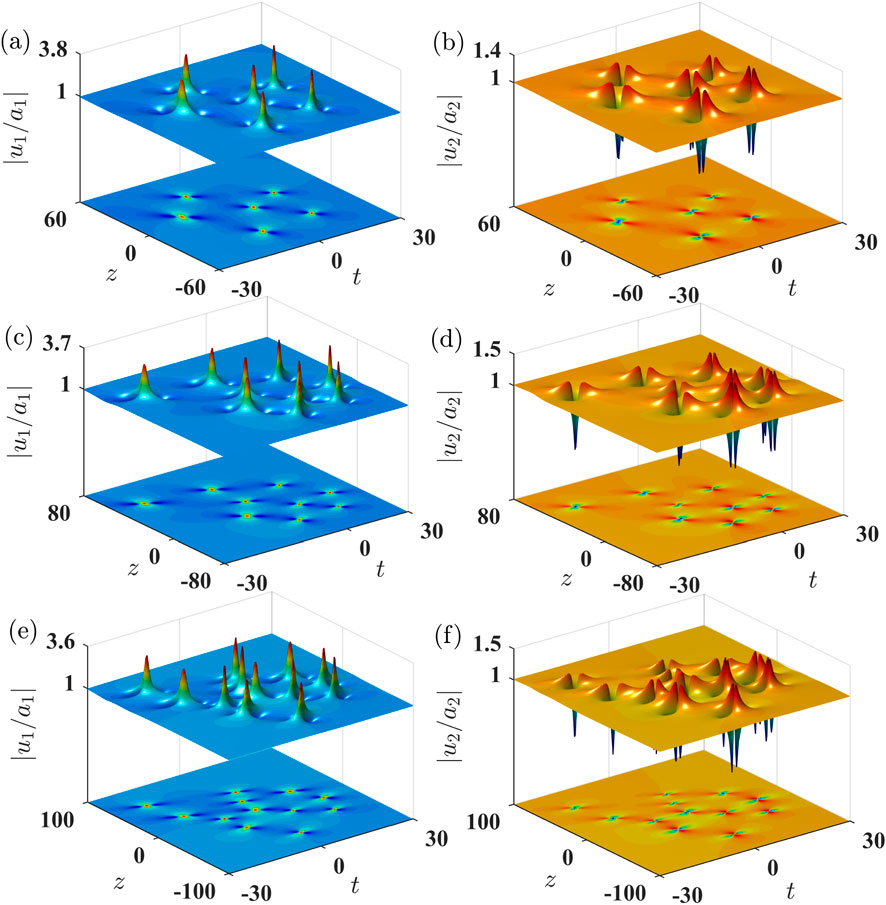
Figure 3. Three-dimensional surface (top) and contour (bottom) plots of the sextet, nonet, and dodecatet rogue wave structures in the normal dispersion regime ($\sigma =-1$). (a,b) ${\gamma }_1=1$, ${\gamma }_8=10000$ (sextets); (c,d) ${\gamma }_1=3$, ${\gamma }_2=1$, and ${\gamma }_8=20000$ (nonets); (e,f) ${\gamma }_1=15\mathrm{i}$, ${\gamma }_2=5$, ${\gamma }_3=1$, and ${\gamma }_8=80000$ (dodecatets). Those unspecified parameters ${\gamma }_s$ are set to zero. The other background parameters are kept the same as in Figure 1.

The emergence of non-even-mode configurations (e.g., the nine-soliton state in Figures 3c,d) is fundamentally attributed to the self-steepening term ($\gamma u_{ıt}$) in Equation 1. This term introduces two key symmetry-breaking mechanisms: (i) the intensity-dependent group velocity shift ${\upsilon }_{ı}=\gamma {\omega }_{ı}-1$ (Equation 6) causes temporal misalignment between components. As demonstrated in Ref. [26], this decouples the phase locking enforced in Manakov systems ($\gamma =0$), allowing independent soliton clustering. (ii) The term $i\gamma u_{ıt}$ breaks the SU(2) rotational symmetry of the vector system [40, 41]. Under triple-root conditions, this permits odd-numbered states (e.g., nonet) that violate even-mode constraints observed in scalar systems [27]. Specifically, the imaginary part ${\lambda }_m=\frac{3\sqrt{3}}{2}\gamma \delta \sigma$ (Equation 17) quantifies the symmetry-breaking strength. When $\gamma \ne 0$, ${\lambda }_m\ne 0$ lifts the degeneracy of soliton positions, enabling the nine-soliton configuration in Figures 3c,d. This contrasts with Manakov systems, where ${\lambda }_m=0$ forces even-mode distributions [44].

Finally, let us comment on the rules involving the number of fundamental Peregrine solitons for multiple rogue wave states. Based on the above results, we find that for the first-order solutions, one and two Peregrine solitons constitute the singlet and doublet rogue wave states; whereas for the second-order solutions, two, four, and six Peregrine solitons constitute the doublet, quartet, and sextet rogue wave states; and for the third-order solutions, six, nine, and twelve Peregrine solitons constitute the sextet, nonet, and dodecatet rogue wave states, respectively. From this perspective, the number of fundamental Peregrine solitons for the $n$th-order solution forms an arithmetic sequence with the general term:

$T_k=n(n-1)+n(k-1)(k=\mathrm{1,2,3}).$

where $k$ denotes the rogue wave state pattern. (i) The first term $T_1=n(n-1)$ corresponds to the terminal mode of the ($n$-1)th-order solutions (e.g., the first term 6 of the third-order = the last term of second-order); (ii) the common difference $d=n$ is due to linear scaling of soliton generation relative to order $n$ in a non-recursive DT framework, governed by the $3n$ structural parameters ${\gamma }_s$ and the $n\times n$ matrix $\mathbf{M}$ in Equation 4; (iii) when all ${\gamma }_s$ parameters activate different Peregrine components, the Taylor expansion order ${ϵ}^{3n}$ (Equation 18) and the determinant det $\mathbf{M}$ (Equation 19) determine the polynomial growth of the soliton number (the highest $n$($n$+1) terms).

3.4 Limitations and outlook

This study employs idealized assumptions that may limit real-world realization. (i) Plane-wave background simplification (Equation 5): real systems exhibit amplified spontaneous emission noise and finite energy, with peak amplitudes 5 times lower than theoretically predicted [17], and future work should incorporate stochastic backgrounds [20]. (ii) Triple-root sensitivity: the condition $\sigma {\upsilon }_{\mathrm{1,2}}<0$ (Equation 16) requires exact parameter matching in waveguides. Small deviations in $\gamma$ (wavelength-dependent [25]) suppress nonet states. (iii) Material nonlinearities: the model neglects Raman scattering and two-photon absorption, critical for pulses $<$100 fs in chalcogenide glasses or semiconductors [24]. Despite these, recent experiments [17, 24] confirm that key phenomena (e.g., amplitude anomalies) persist in noisy environments, supporting the model’s predictive value.

4 Conclusion

In the study of spatiotemporal dynamics in nonlinear optical systems, the vector CLL-NLS model reveals phenomena that are impossible in scalar NLS: anomalous peak amplitudes, inhomogeneous soliton states (e.g., 9-soliton states) and an arithmetic sequence soliton distributions. These phenomena are essentially caused by multi-field coupling and self-steepening effects, making the model crucial for multichannel nonlinear photonics. While the idealized model neglects noise and material nonlinearities (Section 3.4), its predictions - anomalous amplitudes, nonet states, and arithmetic progressions - provide testable benchmarks for nonlinear photonics. Experimental validation in ${\chi }^{(2)}$ waveguides [24, 25, 47] is underway. Unlike the Manakov system’s even-mode solutions [44], the CLL-NLS system’s self-steepening term ($\gamma \ne 0$) enables asymmetric localization, anomalous peak amplification, and odd-mode rogue wave states (e.g., nonets). These differences are rooted in the SU(2) symmetry breaking and cross-component energy transfer mechanisms, as quantified in [27, 44]. Rogue waves of high amplitude can enhance the sensitivity of photonic sensors. For example, in blood glucose detection, the refractive index disturbance caused by the change of urine glucose concentration, high-amplitude solitons can improve the coupling efficiency of the waveguide evanescent field [53]. In addition, in cancer marker detection, the local field enhancement effect of infrared laser in photonic crystal ring cavity [54] matches the spatiotemporal focusing characteristics of rogue waves.

This paper systematically investigates the evolution patterns of higher-order anomalous soliton states through a non-recursive DT method, based on a multi-component optical pulse propagation model constructed by the vector CLL-NLS equation. The research reveals that in nonlinear fiber media, rogue wave states with different orders exhibit predictable Peregrine soliton structures: (i) first-order solutions can form the structures with singlet (one Peregrine soliton) and doublet (two Peregrine soliton) rogue wave states, corresponding to bright-dark alternating spatiotemporal localization characteristics. (ii) Second-order solutions generate soliton clusters with doublet, quartet (four Peregrine soliton), and sextet (six Peregrine soliton) configurations. (iii) Third-order solutions further demonstrate complex soliton structures including sextet, nonet (nine Peregrine soliton), and dodecatet (twelve Peregrine soliton) formations. The number distribution of Peregrine solitons in $n$-order rogue wave states follows an arithmetic progression $T_k=n(n-1)+n(k-1)$ ($k=\mathrm{1,2,3}$), where $T_1=n(n-1)$ is the minimal count (linked to the ($n$-1)th-order terminal state); $T_3=n(n+1)$ is the maximum count; the common difference $n$ reflects the linear growth per state transition, tied to the dimension of the DT matrix $\mathbf{M}$. Notably, while the first-order solution exhibits dual-mode distribution, all higher-order solutions demonstrate tri-mode distribution patterns. We hope these findings may contribute to understanding complex rogue wave dynamics in multi-component nonlinear systems.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author contributions

CP: Methodology, Conceptualization, Writing – review and editing, Data curation, Investigation, Writing – original draft, Software, Visualization, Validation. GW: Writing – original draft, Visualization, Validation. RB: Visualization, Writing – original draft, Validation. BS: Validation, Visualization, Writing – original draft. HZ: Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by the Key Project of Natural Science Research in Colleges and Universities of Anhui Province Department of Education (Grant No. 2023AH051666), and the Talent Research Initiation Fund Project of Tongling University (Grant No. 2023tlxyrc13), and the General Project of Natural Science Research at Tongling University (No. 2024tlxykj04), and the National Natural Science Foundation of China (Grant No. 12404350), and Zhejiang Provincial Natural Science Foundation of China (Grant No. LQ23F050003).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2025.1649398/full#supplementary-material

References

1. Dysthe K, Krogstad HE, Müller P. Oceanic rogue waves. Annu Rev Fluid Mech (2008) 40:287–310. doi:10.1146/annurev.fluid.40.111406.102203

CrossRef Full Text | Google Scholar

2. Chabchoub A, Hoffmann NP, Akhmediev N. Rogue wave observation in a water wave tank. Phys Rev Lett (2011) 106:204502. doi:10.1103/physrevlett.106.204502

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Dematteis G, Grafke T, Onorato M, Vanden-Eijnden E. Experimental evidence of hydrodynamic instantons: the universal route to rogue waves. Phys Rev (2019) 9:041057. doi:10.1103/physrevx.9.041057

CrossRef Full Text | Google Scholar

4. Solli DR, Ropers C, Koonath P, Jalali B. Optical rogue waves. Nature (2007) 450:1054–7. doi:10.1038/nature06402

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Wabnitz S. Nonlinear guided wave optics: a testbed for extreme waves. Bristol, UK: IOP Publishing (2017). p. 387.

Google Scholar

6. Wang Z, Nithyanandan K, Coillet A, Tchofo-Dinda P, Grelu P. Buildup of incoherent dissipative solitons in ultrafast fiber lasers. Phys Rev Res (2020) 2:013101. doi:10.1103/physrevresearch.2.013101

CrossRef Full Text | Google Scholar

7. Lin P-C, I L. Synchronization of multiscale waveform focusing for rogue wave generation in dust acoustic wave turbulence. Phys Rev Res (2020) 2:023090. doi:10.1103/physrevresearch.2.023090

CrossRef Full Text | Google Scholar

8. Copus MG, Camley RE. Creation of magnetic rogue waves. Phys Rev B (2020) 102:220410. doi:10.1103/physrevb.102.220410

CrossRef Full Text | Google Scholar

9. Bludov YV, Konotop VV, Akhmediev N. Matter rogue waves. Phys Rev A (2009) 80:033610. doi:10.1103/physreva.80.033610

CrossRef Full Text | Google Scholar

10. Mihalache D. Localized structures in optical and matter-wave media: a selection of recent studies. Rom Rep Phys (2021) 73:403. Available online at: https://rrp.nipne.ro/2021/AN73403.pdf

Google Scholar

11. Marcucci G, Pierangeli D, Conti C. Theory of neuromorphic Computing by waves: machine learning by rogue waves, dispersive shocks, and solitons. Phys Rev Lett (2020) 125:093901. doi:10.1103/physrevlett.125.093901

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Marcucci G, Pierangeli D, Agranat AJ, Lee R-K, DelRe E, Conti C. Topological control of extreme waves. Nat Commun (2019) 10:5090. doi:10.1038/s41467-019-12815-0

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Akhmediev N, Ankiewicz A, Taki M. Waves that appear from nowhere and disappear without a trace. Phys Lett A (2009) 373:675–8. doi:10.1016/j.physleta.2008.12.036

CrossRef Full Text | Google Scholar

14. Ankiewicz A, Clarkson PA, Akhmediev N. Rogue waves, rational solutions, the patterns of their zeros and integral relations. J Phys A: Math Theor (2010) 43:122002. doi:10.1088/1751-8113/43/12/122002

CrossRef Full Text | Google Scholar

15. Peregrine DH. Water waves, nonlinear Schrödinger equations and their solutions. J Aust Math Soc Ser B Appl Math (1983) 25:16–43. doi:10.1017/s0334270000003891

CrossRef Full Text | Google Scholar

16. Shrira VI, Geogjaev VV. What makes the peregrine soliton so special as a prototype of freak waves? J Eng Math (2010) 67:11–22. doi:10.1007/s10665-009-9347-2

CrossRef Full Text | Google Scholar

17. Kibler B, Fatome J, Finot C, Millot G, Dias F, Genty G, et al. The peregrine soliton in nonlinear fibre optics. Nat Phys (2010) 6:790–5. doi:10.1038/nphys1740

CrossRef Full Text | Google Scholar

18. Tikan A, Billet C, El G, Tovbis A, Bertola M, Sylvestre T, et al. Universality of the peregrine soliton in the focusing dynamics of the cubic nonlinear Schrödinger equation. Phys Rev Lett (2017) 119:033901. doi:10.1103/physrevlett.119.033901

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Bailung H, Sharma SK, Nakamura Y. Observation of Peregrine solitons in a multicomponent plasma with negative ions. Phys Rev Lett (2011) 107:255005. doi:10.1103/physrevlett.107.255005

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Chabchoub A. Tracking breather dynamics in irregular sea state conditions. Phys Rev Lett (2016) 117:144103. doi:10.1103/physrevlett.117.144103

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Guo B-L, Ling L-M. Rogue wave, breathers and bright-dark-rogue solutions for the coupled Schrödinger equations. Chin Phys Lett (2011) 28:110202. doi:10.1088/0256-307x/28/11/110202

CrossRef Full Text | Google Scholar

22. Chan HN, Malomed BA, Chow KW, Ding E. Rogue waves for a system of coupled derivative nonlinear Schrödinger equations. Phys Rev E (2016) 93:012217. doi:10.1103/physreve.93.012217

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Agrawal GP. Nonlinear Fiber optics. 4th ed. San Diego, CA: Academic (2007).

Google Scholar

24. Moses J, Wise FW. Controllable self-steepening of ultrashort pulses in quadratic nonlinear media. Phys Rev Lett (2006) 97:073903. doi:10.1103/physrevlett.97.073903

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Moses J, Malomed BA, Wise FW. Self-steepening of ultrashort optical pulses without self-phase-modulation. Phys Rev A (2007) 76:021802. doi:10.1103/physreva.76.021802

CrossRef Full Text | Google Scholar

26. Chen S, Ye Y, Soto-Crespo JM, Grelu P, Baronio F. Peregrine solitons beyond the threefold limit and their two-soliton interactions. Phys Rev Lett (2018) 121:104101. doi:10.1103/physrevlett.121.104101

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Chen S, Pan C, Grelu P, Baronio F, Akhmediev N. Fundamental Peregrine solitons of ultrastrong amplitude enhancement through self-steepening in vector nonlinear systems. Phys Rev Lett (2020) 124:113901. doi:10.1103/physrevlett.124.113901

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Ye Y, Bu L, Wang W, Chen S, Baronio F, Mihalache D. Peregrine solitons on a periodic background in the vector cubic-quintic nonlinear Schrödinger equation. Front Phys (2020) 8:596950. doi:10.3389/fphy.2020.596950

CrossRef Full Text | Google Scholar

29. Akhmediev N, Ankiewicz A, Soto-Crespo JM. Rogue waves and rational solutions of the nonlinear Schrödinger equation. Phys Rev E (2009) 80:026601. doi:10.1103/physreve.80.026601

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Ohta Y, Yang J. General high-order rogue waves and their dynamics in the nonlinear Schrödinger equation. Proc R Soc (2012) 468:1716–40. doi:10.1098/rspa.2011.0640

CrossRef Full Text | Google Scholar

31. He JS, Zhang HR, Wang LH, Porsezian K, Fokas AS. Generating mechanism for higher-order rogue waves. Phys Rev E (2013) 87:052914. doi:10.1103/physreve.87.052914

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Chabchoub A, Akhmediev N. Observation of rogue wave triplets in water waves. Phys Lett A (2013) 377:2590–3. doi:10.1016/j.physleta.2013.07.027

CrossRef Full Text | Google Scholar

33. Chen S, Soto-Crespo JM, Grelu P. Dark three-sister rogue waves in normally dispersive optical fibers with random birefringence. Opt Express (2014) 22:27632–42. doi:10.1364/oe.22.027632

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Chabchoub A, Hoffmann N, Onorato M, Akhmediev N. Super rogue waves: observation of a higher-order breather in water waves. Phys Rev X (2012) 2:011015. doi:10.1103/physrevx.2.011015

CrossRef Full Text | Google Scholar

35. Chen S, Zhou Y, Bu L, Baronio F, Soto-Crespo JM, Mihalache D. Super chirped rogue waves in optical fibers. Opt Express (2019) 27:11370–84. doi:10.1364/oe.27.011370

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Yan X, Chen Y. Rogue wave patterns of the Fokas-Lenells equation. EPL (2023) 144:62001. doi:10.1209/0295-5075/ad177b

CrossRef Full Text | Google Scholar

37. Li H, Chen Y, Zhou D. Rogue wave patterns of two-component nonlinear Schrödinger equation coupled to the Boussinesq equation. Commun Nonlinear Sci Numer Simul (2024) 140:108406. doi:10.1016/j.cnsns.2024.108406

CrossRef Full Text | Google Scholar

38. Ling L, Su H. Rogue waves and their patterns for the coupled Fokas-Lenells equations. Physica D (2024) 461:134111. doi:10.1016/j.physd.2024.134111

CrossRef Full Text | Google Scholar

39. Duan Z, Tao X, Yang B. Patterns of rogue waves in the sharp-line Maxwell–Bloch system. Chaos Soliton Fract (2024) 187:115407. doi:10.1016/j.chaos.2024.115407

CrossRef Full Text | Google Scholar

40. Pan C, Bu L, Chen S, Mihalache D, Grelu P, Baronio F. Omnipresent coexistence of rogue waves in a nonlinear two-wave interference system and its explanation by modulation instability. Phys Rev Res (2021) 3:033152. doi:10.1103/physrevresearch.3.033152

CrossRef Full Text | Google Scholar

41. Pan C, Bu L, Chen S, Yang W-X, Mihalache D, Grelu P, et al. General rogue wave solutions under SU(2) transformation in the vector Chen–Lee–Liu nonlinear Schrödinger equation. Physica D (2022) 434:133204. doi:10.1016/j.physd.2022.133204

CrossRef Full Text | Google Scholar

42. Kedziora DJ, Ankiewicz A, Akhmediev N. Classifying the hierarchy of nonlinear-Schrödinger-equation rogue-wave solutions. Phys Rev E (2013) 88:013207. doi:10.1103/physreve.88.013207

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Ankiewicz A, Akhmediev N. Multi-rogue waves and triangular numbers. Rom Rep Phys (2017) 69:104. Available online at: https://rrp.nipne.ro/2017/AN104.pdf

Google Scholar

44. Chen S, Mihalache D. Vector rogue waves in the manakov system: diversity and compossibility. J Phys A: Math Theor (2015) 48:215202. doi:10.1088/1751-8113/48/21/215202

CrossRef Full Text | Google Scholar

45. Ye Y, Zhou Y, Chen S, Baronio F, Grelu P. General rogue wave solutions of the coupled fokas-lenells equations and non-recursive Darboux transformation. Proc R Soc (2019) 475:20180806. doi:10.1098/rspa.2018.0806

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Ye Y, Liu J, Bu L, Pan C, Chen S, Mihalache D. Rogue waves and modulation instability in an extended Manakov system. Nonlinear Dyn (2020) 102:1801–12. doi:10.1007/s11071-020-06029-z

CrossRef Full Text | Google Scholar

47. Baronio F, De Angelis C, Marangoni M, Manzoni C, Ramponi R, Cerullo G. Spectral shift of femtosecond pulses in nonlinear quadratic PPSLT crystals. Opt Express (2006) 14:4774–9. doi:10.1364/oe.14.004774

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Kodama Y, Hasegawa A. Nonlinear pulse propagation in a monomode dielectric guide. IEEE J Quan Electron (1987) 23:510–24. doi:10.1109/jqe.1987.1073392

CrossRef Full Text | Google Scholar

49. Kang JU, Stegeman GI, Aitchison JS, Akhmediev N. Observation of Manakov spatial solitons in AlGaAs planar waveguides. Phys Rev Lett (1996) 76:3699–702. doi:10.1103/physrevlett.76.3699

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Onorato M, Osborne AR, Serio M. Modulational instability in crossing sea states: a possible mechanism for the formation of freak waves. Phys Rev Lett (2006) 96:014503. doi:10.1103/physrevlett.96.014503

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Tsuchida T, Wadati M. New integrable systems of derivative nonlinear Schrödinger equations with multiple components. Phys Lett (1999) 257:53–64. doi:10.1016/s0375-9601(99)00272-8

CrossRef Full Text | Google Scholar

52. Matveev VB, Salle MA. Darboux transformation and solitons. Berlin, Germany: Springer (1991).

Google Scholar

53. Sinha S, Panda TK, Sarkar P, Palai G, Pal M, Kumar BA, et al. Designing efficient photonic waveguides for glucose detection in human urine for diabetic management. J Opt (2025) 1–13. doi:10.1007/s12596-025-02683-x

CrossRef Full Text | Google Scholar

54. Rupali, , Sahu SK, Palai G, Kumar BA, Mishra BK. Modelling of photonic crystal based ring resonator sensor for cancer detection using infrared laser. J Opt (2024) 1–7. doi:10.1007/s12596-024-02107-2

CrossRef Full Text | Google Scholar