Equilibrium trajectories quantify second-order violations of the fluctuation–dissipation theorem without the need for a model

Quantifying and characterizing fluctuations far away from equilibrium is a challenging task. We discuss and experimentally confirm a series expansion for a driven classical system, relating the different nonequilibrium cumulants of the observable conjugate to the driving protocol. This series is valid from micro- to macroscopic length scales, and it encompasses the fluctuation–dissipation theorem (FDT). We apply it in experiments of a Brownian probe particle confined and driven by an optical potential and suspended in a nonlinear and non-Markovian fluid. The expansion states that the form of the FDT remains valid away from equilibrium for Gaussian observables, up to the order presented. We show that this expansion agrees with that of a known fluctuation theorem up to an unresolved difference regarding moments versus cumulants.

Introduction

The fluctuation–dissipation theorem (FDT) [1, 2], connecting response and fluctuations of equilibrium systems, is of fundamental importance for condensed matter, fluids, plasmas, or electromagnetic fields [3–6]. One of its remarkable properties is its validity at any length scale, ranging from the nanoscale, for electric charges, to the macroscale, for macroscopic magnetization. It is, however, restricted to the linear regime, i.e., to situations close to equilibrium. Most previous research has been largely devoted to determining similar relations for nonequilibrium steady states [7–29] and for nonlinear responses [30–51]. A typical observation in the found relations is the explicit appearance of microscopic details—sometimes referred to as frenetic components [52, 53] or information on the specific rule governing the time evolution [40]—often hampering a model-independent formulation and systematic changes in length scales such as coarse graining to macroscopic scales [46, 47, 49]. As a consequence, experimental tests and application of such relations have indeed been successful for systems with a small number of accessible Markovian degrees of freedom [51, 54–57], for which the dynamics can be modeled.

In a different spirit, nonlinear fluctuation dissipation relations [31–34, 58] and fluctuation theorems [33, 41, 59–61] have been found, which can often be applied in the absence of a specific model. However, they have, to our knowledge, not been used to quantify the error of the FDT.

In this manuscript, we discuss and experimentally confirm a series expansion for a driven classical system, which relates the different nonequilibrium cumulants of the observable conjugate to the driving protocol, up to a certain order in driving velocity. This series (i) is valid from micro- to macroscopic length scales, (ii) is model-independent, and (iii) encompasses the FDT. We apply it in an experimental many-body system of a Brownian probe particle interacting with worm-like micelles and confined and driven by an optical potential. In these experiments, we demonstrate that the equilibrium third force cumulant quantifies the second-order deviation from the FDT under driving. Notably, our theoretical predictions demonstrate that the form of the FDT remains valid for purely Gaussian observables within the displayed order.

System and fluctuation series

Consider a classical system of stochastic degrees ${\mathbf{x}}_t$ at time $t$ (weakly) coupled to a heat bath at temperature $T$. The system’s potential energy $U$ depends on ${\mathbf{x}}_t$ and on a time-dependent deterministic protocol $X_t$, i.e., $U({\mathbf{x}}_t,X_t)$. The system is prepared in equilibrium at time $t\to -\infty$, with a protocol value $X_{-\infty }=X_t$, for simplicity [62]. The time dependence of the protocol drives the system away from equilibrium.

The derivative of $U$ in terms of $X_t$, $F_t:={\partial }_{X_t}U({\mathbf{x}}_t,X_t)$ is the observable conjugate to $X_t$. For example, if $X_t$ is a position as in our experiments, $F_t$ is (minus) the corresponding force. $F_t$ can be micro- or macroscopic; for example, let $X$ couple linearly to an observable $A(\mathbf{x})$; $U({\mathbf{x}}_t,X_t)=U({\mathbf{x}}_t,0)-X_{t}A({\mathbf{x}}_t)$, i.e., $F_t=-A({\mathbf{x}}_t)$. Thus, if $A(\mathbf{x})$ is a macroscopic field, such as macroscopic magnetization, $F_t$ is macroscopic. If $A(\mathbf{x})$ is the position of a molecular particle, $F_t$ is microscopic. The following remains valid if $X_t$ enters $U$ nonlinearly.

The statistical properties of $F_t$ in this nonequilibrium situation are encoded in its cumulants and in its correlations with another state observable, $B_t=B({\mathbf{x}}_t,X_t)$, which we aim to study here. The well-known FDT connects the covariance in the unperturbed system and the first moment of $B$ under weak driving [1, 2],

${\beta }^2{\int }_{-\infty }^t\mathrm{d}s{\dot{X}}_s{⟨B_t;F_s⟩}_{\text{eq}}=\beta \left[⟨B_t⟩-{⟨B_t⟩}_{\text{eq}}\right]+\mathcal{O}({\dot{X}}^2),(1)$

with $\beta =1/k_{B}T$ and Boltzmann constant $k_B$. $⟨\dots ;\dots ⟩$ denotes the second cumulant, and similarly for higher orders below. Expectation values ${⟨\dots ⟩}_{\text{eq}}$ are evaluated using equilibrium trajectories with a protocol value fixed at $X_t$. Expectation values $⟨\dots ⟩$ are measured in the driven system, i.e., under the given time-dependent protocol [62].

In Ref. [62], we derive identities connecting the nonequilibrium cumulants of $F_t$ and $B_t$ to different orders. These give rise to the following series involving the mentioned cumulants [62],

$\begin{array}{cc}\hfill & {\beta }^2{\int }_{-\infty }^t\mathrm{d}s{\dot{X}}_s⟨B_t;F_s⟩=\beta \left[⟨B_t⟩-{⟨B_t⟩}_{\text{eq}}\right]\hfill \\ \hfill & +\frac{{\beta }^3}{2}{\int }_{-\infty }^t\mathrm{d}s{\int }_{-\infty }^t\mathrm{d}{s}^{\prime }{\dot{X}}_s{\dot{X}}_{s^{\prime }}⟨B_t;F_s;F_{s^{\prime }}⟩\hfill \\ \hfill & -\frac{{\beta }^4}{6}{\int }_{-\infty }^t\mathrm{d}s{\int }_{-\infty }^t\mathrm{d}{s}^{\prime }{\int }_{-\infty }^t\mathrm{d}{s}^{″}{\dot{X}}_s{\dot{X}}_{s^{\prime }}{\dot{X}}_{s^{″}}\hfill \\ \hfill & \times ⟨B_t;F_s;F_{s^{\prime }};F_{s^{″}}⟩+\mathcal{O}({\dot{X}}^4),\hfill \end{array}(2)$

As presented in Ref. [62], this series expansion can also be obtained from a known fluctuation theorem [33, 41], albeit with an open question regarding cumulants versus moments.

Equation 2 is, as indicated, correct up to the fourth order in driving ${\dot{X}}_t$, under the assumption of local detailed balance [63]. Expanding¹ Equation 2 to the first order yields the FDT in Equation 1 so that it is included in Equation 2. To higher orders, first and second cumulants do not fulfill the FDT, and Equation 2 quantifies their difference in terms of third and fourth cumulants of $F$ and $B$. Notably, the second to fourth lines of Equation 2 vanish for purely Gaussian distributed $F$ and $B$ so that first and second cumulants obey the FDT to the given nonequilibrium order. It is important to note that, in Equation 2, the protocol $\dot{X}$ appears as pre-factors and in the nonequilibrium cumulants themselves; i.e., the latter are evaluated under application of driving. As Equation 2 only requires measurement of $F$ and $B$, we use the notion of model free.

Experimental setup

We exploit Equation 2 with experiments of Brownian particles interacting with micellar fluid. In particular, we use silica particles of diameter $\sim$ 1 µm suspended in a 5-mM equimolar solution of cetylpyridinium chloride monohydrate (CPyCl) and sodium salicylate (NaSal). At concentrations above the critical micellar concentration ($\gtrsim$ 4 mM), this fluid is known to form giant worm-like micelles, leading to a viscoelastic nonlinear behavior at ambient temperatures [64]; see SM. At 5 mM, we determine the relaxation time of the fluid from microrheological recoil experiments, where a particle is first driven with a constant external force which is then suddenly removed, to be $\sim$ (3$\pm$0.2)s [65]. A small amount of silica particles is added to the micellar solution, which is contained in a rectangular capillary with 100 µm height and kept at a temperature of 25 °C. This sample is placed on a custom-built optical tweezer setup that uses a Gaussian laser beam of wavelength 532 nm and a 100$\times$ oil immersion objective (NA $=$ 1.45). The laser beam yields a potential $U(x_t-X_t)$, as shown in Figure 1a, centered at $X_t$, trapping one of the silica particles with coordinate $x_t$. $F_t={\partial }_{X_t}U(x_t-X_t)$ is thus the force acting on the particle by the trapping potential (or vice versa). As the micellar degrees do not couple to $X$, they do not enter $F_t$ explicitly, and knowing how they enter $U$ is not required to apply Equation 2. Thus, the use of Equation 2 does not require the detection of the positions of micellar particles, and applying it to such a complex fluid demonstrates its strength. We consider $B\equiv F$, and made the potential asymmetric, to obtain a finite second-order response of $\beta ⟨F_t⟩$. This allows to test Equation 2 to the second order in our experiments, and it is achieved by a controlled lateral displacement of the vertically incident laser beam from the center of the objective lens (see SM). Notably, Equation 2 could also be tested in a purely viscous fluid, which also shows a second-order response due to the nonlinear potential. However, to demonstrate that Equation 2 is valid beyond simple systems, we have chosen the more challenging case of a micellar fluid.

Figure 1

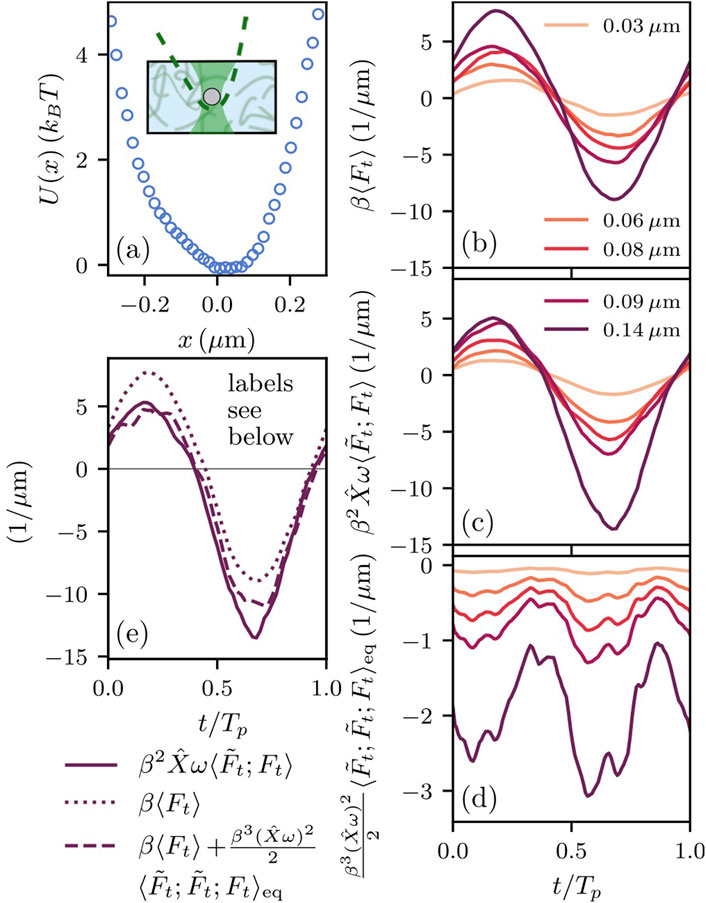
Figure 1. (a) Asymmetric optical potential $U(x)=-k_{B}T\ln P(x)$ felt by the probe particle (inset sketch), with $P(x)$ the probability distribution with the trap at rest. (b) Mean force $\beta ⟨F_t⟩$, (c) force covariance ${\beta }^2\widehat{X}\omega ⟨{\tilde{F}}_t,F_t⟩$, and (d) equilibrium third cumulant ${\beta }^2{(\widehat{X}\omega )}^2{⟨{\tilde{F}}_t;{\tilde{F}}_t;F_t⟩}_{\mathrm{e}\mathrm{q}}/2$, as functions of time, for driving frequency $\omega =$8.4 rad/s and amplitudes $\widehat{X}=\{0.03,0.06,0.08,0.09,0.14\}$µm as labeled. $T_p=\frac{2\pi }{\omega }$. (e) Force covariance (solid line), mean force (dotted line), and the sum of mean force and third force cumulant (dashed line, Equation 4) for $\widehat{X}$ = 0.14 µm.

To apply the driving protocol, the sample cell is moved, whereas the optical trap remains stationary in our experiments. This is achieved using a piezo-driven stage, on which the sample is mounted and translated in an oscillating manner relative to the trap. In the fluid’s rest frame, this yields a periodic motion of the potential minimum $X_t$, i.e., the protocol,

$X_t=\widehat{X}\sin (\omega t),(3)$

with the amplitude $\widehat{X}$ and the frequency $\omega$. Particle trajectories are recorded with a frame rate of $\sim$ 150 Hz using a video camera, and particle positions are determined using a custom MATLAB algorithm. To yield sufficient statistics, each protocol ($\widehat{X}$, $\omega$) was measured over 1400s. We allowed the system to reach a steady state by recording trajectories only after at least five oscillation periods had passed. Thereafter, no further equilibration was visible in the data. Prior to each nonequilibrium protocol, we recorded particle trajectories for another 1000s with $X_t$ at rest. These equilibrium data were used to check that the form of $U$ does not vary between measurements and also to obtain the force cumulants under equilibrium conditions.

Data analysis

With the protocol of Equation 3, Equation 2 takes, expanded to the second order, the form

$\begin{array}{cc}\hfill {\beta }^2\widehat{X}\omega ⟨{\tilde{F}}_t;F_t⟩& =\beta ⟨F_t⟩+\frac{{\beta }^3{\widehat{X}}^2{\omega }^2}{2}⟨{\tilde{F}}_t;{\tilde{F}}_t;F_t⟩\hfill \\ \hfill & +\mathcal{O}({(\widehat{X}\omega )}^3),\hfill \end{array}(4)$

where the tilde denotes the cosine transform, i.e., ${\tilde{F}}_t\equiv {\int }_{-\infty }^t\mathrm{d}s\cos (\omega s)F_s$. We restrict the analysis to the lowest nontrivial, i.e., second, order and expand Equation 2 accordingly, also using ${⟨F_t⟩}_{\text{eq}}=0$. Notably, to extract the second-order contribution from the last term in Equation 4, the third cumulant in Equation 4 is replaced by its equilibrium version. This is because of the pre-factor ${\widehat{X}}^2{\omega }^2$ and will be done in the following analysis.

The cumulants in Equation 4 depend on time $t$ in a periodic manner, as shown in Figures 1b–d, for $\omega =$ 8.4 rad/s and driving² amplitudes ranging from $\widehat{X}=$ 0.03 µm (light) to $\widehat{X}=$ 0.14 µm (dark). Figure 1b shows the mean force, which, as expected for a driven oscillator, is a periodic function with period $T_p=\frac{2\pi }{\omega }$. For the smallest amplitude shown, the mean force is nearly harmonic with frequency $\omega$, as expected from linear response. With growing amplitude, higher harmonics occur, as expected from nonlinear response. This asymmetric system shows the second-order response with expected frequencies of $2\omega$ and $0\omega$.

Figure 1c shows the force covariance for the same parameters and color code. For small amplitude $\widehat{X}$, the curves in Figures 1b,c are equal within the experimental accuracy, as analyzed in detail below. For larger driving amplitude, the force covariance develops higher harmonics with signatures of second order. Very little is known about the properties of such nonequilibrium fluctuations, and quantifying these is difficult. It is notable that the curves in Figure 1c, for larger amplitudes, deviate from Figure 1b, a deviation that we claim to be quantified by Equation 4.

Figure 1d shows the third cumulant of force for the same parameters and color code. We have here restricted to the equilibrium cumulant as it appears in Equation 4, multiplied by ${(\widehat{X}\omega )}^2$. The curves in Figure 1d thus differ only because of the factor ${(\widehat{X}\omega )}^2$. They thus scale quadratically in driving velocity and only show frequencies of $2\omega$ and $0\omega$.

Equation 4 states that in the shown range of amplitudes, the curves in Figure 1c are given by the sum of the curves in Figures 1b,d. For $\widehat{X}=$0.14 µm, the respective summed curve is shown as a dashed line together with the mean force and the force covariance in Figure 1e. The agreement is convincing and a confirmation of Equation 4.

To test this prediction systematically, we dissect the curves in Figures 1b–d into the contributions from harmonics with frequencies $0\omega$, $\omega$, and $2\omega$, respectively, i.e., we expand the cumulant of order $n$ into harmonics with the frequency $m\omega$,

$\begin{array}{cc}\hfill {\beta }^n{(\widehat{X}\omega )}^{n-1}⟨{({\tilde{F}}_t;)}^{n-1}{F}_t⟩& ={\displaystyle \sum _{m=0}^{\infty }}{A}_m^{(n)}\sin (m\omega t+{\varphi }_m^{(n)}),\hfill \end{array}(5)$

where the coefficients $A_m^{(n)}$ depend on $\widehat{X}\omega$. We set ${\varphi }_0^{(n)}\equiv \pi /2$ for consistency. Equation 4, projected on the harmonic of order $m$, yields relations between coefficients and phases for each $m$, which we can test.

Results

Figure 2 shows the coefficients $A_m^{(n)}$ as a function of the driving amplitude $\widehat{X}$. The top panel gives the order $m=1$, which is considered to be linear in $\widehat{X}$ for the range shown, as expected from linear response. The graph shows the mean force (data points) and the force covariance (line). The latter is evaluated from equilibrium trajectories. The agreement in this panel, for the range of sufficiently small $\widehat{X}$, is expected from the FDT.

Figure 2

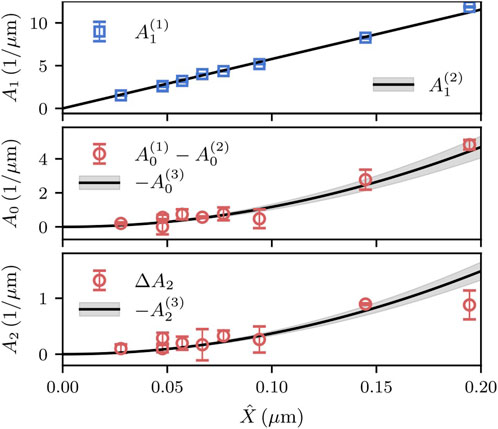
Figure 2. Coefficients $A_m$ corresponding to harmonics with the frequency $m\omega$, as a function of driving amplitude $\widehat{X}$, for $\omega =$8.4 rad/s. Top panel: $m=1$, demonstrating FDT. Lower panels: difference in first and second cumulants (data points), and third cumulant (lines) for $m=0$ and $m=2$. The agreement confirms Equation 4. $\mathrm{\Delta }{A}_2\equiv [{(A_2^{(1)})}^2+{(A_2^{(2)})}^2$$-2A_2^{(1)}{A}_2^{(2)}\cos ({\varphi }_2^{(1)}-{\varphi }_2^{(2)}){]}^{1/2}$. Error bars and bands are obtained from partitioning trajectories into two pieces.

The center and lower panels in Figure 2 show the orders $m=0$ and $m=2$, respectively. In particular, these panels present the difference of first and second cumulants in Equation 4 (data points), i.e., $\beta ⟨F_t⟩-{\beta }^2\widehat{X}\omega ⟨{\tilde{F}}_t;F_t⟩$, together with the third cumulant (line), $-{\beta }^3{(\widehat{X}\omega )}^2{⟨{\tilde{F}}_t;{\tilde{F}}_t;F_t⟩}_{\text{eq}}/2$, evaluated from equilibrium measurements³. The latter is shown as a parabola with curvature obtained from the third force cumulant at equilibrium. The data points in this graph thus quantify the deviation from the FDT, with the line giving the prediction of Equation 4 for this deviation. The agreement is convincing for both $m=0$ and $m=2$, supporting the validity of Equation 4.

As data in the top panel of Figure 2 grow linearly and those in the center and lower panels grow quadratically with $\widehat{X}$, we fit a line and a parabola to obtain the, respective, slope and curvature for each $m$. The obtained values—divided by the respective power in $\omega$—are shown in Figure 3 as a function of the frequency $\omega$. We observe convincing agreement for the measured frequencies further supporting Equation 4. In tendency, the coefficients decrease with increasing $\omega$. Notably, the statistical accuracy of the data points decreases with decreasing $\omega$; with smaller $\omega$, longer trajectories are required, especially in a fluid with pronounced memory, as the period of the cosine transform increases.

Figure 3

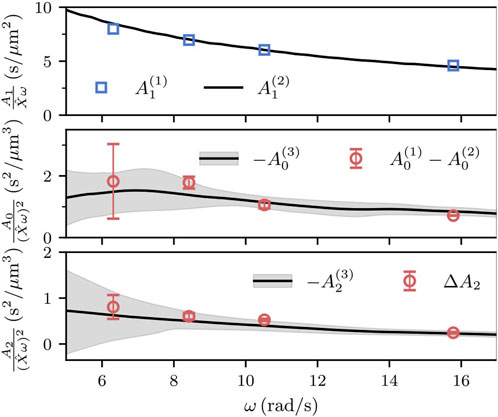
Figure 3. Coefficients $A_m$, normalized as labeled, as a function of the frequency $\omega$. The agreement in the top panel confirms the FDT, and the agreement in the lower panels confirms Equation 4. Each data point is obtained from averaging over driving amplitudes taking the respective scaling of $A_m$ with $\widehat{X}$ into account (see SM). Error bars are obtained from partitioning trajectories into two pieces (data points) and from the standard deviation between separate series of measurements (gray area).

Figure 4 provides the final test of Equation 4, namely, the phases ${\varphi }_m^{(n)}$ of Equation 5. These hardly depend on driving amplitude, and the shown data are averaged over the measured values of $\widehat{X}$. The top panel of Figure 4 shows the order $m=1$, i.e., the linear response, with convincing agreement. The phase angle for $m=1$ is small for the frequencies measured, indicating that the force $F_t$ is almost in phase with the protocol $X_t$, as for an elastic material. The black curve, extracted from equilibrium data, shows that with smaller $\omega$, the phase increases, presumably reaching $\pi /2$ in the limit of $\omega \to 0$. The slow increase with decreasing $\omega$ displays the slow nature of the investigated system.

Figure 4

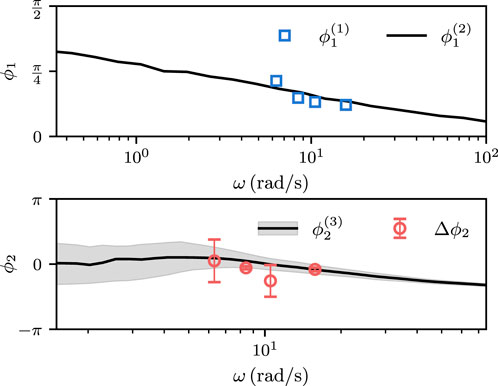
Figure 4. Phase angles ${\varphi }_1$ and ${\varphi }_2$ of the harmonics in Equation 5, as functions of $\omega$. Top panel shows the phases of the linear response. Lower panel shows the phase of the second-order response, comparing the contributions of the terms in Equation 4. $\mathrm{\Delta }{\varphi }_2\equiv \arctan \frac{A_2^{(1)}\sin {\varphi }_2^{(1)}-A_2^{(2)}\sin {\varphi }_2^{(2)}}{A_2^{(1)}\cos {\varphi }_2^{(1)}-A_2^{(2)}\cos {\varphi }_2^{(2)}}$. Error bars are obtained from partitioning trajectories into two pieces. The gray error band is obtained as the standard deviation between separate series of measurements.

The lower panel shows the phase for $m=2$, i.e., to second order. Although the agreement between the line and data confirms Equation 4, the graph shows that the differences in phases of first and second cumulants are rather small. In other words, first and second cumulants deviate noticeable in amplitude, as shown in Figure 2, but not so much in phase.

Conclusion

We presented and tested a nonequilibrium fluctuation expansion for a driven classical system, emphasizing the validity on various length scales. Indeed, such relations are necessary, e.g., for a systematic coarse graining of nonequilibrium systems. The identity is confirmed for experiments of a Brownian particle interacting with a complex surrounding. Future work can explore other systems and aim to clarify the relation to the mentioned fluctuation theorems [33, 41]. It is also important to investigate the use of Equation 2 for treating systems far away from equilibrium.

This project was funded by the Deutsche Forschungsgemeinschaft (DFG), Grant No. SFB 1432 (Project ID 425217212)—Project C05.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

JC: Writing – review and editing, Writing – original draft. KK: Writing – original draft, Writing – review and editing. CB: Writing – original draft, Writing – review and editing. MK: Writing – review and editing, Writing – original draft.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This project was funded by the Deutsche Forschungsgemeinschaft (DFG), Grant No. SFB 1432 (Project ID 425217212)—Project C05. The authors acknowledge support by the Open Access Publication Funds of the Göttingen University.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2025.1667224/full#supplementary-material

Footnotes

¹The expansion in Equation 2 suggests the dimensionless expansion parameter $\beta F{\int }_{t-\tau }^t\mathrm{d}s{\dot{x}}_s$ with cumulant relaxation time τ.

²ω is determined from the power spectral density, thus carrying an error depending on the length of the measurement.

³As the phases ${\varphi }_2^{(1)}$ and ${\varphi }_2^{(2)}$ may differ, the coefficient ΔA₂ of the difference of first and second cumulants is found via $\mathrm{\Delta }{A}_2\equiv \sqrt{{\left(A_2^{(1)}\right)}^2+{\left(A_2^{(2)}\right)}^2-2A_2^{(1)}{A}_2^{(2)}\cos \left({\varphi }_2^{(1)}-{\varphi }_2^{(2)}\right)}$. For m = 0, i.e., the zero frequency contribution, there is no phase by definition, and the coefficients $A_0^{(n)}$ can be compared directly.

References

1. Callen HB, Welton TA. Irreversibility and generalized noise. Phys Rev (1951) 83:34–40. doi:10.1103/physrev.83.34

CrossRef Full Text | Google Scholar

2. Kubo R. The fluctuation-dissipation theorem. Rep Prog Phys (1966) 29:255–84. doi:10.1088/0034-4885/29/1/306

CrossRef Full Text | Google Scholar

3. Landau LD, Lifshitz EM. Statistical physics. Pergamon (1980).

Google Scholar

4. Sitenko AG. Electromagnetic fluctuations in plasma. New York: Academic Press (1967).

Google Scholar

5. Rytov SM, Kravtsov IA, Tatarskii V. Principles of statistical radiophysics. Springer-Verlag (1987).

Google Scholar

6. Hansen JP, McDonald IR. Theory of simple liquids: with applications to soft matter. Elsevier Science (2013).

Google Scholar

7. Cugliandolo LF, Dean DS, Kurchan J. Fluctuation-dissipation theorems and entropy production in relaxational systems. Phys Rev Lett (1997) 79:2168–71. doi:10.1103/physrevlett.79.2168

CrossRef Full Text | Google Scholar

8. Ruelle D. General linear response formula in statistical mechanics, and the fluctuation-dissipation theorem far from equilibrium. Phys Lett A (1998) 245:220–4. doi:10.1016/s0375-9601(98)00419-8

CrossRef Full Text | Google Scholar

9. Crisanti A, Ritort F. Violation of the fluctuation–dissipation theorem in glassy systems: basic notions and the numerical evidence. J Phys A: Math Gen (2003) 36:R181–290. doi:10.1088/0305-4470/36/21/201

CrossRef Full Text | Google Scholar

10. Harada T, Sasa S-I. Equality connecting energy dissipation with a violation of the fluctuation-response relation. Phys Rev Lett (2005) 95:130602. doi:10.1103/physrevlett.95.130602

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Speck T, Seifert U. Restoring a fluctuation-dissipation theorem in a nonequilibrium steady state. EPL (2006) 74:391–6. doi:10.1209/epl/i2005-10549-4

CrossRef Full Text | Google Scholar

12. Deutsch JM, Narayan O. Energy dissipation and fluctuation response for particles in fluids. Phys Rev E (2006) 74:026112. doi:10.1103/physreve.74.026112

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Chetrite R, Falkovich G, Gawedzki K. Fluctuation relations in simple examples of non-equilibrium steady states. J Stat Mech (2008):P08005. doi:10.1088/1742-5468/2008/08/P08005

CrossRef Full Text | Google Scholar

14. Marconi UMB, Puglisi A, Rondoni L, Vulpiani A. Fluctuation–dissipation: response theory in statistical physics. Phys Rep (2008) 461:111–95. doi:10.1016/j.physrep.2008.02.002

CrossRef Full Text | Google Scholar

15. Saito K. Energy dissipation and fluctuation response in driven quantum langevin dynamics. Europhys Lett (2008) 83:50006. doi:10.1209/0295-5075/83/50006

CrossRef Full Text | Google Scholar

16. Baiesi M, Maes C, Wynants B. Fluctuations and response of nonequilibrium states. Phys Rev Lett (2009) 103:010602. doi:10.1103/physrevlett.103.010602

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Prost J, Joanny J-F, Parrondo JMR. Generalized fluctuation-dissipation theorem for steady-state systems. Phys Rev Lett (2009) 103:090601. doi:10.1103/physrevlett.103.090601

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Harada T. Macroscopic expression connecting the rate of energy dissipation with the violation of the fluctuation response relation. Phys Rev E (2009) 79:030106. doi:10.1103/physreve.79.030106

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Krüger M, Fuchs M. Fluctuation dissipation relations in stationary states of interacting brownian particles under shear. Phys Rev Lett (2009) 102:135701. doi:10.1103/physrevlett.102.135701

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Seifert U, Speck T. Fluctuation-dissipation theorem in nonequilibrium steady states. EPL (2010) 89:10007. doi:10.1209/0295-5075/89/10007

CrossRef Full Text | Google Scholar

21. Baiesi M, Maes C, Wynants B. The modified sutherland–einstein relation for diffusive non-equilibria. Proc R Soc A: Math Phys Eng Sci (2011) 467:2792–809. doi:10.1098/rspa.2011.0046

CrossRef Full Text | Google Scholar

22. Cugliandolo LF. The effective temperature. J Phys A: Math Theor (2011) 44:483001. doi:10.1088/1751-8113/44/48/483001

CrossRef Full Text | Google Scholar

23. Verley G, Chétrite R, Lacoste D. Modified fluctuation-dissipation theorem for general non-stationary states and application to the glauber–ising chain. J Stat Mech (2011):10025. doi:10.1088/1742-5468/2011/10/P10025

CrossRef Full Text | Google Scholar

24. Altaner B, Polettini M, Esposito M. Fluctuation-dissipation relations far from equilibrium. Phys Rev Lett (2016) 117:180601. doi:10.1103/physrevlett.117.180601

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Lippiello E, Baiesi M, Sarracino A. Nonequilibrium fluctuation-dissipation theorem and heat production. Phys Rev Lett (2014) 112:140602. doi:10.1103/physrevlett.112.140602

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Wu W, Wang J. Generalized fluctuation-dissipation theorem for non-equilibrium spatially extended systems. Front Phys (2020) 8:567523. doi:10.3389/fphy.2020.567523

CrossRef Full Text | Google Scholar

27. Caprini L. Generalized fluctuation–dissipation relations holding in non-equilibrium dynamics. J Stat Mech (2021):063202. doi:10.1088/1742-5468/abffd4

CrossRef Full Text | Google Scholar

28. Baldovin M, Caprini L, Puglisi A, Sarracino A, Vulpiani A. In nonequilibrium thermodynamics and fluctuation kinetics: modern trends and open questions. Springer International Publishing (2022).

Google Scholar

29. Johnsrud MK, Golestanian R, Generalized fluctuation dissipation relations for active field theories (2024), arXiv:2409.14977.

Google Scholar

30. Kubo R. Statistical-mechanical theory of irreversible processes. I. General theory and simple applications to magnetic and conduction problems. J Phys Soc Jpn (1957) 12:570–86. doi:10.1143/jpsj.12.570

CrossRef Full Text | Google Scholar

31. Bernard W, Callen HB. Irreversible thermodynamics of nonlinear processes and noise in driven systems. Rev Mod Phys (1959) 31:1017–44. doi:10.1103/revmodphys.31.1017

CrossRef Full Text | Google Scholar

32. Efremov GF, Eksp Z. A fluctuation dissipation theorem for nonlinear media. Theor Fiz (1968) 55:2322.

Google Scholar

33. Bochkov GN, Kuzovlev YE. Nonlinear fluctuation-dissipation relations and stochastic models in nonequilibrium thermodynamics. Phys A: Stat Mech Appl (1981) 106:443–79. doi:10.1016/0378-4371(81)90122-9

CrossRef Full Text | Google Scholar

34. Stratonovich RL. Nonlinear nonequilibrium thermodynamics I: Linear and nonlinear fluctuation-dissipation theorems. Springer (1992).

Google Scholar

35. Evans DJ, Morriss G. Statistical mechanics of nonequilibrium liquids. 2nd ed. Cambridge University Press (2008).

Google Scholar

36. Fuchs M, Cates ME. Integration through transients for Brownian particles under steady shear. J Phys Condens Matter (2005) 17:S1681–96. doi:10.1088/0953-8984/17/20/003

CrossRef Full Text | Google Scholar

37. Holsten T, Krüger M. Thermodynamic nonlinear response relation. Phys Rev E (2021) 103:032116. doi:10.1103/PhysRevE.103.032116

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Oppenheim I. Nonlinear response and the approach to equilibrium. Prog Theor Phys Supp (1989) 99:369–81. doi:10.1143/ptps.99.369

CrossRef Full Text | Google Scholar

39. Bouchaud J-P, Biroli G. Nonlinear susceptibility in glassy systems: a probe for cooperative dynamical length scales. Phys Rev B (2005) 72:064204. doi:10.1103/physrevb.72.064204

CrossRef Full Text | Google Scholar

40. Lippiello E, Corberi F, Sarracino A, Zannetti M. Nonlinear response and fluctuation-dissipation relations. Phys Rev E (2008) 78:041120. doi:10.1103/physreve.78.041120

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Andrieux D, Gaspard P. Quantum work relations and response theory. Phys Rev Lett (2008) 100:230404. doi:10.1103/physrevlett.100.230404

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Lucarini V, Colangeli M. Beyond the linear fluctuation-dissipation theorem: the role of causality. J Stat Mech (2012):p05013. doi:10.1088/1742-5468/2012/05/P05013

CrossRef Full Text | Google Scholar

43. Diezemann G. Nonlinear response theory for markov processes: simple models for glassy relaxation. Phys Rev E (2012) 85:051502. doi:10.1103/physreve.85.051502

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Wang E, Heinz U. Generalized fluctuation-dissipation theorem for nonlinear response functions. Phys Rev D (2002) 66:025008. doi:10.1103/physrevd.66.025008

CrossRef Full Text | Google Scholar

45. Andrieux D, Gaspard P. A fluctuation theorem for currents and non-linear response coefficients. J Stat Mech (2007):P02006. doi:10.1088/1742-5468/2007/02/P02006

CrossRef Full Text | Google Scholar

46. Colangeli M, Maes C, Wynants B. A meaningful expansion around detailed balance. J Phys A: Math Theor (2011) 44:095001. doi:10.1088/1751-8113/44/9/095001

CrossRef Full Text | Google Scholar

47. Basu U, Krüger M, Lazarescu A, Maes C. Frenetic aspects of second order response. Phys Chem Chem Phys (2015) 17:6653. doi:10.1039/C4CP04977B

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Basu U, Helden L, Krüger M. Extrapolation to nonequilibrium from coarse-grained response theory. Phys Rev Lett (2018) 120:180604. doi:10.1103/PhysRevLett.120.180604

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Maes C. Response theory: a trajectory-based approach. Front Phys (2020) 8:229. doi:10.3389/fphy.2020.00229

CrossRef Full Text | Google Scholar

50. Caspers J, Krüger M. Nonlinear langevin functionals for a driven probe. J Chem Phys (2024) 161:124109. doi:10.1063/5.0227674

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Helden L, Basu U, Krüger M, Bechinger C. Measurement of second-order response without perturbation. EPL (2016) 116:60003. doi:10.1209/0295-5075/116/60003

CrossRef Full Text | Google Scholar

52. Maes C. On the second fluctuation–dissipation theorem for nonequilibrium baths. J Stat Phys (2014) 154:705–22. doi:10.1007/s10955-013-0904-8

CrossRef Full Text | Google Scholar

53. Maes C. Frenesy: time-Symmetric dynamical activity in nonequilibria. Phys Rep (2020) 850:1–33. doi:10.1016/j.physrep.2020.01.002

CrossRef Full Text | Google Scholar

54. Gomez-Solano JR, Petrosyan A, Ciliberto S, Chetrite R, Gawedzki K. Experimental verification of a modified fluctuation-dissipation relation for a micron-sized particle in a nonequilibrium steady state. Phys Rev Lett (2009) 103:040601. doi:10.1103/physrevlett.103.040601

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Blickle V, Speck T, Lutz C, Seifert U, Bechinger C. Einstein relation generalized to nonequilibrium. Phys Rev Lett (2007) 98:210601. doi:10.1103/physrevlett.98.210601

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Mehl J, Blickle V, Seifert U, Bechinger C. Experimental accessibility of generalized fluctuation-dissipation relations for nonequilibrium steady states. Phys Rev E (2010) 82:032401. doi:10.1103/physreve.82.032401

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Gomez-Solano JR, Petrosyan A, Ciliberto S, Maes C. Fluctuations and response in a non-equilibrium micron-sized system. J Stat Mech (2011):P01008. doi:10.1088/1742-5468/2011/01/P01008

CrossRef Full Text | Google Scholar

58. Bochkov GN, Kuzovlev YE. General theory of thermal fluctuations in nonlinear systems. Zh Eksp Teor Fiz (1977) 72:238.

Google Scholar

59. Jarzynski C. Nonequilibrium equality for free energy differences. Phys Rev Lett (1997) 78:2690–3. doi:10.1103/physrevlett.78.2690

CrossRef Full Text | Google Scholar

60. Crooks GE. Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences. Phys Rev E (1999) 60:2721–6. doi:10.1103/physreve.60.2721

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Seifert U. Stochastic thermodynamics, fluctuation theorems and molecular machines. Rep Prog Phys (2012) 75:126001. doi:10.1088/0034-4885/75/12/126001

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Caspers J, Krüger M. Identities for nonlinear memory kernels. Phys Rev E (2025) 112:024124. doi:10.1103/pzs6-l3ws

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Maes C. Local detailed balance. Scipost Phys Lect Notes (2021) 32. doi:10.21468/scipostphyslectnotes.32

CrossRef Full Text | Google Scholar

64. Cates ME, Candau SJ. Statics and dynamics of worm-like surfactant micelles. J Phys Condens Matter (1990) 2:6869–92. doi:10.1088/0953-8984/2/33/001

CrossRef Full Text | Google Scholar

65. Gomez-Solano JR, Bechinger C. Transient dynamics of a colloidal particle driven through a viscoelastic fluid. New J Phys (2015) 17:103032. doi:10.1088/1367-2630/17/10/103032

CrossRef Full Text | Google Scholar