- Cognitive Psychology and Ergonomics, University of Twente, Enschede, Netherlands
This study addresses the role of cognitive control in the initiation and execution of familiar and unfamiliar movement sequences. To become familiar with two movement sequences participants first practiced two discrete key press sequences by responding to two fixed series of 6-key specific stimuli. In the ensuing test phase they executed these two familiar and also two unfamiliar keying sequences while there was a two-third chance a tone was presented together with one randomly selected key specific stimulus in each sequence. In the counting condition of the test phase participants counted the low pitched (i.e., target) tones. By and large the results support the dual processor model in which the prime role of the cognitive processor shifts from executing to initiating sequences while the gradual development of motor chunks allows a motor processor to execute the sequences. Yet, the results extend this simple model by suggesting that with little practice sequence execution is based also on some non-cognitive (perhaps associative) learning mechanism and, for some participants, on the use of explicit sequence knowledge. Also, after extensive practice the cognitive processor appears to still contribute to slower responses. The occurrence of long interkey intervals was replicated suggesting that fixed 6-key sequences include several motor chunks. Yet, no indication was found that the cognitive processor is responsible for concatenating these chunks.
Introduction
To what extent, and for which purposes, is cognitive control required when executing new and familiar movement patterns? To investigate this question we examined the effects of a secondary tone counting task on the production of highly practiced and new discrete sequences of 6-key presses, relative to a condition in which these tones were presented but ignored. The use of a sequential key press task seems appropriate for studying the role of cognitive control in movement skill because a key press takes little time to execute and response times are therefore more likely to be influenced by the underlying control processes than when the execution of the constituents takes considerable time (Rhodes et al., 2004). Moreover, the relatively short movement sequences studied here are assumed to be the building blocks of more complex, hierarchically controlled sequential action (e.g., Gallistel, 1980; Wolpert and Kawato, 1998). For instance, changing gears is a building block of driving, and playing a particular arpeggio on a piano may be a building block of an otherwise unfamiliar piece of music.
In the present study we asked participants to practice two fixed keying sequences as part of the so-called discrete sequence production (DSP) task (e.g., Verwey, 1999). In this task participants typically have six or eight fingers resting on six or eight keys of a computer keyboard. They start off by responding to each of a series of (typically 2 to 7) key specific stimuli. This can be denoted the reaction mode of processing (Verwey, 2003a). Given the limited number of key presses in a sequence participants quickly learn that the order of each sequence is fixed and they gradually switch to the sequencing mode by executing in response to the first stimulus the entire series of key presses. In that mode stimuli past the first may eventually be ignored and response times may become shorter than 100 ms (Verwey, 1999). Given the typical zero response stimulus interval (RSI) each stimulus past the first is presented immediately upon pressing the preceding key and response times equal interkey intervals (IKI). Hence, a DSP task with two alternative keying sequences, each including 6-key presses, turns with practice from two series of 6-choice RT tasks into a single 2-choice RT task in which an entire keying sequence constitutes the response. This transition from reaction to sequencing mode is possible because an integrated memory representation of a series of movements (i.e., a motor chunk) develops that can be selected and executed as a whole. We believe that the control of DSP sequences is a model for the way automated real-world movement patterns are controlled. Indeed indications for chunk-based motor control have been observed also in studies that employed very different discrete sequential movement tasks like moving a lever to sequentially presented targets using elbow flexions and extensions (e.g., Park and Shea, 2005; Panzer et al., 2009), moving a pen through a cut-out maze pattern with the eyes closed (e.g., van Mier and Hulstijn, 1993; van Mier and Petersen, 2006), and uttering speech (e.g., Bohlanda and Guenther, 2006).
An important observation is that with sequences consisting of more than three to five successive key presses, one of the key presses is often preceded by a relatively long IKI. If there are marked regularities in a sequence in spatial, temporal, or conceptual ways (like reversals or runs), participants have been found to develop this longest IKI at the same location. This has been taken as an indication that they segmented the sequence in the same way (Povel and Collard, 1982; Koch and Hoffmann, 2000; Verwey et al., 2002; de Kleine and Verwey, 2009a; see similar findings with sequential aiming movements in Park and Shea, 2005; Panzer et al., 2006). In other sequences such long IKIs are not observed at the same sequential location but detailed analyses showed that participants often have a relatively long IKI at some individually determined location. The fact that this longest IKI occurs at different sequential locations suggests that without a clear regularity participants segment such sequences in individually different ways (Verwey, 2001, 2003b; Verwey and Eikelboom, 2003; Sakai et al., 2003; Kennerley et al., 2004; Bo and Seidler, 2009).
Attempts have failed to attribute this longest IKI to the development of a temporal pattern associated with the sequence, i.e., a rhythm. First, the ratios of long and short IKIs were found not to adhere to the 1:1 and 1:2 ratios that are expected with rhythm learning, but they varied continuously between 1:2 and 1:8 for individual participants (Verwey, 1996; Verwey and Dronkert, 1996). Furthermore, while a rhythm can be expected to be independent of the sequence it occurs in, the pattern of IKIs in the DSP task appeared not to transfer to simultaneously and subsequently performed sequences (Verwey et al., 2009). Also, recent research did not find a correlation between the chunking pattern in the sequence and the individual’s temporal control abilities. This was taken to indicate that a timing mechanism does not play a significant role in determining the temporal structure of acquired motor sequences (Bo et al., 2009; Bo and Seidler, 2009). Finally, on basis of different patterns of activity in brain scans, Sakai et al. (2004) argued that the spontaneous development of an IKI pattern – an “implicit rhythm” with non-integer ratios – should be distinguished from explicitly learning rhythms with integer ratios.
A more plausible explanation for the occurrence of the longest IKI in longer keying sequences is that motor chunks can represent only about three to five individual movements. Longer sequences would necessarily include several motor chunks (Verwey et al., 2002; Verwey, 2003b; Bo and Seidler, 2009). The idea that the longest IKI in 6-key sequences indexes a process not occurring with short IKIs – namely the transition between successive motor chunks – is in line with findings that the longest and shortest IKIs react differently to various experimental manipulations. That is, the longest IKI reduced more than the short IKIs after stimulating part of the supplementary motor area (i.e., the pre-SMA) with transcranial magnetic stimulation (TMS) (Kennerley et al., 2004). In contrast, the short IKIs were lengthened more than the longest IKI after changing the location of the hand relative to the body (de Kleine and Verwey, 2009a), when using fingers adjacent to the ones used during practice (Verwey et al., 2009), and when discrete sequences were executed by dyslexics (de Kleine and Verwey, 2009b).
The spontaneous occurrence of a longest IKI in longer sequences is reminiscent of the long IKI observed when two separately practiced keying sequences were executed in rapid succession (Verwey, 2001). That study showed that the selection of a familiar sequence may occur while an earlier familiar sequence is being executed (cf. Verwey, 1995). This led to the proposal of a dual processor model that assumes that a cognitive processor selects each motor chunk and loads its responses into a short-term (motor) buffer. Subsequently, the motor processor retrieves the codes for each response from that buffer until the entire motor chunk has been carried out (cf. Sternberg et al., 1978). This allows the cognitive processor to, for example, select the next sequence or perform another task during sequence execution. The fact that the transition between the two familiar sequences was marked by a relatively long IKI was taken to suggest that the second sequence can be loaded into the motor buffer only after the first sequence is entirely completed.
If indeed the relatively long IKI between two successive sequences reflects initiation of the next sequence by the cognitive processor one might argue also that the longest IKI in longer sequences reflects the transition between successive motor chunks by a cognitive processor. This would be in line with the notion that “performance is more automatic within a chunk than between chunks” (Sakai et al., 2004, p. 551). In other words, the contribution of a cognitive processor to sequence performance may be larger between chunks than within chunks. Alternatively, it could be that the consistent order of motor chunks in a fixed sequence might cause the transition to automate with practice too, thereby reducing cognitive influences. So, despite indications for an additional process during long IKIs in fixed sequences, it can not be presumed that long IKIs involve a larger cognitive contribution than the remaining IKIs.
There is some tentative support for the view that the cognitive processor is responsible for concatenating motor chunks during the relatively long IKI in a keying sequence. This comes from a study in which the already relatively slow fourth of six aiming movements was slowed more than other movements by a secondary memory task (Brown and Carr, 1989). However, contradictory results have been found in that the spontaneously developing longest IKI in longer keying sequences did not lengthen more than the other IKIs when participants had a memory task during sequence execution (Verwey, 2003b). Yet, the latter result may be explained by the notion that the rehearsal that is typical for a memory task (e.g., Baddeley, 1986) was postponed until after the sequence had been completed. This usually is not problematic for memory if it lasts just 1 or 2 s because short-term memory content remains active for such an interval (e.g., Hommel, 1994).
In the present article we will further explore when exactly the cognitive processor is involved in sequence production. Within DSP sequences we distinguish sequence initiation (i.e., the first response time T1), the concatenation phase that involves the transition from one to the next motor chunk (assumed to be indicated by the longest IKI), and the execution phase that includes the remaining elements of a motor chunk (indicated by so-called execution IKIs, cf. Verwey et al., 2009). The initiation and concatenation phases are assumed to both involve the loading and initiation of the upcoming motor chunk, but the initiation phase will most likely include more general preparatory processes too (Verwey, 2003b). In the test phase of the present study, the role of the cognitive processor in these three phases of familiar and unfamiliar keying sequences was explored with a secondary tone counting task that does not allow participants to postpone processing until after sequence completion (like perhaps in a secondary memory task). Furthermore, this task allows clear determination of the exact moment at which the cognitive processor is loaded by the secondary task by exploring fluctuations in response times.
The secondary tone counting task we used involved presenting a tone in 66% of the sequences together with one randomly selected key specific stimulus. In the counting condition participants are instructed to identify each tone and count the number of target tones across a block of trials. If only the key presses following a tone is slowed (relative to a no-counting control condition in which tones are to be ignored), this would indicate that key pressing continues only after the cognitive processor has switched back to the sequencing task. However, if several key presses are slowed one could surmise that a non-cognitive processor continues with the sequencing task while the speed reduction indicates that the cognitive processor contributed to triggering keys as well. The tone counting task is assumed to require immediate processing upon tone presentation so that a lack of interference can not be attributed to postponed processing. In addition, unlike the probe RT task in which an overt response is immediately given to the tone (Posner and Keele, 1969), slowing of the primary task by a tone in the tone counting task can not be attributed to interference at the response level but is likely to have been caused by interference at the cognitive level (McLeod, 1980). In anticipation of our results we note here already that this tone counting task showed the intended effects.
The tone counting task was performed while participants executed familiar and unfamiliar keying sequences. Of the two sequences that were first practiced by each participant one was an unstructured sequence in which all response-to-stimulus intervals (RSIs) were 0. To examine whether in these sequences the spontaneously emerging longest IKI involves concatenation by the cognitive processor, the location of the longest IKI was determined for each participant separately (cf. Kennerley et al., 2004; Sakai et al., 2004; Bo and Seidler, 2009). The other sequence of each participant was prestructured in that it was practiced with one or two brief RSIs at fixed positions (i.e., one or two pauses between a key press and the next stimulus). Earlier research showed that when in a subsequent test phase these pauses are removed participants have the longest IKIs at the positions where these pauses had been during the practice phase. This has led to the proposal that the pause may eventually determine the boundary between successive motor chunks at the same position for all participants (e.g., Verwey, 1996; Verwey et al., 2009). To assure that it is indeed the pause that determines segmentation of the prestructured sequence we had two practice groups with pauses at different sequential locations in their prestructured sequences. We included both an unstructured and a prestructured sequence in the present experiment because it can not be claimed beyond doubt that spontaneously developing long IKIs in unstructured sequences and the imposed long IKIs in prestructured sequences indeed entail the same concatenation process. This allowed us to examine whether the longest IKI in the two prestructured and the unstructured sequences show the same effects of the secondary task.
The present study addressed several issues. The first question was whether a secondary tone counting task would lengthen the longest IKI in unstructured and prestructured familiar sequences more than the execution IKIs (as found by Brown and Carr, 1989 but not by Verwey, 2003b). While initiation of aiming movements (e.g., Glencross, 1980; for an overview see Ketelaars et al., 1997) and familiar 3-key sequences (Verwey, 1993) has repeatedly been found to be slowed by a secondary task, this does not necessarily mean that concatenation is slowed too, because (a) movement initiation involves general preparation processes that do not occur in concatenation, and (b) concatenation could become independent of the cognitive processor with practice because of consistent chunk order. A second question concerned whether execution of unfamiliar sequences is slowed more than of familiar sequences. This question is motivated by the assumption of the dual processor model that in unfamiliar sequences (executed in reaction mode) the cognitive processor is solely responsible for each individual response and needs to switch between tasks, whereas in familiar sequences (executed in sequencing mode) it is still responsible for sequence preparation (and perhaps concatenation), but not for sequence execution. This implies a third question which is whether in unfamiliar sequences only the key press following a tone will be slowed because the cognitive processor switches to another task while in familiar sequences several responses may be slowed when the cognitive processor has switched to the secondary task as the motor processor continues sequence execution. Fourth, to examine whether explicit sequence knowledge contributes to sequence execution, the present experiment assessed awareness of the individual movements in these familiar sequence and how this is related to performance of that sequence.
Materials and Methods
Participants
In exchange for course credits or ?15, 48 undergraduate students took part (average 20 years). They were 24 women and 24 men. The study had been approved by the ethics committee of the University of Twente.
Tasks
In the practice phase, six black 0.9 cm × 0.9 cm placeholders were presented horizontally in the center of the screen against a white background. To mimic the positions of the response keys on the key board (DFG and JKL) there were 0.7 cm gaps between the placeholders with the exception of a gap in the middle that was 2.2 cm. Participants sat with their left and right ring, middle, and index fingers resting lightly on the D, F, G, J, K, and L keys of a regular computer key board. A stimulus involved filling of one placeholder with green. Participants responded by pressing the spatially compatible key. When the correct key had been pressed, the color in the square changed back to the background color (white). Errors resulted in the message “wrong key” (in Dutch) for 500 ms, and the sequence continued only when the correct key was depressed.
As indicated in Figure 1, in each practice block stimuli were presented in two fixed series of six (i.e., S1–S6), thus requiring two fixed sequences of six key presses (R1–R6). The time between stimulus n and response n is indicated by Tn which signifies the response time and in case of RSI 0 the IKI (e.g., the time between S2 and R2 is T2). The two 6-key sequences were presented in random order. The term trial is used to denote the entire sequence. The unstructured sequence did not involve any pauses, whereas during practice the prestructured sequence included for the 33 group one pause between R3 and S4 (i.e., an RSI > 0), and for the 222 group two pauses, one between R2 and S3 and one between R4 and S5. To counteract the development of a fixed execution rhythm, the pauses in the practice phase consisted of non-aging intervals of at least 300 ms (and truncated at 2000 ms) so that participants could not anticipate the moment the key-specific stimulus would be presented after the pause (Gottsdanker et al., 1986). If a key was prematurely pressed during the pause an error message was displayed, the non-aging interval started again, and the proper key was to be pressed again.
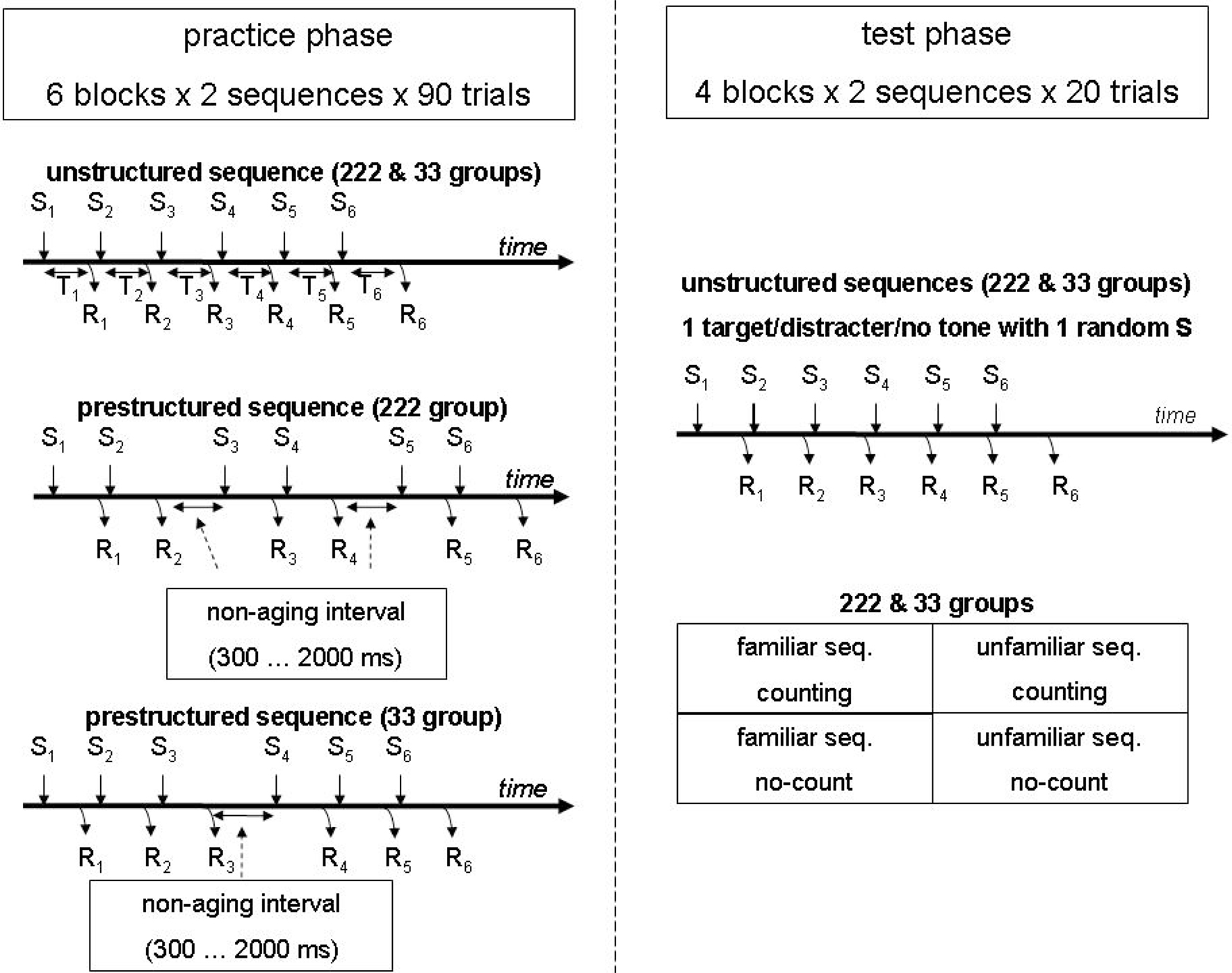
Figure 1. Schematic representation of the experiment. The participants practiced one unstructured sequence as well as one prestructured sequence with either one (33 group) or two (222 group) non-aging (response stimulus) intervals (i.e., a pause). The test phase included for all participants the same two blocks with the two familiar and two blocks with two unfamiliar sequences. Here, none of the test sequences included a non-aging interval. In each test sequence one randomly selected key specific stimulus was accompanied by either a target tone, a distracter tone (of both 100 ms), or no tone (ps = 0.33). In one of the familiar and one of the unfamiliar sequence blocks target tones were counted whereas they were ignored in the other two blocks.
Different sequences were used for different participants so that eventually each of the six fingers was used equally often at each sequential location, and response time differences between sequential locations can not be attributed to the use of particular fingers. For example, one participant had KFGDJL and FKL-JDG (“-” indicating a pause), while the next participant had LGJFKD and GLD-KFJ. The latter two sequences were derived by replacing each key of the first participant by the key and finger at its right (except L which was replaced by D). Following each sequence, the display was erased for 500 ms to indicate completion of the sequence, then the placeholders were presented again for 1000 ms, and the first stimulus of the next sequence was displayed.
The test phase included four blocks of trials: Two contained the two familiar sequences and two contained two unfamiliar (new) 6-key sequences (Figure 1). The pauses no longer occurred in the prestructured sequences. The interval between depressing the last key of one sequence and presenting the first key specific stimulus of the next sequence again amounted to 1500 ms. In all test phase blocks the onset of one of the six key-specific stimuli in each sequence was accompanied either by the onset of a 100 ms tone of 698 Hz (F5, p = 0.33) or 660 Hz (E5, p = 0.33), or no tone was presented at all (p = 0.33). Participants were instructed to continue keying when a tone was presented. In two test blocks, one with the familiar and one with the unfamiliar sequences, participants were instructed to count the low pitched (i.e., target) tones and ignore the high pitched (distracter) tones. In the other two blocks participants were told to ignore all tones. The instruction to count or ignore tones in a particular block remained visible at the bottom of the screen. At the end of a counting block, the participants typed in the number of target tones they had counted. All blocks were followed by presenting the percentage of errors and mean RT, while in the counting blocks the correct number of target tones was displayed too.
Procedure
Upon entering the lab, participants filled out an informed consent form and received a written instruction on the task to be performed which, if necessary, was extended orally by the experimenter. Subsequently 6 practice blocks followed, each including 90 unstructured and 90 prestructured sequences, yielding a total of 540 practice trials for each sequence. Each practice block lasted 10–15 min and was followed by a 7 min rest period.
After practice participants were asked to write down as accurately as possible the familiar sequences by using the letters of the keys employed in the experiment. The locations of the relevant key with the associated letters were displayed on the questionnaire and the computer key board remained in sight for consultation. Participants were then asked to indicate the strategy they had used for writing down their sequences. This involved checking one or more of five given alternatives: (A) “I remembered the order of the letters on the keys,” (B) “I tapped the sequence with my fingers on the table,” (C) “I tapped the sequence in my mind,” (D) “I remembered the positions of the squares and keys,” and (E) “I used another strategy, namely…”.
The test phases started off by participants putting on a pair of headphones allowing them to hear the tones presented in the test phase. Each of the four test blocks included 20 instances of each of the two sequences of a block. The order of the four test blocks was counter-balanced across participants and there was no pause in between the blocks other than a short instruction to count or ignore tones in the ensuing block. Sequences were balanced across participants such that a particular sequence was as often used as prestructured and unstructured sequence in the practice phase and as unfamiliar and familiar sequence in the test phase. So, effects of pauses and familiarity cannot be attributed to differences amongst sequences in different conditions. It took a participant about two and a half hours to complete the experiment.
Apparatus
Stimulus presentation, timing, and data collection was achieved using the E-prime© 1.1 experimental software package on a standard Pentium© IV Windows XP© PC. Unnecessary Windows services were shut down to improve RT measurement accuracy. Stimuli were presented on a 17 inch Philips 107T5 display running at 1024 by 768 pixel resolution in 32 bit color, and refreshing at 85 Hz. The viewing distance was approximately 50 cm, but this was not strictly controlled. Tones were presented with a Sennheiser HD202 over-the-ear headphone at a level that was clearly audible, but not disturbingly loud.
Results
Below, we generally report first the design and relevant results of the omnibus ANOVAs after which we zoom in on the specific research questions with planned comparisons.
Practice Phase
The development of keying skill in the practice phase was examined with a 2 (Group: 222 vs. 33) × 2 (Structure: prestructured vs. unstructured) × 6 (Block) × 6 (Key: R1 –R6) ANOVA with Group as between-subjects variable. In addition to main effects of Block, F(5,230) = 215.2, p < 0.001, ηp2= 0.82, and Key, F(5,230) = 198.3, p < 0.001, ηp2 = 0.81, interactions were in line with the expectation that the 222 and 33 groups used different segmentation patterns, Group × Key, F(5,230) = 24.3, p < 0.001, ηp2 = 0.35, and that this difference changed with practice, Group × Block × Key, F(25,1150) = 4.7, p < 0.001, ηp2 = 0.35. The effect of imposing a pause was significant as a Structure main effect, F(1,46) = 8.1, p < 0.01, ηp2 = 0.15. This effect differed for the two groups, Group × Structure, F(1,46) = 10.5, p < 0.01, ηp2 = 0.19, and it affected different keys for the two groups, Group × Structure × Key, F(5,230) = 33.2, p < 0.001, ηp2 = 0.42. So, these effects are in line with the intended effects of Structure and Group.
The practice phase was basically meant for motor chunk development, but allowed an additional test of the earlier finding that the rhythm of one sequence does not transfer to a simultaneously practiced sequence (Verwey et al., 2009; cf. Sakai et al., 2004). That is, given that the main difference between a 222 and a 33 prestructured sequence concerns T3–T5 (i.e., T3/T5 are longer than T4 in 222, and shorter in 33), transfer of the rhythm of the prestructured to the unstructured sequence should affect especially the difference between T3/T5 and T4 in the unstructured sequences of the 222 and 33 groups. For Blocks 1 and 2, planned comparisons were still in line with an effect of the prestructured on the unstructured sequence because for the 33 group T4 of the unstructured sequences was longer than T3/T5, F(1,46) = 7.8, p < 0.01, ηp2 = 0.14, whereas for the 222 group T4 was significantly shorter than (at least) T3, F(1,46) = 4.3, p < 0.05, ηp2 = 0.09. This group difference was significant, F(1,46) = 5.8, p < 0.05, ηp2 = 0.11. Importantly, this group difference reduced across the practice blocks, F(5,230) = 2.4, p < 0.05, ηp2 = 0.05, and was no longer significant across Blocks 5 and 6, F(1,46) = 0.9, p > 0.20, ηp2 = 0.02. Planned comparison on subsequent test phase results confirmed this: There too the T3/T5 vs. T4 difference in the unstructured sequence was not different in the 222 and 33 groups (across the no-tone sequences in the count and no-count conditions), F(1,46) = 0.3, p > 0.20, ηp2 = 0.01. So, the practice and test phase results confirm that the structure of the prestructured sequence did influence IKIs of the unstructured sequence in early practice and that this influence had vanished by the end of the practice phase. This supports the earlier conclusion that the temporal structure of the prestructured sequence did not transfer to the unstructured sequence.
Proportions of errors were transformed with an arcsine function before being subjected to variance analytic analyses (Winer et al., 1991). These transformed error proportions were submitted to an ANOVA with the above mentioned design. It appeared that error rate per key was always below 3.7%, and the ANOVA showed no interesting findings other than a Group × Structure × Key interaction, F(5,230) = 10.6, p < 0.001, ηp2 = 0.19, indicating that error rate in the prestructured sequence was highest for the key presses immediately following the pause (222: R3 and R5; 33: R4).
Test Phase
Figure 2 presents response times in the counting and no-counting conditions. Mean response times per participant, key position, and test condition were analyzed first with a mixed 2 (Group) × 2 (Counting: counting vs. no-counting) × 2 (Familiarity: familiar vs. unfamiliar sequence) × 2 (Structure: prestructured vs. unstructured sequence) × 6 (Key) ANOVA with Group as between subjects variable. The ANOVA showed by way of a Structure main effect that practicing the prestructured sequence with a pause affected response times, F(1,46) = 24.4, p < 0.001, ηp2 = 0.35. As expected, the size of the Structure effect was different for familiar and unfamiliar sequences, Structure × Familiarity interaction, F(1,46) = 9.6, p < 0.01, ηp2 = 0.17, which in turn differed for the 222 and 33 groups Group × Structure × Familiarity interaction, F(1,46) = 4.1, p < 0.05, ηp2 = 0.08. Also, the difference between Keys, F(5,230) = 113.4, p < 0.001, ηp2 = 0.71, was affected by sequence structure, Structure × Key, F(5,230) = 4.4, p < 0.001, ηp2 = 0.09, which differed as a function of familiarity, Familiarity × Structure × Key, F(5,230) = 6.0, p < 0.001, ηp2 = 0.12.
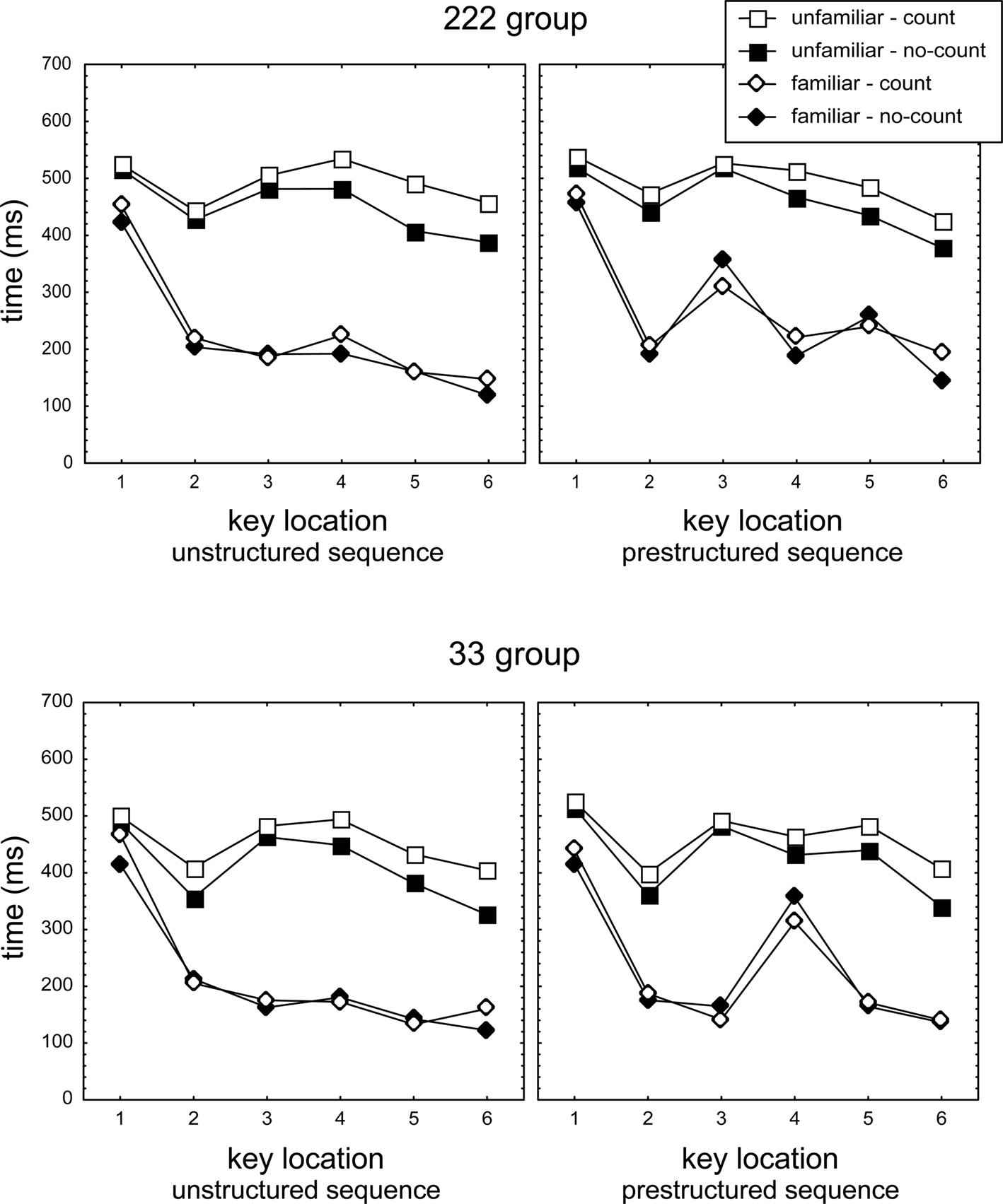
Figure 2. Response times (i.e., T1 and IKIs T2–T6) in the no-counting and the counting conditions of the test phase for the unfamiliar and familiar (prestructured and unstructured) sequences. T3 and T5 in the 222 prestructured familiar, and T4 in the 33 familiar prestructured sequences constitute the longest IKIs. For unfamiliar sequences, the distinction between prestructured and unstructured is artificial as these sequences had not been practiced before.
As the long IKIs occurred at different positions in the unstructured and prestructured sequences in the 222 and 33 groups, a second ANOVA was used in which the Key variable was replaced by a 3-level Phase variable (including T1 vs. execution IKI vs. longest IKI). For familiar/prestructured sequences execution IKIs included T2T4T6 in 222 and T2T3T5T6 in 33, longest IKIs (assumed to index the concatenation phase) included T3T5 in 222 and T4 in 33. For familiar, unstructured sequences the “longest IKI” involved the single longest IKI of T2-T6, while “execution IKIs” consisted of the three shortest IKIs of T2–T6 of each participant (three instead of four intervals were used as the second longest IKI might index a second transition between motor chunks). This ANOVA confirmed that the Phase effect, F(2,92) = 233.9, p < 0.001, ηp2 = 0.84, was different for familiar and unfamiliar sequences, Familiarity × Phase, F(2,92) = 102.4, p < 0.001, ηp2 = 0.69, which effect in turn differed for prestructured and unstructured groups, Familiarity × Structure × Phase, F(2,92) = 20.2, p < 0.001, ηp2 = 0.31.
As these two ANOVAs involved all responses irrespective of whether they followed a tone, two additional ANOVAs were carried out with the same design that included only the intervals that immediately followed a tone (rather than all intervals in the sequence). These ANOVAs are more sensitive to the effects of the secondary task on sequence execution and appeared to confirm the above results. These four ANOVAs served as starting point for most planned comparisons below that tested the hypothesis formulated in the Introduction though some additional ANOVAs are reported below too.
Longest IKIs
A first set of planned comparisons was used to verify that the pauses that had occurred during practice in the prestructured sequences had indeed induced the longest IKIs of these sequences in the test phase. Indeed, in 33 T4 was longer than T2T3T5T6, F(1,46) = 74.5, p < 0.001, ηp2 = 0.62 and in 222 T3T5 were longer than T2T4T6, F(1,46) = 40.4, p < 0.001, ηp2 = 0.47. Next, we determined for the unstructured sequences of the 222 and 33 groups that the longest IKIs were indeed significantly longer than the remaining IKIs (no-tone sequences), F(1,46) = 110.25, p < 0.001, ηp2 = 0.71. This demonstration that the longest IKIs in the prestructured and unstructured sequences were longer than the remaining IKIs allowed us to examine the secondary task effects separately for the alleged concatenation and execution intervals.
Global secondary task effects
No-tone sequences. We assessed the effect on sequence performance of carrying out the counting task when no actual tones were presented. This was done separately for the three phases of sequence production (i.e., T1, execution IKIs, and in familiar sequences longest IKIs) by comparing no-tone sequences in the counting and no-counting conditions. It appeared that even when no tone was presented the counting task slowed initiation of familiar sequences relative to the no-counting condition, F(1,46) = 12.7, p < 0.001, ηp2 = 0.22. This slowing was not observed for initiating unfamiliar sequences, F(1,46) = 0.4, p > 0.20, ηp2 = 0.01, nor for performing familiar and unfamiliar sequences, F(1,46) = 0.14, p > 0.20, ηp2 = 0.00. These findings suggest that only in familiar sequences some general preparation was affected by the mere involvement of a secondary task.
Tone vs no-tone sequences. To explore the effect of increased cognitive load (due to the secondary task) across different phases of the sequences, the planned comparisons below compare the difference between IKIs following a “tone” in tone and no-tone sequences of the counting condition, with that difference for the no-counting condition. The “tone” in the no-tone base line condition involved the computer determined tone position at which no actual tone was presented.
A first set of analyses including this comparison of tone effects in counting- and no-counting conditions confirmed that the tone slowed all responses of unfamiliar sequences more in the counting than in the no-counting condition, T1: F(1,46) = 4.1, p < 0.05, ηp2 = 0.08, all IKIs: F(1,46) = 20.0, p < 0.001, ηp2 = 0.30, resp. Similarly, in familiar sequences the tone lengthened longest and execution IKIs more in the counting than in the no-counting condition, F(1,46) = 8.5, p < 0.01, ηp2 = 0.16, while here lengthening was marginally significant for T1, F(1,46) = 3.1, p = 0.08, ηp2 = 0.06. The lengthening by a tone in the counting (as compared with the no-counting) condition was stronger for IKIs of unfamiliar than of familiar sequences, F(1,46) = 10.3, p < 0.01, ηp2 = 0.18, while lengthening of T1 was not significantly different (p > 0.20). Importantly, in familiar sequences lengthening of longest and execution IKIs in the counting as compared with the no-counting condition was not significantly different, F(1,46) = 3.7, p > 0.06, ηp2 = 0.07. In fact, the latter marginally significant effect actually indicated a trend in the opposite direction suggesting that concatenation would suffer less than execution from the secondary task, instead of more (see right panels of Figure 2, but see below). So, execution of unfamiliar sequences was generally slowed more than of familiar sequences, but there was no indication that the longest IKIs (assumed to reflect concatenation) were lengthened more than execution IKIs and hence that concatenation is carried out by the cognitive processor.
The above mentioned indication that concatenation in the familiar prestructured sequences was fastened instead of slowed in the counting condition (relative to the no-counting condition, see the right hand panels in Figure 2) appeared to occur irrespective of whether a tone had been presented. That is, in the 33 group T4 of the prestructured familiar sequence was indeed significantly faster in the counting than in the no-counting condition (relative to T2T3T5T6), F(1,46) = 11.0, p < 0.01, ηp2 = 0.19. However, this effect was significant in the no-tone sequences of the counting condition too, F(1,46) = 8.7, p < 0.01, ηp2 = 0.16, and was not different for tone and no-tone sequences, F(1,46) = 0.8, p > 0.20, ηp2 = 0.02. Likewise, for the familiar prestructured 222 sequences T3T5 were shorter in the counting than in the no-counting condition (relative to T2T4T6), F(1,46) = 12.5, p < 0.001, ηp2 = 0.21, but the effect was significant also for the no-tone sequences alone, F(1,46) = 4.4, p < 0.05, ηp2 = 0.09, and not different for tone and no-tone sequences, F(1,46) = 1.6, p > 0.20, ηp2 = 0.03. Thus, the apparent fastening of the longest IKIs in the familiar, prestructured sequences in the counting condition did not result from actual tone presentation but rather from performing in the counting condition. This observation may be associated with the earlier reported slowed initiation of these sequences which may imply that the secondary task affected sequence preparation and therewith sequence execution.
In short, first, performing in the tone counting condition slowed initiation of familiar keying sequences (even when there was no tone). Second, if a tone was actually presented the immediately ensuing response slowed more in the counting than in the no-counting condition (in all phases of familiar and of unfamiliar sequences), and this slowing was larger for IKIs in unfamiliar than in familiar sequences. This supports the hypothesis that the cognitive processor is involved less in executing familiar than unfamiliar sequences. Third, the data do not endorse the notion that concatenation in familiar sequences is carried out by the cognitive processor in that the longest IKI was not slowed more than the execution IKIs.
Immediate effects of a tone
To examine in detail whether we can find support for the notion that the cognitive processor switches from triggering key presses in sequences, to identifying tones and counting target tones, and then back to triggering key presses, we examined slowing of the IKIs that followed each tone as a function of their position relative to the tone. This was done irrespective of the absolute location of tone presentation and ignored the difference between execution IKIs and longest IKIs (as these were lengthened by a tone to a similar degree, see above). In this analysis, all IKIs preceding tone presentation were averaged at Location −1 (i.e., L−1). IKIs immediately following tone presentation were averaged and indicated as IKI at Location 0. Likewise, subsequent IKIs were averaged as a function of their location relative to the tone onset. Tones at S1 were not included in this analysis because the relatively long T1 would slow L0–L5 and not L−1 and because it is unclear whether the motor processor is involved in R1. A distinction was made between target tones, distracter tones, and no-tones to distinguish between effects of identification of distracter tones, and effects of identifying and counting target tones. This recoding of response times yielded IKI as a function of relative locations L−1 to L5 (see Figure 3).
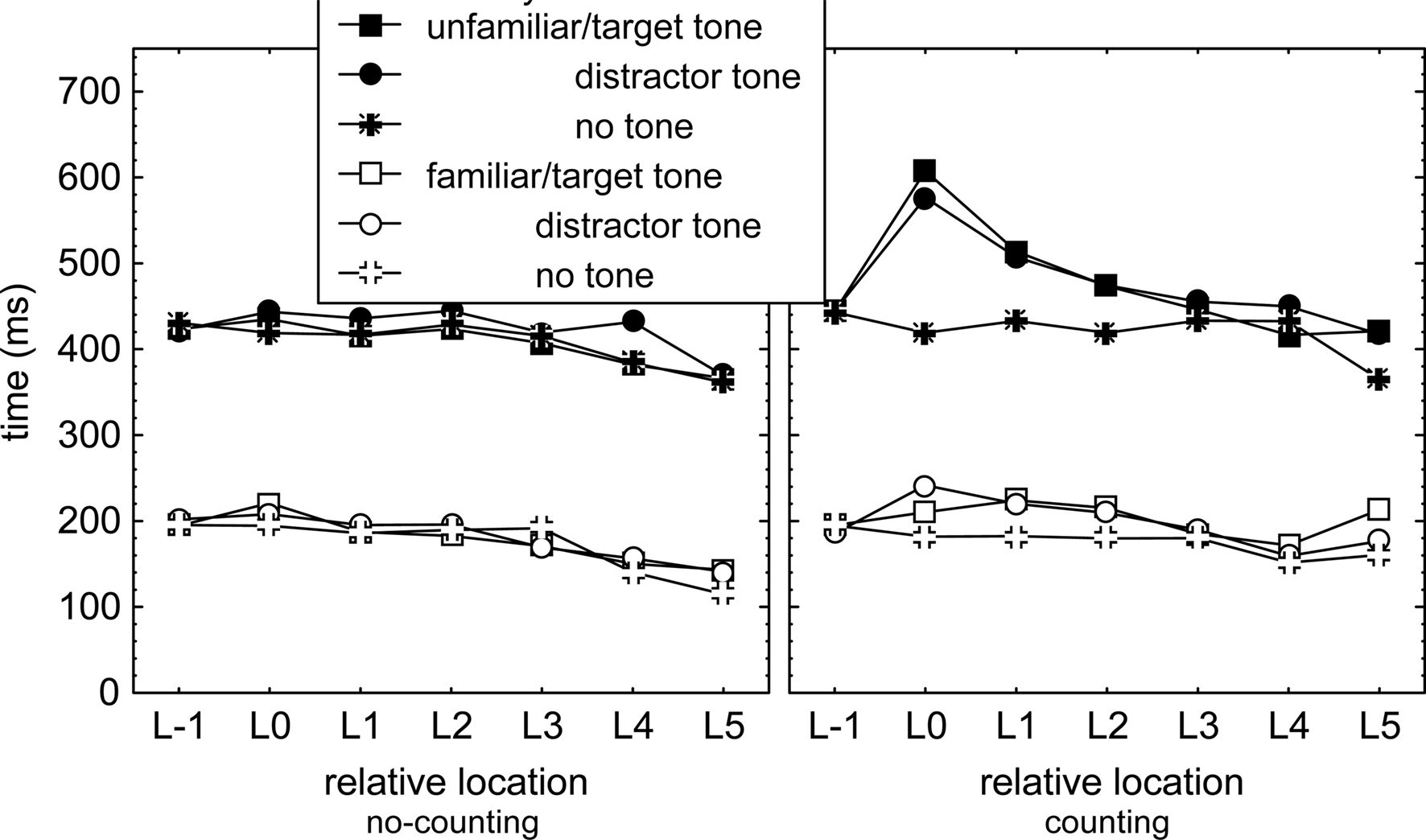
Figure 3. Response times as a function of location relative to tone presentation (L−1: average of all interkey intervals preceding the tone, L0: interkey interval immediately following the tone, and so on), tone identity, sequence familiarity, counting condition, and secondary task.
Interkey intervals following a tone (or at least the computer determined tone position that did not involve actual tone presentation in the no-tone condition) were analyzed with a mixed 2 (Group) × 2 (Counting) × 2 (Familiarity) × 2 (Structure) × 3 (Tone: target, distracter, no tone) × 7 (Location: L-1–L5) ANOVA on the IKIs relative to the location of the tone. Most importantly, the ANOVA (in combination with the planned comparisons below) showed that IKIs differed at the various locations relative to the tone, F(6,276) = 31.4, p < 0.001, ηp2 = 0.41, and this effect was larger in the counting than in the no-counting conditions, Counting × Location, F(6,276) = 4.4, p < 0.001, ηp2 = 0.09, larger in unfamiliar than in familiar sequences, Familiarity × Location, F(6,276) = 3.5, p < 0.01, ηp2 = 0.07, and in line with Figure 3, largest for particular locations in the counting condition for unfamiliar sequences, Familiarity × Counting × Location, F(6,276) = 6.2, p < 0.001, ηp2 = 0.12.
Planned comparisons showed that in the no-counting condition presentation of a tone did not affect IKIs. This was indicated by comparison of the IKIs at L0 and at L−1 in familiar and unfamiliar sequences, Fs(1,46) = 3.3, ps > 0.07, ηp2s < 0.07 (left panel of Figure 3). In contrast, presenting a (target or distracter) tone in the counting condition significantly lengthened IKI at L0 relative to the IKIs at L−1 in both familiar and unfamiliar sequences, Fs(1,46) > 12.4, ps < 0.001, ηp2s > 0.21 (right panel of Figure 3). This lengthening was larger in unfamiliar than in familiar sequences, F(1,46) = 12.1, p < 0.01, ηp2 = 0.21, but did not differ for target and distracter tones in either sequence condition, Fs(1,46) < 1.7, ps > .19, ηp2s < .04. Further planned comparisons showed that IKIs at L0, L1, and L2 were each longer following a (target and distracter) tone than when no tone was presented in the counting condition. This was significant in unfamiliar sequences, Fs(1,46) > 19.6, ps < .01, pη2s > .30, and also in familiar sequences, Fs(1,46) = 9.3, ps < .01, ηp2s > .17. This pattern of results was obtained also in similar analyses with just execution IKIs.
Hence, presenting target and distracter tones slowed the ensuing three responses in the counting condition relative to the no-counting condition, and more so in unfamiliar than in familiar sequences. The finding that a tone slowed three responses in both the familiar and unfamiliar sequences suggests that the presentation of a tone caused the cognitive processor to be allocated away from contributing to sequence execution for a short time while sequence execution continued (though slower). Absence of a target-distracter tone difference suggests that the cognitive processor did not perform the tone counting operation during sequence execution.
Interference as a function of response rate
The above finding that three responses following a tone were slowed suggests that execution of even the unfamiliar sequence continued while the cognitive processor was dedicated to tone processing, and hence that already during the test phase participants learned to execute responses of the new sequence independent of the cognitive processor. Alternatively, this finding might indicate that the cognitive processor had sufficient capacity to be involved both in tone counting and sequence execution processes (in parallel or in rapid succession). Learning of unfamiliar sequences in the test blocks is indicated by the finding in Figure 2 that R2 of the unfamiliar sequences was relatively fast and execution rate increased as the sequence progressed. Furthermore, rapid learning of only some response transitions predicts that when the IKI following the tone is short (because it is triggered by a fast non-cognitive sequence learning mechanism), it will be lengthened less by the tone than when the IKI is long (indicating the response relies on the cognitive processor). This hypothesis was tested following a mixed 2 (Group) × 2 (Structure) × 2 (Tone: Sequences with vs. without any tone) × 2 (Familiarity) × 5 (IKI duration) analysis of the single IKI that immediately followed a tone while IKIs of each participant were sorted from short to long.
This ANOVA confirmed the indication in Figure 4 that, across the 5 IKIs of unfamiliar sequences, the presentation of a tone slowed the ensuing response more in the counting than in the no-counting condition, F(1,46) = 26.6, p < 0.001, ηp2 = 0.37. In line with the notion that in the unfamiliar sequence the faster transitions had been learned by a non-cognitive mechanism during the test block, lengthening of the IKI by a tone in the counting condition increased with IKI duration. This followed from the comparison of the tone no-tone difference in the counting and the no-counting conditions (see the upper right panel of Figure 4), F(4,184) = 12.5, p < 0.001, ηp2 = 0.21. For familiar sequences, this increasing slowing by a tone with IKI duration was significant too (lower right panel of Figure 4), F(4,184) = 4.4, p < 0.01, ηp2 = 0.09, but the size of the effect was smaller than in the unfamiliar sequence, F(4,184) = 3.3, p < 0.01, ηp2 = 0.07. Hence, these results support the notion that, when assessed across the entire test block, even in unfamiliar sequences some responses were not triggered by the cognitive processor but by some faster (non-cognitive) processor that was not disrupted by the secondary task. Likewise, in familiar sequences slow responses appeared to still involve a clear influence of the cognitive processor.
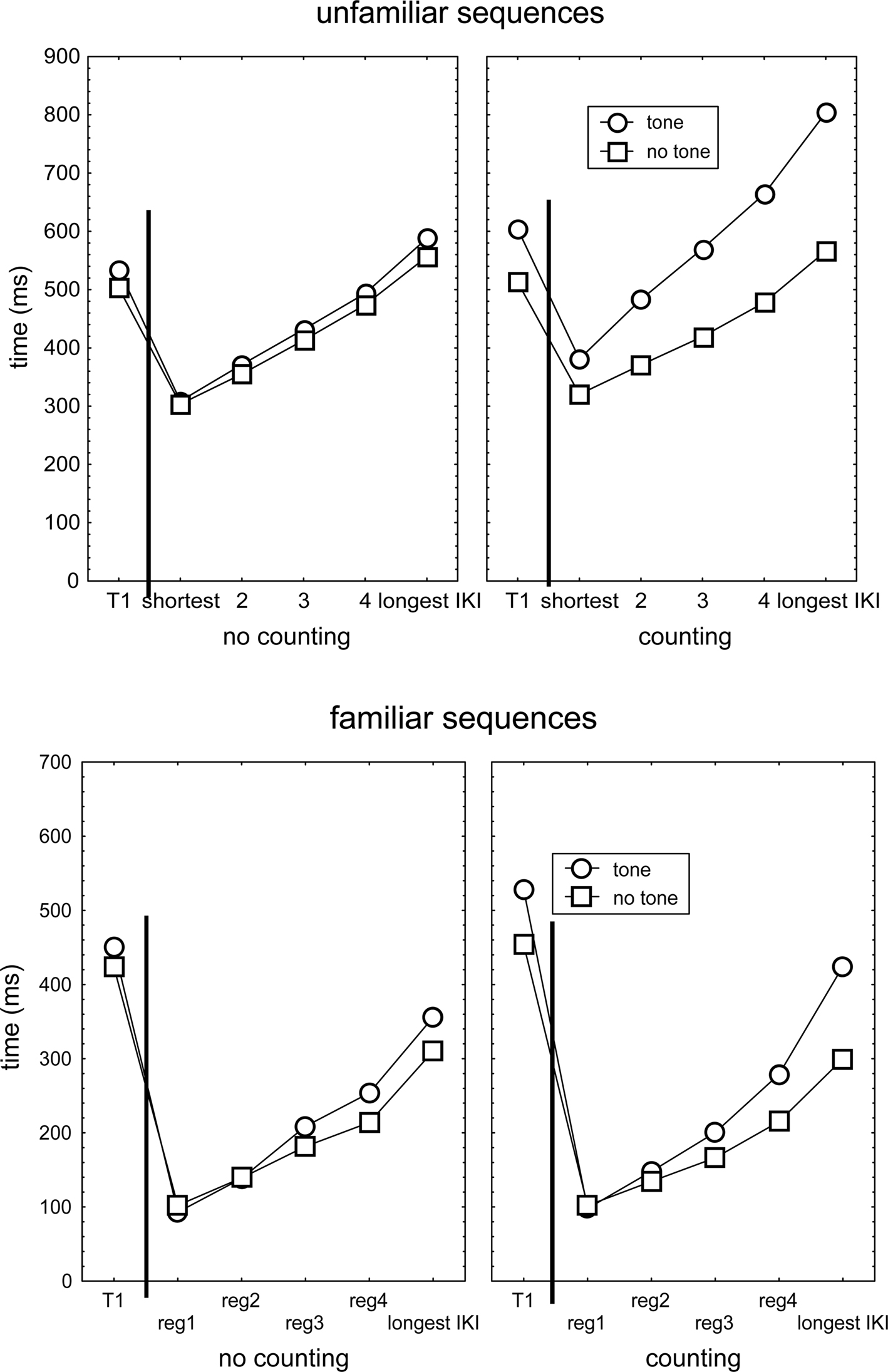
Figure 4. The durations of T1 and IKIs in no-counting and counting conditions that immediately followed the computer determined tone location in (unfamiliar and familiar) sequences in which the tone was actually presented, and in sequences which no tone was presented. IKIs had first been sorted for each individual participant as function of their duration and then averaged across participants.
Awareness
Of the 48 participants, 29% (14) of the participants were not able to write down even one of their sequences at the end of the practice phase, 25% (12) wrote down one sequence correctly, and 46% (22) reproduced both sequences correctly. Including awareness as between subject variable in the earlier practice phase ANOVA on responses times yielded a mixed 3 (Awareness: number of correctly written sequences: 0-2) × 2 (Group) × 2 (Structure) × 6 (Block) × 6 (Key) ANOVA. It showed that participants with awareness of both sequences were faster than those with awareness of one or of neither sequence, 198, 303, 293 ms, resp., F(2,42) = 18.4, p < 0.001, ηp2 = 0.47. Those writing down just one sequence correctly were not faster than those who could not write down one sequence correctly, F(1,42) = 0.2, p > 0.20, ηp2 = 0.0. This advantage of the fully aware over the less aware and unaware participants reduced from Block 1 (316, 463, 456 ms, resp.) to Block 6 (162, 221, 219 ms), F(10,210) = 7.2, p < 0.001, ηp2 = 0.26, but the awareness effect was still significant when tested for Block 6 alone, F(1,42) = 14.2, p < 0.001, ηp2 = 0.25.
Replies as to how the 48 participants had tried to write down their sequences showed that most participants either remembered the spatial positions of the stimuli and/or keys (25%, 12 participants), or tried to reconstruct the sequence by playing it back in their mind or on the table top (42%, 20 participants). The remaining participants indicated to have tried a combination of strategies. Using the spatial knowledge strategy was more successful for writing down both sequences (9 of the 12 “spatial” participants wrote down both sequences correctly) than tapping (8 of the 20 “play-back” participants), which group difference was significant according to a 2 (Strategy) × 2 (Correct reproduction: 0 vs. 2) χ2 test, χ2(1) = 3.7, p = 0.05.
So, only participants who wrote down both their sequences were executing their sequences faster, but this benefit reduced with practice. Participants claiming to have remembered the spatial order of stimuli and/or keys were more successful in writing down their sequences than those who indicated to have tried to reconstruct their sequences by tapping them.
Errors
The mixed 2 (Group) × 2 (Counting) × 2 (Familiarity) × 2 (Structure) × 6 (Key) ANOVA on arcsin transformed error proportions of the test phase showed only two main effects: There were more errors in unfamiliar than in familiar sequences (4.8% vs. 3.4% per key press), F(1,46) = 32.9, p < 0.001, ηp2 = 0.42, and error rate varied across key locations, F(1,46) = 8.9, p < 0.001, ηp2 = 0.16, and peaked at R4 (6.3% vs. below 4.3% for the rest).
Discussion
The present experiment tested several predictions made by the dual processor model for the situation that familiar and unfamiliar keying sequences are being executed while at the same time a secondary task is performed. As to the hypotheses in the introduction, it can be concluded that, first, the present study does not support the notion that the cognitive processor is responsible for concatenating motor chunks, neither in unstructured nor in prestructured (222 and 33) sequences. Second, the hypothesis that unfamiliar sequences would be slowed more than familiar sequences by the secondary tone-counting task was confirmed, and it appeared that, third, actual tone presentation slowed the three responses following a tone in both familiar and unfamiliar sequences, and significantly more so in the latter. Finally, a subgroup of participants seems to have used explicit knowledge for executing sequences with limited practice in that participants with explicit knowledge of both sequences were faster than those who had explicit knowledge of one or none of the sequences. This benefit of explicit knowledge reduced with practice suggesting that with practice the motor processor outperformed the application of explicit knowledge. Below these results are discussed in more detail.
First, the main impetus for the present study were the contrasting results with respect to the effect of a secondary memory task on the slowest response in an unstructured movement sequence (Brown and Carr, 1989; Verwey, 2003b). We used a tone counting task to assure that this time at least some secondary task processes were immediately carried out. Execution IKIs showed the expected lengthening by the secondary task, but the secondary task did not cause additional lengthening of the longest IKIs in the unstructured and prestructured sequences. This does not rule out the notion that the longest IKIs index concatenation of successive motor chunks and, hence, hierarchical control (e.g., Broadbent, 1977; Rosenbaum et al., 1983). Yet, it does indicate that the longest IKI does not reflect concatenation of motor chunks by the cognitive processor. Instead, the longest IKI in fixed sequences may indicate activation via an association of the next motor chunk, or perhaps concatenation by some dedicated “concatenation” processor.
Second, as expected IKIs of unfamiliar keying sequences were lengthened more than IKIs of familiar keying sequences by the counting task, indicating that cognitive involvement was higher in the former. Importantly, this finding was accompanied by a slowed initiation of familiar sequences in the counting condition (even when no tone was presented). This shift of slowing from sequence execution to sequence initiation with practice indicates that the first response of familiar sequences is preceded by more extensive preparation by the cognitive processor with familiar than with unfamiliar sequences, while the cognitive processor is involved much less in executing familiar than unfamiliar sequences. This is entirely in line with the dual processor model in which familiar keying sequences are executed mainly on the basis of motor chunks, and also with the notion that preparation of a timed sequence involves a time frame specifying the moment each element is initiated (Klapp, 1995).
Third, it was observed that the three responses following actual tone presentation were slowed in the counting condition for both familiar and unfamiliar sequences, but more so for the latter. These results are well in line with the idea that the cognitive processor is affected by the secondary task. For familiar sequences the impact of a secondary task is small as the cognitive processor is mostly (but not always) outraced by the motor processor (which is well trained for familiar sequences). Instead, execution of unfamiliar sequences is much more dependent on the cognitive processor and therefore suffers greatly from an interfering secondary task.
In familiar sequences slowing of the three responses that follow a tone rejects the strong version of the dual processor model that assumes that the cognitive processor is not at all involved in executing familiar sequences. Rather, this finding supports the conclusion that without the need to process a tone, the cognitive processor contributes to triggering individual responses in a race with the motor processor (Verwey, 2003a). Originally, such a race model was proposed to explain the IKI distributions in familiar keying sequences when participants switched from reaction to sequencing mode during execution (Verwey, 2003a; also see Raab, 1962; Logan, 1988; Miller and Ulrich, 2003). However, the race model also explains the small execution rate decrease when a secondary task is carried out (Verwey, 1993, 2003b, present study), when key-specific stimuli are not presented (Verwey, 1999), when a choice RT task precedes sequence execution (Verwey and Eikelboom, 2003), and when another sequence follows sequence execution (Verwey, 2001). According to this race model a keying sequence will be slowed less by a secondary task if the cognitive processor wins the race less often, which is, when the sequence has been practiced more extensively and the motor processor has become faster. This is precisely what we found.
Interestingly, actual tone presentation also slowed up to three responses in the unfamiliar sequences. This can not easily be explained by the idea that the cognitive processor is solely responsible for triggering responses, upon tone presentation devotes its resources to tone processing (i.e., identification), and then switches back to sequence production. That would predict only one slowed response. Several alternative explanations for this unexpected result can be considered. First, it could be explained by individual differences in the moment of tone processing, with most participants starting the tone processing directly after tone presentation (i.e., causing a slowed response only at L0; see Figure 3), and others delaying tone processing until one or two responses had been executed (i.e., causing a slowed response at L1 and L2, respectively). Second, it could be that the cognitive system shared its resources between tone processing and sequence execution in a parallel fashion. However, this would indicate that against current notions the cognitive processor is not a single resource system. Third, the slowing of up to three responses in unfamiliar sequences could be explained by very rapid switching between (sub-) processes of both tone processing and sequence execution. Finally, it is possible that the test phase had provided enough practice to have at least some responses in unfamiliar sequences being triggered by some non-cognitive mechanism. That indeed learning occurred during the test phase is demonstrated by the finding that R2 of the unfamiliar sequence was relatively fast and execution rate increased as the sequence progressed (Figure 2; Verwey, 2010, reports similar results with elderly executing a DSP sequence). The notion that learning of unfamiliar sequences was not mediated by the cognitive processor is suggested by the finding that fast responses in the unfamiliar sequences suffered less from a tone than slow responses. This result implies that slow responses were slow because they depended heavily on the cognitive processor (because the non-cognitive sequence learning mechanism had not yet learned that transition), while the fast transitions involved transitions triggered by another (obviously non-cognitive) mechanism. This learning by a non-cognitive mechanism is in line with the associative learning that is assumed to underlie skill in the serial RT task too (cf. Jiménez, 2008; Verwey, 2010). Given the abundance of support for the notion that implicit learning in the serial RT task rests on the rapid development of associative sequence knowledge, the latter explanation of the slowing by a tone of three ensuing responses in unfamiliar sequences seems quite plausible.
Note that slowing was the same for target and distracter tones. This indicates that the cognitive processor was involved in identifying the tone, but did not increment the target counter in working memory during sequence execution. Given the reliance on working memory it then seems likely that the cognitive processor incremented the target counter after sequence completion.
Fourth, as awareness is limited in the serial RT task (e.g., Curran and Keele, 1993; Rüsseler et al., 2003; Tubau et al., 2007), we decided to also assess awareness in the present experiment. In contrast to the serial RT task it is obvious to participants in DSP studies that they are executing fixed keying sequences. Still, in line with findings reported in Verwey et al. (2009), awareness appeared to be limited in that not even half the participants was able to write down both their sequences. Those who did have explicit sequence knowledge of both sequences appeared to also be faster executing their familiar keying sequences than those who could correctly write down only one sequence or no sequence at all. This is interesting as it suggests a strategic difference: Only participants with full explicit knowledge used explicit knowledge for sequence execution (i.e., a memory based execution mode), perhaps instead of, or in parallel with, translating key specific stimuli into key presses (i.e., in reaction mode). The finding that the beneficial effect of explicit knowledge on sequence execution reduced with practice indicates that it was not the motor processor that used explicit sequence knowledge for executing familiar sequences. Using explicit knowledge for sequence execution may have been fairly easy for the more aware participants as the questionnaire results suggest that explicit knowledge in the aware participants was already in a spatial code. Instead, those who indicated to have played back the sequence during the awareness test (mentally or on the table top) indeed seem not to have explicit sequence knowledge available in an easy accessible format and therefore could not increase execution rate (cf. Heuer and Schmidtke, 1996; Park and Shea, 2005).
All taken together, these findings are in line with, and extend, the dual processor model that was originally developed to explain that selecting a forthcoming familiar keying sequence can occur during execution of a previous familiar sequence (Verwey, 2001). The present results confirm that the cognitive processor is a general, versatile processor that is responsible for preparing and initiating unfamiliar and familiar keying sequences, triggering individual key presses in these sequences (using external stimuli or perhaps explicit knowledge), and identifying tones. Yet, it can probably perform only one task at the time and needs to switch in secondary task conditions. In familiar sequences the cognitive processor races with the motor processor to trigger individual key presses – unless it is involved in other tasks (like identifying tones and preparing forthcoming sequences). It now seems that even with little practice some response transitions have been learned at a non-cognitive (motor chunk- or associative learning based) level, and for some participants also at an explicit level. In the present study, this allowed execution of even unfamiliar sequences to continue when the cognitive processor was identifying a tone. So, depending on the level of practice and awareness of the participant, execution of discrete keying sequences seems to be based on a combination of motor chunks, associative knowledge and explicit knowledge, but with practice the use of motor chunks becomes dominant. A similar model of mixed mechanisms in which control becomes increasingly independent of external stimuli has been argued to also underlie skill in the serial RT task (Tubau et al., 2007). In conclusion one could say that the effects in the present study can be explained by a relatively complex processing architecture that does justice to the complexity and redundancy of the brain.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This experiment was carried out by students in Willem Verwey’s laboratory classes. We would like to thank Jennifer Bissling, Cynthia Dekker, Ariane Chantal Dücker, Kristina Frangenberg, Nicole Jöersen, Karin van Leeuwen, Annemiek Punter, and Arzu Tanriverdi for running the experiment. This research was supported in part by grant 461-04-620 from the Netherlands Organization for Scientific Research NWO.
References
Bo, J., Borza, V., and Seidler, R. D. (2009). Age-related declines in visuospatial working Memory correlate with deficits in explicit motor sequence learning. J. Neurophysiol. 102, 2744–2754.
Bo, J., and Seidler, R. D. (2009). Visuospatial working memory capacity predicts the organization of acquired explicit motor sequences. J. Neurophysiol. 101, 3116–3125.
Bohlanda, J. W., and Guenther, F. H. (2006). An fMRI investigation of syllable sequence production. Neuroimage 32, 821–841.
Broadbent, D. E. (1977). Levels, hierarchies, and the locus of control. Q. J. Exp. Psychol. 29, 181–201.
Brown, T. L., and Carr, T. H. (1989). Automaticity in skill acquisition: mechanisms for reducing interference in concurrent performance. J. Exp. Psychol. Hum. Percept. Perform. 15, 686–700.
Curran, T., and Keele, S. W. (1993). Attentional and nonattentional forms of sequence learning. J. Exp. Psychol. Learn. Mem. Cogn. 19, 189–202.
de Kleine, E., and Verwey, W. B. (2009a). Representations underlying skill in the Discrete Sequence Production task: effects of hand used and hand position on the discrete sequence production task. Psychol. Res. 73, 685–694.
de Kleine, E., and Verwey, W. B. (2009b). Motor learning and chunking in dyslexia. J. Mot. Behav. 41, 331–337.
Glencross, D. J. (1980). “Response planning and the organization of speed movements.” in Attention and Performance VIII, ed. R. S. Nickerson (Hillsdale, NJ: Erlbaum), pp. 107–125.
Gottsdanker, R., Perkins, T., and Aftab, J. (1986). Studying reaction time with nonaging intervals: an effective procedure. Behav. Res. Methods Instrum. Comput. 18, 287–292.
Heuer, H., and Schmidtke, V. (1996). Secondary-task effects on sequence learning. Psychol. Res. 59, 119–133.
Jiménez, L. (2008). Taking patterns for chunks: is there any evidence of chunk learning in continuous serial reaction time tasks? Psychol. Res. 72, 387–396.
Kennerley, S. W., Sakai, K., and Rushwordth, M. F. S. (2004). Organization of action sequences and the role of pre-SMA. J. Neurophysiol. 91, 978–993.
Ketelaars, M. A. C., Garry, M. I., and Franks, I. M. (1997). On-line programming of simple movement sequences. Hum. Mov. Sci. 16, 461–483.
Klapp, S. T. (1995). Motor response programming during simple and choice reaction time: the role of practice. J. Exp. Psychol. Hum. Percept. Perform. 21, 1015–1027.
Koch, I., and Hoffmann, J. (2000). Patterns, chunks, and hierarchies in serial reaction-time tasks. Psychol. Res. 63, 22–35.
Kuriyama, K., Stickgold, R., and Walker, M. P. (2004). Sleep-dependent learning and motor-skill complexity. Learn. Mem. 11, 705–713.
McLeod, P. (1980). “What can probe RT tell us aboput the attentional demonds of movement?” in Tutorials in Motor Behavior, eds G. E. Stelmach and J. Requin (Amsterdam: North-Holland), pp. 579–589.
Miller, J., and Ulrich, R. (2003). Simple reaction time and statistical facilitation: a parallel grains model. Cogn. Psychol. 46, 101–151.
Panzer, S., Krueger, M., Muehlbauer, T., Kovacs, A., and Shea, C. H. (2009). Inter-manual transfer and practice: coding of simple motor sequences. Acta Psychol. 131, 99–109.
Panzer, S., Wilde, H., and Shea, C. H. (2006). Learning of similar complex movement sequences: proactive and retroactive effects on learning. J. Mot. Behav. 38, 60–70.
Park, J. -H., and Shea, C. H. (2005). Sequence learning: response structure and effector transfer. Q. J. Exp. Psychol. 58A, 387–419.
Posner, M. I., and Keele, S. W. (1969). “Attention demands of movement,” in Proceedings of XVIth Congress of Applied Psychology (Amsterdam: Swets and Zeitlinger).
Povel, D. J., and Collard, R. (1982). Structural factors in patterned finger tapping. Acta Psychol. 52, 107–123.
Raab, D. H. (1962). Statistical facilitation of simple reaction times. Trans. N. Y. Acad. Sci. 24, 574–590.
Rhodes, B. J., Bullock, D., Verwey, W. B., Averbeck, B. B., and Page, M. P. A. (2004). Learning and production of movement sequences: behavioral, neurophysiological and modeling perspectives. Hum. Mov. Sci. 23, 699–746.
Rosenbaum, D. A., Kenny, S. B., and Derr, M. A. (1983). Hierarchical control of rapid movement sequences. J. Exp. Psychol. Hum. Percept. Perform. 9, 86–102.
Rüsseler, J., Hennighausen, E., Münte, T. F., and Rösler, F. (2003). Differences in incidental and intentional learning of sensorimotor sequences as revealed by event-related brain potentials. Cogn. Brain Res. 15, 116–126.
Sakai, K., Hikosaka, O., and Nakamura, K. (2004). Emergence of rhythm during motor learning. Trends Cogn. Sci. 8, 547–553.
Sakai, K., Kitaguchi, K., and Hikosaka, O. (2003). Chunking during human visuomotor sequence learning. Exp. Brain Res. 152, 229–242.
Sternberg, S., Monsell, S., Knoll, R. L., and Wright, C. E. (1978). “The latency and duration of rapid movement sequences: comparisons of speech and typewriting.” in Information Processing in Motor Control and Learning, eds G. E. Stelmach (New York: Academic Press), pp. 117–152.
Tubau, E., Hommel, B., and Lopez-Moliner, J. (2007). Modes of executive control in sequence learning: from stimulus-based to plan-based control. J. Exp. Psychol. Gen. 136, 43–63.
van Mier, H., and Hulstijn, W. (1993). The effects of motor complexity and practice on initiation time in writing and drawing. Acta Psychol. (Amst) 84, 231–251.
van Mier, H. I., and Petersen, S. E. (2006). Intermanual transfer effects in sequential tactuomotor learning: evidence for effector independent coding. Neuropsychologia 44, 939–949.
Verwey, W. B. (1993). Effects of extended practice in a one-finger keypressing task. Acta Psychol. 84, 179–197.
Verwey, W. B. (1995). A forthcoming keypress can be selected while earlier ones are executed. J. Mot. Behav. 27, 275–284.
Verwey, W. B. (1996). Buffer loading and chunking in sequential keypressing. J. Exp. Psychol. Hum. Percept. Perform. 22, 544–562.
Verwey, W. B. (1999). Evidence for a multi-stage model of practice in a sequential movement task. J. Exp. Psychol. Hum. Percept. Perform. 25, 1693–1708.
Verwey, W. B. (2001). Concatenating familiar movement sequence: the versatile cognitive processor. Acta Psychol. 106, 69–95.
Verwey, W. B. (2003a). Processing modes and parallel processors in producing familiar keying sequences. Psychol. Res. 67, 106–122.
Verwey, W. B. (2003b). The effect of sequence length on execution familiar keying sequences: lasting segmentation and preparation? J. Mot. Behav. 35, 343–354.
Verwey, W. B. (2010). Diminished motor skill development in elderly: indications for limited motor chunk use. Acta Psychol. 134, 206–214.
Verwey, W. B., Abrahamse, E. L., and Jiménez, L. (2009). The effect of full visual feedback on the locus of an acquired nonlinear visuomotor transformation. Hum. Mov. Sci. Hum. Mov. Sci. 28, 348–361.
Verwey, W. B., and Dronkert, Y. (1996). Practicing a structured continuous keypressing task: motor chunking or rhythm consolidation? J. Mot. Behav. 28, 71–79.
Verwey, W. B., and Eikelboom, T. (2003). Evidence for lasting sequence segmentation in the discrete sequence production task. J. Mot. Behav. 35, 171–181.
Verwey, W. B., Lammens, R., and van Honk, J. (2002). On the role of the SMA in the discrete sequence production task. A TMS study. Neuropsychologia 40, 1268–1276.
Winer, B. J., Brown, D. R., and Michels, K. M. (1991). Statistical Principles in Experimental Design. New York: McGraw-Hill.
Keywords: keying sequences, discrete sequence production task, task switching, secondary task, motor skills, chunking
Citation: Verwey WB, Abrahamse EL and de Kleine E (2010) Congnitive processing in new and practiced discrete keying sequences. Front. Psychology 1:32. doi: 10.3389/fpsyg.2010.00032
Received: 02 March 2010;
Paper pending published: 16 April 2010;
Accepted: 29 June 2010;
Published online: 15 July 2010
Edited by:
Wilfried Kunde, Technische Universitaet Dortmund, GermanyReviewed by:
Charles Shea, Texas A&M University, USAMatthew J. C. Crump, Vanderbilt University, USA
Copyright: © 2010 Verwey, Abrahamse and de Kleine. This is an open-access article subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Willem B. Verwey, Faculty of Behavioral Sciences, Department of Cognitive Psychology and Ergonomics, University of Twente, P.O. Box 217, 7500 AE Enschede, Netherlands. e-mail:dy5iLnZlcndleUB1dHdlbnRlLm5s


