- School of Public Health, University of Saskatchewan, Saskatoon, SK, Canada
Discriminant analysis (DA) encompasses procedures for classifying observations into groups (i.e., predictive discriminative analysis) and describing the relative importance of variables for distinguishing amongst groups (i.e., descriptive discriminative analysis). In recent years, a number of developments have occurred in DA procedures for the analysis of data from repeated measures designs. Specifically, DA procedures have been developed for repeated measures data characterized by missing observations and/or unbalanced measurement occasions, as well as high-dimensional data in which measurements are collected repeatedly on two or more variables. This paper reviews the literature on DA procedures for univariate and multivariate repeated measures data, focusing on covariance pattern and linear mixed-effects models. A numeric example illustrates their implementation using SAS software.
Introduction
Linear discriminant analysis (DA), first introduced by Fisher (1936) and discussed in detail by Huberty and Olejnik (2006), is a multivariate technique to classify study participants into groups (predictive discriminant analysis; PDA) and/or describe group differences (descriptive discriminant analysis; DDA). DA is widely used in applied psychological research to develop accurate and efficient classification rules and to assess the relative importance of variables for discriminating between groups.
To illustrate, consider the study of Onur et al. (2007). The authors investigated clinical measures to distinguish patients with respiratory panic disorder from patients with non-respiratory panic disorder. The authors developed a classification rule in a training dataset, that is, in a sample of patients with panic disorder (N = 124) in which patients with the respiratory subtype (n1 = 79) could be identified. Data were collected for all patients on eight measures of panic-agoraphobia spectrum symptoms and traits. Using PDA, a classification rule was developed with these eight measures; the rule accurately assigned 86.1% of patients to the correct subtype. DDA results showed that four of the domains were most important for discriminating between patients with and without respiratory panic disorder. The rule developed in the training dataset is used to classify new patients with panic disorder into subtype groups in order to “tailor more specific treatment targets” (p. 485).
Discriminant analysis has been applied to a diverse range of studies within the psychology discipline. For example, in neuropsychology it has been used to distinguish children with autism from healthy controls (Williams et al., 2006), in educational psychology it has been applied in studies about intellectually gifted students (Pyryt, 2004), and in clinical psychology it has been applied in addictions research (Corcos et al., 2008). Sherry (2006) discusses some applications in counseling psychology.
Discriminant analysis is usually applied to multivariate problems in which data are collected at a single point in time. Multivariate textbooks that include sections on DA (Rencher, 2002; Timm, 2002; Tabachnick and Fidell, 2007) as well as DA textbooks (McLachlan, 1992; Huberty and Olejnik, 2006) provide little, if any, discussion about procedures for repeated measures designs, in which study participants provide responses at two or more measurement occasions. Repeated measures designs arise in many disciplines, including social and behavioral science disciplines. A review of DA procedures for repeated measures data is therefore timely given that a number of developments have occurred in procedures for data characterized by missing observations and/or unbalanced measurement occasions and high-dimensional data in which measurements are collected repeatedly on two or more variables.
The purpose of this manuscript is to (a) provide examples of the types of research problems to which repeated measures DA procedures can be applied, (b) describe several repeated measures DA procedures, focusing on those based on covariance pattern and linear mixed-effects regression models, and (c) illustrate the implementation of these procedures.
Statistical Concepts in DA
Let yij be a q × 1 vector of observed measurements on q variables in a training dataset, in which group membership is known, for the ith study participant (i = 1,..., nj) in the jth group (j = 1, 2). While this manuscript focuses on the analysis of two-group designs, the procedures have been generalized to multi-group problems (McLachlan, 1992; Huberty and Olejnik, 2006). It is assumed that yij∼ Nq(μj, Σj), where μj and Σj are the population mean vector and covariance matrix for the jth group and are estimated by 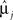 and
and 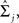 respectively.
respectively.
The linear DA classification rule is: Assign the ijth study participant to group 1 if
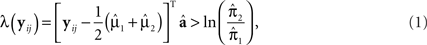
else assign the study participant to group 2. In Eq. 1, T is the transpose operator, 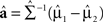 , the estimate of the linear discriminant function, a, where
, the estimate of the linear discriminant function, a, where

The parameters π1 and π1 are the a priori probabilities that observations belong to populations 1 and 2, respectively and may be estimated by,

where N = n1 + n2. Standardized discriminant function coefficients are obtained by multiplying 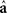 by a diagonal matrix of variable standard deviations. The relative importance of the variables for discriminating between groups can be assessed by the magnitude of the absolute value of these standardized coefficients, although other measures of relative importance have also been proposed (Huberty and Wisenbaker, 1992; Thomas, 1992).
by a diagonal matrix of variable standard deviations. The relative importance of the variables for discriminating between groups can be assessed by the magnitude of the absolute value of these standardized coefficients, although other measures of relative importance have also been proposed (Huberty and Wisenbaker, 1992; Thomas, 1992).
The accuracy of the classification rule is described by the misclassification error rate (MER), the probability that an individual is incorrectly allocated to the jth population. The MER is estimated by the apparent error rate (APER; Rencher, 2002; Timm, 2002),

where n11 and n22 are the number of study participants correctly assigned to groups 1 and 2, respectively.
The group membership of a new study participant is predicted using the classification rule developed in the training dataset. However, prior to applying this rule to new data, the rule should be validated in order to assess its generalizability. Internal and external validation techniques are discussed in a number of sources, including Timm (2002) and McLachlan (1992).
Papers that provide a more detailed introduction to the theory and application of classical linear DA include Huberty (1984) and Sherry (2006). A critical evaluation of the differences between DA and logistic regression, another method that is commonly applied to classification problems, is provided by Lei and Koehly (2003). In general, DA is preferred when its underlying derivational assumptions are satisfied because DA will have greater statistical power than logistic regression.
Examples of Potential Applications of Repeated Measures DA
Repeated measures DA procedures are applied to data collected on multiple occasions for the same individual; often these data will arise in studies about development, maturation, or aging processes. Below, we discuss a number of examples of the kinds of studies in which repeated measures DA can be used.
Levesque et al. (2008) were interested in classifying husbands, who were care providers for functionally or cognitively impaired wives, into three psychological distress groups based on changes in exposure to stress over time. The variables in the study included objective stressors, such as wives’ functional impairment and memory and behavioral problems, as well as subjective stressors such as role overload and relationship deprivation. All variables were collected at two measurement occasions. Measures of change over time, as well as some of the baseline measurements, were used to develop the classification model using classical linear DA. A total of N = 205 study participants provided data at the baseline measurement occasion. More than one quarter (28.2%) of participants dropped out of the study between the first and second measurement occasions; these individuals were excluded from the analysis.
A second example comes from the study of Rietveld et al. (2000). The researchers were interested in discriminating monozygotic from dizygotic twins using measures of twin similarity and confusion collected at ages 6, 8, and 10 years. Self-report data on these measures were obtained from both mothers and fathers. Classical linear DA was used to construct a separate classification rule for each measurement occasion and for each parent, resulting in a total of six rules. The rules were used to describe differences in classification accuracy over time and between parents. Loss to follow up was substantial. While 691 twin pairs were initially recruited into the study, by the third measurement occasion (i.e., age 10), mothers’ evaluations were only available for 324 (46.9%) twin pairs and fathers’ evaluations were only available for 279 (40.4%) pairs. The classification rules were validated using a leave-one-out internal validation method.
de Coster et al. (2005) applied classical linear DA to develop a classification rule for first-time stroke patients using data collected on the 17 items of the Hamilton Rating Scale for Depression (HAM-D) at 1, 3, 6, and 9-months post stroke. A total of 206 patients were classified as depressed or not depressed; the depression diagnosis was assigned based on the Structured Clinical Interview for the DSM-IV. The measurements collected prior to the diagnosis of depression were used to classify patients into groups using classical linear DA. The following HAM-D items were most important for discriminating between depressed and non-depressed patients: depressed mood, reduced appetite, thoughts of suicide, psychomotor retardation, psychic anxiety, and fatigue. Loss to follow up was small (i.e., about 10%).
Repeated Measures DA
While the previous section illustrates the kinds of studies in which repeated measures DA procedures can be applied, the authors of these studies used the classical linear DA procedure instead. The application of classical linear DA to repeated measures data has been criticized for a number of reasons (Tomasko et al., 1999; Roy, 2006): (a) observations with missing values are removed from analysis via casewise deletion, (b) covariates are difficult to include, and (c) the classical DA procedure cannot be applied to high-dimensional data in which N is less than the product of the number of repeated measurements and the number of variables.
Research about repeated measures DA has primarily been undertaken for PDA procedures, rather than DDA procedures. Early research about PDA focused on procedures based on the growth curve model (Azen and Afifi, 1972; Lee, 1982; Albert, 1983) as well as a stagewise discriminant, regression, discriminant (DRD) procedure (Afifi et al., 1971). Under the latter procedure, DA is applied separately to the data from each measurement occasion. The discriminant function coefficients estimated at each measurement occasion are then entered into a linear regression model and DA is applied to the slope and intercept coefficients from this regression model. In terms of DDA procedures, Albert and Kshirsagar (1993) developed two procedures for univariate repeated measures data, which are used to evaluate the relative importance of the measurement occasions for discriminating amongst groups. The first procedure is based on repeated measures multivariate analysis of variance (MANOVA) while the second procedure is based on the growth curve model of Potthoff and Roy (1964).
To introduce DA procedures for repeated measures data, denote yl (l = 1,…, N) as the vector of observations for the lth study participant, where the first nj observation vectors are for participants in group 1 and the remaining observation vectors are for individuals in group 2. In the case of univariate repeated measures data, that is, data that are collected on multiple measurement occasions for a single variable, yl has dimension pl × 1, where pl is the number of measurement occasions for the lth individual. In multivariate repeated measures data, that is, data that are collected on multiple measurement occasions for two or more variables, yl has dimension qpl × 1, where q is the number of variables. For simplicity, all procedures will be described for the case pl = p.
The Covariance Pattern Model
The covariance pattern model was originally proposed by Jenrich and Schluchter (1986). For univariate repeated measures data, the model is given by

where β is the k × 1 vector of parameters to be estimated, Xl is the p × k design matrix that defines groups membership, and εl ∼ Np(0, Σ). Group means are computed from estimates of the fixed-effects parameters, that is, 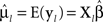 . This model assumes Σ has a functional form such as compound symmetric (CS) or first-order autoregressive (AR-1). The CS covariance structure assumes equal correlation between pairs of measurement occasions and constant variance across the occasions. The assumption of equi-correlation, regardless of the time lag between measurement occasions, may not be realistic in data collected over time, where the magnitude of correlation often decreases as the time lag between measurement occasions increases. The AR-1 covariance structure assumes the correlation between pairs of measurement occasions decays over time but the variance remains constant across the occasions (Fitzmaurice et al., 2004). By assuming a functional form for Σ, the number of variance and covariance parameters to estimate is reduced, which may result in improved classification accuracy and is advantageous to ensure the data are not overfit when total sample size is small relative to the number of measurement occasions. For example, in a study with p = 4 repeated measurements, there are p(p + 1)/2 = 4(5)/2 = 10 parameters to estimate when Σ is unstructured as compared to two parameters to estimate (one correlation and one variance) when a CS or AR-1 structure is assumed.
. This model assumes Σ has a functional form such as compound symmetric (CS) or first-order autoregressive (AR-1). The CS covariance structure assumes equal correlation between pairs of measurement occasions and constant variance across the occasions. The assumption of equi-correlation, regardless of the time lag between measurement occasions, may not be realistic in data collected over time, where the magnitude of correlation often decreases as the time lag between measurement occasions increases. The AR-1 covariance structure assumes the correlation between pairs of measurement occasions decays over time but the variance remains constant across the occasions (Fitzmaurice et al., 2004). By assuming a functional form for Σ, the number of variance and covariance parameters to estimate is reduced, which may result in improved classification accuracy and is advantageous to ensure the data are not overfit when total sample size is small relative to the number of measurement occasions. For example, in a study with p = 4 repeated measurements, there are p(p + 1)/2 = 4(5)/2 = 10 parameters to estimate when Σ is unstructured as compared to two parameters to estimate (one correlation and one variance) when a CS or AR-1 structure is assumed.
Repeated measures DA procedures based on the covariance pattern model can accommodate time-invariant covariates, that is, explanatory variables that do not change across the measurement occasions (Fitzmaurice et al., 2004). The inclusion of covariates in the model may help to improve classification accuracy. As well, it is possible to specify a mean structure for the model, such as assuming that the means remain constant over time (Roy and Khattree, 2005a), which reduces the number of mean parameters to estimate and therefore may further improve classification accuracy.
Repeated measures DA based on the covariance pattern model for univariate repeated measures data is described by Roy and Khattree (2005a). Under a CS structure, the authors showed, via statistical proof, that the classification rule does not depend on Σ. That is, assign the lth subject to group 1 if

else, allocate to group 2. In Eq. 6, ylk is the observation for the lth study participant on the kth repeated measurement, 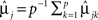 and
and 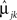 is the estimated mean for the jth group on the kth repeated measurement. By comparison, for an AR-1 structure the classification rule depends on the correlation parameter, ρ, as well as the estimated group means.
is the estimated mean for the jth group on the kth repeated measurement. By comparison, for an AR-1 structure the classification rule depends on the correlation parameter, ρ, as well as the estimated group means.
Repeated measures DA based on the covariance pattern model have also been described for multivariate repeated measures data (Roy and Khattree, 2005b, 2007; Krzysko and Skorzybut, 2009). Briefly, the covariance matrix of the repeated measurements is assumed to have a Kronecker product structure, denoted by the notation Σ = Σp⊗Σq, where Σp is the covariance matrix of the repeated measurements and Σq is the covariance matrix of the variables. A Kronecker product structure assumes that the covariance matrix of the repeated measurements is constant across all variables; adopting this structure results in a substantial reduction in the number of parameters to estimate. For example, with p = 4 and q = 3, there are a total of 4(5)/2 + 3(4)/2 = 16 covariance parameters to estimate under a Kronecker product structure as compared to 12(13)/2 = 78 parameters to estimate when an unstructured covariance is assumed. Roy and Khattree (2005b) also describe models in which the multivariate mean vector is assumed to have a specific function form (i.e., constant mean) over time, although they do not investigate the effects of classification accuracy when the mean structure is misspecified.
Misspecification of the covariance structure in both univariate and multivariate repeated measures analyses may result in increased misclassification rates. The effects of misspecification are considered in a subsequent section of this manuscript. Graphic exploration of the data, likelihood ratio tests, and penalized log-likelihood measures such as the Aikaike information criterion (AIC) have been recommended to guide the selection of a well-fitted model with an appropriate covariance structure (Roy, 2003; Fitzmaurice et al., 2004).
Linear Mixed-Effects Model
For univariate repeated measures data, the linear mixed-effects model is

where β is the k × 1 vector of fixed effect parameters, Xl is the p × k matrix of corresponding covariates, and Zl is the p × s design matrix associated with the s × 1 vector of subject-specific random effects dl. The error vector εl ∼ Np(0, Ul) and the random effects vector dl ∼ Ns(0, Gl) are assumed to be independent. The subject-specific covariance matrix is defined as

A repeated measures DA procedure based on the mixed-effects model was first proposed by Choi (1972). Subsequently, Tomasko et al. (1999) developed procedures that assume various covariance structures (such as CS and AR-1) for U, the covariance matrix of the residual errors; the application of these procedures was illustrated by Wernecke et al. (2004). The classification rule is: Assign the lth study participant to group 1 if
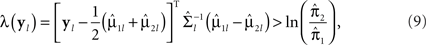
else, assign the participant to group 2. In Eq. 9, 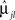 is the lth subject-specific mean for the jth group. Maximum likelihood methods are used to estimate
is the lth subject-specific mean for the jth group. Maximum likelihood methods are used to estimate 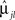 and
and 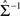 . A strength of DA based on the linear mixed-effects model is that both time-varying and time-invariant covariates can be accommodated in the model; covariate information may help to reduce misclassification error. Moreover, this model can accommodate an unequal number of measurements per individual.
. A strength of DA based on the linear mixed-effects model is that both time-varying and time-invariant covariates can be accommodated in the model; covariate information may help to reduce misclassification error. Moreover, this model can accommodate an unequal number of measurements per individual.
Gupta (1986) extended Choi’s (1972) methodology to develop DA procedures based on the linear mixed-effects model for multivariate repeated measures data. Roy (2006) proposed a classification procedure for incomplete multivariate repeated measures data based on the multivariate linear mixed-effects model that assumes a Kronecker product structure for the covariance matrix of the residual errors. Marshall et al. (2009) developed classification procedures based on the bivariate non-linear mixed-effects model that assumes a Kronecker product structure for the residual error covariance matrix.
Comparisons Amongst Procedures
Research about the performance of different repeated measures DA procedures has been limited. Roy and Khattree (2005a, 2007) used simulation techniques to compare procedures based on different covariance structures for univariate and multivariate repeated measures data. They found that for univariate repeated measures data, the average APER for a procedure based on an unstructured covariance was larger than the APER for procedures based on CS and AR-1 structures, regardless of the form of the population covariance. However, for multivariate repeated measures data, a misspecified Kronecker product covariance structure resulted in a higher APER than a correctly specified Kronecker product covariance structure. One study that investigated DA procedures based on the mixed-effects model (Tomasko et al., 1999) found that when sample size was small, procedures that specified a specific covariance structure for the residual errors generally had lower APERs than a procedure that adopted an unstructured covariance. However, for moderate to large sample sizes, the increase in classification accuracy was often negligible. None of the comparative studies that have been conducted to date have investigated the effect of a misspecified mean structure on the APER.
The effect of missing data on classification accuracy was studied by Roy (2006). She compared the accuracy of a classification procedure based on the multivariate mixed-effects model to the accuracy of a non-parametric classification procedure that used a multiple imputation method to fill in the missing observations. The assumption underlying both models is that the data are missing at random (MAR; Little and Rubin, 1987). She found that the APER for the mixed-effects procedure was less than the median error rate for the procedure based on the multiple imputation method. Roy suggested that because the multiple imputation method introduces noise into the data, it may not always be the optimal method to use.
Implementing Repeated Measures DA
Covariance pattern models and mixed-effects models can be fit to univariate and multivariate repeated measures data using the MIXED procedure in SAS (SAS Institute Inc., 2008). These models have been described in several sources (Singer, 1998; Littell et al., 2000; Thiebaut et al., 2002). Covariance pattern models are specified using a REPEATED statement to identify the repeated measurements and define a functional form for the covariance matrix. Mixed-effects models are specified using a RANDOM statement to identify one or more subject-specific effects; a REPEATED statement may also be included to define a functional form for the covariance matrix of the residuals. In multivariate repeated measures data, the MIXED procedure can also be used to specify a Kronecker product structure for the covariance matrix. However, the MIXED statement is limited to specifying Σp as unstructured, AR-1, or CS, and Σq as unstructured. The parameter estimates and covariances are extracted from the MIXED output using ODS output and the classification rule is defined to calculate the APER. This last step can be completed using programming software such as SAS/IML.
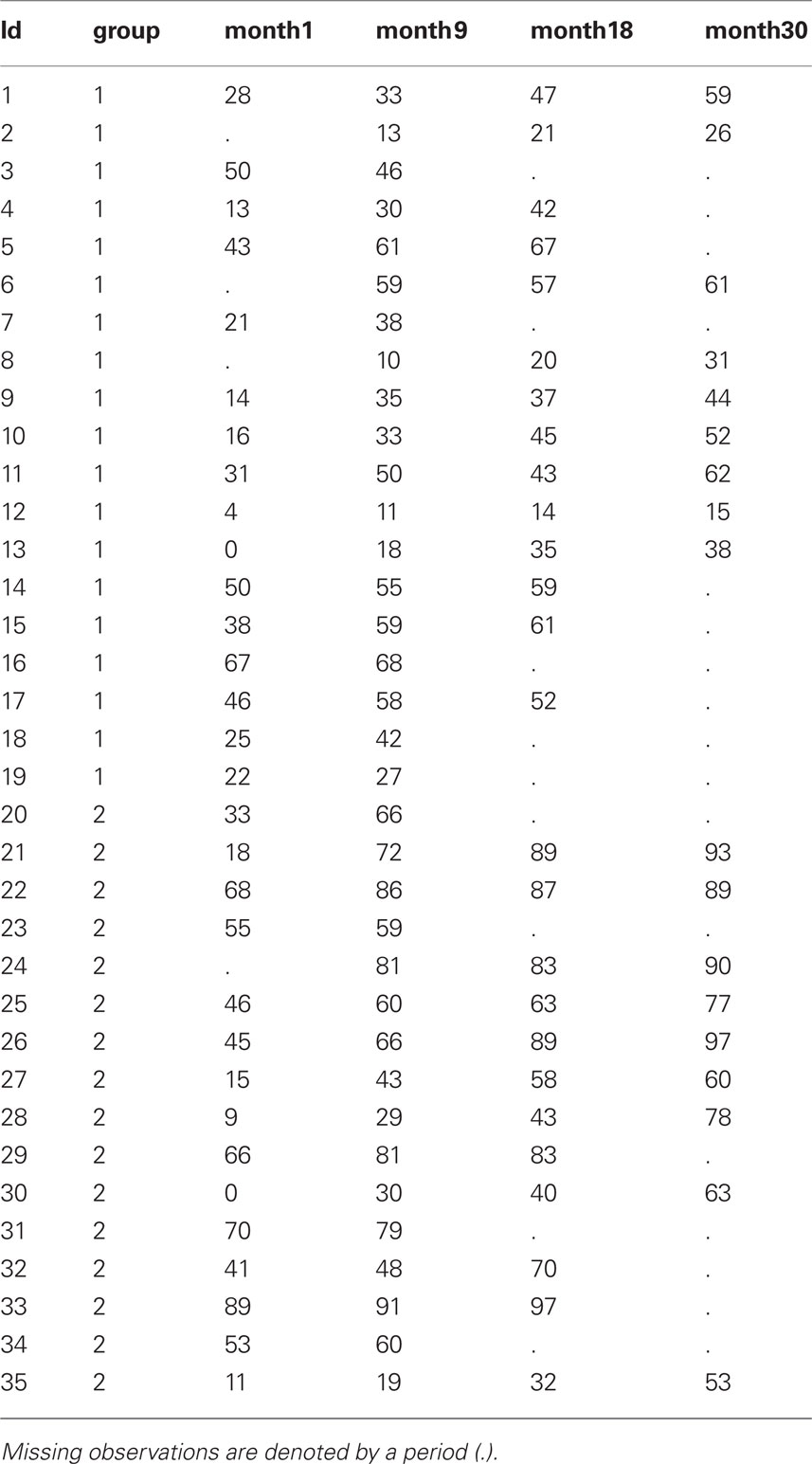
To illustrate, we use a numeric example based on the dataset described by Nunez-Anton and Woodworth (1994), which consists of the percent correct scores on a sentence test administered to two groups of study participants wearing different hearing implants1. The purpose of the analysis is to develop a classification rule to distinguish between the two type of implants. All study participants were deaf prior to connection of the implants. Data are available for 19 participants in group 1 and 16 participants in group 2, and measurements were obtained at 1, 9, 18, and 30 months after connection of the implants. A total of 14 study participants had complete data at all four measurement occasions. The pattern of missing data is intermittent. For this analysis we assume that the data follow a multivariate normal distribution and also that the missing observations are MAR (Little and Rubin, 1987).
Table 1 provides information about the number of complete observations, means, and standard deviations for each measurement occasions for the two groups. The raw data are provided in “Example dataset for repeated measures discriminant analysis” in Appendix, along with the SAS code to define the dataset, audio.
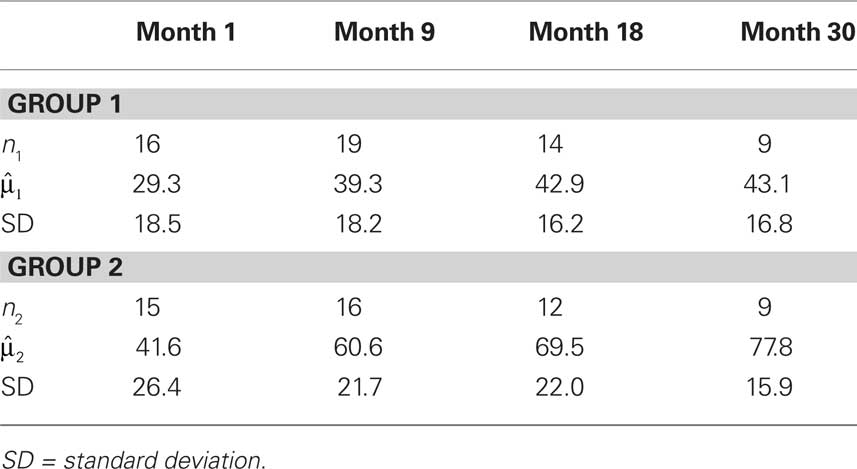
Table 1. Means and standard deviations for percent correct sentence test scores in two cochlear implant groups.
First we define the SAS syntax for classical linear DA. This syntax specifies a pooled covariance matrix, assumes a normal distribution of responses, and adopts a priori probabilities that are proportional to group sizes.
proc discrim data=audio method=normal pool = yes;
class group;
priors proportional;
var month1 month9 month18 month30;
run;
Using this code, APER = 20.2%. However, this error rate does not take into account the 21 study participants who were excluded from the analysis because of one or more missing observations and therefore could not be classified.
A repeated measures DA procedure based on a mixed-effects model is an appropriate choice for these data given that there are an unequal number of measurements for study participants. A model with an AR-1 covariance structure is implemented using the following SAS syntax.
data audio_long1;
set audio;
time=1; y=month1; output;
time=9; y=month9; output;
time=18; y=month18; output;
time=30; y=month30; output;
drop month1 month9 month18 month30;
run;
data audio_long; set audio_long1;
int=1;
timeg=time*group;
run;
proc sort data=audio_long;
by id;
run;
proc mixed data=audio_long method=ml;
class id group;
model y=time group time*group/ solution;
random intercept / subject=id v=1 solution;
repeated / type=ar(1) subject=id;
ods output v=vmat solutionf=parms_mat;
run;
The dataset audio_long1 converts the data into a person-period format and in audio_long, we create new variables called timeg (interaction) and int (model intercept). The MIXED syntax specifies the use of maximum likelihood estimation and implements a model containing the fixed effects of time, group, and their interaction. The RANDOM statement specifies a random intercept and requests the estimated covariance matrix for subject 1. The REPEATED statement specifies an AR-1 structure for the residual errors. The ODS statement indicates that  will be output to a new dataset named vmat, while the fixed-effects parameters are output to the dataset parms_mat. Two additional models were fit to these data (syntax not shown), to identify a well-fitting model for these data. One model included a random intercept and random slope, and the second included the quadratic term for time as an additional model covariate. The former did not result in improved model fit, as judged by the AIC, and the latter resulted in problems with estimation of the covariance parameters. “Illustration of SAS syntax to implement discriminant analysis procedures based on mixed-effects and covariance structure models” in Appendix provides example code used to extract the ODS output into SAS/IML to implement the linear classification rule.
will be output to a new dataset named vmat, while the fixed-effects parameters are output to the dataset parms_mat. Two additional models were fit to these data (syntax not shown), to identify a well-fitting model for these data. One model included a random intercept and random slope, and the second included the quadratic term for time as an additional model covariate. The former did not result in improved model fit, as judged by the AIC, and the latter resulted in problems with estimation of the covariance parameters. “Illustration of SAS syntax to implement discriminant analysis procedures based on mixed-effects and covariance structure models” in Appendix provides example code used to extract the ODS output into SAS/IML to implement the linear classification rule.
Fit statistics and APERs are provided in Table 2 for three models, to illustrate the effect of modifying the covariance structure on classification accuracy. Overall, the model with an unstructured covariance had the lowest value of the AIC and also resulted in the lowest APER. While no guidelines exist about acceptable magnitude of the APER, it is possible to test for differences in APER values across models (Lachenbruch and Mickey, 1968; McLachlan, 1992).
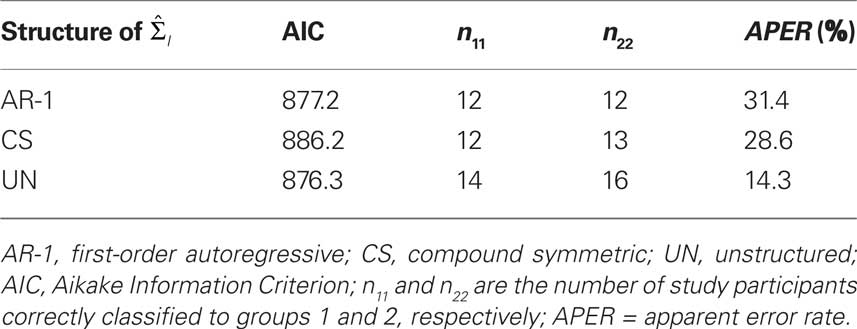
Table 2. Fit statistics and apparent error rates (APER) for the mixed-effects model with three covariance structures.
Example syntax is provided in “Illustration of SAS syntax to implement discriminant analysis procedures based on mixed-effects and covariance structure models” in Appendix that could be used to fit both a CS and AR-1 covariance pattern to these data. Given that the covariance pattern model is only applicable to datasets with complete observations, this syntax is provided for illustration purposes.
Discussion
While research about repeated measures DA spans more than a 30-year period, there have been a number of recent developments in PDA procedures based on covariance pattern and mixed-effects models for univariate and multivariate repeated measures data. These developments provide applied researchers with a number of options to develop accurate and efficient classification rules when data are collected repeatedly on the same subjects. Several of these procedures can be implemented using standard statistical software, although some supplementary programming is required to implement the classification rule.
There are opportunities for further research about repeated measures DA procedures. For example, there has been limited research about procedures for non-normal data and heterogeneous group covariances. While the MER of classical linear DA appears to be reasonably robust (i.e., insensitive) to outliers (Lee and Ord, 1990), heavy-tailed distributions may result in some loss of classification accuracy and inflate the standard errors of discriminant function coefficients. Non-parametric DA procedures, which do not assume a normal distribution of responses, such as nearest neighbor classification procedures, have been investigated for repeated measures data (Bagui and Mehra, 1999). PDA procedures based on the multivariate Box and Cox transformation (Velilla and Barrio, 1994) and a rank transformation method (Conover and Iman, 1980), which Baron (1991) found to perform well for a number of different non-normal distributions, as well as distribution-free methods (Burr and Doak, 2007), have not yet been investigated for repeated measures data. Roy and Khattree (2005a,b) developed PDA procedures for heterogeneous group covariances based on the covariance pattern model while Marshall and Baron (2000) proposed PDA procedures based on the mixed-effects model for conditions of covariance heterogeneity, which can be implemented using SAS software. Roy and Khattree (2005b) showed in a single numeric example that when covariances are heterogeneous, a PDA procedure for unequal group covariances had a lower APER than a procedure that assumed homogeneity of group covariances. Additional research is needed to compare the classification accuracy of these procedures across a range of conditions of heterogeneity, particularly when group sizes are unequal, and to develop software to implement these procedures. As well, comparisons with conventional linear DA could also be undertaken.
Non-ignorable missing data, that is, data that are missing not at random (Little and Rubin, 1987) is likely to affect the accuracy of DA classification rules. Pattern mixture and selection models (Hedeker and Gibbons, 1997; Little, 1993, 1995) have been proposed to adjust for potential bias in mixed-effects models when it cannot be assumed that the mechanism of missingness is ignorable. Further research could investigate the development of DA procedures based on these models.
Finally, other models could be investigated for repeated measures data. Examples include extensions of the growth curve model (Albert and Kshirsagar, 1993) to include random effects and machine learning models for high-dimensional data (Hastie, Tibshirani and Friedman, 2001).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research was supported by funding from the Manitoba Health Research Council, a Canadian Institutes of Health Research (CIHR) New Investigator Award to the first author, and a CIHR Vanier Graduate Scholarship to the second author.
Footnote
- ^In the dataset reported by Nunez-Anton and Woodworth (1994), there was no significant difference between the two groups. Therefore, the original observations were modified to ensure a difference exists. We maintained the same number of study participants and pattern of missing data as in the original dataset.
References
Afifi, A. A., Sacks, S. T., Liu, V. Y., Weil, M. H., and Shubin, H. (1971). Accumulative prognostic index for patients with barbiturate, glutethimide and meprobamate intoxication. N. Engl. J. Med. 285, 1497–1502.
Albert, A. (1983). Discriminant analysis based on multivariate response curves: a descriptive approach to dynamic allocation. Stat. Med. 2, 95–106.
Albert, J. M., and Kshirsagar, A. M. (1993). The reduced-rank growth curve model for discriminant analysis of longitudinal data. Aust. J. Stat. 35, 345–357.
Azen, S. P., and Afifi, A. A. (1972). Two models of assessing prognosis on the basis of successive observations. Math. Biosci. 14, 169–176.
Bagui, S. C., and Mehra, K. L. (1999). Classification of multiple observations using multi-stage nearest rank neighbor rule. J. Stat. Plan. Inference 76, 163–183.
Baron, A. E. (1991). Misclassification among methods used for multiple group discrimination: the effects of distributional properties. Stat. Med. 10, 757–766.
Burr, T., and Doak, J. (2007). Distribution-free discriminant analysis. Intell. Data Anal. 11, 651–662.
Conover, W. J., and Iman, R. L. (1980). The rank transformation as a method of discrimination with some examples. Commun. Stat. Theory Methods 9, 465–487.
Corcos, M., Loas, G., Sperana, M., Perez-Diaz, F., Stephan, P., Vernier, A., Lang, F., Nezelof, S., Bizouard, P., Veniss, J, L., and Jeammet, P. (2008). Risk factors for addictive disorders: a discriminant analysis on 374 addicted and 513 nonpsychiatric participants. Psychol. Rep. 102, 435–449.
de Coster, L., Leentjens, A. F. G., Lodder, J., and Verhey, F. R. J. (2005). The sensitivity of somatic symptoms in post-stroke depression: a discriminant analytic approach. Int. J. Geriatr. Psychiatry 20, 358–362.
Fisher, R. A. (1936). The use of multiple measurements in taxonomic problems. Ann. Eugen. 7, 179–188.
Fitzmaurice, G. M., Laird, N. M., and Ware, J. H. (2004). Applied Longitudinal Analysis. New Jersey: Wiley.
Gupta, A. K. (1986). On a classification rule for multiple measurements. Comput. Math. Appl. 12, 301–308.
Hastie, T., Tibshirani, R., and Friedman, J. H. (2001). Elements of Statistical Learning: Data Mining, Inference, and Prediction. New York: Springer.
Hedeker, D., and Gibbons, R. D. (1997). Application of random-effects pattern-mixture models for missing data in longitudinal studies. Psychol. Bull. 2, 64–78.
Huberty, C. J. (1984). Issues in the use and interpretation of discriminant analysis. Psychol. Bull. 95, 156–171.
Huberty, C. J., and Olejnik, S. (2006). Applied MANOVA and Discriminant Analysis. New Jersey: Wiley.
Huberty, C. J., and Wisenbaker, J. M. (1992). Variable importance in multivariate group comparisons. J. Educ. Stat. 17, 75–91.
Jenrich, R. I., and Schluchter, M. D. (1986). Unbalanced repeated measures models with structural covariance matrices. Biometrics 42, 805–820.
Krzysko, M., and Skorzybut, M. (2009). Discriminant analysis of a multivariate repeated measures data with a Kronecker product structured covariance matrices. Stat. Papers 50, 817–855.
Lachenbruch, P. A., and Mickey, M. R. (1968). Estimation of error rates in discriminant analysis. Technometrics 10, 1–11.
Lee, C. K., and Ord, J. K. (1990). Discriminant analysis via least absolute deviations. Decis. Sci. 21, 86–96.
Lee, J. C. (1982). “Classification of growth curves. In classification, pattern recognition, and reduction of dimensionality,” in Handbook of Statistics, Vol. 2, eds P. R. Krishnaiah and L. N. Kanal (Amsterdam: North – Holland), 121–137.
Lei, P., and Koehly, L. M. (2003). Linear discriminant analysis versus logistic regression: A comparison of classification errors in the two-group case. J. Exp. Educ. 72, 25–49.
Levesque, L., Ducharme, F., Zarit, S. H., Lachance, L., and Giroux, F. (2008). Predicting longitudinal patterns of psychological distress in older husband caregivers: further analysis of existing data. Aging Ment. Health 12, 333–342.
Littell, R. C., Pendergast, J., and Natarajan, R. (2000). Tutorial in biostatistics: modelling covariance structure in the analysis of repeated measures data. Stat. Med. 19, 1793–1819.
Little, R. J. A. (1993). Pattern-mixture models for multivariate incomplete data. J. Am. Stat. Assoc. 88, 125–134.
Little, R. J. A. (1995). Modeling the dropout mechanism in repeated-measures studies. J. Am. Stat. Assoc. 90, 1112–1121.
Marshall, G., and Baron, A. E. (2000). Linear discriminant models for unbalanced longitudinal data. Stat. Med. 19, 1969–1981.
Marshall, G., De la Cruz-Mesia, R., Quitanna, F. A., and Baron, A. E. (2009). Discriminant analysis for longitudinal data with multiple continuous responses and possibly missing data. Biometrics 65, 69–80.
McLachlan, G. J. (1992). Discriminant Analysis and Statistical Pattern Recognition. New York: Wiley.
Nunez-Anton, V., and Woodworth, G. G. (1994). Analysis of longitudinal data with unequally spaced observations and time-dependent correlated errors. Biometrics 50, 445–456.
Onur, E., Alkin, T., and Tural, U. (2007). Panic disorder subtypes: further clinical differences. Depress. Anxiety 24, 479–486.
Potthoff, R. F., and Roy, S. N. (1964). A generalized multivariate analysis of variance model useful especially for growth curve problems. Biometrika 51, 313–326.
Pyryt, M. C. (2004). Pegnato revisited: using discriminant analysis to identify gifted children. Psychol. Sci. 46, 342–347.
Rietveld, M. J. H., van der Valk, J. C., Bongers, I. L., Stroet, T. M., Slagboom, P. E., and Boomsma, D. I. (2000). Zygosity diagnosis in young twins by parental report. Twin Res. 3, 134–141.
Roy, A. (2006). A new classification rule for incomplete doubly multivariate data using mixed effects model with performance comparisons on the imputed data. Stat. Med. 25, 1715–1728.
Roy, A., and Khattree, R. (2003). Tests for mean and covariance structures relevant in repeated measures based discriminant analysis. J. Appl. Stat. Sci. 12, 91–104.
Roy, A., and Khattree, R. (2005a). Discrimination and classification with repeated measures data under different covariance structures. Commun. Stat. Simul. Comput. 34, 167–178.
Roy, A., and Khattree, R. (2005b). On discrimination and classification with multivariate repeated measures data. J. Stat. Plan. Inference 134, 462–485.
Roy, A., and Khattree, R. (2007). Classification of multivariate repeated measures data with temporal autocorrelation. J. Appl. Stat. Sci. 15, 283–294.
Sherry, A. (2006). Discriminant analysis in counseling psychology research. Couns. Psychol. 34, 661–683.
Singer, J. D. (1998). Using SAS PROC MIXED to fit multilevel models, hierarchical models, and individual growth models. J. Educ. Behav. Stat. 24, 323–355.
Tabachnick, B. G., and Fidell, L. S. (2007). Using Multivariate Statistics, 5th Edn. Boston: Allyn & Bacon.
Thiebaut, R., Jacqmin-Gadda, H., Chene, G., Leport, C., and Commenges. D. (2002). Bivariate linear mixed models using SAS PROC MIXED. Comput. Methods Programs Biomed. 69, 249–256.
Thomas, R. D. (1992). Interpreting discriminant functions: a data analytic approach. Multivariate Behav. Res. 27, 335–362.
Tomasko, L., Helms, R. W., and Snappin, S. M. (1999). A discriminant analysis extension to mixed models. Stat. Med. 18, 1249–1260.
Velilla, S., and Barrio, J. A. (1994). A discriminant rule under transformation. Technometrics 36, 348–353.
Wernecke, K. D., Kalb, G., Schink, B., and Wegner, B. (2004). A mixed model approach to discriminant analysis with longitudinal data. Biom. J. 46, 246–254.
Williams, D. L., Goldstein, G., and Minshew, N. J. (2006). The profile of memory function in children with autism. Neuropsychology 20, 21–29.
Appendix
Example Dataset for Repeated Measures Discriminant Analysis
The SAS code used to define the dataset is:
data audio;
input id group month1 month9 month18 month30;
cards;
Illustration of SAS Syntax to Implement Discriminant Analysis Procedures Based on Mixed-Effects and Covariance Structure Models
Mixed-effects model
This SAS/IML syntax reads the SAS datasets from the ODS output (see section 5) for the MIXED procedure and demonstrates the application of the classification rule to the data for the first study participant.
proc iml;
reset noname;
use audio_long;
read all var {id int time group timeg y} into
tempmat where (y>=0);
use parms_mat;
read all var {‘estimate’} into beta;
beta1a=beta[1:3];
beta1b=beta[5];
beta1=beta1a//beta1b;
use vmat;
read all var {‘index’ ‘col1’ ‘col2’ ‘col3’
‘col4’} into vmat;
ntot=35;
n1=19;
n2=16;
discrim=j(ntot,1,.);
count=j(ntot,1,.);
**this portion of the code applies the
classification rule to the data for subject
id=1**;
subj=1;
xmatss1=tempmat[1:4,2:5];
xmatss2=xmatss1;
xmatss2[,3]=0;
ymatss=tempmat[1:4,6];
vmatss=vmat[1:4,3:6];
mu1=xmatss1*beta1;
mu2=xmatss2*beta1;
discrim[subj]=(ymatss-0.5*(mu1+mu2))`*
(inv(vmatss)*(mu1-mu2));
print ‘Discriminant function for subject id=1’;
print discrim[format=6.2];
if discrim[subj]>=ln(n2/n1) then count[subj]=1;
else count[subj]=0;
quit;
Covariance pattern model
This SAS/IML syntax applies the DA classification rule defined in Eq. 6, which is based on a CS covariance structure. It also applies a classification rule based on an AR-1 covariance structure. Unlike the previous analyses, neither of these models includes subject-specific effects.
**DA BASED ON COVARIANCE PATTERN MODEL WITH CS
STRUCTURE**;
proc iml;
reset noname;
use audio;
read all var {month1 month9 month18 month30}
into y;
p=4;
n1=19;
n2=16;
nsum=n1+n2;
dsum=j(nsum,1,.);
do i=1 to nsum;
d1=sum(y[i,]);
if i=1 then dsum=d1;
else dsum=dsum//d1;
end;
y1=y[1:n1,];
y2=y[(n1+1):nsum,];
ybar1=y1[+,]/n1;
ybar2=y2[+,]/n2;
ybar=ybar1//ybar2;
yp=j(1,p,1);
mu1=yp*(ybar1`)/p;
mu2=yp*(ybar2`)/p;
d=j(nsum,1,.);
countn=0;
countn1=0;
do t=1 to nsum;
if dsum[t]>= (mu1+mu2)#p/2 then
countn=countn+1;
end;
do t=1 to n1;
if dsum[t]>= (mu1+mu2)#p/2 then
countn1=countn1+1;
end;
a=n1 - countn1;
aper=(countn - countn1+a)*100/nsum;
print ‘APER’;
print aper[format=6.2];
quit;
**DA BASED ON COVARIANCE PATTERN MODEL WITH AR-1
STRUCTURE**;
proc mixed data=audio_long method=ml;
class id group;
model y=time group time*group /solution;
repeated/type=ar(1) subject=id;
ods output covparms=cov;
run;
proc iml;
reset noname;
use audio;
read all var {month1 month9 month18 month30}
into z;
use cov;
read all var {‘estimate’} into v;
rho=v[1];
n1=19;
n2=16;
nsum=n1+n2;
p=4;
dtot=j(nsum, 1,.);
dtot2=j(nsum,1,.);
do i=1 to nsum;
dtot[i]=sum(z[i,]);
end;
do k=1 to nsum;
dtot2[k]=sum(z[k,2:p-1]);
end;
mdtot=dtot/p;
mdtot2=dtot2/(p-2);
z1=z[1:n1,];
z2=z[(n1+1):nsum,];
zbar1=z1[+,]/n1;
zbar2=z2[+,]/n2;
zbar=zbar1//zbar2;
zp=j(1,p,1);
mu1=zp*(zbar1`)/p;
mu2=zp*(zbar2`)/p;
/**Allocation Rule****/
zcount=0;
zcount1=0;
do ir=1 to nsum;
if (p*mdtot[ir] - rho*(p-2)*mdtot2[ir])>=
(1/2)*(p - rho*(p-2))*(mu1+ mu2) then
zcount=zcount+1;
end;
do ir=1 to n1;
if (p*mdtot[ir] - rho*(p-2)*mdtot2[ir])>=
(1/2)*(p - rho*(p-2))*(mu1+mu2) then
zcount1=zcount1+1;
end;
z1= n1 - zcount1;
aper=(zcount - zcount1+ z1)*100/nsum;
print ’APER’;
print aper[format=6.2];
quit
Keywords: repeated measures, longitudinal, multivariate, classification, missing data
Citation: Lix LM and Sajobi TT (2010) Discriminant analysis for repeated measures data: a review. Front. Psychology 1:146. doi: 10.3389/fpsyg.2010.00146
Received: 14 March 2010;
Paper pending published: 05 April 2010;
Accepted: 10 August 2010;
Published online: 09 September 2010
Edited by:
D. Betsy Mccoach, University of Connecticut, USAReviewed by:
Anne C. Black, Yale University School of Medicine, USAScott J. Peters, University of Wisconsin White Water, USA
Jeffrey Harring, University of Maryland College Park, USA
James Stamey, Baylor University, USA
Copyright: © 2010 Lix and Sajobi. This is an open-access article subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Lisa M. Lix, School of Public Health, University of Saskatchewan, 107 Wiggins Road, Saskatoon, SK S7N 5E5, Canada. e-mail:bGlzYS5saXhAdXNhc2suY2E=