- 1 Department of Psychological Sciences, Purdue University, West Lafayette, IN, USA
- 2 Swedish Collegium for Advanced Study, Uppsala, Sweden
- 3 University of Jyväskylä, Jyväskylä, Finland
A general definition and a criterion (a necessary and sufficient condition) are formulated for an arbitrary set of external factors to selectively influence a corresponding set of random entities (generalized random variables, with values in arbitrary observation spaces), jointly distributed at every treatment (a set of factor values containing precisely one value of each factor). The random entities are selectively influenced by the corresponding factors if and only if the following condition, called the joint distribution criterion, is satisfied: there is a jointly distributed set of random entities, one entity for every value of every factor, such that every subset of this set that corresponds to a treatment is distributed as the original variables at this treatment. The distance tests (necessary conditions) for selective influence previously formulated for two random variables in a two-by-two factorial design (Kujala and Dzhafarov, 2008, J. Math. Psychol. 52, 128–144) are extended to arbitrary sets of factors and random variables. The generalization turns out to be the simplest possible one: the distance tests should be applied to all two-by-two designs extractable from a given set of factors.
A system’s behavior, be the system biological, social, or technological, can be thought of as a network of stochastically interdependent random entities. The external world provides inputs (influences, interventions, conditions) presumably affecting some of the components of the network and not affecting the others. The question arises therefore as to how, based on the joint distributions of all these random entities, to distinguish the components affected and not affected by each of these external inputs.
The notion of selective influence under stochastic interdependence was introduced and systematically analyzed in the behavioral context by Townsend (1984), although implicitly it had been used before (Lazarsfeld, 1965; Bloxom, 1972; Schweickert, 1982). Townsend’s approach to selective influence (further developed in Townsend and Thomas, 1994, and mathematically characterized in Dzhafarov, 1999) is, however, very different from the present one. In fact, in all non-trivial cases they are incompatible. Our approach gradually developed starting with Dzhafarov (2001), based on Dzhafarov’s earlier work on response time analysis (see Dzhafarov, 1997, for an overview). In Dzhafarov (2003) the definition of selective influence adopted in the present paper was given for finite systems of random entities. This notion was put on a more solid probabilistic foundation in Dzhafarov and Gluhovsky (2006), and further developed in Kujala and Dzhafarov (2008). In the latter work, for the first time, workable tests for selective influence were formulated.
The present paper continues this line of research on a higher level of mathematical rigor and arguably the highest possible level of generality. The abstract nature of the mathematical theory makes it rather difficult reading, with notation which, though carefully chosen, may appear complicated. As a partial remedy, we precede the formal development in Sections 2–5 by Section 1 in which we provide a more intuitive account of some of the basic notions and results. We do this on simple examples involving just two random variables influenced by two factors.
1. Intuitive Introduction
1.1. What is Selective Influence?
Consider a simple double-detection experiment: there are two stimuli each of which may possess or lack a certain feature (signal property), and an observer has to respond Yes (signal present) or No (signal absent) to each of the two stimuli. For instance, the stimuli may be two spatially separated line segments in a frontal plane each of which may be either vertical (signal absent) or tilted by a fixed small angle (signal present); the observer says Yes − Yes if both lines appear to be tilted, Yes − No if the left line appears tilted and the right one not, etc. These responses are random variables: A (response to the left stimulus) and B (response to the right one), each with two possible values {Yes, No} occurring with some probabilities. They are jointly distributed, in the sense that by the virtue of co-occurring in the same trial the values of A and B are naturally paired, enabling one to meaningfully pose questions like “What is the joint probability of A = Yes and B = No?”. The joint distribution of A and B may change depending on the values of the following external factors: α = Tilt of the left line, with two possible values, {absent, present}, and β = Tilt of the right line, with the same two values. The combination of factor values chosen, one for each of the factors, is traditionally referred to as a treatment. With this terminology and notation, the population-level (idealized) results of the experiment in question can be presented in the form of four matrices:

The letters p, q, r, s here represent theoretical probabilities, with the usual meaning of the subscripts: p1· = p11 + p12, p2· = p21 + p22, p1· + p2· = 1, etc. It is natural to surmise that, unless the observer does not look at the stimuli at all, the random variable A should depend on (be influenced by) the value of α, and B should be influenced by the value of β. It is not obvious, however, whether factor α only (or selectively) influences random variable A, without affecting B, and whether factor β only (selectively) influences random variable B, without affecting A:
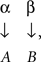
as opposed to the possibilities
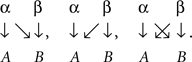
Thus, we will have one of the latter scenarios if the “present” value of α visually masks or enhances the salience of the “present” value of β, or if the values of β somehow affect the level of attention the observer pays to the factor α.
We denote the case when (α, β) selectively influence (A, B), respectively, by
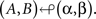
What does this mean? The meaning of the relation is only obvious if A and B are stochastically independent for all four treatments, i.e., if pij = pi· p·j, qij = qi·q·j, etc., where i, j ∈{1, 2}. In this case all one has to establish to prove (A, B) ↫ (α, β) is that the marginal distribution of A is not affected by changes in β and the marginal distribution of B is not affected by changes in α.
To look at this in detail, let the pair of our random variables (A, B) at the four treatments be denoted (A, B)11, (A, B)12, (A, B)21, and (A, B)22, where 1, 2 denote “absent” and “present,” respectively. If A and B are independent at all four treatments, then the selectiveness (A, B) ↫ (α, β) simply means that the marginal distribution of A does not depend on β (i.e., p1· = q1· and r1· = s1·) and the marginal distribution of B does not depend on α (i.e., p·1 = q·1 and r·1 = s·1). The problem arises when A and B are not independent for at least one of the treatments: how should one determine then if (A, B) ↫ (α, β)? This is the problem addressed in this paper, only we do not confine the consideration to the case of two factors and two random variables. Rather we generalize the problem to an arbitrary set of external factors and an arbitrary (but one-to-one corresponding to the set of factors) set of random entities.1
For a finite set of random variables the definition of selective influence was given in Dzhafarov (2003) and then refined in Dzhafarov and Gluhovsky (2006) and Kujala and Dzhafarov (2008). Applying it to our example, (A, B) is selectively influenced by (α, β) if and only if one can find functions f and g and a random entity C whose distribution does not depend on α, β, such that
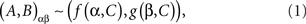
where ∼ stands for “is distributed as”.2 That is, denoting f(α = 1, C) by f1(C), g(β = 2, C) by g2(C), etc.,
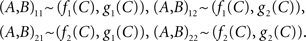
As an example, let C be a random vector (C0, CI, C2) with stochastically independent components having the following interpretation: C0 is a random entity representing the general level of visual attention, while C1 and C2 are stimulus-specific sources of randomness (which, with no loss of generality, can be taken to be uniformly distributed between 0 and 1). Let
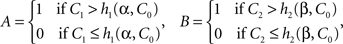
where h1, h2 are some measurable functions from the set of possible values of C into interval [0, 1]. One can see that A and B are generally stochastically interdependent by virtue of depending on one and the same random entity, C0, but that A does not depend on β, in the sense that for any given values of the other arguments, C0 = c0, C1 = c1, C2 = c2, and α = 1 or 2, the value of A does not change as a function of β; and B does not depend on α in the analogous sense.
The definition of selective influence can also be looked at in a simpler and more fundamental way. The fact that for any given treatment A and B are stochastically related (i.e., paired, whether independent or interdependent) means in Kolmogorov’s probability theory that A and B are measurable functions of one and the same random entity. It is always true therefore that
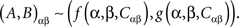
The random entities C11, C12, C21, C22, can always be replaced with a single C, e.g., by putting C = (C11, C12, C21, C22) and redefining the functions f, g accordingly:
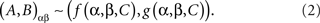
Comparing this universal representation with (1) we see that the assumption of selective influence is that β in f and α in g are dummy arguments.
1.2. Main Properties of Selective Influence
There are three main properties of the selective influence relation, (A, B) ↫ (α, β).
First, selective influence is invariant with respect to all (measurable) transformations of the random variables A,B, even if transformations of A are allowed to depend on values of factor α and transformations of B are allowed to depend on values of factor β. In our example the values of A and B are denoted yes and no. Clearly, we can encode them 0 and 1, respectively, or by any other two numbers or words. Moreover, we can, if we so choose, denote {yes, no} for A by {1, 0} if α = absent but by {−3, 5} if α = present; analogously, we can denote {yes, no} for B by {lion, crocodile} if β = absent but by {zebra, cheetah} if β = present. Selective influence, (A, B) ↫ (α, β), if it holds for the original values for A and B must also hold after any such transformations. This follows from the fact that if (1) holds then after any factor-value-specific transformations F(α, A) and G(β, B) we have
Second, selective influence implies marginal selectivity, the term coined by Townsend and Schweickert (1989) for the situation when the marginal distribution of A does not depend on β and the marginal distribution of B does not depend on α. This is an obvious consequence of (1). The reverse is not true, as illustrated by examples in Dzhafarov (2003) and, more systematically, in Kujala and Dzhafarov (2008). Other examples are given in this paper: in fact, in all our examples where the selective influence relation does not hold marginal selectivity is satisfied.
Third, selective influence relation satisfies the nestedness property: if some random variables are selectively influenced by corresponding factors (say, (A, B, C) ↫ (α, β, γ) – we need more than two factor-variable pairs for this property to be non-trivial), then any subset of these variables is selectively influenced by the corresponding subset of factors: (A, B) ↫ (α, β), (A, C) ↫ (α, γ), and (B, C) ↫ (β, z). This property is obvious as soon as (1) is generalized to larger sets.
In this paper the three properties of selective influence will be demonstrated on the maximal level of generality, for arbitrary sets of random entities and corresponding sets of factors of arbitrary nature.
1.3. Distance Tests for Selective Influence
How can one determine that (A, B) ↫ (α, β)? In Kujala and Dzhafarov (2008) two types of necessary conditions for selective influence were formulated, termed cosphericity tests and distance tests. As we only generalize in this paper the latter class of tests, we need not discuss the former. To apply a distance test to our example means to do the following. First, the values of A and B have to be encoded by real numbers. In accordance with what we know about the transformations we can use any functions f(α, A) and g(β, B) with numerical values. Second, one chooses a number ρ ≥ 1. Third, for each of the four treatments αβ = 11, 12, 21, 22 one computes the quantity
where E denotes expected value and (Aαβ, Bαβ) is an alternative (and more convenient) way of designating (A, B)αβ. Note that Dαβ (the same as αβ, 21, etc.) is a string of symbols, with no multiplication involved.
It has been shown in Kujala and Dzhafarov (2008) that if (A, B) ↫ (α, β), then, considering each random variable at each value of the corresponding factor as a point (this yields four points, A1, A2, B1, B2), these points can be placed in a metric space in which the values D11, D12, D21, D22 are, with some caveats, distances between A points and B points (D11 between A1 and B1, D12 between A1 and B2, etc.). As these distances, by definition, should satisfy the triangle inequality, we conclude with a bit of algebra (see Section 5) that
A distance test consists in checking if this inequality is satisfied: if not (at least for one choice of the numerical values and the exponent ρ), then the selective influence relation is ruled out.
In this paper we generalize this test to arbitrary sets of random entities selectively influenced by arbitrary sets of external factors. As it turns out, all one has to do to prove that all random entities, taken one for each value of the corresponding factor, can be embedded in a metric space is to apply the test just described to all pairs of 2 × 2 treatments for all pairs of factors. To present this result in an unambiguous form we have to introduce some notation that may appear cumbersome at first: since a value of a factor generally does not itself indicate which factor it is a value of (e.g., absent or 1 can be a value of both α and β), we superscript each factor value by the corresponding factor name. In our example it would be 1α, 2α, 1β, 2β. We call these pairs, factor value with factor name, factor points. The four distances will now be written D1α1β, D1α2β, D2α1β, D2α2β. Note that we could only get away with the previous notation because the identity of the factors in it was encoded by the order of their values within pairs: in D11 the first 1 belonged to α and the second one to β. This convention cannot work, of course, for more than two factors. In the new notation the distance test acquires the form
where
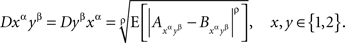
1.4. The Joint Distribution Criterion for Selective Influence
Compliance with a given set of distance tests is only a necessary condition for selective influence. Is there a way to definitively prove that selective influence (A, B) ↫ (α, β) does hold if it is not ruled out by distance tests? As it turns out, the answer is affirmative, and it is an almost immediate consequence of our definition of selective influence, if presented at a sufficiently high level of mathematical rigor. Stated in intuitive terms and applied to our example, consider four hypothetical random variables, one for each of our factor points: 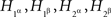 . Suppose that they are jointly distributed, i.e., we can speak of co-occurring quadruples of values. There are six pairwise combinations of the four factor points but only four of them, those of the form xαyβ (x, y ∈{1, 2}), form treatments, whereas the remaining two, 1α2α and 1β2β, do not. The four treatments correspond to pairs
. Suppose that they are jointly distributed, i.e., we can speak of co-occurring quadruples of values. There are six pairwise combinations of the four factor points but only four of them, those of the form xαyβ (x, y ∈{1, 2}), form treatments, whereas the remaining two, 1α2α and 1β2β, do not. The four treatments correspond to pairs 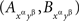 whose joint distributions are well defined. Suppose now that for all those cases when a pair of factor points forms a treatment we have
whose joint distributions are well defined. Suppose now that for all those cases when a pair of factor points forms a treatment we have
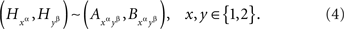
Then and only then (A, B) ↫ (α, β), and we can write then 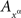 instead of
instead of 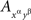 and
and 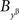 instead of
instead of 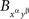 . We call this the joint distribution criterion for selective influence. The joint distributions of
. We call this the joint distribution criterion for selective influence. The joint distributions of 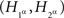 and
and 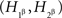 must also be well defined, even though they do not correspond to any pairs of random variables one can choose from the observable
must also be well defined, even though they do not correspond to any pairs of random variables one can choose from the observable 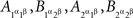 .
.
Let us look at this in detail. The observed joint distributions of 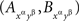 are represented by four probabilities each, denoted in the four matrices introducing our example by pij , qij , rij , sij . We now switch to a more convenient notation (although again, more cumbersome at first glance):
are represented by four probabilities each, denoted in the four matrices introducing our example by pij , qij , rij , sij . We now switch to a more convenient notation (although again, more cumbersome at first glance):
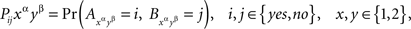
where Pijxαyβ is a string of symbols, with no multiplication implied. To ascertain if (A, B) ↫ (α, β) using (4), we have to see if we can find 16 probabilities
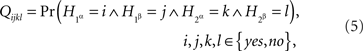
for four binary variables 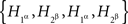 , subject to the basic constraints
, subject to the basic constraints
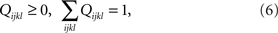
and such that
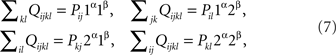
for all i, j, k, l ∈{yes, no}. Indeed,
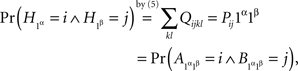
which shows that the first of the equations (7) is equivalent to 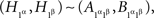 the application of (4) to xαyβ = 1α1β; and analogously for the other three equations.
the application of (4) to xαyβ = 1α1β; and analogously for the other three equations.
Note that (7) implies marginal selectivity. For instance, it follows from (7) that
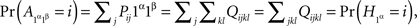
and
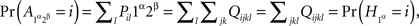
that is, 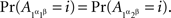
Example 1.1. Let the dependence of {A, B} on {α, β} be described by the distributions
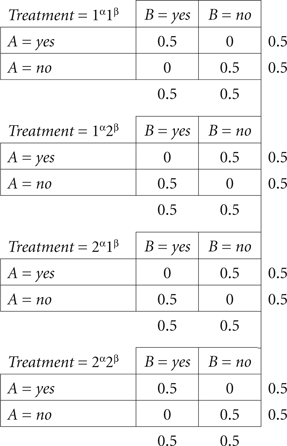
Note that marginal selectivity here is satisfied trivially, as the marginal distributions remain fixed. Consider the distribution of 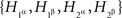 with
with
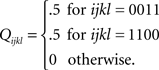
It is easy to check that this distribution satisfies (6) and (7), hence also (4). By the joint distribution criterion, we conclude that {A, B} ↫ {α, β}.
Example 1.2. No such probabilities Qijkl can be found for the distributions

so {A, B} are not selectively influenced by {α, β} in this case. This can be shown by direct algebra, but there is a simpler method: this dependence of {A, B} on {α, β} fails a distance test. Indeed, let us transform yes into 0 and no into 1, and let us choose the exponent ρ = 1 (although in this example the value of ρ does not matter). Then
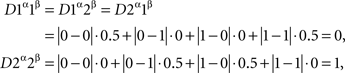
and
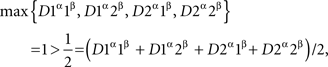
which contravenes (3).
In this paper the joint distribution criterion is formulated in complete generality, for arbitrary sets of random entities and corresponding sets of external factors.
1.5. The Need for Generalization
In a controlled experiment or systematic survey we usually focus on a small number of random entities, such as which of several responses is given and how long it has taken, and try to selectively target some of them by experimental manipulations, or selectively relate them to concomitant factors. Relatively small networks of random entities and external factors are therefore of paramount practical importance. But a network of random entities and the set of external factors that may be thought to affect them selectively can be quite large, even infinitely large, in theoretical considerations dealing with complex observable behaviors, such as a person’s activities within a typical day, or unobservable “mental networks” behind even relatively simple tasks, such as pushing a key in response to a stimulus varying in two binary properties (see Dzhafarov, Schweickert, and Sung, 2004, for an example). Random processes are routinely used in modeling simple forms of decision making (see, e.g., Diederich and Busemeyer, 2003). Any random process can be viewed as a system of stochastically interdependent random entities indexed by “intervention values” (including “no intervention”) at every moment of time. An intervention α at moment t1 can be thought to selectively affect a portion of the random process in some interval [t1, t2] (perhaps even with t2 = t1), and the problem arises as to how to identify such an interval from the observed joint distribution of the random entities constituting the process. It is important therefore to be able to apply the notion of selective influence to arbitrary, finite and infinite, systems of random entities, and external factors.
2. Conventions and Notation
A factor is defined as a non-empty set of factor points (a dummy factor can be defined as a set containing a single point). Denoting factors by lowercase Greek letters, α, β, γ, …, the factor points of, say, factor α are formally pairs (x, ‘α’) consisting of a factor value (or level), x, and a unique factor name, ‘α’ (read: value/level x of factor α). This ensures that no two distinct factors have common points: e.g., level 1 of factor ‘size’ (1, ‘size’), is distinct from level 1 of factor ‘shape’ (1, ‘shape’). It is convenient to write xα in place of (x, ‘α’): 1shape, (50 db)intensity, presentleft stilumus, etc.
Let Φ be a non-empty set of factors. A set ɸ containing precisely one factor point 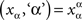 for each factor α in Φ,
for each factor α in Φ,
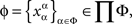
is called a treatment.3 When the set of factors Φ is finite, treatments will be presented as strings of factor points, without commas or parentheses: xαyβzγ, 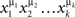 , etc.
, etc.
Example 2.1. If Φ = {α, β, γ} with α = {1α, 2α}, β = {1β, 2β}, and γ = {1γ}, then the treatments ɸ (written as strings) are 1α1β1γ, 1α2β1γ, 2α1β1γ, and 2α2β1γ.
A random entity A is a triad consisting of a measurable function 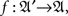 a sample (probability) space
a sample (probability) space 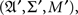 and an observation (measurable) space (𝔄, Σ), on which f induces a probability measure M. Traditionally, A is simply identified with f, the sample space and the observation space being assumed implicitly, or A is viewed as the identity function on 𝔄, with (𝔄′, Σ′, M′) = (𝔄, Σ, M). The latter view is often the only practical one, as we almost never know anything about a sample space as separate from the observation space.
and an observation (measurable) space (𝔄, Σ), on which f induces a probability measure M. Traditionally, A is simply identified with f, the sample space and the observation space being assumed implicitly, or A is viewed as the identity function on 𝔄, with (𝔄′, Σ′, M′) = (𝔄, Σ, M). The latter view is often the only practical one, as we almost never know anything about a sample space as separate from the observation space.
A random variable is a random entity whose observation space is a subset of reals endowed with the Borel sigma-algebra.4
Given an arbitrary indexing set Ω, any set of random entities whose measurable functions {fω:𝔄′→𝔄ω}ω∈Ω map from one and the same sample space (𝔄′, Σ′, M′) into respective observation spaces {(𝔄ω, Σω)}ω∈Ω possesses a joint distribution, i.e., a probability measure M induced by M′ on the product space ⊗ω∈Ω(𝔄ω, Σω).5
Example 2.2. Let the sample space consist of 𝔄′ = {0, 1} × {0, 1} × {0, 1}, Σ′ = 2𝔄′, and M′ derived from elementary probabilities pijk (i, j, k ∈{0, 1}). Then the random variables A, B, C defined on (𝔄′, Σ′, M′) by the coordinate projections 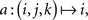 ,
, 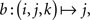 , and
, and 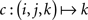 , respectively (i, j, k ∈{0, 1}), possess the joint distribution M = M′ on ({0, 1}, 2{0,1}) ⊗ ({0, 1}, 2{0,1}) ⊗ ({0, 1}, 2{0,1}) = (𝔄′, Σ′).
, respectively (i, j, k ∈{0, 1}), possess the joint distribution M = M′ on ({0, 1}, 2{0,1}) ⊗ ({0, 1}, 2{0,1}) ⊗ ({0, 1}, 2{0,1}) = (𝔄′, Σ′).
Two random entities A and B defined on different sample spaces are called (stochastically or probabilistically) unrelated (see Dzhafarov and Gluhovsky, 2006). They do not possess a joint distribution. Note that two unrelated random variables can be identically distributed – if they map into one and the same observation space on which they induce one and the same probability measure.
Throughout this paper we deal with a set of probabilistically unrelated random entities {Aɸ}ɸ∈ΠΦ indexed by treatments ɸ∈ΠΦ, with measures {Mɸ}ɸ∈ΠΦ induced on one and the same observation space (𝔄, Σ). For convenience, we refer to Aɸ as “a random entity A at ɸ”, as if Aɸ and 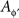 for ɸ ≠ ɸ′ were “a single” entity A at two different treatments. Note that Aɸ and
for ɸ ≠ ɸ′ were “a single” entity A at two different treatments. Note that Aɸ and 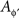 are defined on different sample spaces: they do not possess a joint distribution. In particular, they are not mutually independent.6
are defined on different sample spaces: they do not possess a joint distribution. In particular, they are not mutually independent.6
Example 2.3. The random variables A and B in the examples of Section 1 are called A and B by the abuse of language just mentioned. Strictly speaking we deal with four pairwise stochastically unrelated 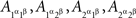 and four pairwise stochastically unrelated
and four pairwise stochastically unrelated 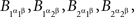 such that
such that 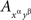 and
and 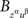 possess a joint distribution if and only if xαyβ = zαuβ.
possess a joint distribution if and only if xαyβ = zαuβ.
A set of random entities {Aω}ω∈Ω on one and the same sample space is a random entity whose observation space (𝔄, Σ) is the conventionally understood product of the observation spaces (𝔄ω, Σω) for Aω, ω ∈ Ω. If the set of random entities {Aω}ω∈Ω depends on Φ, we present {Aω}ω∈Ω at a treatment ɸ as 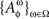 instead of the more correct but less convenient ({Aω}ω∈Ω)Φ.
instead of the more correct but less convenient ({Aω}ω∈Ω)Φ.
Example 2.4. The variables {A, B, C} of Example 2.2 depend on the factors Φ = {α, β, γ} of Example 2.1 if 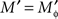 is viewed as a function of ɸ = 1α1β1γ, 1α2β1γ, …. In this example
is viewed as a function of ɸ = 1α1β1γ, 1α2β1γ, …. In this example 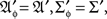 and {aɸ, bɸ, cɸ} = {a, b, c}.
and {aɸ, bɸ, cɸ} = {a, b, c}.
3. Selective Influence
In accordance with the previous section, given a set of factors Φ, a corresponding set of random entities is denoted {Aα}α∈Φ. For each α∈Φ, the entity Aα may in fact be a shortcut notation for a set of stochastically unrelated random entities indexed by different treatments, 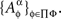 In other words,
In other words, 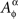 is treated as a random entity A corresponding to factor α and taken at treatment ɸ. The complete notation for the set of random entities {Aα}α∈Φ then is
is treated as a random entity A corresponding to factor α and taken at treatment ɸ. The complete notation for the set of random entities {Aα}α∈Φ then is

where the elements of 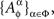 for a given ɸ, are stochastically interrelated (possess a joint distribution), while the sets
for a given ɸ, are stochastically interrelated (possess a joint distribution), while the sets 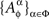 and
and 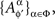 for distinct ɸ, ɸ′, are stochastically unrelated. It is more convenient, however, not to use this explicit notation and to speak instead of {Aα}α∈Φ depending on Φ.
for distinct ɸ, ɸ′, are stochastically unrelated. It is more convenient, however, not to use this explicit notation and to speak instead of {Aα}α∈Φ depending on Φ.
Definition 3.1. Let a set of random entities {Aα}α∈Φ indexed by a set of factors Φ depend on this set of factors (i.e., be presentable as (8)). We say that the dependence of {Aα}α∈Φ on Φ is marginally selective (satisfies the property of marginal selectivity) if, for any subset Φ1 ⊂ Φ and any ɸ1∈ΠΦ1, the distribution of 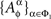 is the same for all treatments ɸ containing ɸ1 (that is, it does not depend on {xβ∈ɸ : β∈Φ−Φ1}).
is the same for all treatments ɸ containing ɸ1 (that is, it does not depend on {xβ∈ɸ : β∈Φ−Φ1}).
The notion of marginal selectivity was introduced by Townsend and Schweickert (1989), for two random variables. In Dzhafarov (2003) it was generalized to a finite set of random variables under the name of complete marginal selectivity. The adjective “complete” (omitted in the present paper for simplicity) distinguishes this notion from a weaker and less useful generalization of Townsend and Schweickert’s term: for any factor α∈Φ and any treatment ɸ, the distribution of 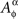 does not depend on {xβ∈ɸ : β∈Φ−{α}}.
does not depend on {xβ∈ɸ : β∈Φ−{α}}.
Note that Definition 3.1 does not mean that for distinct treatments ɸ and ɸ′ which include ɸ1 = {xβ ∈ɸ : β ∈Φ1} = {xβ ∈ɸ′ :β ∈Φ1},
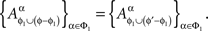
This equality is not legitimate as the two sets of random variables do not possess a joint distribution. One can only say that
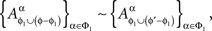
where, as before, ∼ means “is distributed as.”
Example 3.2. Let the variables {A, B, C} of Example 2.2 be indexed by the factors Φ = {α, β, γ} of Example 2.1, respectively. That is, {A, B, C} stands for {Aα, Aβ, Aγ}, in accordance with the general notation of Definition 3.1. Then the dependence of {Aα, Aβ, Aγ} on {α, β, γ} is marginally selective if and only if
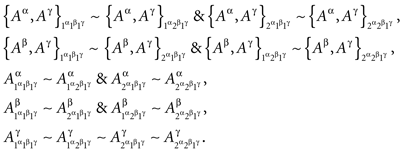
Under marginal selectivity, it is sometimes admissible, by abuse of notation, to write 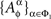 as
as 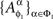 where ɸ1 = {xα ∈ɸ : α ∈Φ1}. Thus, in Example 3.2, it may be convenient to present both
where ɸ1 = {xα ∈ɸ : α ∈Φ1}. Thus, in Example 3.2, it may be convenient to present both 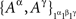 and
and 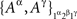 as
as 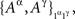 present both
present both 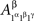 and
and 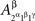 as
as 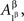 etc. This does not lead to complications provided one remembers that, say,
etc. This does not lead to complications provided one remembers that, say, 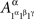 and
and 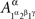 are identically distributed rather than identical. One can therefore deal with
are identically distributed rather than identical. One can therefore deal with 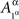 and
and 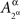 in all considerations involving only Aα, or with
in all considerations involving only Aα, or with 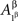 and
and 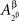 in all considerations involving only Aβ. It would be incorrect, however, to speak of stochastic relationships between
in all considerations involving only Aβ. It would be incorrect, however, to speak of stochastic relationships between 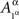 or
or 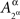 and
and 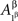 or
or 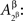 to depict such relationships one needs both Aα and Aβ to be double-indexed by the factor points involved (unless we have selective influence in addition to marginal selectivity, as explained in the next section).
to depict such relationships one needs both Aα and Aβ to be double-indexed by the factor points involved (unless we have selective influence in addition to marginal selectivity, as explained in the next section).
Example 3.3. Continuing Example 3.2, let us return to writing {A, B, C} instead of {Aα, Aβ, Aγ}. We can omit the factor γ when dealing with {A, B} only and write 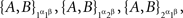
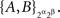 Let the distributions of these random pairs be
Let the distributions of these random pairs be

We verify that marginal selectivity holds for A and B and introduce the abridged indexing, 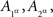 etc.:
etc.:

We can use the abridged indexing in all considerations involving A alone and B alone. Consider, however, this: from the joint distribution matrices we have
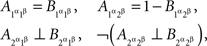
where ⊥ indicates stochastic independence and ¬ negation (i.e., 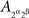 and
and 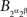 are not stochastically independent). If now we attempt to use in these relations the abridged indexing, we will run into a contradiction: from
are not stochastically independent). If now we attempt to use in these relations the abridged indexing, we will run into a contradiction: from 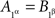 and
and 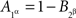 we conclude
we conclude 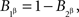 but then it is impossible for
but then it is impossible for 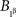 to be independent of
to be independent of 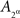 and for
and for 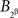 not to be. It is therefore necessary to retain the notation
not to be. It is therefore necessary to retain the notation 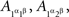 etc. in all considerations involving both A and B even though we know that the dependence of {A, B} on {α, β} is marginally selective.
etc. in all considerations involving both A and B even though we know that the dependence of {A, B} on {α, β} is marginally selective.
Definition 3.4. Let a set of random entities {Aα}α∈Φ indexed by a set of factors Φ depend on this set of factors. We say that the set {Aα}α∈Φ is selectively influenced by Φ, and write

if, for some random entity C and every xα∈α∈Φ there is a measurable function 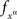 such that, for every treatment ɸ,
such that, for every treatment ɸ,
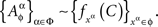
Remark 3.5. Alternatively, one could posit, for every treatment ɸ,
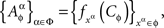
where
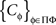
is a set of pairwise unrelated random entities all distributed as C. This formulation is more cumbersome but it correctly emphasizes the stochastic unrelatedness of 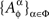 for different treatments ɸ. Definition 3.4, however, is more parsimonious, as the stochastic unrelatedness property is known from the context.
for different treatments ɸ. Definition 3.4, however, is more parsimonious, as the stochastic unrelatedness property is known from the context.
Remark 3.6. If applied to finite sets Φ, Definition 3.4 becomes equivalent to the formulations of selective influence given in Dzhafarov (2003), Dzhafarov and Gluhovsky (2006), and Kujala and Dzhafarov (2008). Even for the finite case, however, the present definition is mathematically more rigorous, and it profits from the precision offered by the notation xα = (x, ‘α’) for factor points. More importantly, it can be seen more immediately than the previous definitions to be reformulable into the joint distribution criterion for selective influence, as discussed in the next section.
The following statements are obvious.
Lemma 3.7. If {Aα}α∈Φ↫ Φ, then
(i) 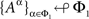 for any Φ1 ⊂ Φ;
for any Φ1 ⊂ Φ;
(ii) the dependence of {Aα}α∈Φ on Φ is marginally selective.
That is (refer to Section 1.2), selective influence has the nestedness property and implies marginal selectivity.
The next lemma says that if a set of random entities {Aα}α∈Φ is selectively influenced by Φ, then the set of individually transformed versions of these random variables is also selectively influenced by Φ (refer to the first property in Section 1.2). “Individual transformations” of Aα can be different for different factor points xα.
Lemma 3.8. If {Aα}α∈Φ ↫ Φ then {Bα}α∈Φ ↫ Φ, where, for any α∈Φ, any xα∈α, and any treatment ɸ containing xα,
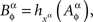
for some measurable function 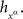
Proof. By definition,
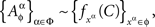
which implies
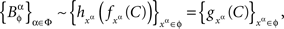
where 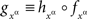 is a measurable function. ☐
is a measurable function. ☐
4. The Joint Distribution Criterion
Definition 3.4 suggests a way of looking at the selective influence relation directly in terms of the (product) observation space for the system of the random entities involved, making the overt reconstruction of C and the functions 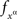 unnecessary (or trivial, as in the proof of the theorem below).
unnecessary (or trivial, as in the proof of the theorem below).
Theorem 4.1. A necessary and sufficient condition for
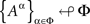
is the existence of a jointly distributed system
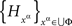
such that for every subset ɸ of 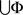 that forms a treatment (i.e., belongs to ΠΦ),
that forms a treatment (i.e., belongs to ΠΦ),
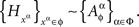
Remark 4.2. We call this the joint distribution criterion for selective influence.
Proof. The necessity is proved by observing that if {Aα}α∈Φ ↫ Φ, then the system
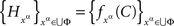
is a jointly distributed system of random entities. To prove the sufficiency, define
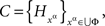
and, for every xα, define
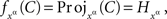
where 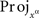 denotes the xαth coordinate projection. ☐
denotes the xαth coordinate projection. ☐
As a very simple application of the joint distribution criterion we prove the following (intuitively quite obvious) statement.
Lemma 4.3. If the dependence of {Aα}α∈Φ on Φ is marginally selective and 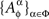 is a set of mutually independent random entities for every treatment Φ, then {Aα}α∈Φ↫ Φ.
is a set of mutually independent random entities for every treatment Φ, then {Aα}α∈Φ↫ Φ.
Proof. For any factor α ∈Φ, marginal selectivity implies that the distribution of 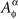 depends only on the factor point xα ∈Φ. Form the set
depends only on the factor point xα ∈Φ. Form the set 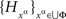 consisting of mutually independent random entities such that, for any xα,
consisting of mutually independent random entities such that, for any xα, 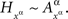 Then, for every treatment ɸ,
Then, for every treatment ɸ, 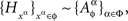 and Theorem 4.1 implies {Aα}α∈Φ↫ Φ. · ☐
and Theorem 4.1 implies {Aα}α∈Φ↫ Φ. · ☐
In Section 1.4 we have seen illustrations of the criterion on interdependent random entities. Here is another example.
Example 4.4. Let Φ = {α, β}, α = {1α,2α}, β = {1β, 2β}, and let {Aɸ, Bɸ} for every treatment ɸ be a pair of Bernoulli variables. Consider the distributions below:

The criterion of the joint distribution of 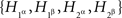 rejects the possibility of {A, B} ↫ {α, β}, as it can be shown by direct algebra that there are no 16 probabilities Qijkl generating the distributions in question (cf. Examples 1.1 and 1.2). We do not need to provide such a demonstration as it is obvious in this case from probabilistic considerations that
rejects the possibility of {A, B} ↫ {α, β}, as it can be shown by direct algebra that there are no 16 probabilities Qijkl generating the distributions in question (cf. Examples 1.1 and 1.2). We do not need to provide such a demonstration as it is obvious in this case from probabilistic considerations that 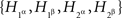 cannot be jointly distributed and satisfy
cannot be jointly distributed and satisfy
Otherwise the four joint distribution matrices shown above would have implied, respectively,  and
and  , which are not mutually compatible equations.
, which are not mutually compatible equations.
If we take the numerical values of A and B in the last example as they are, then with any exponent ρ ≥ 1 (see Section 1.3) the distance test is passed:
This is just another demonstration that a distance test is only a necessary condition for selective influence: a dependence of random entities on external factors can pass such a test but still fail the joint distribution criterion. It is instructive to see, however, in reference to Lemma 3.8, that with appropriately chosen transformations of the random variables the distributions in question can be made to fail the respective distance tests. Thus, the possibility of selective influence in Example 4.4 will be rejected if we apply the simple transformation
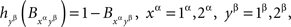
while leaving 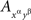 untransformed. The distributions then become essentially the same as in Example 1.2. The distance tests therefore can be conjectured to have considerable rejection power if one combines it with adeptly chosen transformations (see the open question we pose at the conclusion of the paper). In any case, the exceptional simplicity of these tests makes it worthwhile to always consider them before applying the joint distribution criterion.
untransformed. The distributions then become essentially the same as in Example 1.2. The distance tests therefore can be conjectured to have considerable rejection power if one combines it with adeptly chosen transformations (see the open question we pose at the conclusion of the paper). In any case, the exceptional simplicity of these tests makes it worthwhile to always consider them before applying the joint distribution criterion.
5. Distance Tests
In Kujala and Dzhafarov (2008) the distance tests were formulated for two variables influenced by two factors in a two-by-two factorial design. In this section we generalize these tests to arbitrary random variables {Aα}α∈Φ whose dependence on factors Φ is marginally selective. Perhaps surprisingly, we show that this generalization requires nothing more and nothing less than applying the original tests to all possible two-by-two factorial designs one can extract from Φ.
Distance tests can be applied to non-numerical random entities only after they have been numerically transformed (thus, for the distance test applied to Example 1.2 we transformed yes into 0 and no into 1). In this section therefore we confine our discussion to random variables.
We will need some auxiliary notions and notation conventions. Any finite sequence of factor points 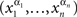 is called a chain. Chains will be written as strings,
is called a chain. Chains will be written as strings, 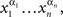 without commas and parentheses (this generalizes the convention we have already used for chains which are finite treatments). Chains can be denoted by capital Roman letters,
without commas and parentheses (this generalizes the convention we have already used for chains which are finite treatments). Chains can be denoted by capital Roman letters, 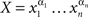 (from the second half of the alphabet, to distinguish them from random variables and entities for which we use the first half). A chain X may be empty or consist of a single element (factor point), xα. A subsequence of points belonging to a chain forms its subchain.
(from the second half of the alphabet, to distinguish them from random variables and entities for which we use the first half). A chain X may be empty or consist of a single element (factor point), xα. A subsequence of points belonging to a chain forms its subchain.
A concatenation of two chains X and Y is written as XY. So, we can have chains xαXyβ, xαXYyβ, XxαyβY, xαXyβZ, etc.
The number of points in a chain X is its cardinality, | X |, and any chain with the smallest cardinality within a set of chains is referred to as a minimal chain (in this set). In particular, one can speak of a minimal subchain of a chain among all subchains with a certain property (this notion is used in the proof of Theorem 5.11 below).
Definition 5.1. Let the dependence of a set of random variables {Aα}α∈Φ on factors Φ be marginally selective. Let ρ ≥ 1 be fixed. For any (xα, yβ) with α ≠ β, we define
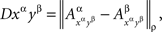
where 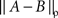 for any jointly distributed A and B is defined as
for any jointly distributed A and B is defined as
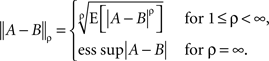
Remark 5.2. Here ess sup is the essential supremum, the lowest upper bound that holds almost surely; it is the limit of 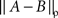 as ρ → ∞.
as ρ → ∞.
Remark 5.3. Note that Dxαyβ is well-defined only under the assumption that the dependence of a set of random variables {Aα}α∈Φ on factors Φ is marginally selective. Otherwise 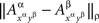 would not be determined by xαyβ only, and it would not even be legitimate to index the two variables by xαyβ alone.
would not be determined by xαyβ only, and it would not even be legitimate to index the two variables by xαyβ alone.
We will rely on the following result, whose proof we omit as its only non-trivial part follows from the Minkowski inequality (a somewhat abridged proof can be found in Kujala and Dzhafarov, 2008).
Lemma 5.4. Given a sample space, let ℜ be a set of all random variables A, B, … (jointly distributed) on this space. For any 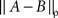 is an extended metric on ℜ, provided we do not distinguish A,B identical on a set of measure 1.
is an extended metric on ℜ, provided we do not distinguish A,B identical on a set of measure 1.
Remark 5.5. The adjective “extended” means that ∞ is included in the set of possible values. The norms 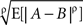 and
and 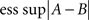 , as they only involve non-negative values, always exist, finite or infinite.
, as they only involve non-negative values, always exist, finite or infinite.
Convention 5.6. In the remainder of this section we will tacitly assume that the dependence of {Aα}α∈Φ on Φ is marginally selective. We will also tacitly assume that ρ in the definition of 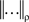 and D is fixed.
and D is fixed.
For any chain 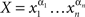 such that
such that 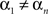 and
and 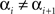 for i = 1,…,n −1, define
for i = 1,…,n −1, define
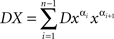
(with the understanding that the sum is zero if n is 0 or 1). The operator D always acts upon the entire chain following it, e.g., 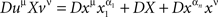 .
.
Definition 5.7. A chain xαXyβ is said to be compliant with the chain inequality (or simply, compliant) if DxαXyβ ≥ Dxαyβ. The chain is said to be contravening (the chain inequality) if DxαXyβ < Dxαyβ.
It follows from this definition that if xαXyβ is contravening or compliant, then α ≠ β (otherwise Dxαyβ is not defined), and no factor in xαXyβ occurs twice in succession. For a chain to be contravening, in addition, X must be non-empty (i.e., | xαXyβ | ≥ 3; Lemma 5.9 below shows that in fact | xαXyβ | ≥ 4). A non-contravening chain need not be compliant: it may, e.g., be any chain with fewer than 3 elements, or it can be any chain of the form xαXyα. Analogously, a non-compliant chain is not necessarily contravening.7
Lemma 5.8. Let U = XyβYzγZ be a contravening chain with a compliant subchain yβYzγ. Then U* = XyβzγZ (i.e., U without Y) is a contravening subchain of U.
Proof. Let xα and uδ be the first and the last elements of U, respectively (then necessarily α ≠ δ). Note that xα may coincide with yβ or uδ with zγ (but not both). From
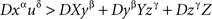
and
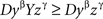
we get
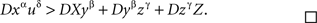
Lemma 5.9. Every triadic chain xαyβzγ with pairwise distinct α, β, γ is compliant.
Proof. Denoting the random variables corresponding to the factors α, β, γ, by A, B, C, respectively, marginal selectivity implies
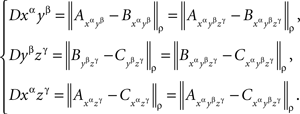
Since 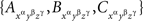 are jointly distributed, the statement follows from Lemma 5.4.8 ☐
are jointly distributed, the statement follows from Lemma 5.4.8 ☐
We are ready now to prove the main theorems regarding the distance tests for selective influence.
Theorem 5.10. Let {Aα}α∈Φ be selectively influenced by Φ. Then any chain 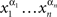 such that αi ≠ αi+1 for i = 1,…,n − 1, and α1 ≠ αn is compliant,
such that αi ≠ αi+1 for i = 1,…,n − 1, and α1 ≠ αn is compliant,
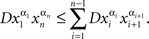
Proof. By the joint distribution criterion, there is a jointly distributed system 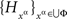 such that for any {xα, yβ} within a treatment (i.e. with α ≠ β),
such that for any {xα, yβ} within a treatment (i.e. with α ≠ β),
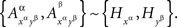
But then
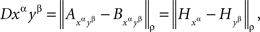
and the statement of the lemma follows from Lemma 5.4. ☐
For the next theorem, recall that we are following Convention 5.6.
Theorem 5.11. Every contravening chain X contains a contravening tetradic subchain X′ of the form xαyβvαuβ.
Proof. Let X′ = xαPuβ be a minimal contravening subchain of X. Then α ≠ β, and by Lemma 5.9, | X ′| ≥ 4. If for some zγ in X′ we had α ≠ γ ≠ β, then the subchains xαQzγ and zγRuβ with QzγR = P would have to be compliant (otherwise X′ would not be minimal). Then, by Lemma 5.8, we would have a contravening triadic chain xαzγuβ, which is impossible by Lemma 5.9. For every zγ in X′ therefore, either γ = α or γ = β. Since a contravening chain cannot contain repeating superscripts, X′ is of the form xαyβvαSuβ. But then vαSuβ must be compliant (otherwise X′ would not be minimal), and by Lemma 5.8 xαyβvαuβ is contravening. Since X′ is minimal, we conclude that S is empty and X′ = xαyβvαuβ.
It follows that the task of testing the compliance of D with all possible chain inequalities, as stated in Theorem 5.10, is reduced to testing the compliance with only the inequalities involving tetradic chains: if {Aα}α∈Φ↫ Φ, then, for any chain xμyνuμvν with distinct μ and ν,
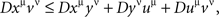
and if all such inequalities are satisfied, then there can be no other contravening chains. Given any four factor points xμ, yν, uμ, vν, one can form four different chains with alternating factors and four corresponding inequalities,
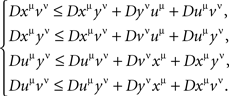
Following Kujala and Dzhafarov (2008), these are easy to see (by adding the left-hand sides to themselves and to the right-hand sides) to be equivalent to the single inequality
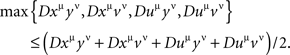
We call this a tetradic inequality. Note that it is always satisfied if xμ = uμ or yν = vν, so we only have to look at xμ, yν, uμ, vν with two distinct points of each factor.
The theorem below shows that we have to check all such tetradic inequalities (for any given ρ).
Theorem 5.12. The tetradic inequalities are mutually independent, in the sense that any one of them can be violated while the rest of them hold.
Proof. Let μ and ν be distinct factors in Φ, and let, for all points xμ and yν,
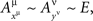
where E is some non-singular random variable (i.e., no constant equals E with probability 1). Let 1μ, 2μ, 1ν, 2ν be distinct fixed points of μ and ν, and let
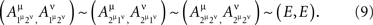
Let 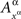 for any point of any factor α ∉{μ, ν} be distributed arbitrarily, and let the random variables
for any point of any factor α ∉{μ, ν} be distributed arbitrarily, and let the random variables 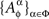 be mutually independent for any treatment ɸ, except if the latter includes one of the pairs {1μ, 2ν}, {2μ, 1ν}, or {2μ, 2ν}: in those cases the joint distribution of
be mutually independent for any treatment ɸ, except if the latter includes one of the pairs {1μ, 2ν}, {2μ, 1ν}, or {2μ, 2ν}: in those cases the joint distribution of 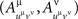 is given by (9), while
is given by (9), while 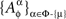 and
and 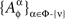 remain the sets of mutually independent variables. It is easy to see that
remain the sets of mutually independent variables. It is easy to see that 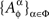 thus defined satisfy the marginal selectivity property.
thus defined satisfy the marginal selectivity property.
Now,
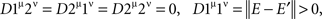
where E and E′ are identically distributed and independent. The tetradic inequality on {1μ, 1ν, 2μ, 2ν} is therefore violated:
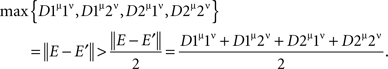
Clearly, the tetradic inequality holds on any set {xα, yβ, sα, tβ} that does not include {1μ, 2ν}, {2μ, 1ν}, or {2μ, 2ν}, as this inequality then only involves mutually independent random variables (Lemma 4.3 and Theorem 5.10). Denoting by 3μ any point other than 1μ and 2μ (if such a point exists), and analogously for 3ν, it remains to consider the cases {1μ, 2ν, 3μ, 3ν}, {1μ, 2ν, 2μ, 3ν}, {1μ, 2ν, 3μ, 1ν}, {2μ, 1ν, 3μ, 3ν}, {2μ, 1ν, 1μ, 3ν}, {2μ, 1ν, 3μ, 2ν}, and {2μ, 2ν, 3μ, 3ν} (note that the order of the points is immaterial here). It is easy to check that the four distances in each of these quadruples equal either 0 or ‖ E − E′ ‖> 0 (with E, E′ independent identically distributed), and that the number of zero distances in these quadruples is never greater than two. The tetradic inequality, therefore, always holds: either
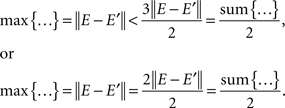
This completes the proof. ☐
Theorem 5.12 is proved for a fixed ρ ≥ 1, and for “untransformed” {Aα}α∈Φ. The application scope of the distance tests can be significantly broadened by using various values of ρ and by applying to {Aα}α∈Φ various transformations as specified in Lemma 3.8. It is clear that the tetradic inequalities cannot be independent across all ρ and/or all transformations. Since a violation of a tetradic inequality means a strict inequality, the inequality involving the same quadruple of factor points will have to hold also for sufficiently close values of ρ and sufficiently “slight” transformations. This also applies to ρ = ∞: every violated inequality for ρ = ∞ will have to remain violated for all sufficiently large values of ρ, since the difference between ess sup | A − B | and  can be made arbitrarily small (or, if the former is infinite, the latter can be made arbitrarily large).
can be made arbitrarily small (or, if the former is infinite, the latter can be made arbitrarily large).
6. Conclusion
We have advanced the theory of selective influence in three ways.
1. The notion of selective influence (together with the related but weaker notion of marginal selectivity) has been generalized to arbitrary sets of random entities whose joint distributions depend on arbitrary sets of external factors by which the random entities are indexed (Definition 3.4).
2. The joint distribution criterion has been formulated for random entities to be selectively influenced by their indexing external factors: this happens if and only if there is a jointly distributed set of random entities, one for every value of every factor, such that every subset of this set that corresponds to a treatment is distributed as the original entities at this treatment (Theorem 4.1).
3. The distance tests previously formulated for pairs of random variables in two-by-two factorial designs have been generalized to arbitrary sets of random variables. For any quadruple of distinct factor points xμ, yν, uμ, vν, we check whether
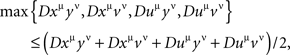
where the function D is as in Definition 5.1, for some choice of ρ ≥ 1 and of transformations 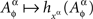 as specified in Lemma 3.8. If this tetradic inequality is violated, the variables are not selectively influenced by the factors indexing them. It is shown that we do not need to check for compliance with any other chain inequalities (Definition 5.7, Theorems 5.10 and 5.11), and that the tetradic inequalities for different quadruples of factor points (for a given ρ and a given set of transformations) are logically independent (Theorem 5.12).
as specified in Lemma 3.8. If this tetradic inequality is violated, the variables are not selectively influenced by the factors indexing them. It is shown that we do not need to check for compliance with any other chain inequalities (Definition 5.7, Theorems 5.10 and 5.11), and that the tetradic inequalities for different quadruples of factor points (for a given ρ and a given set of transformations) are logically independent (Theorem 5.12).
We conclude by posing an open question. Example 4.4 in Section 4 shows that the distance tests can be passed for all values of ρ while the random variables in question do not selectively depend on the respective factors. At the same time, in this example a distance test can be found to fail after the random variables have been transformed in accordance with Lemma 3.8. The open question is: for random variables which are not selectively influenced (but whose dependence on the corresponding factors is marginally selective), can the distance test be passed under all possible measurable transformations of the variables?
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research has been supported by NSF grant SES 0620446 and AFOSR grant FA9550-09-1-0252 to Purdue University, as well as by the Academy of Finland grant 121855 to University of Jyväskylä.
Footnotes
- ^As explained in Section 2, we distinguish random entities and their special case, random variables. Random entities take on values in arbitrary measurable spaces, while random variables map, or can be redefined to map, into real numbers endowed with the Borel sigma-algebra. Note also that the notion of a random entity (or variable) should always be taken to include deterministic entities (variables) as a special case, the same as the notion of stochastic interdependence, unless otherwise indicated, should be taken to include stochastic independence as a special case.
- ^It is usually the case that the possibility of selectiveness is considered when it is known that the factors are effective in their influence upon (A, B), meaning that for at least one value of either of the two factors the change of the other factor from 1 to 2 changes the joint distribution of (A, B). This aspect of the dependence of (A, B) on (α, β) being relatively trivial, we do not include it in the definition of selective influence. In other words, (A, B) ↫ (α, β) is taken to mean that β does not influence A and α does not influence B, leaving open the question of whether α influences A and/or β influences B (see Dzhafarov, 2003, p. 10).
- ^Strictly speaking, an element of the Cartesian product ΠΦ is a choice function,
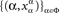 whereas a treatment ɸ is the range of a choice function,
whereas a treatment ɸ is the range of a choice function, 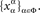 We conveniently confuse the two notions. Also for convenience only, in this paper we assume “completely crossed design”, i.e., that every member of ΠΦ is a possible treatment. With only slight modifications ΠΦ can be replaced with any nonempty subset thereof.
We conveniently confuse the two notions. Also for convenience only, in this paper we assume “completely crossed design”, i.e., that every member of ΠΦ is a possible treatment. With only slight modifications ΠΦ can be replaced with any nonempty subset thereof. - ^A random entity A with 𝔄 a finite or infinite denumerable set and Σ the set of all its subsets can also be (and traditionally is) considered a random variable, because such an 𝔄 can always be injectively mapped into the set of reals, or into a partition of an interval of reals.
- ^Recall that in the product measurable space ⊗ω∈Ω(𝔄ω, Σω) = (𝔄, Σ) the set 𝔄 is the Cartesian product Πω∈Ω𝔄ω, while Σ = ⊗ω∈ΩΣω is the smallest sigma algebra containing all sets of the form
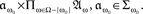
- ^We could have extended the scope of this definition by allowing
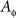 to be a function
to be a function 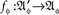 relating
relating 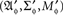 to (𝔄ɸ, Σɸ), i.e., by allowing the set and the sigma algebra, not only the measure Mɸ, to depend on treatment ɸ. This would have, however, made our abuse of language (in treating different Aɸ’s as a single A at different ɸ’s) even more abusive. Moreover, this general approach can always be reduced to the set-up with a ɸ-independent (𝔄, Σ) by putting
to (𝔄ɸ, Σɸ), i.e., by allowing the set and the sigma algebra, not only the measure Mɸ, to depend on treatment ɸ. This would have, however, made our abuse of language (in treating different Aɸ’s as a single A at different ɸ’s) even more abusive. Moreover, this general approach can always be reduced to the set-up with a ɸ-independent (𝔄, Σ) by putting 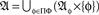 and Σ the sigma algebra consisting of all countable unions of the sets
and Σ the sigma algebra consisting of all countable unions of the sets 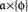 for all
for all 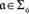 and all ɸ∈ΠΦ.
and all ɸ∈ΠΦ. - ^We cannot resist mentioning at this point a surprising mathematical similarity between the conceptual apparatus of (hence also the notation adopted in) the present theory, especially in this section, and that of the completely unrelated theory of “regular well-matched spaces” developed in Dzhafarov and Dzhafarov (2010) for comparative judgments. In particular, factors and factor points seem to be formally homologous to “stimulus areas” and “stimuli,” respectively, and the contravening chains of the present theory essentially mirror the “soritical” sequences for comparative judgments, so that the proof of Theorem 5.11 below is almost identical to that of Lemma 3.3 of Dzhafarov and Dzhafarov (2010).
- ^One can easily generalize this reasoning to show that every chain
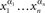 with pairwise distinct {α1, … αn} is compliant. As will be apparent from the proof of Theorem 5.11, however, in the present development we should only be concerned with n = 3.
with pairwise distinct {α1, … αn} is compliant. As will be apparent from the proof of Theorem 5.11, however, in the present development we should only be concerned with n = 3.
References
Diederich, A., and Busemeyer, J. R. (2003). Simple matrix methods for analyzing diffusion models of choice probability, choice response time and simple response time. J. Math. Psychol. 47, 304–322.
Dzhafarov, E. N. (1997). “Process representations and decompositions of response times,” in Choice, Decision and Measurement: Essays in Honor of R. Duncan Luce, ed. A. A. J. Marley (New York: Erlbaum), 255–278.
Dzhafarov, E. N. (1999). Conditionally selective dependence of random variables on external factors. J. Math. Psychol. 43, 123–157.
Dzhafarov, E. N. (2001). Unconditionally selective dependence of random variables on external factors. J. Math. Psychol. 45, 421–451.
Dzhafarov, E. N. (2003). Selective influence through conditional independence. Psychometrika 68, 7–26.
Dzhafarov, E. N., and Dzhafarov, D. D. (2010). Sorites without vagueness II: Comparative sorites. Theoria 76, 25–53.
Dzhafarov, E. N., and Gluhovsky, I. (2006). Notes on selective influence, probabilistic causality, and probabilistic dimensionality. J. Math. Psychol. 50, 390–401.
Dzhafarov, E. N., Schweickert, R., and Sung, K. (2004). Mental architectures with selectively influenced but stochastically interdependent components. J. Math. Psychol. 48, 51–64.
Kujala, J. V., and Dzhafarov, E. N. (2008). Testing for selectivity in the dependence of random variables on external factors. J. Math. Psychol. 52, 128–144.
Lazarsfeld, P. F. (1965). “Latent structure analysis,” in Mathematics and Social Sciences, Vol. 1, eds S. Sternberg, V. Capecchi, T. Kloek, and C. T. Leender (Paris: Mouton), 37–54.
Schweickert, R. (1982). The bias of an estimate of coupled slack in stochastic PERT networks. J. Math. Psychol. 26, 1–12.
Townsend, J. T. (1984). Uncovering mental processes with factorial experiments. J. Math. Psychol. 28, 363–400.
Townsend, J. T., and Schweickert, R. (1989). Toward the trichotomy method of reaction times: Laying the foundation of stochastic mental networks. J. Math. Psychol. 33, 309–327.
Keywords: external factors, joint distribution, probabilistic causality, selective influence, systems of random variables, stochastic dependence, stochastically unrelated
Citation: Dzhafarov EN and Kujala JV (2010) The joint distribution criterion and the distance tests for selective probabilistic causality. Front. Psychology 1:151 doi: 10.3389/fpsyg.2010.00151
Received: 08 July 2010;
Paper pending published: 26 July 2010;
Accepted: 21 August 2010;
Published online: 17 September 2010
Edited by:
Hans Colonius, Carl von Ossietzky Universitaet Oldenburg, GermanyReviewed by:
Hans Colonius, Carl von Ossietzky Universitaet Oldenburg, GermanyAli Ünlü, University of Dortmund, Germany
Copyright: © 2010 Dzhafarov and Kujala. This is an open-access article subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Ehtibar N. Dzhafarov, Department of Psychological Sciences, Purdue University, 703 Third Street, West Lafayette, IN 47907, USA. e-mail:ZWh0aWJhckBwdXJkdWUuZWR1

