- 1 Center for Cognitive Neuroscience, Duke University, Durham, NC, USA
- 2 Department of Psychology and Neuroscience, Duke University, Durham, NC, USA
- 3 Department of Radiology and Neuroscience, Columbia University, New York, NY, USA
Performance on traditional selective attention tasks, like the Stroop and flanker protocols, is subject to modulation by trial history, whereby the magnitude of congruency (or conflict) effects is often found to decrease following an incongruent trial compared to a congruent one. These “congruency sequence effects” (CSEs) typically appear to reflect a mesh of memory- and attention-based processes. The current study aimed to shed new light on the nature of the attention-based contribution to CSEs, by characterizing the shape of the CSE time-course while controlling for mnemonic influences. Existing attention-based accounts of CSEs are either ambiguous in their predictions of CSE time-courses, or predict CSEs to persist or grow over the post-stimulus/response interval in anticipation of an upcoming stimulus. We gauged CSE time-courses by systematically varying inter-stimulus (Experiment 1) and response-to-stimulus (Experiment 2) intervals across a wide temporal range, in a face–word Stroop task. In spite of an exponential increase in the likelihood of stimulus appearance with increasing interval duration (i.e., an exponential hazard function), results from both experiments showed CSEs to be most pronounced at the shortest intervals, to quickly decay in magnitude with increasing interval length, and to be absent at longer intervals. These data refute the idea that attentional contributions to CSEs remain static over post-stimulus/response intervals and are incompatible with the notion that CSEs reflect expectation-guided preparatory biasing in anticipation of a forthcoming stimulus. The data are compatible, however, with the notion that attentional contributions to CSEs reflect a short-lived, phasic enhancement of attentional set in reaction to processing conflict.
Introduction
The efficiency of attention and response selection processes is strongly affected by our recent interactions with the environment. For example, in the classic color-naming Stroop task (Stroop, 1935; MacLeod, 1991), subjects indicate the print color of a word stimulus whose meaning is either congruent (e.g., the word RED printed in red ink) or incongruent (e.g., the word BLUE printed in red ink) with that color. Performance is reliably slower in the incongruent condition (the Stroop congruency effect), because the necessary disambiguation of the conflicting relevant and irrelevant stimulus features, and their respective response associations, imposes additional attentional processing demands (Cohen et al., 1990; MacLeod, 1991). Importantly, this congruency (or conflict) effect is modulated by trial history, whereby the degree of conflict is often found to be reduced following an incongruent as compared to a congruent stimulus trial (Gratton et al., 1992; for reviews, see Egner, 2007, 2008). However, the precise nature of the mechanisms mediating these congruency sequence effects (CSEs) remains contested.
A major distinction can be drawn between top-down attention-based (Gratton et al., 1992; Botvinick et al., 2001) and bottom-up mnemonic/associational accounts (Mayr et al., 2003; Hommel, 2004; Hommel et al., 2004) for CSEs, although empirical studies aimed at disentangling these proposed sources of the effect have generally fostered the conclusion that both mnemonic and attentional influences contribute to this data pattern (Wühr, 2005; Wühr and Ansorge, 2005; Notebaert et al., 2006; Akcay and Hazeltine, 2007; Egner, 2007; Notebaert and Verguts, 2007; Bugg, 2008; Chen and Melara, 2009; Davelaar and Stevens, 2009). The experiments reported in the current study explicitly controlled for possible contributions of associative effects across successive trials (see Materials and Methods), and we will here therefore forego an in-depth discussion of mnemonic models of CSEs. Rather, the present work aimed to characterize more closely the nature of the attention-based contribution to CSEs. Specifically, we were interested in delineating the typical time-course of CSEs, and relating it to current attention-based models of CSEs.
Two main accounts of attentional influences on CSEs can be distinguished in the current literature, namely, a conflict-driven model (Botvinick et al., 2001) and an expectation-based account (Gratton et al., 1992). The former view casts CSEs as reflecting “conflict adaptation”, the workings of a regulatory mechanism that uses internal processing conflicts as control-recruiting signals in the online regulation of a current task-set. Specifically, the conflict-monitoring model of cognitive control (Botvinick et al., 2001) argues that CSEs are due to conflict (defined as concurrent activation of mutually incompatible stimulus or response representations) that occurs during an incongruent trial triggering a reinforcement of the current task-set. In the Stroop task, this would correspond to enhancing the focus of top-down attention toward the processing of the task-relevant relative to the task-irrelevant stimulus feature (reflecting the current task-set). This conflict-triggered reinforcement of top-down attention following an incongruent trial results in a dampening of the influence of the task-irrelevant stimulus feature on response selection, reflected in the subsequent trial in the shape of improved performance on incongruent trials (due to reduced interference from incongruent task-irrelevant stimulus features) and poorer performance on congruent trials (due to reduced facilitation from congruent task-irrelevant stimulus features), thus producing the CSE.
By contrast, Gratton et al. (1992) have conceptualized CSEs as stemming from specific expectations regarding the congruency of the forthcoming stimulus. According to this view, subjects harbor the expectation that the congruency of an upcoming stimulus will match that of the preceding stimulus (cf. Remington, 1969) and, accordingly, they bias their attentional focus in anticipation of the expected stimulus type. If the stimulus is expected to be congruent, the attentional focus is “loosened” in order to derive the benefit of congruent task-irrelevant stimulus features, which results in fast responses to congruent but slow responses to incongruent stimuli. If an incongruent stimulus is expected, attention is strategically focused more tightly on the task-relevant stimulus feature, speeding up the response to incongruent trials but slowing the response to congruent ones, thus producing the CSE data pattern (Gratton et al., 1992). Under this view then, the CSE is an expression of a proactive process, namely, the strategic preparation for an expected stimulus, and Gratton et al. (1992) have argued that this process is in fact precisely equivalent to the type of preparation that takes place when subjects are explicitly cued about the congruency of a forthcoming stimulus (Experiment 3).
What kind of a time-course of CSEs do these models imply? It is not straightforward to derive the relevant prediction from the conflict-monitoring model, which could be read in two ways. On the one hand, the model describes conflict adaptation as a reactive, quasi-homeostatic process where the reinforcement of top-down attention is an obligatory and immediate consequence of conflict. Pairing this conception with the reasonable assumption that this reinforced attention is subject to temporal decay, one could come to the conclusion that the model predicts CSEs to be of high magnitude at short post-stimulus/response intervals, and to diminish over time thereafter (see also Gao et al., 2009), thus producing a phasic or transient post-stimulus/response CSE. On the other hand, the original computational implementation of the conflict-monitoring model of CSEs simulated conflict-triggered control as decaying not over units of time (or processing cycles) between trials but rather as diminishing across units of trials (Botvinick et al., 2001). According to this conception, the precise amount of time passing between trial n and n + 1 would be irrelevant to the magnitude of CSEs at n + 1, that is, CSE magnitude would remain static across the inter-trial interval. Predictions from the expectation-based model are less ambiguous. Since this model views CSEs as resulting from an active, preparatory process, one would expect the effect to take some time to establish itself, and then to build up (or at least persist) over time in anticipation of the forthcoming stimulus, akin to probabilistic cueing effects in the attention literature (e.g., Sanders, 1971; Muller and Rabbitt, 1989).
Extant relevant data pertaining to CSE time-courses are sparse. While the jittering of inter-trial intervals across a range of a few seconds is standard practice in neuroimaging studies of CSEs (e.g., Egner and Hirsch, 2005a,b; Egner et al., 2007, 2008), their minimum interval length typically lies around 3 s, thus precluding an analysis at shorter ranges. Moreover, previous behavioral studies addressing the time-course of CSEs tested only very few (two) time points, and at vastly different ranges, specifically, 50 vs. 200 ms (Notebaert et al., 2006), and 1,500 vs. 6,000 ms (Wühr and Ansorge, 2005). In order to obtain a finer-grained picture of the time-course of CSEs, we here manipulated stimulus timing in two Stroop-type experiments across a wide temporal range. In the first experiment, we employed a fixed stimulus duration and varied the inter-stimulus interval (ISI) (following Wühr and Ansorge, 2005) as defined by the duration between the offset of the previous stimulus and the onset of the next one, across a range of 500–7,000 ms. In the second experiment, stimulus duration was determined by response time (RT), and we varied the interval between the response to the previous stimulus and the onset of the next stimulus (response-to-stimulus interval, RSI) (following Notebaert et al., 2006), across a range of 500–5,000 ms.
Materials and Methods
Participants
The sample consisted of 20 healthy subjects, 10 per experiment (Experiment 1: six males, four females, mean age = 23.7; Experiment 2: five males, five females, mean age = 18.7). Subjects had been screened via self-report to exclude participants with a history of serious medical illness (including psychiatric diagnoses), previous or current drug abuse, and current usage of drugs that might affect their alertness levels. Inclusion criteria consisted of fluent English language proficiency and normal or corrected-to-normal vision. Subjects were recruited by flyer and email advertisement, and performed the tasks in exchange for course credits or a payment of $10. The study was approved by the institutional review board of Duke University (Pro00018918).
Apparatus and Stimuli
For both experiments, stimulus presentation and response data collection were accomplished using Presentation software (NeuroBehavioral Systems, Albany, CA, USA) and Dell Optiplex 960 personal computers, running on Intel Dual Core processors. Subjects viewed stimuli displayed on Dell 19' LCD monitors, while having their chin placed on a table-clamp chinrest (Veatch Ophthalmic Instruments, Tempe, AZ, USA) to assure a constant distance between their eyes and the monitor (at ∼60 cm). Responses were collected via a Dell QWERTY US keyboard, with the right index finger response collected from the “.” key, and the right middle finger response collected from the “/” key. Data were analyzed using SPSS statistical software (SPSS Inc., Chicago, IL, USA). The stimulus set consisted of 24 photographic, black and white images of male and female faces (12 for each gender). Each face image was paired with a congruent and an incongruent gender label (“male”, “female”) that could be either printed in lower or upper case (in Ariel font), resulting in a total of 96 unique stimuli (see Figure 1 for two examples). The gender labels were presented in red ink and placed across the center of the faces (the bridge of the nose) without obscuring the eyes or mouth regions of the face stimuli. The faces subtended circa 9° of visual angle vertically and 6° horizontally. The gender labels subtended circa 2° of visual angle vertically, and 5–7° horizontally.

Figure 1. Example stimuli and trial sequence. A congruent stimulus on trial n is followed by an incongruent stimulus on trial n + 1, resulting in a CI (congruent–incongruent) trial at n + 1. This example CI trial is associated with a response repetition, while both relevant (face) and irrelevant (gender label) stimulus features change across trials.
Procedure and Design
In both experiments, subjects performed a gender face–word Stroop task (Egner et al., 2008). On each trial, participants were presented with a compound face–word stimulus, consisting of a face and an overlaid gender label (Figure 1), where the relation between the task-relevant face stimulus and the task-irrelevant gender label could be either congruent (e.g., a male face with a “male” label) or incongruent (e.g., a male face with a “female” label). Subjects were required to categorize, as fast as possible while maintaining high accuracy, whether the face stimulus depicted a male or female person, by means of a button press (using index and middle fingers of the right hand). In Experiment 1, the stimuli were on screen for a fixed duration of 1,000 ms, whereas for Experiment 2, stimuli were shown until a response was recorded. Each stimulus was followed by variable intervals during which a small central fixation cross (circa 0.3° × 0.3° of visual angle) was displayed. In Experiment 1, the interval timing was determined by the ISI (offset-to-onset), which was varied across 10 levels (500, 1,000, 1,500, 2,000, 2,500, 3,000, 4,000, 5,000, 6,000, and 7,000 ms). In Experiment 2, the interval timing was manipulated as a function of RSI, varying across 10 RSI levels (500, 1,000, 1,500, 2,000, 2,500, 3,000, 3,500, 4,000, 4,500, and 5,000 ms). In Experiment 1, each subject performed 16 blocks of 101 trials, in Experiment 2, each subject performed 8 blocks of 101 trials. The different ISI (or RSI) levels were drawn in random order from a uniform distribution. It is noteworthy that the latter results in an exponential increase in the hazard function (the likelihood of the stimulus appearing at the next interval) with increasing interval length.
One motivation for conducting one experiment manipulating ISI and another experiment manipulating RSI duration, beyond the attempt to relate the current results to previous studies (Wühr and Ansorge, 2005; Notebaert et al., 2006), is that, a priori, it is not certain which of these interval variables will be more effective in modulating CSE magnitudes. In addition, the two approaches incorporate opposing biases with respect to slow and fast responses. Specifically, if one manipulates ISI duration, then faster trials (e.g., congruent ones) end up being associated with a longer RSI than slower trials (e.g., incongruent ones). On the other hand, if one manipulates RSI duration, then faster trials (e.g., congruent ones) will be associated with a shorter ISI than slower trials (e.g., incongruent ones). We reasoned that performing both types of manipulation guards against the possibility of our conclusions being biased by the particular choice of interval measure.
Stimuli were presented in pseudo-random sequences that obeyed the following constraints. First, half of all trials were congruent, and half incongruent, and the stimulus sequences for each block produced equal numbers of congruent stimuli preceded by a congruent stimulus (CC trials), incongruent stimuli preceded by a congruent stimulus (CI trials), congruent stimuli preceded by an incongruent stimulus (IC trials), and incongruent stimuli preceded by an incongruent stimulus (II trials) (after dropping the first trial in each block). Second, each of these trial types was paired equally often with each ISI (or RSI) level. This resulted in equal cell counts across a three-factor 2 × 2 × 10 (previous trial congruency × current trial congruency × ISI/RSI level) repeated-measures factorial design. Third, each cell in the design was associated with equal numbers of male and female face target stimuli. Fourth, individual face stimuli (i.e., the task-relevant stimulus feature) were never repeated across successive trials, and gender labels (i.e., the task-irrelevant stimulus feature) always alternated between lower and upper case lettering from trial to trial (irrespective of whether the gender label category switched or not). This ensured that no exact visual stimulus features were ever repeated across successive trials. Finally, each condition in the factorial design was associated with a response repetition on half of the trials, and a response switch for the other half. In the lingo of associational accounts for CSEs (Hommel et al., 2004), this stimulus sequencing ensured that each condition in our design consisted of 50% “complete alternations” (all stimulus features and the response switch across trials) and 50% “partial repetitions” (all stimulus features switch but the response repeats across trials). Figure 1 depicts an example of a CI partial repetition trial. Thus, potential associational influences on CSEs were balanced out between all of the conditions of interest in this design.
It should be noted though that the control over associational sequence effects at the level of specific stimulus features does not necessarily preclude the possibility of similar effects occurring at the level of stimulus categories (e.g., Schuch and Koch, 2004; Egner and Hirsch, 2005a), for example, the incurrence of categorical “partial repetition” costs for response repetitions accompanied by changes in stimulus category (male vs. female). However, such categorical priming or binding effects are unlikely to confound CSEs in the current study. First, because the task is categorical in nature, a change in the relevant, target stimulus feature category (face gender) is always associated with a change in response, and a repetition of category is always associated with a response repetition, thus precluding partial repetitions. Moreover, as noted above, the incidence of response (and thus target feature) repetitions and alternations were evenly distributed within each of our conditions of interest. With respect to the relation between categorical transitions of the irrelevant stimulus feature (the word labels) and response transitions, if such effects existed, they would bias against obtaining a CSE in the current experiment, because such “irrelevant partial repetitions” of category never occur in CC trials, occur on average in 25% of CI and IC trials, and in 50% of II trials. These hypothetical RT costs would thus produce a pattern of results counter-productive to the CSE effect (where II trials are faster than CI trials). Potential priming effects involving the irrelevant stimulus category transitions would therefore not be able to mimic CSEs in the current experiment, but we cannot exclude the possibility that they affect the data per se.
Analysis
Data analyses focused on mean RTs, being the most commonly employed indicator of CSEs in the literature. Accuracy in both experiments was near ceiling (Experiment 1: 96.1%, SD = 2.1; Experiment 2: 97.6%, SD = 1.3), and error rates were considered only for ruling out speed-accuracy trade-offs as mediating the RT results. For each subject, mean RT was computed for each condition of the design. Error trials and trials immediately following an error were excluded from the RT averaging. Trials where responses were >2 SDs removed from the subject’s grand mean RT were also removed from the averaging process. These procedures resulted in the removal of <3% of RT data points in both experiments. For the sake of statistical reliability and clarity of presentation, we temporally smoothed the ISI/RSI factor, by averaging adjacent pairs of intervals together (i.e., we averaged intervals 1 and 2, intervals 3 and 4, etc.), thus resulting in five time bins in each experiment. Mean RT data were analyzed in 2 × 2 × 5 (previous trial congruency × current trial congruency × ISI/RSI interval) repeated measures ANOVAs, followed by planned pair-wise comparisons between CSE scores ([CI − CC] − [II − IC]) at different time bins, and planned previous × current trial congruency analyses within each time bin.
Results
Experiment 1 – ISI Manipulation
Experiment 1 manipulated the time interval between the offset of the previous stimulus and the onset of the forthcoming stimulus (ISI), without consideration of the timing of the subjects’ response to the stimuli, and with a fixed stimulus duration of 1 s, akin to the approach taken by Wühr and Ansorge (2005). Analyzing the RT data, a three-way 2 × 2 × 5 (previous trial congruency × current trial congruency × ISI) repeated measures ANOVA revealed a standard interference effect, reflected in a main effect of current trial congruency (F[1, 9] = 15.8, p < 0.005), due to slower RTs for incongruent (mean = 597 ms, SD = 58) than for congruent trials (mean = 581 ms, SD = 55). The classic CSE was also observed (Figure 2A), as evidenced by a significant previous × current trial congruency interaction effect (F[1, 9] = 16.5, p < 0.005) that was due to smaller conflict scores following incongruent trials (mean = 6 ms) than following congruent trials (mean = 23 ms).
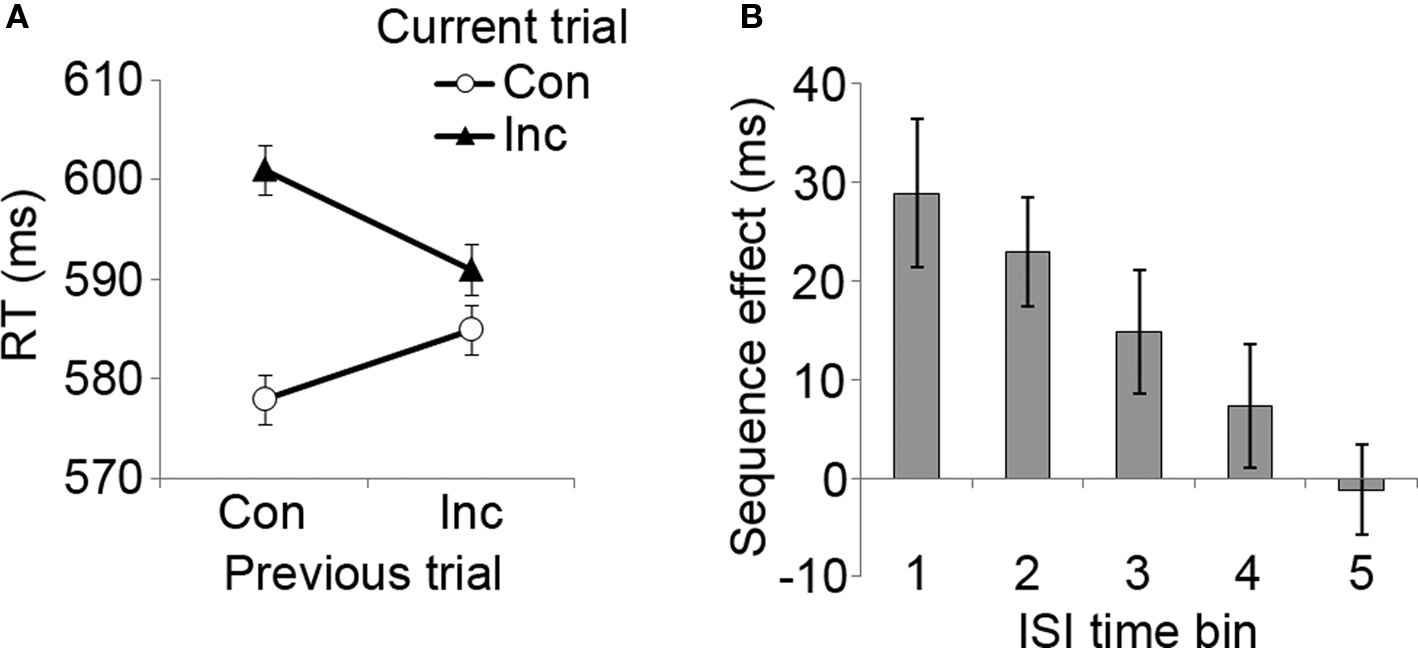
Figure 2. Congruency sequence effects as a function of ISI length. (A) Mean RT data as a function of previous and current trial congruency, displaying the classic CSE data pattern. Con, congruent trial; Inc, incongruent trial. (B) The magnitude of the CSE ([CI − CC] − [II − IC]) as a function of ISI duration (positive values indicate the magnitude of RT reduction following an incongruent compared to a congruent trial). ISI time bins: 1 = 500–1,000 ms, 2 = 1,500–2,000 ms, 3 = 2,500–3,000 ms, 4 = 4,000–5,000 ms, 5 = 6,000–7,000 ms. Error bars reflect mean standard errors (after Masson and Loftus, 2003) for CSE interaction effects.
Importantly, we also observed a three-way previous × current trial congruency × ISI interaction effect (F[4, 36] = 4.7, p < 0.005). As can be seen in Figure 2B, this interaction appeared to stem from the fact that the CSE steadily declined with increasing ISI length (polynomial linear trend, F[1, 9] = 10.0, p < 0.05). A significant CSE was present at time bin 1 (500–1,000 ms, F[1, 9] = 14.7, p < 0.005), bin 2 (1,500–2,000 ms, F[1, 9] = 17.6, p < 0.005), and bin 3 (2,500–3,000 ms, F[1, 9] = 5.6, p < 0.05), but the effect was absent during time bins 4 (4,000–5,000 ms) and 5 (6,000–7,000 ms). Pair-wise t-tests between CSE scores showed that the effect was significantly larger at time bin 1 than at bin 3 (t[9] = 2.5, p < 0.05), bin 4 (t[9] = 2.4, p < 0.05), and bin 5 (t[9] = 2.7, p < 0.05). The effect was also stronger at time bin 2 than at bin 4 (marginally, t[9] = 2.1, p = 0.07) and bin 5 (t[9] = 3.7, p < 0.01). Finally, the ANOVA also detected an unexpected interaction between previous trial congruency and ISI (F[4, 36] = 4.1, p < 0.01), which appeared to be attributable to generally faster RTs following incongruent trials in time bin 1 (t[9] = 5.4, p < 0.001), accompanied by an absence of such effects in all of the later time intervals. In summary, the RT data from Experiment 1 show that the CSE steadily diminishes with increasing ISI.
In order to ascertain that the RT CSE, and its variation across ISI intervals, was not mediated by an inverse tendency for response accuracy (i.e., a speed-accuracy trade-off), we correlated the RT CSE magnitude (i.e., the relative reduction in conflict following incongruent as compared to congruent trials) at each ISI with the corresponding effect in error rates across subjects. These correlations were either non-significant or positive (time bin 1: r[10] = 0.79, p < 0.01; time bin 3: r[10] = 0.62, p = 0.06), meaning that subjects with a higher reduction in RT congruency effects following an incongruent trial tended to also display a greater reduction in the error rate congruency effect. This pattern runs opposite to a speed-accuracy trade-off, but is in line with many previous studies documenting that CSEs in RT are typically accompanied by corresponding effects in accuracy (Egner, 2007).
Experiment 2 – RSI Manipulation
In Experiment 2, we aimed to establish whether the data pattern observed in Experiment 1 would be robust to some procedural modifications that would bring the experimental design in line with the approach taken by Notebaert et al. (2006). Specifically, instead of manipulating ISI and having a fixed stimulus duration, Experiment 2 displayed stimuli until a response occurred, and varied the interval between the response and the forthcoming stimulus (RSI), thus tying the timing intervals directly to subjects’ responses. Analyzing the RT data, a three-way 2 × 2 × 5 (previous trial congruency × current trial congruency × RSI) repeated measures ANOVA revealed a standard interference effect of current trial congruency (F[1, 9] = 10.3, p < 0.05), as incongruent trials were associated with slower RT (mean = 767, SD = 158) than congruent ones (mean = 697, SD = 113). The overall CSE was only marginally significant (previous × current trial congruency interaction: F[1, 9] = 3.3, p = 0.10), with numerically smaller conflict scores following incongruent (mean = 80 ms) than congruent trials (mean = 60 ms) (see Figure 3A).
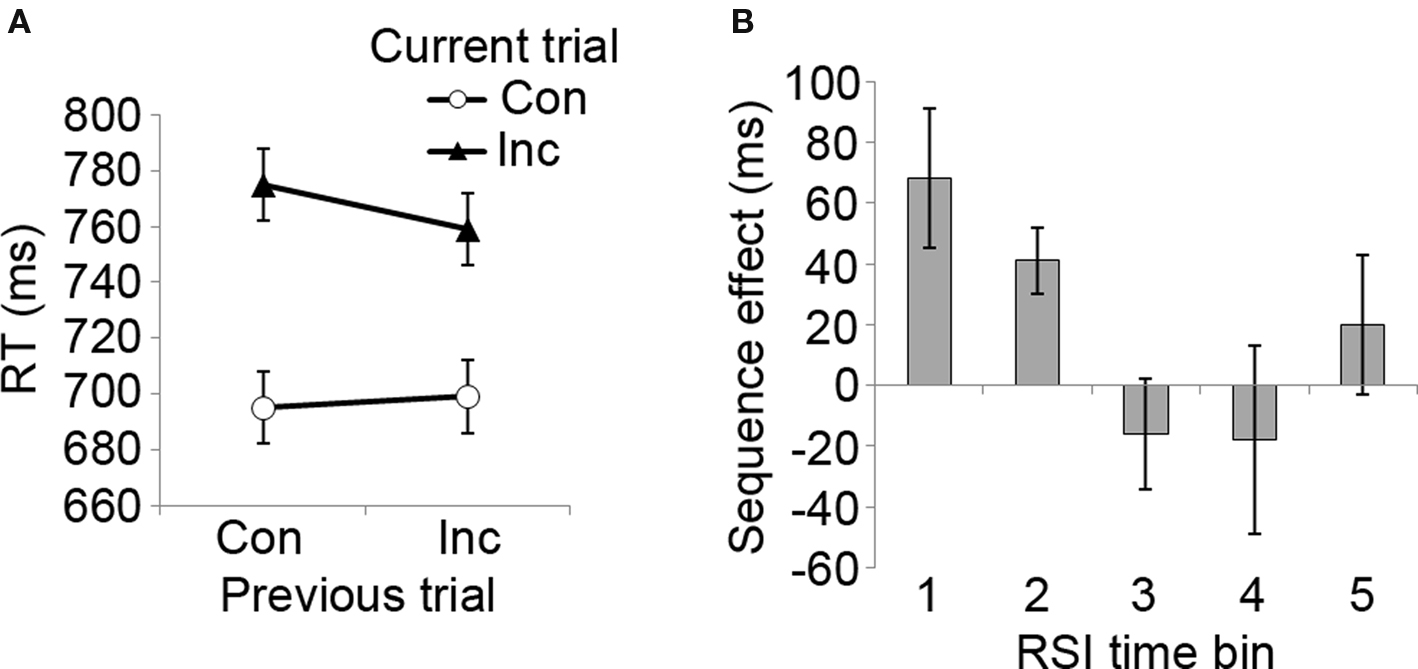
Figure 3. Congruency sequence effects as a function of RSI length. (A) Mean RT data as a function of previous and current trial congruency, displaying the classic CSE data pattern. Con, congruent trial; Inc, incongruent trial. (B) The magnitude of the CSE ([CI − CC] − [II − IC]) as a function of RSI duration (positive values indicate the magnitude of RT reduction following an incongruent compared to a congruent trial). RSI time bins: 1 = 500–1,000 ms, 2 = 1,500–2,000 ms, 3 = 2,500–3,000 ms, 4 = 3,500–4,000 ms, 5 = 4,500–5,000 ms. Error bars reflect mean standard errors (after Masson and Loftus, 2003) for CSE interaction effects.
Importantly, there was a significant three-way interaction between previous and current trial congruency, and RSI (F[4, 36] = 2.77, p < 0.05). As displayed in Figure 3B, CSEs varied with RSI, being present at shorter but not at longer RSIs. Significant previous × current trial congruency interactions were found at RSI time bin 1 (500–1,000 ms, F[1, 9] = 5.6, p < 0.05) and time bin 2 (1,500–2,000 ms, F[1, 9] = 13.8, p < 0.01), but not at time bins 3 (2,500–3,000 ms), 4 (3,500–4,000 ms), and 5 (4,500–5,000 ms). Pair-wise t-tests between CSE scores showed that the effect was significantly larger at time bin 1 than at bin 3 (t[9] = 2.6, p < 0.05) and (marginally) bin 4 (t[9] = 2.1, p = 0.06), and that the effect was larger at bin 2 than bin 3 (t[9] = 2.9, p < 0.05). Given the visual impression in Figure 3B that CSEs may have tended to increase around bin 5, we decomposed this bin into its constituents (4,500 and 5,000 ms RSI bins) and tested each of them for CSEs. Neither RSI bin was associated with significant CSEs, however (both p values >0.4). Finally, similar to Experiment 1, an interaction effect was also observed between previous trial congruency and RSI interval (F[4, 36] = 3.23, p < 0.05), which was related to a general speed-up in RT following incongruent trials in time bin 1 (t[9] = 2.3, p < 0.05) and a general slow-sown following incongruent trials in time bin 2 (t[9] = 2.8, p < 0.05). To summarize, RT data from Experiment 2 show that CSEs decrease with increasing RSI length, similar to the data pattern observed for varying ISIs in Experiment 1.
As in Experiment 1, we correlated RT and error rate congruency sequent effect scores across subjects to rule out speed-accuracy trade-offs as a source of the RT findings. No significant associations were detected.
Discussion
To characterize the shape of the time-course of (attention-mediated) CSEs, we manipulated ISI (Experiment 1) and RSI (Experiment 2) duration in a Stroop-type task, across a relatively large temporal range, and measured how CSE magnitude varied with post-stimulus/response interval duration. The results were clear-cut, in that both experiments produced interaction effects between the CSE (the previous × current trial congruency interaction) and the ISI/RSI factor, with significant CSEs evident at the shortest post-stimulus/response intervals, but not at longer intervals. These results are not commensurate with the original computational implementation of the conflict-based account of CSEs, where adaptation effects were modeled as decreasing as a function of trials rather than as a function of time between trials (Botvinick et al., 2001). Similarly, the current data speak against the view that CSEs are a reflection of a proactive preparatory process based on expectations (Gratton et al., 1992), because one would assume the effects of such an anticipatory process to grow (or at least persist) over the post-stimulus/response interval. However, our results are compatible with a version of conflict adaptation where the decay of the adaptation effect is not trial-bound but time-sensitive and fairly steep. This view of conflict adaptation would indeed predict CSEs to be most pronounced shortly after the control-triggering conflict event, and to subsequently decay over time, irrespective of the appearance of a subsequent stimulus. This type of temporal dynamic of conflict-induced control processes has in fact recently been used to successfully model some aspects of first- and higher-order sequential effects in non-conflict 2-alternative forced choice (2AFC) task data (Gao et al., 2009).
While the conflict-monitoring model views CSEs explicitly as an expression of across-trial processing adjustments (Botvinick et al., 2001), it should be noted that the current results are also compatible with the possibility that conflict adaptation occurs within trial n-1 and it is the steadily decaying aftereffects of such within-trial control processes that produce the CSE on trial n. Some recent work has produced support for the basic existence of rapid within-trial processing adjustments (Taylor et al., 2007; Appelbaum et al., in press), and has suggested that these may be mediated by principally distinct mechanisms than those that underpin across-trial adjustments (Boy et al., 2010). However, whether CSEs are an expression of the former or the latter currently remains an open question.
In addition to these findings directly pertinent to our a priori hypotheses, an unexpected interaction effect involving previous trial congruency and ISI/RSI was found in both experiments, which was due to faster mean RTs following an incongruent trial at the shortest post-stimulus/response intervals only. We speculate that this effect could feasibly reflect a very short-lived increase in arousal accompanying the processing of a conflicting stimulus (cf. Verguts and Notebaert, 2009), which then translates into a brief non- selective speed-up of RTs at short post-stimulus/response intervals.
With respect to an expectation-based, preparatory account of CSEs, it should be pointed out that our experimental design was in fact quite favorable to the possibility of expectation-mediated improvements in performance at longer intervals, because the uniform distribution of ISI/RSI intervals produced an exponentially growing hazard function across the post-stimulus/response intervals. In other words, the likelihood of stimulus occurrence grew exponentially with each passing interval where no stimulus was presented. There was in fact some evidence that subjects did form expectations in this regard, as mean RT in Experiment 2 (though not in Experiment 1) displayed the expected speed-up (numerically) with increasing interval duration (mean RT being 754, 730, 730, 731, and 717 ms for bins 1–5, respectively). Nevertheless, we did not detect any evidence that subjects made strategic use of this temporal profile with respect to the implementation of purported anticipatory attentional biasing as reflected in CSE magnitude. The lack of a positive correlation between the CSE magnitude and RSI duration in the current study stands in stark contrast with findings in fairly similar contexts, where the effects of expectation have been clearly observed to build up over post-stimulus/response intervals. For instance, in 2AFC tasks, “subjective expectancy” effects for the continuation of a particular higher-order stimulus sequence increase reliably with RSI duration (e.g., Soetens et al., 1985). These findings further support the conclusion that expectations are unlikely to be the prime mediator of CSEs. In their rejection of the expectation-based account of CSEs, the present data are also in line with other recent findings that suggest the processes mediating CSEs are not equivalent to the processes that mediate the effects of cue-induced expectations. Specifically, Alpay et al. (2009) demonstrated that explicit cueing of congruency, on the one hand, and congruency sequence per se, on the other hand, produce additive effects on performance. This raises substantial doubts concerning the validity of the central assumption of the expectation-based account, that CSEs are mediated by the same processes that underlie the effects of explicitly cueing stimulus congruency (Gratton et al., 1992).
As noted in the Section “Introduction”, previous studies have not explored the time-course of CSEs in any great detail. Notebaert et al. (2006) varied RSIs between 50 and 200 ms and reported a significant CSE only at the longer interval, concluding that the control processes presumed to mediate the CSE require more than 50 ms following response execution to be implemented but to be already effective at 200 ms post-response. Wühr and Ansorge (2005) varied stimulus onset asynchrony between 1,500 and 6,000 ms, with a fixed stimulus duration of 250 ms, corresponding to ISI lengths of 1,250 and 5,750 ms. These authors reported higher CSE magnitudes at the shorter than at the longer ISI, but still observed a CSE at an ISI of 5,750 ms. The latter finding differs from data observed in the current study, where significant CSEs were not detected beyond a 2,500–3,000 ms ISI. This could be due to procedural differences between studies, including the fact that Wühr and Ansorge (2005) used a Simon task. More interestingly though, this could alternatively suggest that, while the general shape of the CSE time-course may always reflect a decline with increasing length of the post-stimulus/response interval (excepting extremely short intervals, cf. Notebaert et al., 2006), the exact rate of decay may be context-dependent. In particular, it appears likely that the rate of decay of the CSE would vary as a function of the mean duration and overall distribution of ISI/RSI intervals. That the decay rate of CSEs across post-stimulus/response intervals is not constant across experiments is certainly evident from the findings of significant mean CSEs in many neuroimaging studies that employed intervals in the 3,000–6,000 ms range (e.g., Egner and Hirsch, 2005a,b; Egner et al., 2007, 2008), a range at which we did not detect significant CSEs in the current study. To explore this issue a little further, we re-analyzed behavioral data from a previous neuroimaging study using a highly similar face–word gender Stroop task and a uniform distribution of ISIs of 4,000, 5,000, and 6,000 ms (Egner et al., 2008). While CSE magnitude decreased numerically with interval duration, the interaction involving ISI and CSE magnitude did not reach significance. However, since imaging studies typically only involve a very limited range of intervals and relatively low trial counts within each interval, they do of course not provide an ideal vehicle for testing ISI/RSI effects on CSEs. Thus, the exact way in which the temporal decay function of CSEs might vary with different interval distributions, and how such a temporal-context modulation of conflict-triggered control might be implemented neurally and computationally, pose interesting questions for future research. An alternative possibility that should also be entertained in this regard is that short-lived “reactive” CSEs that immediately follow a conflicting event might be ubiquitous, but that the presence of CSEs at longer intervals might be reliant on a different mechanism, such as the ability to maintain an attentional set over time, which may vary more widely across participants as well as between experimental contexts.
While the overall pattern of results was quite similar across the two present experiments, there were also some notable differences. First, overall RTs, congruency effects, and standard deviations were much larger in Experiment 2. Second, in Experiment 1, significant CSEs were evident up to time bin 3, corresponding to ISI durations of 2,500–3,000 ms, whereas in Experiment 2, effects were only evident up until time bin 2, that is, an RSI duration of 1,500–2,000 ms. In order to compare these data more directly, we can infer the mean effective RSIs from the ISI data in Experiment 1. Mean RTs across the different time bins in Experiment 1 were very homogenous, ranging from 586 to 593 ms. Given a fixed stimulus duration of 1 s, followed by the ISIs, the mean RSIs for the different time bins in Experiment 1 were therefore approximately 400 ms longer than those of corresponding bins in Experiment 2. While an overall increase in RT, conflict, and variability in Experiment 2 could thus perhaps be expected at the shortest RSI level (being a fair bit shorter than the shortest RSIs in Experiment 1), there is no obvious reason for why responses would be slower and noisier at the longer intervals, although higher standard deviations could at least in part stem from a smaller trial count in Experiment 2. We can only speculate that these differences may have primarily arisen due to motivational differences between our samples; participants in Experiment 1 were predominantly graduate students performing for cash payment, whereas the subject pool in Experiment 2 consisted of undergraduate students participating in exchange for course credits.
To conclude, while controlling for differential mnemonic effects, we characterized the shape of the time-course of CSEs, in order to evaluate hypotheses derived from different accounts of top-down attentional contributions to the CSE. Results across two experiments indicated that CSEs are most pronounced at short post-stimulus/response intervals, and decay (and disappear) thereafter. We interpret these data as incommensurate with a trial-bound, static version of conflict adaptation, and with an expectation-based account of CSEs, but as compatible with a “phasic” version of conflict adaptation, where processing conflicts elicit a short-lived reinforcement of top-down attentional set.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank two reviewers for insightful comments. This work was supported by NIMH R01 MH087610-01 (Tobias Egner).
References
Akcay, C., and Hazeltine, E. (2007). Conflict monitoring and feature overlap: two sources of sequential modulations. Psychon. Bull. Rev. 14, 742–748.
Alpay, G., Goerke, M., and Sturmer, B. (2009). Precueing imminent conflict does not override sequence-dependent interference adaptation. Psychol. Res. 73, 803–816.
Appelbaum, L. G., Smith, D. V., Boehler, C. N., Chen, W. D., and Woldorff, M. G. (in press). Rapid modulation of sensory processing induced by stimulus conflict. J. Cogn. Neurosci.
Botvinick, M. M., Braver, T. S., Barch, D. M., Carter, C. S., and Cohen, J. D. (2001). Conflict monitoring and cognitive control. Psychol. Rev. 108, 624–652.
Boy, F., Husain, M., and Sumner, P. (2010). Unconscious inhibition separates two forms of cognitive control. Proc. Natl. Acad. Sci. U.S.A. 107, 11134–11139.
Bugg, J. M. (2008). Opposing influences on conflict-driven adaptation in the Eriksen flanker task. Mem. Cogn. 36, 1217–1227.
Chen, S., and Melara, R. D. (2009). Sequential effects in the Simon task: conflict adaptation or feature integration? Brain Res. 1297, 89–100.
Cohen, J. D., Dunbar, K., and McClelland, J. L. (1990). On the control of automatic processes: a parallel distributed processing account of the Stroop effect. Psychol. Rev. 97, 332–361.
Davelaar, E. J., and Stevens, J. (2009). Sequential dependencies in the Eriksen flanker task: a direct comparison of two competing accounts. Psychon. Bull. Rev. 16, 121–126.
Egner, T. (2007). Congruency sequence effects and cognitive control. Cogn. Affect. Behav. Neurosci. 7, 380–390.
Egner, T. (2008). Multiple conflict-driven control mechanisms in the human brain. Trends Cogn. Sci. 12, 374–380.
Egner, T., Delano, M., and Hirsch, J. (2007). Separate conflict-specific cognitive control mechanisms in the human brain. Neuroimage 35, 940–948.
Egner, T., Etkin, A., Gale, S., and Hirsch, J. (2008). Dissociable neural systems resolve conflict from emotional versus nonemotional distracters. Cereb. Cortex 18, 1475–1484.
Egner, T., and Hirsch, J. (2005a). Cognitive control mechanisms resolve conflict through cortical amplification of task-relevant information. Nat. Neurosci. 8, 1784–1790.
Egner, T., and Hirsch, J. (2005b). The neural correlates and functional integration of cognitive control in a Stroop task. Neuroimage 24, 539–547.
Gao, J., Wong-Lin, K. F., Holmes, P., Simen, P., and Cohen, J. D. (2009). Sequential effects in two-choice reaction time tasks: decomposition and synthesis of mechanisms. Neural Comput. 21, 2407–2436.
Gratton, G., Coles, M. G., and Donchin, E. (1992). Optimizing the use of information: strategic control of activation of responses. J. Exp. Psychol. Gen. 121, 480–506.
Hommel, B. (2004). Event files: feature binding in and across perception and action. Trends Cogn. Sci. 8, 494–500.
Hommel, B., Proctor, R. W., and Vu, K. P. (2004). A feature-integration account of sequential effects in the Simon task. Psychol. Res. 68, 1–17.
MacLeod, C. M. (1991). Half a century of research on the Stroop effect: an integrative review. Psychol. Bull. 109, 163–203.
Masson, M. E. J., and Loftus, G. R. (2003). Using confidence intervals for graphically based data interpretation. Can. J. Exp. Psychol. 57, 203–220.
Mayr, U., Awh, E., and Laurey, P. (2003). Conflict adaptation effects in the absence of executive control. Nat. Neurosci. 6, 450–452.
Muller, H. J., and Rabbitt, P. M. (1989). Reflexive and voluntary orienting of visual attention: time course of activation and resistance to interruption. J. Exp. Psychol. Hum. Percept. Perform. 15, 315–330.
Notebaert, W., Gevers, W., Verbruggen, F., and Liefooghe, B. (2006). Top-down and bottom-up sequential modulations of congruency effects. Psychon. Bull. Rev. 13, 112–117.
Notebaert, W., and Verguts, T. (2007). Dissociating conflict adaptation from feature integration: a multiple regression approach. J. Exp. Psychol. Hum. Percept. Perform. 33, 1256–1260.
Remington, R. J. (1969). Analysis of sequential effects in choice reaction times. J. Exp. Psychol. 82, 250–257.
Sanders, A. F. (1971). Probabilistic advance information and the psychological refractory period. Acta Psychol. 35, 128–137.
Schuch, S., and Koch, I. (2004). The cost of changing the representation of action: response repetition and response-response compatibility in dual tasks. J. Exp. Psychol. Hum. Percept. Perform. 30, 566–582.
Soetens, E., Boer, L.C., and Hueting, J. E. (1985). Expectancy or automatic facilitation? Separating sequential effects in two-choice reaction time. J. Exp. Psychol. Hum. Percept. Perform. 11, 598–616.
Stroop, J. R. (1935). Studies of interference in serial verbal reactions. J. Exp. Psychol. 18, 643–662.
Taylor, P. C., Nobre, A. C., and Rushworth, M. F. (2007). Subsecond changes in top down control exerted by human medial frontal cortex during conflict and action selection: a combined transcranial magnetic stimulation electroencephalography study. J. Neurosci. 27, 11343–11353.
Verguts, T., and Notebaert, W. (2009). Adaptation by binding: a learning account of cognitive control. Trends Cogn. Sci. 13, 252–257.
Wühr, P. (2005). Evidence for gating of direct response activation in the Simon task. Psychon. Bull. Rev. 12, 282–288.
Keywords: cognitive control, congruency sequence effect, conflict adaptation, attention, expectation
Citation: Egner T, Ely S and Grinband J (2010) Going, going, gone: characterizing the time-course of congruency sequence effects. Front. Psychology 1:154. doi: 10.3389/fpsyg.2010.00154
Received: 27 July 2010;
Paper pending published: 05 August 2010;
Accepted: 25 August 2010;
Published online: 16 September 2010.
Edited by:
Wery P. M. van den Wildenberg, University of Amsterdam, NetherlandsReviewed by:
Thomas Kleinsorge, Leibniz Research Centre for Working Environment and Human Factors, GermanyMarco Steinhauser, University of Konstanz, Germany
Copyright: © 2010 Egner, Ely and Grinband. This is an open-access article subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Tobias Egner, Center for Cognitive neuroscience, Duke University, LSRC Box 90999, Durham, NC 27708, USA. e-mail:dG9iaWFzLmVnbmVyQGR1a2UuZWR1


