- Department of Measurement, Statistics & Evaluation, University of Maryland, College Park, MD, USA
The current study assessed the viability of mixture confirmatory factor analysis (CFA) for measurement invariance testing by evaluating the ability of mixture CFA models to identify differences in factor loadings across populations with identical mean structures. Using simulated data from a model with known parameters, convergence rates, parameter recovery, and the power of the likelihood-ratio test were investigated as impacted by sample size, latent class proportions, magnitude of factor loading differences, percentage of non-invariant factor loadings, and pattern of non-invariant factor loadings. Results suggest that mixture CFA models may be a viable option for testing the invariance of factor loadings; however, without differences in latent means and measurement intercepts, results suggest that larger sample sizes, more non-invariant factor loadings, and larger amounts of heterogeneity are needed to successfully estimate parameters and detect differences across latent classes.
Introduction
Modeling and testing for heterogeneity in the relationship between latent variables and their continuous measured indicator variables in cross-sectional confirmatory factor analysis (CFA) models is of interest when the assumption of a homogeneous measurement scale may not be tenable. Measurement invariance testing is both practically and theoretically important to insure that inferences drawn are about the intended population and that cross-population comparisons are accurate and valid. Validity can be substantially comprised if a measurement instrument is assumed to be invariant across populations that are being compared at the structural level when it truly is not or when inferences about a homogeneous population are drawn from a single-population model using data that is truly derived from two or more populations.
Testing for measurement invariance across known groups using multigroup CFA has been widespread (for summaries of applications see Vandenberg and Lance, 2000; Schmitt and Kuljanin, 2008). However, there may be substantive reasons why it is not tenable to assume that a manifest group is homogeneous with respect to indicator variable performance, particularly when broad groups such as gender or race are used out of convenience or post hoc consideration. For example, early interest in latent sources of measurement heterogeneity included work by French (1965) who hypothesized that factor loading values were influenced by populations of test-takers who differed with respect to their problem-solving skills and abilities. The use of multigroup CFA when manifest groups are not homogeneous may result in incorrect inferences about population heterogeneity or may lead to incorrect parameter estimates in the structural portion of a latent variable model. Alternatively, mixture CFA can be used to incorporate theoretically important unmeasured characteristics to capture heterogeneity and test for measurement invariance across latent classes.
In some disciplines, manifest groups may be sufficient for modeling heterogeneity and statistical analyses can verify substantive theories about population differences. For example, sources of self-esteem are hypothesized to be different for Western and Eastern cultures implying that items on a questionnaire translated from English to Chinese may have weaker factor loadings (Chen, 2008). However, oftentimes manifest groups are used in empirical research as proxies for other more nuanced characteristics that are not included in a dataset. The psychometric insufficiency of using manifest groups to define sources of measurement heterogeneity has been discussed in the social and behavioral sciences, for example, when modeling data from psychological instruments (e.g., Muthén, 1989), marketing research (e.g., Moore, 1980) and test items (e.g., Mislevy and Verhelst, 1990).
In educational testing, latent classes can represent heterogeneous qualitative characteristics, such as instructional background (Muthén, 1989) or solution strategies (Mislevy and Verhelst, 1990; Rost, 1990). The use of latent classes instead of manifest groups has been advocated in the test theory literature for detecting differential item functioning (DeAyala et al., 2002; Samuelsen, 2007) and has been shown to provide more meaningful inferences in applications (Webb et al., 2008; Scarpati et al., 2009). An advantage of mixture models is that latent classes can be detected without knowing the source of the heterogeneity.
There is extensive methodological and applied literature on using item response theory (IRT) and CFA to model heterogeneous discrete item responses across populations with both observed and unobserved membership (e.g., Muthén and Christoffersson, 1981; Mislevy and Verhelst, 1990; Rost, 1990; Mislevy and Wilson, 1996; French and Finch, 2006; Muthén and Asparouhov, 2006; Lubke and Neale, 2008), using multigroup CFA to model heterogeneous continuous indicator variables across observed populations (e.g., Jöreskog, 1971; Sörbom, 1974; Byrne et al., 1989; Cheung and Rensvold, 2002; Meade and Lautenschlager, 2004; French and Finch, 2006; Meade and Bauer, 2007), and using mixture CFA to model heterogeneous latent means across unobserved populations (e.g., Gagné, 2004; Lubke and Muthén, 2005; Lubke and Neale, 2006; Lubke and Muthén, 2007). However, little is known about how well mixture CFA can successfully model heterogeneous factor loadings and test for measurement invariance when the source of population heterogeneity is unobserved. As such, the current study examined the feasibility of mixture CFA to successfully model (in terms of convergence and parameter recovery) and test for heterogeneous factor loadings. While heterogeneity in a measurement model can be due to cross-population differences in factor loadings, measurement intercepts, or error variances/covariances, the focus of the current study was on modeling heterogeneous factor loadings, as factor loadings are the first and most commonly tested set of parameters when investigating the equivalence of measurement models across populations (e.g., Vandenberg and Lance, 2000; Schmitt and Kuljanin, 2008).
Theoretical Framework
The following equations define the general form of the finite mixture CFA model with continuous indicator variables for cross-sectional data. The measurement model with p indicators of m exogenous latent variables for observation i in latent class c is Xic = τc + Λcξic+δic, where i = 1 to Nc, τc is a p × 1 vector of measurement intercepts, Λc is a p × m matrix of factor loadings, ξic is an m × 1 vector of factor scores (i.e., values for individuals on a latent continuum), and δic is a p × 1 vector of residuals. Xic has an associated mean vector, μxc = τxc + Λc κc, where κc is an m × 1 vector of factor means, and covariance matrix Σc = ΛcΦcΛc + Θc, where Φc is an m × m factor variance/covariance matrix, and Θc is a p × p residual variance/covariance matrix. Assuming that ξic ∼ iid MVN(κc, Φc) and δic ∼ iid MVN(0, Θc), the finite mixture CFA density function is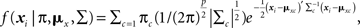 
with latent class proportion 0 ≤ πc ≤ 1.
Maximum-likelihood (ML) estimation of mixture CFA models can be accomplished via the expectation-maximization (EM) algorithm or some modification of it (McLachlan and Krishnan, 2008). Mplus 5.1 (Muthén and Muthén, 2007) is one of several existing software programs with the capacity to estimate mixture CFA parameters with ML methods. Mplus uses ML estimation via the EM algorithm; a description of the estimation in general for latent variable mixture modeling is described in the Mplus 5.1 technical appendices (Muthén, 1998-2004) with more details provided in Muthén and Shedden (1999). The EM algorithm is described in detail specifically for mixture CFA models in Yung (1997).
Failure to converge to a stable solution within a given number of iterations or converging to a local maximum are common problems when estimating any type of mixture model using ML. In univariate and multivariate normal mixtures with heterogeneous covariance matrices, the likelihood function is unbounded, which frequently can lead to non-convergence or convergence to one of multiple local maxima that likely exist rather than a global solution (McLachlan and Peel, 2000). As such, while non-convergence has been a non-issue in previous methodological studies that have estimated multigroup CFA with observed group membership and continuous indicator variables using ML estimation (e.g., French and Finch, 2006; Meade and Bauer, 2007), failure to obtain a global solution is a concern when studying and using mixture CFA models.
There are two main purposes for modeling factor loading heterogeneity within a CFA framework. A heterogeneous indicator-latent variable relationship may be modeled for substantive reasons, such as when theory suggests that a construct differs across populations. For example, scale items may function differently across ethnic groups due to secondary attributes in addition to the primary construct. Alternatively, a researcher addressing questions of moderation in structural relations or latent means must first examine the cross-population equality of parameters residing in the CFA portion of the model. For example, mean levels of self-concept can be compared across gender groups if the latent reading self-concept scales are similar for girls and boys. In the former case, the intent is to find evidence of non-invariance to support a hypothesis. In the latter, the intent is to find sufficient statistical support for invariance or partial invariance so that inferences about structural parameters or latent means are accurate and meaningful (Byrne et al., 1989).
When the number of latent classes is assumed to be known, invariance testing with a mixture CFA model involves only cross-population constraints. Comparing goodness-of-fit between alternative configurations of cross-population constraints requires estimation of a null hypothesized model with all parameters of theoretical interest constrained equal across populations while all other parameters except those needed for identification1 are free to vary. An alternative model also is estimated with the same identification constraints as the null hypothesized model but with all parameters of theoretical interest free to vary across populations in order to compare goodness-of-fit across the models.
The most commonly used method of invariance testing in multigroup CFA is the likelihood-ratio (LR) test (Vandenberg and Lance, 2000) which allows for goodness-of-fit comparisons of nested models by comparing chi-square values and can be used in mixture CFA when the number of latent classes is assumed to be known. Invariance testing within a mixture modeling framework when the number of latent classes is theoretically unknown poses challenges because model selection involves both choosing the number of latent classes and choosing between different configurations of cross-population invariance constraints. Models with different numbers of latent classes are nested; however, the standard LR statistic for comparing models with different numbers of latent classes does not follow the theoretical chi-square distribution and as such, the models cannot be compared with chi-square values (e.g., Dayton, 1998).
To test for the number of latent classes, information-based indices have been commonly used (see, for example, Henson et al., 2007), including the Akaike Information Criterion (Akaike, 1987), the Bayesian Information Criterion (Schwartz, 1978), the consistent Akaike Information Criterion (Bozdogan, 1987), and the sample-size adjusted BIC (Sclove, 1987). LR-based tests to determine the number of latent classes that approximate the chi-square distribution have also been proposed. These include the Lo–Mendell–Rubin test (Lo et al., 2001), the bootstrapped LR test (McLachlan, 1987) and a modified LR test (Stoel et al., 2006). Approaches for deciding on the number of latent classes in structured means mixture modeling and growth mixture modeling have been studied empirically by several authors (e.g., Henson et al., 2007; Nylund et al., 2007; Tofighi and Enders, 2008).
Mean separation is not a requirement in multigroup CFA modeling when solely testing parameters in the covariance structure. In mixture CFA modeling, a mean structure is imposed even when the focus is on heterogeneity in the covariance structure (e.g., Yung, 1997). In the current study, the performance of mixture CFA was evaluated in the presence of a completely invariant mean structure. Testing for cross-population factor loading differences in the presence of an invariant mean structure represents a substantively interesting and methodologically extreme case. Examples of applications in which factor loadings are hypothesized to differ while the mean structure may be invariant include extreme response style in survey research (Cheung and Rensvold, 2000), racial differences on intelligence tests (Drasgow, 1984), and non-uniform differential item functioning (González-Romá et al., 2005). It was expected that heterogeneous factor loadings would be most difficult to detect with mixture CFA when the mean structure is invariant because the aggregate distribution would appear unimodal, making it difficult to differentiate between latent classes. Such an overlap of latent class distributions is also expected to negatively impact convergence and parameter coverage rates.
If mixture CFA modeling can successfully estimate the model parameters and determine the existence of heterogeneous factor loadings when the location of latent classes is the same, then it is expected that mixture CFA can be used with confidence whether or not differences in latent means are hypothesized to exist. The performance of mixture CFA models in this context in terms of convergence, parameter recovery, and power to detect heterogeneous factor loadings was evaluated with data generated under a variety of study conditions that represent a broad range of research scenarios found in practice to assess the potential of mixture CFA for use in measurement invariance testing. These study conditions comprise an important subset of conditions that would require further methodological evaluation given evidence in support of the feasibility of mixture CFA modeling for measurement invariance testing in the presence of an invariant mean structure.
Methods
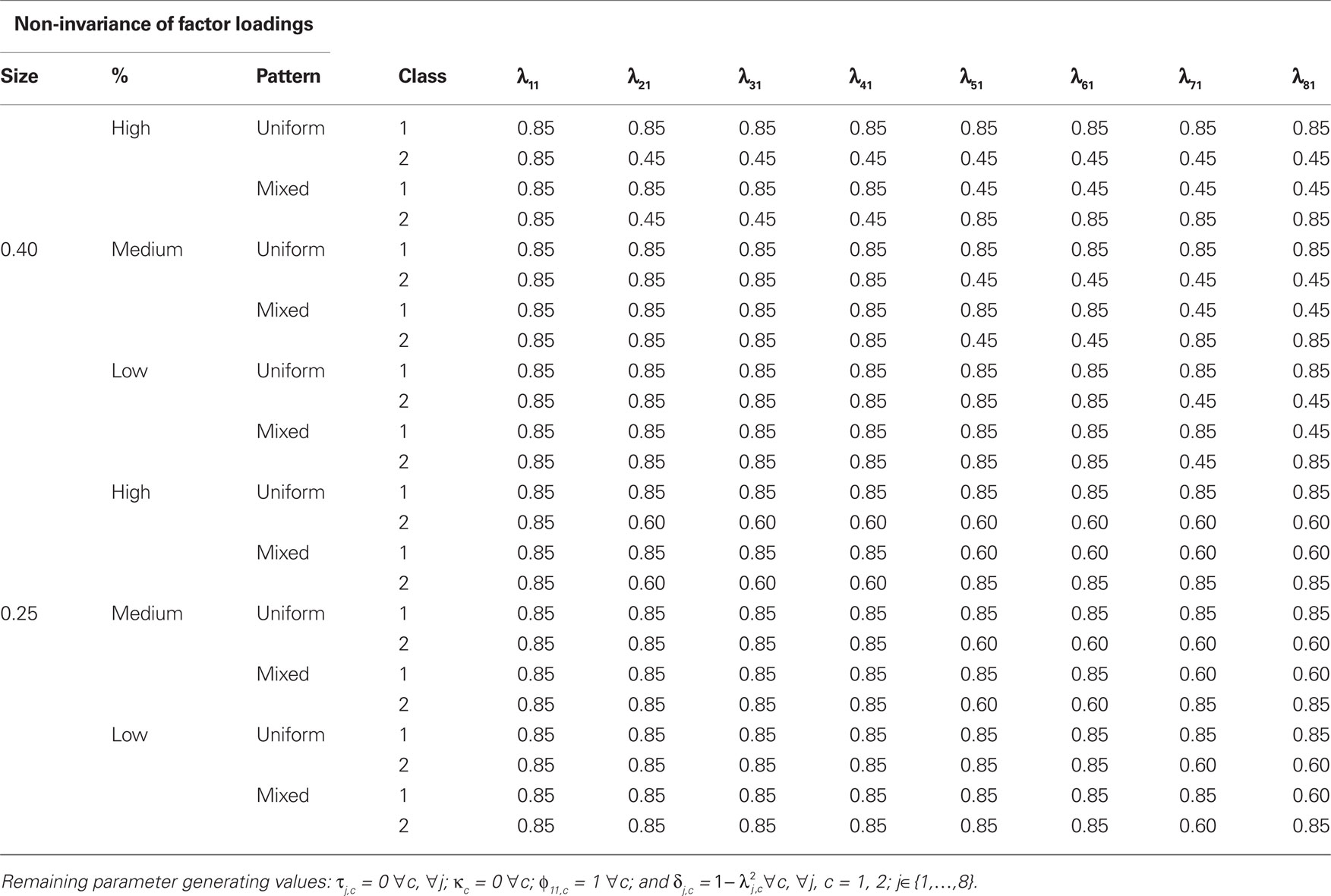
A two-class one-factor model was used to generate eight continuous indicator variables from a multivariate normal distribution depending on class membership for each study condition. Population generating values for the factor loadings (λ11 to λ81), factor variance (φ11), factor mean (κ), measurement intercepts (τ1 to τ8), and error variances (δ1 to δ8) are shown in Table 1. A factor loading below 0.6 is indicative of a mediocre to weak relationship between a latent variable and its measured indicator (Ximénez, 2006).
Table 1. Factor loading model generating values.
The non-invariance of factor loadings was manipulated in three ways: the pattern of non-invariance across classes was either uniform or mixed, factor loadings differed by either 0.25 or 0.40 and the percentage of non-invariant factor loadings was either low, medium, or high. In conditions with uniform non-invariance, the population generating values of all non-invariant class 1 factor loadings were higher than those for class 2. In mixed conditions, half of the non-invariant factor loadings were higher for class 1 and half were higher for class 2. The percentages of factor loadings chosen to be non-invariant were 25% and 50% for conditions with low or medium percentages, with the addition of high conditions with 88% of the factor loadings non-invariant.
Samples sizes and latent class proportions were chosen to represent moderate to large numbers of individuals. Total sample sizes of 200, 400, and 800 were used with equal class proportions. An unequal group size condition was also considered with latent class proportions equal to 0.25 and 0.75 for total sample sizes of 400 and 800. As such, the smallest class studied had 100 observations2. For conditions with unequal latent class proportions and a uniform pattern of non-invariance, the larger class had the smaller factor loadings. There are 36 conditions with equal latent class proportions and 24 conditions with unequal latent class proportions for a total of 60 study conditions.
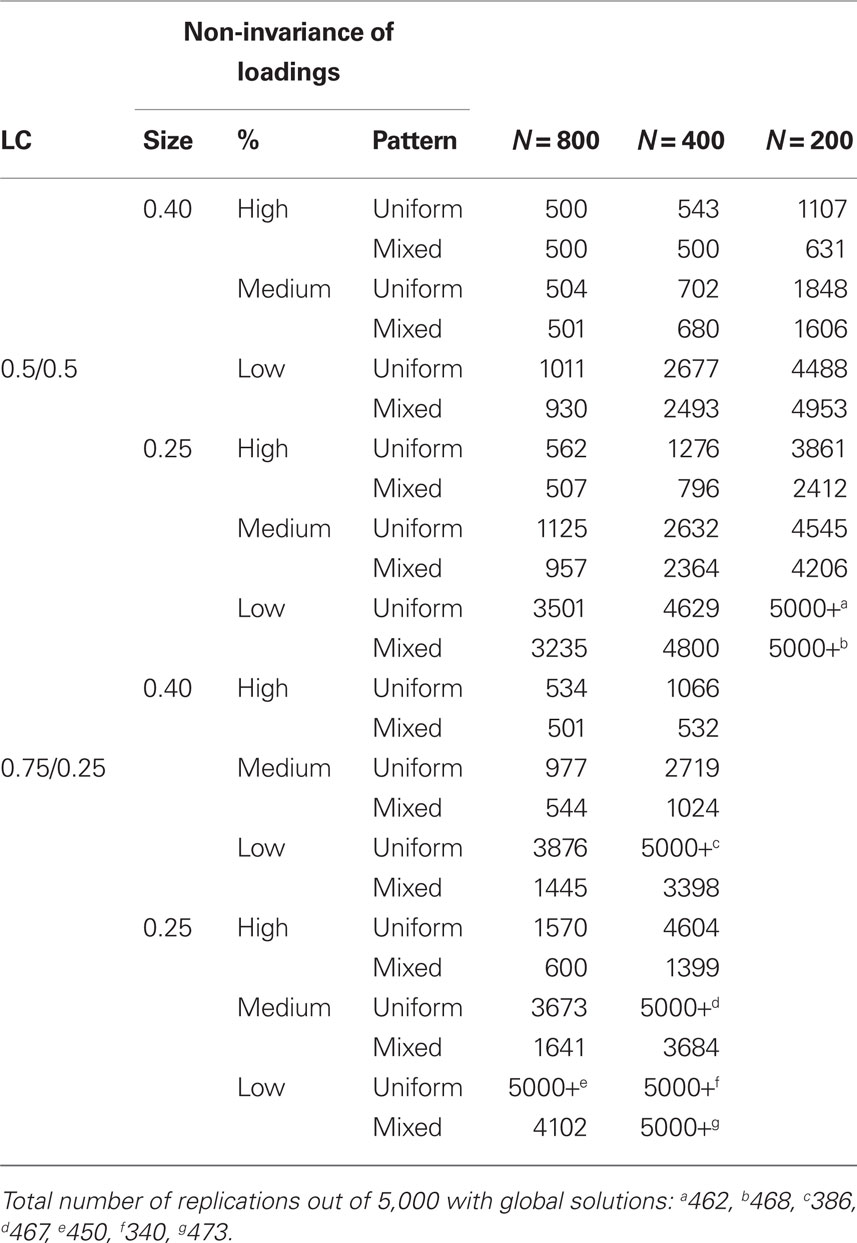
Based on pilot analyses, the rates of non-convergence or local maxima in the current study were hypothesized to be higher than in existing work on mixture CFA for testing differences in latent means (e.g., Gagné, 2004; Lubke and Muthén, 2007), given a completely invariant mean structure. As such, model estimation occurred concurrently with data generation. Specifically, datasets were generated in SAS 9.0 for each study condition and the model was estimated until global solutions were achieved for 500 replications, with an upper limit of 5,000 replications. Conditions under which 5,000 replications were reached without achieving 500 global solutions would then have a 90% or higher rate of unsuccessful estimation. The number of replications required to reach 500 global solutions was recorded for each study condition and the datasets with properly converged solutions were used to evaluate the outcome measures.
Mplus 5.1 (Muthén and Muthén, 2007) was applied to the generated data to obtain ML estimates of parameters in the true two-class models. Fifty sets of random starting values were used with ten iterations for each set, consistent with previous research on mixture CFA modeling (e.g., Lubke and Neale, 2006; Lubke and Muthén, 2007). During estimation, the first loading associated with each factor was fixed to the true value (0.85) for each class to provide a metric for the factor; this value was used rather than the customary value of 1 merely to put parameters on the scale of the original population values, and in no way affects the estimation process. In the current study, factor means were constrained equal across classes and set to 0 for model identification because the focus was on measurement model heterogeneity. Residual variances were freely estimated. The factor variance and all measurement intercepts, although truly invariant, were freely estimated and unconstrained across classes, consistent with the hierarchy recommended in the invariance testing literature (e.g., Bollen, 1989).
In order to conduct the analyses described below, two nested models were estimated with varying degrees of severity of cross-population constraints on the factor loadings (excluding the referent factor loading). Specifically, models with all factor loadings except the referent freely estimated across latent classes (herein referred to as unconstrained models) and models with all factor loadings constrained equal across latent classes (herein referred to as constrained models) were estimated. The remaining parameters except those fixed for identification were freely estimated as described above identically in both model configurations.
The impact of study conditions on the ability of mixture CFA to accurately estimate parameters of the unconstrained model was evaluated3. Ninety five percent confidence intervals were computed using parameter estimates and their standard errors for each of the (up to) 500 replications that achieved a global solution. The percentage of confidence intervals that contained the parameter generating value across replications was recorded for each individual parameter for each study condition. These coverage rates were then averaged across latent classes and parameters in each of the following matrices: factor loadings, measurement intercepts, residual variances, factor variance, and latent class proportions.
An omnibus LR test on the entire factor loading matrix was performed, comparing a two-class model with all factor loadings constrained to be equal across classes (H0; the constrained model) to a two-class model with all factor loadings free to vary across classes except for referent factor loadings (HA; the unconstrained model). All other parameters were estimated freely except for factor means which were fixed to 0 for identification as described above for both null and alternative models. Power of the omnibus test for each study condition was computed as the percentage of correctly rejected LR tests across replications with global solutions using α = 0.05.
The number of replications required to achieve 500 global solutions is reported for all study conditions. Analysis of variance (ANOVA) with a five-way [2 (latent class proportions) × 3 (sample size) × 2 (size of factor loading differences) × 2 (pattern of factor loading non-invariance) × 3 (percentage of non-invariant factor loadings)] unbalanced design was performed to evaluate the impact of study conditions on parameter recovery and power. Results for these outcome measures are reported for study conditions that are included in the highest significant interaction from each five-way ANOVA.
Results
The number of replications required to achieve 500 global solutions, with an upper limit of 5,000 replications, is reported in Table 2 for each study condition. Counts closer to 500 indicate better rates of convergence to the global maximum. As counts increase, the feasibility of estimating a CFA mixture model under a given study condition decreases. In general, as expected, larger sample sizes, larger differences in factor loadings, a mixed pattern of non-invariance, and more non-invariant factor loadings were associated with higher rates of convergence to the global solution.
Table 2. Number of replications out of 5,000 needed to achieve 500 global solutions.
Six of the 60 study conditions had less than a 10% rate of convergence to the global solution. Data generated under these conditions were characterized by one or more of the following: fewer than 100 observations in the smallest latent class, small differences in factor loadings, few non-invariant factor loadings, and a uniform pattern of non-invariant factor loadings. Eleven of 60 conditions had a 90% or better rate of convergence to the global solution. Data generated under these conditions were characterized by more than 200 observations in the smaller latent class, many non-invariant factor loadings, and large differences in factor loadings. Conditions with 100 observations in the smaller latent class achieved acceptable rates of convergence to the global solution only when the difference between factor loadings was large and there were many non-invariant factor loadings following a mixed pattern of non-invariance.
For a given total sample size, conditions with unequal latent class proportions had fewer successfully converged replications than conditions with equal latent class proportions. In particular, with a total sample size of 800 and unequal latent class proportions, the numbers of replications needed to achieve convergence to the global solution were higher than for conditions with N = 800 and equal class proportions. When comparing conditions with the same number of observations in the smaller class, conditions with unequal latent class proportions (and therefore a higher total sample size) had higher rates of convergence to the global solution than conditions with equal latent class proportions when the pattern of non-invariance was mixed and there were many non-invariant factor loadings.
The results suggest a trade-off among sample size, size of factor loading differences, and percentage and pattern of non-invariant factor loadings. When the pattern of non-invariance was uniform, the average communality in one class was smaller than in the other, and was particularly low when there were many non-invariant factor loadings and large factor loading differences. As such, larger sample sizes were required to compensate for the difficulty in estimating parameters for the class with the lower factor loadings. Conditions with few non-invariant factor loadings posed problems for attaining global solutions, even with as many as 400 observations per class. This suggests the need for a more theory-based and parsimonious model, at least when the mean structure is completely invariant. Overall, data that were characterized by larger sample sizes, larger differences between factor loadings, and many non-invariant factor loadings showed promise in the ability to achieve convergence to the global solution.
Parameter coverage rates are reported separately for each parameter matrix in Table 3. The five-way interaction was statistically significant for the factor loadings (F = 7.71, df = 2, p < 0.01, ω2 = 0.0003), measurement intercepts (F = 18.85, df = 2, p < 0.01, ω2 = 0.001), factor variance (F = 7.20, df = 2, p < 0.01, ω2 = 0.0004), error variance (F = 8.94, df = 2, p < 0.01, ω2 = 0.0004) and latent class proportion (df = 2, F = 5.93, p < 0.01, ω2 = 0.0003). As such, percentages are reported for all study conditions for each of the parameter matrices. Together, the five study conditions and their interactions accounted for 18–33% of the variation in recovery rates across the five parameter matrices with the percentage of non-invariant factor loadings accounting for the most variation4.
Table 3. Percentage of replications out of 500 in which 95% confidence interval covers parameter (Λ, factor loading; τ, measurement intercept; δ, error variance, Φ, factor variance, π, latent class proportion).
Average parameter coverage rates for the factor loading matrix ranged from 79% to 96% across conditions. For measurement intercepts, average parameter coverage rates ranged from 52% to 97%. Average coverage rates for the remaining parameter matrices were 68–95% for residual variances, 72–97% for the variance of the factor, and 25–99% for latent class proportions.
Latent class proportions had the widest range of coverage rates among the parameter matrices. Many study conditions had coverage rates lower than 50%, pointing to difficulty in distinguishing two separate latent class distributions from the unimodal aggregate distribution. For all parameter matrices, the lowest coverage rates occurred for conditions with N = 200, small differences in factor loadings, and few non-invariant factor loadings. The highest coverage rates occurred for conditions with N = 800, large factor loading differences, and a moderate to high percentage of non-invariant factor loadings. For the smallest class size of 100 with either equal or different latent class proportions, coverage rates for all parameter matrices were 90% or above when the data exhibited all of the following: all factor loadings non-invariant (except the referent) in a mixed pattern across latent classes with a difference in factor loadings equal to 0.40. Coverage rates for the factor loading matrix and the residual variance matrix were generally higher than for the other parameter matrices, as expected, since those matrices were truly non-invariant. For parameters in the factor loading matrix, as differences between factor loadings became larger, the accuracy of parameter estimates was higher. A mixed pattern of non-invariant factor loadings across latent classes was also associated with higher coverage rates in general. Alternatively, coverage rates for the factor loadings were never above 90% when there were only two truly non-invariant factor loadings in the entire parameter matrix.
Power of the omnibus LR test is reported in Table 4 with the total number of replications in which the constrained model converged to a global solution in parentheses. When all factor loadings were constrained equal across latent classes in order to estimate the null hypothesized model for the omnibus LR test, fewer replications converged to the global maximum than when the factor loadings were freely estimated for some study conditions. This is not surprising since non-invariant factor loadings in the constrained model were misspecified while only residual variances (both invariant and non-invariant depending on the study conditions) and parameters that were truly invariant (measurement intercepts and the factor variance) were allowed to vary across classes during estimation. As such, the only source of heterogeneity in the estimated null hypothesized model was from deviations due to random sampling error and differences in the residual variances across classes, leading to more replications in which the global solution was not found.
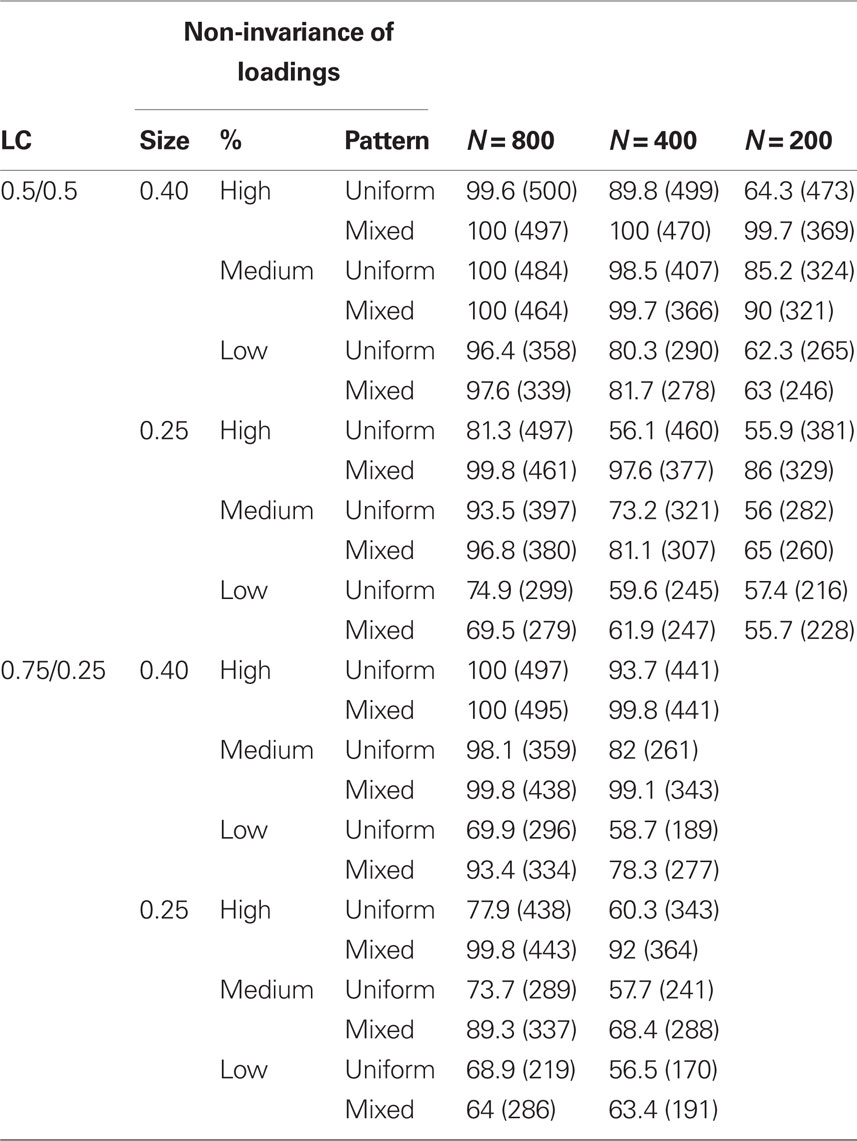
Table 4. Percentage of correctly rejected LR tests for invariance of the factor loading matrix, number of replications in parentheses.
All five study conditions explained 19% of the variation in power rates. Results are disaggregated across study conditions since the interaction of all five study conditions from ANOVA was statistically significant (F = 4.24, df = 2, p < 0.05, ω2 = 0.0003). Across all study conditions, power ranged from 56% to 100%. Power was lowest for conditions with a combination of small sample size, small factor loading differences, and a uniform pattern of non-invariance, as expected. A mixed pattern of non-invariant factor loadings was associated with higher power relative to a uniform pattern of non-invariance except when only two factor loadings exhibited small differences. When the pattern of non-invariance was uniform, power was considerably lower for conditions with many non-invariant factor loadings.
Conditions with unequal latent class proportions had similar power levels to conditions with equal latent class proportions when total sample size was 800, the percentage of non-invariant factor loadings was high and their difference was large. Conditions with a mixed pattern of non-invariance also had similar levels of power for both equal and unequal latent class proportions when there were many factor loadings with small cross-population differences or a moderate percentage of factor loadings with a large difference across population. Overall, power was highest under conditions with total sample size equal to 800 and many factor loadings that differed by 0.40, as well as conditions that achieved more global solutions and produced accurate parameter estimates.
Discussion
The current study provided an analysis of convergence, parameter recovery, and power when testing for heterogeneous factor loadings with mixture CFA in the presence of a completely invariant mean structure, thereby assessing the potential of using latent classes when conducting measurement invariance testing with continuous, cross-sectional data. When conducting research on multiple populations in the social and behavioral sciences, much attention is paid in particular to whether or not populations differ with respect to their factor loadings. Researchers who wish to make inferences about cross-population differences in construct representation, values of latent means, or structural relations must assess measurement invariance to ensure inferences are valid for the intended populations.
Results from estimating two-class one-factor mixture CFA models with simulated data revealed some situations under which mixture CFA models can successfully estimate parameters and detect heterogeneous factor loadings when the mean structure is completely invariant. In general, parameters that were truly non-invariant (factor loadings and residual variances) were estimated most successfully while latent class proportions were least accurately estimated. Convergence and parameter coverage rates were low when there were only two heterogeneous factor loadings and all factor loadings (except referent loadings) were free to vary across classes. A uniform pattern of non-invariance also made it difficult to successfully estimate the mixture CFA model.
The true number of latent classes was used when estimating all models in the current study, which allowed for use of the standard LR statistic to conduct invariance testing. In practice, the number of latent classes may be assumed known, for example, when there is substantive support for known qualitative differences between populations. The LR test had adequate power when there was more heterogeneity across latent classes in the residual variances which allowed for the completely restricted model to be estimated successfully. The invariant mean structure had the least negative consequences for successful estimation and invariance testing when total sample size was equal to 800, latent class proportions were equal, and factor loadings differed by 0.40.
The results showed that a total sample size of at least 800 with equal latent class proportions was adequate to derive accurate conclusions about parameter values and their cross-population equality when there were moderate to many non-invariant factor loadings. This suggests that any deviations of these characteristics toward fewer observations and less heterogeneity would lead to problems with convergence, recovery of parameter estimates, and power to detect factor loading heterogeneity when the mean structure is completely invariant. Problems with convergence and accuracy of estimates when there were only a few non-invariant factor loadings even with large sample sizes and large cross-population differences suggest that, at least when the mean structure is invariant, mixture CFA cannot be used for exploratory analyses.
When the number of classes is assumed to be known a priori, the LR test may be a viable option when it is expected that there are other sources of heterogeneity beyond the parameters being tested. When there is little or no heterogeneity in other parameters, then the LR test may not be a good choice, and researchers should instead consider the multivariate Wald test, which does not require the null model to be estimated, to evaluate the equality of factor loadings. When the number of classes in not known a priori, bootstrapped and adjusted LR tests (e.g., McLachlan, 1987; Lo et al., 2001; Stoel et al., 2006) can be used. Such tests allow for comparisons of models across different numbers of latent classes and have been shown to be successful in latent variable mixture modeling (e.g., Nylund et al., 2007).
While mixture CFA has the potential to accurately model and test for heterogeneous factor loadings when the mean structure is invariant, many study conditions led to unsuccessful estimation. A potential way to improve convergence and accuracy when using mixture CFA models is to include observed covariates to explain latent class membership. For example, Lubke and Muthén (2007) showed improved convergence rates when covariates were included to model heterogeneous factor loadings with mixture CFA and a non-invariant mean structure.
Conditions in the current study were chosen in order to provide an analysis of the potential for using mixture CFA modeling to test factor loading heterogeneity as an alternative to multigroup CFA models. Given the current paucity of research on mixture CFA models for continuous data when the focus is on factor loading heterogeneity, the current study focused on an extreme methodological case to offer preliminary analyses on the viability of testing the invariance of factor loadings across latent classes, with the expectation that the method would be used more frequently by applied researchers if it can be carried out similarly to multigroup CFA and would be applicable in the same substantive situations. The invariant mean structure only allowed for investigation of moderate to large sample sizes in the current study, with the smallest latent class comprised of 100 observations. Questions still remain about the performance of mixture CFA for testing the invariance of measurement model parameters when samples are small as well as the nature of the trade-off between mean separation and sample sizes.
There are several limitations of the current study. High rates of convergence to local maxima may have impacted the generalizability of inferences about parameter coverage and power. Specifically, using only replications that resulted in proper solutions may have inflated parameter recovery percentages and power. In practice, non-convergence may indicate that the model is misspecified or that the estimation algorithm is on the edge of the parameter space. Increasing the number of iterations or decreasing the change in stop criterion may result in convergence to a global solution in practice that is less accurate than the results of this study may suggest. In addition, the current study was limited to one type of fit statistic for invariance testing, the LR test statistic. While popular in applications, there are conflicting results about its success in multigroup CFA (e.g., Cheung and Rensvold, 2002; French and Finch, 2006; Chen, 2007). In addition, since the standard LR statistic used in the current study cannot be used to compare models with different numbers of latent classes, the results cannot be generalized to exploratory modeling with mixture CFA models.
Results from this simulation study offer foundational evidence that mixture CFA models can be used for testing for heterogeneous factor loadings across latent classes when the mean structure is hypothesized to be equal across populations provided that sample sizes are large and the magnitude of heterogeneity is expected to be large in order to compensate for the potential lack of mean differences. More research would be needed to find strategies to improve the capabilities of mixture CFA modeling for invariance testing in order for it to be used under a wider variety of situations found in practice, in particular because most conditions in the current study that had a significant impact on successful estimation cannot be controlled through research design. Such follow-up research includes, for example, a comparison of mixture CFA to multigroup CFA for invariance testing (see Buzick, 2010, for a simulation study and application), a comparison of strategies for testing for parameter invariance concurrently with class enumeration, an evaluation of the performance of mixture CFA with more complex models (e.g., more factors, more latent classes), and an evaluation of the performance of mixture CFA when testing other measurement model parameters. The results of the current study provide support for such further methodological research and also for the consideration of latent classes in applications of measurement invariance testing, not only when important moderator variables are unobserved, but to add theoretically important qualitative information in order to improve parameter estimates and enrich inferences.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research was supported in part by the Graduate School at the University of Maryland via an Ann G. Wylie Dissertation Fellowship. The author would like to thank Gregory R. Hancock, dissertation chair and advisor, for providing substantive guidance and thoughtful advice throughout the course of this research.
Footnotes
- ^Identification of a CFA model with mean structure is accomplished by assigning a metric and an origin for the factors. In multigroup modeling, the metric is usually set by choosing a referent loading and fixing it to a constant for each factor in each population, typically unity. The choice of referent may impact inferences drawn from invariance testing using heterogeneous CFA models (Yoon and Millsap, 2007). Statistical procedures have been proposed to detect factor loadings that are truly invariant across populations to use as referents (see French and Finch, 2008 for a review and performance results from simulated data), yet the degree to which they are successful is unclear. There are two statistically equivalent ways in which parameters can be fixed to set the origin of the factors in a CFA model with mean structure: (1) set the factor means of each population to 0 and allow all measurement intercepts in all populations to be freely estimated, or (2) set the factor mean of one population to 0 while constraining the measurement intercept associated with the referent indicator(s) equal across populations. Fixing the latent means to 0 in all populations may be appropriate when substantive theory suggests that factor means should not differ across populations or when the focus is on measurement model heterogeneity (e.g., Yung, 1997; Muthén, 2008). In the latter case, if true differences in factor means were to exist, this difference would be reflected in differences in the estimated measurement intercepts.
- ^Pilot analyses suggested that smaller sample sizes were infeasible under the current study design with a completely invariant mean structure.
- ^In practice, a model with all factor loadings except for the referent free to vary across populations is typically used as the alternative model in the omnibus test of complete invariance of the factor loading matrix (Cheung and Rensvold, 2002).
- ^ω2 = 0.15 for intercepts, ω2 = 0.10 for error variances, ω2 = 0.07 for factor loadings and latent class proportions, and ω2 = 0.03 for the factor variance.
References
Bozdogan, H. (1987). Model selection and Akaike’s information criterion (AIC): the general theory and its analytic extensions. Psychometrika 52, 345–370.
Buzick, H. M. (2010). A comparison of multigroup CFA and mixture CFA with a covariate for testing measurement invariance. Paper presented at the annual meeting of the American Educational Research Association, Denver, CO.
Byrne, B. M., Shavelson, R. J., and Muthén, B. O. (1989). Testing for the equivalence of factor covariance and mean structures: The issue of partial measurement invariance. Psychol. Bull. 105, 456–466.
Chen, F. F. (2007). Sensitivity of goodness of fit indexes to lack of measurement invariance. Struct. Equ. Modeling 14, 464–504.
Chen, F. F. (2008). What happens if we compare chopsticks with forks? The impact of making inappropriate comparisons in cross-cultural research. J. Pers. Soc. Psychol. 95, 1005–1018.
Cheung, G. W., and Rensvold, R. B. (2000). Assessing extreme and acquiescence response sets in cross-cultural research using structural equation modeling. J. Cross Cult. Psychol. 31, 187–212.
Cheung, G. W., and Rensvold, R. B. (2002). Evaluating goodness-of-fit indexes for testing measurement invariance. Struct. Equ. Modeling 9, 233–255.
DeAyala, R. J., Kim, Seock-Ho, Stapleton, L. M., and Dayton, C. M. (2002). Differential item functioning: a mixture distribution conceptualization. Int. J. Testing 2, 243–276.
Drasgow, F. (1984). Scrutinizing psychological tests: Measurement equivalence and equivalent relations with external variables are the central issues. Psychol. Bull. 95, 134–135.
French, J. W. (1965). The relationship of problem-solving styles to the factor composition of tests. Educ. Psychol. Meas. 25, 9–28.
French, B. F., and Finch, W. H. (2006). Confirmatory factor analytic procedures for the determination of measurement invariance. Struct. Equ. Modeling 13, 378–402.
French, B. F., and Finch, W. H. (2008). Multigroup confirmatory factor analysis: locating the invariant referent sets. Struct. Equ. Modeling 15, 96–113.
Gagné, P. E. (2004). General Confirmatory Factor Mixture Models: A Tool for Assessing Factorial Invariance Across Unspecified Populations. Doctoral dissertation, University of Maryland, 2004. Dissertation Abstracts International, 65, 1389B.
González-Romá, V., Tomás, I., Ferreres, D., and Hernández, A. (2005). Do items that measure self-perceived physical appearance function differentially across gender groups? An application of the MACS model. Struct. Equ. Modeling 12, 148–162.
Henson, J. M., Reise, S. P., and Kim, K. H. (2007). Detecting mixtures from structural model differences using latent variable mixture modeling: A comparison of relative model fit statistics. Struct. Equ. Modeling 14, 202–226.
Jöreskog, K. G. (1971). Simultaneous factor analysis in several populations. Psychometrika 57, 409-426.
Lo, Y., Mendell, N. R., and Rubin, D. B. (2001). Testing the number of components in a normal mixture. Biometrika 88, 767–778.
Lubke, G. H., and Muthén, B. O. (2005). Investigating population heterogeneity with factor mixture models. Psychol. Methods 10, 21–39.
Lubke, G. H., and Muthén, B. O. (2007). Performance of factor mixture models as a function of model size, covariate effects, and class-specific parameters. Struct. Equ. Modeling 14, 26–47.
Lubke, G. H., and Neale, M. C. (2006). Distinguishing between latent classes and continuous factors: resolution by maximum likelihood? Multivariate Behav. Res. 41, 499–532.
Lubke, G. H., and Neale, M. C. (2008). Distinguishing between latent classes and continuous factors with categorical outcomes: class invariance of parameters of factor mixture models. Multivariate Behav. Res. 43, 592–620.
McLachlan, G. J. (1987). On bootstrapping the likelihood ratio test statistic for the number of components in a normal mixture. J. Appl. Stat. 36, 318–324.
McLachlan, G., and Krishnan, T. (2008). The EM Algorithm and Extensions. New York: John Wiley & Sons.
Meade, A. W., and Bauer, D. J. (2007). Power and precision in confirmatory factor analytic tests of measurement invariance. Struct. Equ. Modeling 14, 611–635.
Meade, A. W., and Lautenschlager, G. J. (2004). A Monte-Carlo study of confirmatory factor analytic tests of measurement equivalence/invariance. Struct. Equ. Modeling 11, 60–72.
Mislevy, R. J., and Verhelst, N. (1990). Modeling item responses when different subjects employ different solution strategies. Psychometrika 55, 195–215.
Mislevy, R. J., and Wilson, M. (1996). Marginal maximum likelihood estimation for a psychometric model of discontinuous development. Psychometrika 61, 41–71.
Moore, W. L. (1980). Levels of aggregation in conjoint analysis: An empirical comparison. J. Market. Res. 17, 516–523.
Muthén, B. O. (1989). Latent variable modeling in heterogeneous populations. Psychometrika 54, 557–585.
Muthén, B. O. (2008). “Latent variable hybrids: Overview of old and new models,” in Advances in Latent Variable Mixture Models, eds G. R. Hancock and K. M. Samuelsen (Charlotte, NC: Information Age Publishing, Inc), 1–26.
Muthén, B. O., and Asparouhov, T. (2006). Item response mixture modeling: application to tobacco dependence criteria. Addict. Behav. 31, 1050–1066.
Muthén, B. O., and Christoffersson, A. (1981). Simultaneous factor analysis of dichotomous variables in several groups. Psychometrika 46, 407–419.
Muthén, B. O., and Shedden, K. (1999). Finite mixture modeling with mixture outcomes using the EM algorithm. Biometrics 55, 463–469.
Muthén, L. K., and Muthén, B. O. (2007). Mplus version 5.1 [Computer Software]. Los Angeles: Muthén & Muthén.
Nylund, K., Asparouhov, T., and Muthén, B. O. (2007). Deciding on the number of classes in latent class analysis and growth mixture modeling: a Monte Carlo simulation study. Struct. Equ. Modeling 14, 535–569.
Rost, J. (1990). Rasch models in latent classes: an integration of two approaches to item analysis. Appl. Psychol. Meas. 14, 271–282.
Samuelsen, K. M. (2007). “Examining differential item functioning from a latent mixture perspective,” in Advances in Latent Variable Mixture Models, eds G. R. Hancock and K. M. Samuelsen (Charlotte, NC: Information Age Publishing) 177–198.
Scarpati, S. E., Wells, C. S., Lewis, C., and Jirka, S. (2009). Accommodations and item-level analyses using mixture differential item functioning. J. Special Educ. doi: 10.1177/0022466909350224.
Schmitt, N., and Kuljanin, G. (2008). Measurement invariance: review of practice and implications. Hum. Resource Manag. Rev. 18, 210–222.
Sclove, L. S. (1987). Application of model-selection criteria to some problems in multivariate analysis. Psychometrika 52, 333–343.
Sörbom, D. (1974). A general model for studying differences in factor means and factor structures between groups. Br. J. Math. Stat. Psychol. 27, 229–239.
Stoel, R. D., Galindo-Garre, F., Dolan, C., and Van den Wittenboer, G. (2006). On the likelihood ratio test in structural equation modeling when parameters are subject to boundary constraints. Psychol. Methods 11, 439–455.
Tofighi, D., and Enders, C. K. (2008). “Identifying the correct number of classes in growth mixture models,” in Advances in Latent Variable Mixture Models, eds G. R. Hancock and K. M. Samuelsen (Charlotte, NC: Information Age Publishing), 317–342.
Vandenberg, R. J., and Lance, C. E. (2000). A review and synthesis of the measurement invariance literature: suggestions, practices, and recommendations for organizational research. Organ. Res. Methods 3, 4–69.
Webb, M-Y. L., Cohen, A., and Schwanenflugel, P. J. (2008). Latent class analysis of differential item functioning on the Peabody Picture Vocabulary Test III. Educ. Psychol. Meas. 68, 335–351.
Ximénez, C. (2006). A Monte Carlo study of recovery of weak factor loadings in confirmatory factor analysis. Struct. Equ. Modeling 13, 587–614.
Yoon, M., and Millsap, R. E. (2007). Detecting violations of factorial invariance using data-based specification searches: A Monte Carlo study. Struc. Equ. Modeling 14, 435–463.
Keywords: mixture CFA, latent class analysis, measurement invariance
Citation: Buzick HM (2010) Testing for heterogeneous factor loadings using mixtures of confirmatory factor analysis models. Front. Psychology 1:165. doi: 10.3389/fpsyg.2010.00165
Received: 24 February 2010;
Accepted: 17 September 2010;
Published online: 29 October 2010.
Edited by:
Prathiba Natesan, University of North Texas, USAReviewed by:
Jill S. Budden, National Council of State Boards of Nursing, USARoy Levy, Arizona State University, USA
Copyright: © 2010 Buzick. This is an open-access article subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Heather M. Buzick, Educational Testing Service, Rosedale Road, MS 10-R, Princeton, NJ 08541, USA. e-mail: hbuzick@ets.org