- Department of Psychology, University of Guelph, Guelph, ON, Canada
Zero-sum bias describes intuitively judging a situation to be zero-sum (i.e., resources gained by one party are matched by corresponding losses to another party) when it is actually non-zero-sum. The experimental participants were students at a university where students’ grades are determined by how the quality of their work compares to a predetermined standard of quality rather than to the quality of the work produced by other students. This creates a non-zero-sum situation in which high grades are an unlimited resource. In three experiments, participants were shown the grade distribution after a majority of the students in a course had completed an assigned presentation, and asked to predict the grade of the next presenter. When many high grades had already been given, there was a corresponding increase in low grade predictions. This suggests a zero-sum bias, in which people perceive a competition for a limited resource despite unlimited resource availability. Interestingly, when many low grades had already been given, there was not a corresponding increase in high grade predictions. This suggests that a zero-sum heuristic is only applied in response to the allocation of desirable resources. A plausible explanation for the findings is that a zero-sum heuristic evolved as a cognitive adaptation to enable successful intra-group competition for limited resources. Implications for understanding inter-group interaction are also discussed.
Introduction
The psychological and economic sciences have a long tradition of documenting descriptive characterizations of cognitive behavior that deviate from normative theories. The “heuristics and biases” approach, for example, seeks to identify the heuristics with which people make intuitive judgments, and the resulting biases that are deviant from normative predictions (Tversky and Kahneman, 1974; Kahneman et al., 1982; Gilovich et al., 2002). The research reported here introduces a zero-sum bias.
Zero-sum, a term from game theory (von Neumann and Morgenstern, 1944), refers to a situation in which resources gained by one party are matched by corresponding losses to another party. Non-zero-sum will be used to refer to any other situation; for example, when both parties gain, when both parties lose, when one party gains and the other neither loses nor gains, when one party loses and the other neither gains nor loses, etc. This paper introduces the term zero-sum bias to describe intuitively judging a situation to be zero-sum when it is actually non-zero-sum.
Unlimited resource situations, in which the gains or losses of one party have no effect on other parties, are non-zero-sum situations that might be prone to bias. Unlimited resource situations are not uncommon for people living in the first-world during the early twenty-first Century. A typical situation in my household goes something like this: My two children ask for a snack, and I slice an apple into sections, giving an equal number of sections to each. Inevitably, one of them (and often both) will claim that their sibling’s sections are larger, accompanied by complaints of unfairness. This conclusion of unfairness seems unperturbed by my reminder that there are eleven more apples waiting in the kitchen should anyone want more, and the complainant rarely asks for more after eating what was initially given.
The experiments reported here were designed to test the hypothesis that people are prone to perceive a competition for limited resources (i.e., employ a zero-sum heuristic) even when there are unlimited resources available. Judgments about academic performance evaluations (grades) by those being evaluated (students) are a perfect testing ground for this hypothesis. For students, grades are important resources, as they are the currency by which access to desired careers are bought. University course grading in the United States is often relative (i.e., an individual student’s grade is determined by how the quality of their work compares to the quality of the work produced by the other students in the course) rather than absolute (i.e., an individual student’s grade is determined by how the quality of their work compares to a predetermined standard of quality). Relative grading systems create a zero-sum competition among students, because a high grade given to one student means one less high grade available to the other students.
The situation is different in Canada, however. At the university where I teach, for example, official grading regulations prohibit course instructors from using a relative grading system. Moreover, the large majority of students at my university have little experience with relative grading, because it is also forbidden at the primary and secondary levels, and the university does not include relatively graded examinations, such as the Scholastic Aptitude Test (SAT), as part of the admissions requirements. Absolute grading systems, which thus constitute the experience of the participants in the experiments reported here, create a non-zero-sum situation because if all students in a course do high-quality work, then they should all receive high grades. Nevertheless, informal conversations with my students have frequently revealed signs of zero-sum bias, and the experiments reported here represent an attempt to empirically characterize its prevalence.
Experiment 1 demonstrated zero-sum bias by showing that high grades given to some students increased the likelihood of low grades being predicted for other students. Experiment 2 examined whether the converse is true; i.e., whether zero-sum bias is a unidirectional or bidirectional phenomenon. An important issue in bias research concerns identifying the conditions under which biases can be reduced. In the case of zero-sum bias among students, the non-zero-sum nature of grading is not often explicitly stated by instructors in individual courses. Experiment 3 tested the hypothesis that reminding students of the non-zero-sum grading policy would be sufficient to reduce zero-sum bias.
Experiment 1
In Experiment 1, student participants were asked to make a judgment about a non-zero-sum situation involving grades in the context of an absolute grading system. They were asked to predict the presentation grade of a student based on the prior performance of other students in the same course. The normative and zero-sum bias hypotheses make different suggestions about how students will use the performance of one party to predict the performance of another. Normative behavior, which takes absolute grading into account, would be shown if predicted grades for the student mimicked the grades of the other students. For example, if the grades were relatively high on the presentation, then participants should conclude that the grading criteria were relatively favorable to students, and thus tend to predict that the student should do relatively well on the presentation (not knowing anything else about the student). Biased behavior, which wrongly assumes relative grading, would be shown if predicted grades for the student differed from the grades of the other students. For example, if the grades were relatively high on the presentation, then participants should conclude that no more high grades will be given, and thus tend to predict that the student should do relatively poorly on the presentation (not knowing anything else about the student).
The condition designed to test for zero-sum bias showed participants a negatively skewed distribution in which a biased individual might assume that all of the desirable resources (i.e., high grades) had already been allocated. Compared to a control condition in which the distribution was symmetrical (and thus that desirable resources might still be available), such a negatively skewed distribution might increase the likelihood of low grade predictions. The converse finding, that a negatively skewed distribution might increase the likelihood of high grade predictions, would provide evidence for normative judgment.
Materials and Methods
Participants were 556 undergraduate students at the University of Guelph, all of whom had completed at least one semester of full-time study. Informed consent was obtained from all participants, and the experiment was reviewed and approved by the Research Ethics Board of the University of Guelph.
Participants were randomly assigned to one of two experimental conditions: (a) negatively skewed distribution (N = 278), or (b) symmetrical distribution (N = 278). Participants in both conditions were presented with the text shown below; this text was accompanied by Figure 1A in the negatively-skewed condition, or Figure 1B in the symmetrical condition.
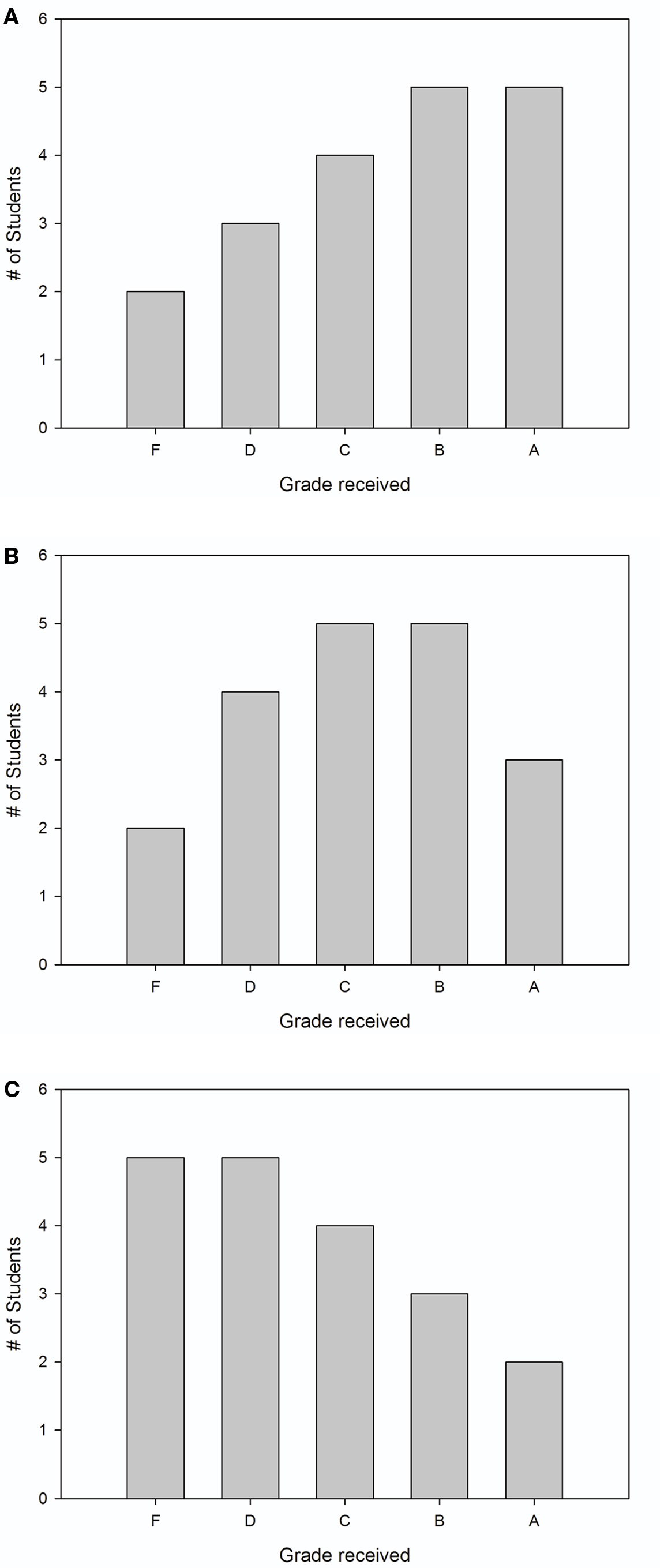
Figure 1. Grade distributions shown to participants. Experiment 1 compared the influence of negatively skewed (A) and symmetrical (B) distributions. Experiment 2 compared the influence of positively skewed (C) and symmetrical (B) distributions. Experiment 3 examined the influence of information provision on the negatively skewed distribution (A). See Section “Materials and Methods” for the accompanying text that was shown to participants.
Consider the following scenario:
A University of Guelph course has 20 students. Each class includes a graded presentation by one student.
The following figure shows the grades received by the first 19 presenters:
The 20th presenter is next.
In your judgment, what is the most likely grade to be received by the 20th presenter?
Choose one of the following: A, B, C, D, F.
Results
The results are shown in Figure 2. Statistical analysis revealed that distribution condition had a significant influence on grade prediction judgments [χ24 = 50.30, N = 556, p < 0.001]. The normative hypothesis predicted that high grade predictions would be more likely, and low grade predictions would be less likely, in the negatively skewed condition compared to the symmetrical condition. The zero-sum hypothesis predicted that high grade predictions would be less likely, and low grade predictions would be more likely, in the negatively skewed condition compared to the symmetrical condition. Separate analyses were done for each grade level to determine whether there was an influence of distribution condition. Predicted grades of A [χ21 = 5.63, N = 86, p < 0.05] and B [χ21 = 6.30, N = 254, p < 0.05] were less frequent in the negatively skewed condition than in the symmetrical condition. Predicted grades of C were not affected by distribution condition [χ21 = 0.46, N = 138]. Predicted grades of D [χ21 = 30.56, N = 55, p < 0.001] and F [χ21 = 7.35, N = 23, p < 0.01] were more frequent in the negatively skewed condition than in the symmetrical condition. These results demonstrated a zero-sum bias.
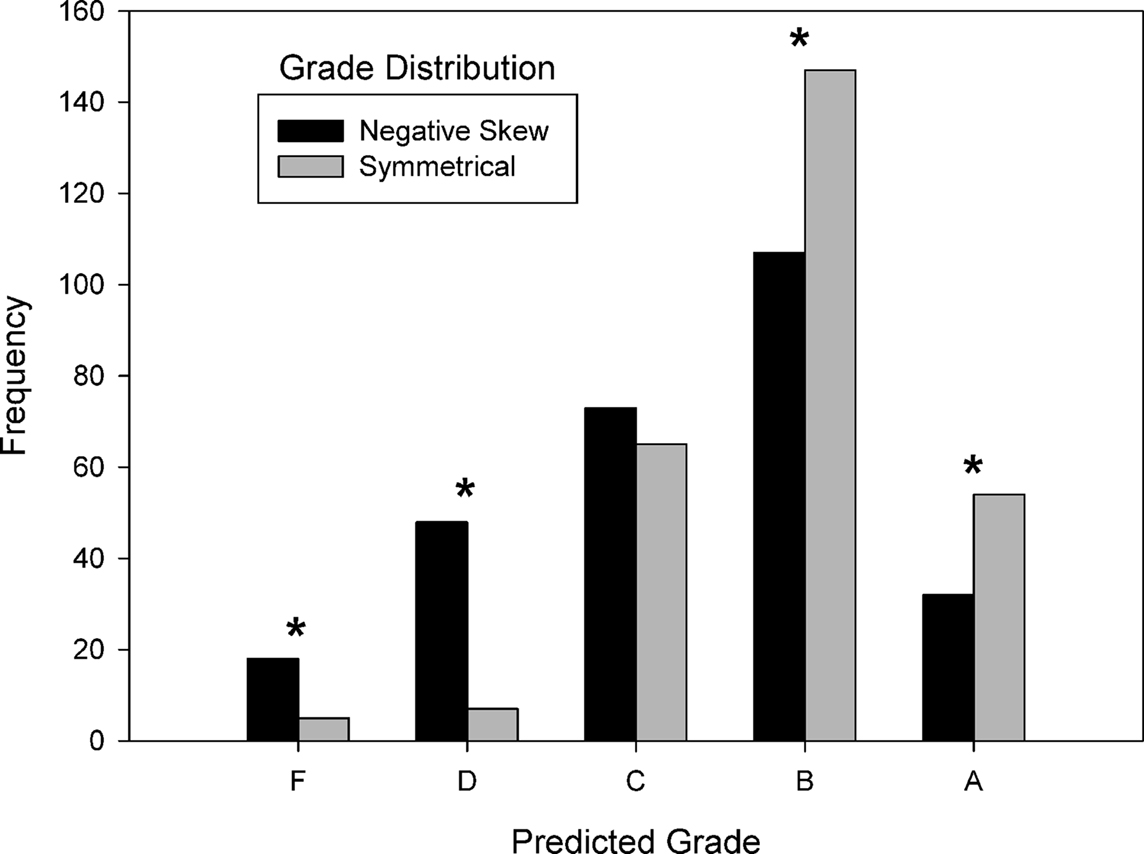
Figure 2. Predicted grade frequency as a function of grade distribution condition in Experiment 1. Distribution condition had a significant influence on grade judgments, particularly at those grade levels marked with an asterisk (indicating p < 0.05). Negative skew increased low grade predictions and decreased high grade predictions, suggesting a zero-sum bias.
Experiment 2
Experiment 1 demonstrated zero-sum bias by showing that high grades given to some students increased the likelihood of low grades being predicted for another student. Experiment 2 examined whether the converse is true. Some previous findings are consistent with the possibility that zero-sum bias could be unidirectional, such that gains predict losses but losses do not predict gains. For example, the costs of loss are perceived to outweigh the benefits of gain (Kahneman and Tversky, 1979). People could thus be relatively over-aware that gains by some mean might mean losses to others, and relatively under-aware that losses by some mean might mean gains to others. In the case of grades, students might be over-concerned about the consequences of high grades given to fellow students, and under-concerned about the consequences of low grades given to fellow students. Experiment 2 examined whether low grades given to some students increased the likelihood of high grades being predicted for another student.
The condition designed to test for zero-sum bias showed participants a positively skewed distribution in which a biased individual might assume that many high grades were still available. Compared to a control condition in which the distribution was symmetrical (and thus that fewer high grades might still be available), such a positively skewed distribution might increase the likelihood of high grade predictions. The converse finding, that a positively skewed distribution might increase the likelihood of low grade predictions, would provide evidence for normative judgment.
Materials and Methods
Participants were 308 undergraduate students at the University of Guelph, all of whom had completed at least one semester of full-time study. Informed consent was obtained from all participants, and the experiment was reviewed and approved by the Research Ethics Board of the University of Guelph.
Participants were randomly assigned to one of two experimental conditions: (a) positively skewed distribution (N = 154), or (b) symmetrical distribution (N = 154). Participants in both conditions were presented with the same text as in Experiment 1; this text was accompanied by Figure 1B in the symmetrical condition, or Figure 1C in the positively skewed condition.
Results
The results are shown in Figure 3. Statistical analysis revealed that distribution condition had a significant influence on grade prediction judgments [χ24 = 13.77, N = 308, p < 0.01]. The normative hypothesis predicted that high grade predictions would be less likely, and low grade predictions would be more likely, in the positively skewed condition compared to the symmetrical condition. The zero-sum hypothesis predicted that high grade predictions would be more likely, and low grade predictions would be less likely, in the positively skewed condition compared to the symmetrical condition. Separate analyses were done for each grade level to determine whether there was an influence of distribution condition. Although the trend at low and high grade levels was consistent with normative judgments, only one grade level reached statistical significance: predicted grades of D [χ21 = 7.20, N = 20, p < 0.01] were more frequent in the positively skewed condition than in the symmetrical condition. Predicted grades of A [χ21 = 1.79, N = 56], B [χ21 = 1.44, N = 136], C [χ21 = 0.56, N = 87], and F [χ21 = 2.78, N = 9, p < 0.10] were not significantly affected by distribution condition. Unlike a negatively skewed distribution, which induced zero-sum tendencies in Experiment 1, a positively skewed distribution did not induce zero-sum tendencies in Experiment 2. In fact there was the opposite tendency toward normative judgment. Perhaps the relatively low grades lead participants to the normative conclusion that the grading criteria were relatively unfavorable to students, and thus to predictions that the student should do relatively poorly on the presentation. The combined results of Experiments 1 and 2 suggest that zero-sum bias is unidirectional in that people are more aware of the consequences of the gains of others than the losses of others.
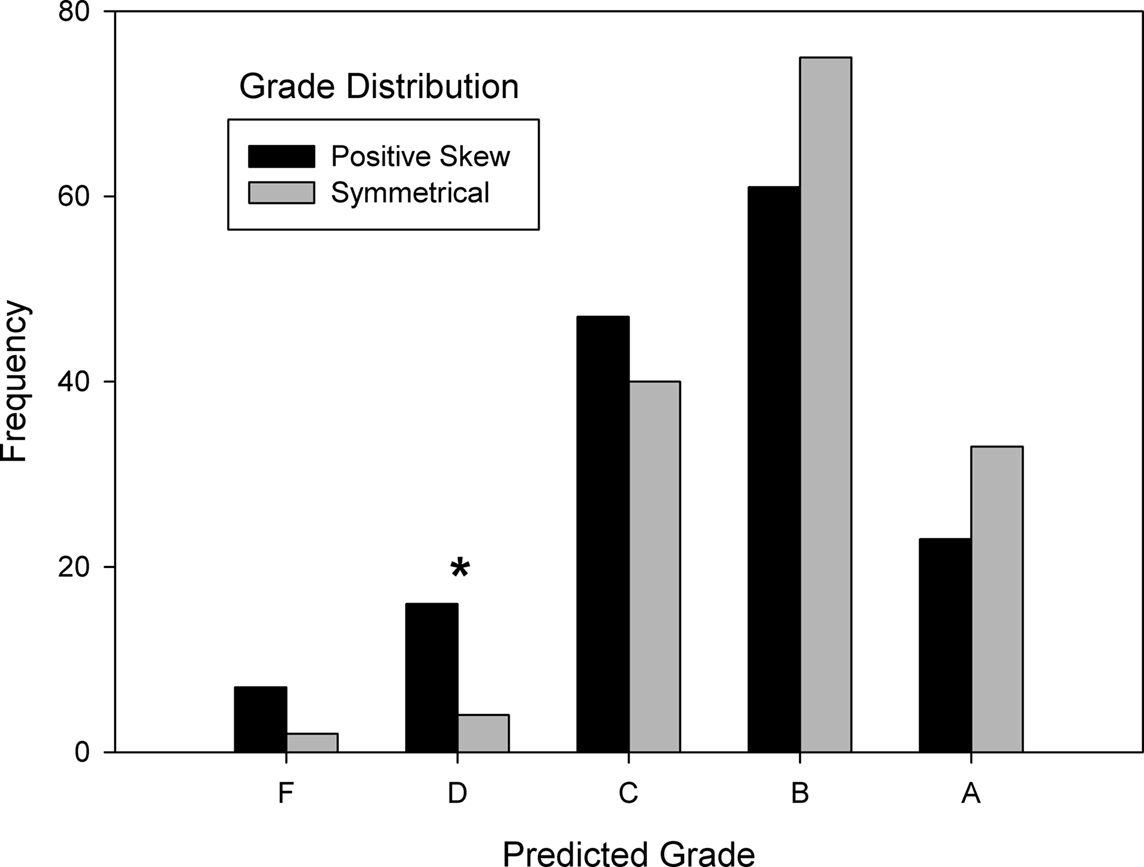
Figure 3. Predicted grade frequency as a function of grade distribution condition in Experiment 2. Distribution condition had a significant influence on grade judgments, particularly at the grade level marked with an asterisk (indicating p < 0.05). Consistent with normative judgment, positive skew increased low grade predictions and decreased high grade predictions.
Experiment 3
An important issue in bias research concerns identifying the conditions under which biases can be reduced. In the case of zero-sum bias among students, the non-zero-sum nature of grading is not often explicitly stated by instructors in individual courses. Experiment 3 tested the hypothesis that reminding students of the non-zero-sum grading policy would be sufficient to reduce zero-sum bias.
Because it was shown to induce zero-sum bias in Experiment 1, participants in Experiment 3 were shown a negatively skewed distribution (Figure 1A). Before making a grade prediction, half of the participants were given information reminding them of the absolute grading policy at the university. If zero-sum bias is susceptible to reduction, then such information should decrease the likelihood of low grade predictions and increase the likelihood of high grade predictions.
Materials and Methods
Participants were 368 undergraduate students at the University of Guelph, all of whom had completed at least one semester of full-time study. Informed consent was obtained from all participants, and the experiment was reviewed and approved by the Research Ethics Board of the University of Guelph.
Participants were randomly assigned to one of two experimental conditions: (a) grading policy information (N = 184), or (b) no grading policy information (N = 184). Participants in both conditions were shown a negatively skewed distribution (Figure 1A), and presented with the same text as in Experiments 1 and 2. Participants in the information condition only were additionally presented with the following text:
Note that University of Guelph grading policy states that “instructors are not to use predetermined, arbitrary distributions in the assignment of grades.” An individual student’s grade is determined by how the quality of their work compares to a predetermined standard of quality, rather than by how the quality of their work compares to the quality of the work produced by the other students in the course. For this reason, exams and assignments are not competitions among students for some predetermined and limited number of A’s, B’s, etc.
Note that the no information condition was identical to the negatively skewed distribution condition of Experiment 1.
Results
The results are shown in Figure 4. Statistical analysis revealed that information condition had a significant influence on grade prediction judgments [χ24 = 18.28, N = 368, p < 0.005]. If zero-sum bias is susceptible to reduction, then there should have been a lower frequency of low grade predictions and a higher frequency of high grade predictions in the information condition than in the no information condition. Separate analyses were done for each grade level to determine whether there was an influence of distribution condition. Although the trend at low and high grade levels was consistent with bias reduction, only the low grade levels reached statistical significance: predicted grades of D [χ21 = 5.77, N = 39, p < 0.05] and F [χ21 = 9.00, N = 16, p < 0.005] were less frequent in the information condition than in the no information condition. Predicted grades of A [χ21 = 2.47, N = 49], B [χ21 = 0.82, N = 147], and C [χ21 = 0.21, N = 117] were not significantly affected by information condition. These results demonstrated that information provision reduced zero-sum bias.
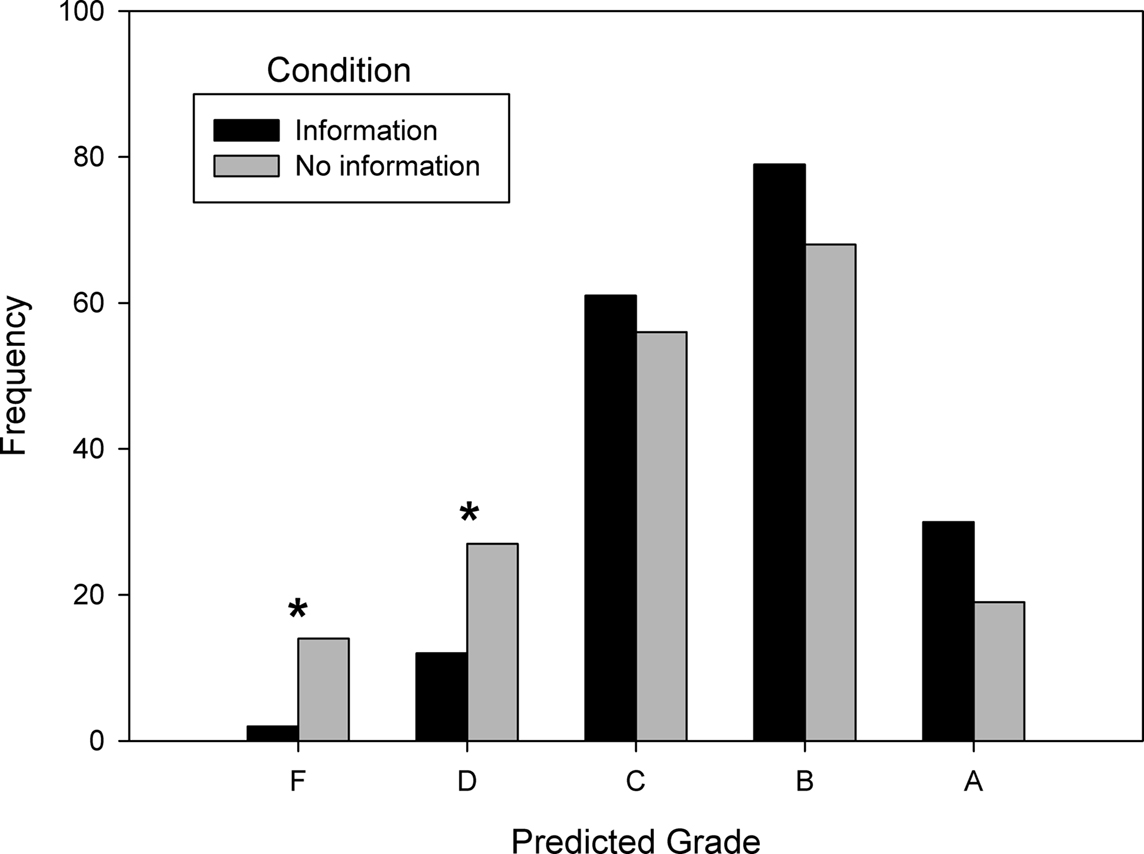
Figure 4. Predicted grade frequency as a function of information condition in Experiment 3. Information condition had a significant influence on grade judgments, particularly at those grade levels marked with an asterisk (indicating p < 0.05). Information decreased low grade predictions and increased high grade predictions.
Discussion
In three experiments, participants were shown the grade distribution after a majority of the students in a university course had completed an assigned presentation, and asked to predict the grade of the next presenter. A negatively skewed distribution, indicating that many high grades (desirable resource) had already been given, increased the likelihood of low grade (undesirable resource) predictions (Experiment 1). I suggest that this tendency is the result of a zero-sum heuristic that is applied indiscriminately when desirable resources have been allocated. Under non-zero-sum conditions, for example when there are unlimited resources available, the application of this heuristic leads to the biased judgment that no more desirable resources are available. In other words, people are prone to perceive a competition for limited resources even when there are unlimited resources available.
A positively skewed distribution, indicating that many low grades had already been given, did not increase the likelihood of high grade predictions (Experiment 2). This suggests that the zero-sum heuristic is not applied when undesirable resources are allocated.
In Experiment 3, participants were reminded that university grading policy prohibits instructors from placing limits on the availability of high grades, and this reminder mitigated the effect of a negatively skewed distribution on grade predictions.
Is the Zero-Sum Heuristic a Cognitive Adaptation?
Popular books (Wright, 2000; Rubin, 2002) have suggested that modern humans have a tendency toward zero-sum intuitions, and that such a tendency is a legacy of intra-group resource allocation and competition for status during a time when evolving humans lived as hunter-gatherers in relatively small groups. Intra-group competition resulted when finite resources (e.g., mates, high-status positions, food) were not guaranteed to be allocated evenly across group members. Uneven resource allocation could have arisen out of necessity (there simply was not enough to go around) or otherwise (high-status members controlled resource allocation and chose uneven allocation). Such conditions would have promoted the evolution of affective and cognitive adaptations to enable successful competition. Affective adaptations could include envy (Hill and Buss, 2008), and cognitive adaptations could include a zero-sum heuristic, because gains by others often meant losses to oneself, especially for indivisible resources such as mates and high-status positions in a well-organized hierarchy.
Although it can lead to bias, a zero-sum heuristic is sensible in that unlimited resource situations were likely rare during the era in which modern humans evolved, and are likely rare today for most people most of the time. Even the student participants examined here, one might argue, are not unwise to be wary of resource availability. For example, although grading policy makes it possible that many students in a course receive very high grades, such an occurrence rarely happens in practice. Instructors know that this is true because the quality of student work is almost always symmetrically distributed around a mid-range mean. From the student perspective, however, the relatively small likelihood of getting a very high grade could justify zero-sum intuitions.
The unidirectionality of zero-sum bias also makes sense from a cognitive/evolutionary perspective, given that limited resource situations are the historical norm. When resources are limited, the allocation of desirable resources means that those resources will soon be depleted. Thus people are wary of the consequences of desirable resource allocation, and zero-sum bias occurs when resources are unlimited. On the other hand, the allocation of undesirable resources has no implications for the depletion of desirable resources because desirable resources are either still available or already depleted. Thus people are less wary of the consequences of undesirable resource allocation, and judgments are normative when resources are unlimited.
In summary, it is possible that a zero-sum heuristic evolved as a cognitive adaptation to enable successful intra-group competition for limited resources. Similar arguments have been made concerning other examples of imperfect intuitive judgments (Cosmides and Tooby, 1996; Gigerenzer et al., 1999; Gigerenzer and Selten, 2002; Todd et al., 2005; Haselton and Nettle, 2006; Wilke and Barrett, 2009). It is important to note, however, that the experiments reported here provide insufficient evidence for the conclusion that a zero-sum heuristic is a cognitive adaptation. Applying the framework suggested by Schmitt and Pilcher (2004) for evaluating evidence for adaptation, the experiments provide insufficient breadth in that only psychological evidence (more specifically cognitive reasoning specificity) has been provided. Other forms of evidence are necessary before it can be concluded that the zero-sum heuristic is an adaptation.
It is also important to consider possible non-evolutionary reasons for why zero-sum bias was demonstrated in these experiments. The most obvious is that the student participants have been raised in a culture in which peers are considered competitors for a limited number of desirable career opportunities, and they have learned to treat all career-oriented activities (e.g., school) as limited resource situations. When resources are unlimited, such as at a university that prohibits relative grading, they are prone to zero-sum bias. Cultural factors and individual differences that could affect the application of a zero-sum heuristic are also considered below.
Societal Implications
The cognitive/evolutionary perspective favors an interpretation of zero-sum bias as a legacy of intra-group competition because psychological adaptations likely evolved at a time when inter-group interactions were relatively rare. Since that time, the likelihood of inter-group interaction has risen significantly. Thus it is interesting to consider how the zero-sum heuristic could affect judgments of inter-group interactions. Applied to inter-group judgments, the zero-sum heuristic would lead to the conclusion that a gain by another group (outgroup) means a corresponding loss for one’s own group (ingroup). Social scientists suspect that zero-sum thinking is the basis of psychological barriers to inter-group interaction. For example, economists blame zero-sum intuitions for public resistance to free trade because people find it hard to comprehend how both trading partners could gain, even though win–win scenarios are a common consequence of trade (Rubin, 2002). Similarly, the outsourcing of jobs to another country is very vulnerable to zero-sum-based resistance because the most direct and visible consequence is a gain of jobs by one country with a corresponding loss of jobs by another. Assuming that the CEOs of major corporations can be considered a group, public anger over high executive pay could stem from the feeling that their gain is our loss. Zero-sum perceptions have also been implicated as a contributing factor to inter-group prejudice (Bobo and Hutchings, 1996; Esses et al., 2005) and public resistance to immigration (Esses et al., 2003).
There is even evidence that consumers apply a zero-sum heuristic when evaluating products (Chernev, 2007). When two products (e.g., laundry detergents) are compared on a particular attribute (e.g., stain removal capability), the product that claims to specialize in that attribute is perceived as superior to a product that claims to have multiple specializations (e.g., stain removal, fading resistance, static prevention). Chernev (2007) suggested that the commitment of resources to the other attributes is perceived to come at a cost to the attribute-of-interest.
The research reported here examined perceptions of those who are affected by resource allocation (non-allocators), rather than those who make decisions about resource allocation (allocators). The complementary study of allocators, specifically those who must allocate resources among ingroup and outgroup members, has a long history in social psychology (Tajfel, 1970; Brewer, 1979). Such studies have demonstrated favoritism toward ingroup members, as well as zero-sum tendencies. Brewer and Silver (1978), for example, had participants choose monetary rewards (from among a choice matrix determined by the experimenters) for one ingroup and one outgroup member. Choices that maximized the reward for the ingroup member also provided large rewards for the outgroup member, and participants instead favored choices that maximized the difference between the ingroup and outgroup members, even when it meant a smaller-than-maximum reward for the ingroup member. Although both parties gained as a result of this choice, I suggest that this difference-maximization strategy is a manifestation of a zero-sum heuristic because it shows an irrational aversion to outgroup gains. Another example can be seen in the results reported by Tajfel (1970), who showed that participants allocating resources to two ingroup members chose to maximize joint profit whereas participants allocating resources to two outgroup members chose instead to split a smaller amount evenly. This is another example of irrational outgroup gain aversion that can be attributed to the zero-sum heuristic.
The pervasiveness of zero-sum thinking leads me to wonder whether it is a cognitive adaptation possessed by all humans (and probably other social animals as well). This offers a slightly different perspective from some social scientists who have emphasized individual differences, cultural differences, and situational factors. For example, individuals high in Social Dominance Orientation (Pratto et al., 1994) are more likely to show zero-sum tendencies when expressing attitudes about immigration (Esses et al., 2003). It also seems likely that people from collectivistic cultures would be less likely to show zero-sum tendencies. As for situational factors, it would not be at all surprising if groups who are chronically or currently low in socioeconomic status are more likely to jump to zero-sum conclusions (Bobo and Hutchings, 1996), or if public resistance to trade and immigration is greatest at times of economic stress. I suggest that the cognitive/evolutionary and social science perspectives are compatible. In other words, a heuristic possessed by all humans is more likely to be used by some individuals, in some cultures, and/or in some situations.
Social scientists have also offered ideas related to the reduction of zero-sum bias. For example, editorials targeting zero-sum beliefs might affect attitudes toward immigrants (Esses et al., 2003). Putting two groups in non-zero-sum situations in which cooperation leads to mutual gain and competition leads to mutual loss, such as in the Robber’s Cave experiment (Sherif et al., 1961), could conceivably reduce zero-sum bias (Wright, 2000). Economists credit economics education, such as providing historical examples of win-win trading, for public acceptance of trade agreements (Rubin, 2002). Future research will explore the efficacy of various strategies for the reduction of zero-sum bias.
On the other hand, there is reason to be concerned that publicizing zero-sum bias could result in the treatment of accurate zero-sum conclusions as inaccurate. For example, there are historical examples of win-lose trading. Proponents of free trade argue that such situations are temporary in that the losers eventually learn to discontinue trade. Nevertheless, when advocating for a proposed trade agreement, it is not sufficient to argue that the continuation of the agreement is contingent upon mutual benefit, or that there are historical examples of mutually beneficial trade agreements. The argument should instead be based on the likelihood that the proposed agreement will be mutually beneficial.
Earlier I suggested that the unidirectionality of zero-sum bias is related to self-interest – in a zero-sum world there is greater incentive to be wary of the gains of others than the losses of others. This could explain why members of the middle class tend to be more concerned about the wealth of the upper class than the poverty of the lower class. One might say that envy is more powerful than guilt. The social science approach, on the other hand, might emphasize the possibility that some individuals or cultures are more concerned about whether personal gain comes at a cost to others. For example, one might hypothesize that zero-sum bias will be bidirectional for people from collectivistic cultures, or for individuals high in egalitarianism (Katz and Hass, 1988), prosociality (Van Lange et al., 1997; Kurzban and Houser, 2005), or collectivism (Triandis, 1995). Future research will test this hypothesis.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research was supported by a grant from the Natural Science and Engineering Research Council of Canada. I thank Annemie Ploeger for helpful comments on an earlier version of the manuscript.
References
Bobo, L., and Hutchings, V. L. (1996). Perceptions of racial group competition: extending Blumer’s theory of group position to a multiracial social context. Am. Sociol. Rev. 61, 951–972.
Brewer, M. B. (1979). In-group bias in the minimal intergroup situation: a cognitive-motivational analysis. Psychol. Bull. 86, 307–324.
Brewer, M. B., and Silver, M. (1978). lngroup bias as a function of task characteristics. Eur. J. Soc. Psychol. 8, 393–400.
Chernev, A. (2007). Jack of all trades or master of one? Product differentiation and compensatory reasoning in consumer choice. J. Consum. Res. 33, 430–444.
Cosmides, L., and Tooby, J. (1996). Are humans good intuitive statisticians after all? Rethinking some conclusions from the literature on judgment under uncertainty. Cognition 58, 1–73.
Esses, V. M., Hodson, G., and Dovidio, J. F. (2003). “Public attitudes towards immigrants and immigration: determinants and policy implications,” in Canadian Immigration Policy for the 21st Century, eds C. M. Beach, A. G. Green, and J. G. Reitz (Montreal: McGill-Queen’s University Press), 507–535.
Esses, V. M., Jackson, L. M., Dovidio, J. F., and Hodson, G. (2005). “Instrumental relations among groups: group competition, conflict, and prejudice,” in On the Nature of Prejudice: Fifty Years After Allport, eds J. F. Dovidio, P. Glick, and L. A. Rudman (Oxford: Blackwell Publishing), 227–243.
Gigerenzer, G., and Selten, R., eds. (2002). Bounded Rationality: The Adaptive Toolbox (Cambridge, MA: MIT Press).
Gigerenzer, G., Todd, P. M., and the ABC Research Group. (1999). Simple Heuristics that Make us Smart (New York: Oxford University Press).
Gilovich, T., Griffin, D., and Kahneman, D., eds. (2002). Heuristics and Biases: The Psychology of Intuitive Judgment. Cambridge: Cambridge University Press.
Haselton, M. G., and Nettle, D. (2006). The paranoid optimist: an integrative evolutionary model of cognitive biases. Pers. Soc. Psychol. Rev. 10, 47–66.
Hill, S. E., and Buss, D. M. (2008). “The evolutionary psychology of envy,” in Envy: Theory and Research, ed. R. H. Smith (Oxford: Oxford University Press), 60–70.
Kahneman, D., Slovic, P., and Tversky, A., eds. (1982). Judgment Under Uncertainty: Heuristics and Biases. Cambridge: Cambridge University Press.
Kahneman, D., and Tversky, A. (1979). Prospect theory: an analysis of decision under risk. Econometrica 47, 263–291.
Katz, I., and Hass, R. G. (1988). Racial ambivalence and American value conflict: correlational and priming studies of dual cognitive structures. J. Pers. Soc. Psychol. 55, 893–905.
Kurzban, R., and Houser, D. (2005). Experiments investigating cooperative types in humans: a complement to evolutionary theory and simulations. Proc. Natl. Acad. Sci. U.S.A. 102, 1803–1807.
Pratto, F., Sidanius, J., Stallworth, L. M., and Malle, B. F. (1994). Social dominance orientation: a personality variable predicting social and political attitudes. J. Pers. Soc. Psychol. 67, 741–763.
Rubin, P. H. (2002). Darwinian Politics: The Evolutionary Origin of Freedom. New Brunswick, NJ: Rutgers University Press.
Schmitt, D. P., and Pilcher, J. J. (2004). Evaluating evidence of psychological adaptation: how do we know one when we see one? Psychol. Sci. 15, 643–649.
Sherif, M., Harvey, O. J., White, J., Hood, W., and Sherif, C. (1961). Intergroup Conflict and Cooperation: The Robber’s Cave Experiment. Norman, OK: University of Oklahoma Book Exchange.
Todd, P. M., Hertwig, R., and Hoffrage, U. (2005). “Evolutionary cognitive psychology,” in The Handbook of Evolutionary Psychology, ed. D. M. Buss (Hoboken, NJ: Wiley), 776–802.
Tversky, A., and Kahneman, D. (1974). Judgment under uncertainty: heuristics and biases. Science 185, 1124–1131.
Van Lange, P. A. M., Otten, W., De Bruin, E. M. N., and Joureman, J. A. (1997). Development of prosocial, individualistic, and competitive orientations: theory and preliminary evidence. J. Pers. Soc. Psychol. 73, 733–746.
von Neumann, J., and Morgenstern, O. (1944). Theory of Games and Economic Behavior. Princeton, NJ: Princeton University Press.
Keywords: heuristics, biases, intuitive judgment, cognitive adaptation, zero-sum
Citation: Meegan DV (2010) Zero-sum bias: perceived competition despite unlimited resources. Front. Psychology 1:191. doi: 10.3389/fpsyg.2010.00191
Received: 08 June 2010;
Accepted: 19 October
2010;
Published online: 05 November 2010.
Edited by:
Bernhard Hommel, Leiden University, NetherlandsReviewed by:
Annemie Ploeger, University of Amsterdam, NetherlandsCopyright: © 2010 Meegan. This is an open-access article subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Daniel V. Meegan, Department of Psychology, University of Guelph, Guelph, ON, Canada, N1G 2W1. e-mail:ZG1lZWdhbkB1b2d1ZWxwaC5jYQ==
