- 1 Institute of Sport Science, University of Bern, Bern, Switzerland
- 2 Faculty of Sport Science, Technische Universität München, Muenchen, Germany
The paralysis-by-analysis phenomenon, i.e., attending to the execution of one’s movement impairs performance, has gathered a lot of attention over recent years (see Wulf, 2007, for a review). Explanations of this phenomenon, e.g., the hypotheses of constrained action (Wulf et al., 2001) or of step-by-step execution (Masters, 1992; Beilock et al., 2002), however, do not refer to the level of underlying mechanisms on the level of sensorimotor control. For this purpose, a “nodal-point hypothesis” is presented here with the core assumption that skilled motor behavior is internally based on sensorimotor chains of nodal points, that attending to intermediate nodal points leads to a muscular re-freezing of the motor system at exactly and exclusively these points in time, and that this re-freezing is accompanied by the disruption of compensatory processes, resulting in an overall decrease of motor performance. Two experiments, on lever sequencing and basketball free throws, respectively, are reported that successfully tested these time-referenced predictions, i.e., showing that muscular activity is selectively increased and compensatory variability selectively decreased at movement-related nodal points if these points are in the focus of attention.
Paralysis by Analysis and Nodal-Point Motor Control
Constrained Actions and Step-by-Step Execution
“Keep your eye on the place aimed at, and your hand will fetch it; think of your hand, and you will very likely miss your aim” – a well known observation, already described by James (1890/2010, p. 520), subsumed in the Bliss–Boder-Hypothesis (Bliss, 1892; Boder, 1935), and termed “paralysis by analysis” by Schmidt (1982, p. 281). In a nutshell, the basic idea behind this phenomenon is that focusing attention on a well-learned action interferes with the quality of performance outcome. Given the multitude of opportunities for experiencing this phenomenon in sports, in music-making or in other everyday life situations, it is surprising that it has for long been neither fully understood nor empirically investigated. Starting from the then surprising finding that giving instructions on technical details of a skill actually impairs learning (Wulf and Weigelt, 1997), primarily Gabriele Wulf and her collaborators have repeatedly been able to show that learners should not focus on a movement itself, but rather on its effects in the environment (for a review, see Wulf and Prinz, 2001; Wulf, 2007). In a study by Wulf et al. (1998, Experiment 1), for example, participants learned to produce slalom-like movements on a ski simulator. Participants were instructed to focus their attention either on their feet exerting force to the platform (internal focus) or on the platform’s wheels to which the force was exerted (external focus). The latter group showed improved performance in both learning and retention. This result was not only replicated in laboratory settings (e.g., Wulf et al., 1998, Experiment 2: stabilometer), but also in externally valid designs (e.g., Wulf et al., 1999: golf pitch shots). Furthermore, Wulf and collaborators have shown that learners seem to generally prefer an external focus of attention (Wulf et al., 2001), that the distance of the focused effect is of importance (McNevin et al., 2003), that it is not the external stimulus itself but the action effect that needs to be focused on (Wulf et al., 2000) and that an external focus is beneficial not only with respect to given instructions but also to augmented feedback conditions (Shea and Wulf, 1999).
Consistent with these findings are results from research on implicit motor learning. In particular, Masters (1992) found that participants with a small pool of explicit knowledge on the performance of golf putting were less likely to fail under a pressure condition than participants who had been given a vast amount of explicit rules concerning movement production. He proposed that the performance of explicit learners breaks down because they are more likely to consciously process movement details, thereby disrupting the acquired automaticity of implicit motor control. Beilock and Carr (2001) assign those kinds of “deautomatization” approaches to the family of explicit monitoring theories for “choking under pressure” (in contrast to distraction theories). The basic assumptions of explicit monitoring theories are that performance pressure increases the anxiety about performing correctly, which in turn enhances the attention paid to the “step-by-step control” of sensorimotor skill. Consequently, proceduralized, automatized processes, which under non-pressure conditions are not necessarily run employing working memory, are disrupted (Beilock et al., 2004; see also Baumeister, 1984; Lewis and Linder, 1997). Compatible with these assumptions for impaired motor control, a “constrained action hypothesis” was formulated by Wulf and colleagues in order to explain the findings of impaired learning under internal focus conditions (see Wulf et al., 2001). Again, two types of processes are stated to underlie motor control and learning, conscious and automatic process, respectively. If performers direct attention to their body movements, this conscious intervention “constrains” the motor system and leads to the disruption of automatic processing. On the other hand, directing attention to the effects the movement yields in the environment allows the more automatic and unconscious processes to take over movement control.
Explicit monitoring theories provide a strong framework for a deeper understanding of the phenomena of choking under pressure and paralysis by analysis as well. However, a suggestion for the detailed sensorimotor mechanisms underlying the resulting breakdown is still lacking. So what exactly are the processes of movement control that are impaired by an internal focus and exactly in which way? The statements that can be found in literature remain rather vague on this topic. Perhaps the most explicit attempt of outlining hypothetical mechanisms on a motor control level has been penned by Beilock et al. (2002, p. 8) in reference to Masters’ (1992) and Masters et al. (1993) proposal,
that attention to high-level skills results in their “breakdown,” in which the compiled real-time control structure of a skill is broken down into a sequence of smaller, separate, independent units – similar to how performance may have been organized early in learning. Once broken down, each unit must be activated and run separately, which slows performance and, at each transition between units, creates the opportunity for error that was not present in the “chunked” control structure.
In the following, we will elaborate this proposal in depth, in the end inferring a “nodal-point hypothesis,” which allows the deduction of some specific predictions that are open for empirical testing. In the course of developing the hypothesis, we are trying to weave together four threads of thought, each being based on classical ideas of motor control literature and each having gained considerable empirical support. These four threads may be labeled as ideo-motor principle and units of behavior (1.2), serial chaining and endpoint control (1.3), “freezing” and muscular co-contractions (1.4), and exploitation and compensatory variability (1.5) (see also Hossner, 2009, for a further illustration of the argument).
Ideo-Motor Principle and Units of Behavior
According to the ideo-motor principle, movements are coded in terms of the effects they evoke. As already stated by James (1890/2010) in his chapter dealing with will, “our idea of raising our arm... or crooking our finger, is a sense... of how the raised arm or the crooked finger feels” (p. 499). James’ basic idea originating from introspection received considerable support during the nineteenth century, fell into disrepute as a consequence of behaviorists’ attacks and has regained importance since the 1960s (for a review, see Greenwald, 1970, pp. 83–85). Today, the ideo-motor principle has been expressed more formally in a number of theoretical works ranging from the common-coding approach by Prinz (1997) to the theory of event coding by Hommel et al. (2001) and the concept of anticipatory behavioral control by Hoffmann (1993, 2003). These theoretical re-formulations of the ideo-motor principle have stimulated a tremendous amount of research on the effect-relatedness of motor control (for a recent review, see Hommel, 2009).
In the present context of paralysis-by-analysis phenomena, the concept of ideo-motor action is important because of the suggestions that (a) an elementary behavioral unit always consists of a response R, its sensory effects E, and the initial conditions given by the situation S, that (b) responses are governed by their intended and anticipated effects in those SRE-triplets, that (c) perceived stimuli and perceived effects basically fall into the same category of perceived “events,” that (d) for this reason, every perception may be considered as the perceived effect of the previous elementary act, that (e), as already stated clearly by Lotze (1852/1966), there is nothing else to perceive from the movement than those effects, and that (f) focusing attention therefore necessarily refers to effects of elementary behavioral acts.
Serial Chaining and Endpoint Control
The second thread develops at least partly from the first. In light of the ideo-motor principle, it has been argued that if in the process of learning effects are accurately attained they can be serially chained to sequential control structures. Greenwald (1970), for example, hypothesized that it is the experience of contingent SRE-triplets that leads to a shift in execution control from stimuli to anticipated effects. When these effects then follow each other reliably, they become associated and form a sequence. Eventually, the final effect takes over the control of the entire sequence.
Obviously, this version of the concept of serial chaining is closely related to the idea of endpoint control of action from the final effect “backward.” This effect has extensively been investigated in studies on table-tennis experts’ strokes conducted by Bootsma (1988), who found a (τ-driven) “homing in” of movement parameters, as the variance in the direction of the bat’s travel declines until the moment of ball–bat contact. Furthermore, the idea of sensorimotor endpoint control is central for the endstate-comfort hypothesis by Rosenbaum and colleagues (Rosenbaum et al., 2001; see also Cohen and Rosenbaum, 2004) and, on a more algorithmic and implementational level, for the vector-integration-to-endpoint (VITE) model by Bullock and Grossberg (1988).
“Freezing” and Muscular Co-Contractions
The argument’s third thread is based on the concept of three motor learning stages as it has been introduced by Bernstein (1944/1967), where bodily degrees of freedom are initially constrained to ensure control, eventually released in order to enable more efficient movements, and exploited in the end with respect to environmental and body dynamics. Empirical support for the transition from the first to the second stage, i.e., “from freezing to freeing,” has been presented, for example, by Vereijken et al. (1992) for slalom-like movements on a ski simulator, and by Cordier et al. (1994) for free climbing. Most interestingly, the latter research group not only managed to show an increase of movement smoothness in the course of learning (expressed by a decrease of a “geometric index of entropy”), but, furthermore, demonstrated a “re-freezing” in already learned climbing movements as a function of increased anxiety induced by climbing height (see also Pijpers et al., 2005).
On a muscular level, one obvious way to “freeze” degrees of freedom appears to be an increase in antagonistic co-contractions, which may be a strong strategy for novices in order to make the motor system controllable. Nevertheless, the strategy is essentially accompanied by the disadvantage of suboptimal efficiency. Not only is more effort needed in order to achieve a certain goal, a “maximum-control strategy” through increased body rigidity is, in addition, by no means sufficient to guarantee an optimal movement outcome. This has been shown, e.g., by Morrison and Newell (2000) for the postural tremor in a pointing task, and by Weinberg (1978) for the comparison of ball-throws performed by high-anxiety vs. low-anxiety participants. More recently, detrimental effects of an increase in muscular activity as a function of a movement-related focus of attention was also found in performing biceps curls (Vance et al., 2004), basketball free throws (Zachry et al., 2005), dart throws (Lohse et al., 2010), and force production tasks in general (for a review, seeMarchant, 2010). Taken together, these results are in perfect line with the here developed argument that explicit monitoring of movements generally leads to a “re-freezing” of degrees of freedom by an overall increase of muscular activity.
Exploitation and Compensatory Variability
The fourth thread of the argument is closely related to the points discussed before. It concerns the exploitation of system dynamics in Bernstein’s (1944/1967) final stage of motor learning. On the basis of the experimental results reported in the previous paragraph, Morrison and Newell (2000) suggest performing pointing movements with low limb stiffness in order to reduce tremor in the finger-tips and allow for compensatory coupling between limb segments. In those cases of functional covariation or compensatory variability of movement parameters, it appears that component processes of the movement are systematically related in such a way that deviations in one component are compensated for by fluctuations in other components (see Müller and Loosch, 1999, for a review). The resulting, stable and parsimonious performance in the expert stage of motor learning, then again, is a product of coupling of degrees of freedom, yet not in form of the rigid coupling typical for initial learning, but rather in the form of a functional coupling in a task-subserving manner. Empirically, such compensatory processes have been found mainly in the spatial domain (e.g., Arutyunyan et al., 1968; Darling and Cooke, 1987), but also in the temporal (e.g., Bootsma, 1988; Cordo, 1990) and in the spatio-temporal domain (e.g., McDonald et al., 1989; Müller, 2001).
The Nodal-Point Hypothesis
In summary, movements seem to be controlled by their intended effects, so that SRE-units are the basic building blocks of coordinated motor behavior (thread 1). In the process of learning, these units are connected to sensorimotor chains, so that, in the expert stage, an intended final goal and the perception of adequate initial conditions are sufficient to let the whole chain rattle off to the endpoint’s final effect (thread 2). This chaining procedure is not only accompanied by a reduced necessity of checking the attainment of intermediate effects (which is phenomenologically perceived as automatism); furthermore, serial chaining appears to coincide with a freeing of degrees of freedoms of the motor system and, on a muscular level, with less activity caused by non-functional co-contractions of agonist and antagonist muscles (thread 3). Thus, reactive phenomena and given properties of the sensorimotor system, e.g., regarding compensatory variability, may be exploited more effectively in order to ensure stable and parsimonious performance and control (thread 4).
Weaving together these four threads with their sound theoretical background and empirical evidence, we argue for a nodal-point hypothesis for impaired motor performance as a result of a movement-related attentional focus. In a nutshell, the core assumption of the hypothesis is that the phenomenon of paralysis by analysis simply reflects an inversion of the serial chaining mechanism sketched above – to some extent in the same sense as has been discussed in the work on choking under pressure, for example, by Masters (1992), Masters et al. (1993), Beilock et al. (2002), or Pijpers et al. (2005).
In more detail: in the process of formation of chains of SRE-units in motor learning, there is initially a need to attend to the effects of each single triplet. A young child, for example, will have to focus on his or her hands grasping a cup in order not to spill its contents. As chunks of SRE-units evolve during the process of motor learning, there is less need to attend to effects of intermediate responses as the endpoint’s final effect takes over control. As a consequence, optimization processes concerning muscular efficiency, or exploitation of systems dynamics are no longer restricted to processes within the basic units, but may be extended to chunks of units, i.e., an imprecise attainment of a certain sub-goal may be compensated for by a functional adaptation of the subsequent unit. The attainment of those sub-goals then does not need to be attended to anymore as the associated effects appear to happen increasingly reliably. However, the prior effects within the sensorimotor chain may still serve as anchors, or as nodal points of action sequences, i.e., they still may be attended to, either in cases where attention is voluntarily directed to the nodal point or in cases where the anticipated sub-goal’s effect does not occur: while the reader does not need to attend to grasping the coffee cup while reading this article, he or she can certainly do so and definitely will, as soon as the handle is missed or the handle slips.
What are then the consequences of a movement-related attentional focus in a well-learned movement? First of all, on the basis of the nodal-point hypothesis, a movement-related focus can usually be translated as attending to a nodal point of a sensorimotor chain, because, from a temporal point of view, the movement (e.g., putting) typically precedes the intended final outcome (e.g., holing in). Therefore, a movement-related focus typically results in setting an “in-between endpoint” and splitting up the entire chain into two parts: the first part beginning with the prior initial conditions of the first SRE-unit and ending with the effects that are associated with the nodal point in focus, and the second part beginning with the initial conditions of the subsequent SRE-unit and ending with the effects that are associated with the prior endpoint. Provided that serial chaining is accompanied by a decrease of muscular activity and an increase of compensatory variability, as has been stated before, two clear predictions can then be deduced from the hypothesis for a shift from endpoint control to nodal-point control: if the focus of attention is directed to an intermediate effect, exactly at this nodal point, increased muscular activity due to muscular co-contractions, and decreased compensatory variability can be expected, compared to the endpoint-control condition, respectively.
Empirical Predictions
It is worth noting that – in contrast to existing explicit monitoring theories for the phenomena of paralysis by analysis or choking under pressure – predictions derived from the nodal-point hypothesis are formulated on an operational, motor control related level as the underlying mechanisms are defined in a clear-cut manner, and methods for measuring muscular activity and compensatory variability can easily be found. Furthermore, they do not refer to overall consequences of an internal compared to an external focus of attention; instead, specific effects are predicted for specific points in time. Therefore, a strong version of the hypothesis predicts selective effects for the comparison of two nodal-point conditions, i.e., for the comparison of focusing on nodal point NPi vs. focusing on nodal point NPi+1. In this case, the predicted effects should only occur at the nodal point in focus and not at the other one, and this statement even holds for the experimental variant that both nodal points are movement-related and may therefore be assigned to a focus condition that traditionally has been subsumed under the label of internal focusing.
In the following, we present two experiments that directly tested this strong version of the nodal-point hypothesis. Other studies cited above, in particular the basketball experiment conducted by Zachry et al. (2005), may be interpreted as generally supporting our ideas, however, and, most decisively, these studies are not looking at time-referenced effects. In Experiment 1, a laboratory task was used (lever sequencing), while Experiment 2 employs a real-life complex motor skill (basketball free throws). Surface electromyography (EMG) was captured from relevant muscles and compensation scores were calculated in the temporal and spatial domain, respectively. For a set of defined nodal points, NP1–NPn, the predictions were specified that, if NPi is focused and NPi refers to an intermediate, movement-related effect, myoelectric activity should be relatively high at NPi and compensatory variability relatively low at NPi (in-focus), compared to a condition where one of the other nodal points is focused (out-of-focus) and vice versa. Instructions of focusing on an endpoint-related event (external-focus) or of not specifically focusing at all (no-focus) served as additional control conditions.
Due to time-consuming procedures of data acquisition and processing, and to the necessity of well-experienced participants as well, only a small number of participants could be examined. For this reason, overall sample size was optimized a priori. The calculated minimum overall sample size of N = 14 for an experimental within-subject design was then divided into two sub-samples of N1 = 8 for Experiment 1 and N2 = 6 for Experiment (for details of this calculation, see Optimal Sample Sizes and Statistical Power of Appendix). For these small sample sizes, statistical predictions were stated in expected effect sizes (Cohen’s f; Cohen, 1988). For inferential statistical tests on differences (ANOVAs with repeated measures), large effect sizes (f > 0.40) were predicted for the crucial contrasts of in-focus vs. out-of-focus conditions in order to reach an overall significance with p < 0.05 (for details of this calculation, see Optimal Sample Sizes and Statistical Power of Appendix). Although no quantifiable effects for the secondary comparisons of out-of-focus vs. external/no-focus conditions could be derived from the nodal-point hypothesis, obviously, non-significant effects of less size (f < 0.25) were demanded in support of the hypothesis. For all prediction-related inferential statistics in Experiment 1 and 2, besides F- and exact two-tailed p-values of the ANOVA comparisons, corresponding f′-values are reported as measures of effect size (i.e., f-values calculated from the within-subject design’s dependent data columns) and, in addition, Cohen’s effect sizes f that can be derived from that measure (i.e., f-values that fit Cohen’s conventions for independent measures). In the General Discussion, these effect sizes are used to conduct overall tests on significance. Please note that exclusively for these overall inferential tests significance of the in-focus vs. out-of-focus contrast is predicted and, due to small sample sizes, not for the p-values reported in the Sections “Results” of Experiment 1 and Experiment 2 (for details of this rationale, see Optimal Sample Sizes and Statistical Power and Overall Test on Significance of Appendix).
Experiment 1: Lever Sequencing
Introduction
In Experiment 1, the nodal-point hypothesis was tested in an internal valid laboratory set-up in which a sequence of lever positions needed to be produced bimanually. Nodal points in this task are defined clear-cut by the stop positions of two levers. According to the nodal-point hypothesis, after extensive learning, focusing on an intermediate stop position should result in selectively increased muscular activity and reduced compensatory variability at this position. In the lever-sequencing task, room for compensatory processes is left only in the temporal domain.
Materials and Methods
Sample
Eight right-handed undergraduate students (four female, four male, age 20–26 years) volunteered for the experiment. All participants were familiar with the experimental task since they had already taken part in a previous experiment and had performed 400 trials on the same apparatus. They were chosen from a sample of 32 participants on the basis of availability and constant and reliable performance in the final stage of the previous experiment. Consequently, all participants were able to produce the complex sequence without an error and without the necessity of focusing on details of the desired movements. Participants were informed about the experimental procedure and signed a consent form.
Procedure
Participants continuously had to produce a complex lever sequence. The two levers of the apparatus could independently be pushed or pulled, tilted inwards or outwards, and twisted inwards or outwards to mechanical stops (see Figure 1). The experimental sequence consisted of seven consecutive configurations beginning with an inversion in all six dimensions, i.e., a combination of pushing/pulling, tilting and twisting movements of both hands, and being followed by five transitions that required inversions in four dimensions each. Inter-individually, different sequences were used; however, sequences were held constant intra-individually for each participant over the whole experiment. Movement times were measured from the complete positioning of one configuration to the next, resulting in five transition times (after the initial full inversion; for further details, see Apparatus). The initiation of every single trial was determined by the participants.
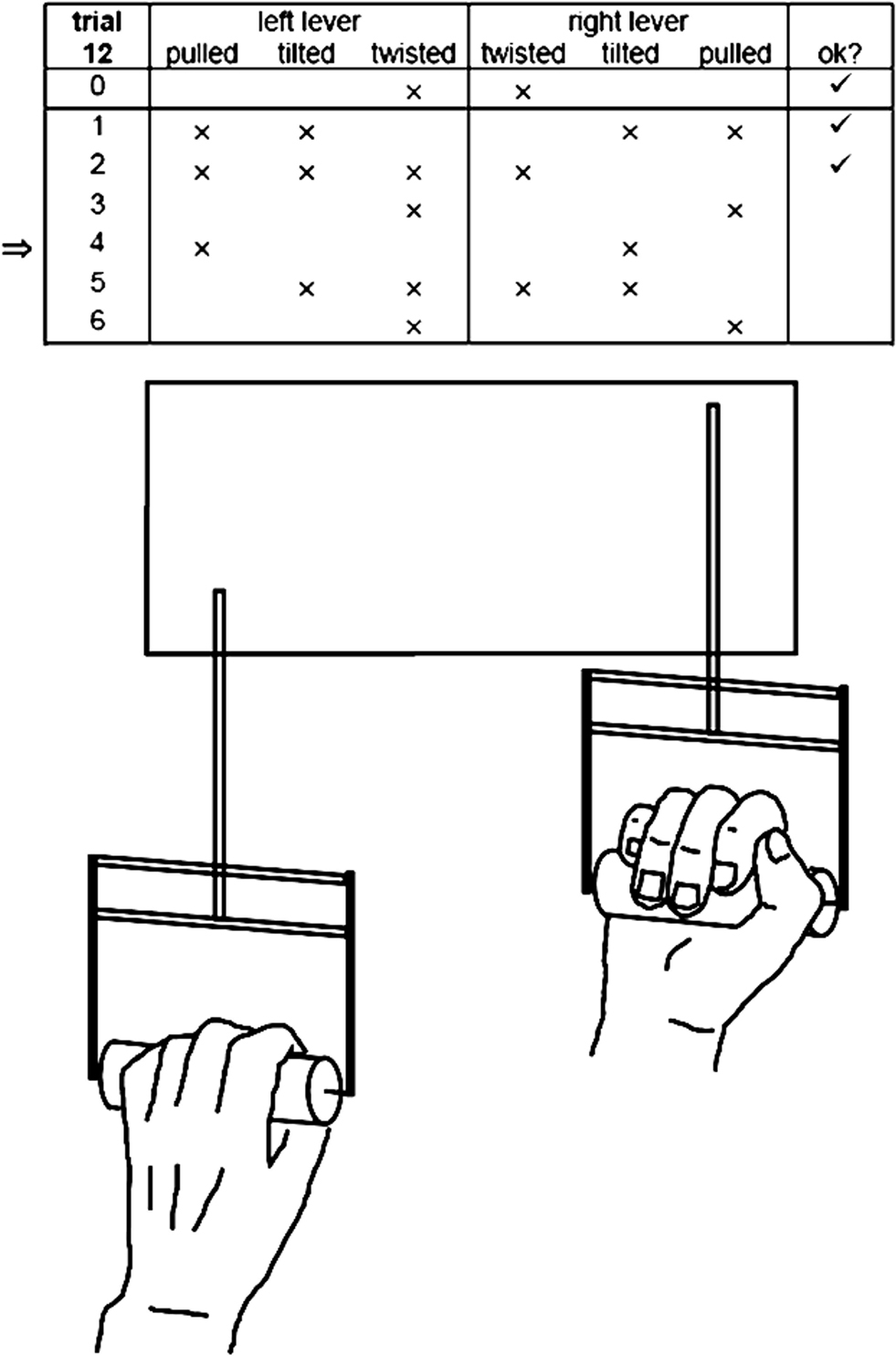
Figure 1. Lever sequencing: two levers can be independently moved in three dimensions each, i. e., pushed/pulled, tilted and twisted to mechanical stops. After an initial configuration 0, six configurations 1–6 must be positioned as indicated by crosses resp. blanks on the computer screen.
Participants had to appear for two sessions taking about 2.5 h each, a training session about 5 weeks after the previous study, and a test session 7 days later. The training session consisted of eight blocks of 50 trials each, beginning with a reminder block in order to get accustomed again to the already familiar lever sequence. For the next six blocks, participants’ task was to produce the sequence as usual while particularly focusing on one certain configuration. The demanded focus was changed blockwise in a random counter-balanced order, different for each participant. The last block of 50 trials was a no-focus block where participants were asked to produce the sequence without focusing on any special configuration.
The test session started with the application of EMG surface electrodes and a couple of familiarization trials in order to check the EMG recordings and get participants accustomed to the new conditions. Afterward, eight test blocks were conducted with no-focus blocks at the beginning and the end, and with six focus blocks in between. For each participant, the order of the focus blocks was the same as in the training session. Contrary to the trainings session, data acquisition in the test blocks was terminated as soon as 16 valid trials were achieved. A trial was rated as valid if the online control of EMG recordings showed no artifacts and if the participant confirmed having complied with the instructions, i.e., having the impression of an efficient (“automatic”) movement production with an accentuated focus on the demanded configuration.
Apparatus
For the sequencing task, a self-developed hardware and software system, the so-called Ξ-apparatus was used (for Ξ = “csi” = complex sequencing inventory, Figure 1). When operating the apparatus, participants sit in front of a computer screen holding the handles of two levers in their hands (length 15 cm, diameter 3 cm, sagittal distance from the trunk to the handles about 25 cm, distance between the handles 47.5 cm). From a neutral, upright position (handles of the levers parallel to the body’s longitudinal axis), the two levers can be moved independently from each other to mechanical stops in three dimensions by pushing or pulling them (translation parallel to the body’s sagittal axis, maximum extent ± 4.0 cm), by tilting them inwards or outwards (rotation in a plane parallel to body’s frontal plane, maximum extent ±60°), and by twisting them inwards or outwards (rotation around the handle’s longitudinal axis, maximum extent ±60°). The first 10 percent of the maximum movement path indicate a “blank” positioning, i.e., the lever is pushed, tilted outwards and twisted inwards; the last 10 percent of the maximum movement path indicate a “cross” positioning, i.e., the lever is pulled, tilted inwards and twisted outwards. In the experiment, the seven target configurations of the sequence (0–6) were displayed as six cells per row in a 6 × 7-matrix on the computer monitor, blanks and crosses representing the desired configurations of the two levers. Check symbols right beside the rows indicated the complete achievement of a desired configuration. In Figure 1, e.g., the check symbol for configuration 2 indicates that target configuration 2 has just been positioned successfully, i.e., that the left lever is pulled, tilted inwards and twisted outwards and the right lever is pushed, tilted outwards and twisted outwards. The configuration participants were asked to focus on was highlighted by an arrow on the left side of the configuration matrix. After a sequence was completed, a refreshed matrix without check symbols appeared on the computer screen as soon as both levers had been moved back into the start configuration (0).
For the calculation of transition times, the current positions of the levers in the six dimensions are captured by potentiometers, after voltage feed, producing signals from 0 to 2.5 V which are collected with a sample rate of 1000 Hz. After online-data smoothing using a second-order Butterworth low-pass filter with a cut-off frequency of 10 Hz, time intervals from the point of leaving the initial configuration to the points of acquisition of the target configurations are calculated online and stored electronically in ms-units. In addition, a spike signal is generated by the apparatus every time a target configuration is positioned successfully. In the experiment, this signal was exported to a free channel of the EMG device, serving as a trigger for synchronizing kinematic and EMG data.
Regarding EMG, data of four muscles (anterior deltoid muscle, lateral head of the triceps brachii, biceps brachii, digital extensor) of the right arm were recorded following the SENIAM guidelines (Hermens et al., 1999). Surface mounted Ag/AgCl-electrodes (∅ 10 mm, intermediate detection-surface distance of 3 cm) were placed on the skin above the belly of each respective muscle (Delagi and Perotto, 1981). A differential electrode was placed above the clavicula. The active amplifiers had a bandwidth of 10–1000 Hz, a common mode rejection ratio of 120 dB and an input impedance of 1012 Ω. Data of surface EMG was sampled at a frequency of 1000 Hz by using Z2 software by Biovision (Wertheim, Germany).
Data analysis
From kinematic data collection, raw data was available for five intervals per sequence, 16 valid trials, and eight focus conditions per participant. As participants had been asked to constantly produce the sequence, the task may be interpreted as a special version of an unpaced rhythm production, as extensively examined following Wing and Kristofferson’s (1973) suggestion of a two-level timing model. The key characteristic of unpaced rhythm production is the negative correlation of successive intervals, which means that a too short interval is typically followed by a relatively long one and vice versa, reflecting sort of temporal compensation in order to maintain an overall constant rhythm. Thus, also for the lever-sequencing task negative correlations were expected for consecutive intervals and, furthermore, a reduction of the absolute values of the coefficients as a consequence of focusing on the configuration in between. Subsequently, correlation coefficients were calculated intra-individually for all four pairs of consecutive time intervals (12–23, 23–34, 34–45, 45–56), always being based on 16 pairs of interval lengths. For the purpose of plausibility check, coefficients for non-consecutive time intervals (12–34, 12–45, 12–56, 23–45, 23–56, 34–56) were also computed. Spearman correlations were preferred because of abnormally distributed data series observed in 19.4% of the cases. In addition, the coefficients were Fisher Z-transformed in order to allow for the conduction of parametric inferential statistical tests.
Lastly, in order to obtain prediction-related data, values for consecutive intervals were pooled with respect to the situation that the configuration in-between – in the present context: the respective nodal point – was in the focus of attention (in-focus), that the respective nodal point was not in focus, but others were (out-of-focus), or that no focus was demanded at all (no-focus). In more detail, the in-focus value was calculated as the mean of the Fisher Z-transformed Spearman correlations for the transitions 12–23, 23–34, 34–45, and 45–56 from the blocks, when participants were asked to focus on configuration 2, 3, 4, and 5, respectively. The mean out of these four coefficients was contrasted with the out-of-focus value, i.e., the mean of the remaining (4 − 1) × 4 = 12 coefficients from the blocks with a demanded focus on configuration 2, 3, 4, and 5, as well as of the 4 × 2 = 8 coefficients from the blocks when participants were asked to focus on configuration 1 and 6, respectively. The no-focus value was obtained by averaging the 4 × 2 = 8 coefficients from the blocks where participants were asked to produce the sequence without focusing on any special configuration. As a result, in-focus and out-of-focus values both refer to conditions traditionally termed as internal focus conditions as in both cases movement-related instructions has been given. Furthermore, the calculations of in-focus and out-of-focus values (in large part) refer to the same trials and only differ with respect to the point in time when the calculation has been performed, i.e., with respect to the time-referenced predictions of the nodal-point hypothesis.
For muscular activity, EMG data was available for four muscles, 16 valid trials, and eight focus conditions per participant. Raw data was filtered twice with a second-order Butterworth filter with a high-pass cut-off frequency of 15 Hz (forward/backward in order to avoid phase shifts). After rectifying the filtered data (fullwave), myoelectric activity (EA) was calculated as the mean amplitude over ±45 ms windows around the trigger signals indicating the six points of successfully positioning a target configuration. A 90-ms interval was used because even the shortest transitions times deliberately produced by participants did not fall below 180 ms so that the 90-ms windows for data analysis were separated by time intervals of the same magnitude at least. Despite the fact that muscular activity typically precedes overt movement, a ±45-ms window was preferred over, e.g., a −90-ms window, as the theory-deduced prediction is on attentional monitoring of effects in the environment and not on focusing on the way these effects are muscularly produced (see General Discussion, for a further examination of this issue).
For further aggregation, the EA values over the course of 16 trials per muscle, nodal point, focus condition, and participant were averaged. Because of significant violations of the normal distribution in 20.2% of the cases, Andrews’ Wave estimation was used as a measure of central tendency. Subsequently, the eight estimators for the eight focus conditions were z-score transformed separately for the four recorded muscles, six nodal points, and eight participants, respectively, resulting in standardized, relative EA values. This step of data aggregation is illustrated in Figure 2, where, for a selected participant (P3), muscle (triceps brachii), and block trial (no. 9), EMG raw data is depicted, from the top to the bottom for six focus conditions (NP1–NP6) as well as for two no-focus conditions (NO1, NO2). Triangles indicate points in time when configurations 1–6 have successfully been achieved; bold triangles flag the respective in-focus configuration. In relation to the other focus conditions, muscular activity at, e.g., nodal point 4 (fourth triangle) is relatively high when this nodal point is in the focus of attention (condition NP4). Because these relative values were of major interest with regard to the research question, z-score transformation was favored over normalizing EMG magnitude by the isometric maximum-effort contraction.
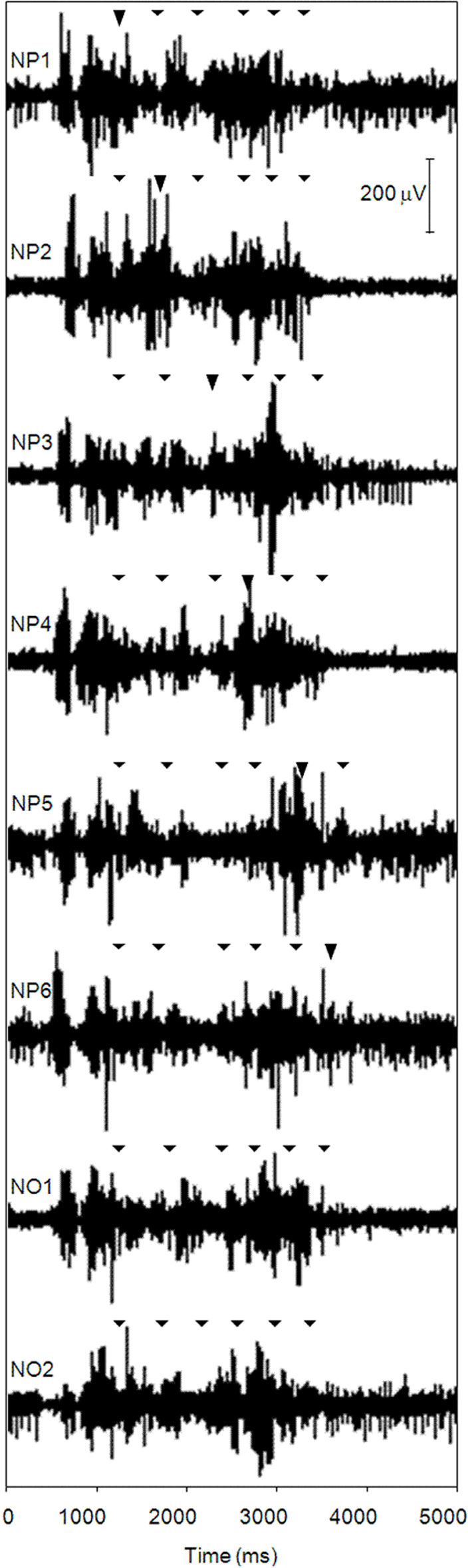
Figure 2. Lever sequencing: raw electromyographic data of a selected participant (P3), muscle (lateral head of the triceps brachii), and trial (no. 9 out of 16 trials per focus block), for six focus conditions (NP1–NP6) and two no-focus conditions (NO1, NO2). Triangles indicate points in time when configuration 1–6 has successfully been positioned; bold triangles flag the respective in-focus configuration.
The average of the z-scores across the four muscles represents overall relative muscular activity as the dependent variable of the experiment. The rationale behind this step of data aggregation is that muscular co-contractions should result in relatively high muscular activities, if the relevant muscles were successfully recorded. If this was not the case, nothing else than stochastical variance can be expected in the muscle-specific z-score with the only consequence of adding noise to the aggregated overall relative muscular activity value and, in turn, making the confirmation of the co-contraction prediction more difficult. Relative muscular activity should therefore be regarded as a sufficient measure for “(re-)freezing” of degrees of freedom (see General Discussion, for a further examination of this issue).
As already been described for the kinematic data, prediction-related data was obtained in the end by pooling cells to in-focus, out-of-focus, and no-focus values. For this purpose, the in-focus value was calculated as mean of the six overall relative EA scores for nodal point 1–6 from focus conditions NP1–NP6 when the respective nodal point was in the focus of attention. The remaining (6 − 1) × 6 = 30 EA scores from the focus trials were used to aggregate the out-of-focus value and the 6 × 2 = 12 EA scores from the no-focus trials for the computation of the no-focus value. Again, it should be noted, that in-focus and out-of-focus values both refer to focus conditions traditionally been labeled as “internal” and that both values only differ with respect to the time-referenced predictions derived from nodal-point hypothesis as both values are drawn from one and the same trials.
Results
Temporal compensation
Fisher Z-transformed correlations between consecutive and non-consecutive time intervals between target configurations are depicted in Figure 3 as mean over all focus conditions. As expected, contrary to non-consecutive intervals, consecutive intervals show negative coefficients, F(9,63) = 16.15, p < 0.01. In the context at hand, this significant result may be interpreted as strong evidence for the assumption of effects of temporal compensation per se.
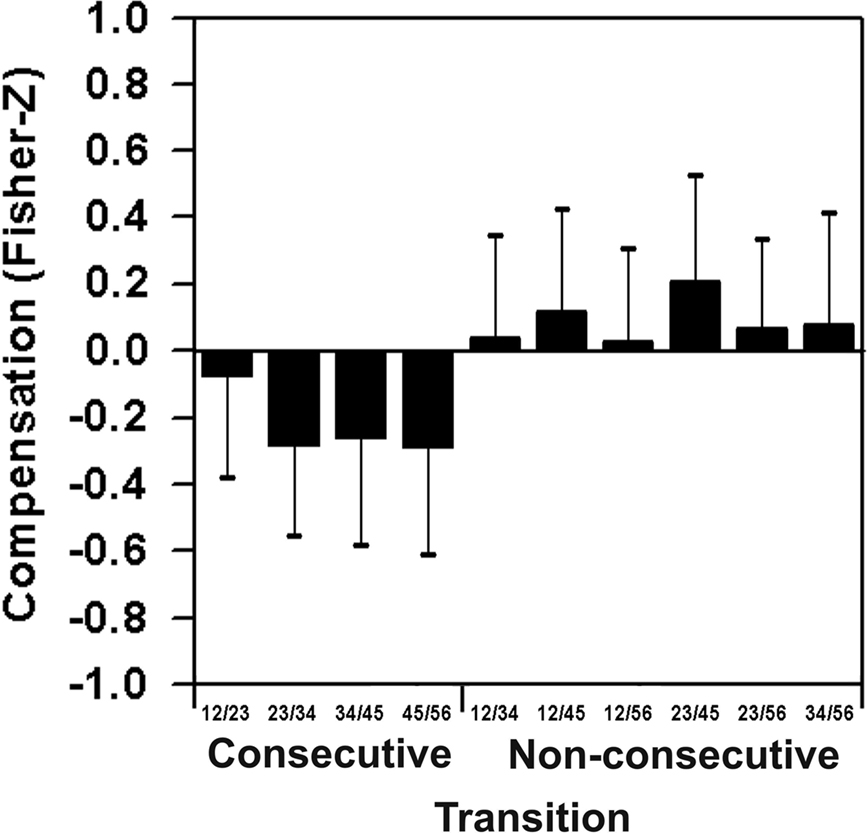
Figure 3. Lever sequencing: temporal compensation between consecutive time intervals between target configurations and missing compensation effects for combinations of non-consecutive time intervals.
The prediction-related data is presented in Figure 4. The expected lowering of compensation effects due to attentional focusing is reflected by the lowest absolute values of Fisher Z-transformed correlation coefficients under in-focus conditions. Statistically, the differences are non-significant, F(2,14) = 0.71, p > 0.05, f′ = 0.32, f = 0.17, but exhibit an almost large effect for the crucial in-focus vs. out-of-focus contrast, F(1,7) = 2.01, p = 0.20, f′’ = 0.54, f = 0.35, and a small effect for the comparison of out-of-focus and no-focus conditions, F(1,7) = 0.45, p = 0.53, f′ = 0.25, f = 0.15.
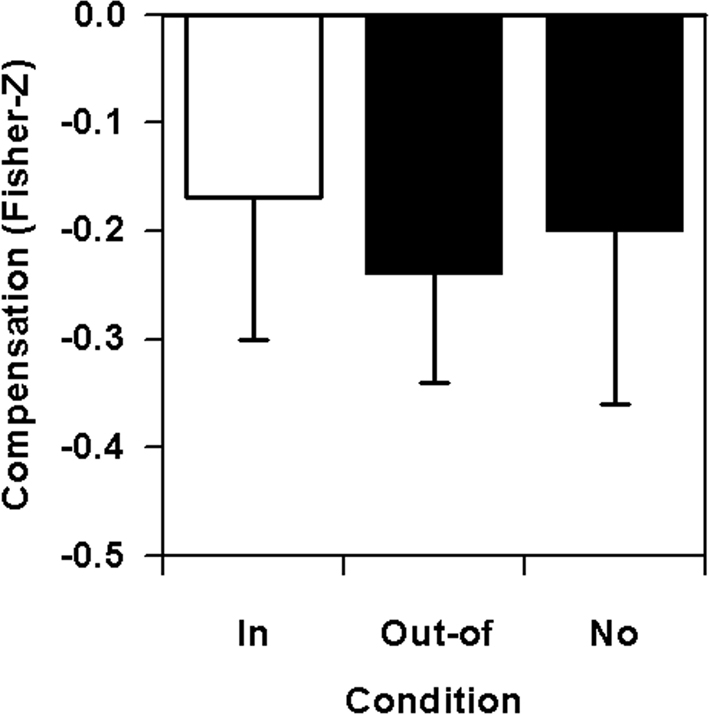
Figure 4. Lever sequencing: temporal compensation combined across the six nodal points as a function of focus of attention on a nodal point (in-focus), on any other nodal point (out-of-focus), or without any special instruction (no).
Muscular activity
Relative muscular activity values after pooling to in-focus, out-of-focus, and no-focus conditions are depicted in Figure 5. Statistically, there are non-significant differences in muscular activity, F(2,14) = 2.64, p = 0.11, f′ = 0.61, f = 0.44; however, the crucial contrast between the in-focus and out-of-focus condition goes in the predicted direction with a large effect size, F(1,7) = 3.85, p = 0.09, f′ = 0.74, f = 0.56.
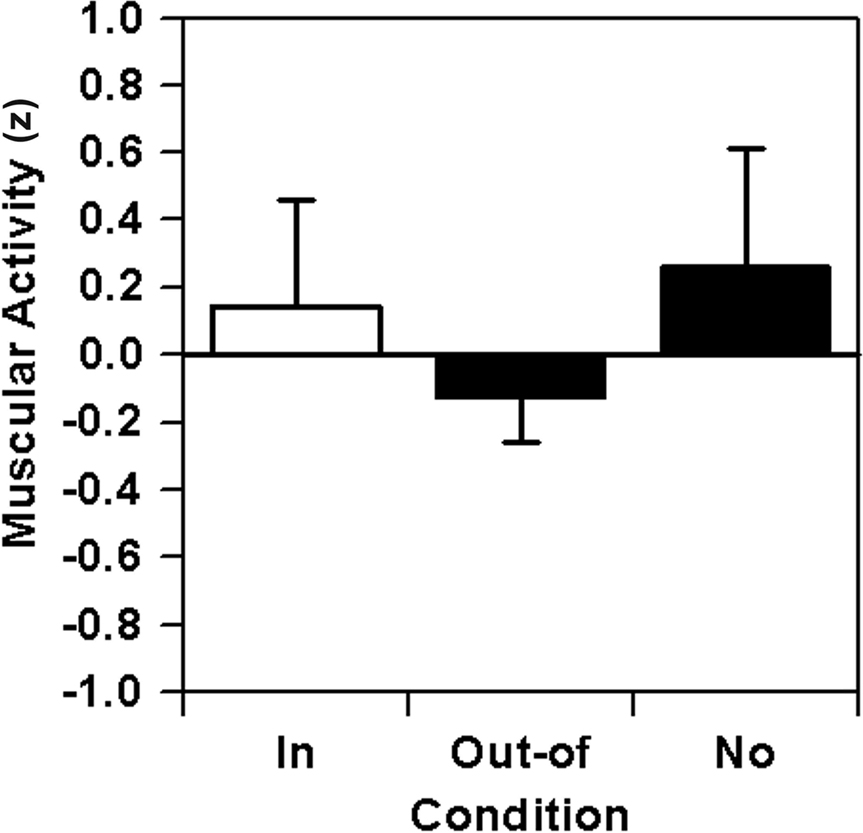
Figure 5. Lever sequencing: relative muscular activity (EA) combined across the six nodal points as a function of focus of attention on the nodal point (in-focus), on any other nodal point (out-of-focus), or without any special instruction (no).
While the in-focus vs. out-of-focus contrast conforms predictions quite well, the unexpected high EA score for the no-focus control condition still remains unexplained, resulting in a very large effect for the difference between the out-of-focus and no-focus condition, F(1,7) = 4.83, p = 0.06, f′ = 0.83, f = 0.81. For this reason, sequence effects were inspected more closely, as the six focus conditions were perfectly balanced over position 2–7 of the order of presentation, however, the no-focus instructions were always been given in the first and last block of the experimental sequence. Consequently, the z-scores of muscular activity were not analyzed by focus condition but by position in the sequence of data acquisition blocks. Statistically, significant differences between the blocks can be found, F(7,49) = 2.35, p = 0.04. Furthermore, when reducing the analysis to the (counter-balanced) focus blocks 2–7, 32 quadratic regression analyses (8 participants × 4 muscles), reveal significant quadratic trends y = a + bx + cx2 with positive coefficients c in 34.3% of cases with a probability value of p < 0.05 and in another 34.3% of cases with a probability value of 0.05 < p < 0.20. These trends only can be interpreted as an overall decrease of muscular activity over the first half and an overall increase of muscular activity over the second half of the test session, resulting in an over-estimation of the muscular activity in the first and last block, i.e., in the no-focus blocks of the experiment. Consequently, in order to obtain trend-free data, residuals were calculated for the focus blocks 2–7 and the resulting z-scores reassigned to the focus conditions. For the no-focus blocks 1 and 8, however, residuals were calculated as differences between raw z-scores and estimated values of the quadratic regression analysis for focus blocks 2–7 in order to eliminate the quadratic trend. Thus, the resulting z-score residuals for the no-focus blocks reflect focus effects after having eliminated sequence effects at the beginning and the end of the test session, respectively.
As illustrated in Figure 6, the adjusted EMG data fits the basic predictions quite well with the highest muscular activity when a target sequence is in focus and, contrary to original data, with no-focus EA values even lower than under out-of-focus conditions. Inferential statistical analyses reveal a non-significant effect for the overall difference, F(2,14) = 1.58, p = 0.24, f′ = 0.48, f = 0.39, with a very large effect size again for the crucial contrast between the in- and out-of-focus condition, F(1,7) = 3.84, p = 0.09, f′ = 0.74, f = 0.74. The formerly detected large effect for the out-of-focus vs. no-focus contrast, however, diminishes and only a small effect remains, F(1,7) = 0.27, p = 0.62, f′ = 0.20, f = 0.13.
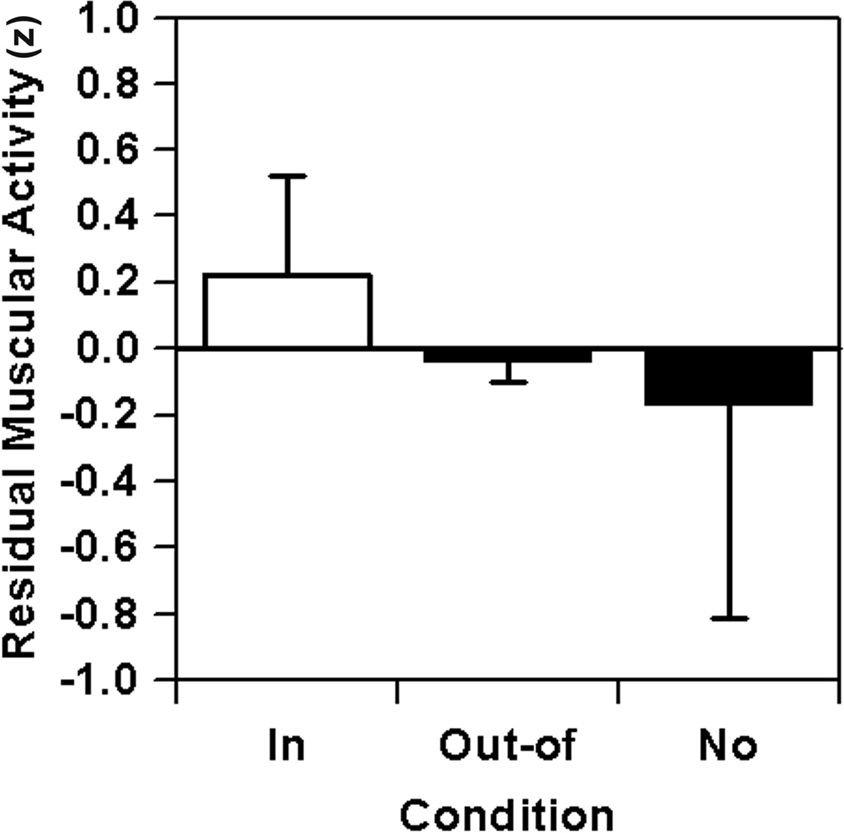
Figure 6. Lever sequencing: residual relative muscular activity (EA) after removal of quadratic trends and combined across the six nodal points as a function of focus of attention on the nodal point (in-focus), on any other nodal point (out-of-focus), or without any special instruction (no).
Discussion
In Experiment 1, participants performed a lever-sequencing task under different focus conditions after having received extensive training in this specific task. Increased muscular activity was found at a stop position, if that position was in the focus of attention. Furthermore, focusing on a stop position resulted in reduced temporal covariation for the related succession of time intervals. Although none of the results reached significance, the reported effect sizes are in line with the a priori expressed prediction of large effect sizes for the in-focus vs. out-of-focus comparisons and less than medium effect sizes for the out-of-focus vs. no-focus comparisons (for overall tests on significance, see General Discussion). Thus, predictions by the nodal-point hypothesis were supported: employing a focus of attention directed to nodal points within a movement sequence leads to specific time-referenced effects.
Experiment 2: Basketball Free Throws
Introduction
Experiment 2 aimed at replicating the findings of Experiment 1 in a more real-life, externally valid setting. Instead of instructing participants to focus on rather artificial nodal points, the rationale was to use nodal points that participants already knew from extensive daily experience. Furthermore, it was tested whether the results on reduced compensatory processes in the temporal domain also hold for the spatial domain. Thus, it was predicted that focusing on well-known nodal points of an over-learned sport skill, basketball free throws, should result in relative high muscular activity and in reduced covariation of spatial parameters selectively at the nodal point in focus.
Materials and Methods
Sample
Six male, semi-professional basketball players (age 18–25 years, all right handed) were recruited from a basketball team playing in the German second division. All participants had played basketball for at least 6 years and three of them had played on junior national teams. They volunteered to take part in the experiment and were not given any compensation for participation. Participants were informed about the experimental procedure and signed a consent form.
Procedure
The task of the participants was to shoot basketball free throws. Within the free-throw movement, two nodal points were defined: “ball over shoulder” and “ball leaves hand,” serving as nodal point 1 and nodal point 2, respectively. These nodal points were derived both from biomechanical analyses of the basketball free throw as well as from experiential evidence (see, e.g., St. Martin and Frangie, 1992).
After being prepared for kinematography and surface EMG and after some warm-up throws, participants performed a series of four blocks of 16 trials of free throws. In the no-focus block 1, participants were given no specific instruction, but were told to “just shoot.” After this, participants were randomly assigned to one of six sequences of three focus conditions in blocks 2–4. In the focus 1 condition, participants were asked to focus on nodal point 1, in the focus 2 condition they were asked to focus on nodal point 2, and in the external condition they were told to focus on the basket. Participants were reminded of the focus instructions after each pair of throws.
Apparatus
The movement was recorded in the sagittal plane with a frequency of 220 Hz using a digital camera (DALSA CCD, Canada) and SIMI-software (Simi Reality Systems). Markers were put above four joints of the throwing arm: the lateral head of the humerus, the lateral epicondyle, the lateral end of the ulna, and on the tip of the middle finger. The bouncing of the ball by the participants resulted in activating a LED that was also recorded by the camera. In order to assess shooting performance, all trials were additionally recorded with a standard video camera.
Electromyographic data was recorded of four muscles of the throwing arm (anterior deltoid muscle, lateral head of triceps brachii, biceps brachii, flexor carpi ulnaris). The same apparatus and electrode configuration was used as in Experiment 1. On a free channel of the EMG device, a spike signal was registered which was generated by an electrical contact every time participants bounced the ball on the floor in front of the free-throw line. This signal served as a trigger for synchronizing kinematic and EMG data.
Data analysis
First of all, 10 of the 16 throws were selected for further analysis. For this purpose, using the standard video, three independent raters scored hits, and misses of the basket on a 1–6 points scale (inter-rater-reliability R = 0.97). Selection of throws was optimized with respect to a high average rating and small variance of average ratings between blocks. For this reason, the following comparisons of movement variables between focus conditions are not simply based on performance differences. Quite the contrary, this selection guaranteed a conservative comparison of focus-dependent measures that do not reflect differences in outcome quality but differences in underlying mechanisms of motor control.
For kinematic data analysis, positions of the markers were digitized frame by frame with SIMI Motion 5 (SIMI Reality Systems). Nodal point 1 was defined as the frame where the distance between shoulder and wrist was minimal after a quadratic fit of the raw 2D positional data over a window of ±25 frames around the roughly estimated point of time. Nodal point 2 was the first frame the ball had just left the fingers. This frame was determined by two independent raters who picked out the same frame in all of the 240 cases of 6 × 4 × 10 free throws. For data smoothing, two time-windows were defined: window 1 consisted of 51 frames around nodal point 1 and window 2 of 16 frames around nodal point 2. For further analyses, the raw displacement data was filtered twice, forward and backward, with a second-order Butterworth filter using a low-pass cut-off frequency in window 1 of 11 Hz and in window 2 of 29 Hz for the shoulder, elbow, and wrist and of 35 Hz for the fingertip. The cut-off frequencies were chosen, because Fast-Fourier analyses of displacement data from 16 randomly chosen throws showed that 90% of the frequency spectrum was accounted for in this way. The kinematic determination of the two nodal points and the trigger signals that were produced by the bouncing of the ball before two consecutive throws provided sufficient temporal information for the determination of the nodal-point related moments in the EMG signals as well.
Raw kinematic data analysis resulted in filtered 2D positional data of the shoulder, elbow, wrist, and fingertip at two nodal points. Analogous to the time-related dependent variable in Experiment 1, an index of spatial compensation was aggregated from this data. This index is based on the comparison between the empirically measured dispersion of joint positions and a covariation-free, potential dispersion, which can be estimated from permuted data sets (for the calculation of the bivariate variable error, BVE, see Hancock et al., 1995, and for the permutation approach, Müller and Sternad, 2003; for further details, see Calculation of a Bivariate Variable Error Score and Calculation of Spatial Compensation of Appendixes). As illustrated in Figure 7 for a selected participant (P2), focus condition (focus on nodal point 1) and analysis window (posture at nodal point 1), the spatial compensation score is derived from sagittal positional data which was available for the shoulder, elbow, wrist, and fingertip for 10 throws per focus condition (Figure 7A). For further analysis, each value was corrected of the variance of the overall body position by transforming the coordinates into a shoulder-fixed system. This transformation was introduced as the resulting relative positional values were of major interest with regard to the research question and not the variance of the overall body position as such. From these shoulder-corrected coordinates, the empirical dispersion can directly be computed as the BVE of the 10 positions of the fingertip (Figure 7B). The covariation-free dispersion was calculated through a complete permutation of the coordinates in relation to the respective proximal joint. It then consisted of the BVE of the 10 elbow × 10 wrist × 10 fingertip = 1000 potential positions of the fingertip (Figure 7C). A generalized correlation coefficient R was computed from these two dispersions, a negative coefficient indicating that the actual variance is reduced by covariation (Müller and Sternad, 2003; for details, see Calculation of Spatial Compensation of Appendix). For reasons of statistical analyses, in the end, Fisher Z-transformed values of the covariation coefficients R were used as measure for spatial compensation.
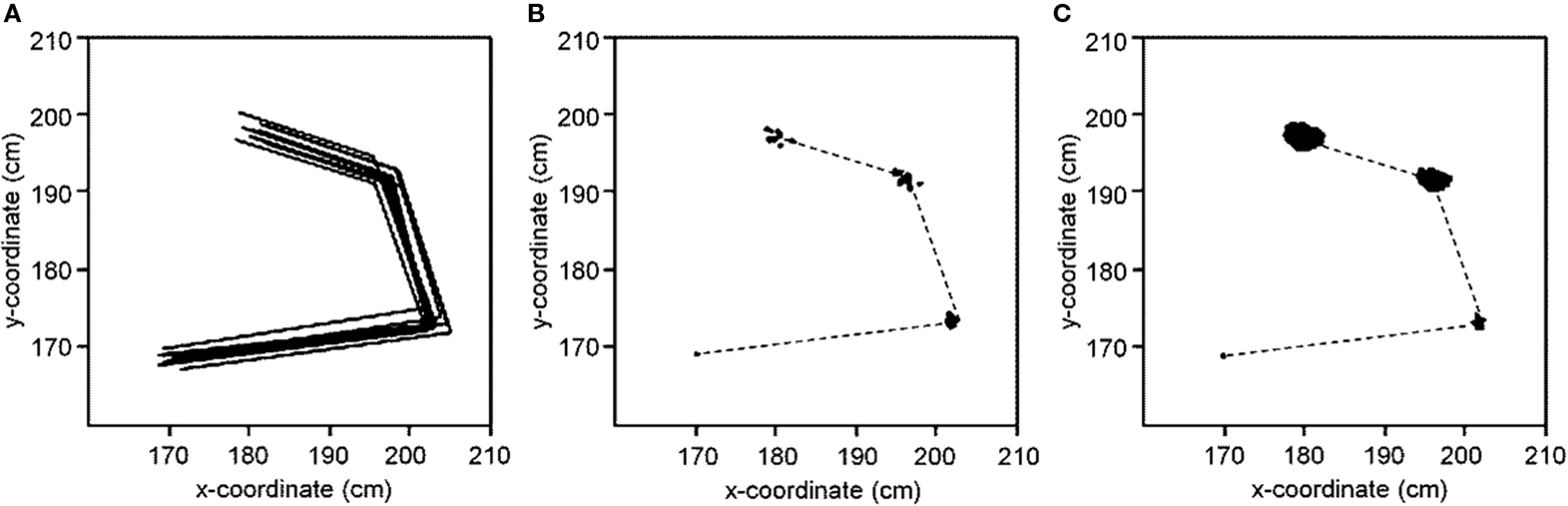
Figure 7. Basketball free throws: calculation of an index of spatial compensation from positional data of 10 throws. Depicted are (A) raw coordinates of shoulder, elbow, wrist, and fingertip for 10 throws of a selected participant (P2), focus condition (focus on nodal point 1: “ball over shoulder”) and analysis window (posture at nodal point 1), (B) the empirical dispersion of the fingertip after introduction of a shoulder-fixed coordinate system (bivariate variable error of 10 data points), and (C) the potential dispersion of the fingertip, calculated through a complete permutation of the joint coordinates (bivariate variable error of 1000 data points).
Electromyographic data was available for 4 muscles, 10 selected trials, and 4 focus conditions per participant. Analogous to Experiment 1, after filtering, the electrical activity (EA) was determined at the two nodal points by using temporal information from the kinematic data. The average values (Andrews’ Wave estimation) for the four muscles were then z-score transformed across the four conditions. The average of these z-scores across the four muscles represents the EMG dependent variable: relative muscular activity (for details on the rationale behind this procedure, see Experiment 1, and for further comments the General Discussion).
Lastly, for the calculation of prediction-related data, compensation and EA values were pooled with respect to in-focus, out-of-focus, external-focus, and no-focus conditions, respectively. The in-focus value was derived as the mean of the scores for nodal point 1 and 2, when the respective nodal point was in the focus of attention, and the out-of-focus value as the mean of the scores for nodal point 1 and 2, when the other respective nodal point was in the focus of attention. The external-focus and no-focus value was calculated by averaging the scores at both nodal points from the trials with external focus and no-focus instructions, respectively. Please note again, that as a consequence of this procedure, in-focus and out-of-focus values for spatial compensation as well as for myoelectric activity refer to the same trials, traditionally, both being assigned to internal focus conditions. Consequently, the only difference between the values for in-focus and out-of-focus conditions are related to the point in time when the calculation has been performed, i.e., with respect to the time-referenced predictions of the nodal-point hypothesis.
Results
Spatial compensation
In Figure 8, spatial compensation scores for four focus conditions are depicted. As negativity of values represents compensation, the least covariation is apparent in the in-focus condition. The overall analysis revealed non-significant effects, F(3,15) = 0.68, p = 0.58, f′ = 0.37, f = 0.18, with an almost large effect for the crucial in-focus vs. out-of-focus comparison, F(1,5) = 1.17, p = 0.33, f′ = 0.48, f = 0.35. Contrast analyses of the out-of-focus against the pooled external and no-focus conditions, however, showed a difference with less than a small effect size, F(1,5) < 0.01, p = 0.95, f′ = 0.10, f = 0.07.
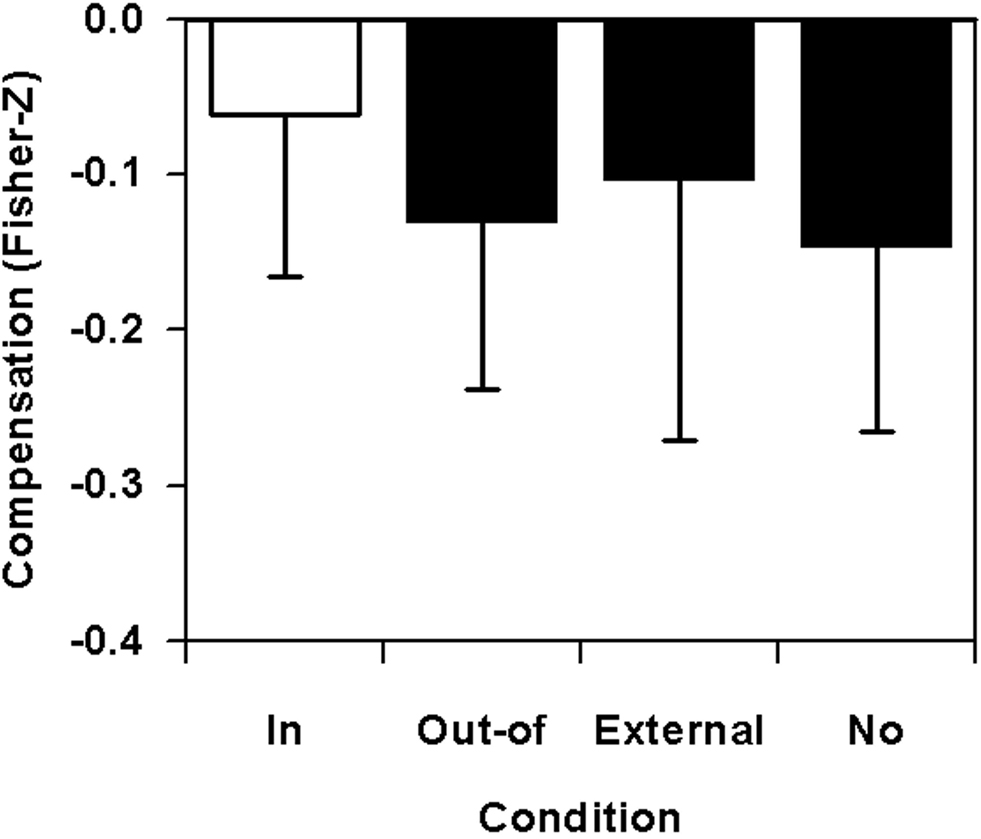
Figure 8. Basketball free throws: spatial compensation combined across the two nodal points as a function of focus of attention on the nodal point (in-focus), on the other nodal point (out-of-focus), on the basket (external), or without any special instruction (no).
Muscular activity
Relative muscular activity values are illustrated in Figure 9. If a nodal point was in focus, more relative muscular activity was found compared to the condition when a nodal point was out of focus. Besides the overall significance of the depicted differences, F(3,15) = 5.63, p = 0.01, f′ = 1.06, f = 0.71, this crucial contrast is significant with a very large effect size, F(1,5) = 15.59, p = 0.01, f′ = 1.77, f = 1.27. Contrary to this effect, a contrast analysis of the out-of-focus condition against the pooled external and no-focus condition showed a non-significant difference of less than medium effect size, F(1,5) = 0.39, p = 0.56, f′ = 0.28, f = 0.24.
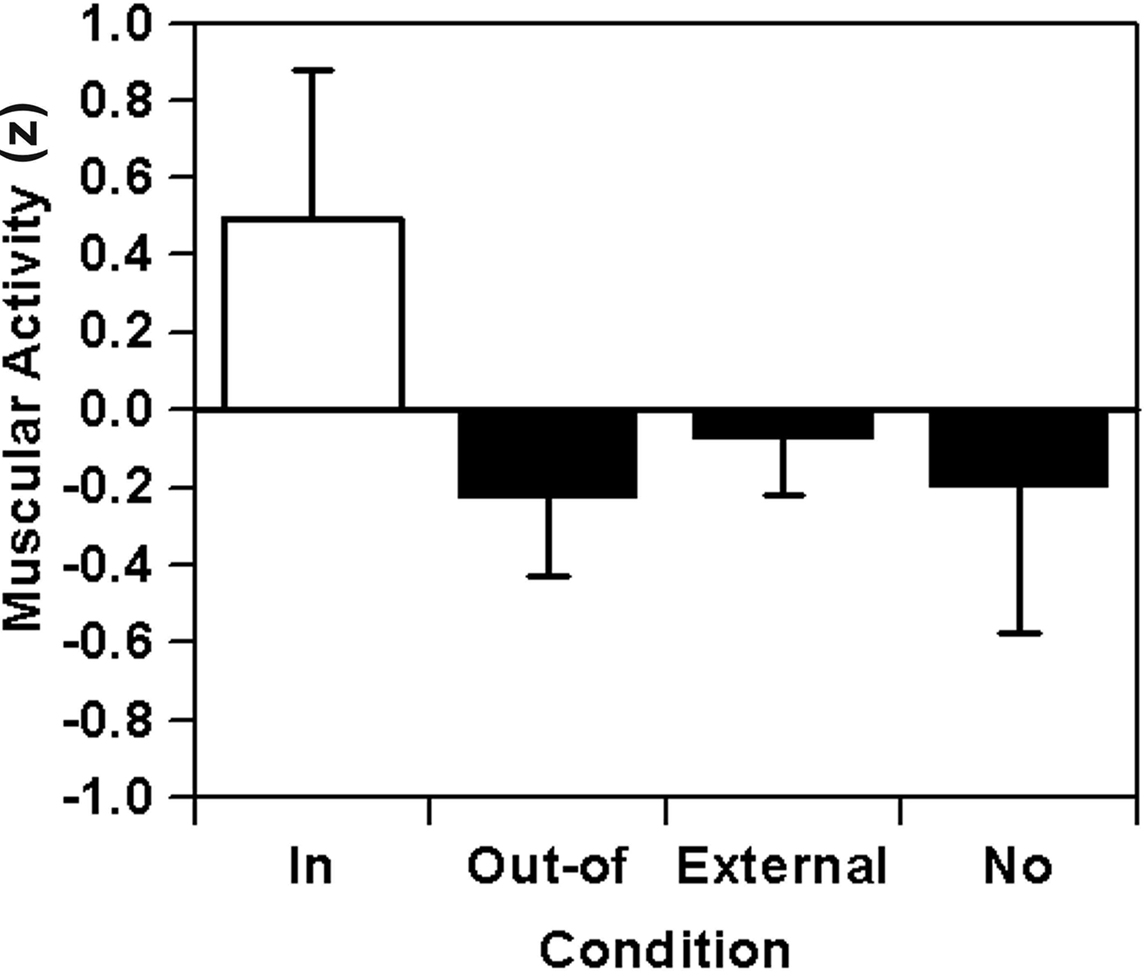
Figure 9. Basketball free throws: relative muscular activity (EA) combined across the two nodal points as a function of focus of attention on the nodal point (in-focus), on the other nodal point (out-of-focus), on the basket (external), or without any special instruction (no).
Discussion
In Experiment 2, experienced basketball players shot free throws under four different instructions: to focus on one of two nodal points within the movement, to focus on the basket, or to perform the task as usual. An increased muscular activity in the throwing arm was found at a nodal point, if that nodal point was in the focus of attention. Furthermore, focusing on a nodal point resulted in a reduction of spatial compensation scores at this nodal point. Although reaching levels of significance only in part, the reported effect sizes absolutely fit the a priori prediction of large effect sizes for the in-focus vs. out-of-focus contrast and less than medium effect sizes for comparisons of out-of-focus vs. control conditions (for overall tests on significance, see General Discussion). Thus, with respect to the nodal-point hypothesis, the results found in Experiment 2 clearly corroborate and extend the supporting findings of Experiment 1.
General Discussion
The two studies presented aimed at investigating time-referenced effects of focusing attention on the execution of well-learned motor skills. In Experiment 1, lever sequencing, a laboratory task was used, while, in Experiment 2, expert basketball players had to perform free throws. Participants in both experiments were asked to focus their attention on certain nodal points of the skill while still trying to perform as usual. Focusing on a nodal point resulted in higher muscular activity and in a reduction of compensatory covariation only at the nodal point in focus, a reduction of temporal compensation in Experiment 1 and a reduction of spatial compensation in Experiment 2.
Most of the results do not pass conventional levels of significance, but the effect sizes are absolutely in line with the a priori expressed prediction of large effect sizes for the in- vs. out-of-focus contrast and of remarkably smaller effect sizes for the out-of- vs. no-/external-focus contrast. Furthermore, it is important to note that the same effects were found in two rather distinct experimental settings. After averaging over the two experiments, the nodal-point specific effect exhibits a very large mean effect size for muscular activity, M(f′) = 1.12, M(f) = 0.95, an almost large mean effect size for compensation scores, M(f′) = 0.51, M(f) = 0.35, and a large mean effect size for the average of both dependent variables, M(f′) = 0.80, M(f) = 0.63. This overall effect can be characterized as reaching significance on an alpha level of α = 0.05 with a power of 1 − β = 0.80 (for the rationale behind averaging procedures and of overall tests on significance, see Overall Test on Significance of Appendix). On the contrary, all comparisons of out-of-focus vs. no-/external-focus conditions yielded F-values of F < 1.00 with two-tailed p-values of p > 0.50 and effect sizes of f < 0.25 – as being a priori defined as critical values for the acceptance of the hypothesis (see Optimal Sample Sizes and Statistical Power of Appendix). Hence, the a priori determination of an overall sample size of N = 14 turns out to be reasonable a posteriori – although an exact a posteriori power analysis leads to the recommendation of conducting future experiments aiming for focus effects on compensation scores with larger sample sizes of N ≥ 24 in order to optimize statistical power (for details of this calculation, see Optimal Sample Sizes and Statistical Power of Appendix). However, the in-focus vs. out-of-focus contrast which is crucial for the prediction of time-referenced effects can claim significance (p < 0.05) even on the basis of the smaller overall sample size of N = 8 + 6 = 14 that has been used in the combined experiments at hand.
In this context, it may be worth to underline again that the conditions of the in-focus vs. out-of-focus comparison both correspond to experimental conditions that traditionally have been characterized as “internal focus conditions.” Furthermore, the derived scores both refer to one and the same movement sample so that the explanation for the discovered differences must be based on time-referenced effects due to the different focus instructions. Thus, it is just fair to say that these results may be interpreted as lending support for the nodal-point hypothesis: detrimental consequences of focusing attention on a movement appear through a “re-freezing” of kinematic degrees of freedom and a reduced exploitation of system features and these effects surface time-referenced at certain nodal points within a sensorimotor chain.
The main empirical appeal of the nodal-point hypothesis is the straightforward deduction of time-referenced predictions which should be taken as a recommendation for future studies on paralysis-by-analysis phenomena not only to investigate general effects of internal focus but also to take specific time-referenced effects into consideration. The main theoretical appeal of the hypothesis is the clear-cut definition of mechanisms underlying the impairment of movement control by a movement-directed focus of attention. As the operations from one anchor of attention to the next, in terms of the nodal-point hypothesis, are conceptualized as being run non-voluntarily by the motor system per se, the disruption of automatic processes is no longer understood as the result of switching from an automatic, implicit, proceduralized, unconscious to a controlled, explicit, declarative, conscious mode. Instead, reduced “automatic processing” under internal focus conditions is suggested to result from disrupting the “automatic” exploitation of system features at certain points in time, the nodal points, by focusing on their effects either as a consequence of voluntary monitoring or of the sudden failure of anticipated effects. Insofar, the nodal-point hypothesis can be understood as an answer to the question what “constraining action” really means, i.e., as a specification of Wulf’s constrained action hypothesis on the functional level of movement control.
However, despite the obvious appeal of the nodal-point hypothesis, some remaining problems should not be concealed. In this regard, it first and foremost has to be stressed, that time-referenced effects of a movement-related focus have been demonstrated here for the first time. As a consequence, further evidence in support of the hypothesis is needed before its potential theoretical contribution can reliably be judged. This is true on the general level of the central prediction of nodal-point related detrimental effects of an “internal” focus as well as on a more specific level concerning the hypothetical mechanism behind the time-referenced deterioration. So, future studies should not only aim at replicating the findings on muscular activity and compensatory variability reported here; beyond that, the assumptions made for the mechanism behind this phenomenon should be empirically challenged. In this regard, those experiments would be of particular interest which referred to the following questions: When exactly do focus-related EMG effects surface in time, i.e., over the time interval when an effect is muscularly produced or over the interval around the point in time when the effect can be perceived by participants (as has been assumed here)? Is an increase in overall muscular activity actually due to a co-contraction of antagonist muscles (as has been hypothesized here), or does a closer look onto the EMG patterns reveal further insights into the mechanism of “re-freezing” as a consequence of a nodal-point related focus? Does the assumption hold that compensatory variability is reduced via muscular “re-freezing” (as has been made here) or do electrical activity and compensation scores turn out to be independent of each other? Answers to questions like this would certainly help to specify and elaborate the nodal-point hypothesis further.
Beyond the empirical problems discussed so far, the authors have to admit that, at least in its current version, the nodal-point hypothesis exhibits a more theoretical issue regarding the derivation of empirical predictions. As the hypothesis’ main prediction has the form “scores in variable x will change at point y as a consequence of focusing on point y,” testability is in particular challenged with respect to the definition of execution variables x as well as the determination of nodal points y. Regarding the execution variable problem, it has to be noticed that a definition for “system exploitation” is needed, for technical reasons, the definition of a variable that can be measured at one single point in time or that at most needs a short time window for being calculated in order to meet the time-referenced nature of the hypothesis. From our point of view, muscular co-contraction and compensatory variability are very plausible candidates for this purpose – but other variables are feasible and may be preferred when it comes to empirical tests of the hypothesis. Similarly to this problem, the question remains how nodal points within a hypothetical movement sequence can be clear-cut identified. Of course, as described in the general introduction, nodal points can theoretically be understood as intended or anticipated effects of elementary behavioral acts, i.e., acts that may not be divided into further parts without changing the purpose of the action. However, what does this exactly mean? For both problems, we would like to propose pursuing a two-step approach. This approach is, on the one hand, based on a combination of phenomenological and kinematic hints, i.e., answers to the question whether I am able to consciously monitor the movement with respect to certain sub-goals, and to the question which variables are characterized by a reduction of dispersion at certain points in time. On the other hand, the strategy proposed by us is based on the comparison of novice’s and expert’s performance: if, in the first step, differences between novice and expert performance can be found in hypothetical execution variables at hypothetical nodal points, this result could be taken as being sufficient for the a priori definition of nodal points for the examination of experimentally induced focus effects in the second step of the strategy. However, future work is needed in order to prove whether and to what extent this two-step strategy holds.
Thus, before our tentative hypothesis may be raised to the rank of a theory some problems still have to be solved and, once again, more empirical data is needed in favor of our approach. By now, however, it should have become obvious from our argument, that a more theoretical discussion of mechanisms underlying paralysis-by-analysis phenomena is needed. In our view, the proposed nodal-point hypothesis offers a promising framework for future work on this topic.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors gratefully thank Daniel Erlacher for his essential support in data collection and his suggestions for improving our whole work and Rainer Wollny for helpful comments on applying EMG methodology.
References
Arutyunyan, G. H., Gurfinkel, V. S., and Mirskii, M. L. (1968). Investigation of aiming at a target. Biophysics 13, 536–538.
Baumeister, R. F. (1984). Choking under pressure: self-consciousness and paradoxical effects of incentives on skillful performance. J. Pers. Soc. Psychol. 46, 610–620.
Beilock, S. L., and Carr, T. H. (2001). On the fragility of skilled performance: what governs choking under pressure? J. Exp. Psychol. Gen. 130, 701–725.
Beilock, S. L., Carr, T. H., MacMahon, C., and Starkes, J. L. (2002). When paying attention becomes counterproductive: impact of divided versus skill-focused attention on novice and experienced performance of sensorimotor skill. J. Exp. Psychol. Appl. 8, 6–16.
Beilock, S. L., Kulp, C. A., Holt, L. E., and Carr, T. H. (2004). More on the fragility of performance: choking under pressure in mathematical problem solving. J. Exp. Psychol. Gen. 133, 584–600.
Bernstein, N. A. (1944/1967). The Co-ordination and Regulation of Movements. Oxford: Pergamon Press (Original work published 1944).
Bliss, C. B. (1892). Investigations in reaction time and attention. Stud. Yale Psychol. Lab. 1, 1–55.
Boder, D. P. (1935). The influence of concomitant activity and fatigue upon certain forms of reciprocal hand movement and its fundamental components. Comp. Psychol. Monogr. 11.
Bullock, D., and Grossberg, S. (1988). “The VITE model: a neural command circuit for generating arm and articulator trajectories,” in Dynamic Patterns in Complex Systems, eds. J. A. S. Kelso, A. J. Madell, and M. F. Schlesinger (Singapore: World Scientific), 305–326.
Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences, 2nd Edn. Hillsdale, NJ: Lawrence Erlbaum.
Cohen, R. G., and Rosenbaum, D. A. (2004). Where grasps are made reveals how grasps are planned: generation and recall of motor plans. Exp. Brain Res. 157, 486–495.
Cordier, P., Mendès France, M., Pailhous, J., and Bolon, P. (1994). Entropy as a global variable of the learning process. Hum. Mov. Sci. 13, 745–764.
Cordo, P. J. (1990). Kinesthetic control of a multijoint movement sequence. J. Neurophysiol. 63, 161–172.
Darling, W. G., and Cooke, J. D. (1987). Movement related EMGs become more variable during learning of fast accurate movements. J. Mot. Behav. 19, 311–331.
Delagi, E. F., and Perotto, M. D. (1981). Anatomic Guide for the Electromyographer – The Limbs. Springfield, IL: Thomas.
Erdfelder, E., Faul, F., and Buchner, A. (1996). GPOWER: a general power analysis program. Behav. Res. Meth. Instrum. Comput. 18, 1–11.
Greenwald, A. G. (1970). Sensory feedback mechanisms in performance control: with special reference to the ideo-motor mechanism. Psychol. Rev. 77, 73–99.
Hancock, G. R., Butler, M. S., and Fischman, M. G. (1995). On the problem of two-dimensional error scores: measures and analyses of accuracy, bias, and consistency. J. Mot. Behav. 27, 241–250.
Hermens, H. J., Freriks, B., Merletti, R., Hägg, G., Stegeman, D. F., Blok, J., Rau, G., and Disselhorst-Klug, C. (1999). SENIAM 8: European Recommendations for Surface ElectromyoGraphy. Enschede: Roessingh Research and Development.
Hoffmann, J. (1993). Vorhersage und Erkenntnis. [Prediction and Reason]. Göttingen, Germany: Hogrefe.
Hoffmann, J. (2003). “Anticipatory behavioral control,” in Anticipatory Behavior in Adaptive Learning Systems, eds. M. Butz, O. Sigaud, and P. Gerard (Berlin: Springer), 44–65.
Hommel, B. (2009). Action control according to TEC (theory of event coding). Psychol. Res. 73, 512–526.
Hommel, B., Müsseler, J., Aschersleben, G., and Prinz, W. (2001). The theory of event coding (TEC): a framework of perception and action. Behav. Brain Sci. 24, 869–937.
Hossner, E.-J. (2009). “A cognitive movement scientist’s view on the link between thought and action: insights form the ‘Badische Zimmer’ metaphor,” in Mind and Motion: The Bidirectional Link Between Thought and Action, eds. M. Raab, J. G. Johnson, and H. R. Heekeren (Amsterdam: Elsevier), 25–34.
James, W. (1890/2010). The Principles of Psychology. Available at http://psychclassics.yorku.ca/James/Principles [Retrieved May 10 2010] (Original work published 1890).
Lewis, B., and Linder, D. (1997). Thinking about choking? Attentional processes and paradoxical performance. Pers. Soc. Psychol. Bull. 23, 937–944.
Lohse, K. R., Sherwood, D., and Healy, A. F. (2010). How changing the focus of attention affects performance, kinematics, and electromyography in dart throwing. Hum. Mov. Sci. 29, 542–555.
Lotze, R. H. (1852/1966). Medicinische Psychologie oder Die Physiologie der Seele [Medical Psychology or Physiology of the Soul]. Amsterdam: Bonset (Original work published 1852).
Marchant, D. C. (2010). Attentional focusing instructions and force production. Front. Psychol. 1:210. doi: 10.3389/fpsyg.2010.00210
Masters, R. S. W. (1992). Knowledge, knerves and know-how: the role of explicit versus implicit knowledge in the breakdown of a complex motor skill under pressure. Br. J. Psychol. 83, 343–358.
Masters, R. S. W., Polman, R. C. J., and Hammond, N. V. (1993). “Reinvestment”: a dimension of personality implicated in skill breakdown under pressure. Pers. Individ. Dif. 14, 655–666.
McDonald, P. V., van Emmerik, R. E., and Newell, K. M. (1989). The effects of practice on limb kinematics in a throwing task. J. Mot. Behav. 21, 245–264.
McNevin, N. H., Shea, C. H., and Wulf, G. (2003). Increasing the distance of an external focus of attention enhances learning. Psychol. Res. 67, 22–29.
Morrison, S., and Newell, K. M. (2000). Limb stiffness and postural tremor in the arm. Motor. Control. 4, 293–315.
Müller, H. (2001). Ausführungsvariabilität und Ergebniskonstanz [Performance Variability and Result Constancy]. Lengerich: Pabst Science.
Müller, H., and Loosch, E. (1999). Functional variability and an equifinal path of movement during targeted throwing. J. Hum. Mov. Stud. 36, 103–126.
Müller, H., and Sternad, D. (2003). A randomization method for calculation of covariation in multiple nonlinear relations: illustrated with the example of goal-directed movements. Biol. Cybern. 89, 22–33.
Pijpers, J. R., Oudejans, R. R. D., and Bakker, F. C. (2005). Anxiety-induced changes in movement behaviour during the execution of a complex whole-body task. Q. J. Exp. Psychol. A 58, 421–445.
Rasch, B., Friese, M., Hofmann, W., and Naumann, E. (2006a). Quantitative Methoden [Quantitative Methods], 2nd Edn, Vol. 1. Heidelberg, Germany: Springer.
Rasch, B., Friese, M., Hofmann, W., and Naumann, E. (2006b). Quantitative Methoden [Quantitative Methods], 2nd Edn, Vol. 2. Heidelberg, Germany: Springer.
Rosenbaum, D. A., Meulenbroek, R. G., Vaughan, J., and Jansen, C. (2001). Posture-based motion-planning: applications to grasping. Psychol. Rev. 108, 709–734.
Schmidt, R. A. (1982). Motor Control and Learning. A Behavioral Emphasis. Champaign, IL: Human Kinetics.
Shea, C. H., and Wulf, G. (1999). Enhancing motor learning through external-focus instructions and feedback. Hum. Mov. Sci. 18, 553–571.
St. Martin, T., and Frangie, F. (1992). The Art of Shooting Baskets: From the Free Throw to the Slam Dunk. Chicago: Contemporary.
Vance, J., Wulf, G., Töllner, T., McNevin, N. H., and Mercer, J. (2004). EMG activity as a function of the performer’s focus of attention. J. Mot. Behav. 36, 450–459.
Vereijken, B., Van Emmerik, R. E. A., Whiting, H. T. A., and Newell, K. M. (1992). Free(z)ing degress of freedom in skill acquisition. J. Mot. Behav. 24, 133–142.
Weinberg, R. S. (1978). The effects of success and failure on the patterning of neuromuscular energy. J. Mot. Behav. 10, 53–61.
Wing, A. M., and Kristofferson, A. B. (1973). Response delays and the timing of discrete motor responses. Percept. Psychophys. 14, 5–12.
Wulf, G. (2007). Attentional focus and motor learning: a review of 10 years of research. J. Bewegung Train. 1, 1–11.
Wulf, G., Höß, M., and Prinz, W. (1998). Instructions for motor learning: differential effects of internal versus external focus of attention. J. Mot. Behav. 30, 169–179.
Wulf, G., Lauterbach, B., and Toole, T. (1999). The learning advantages of an external focus of attention in golf. Res. Q. Exerc. Sport 70, 120–126.
Wulf, G., McNevin, N. H., Fuchs, T., Ritter, F., and Toole, T. (2000). Attentional focus in complex skill learning. Res. Q. Exerc. Sport 71, 229–239.
Wulf, G., McNevin, N., and Shea, C. H. (2001). The automaticity of complex motor skill learning as a function of attentional focus. Q. J. Exp. Psychol. A 54, 1143–1154.
Wulf, G., and Prinz, W. (2001). Directing attention to movement effects enhances learning: a review. Psychon. Bull. Rev. 8, 648–660.
Wulf, G., Shea, C. H., and Park, J.-H. (2001). Attention and motor performance: preferences for and advantages of an external focus. Res. Q. Exerc. Sport 72, 335–344.
Wulf, G., and Weigelt, C. (1997). Instructions in learning a complex motor skill: to tell or not to tell. Res. Q. Exerc. Sport 68, 362–367.
Keywords: motor control, focus of attention, internal focus, external focus, nodal-point hypothesis, electromyography, kinematics, compensatory variability
Citation: Hossner E-J and Ehrlenspiel F (2010) Time-referenced effects of an internal vs. external focus of attention on muscular activity and compensatory variability. Front. Psychology 1:230. doi: 10.3389/fpsyg.2010.00230
Received: 07 September 2010;
Paper pending published: 19 October 2010;
Accepted: 03 December 2010;
Published online: 23 December 2010.
Edited by:
David Marchant, Edge Hill University, UKCopyright: © 2010 Hossner and Ehrlenspiel. This is an open-access article subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Ernst-Joachim Hossner, Institute of Sport Science, University of Bern, Bremgartenstrasse 145, CH-3012 Bern, Switzerland. e-mail:ZXJuc3QuaG9zc25lckBpc3B3LnVuaWJlLmNo

