Attending to One of Many: When Infants are Surprisingly Poor at Discriminating an Item's Size

Despite a prevailing assumption in the developmental literature that changes in continuous quantities (i.e., surface area, duration) are easier to detect than changes in number, very little research has focused on the verity of this assumption. The few studies that have directly examined infants’ discriminations of continuous extent have revealed that infants discriminate the duration of a single event and the area of a single item with similar levels of precision (Brannon et al., 2006; vanMarle and Wynn, 2006). But what about when items are presented in arrays? Infants appear to be much worse at representing the cumulative surface area compared to the numerosity of an array (Cordes and Brannon, 2008a), however this may be due to a noisy accumulation process and not a general finding pertaining to representations of the extent within an array. The current study investigates how well infants detect changes in the size of individual elements when they are presented within an array. Our results indicate that infants are less sensitive to continuous properties of items when they are presented within a set than when presented in isolation. Specifically we demonstrate that infants required a fourfold change in item size to detect a change when items were presented within a set of homogeneous elements. Rather than providing redundant cues that aided discrimination, presenting a set of identical elements appeared to hamper an infant’s ability to detect changes in a single element’s size. In addition to providing some of the first evidence to suggest that the presence of multiple items may hinder extent representations, these results provide converging lines of evidence to support the claim that, contrary to popular belief, infants are better at tracking number than continuous properties of a set.

Introduction

What kind of quantitative information do infants represent when they see a set of objects such as a box of toys or a handful of cheerios? Do infants track the number of cheerios, the overall amount of cereal, or the size of each O? Much research has been dedicated to these questions, primarily focusing on the more specific question of whether infants are capable of representing something as abstract as number. Results of a slew of studies have revealed that, despite significant changes in item size (e.g., Xu and Spelke, 2000), item identity (Starkey et al., 1983), or stimulus modality (Kobayashi et al., 2005; Jordan and Brannon, 2006; Izard et al., 2009) infants do represent number (although see Clearfield and Mix 1999, 2001; Cohen and Marks, 2002; Feigenson et al., 2002a). In fact, findings from studies stringently controlling for other array properties that tend to co-vary with number, such as surface area, density, and item size (in simultaneous visual displays) or duration (in sequential presentations) have revealed that infant discriminations of number are ratio-dependent, such that 6-month-olds are capable of detecting a twofold change in number (e.g., 8 vs. 16) but not a 1.5-fold change (8 vs. 12; e.g., Xu and Spelke, 2000; Lipton and Spelke, 2003; Wood and Spelke, 2005).

A prevailing belief, both in the developmental and animal cognition literature, has been that discriminating continuous quantities is trivial for both non-human animals (Davis and Memmott, 1983) and preverbal infants (Piaget, 1952; Mix et al., 2002a,b). In fact, the default assumption was that infants attend to continuous quantities instead of number. While number was thought to be too abstract for a preverbal child or non-verbal animal, representations of surface area were considered perceptual and thus cognitively effortless.

Despite these prevailing views, until recently there were few empirical tests that actually addressed whether infants were even capable of representing continuous dimensions, such as the size of items, duration, or the total amount of stuff. Results of these new studies have revealed that when required to quantify the continuous amount of a single entity (i.e., the duration of a single event and/or the surface area of a single item), infants discriminate continuous extent with an identical level of precision as that with which they discriminate number. That is, 6-month-olds notice a twofold change in the duration of an event (1 vs. 2 s) but not a 1.5-fold change (1 vs. 1.5 s; vanMarle and Wynn, 2006; Brannon et al., 2007). Similarly, they detect a twofold change in the size of a single element (an Elmo face), but fail to notice a 1.5-fold change (Brannon et al., 2006; see Feigenson, 2007 for review). Based on these findings it would appear that, contrary to Piaget and others, infants are no better at discriminating continuous extent than they are at discriminating number (Cordes and Brannon, 2008b).

An important difference however between the studies addressing numerical discrimination in infancy and those described above that addressed discrimination of duration or size is that stimuli from numerical discrimination tasks necessarily involved sets of multiple items (i.e., numbers greater than 1; e.g., Xu and Spelke, 2000) in contrast to the single elements (event or item) used in the duration or size discrimination studies.

Only two studies to date have made an explicit comparison between the ability to discriminate numerosity and the continuous variables that summarize a set. In Brannon et al. (2004) and Cordes and Brannon (2008a), infant abilities to discriminate changes in the cumulative (total) surface area of arrays of dots were investigated. In both studies, infants were habituated to arrays in which the number of items in the arrays changed across trials, however, the cumulative area of the arrays stayed the same and were then tested with arrays in which the cumulative area was the same or different from that of habituation. Results of these studies were surprising: despite previous findings that infants discriminate a twofold change in the area of a single item (Brannon et al., 2006), infants required as much as a fourfold change in the cumulative area of an array of items in order to detect a change. That is, infant discriminations of the continuous extent of an array were remarkably poor.

Although the precision with which infants represent the cumulative area of arrays is poor relative to that with which they represent number, is this indicative of how they represent all aspects of extent within an array? In particular, are infant representations of other continuous variables in an array, such as item size (individual element area as opposed to cumulative area) similarly imprecise? Whereas it is conceivable that the process by which infants represent cumulative area may involve a noisy (imprecise) summation computation (Cordes et al., 2007), tracking the size of individual items of a display is much less likely to involve extraneous computations that may compromise precision. Thus, in light of these findings, it is still possible that infants discriminate continuous extent within an array with equal or better precision than they represent number.

Here, we explore this question by asking how precisely infants track the size of individual items presented within an array. Seven-month-old infants were presented with homogeneous arrays in which the size of the individual items of the arrays was the same throughout habituation and then tested with arrays in which the size of the items was either the same or different from that of habituation. Controlling for changes in other quantitative aspects of the displays (e.g., number and cumulative area) by varying them throughout habituation and test, we evaluated how well infants keep track of the continuous extent of individual elements presented within the context of an array.

Note that demands in our task do not differ substantially from that of the single-item area discrimination task (Brannon et al., 2006). In order to succeed, infants need not attend to all elements of the display or perform any overt computation, but simply attend to the size of a single element in each of the homogeneous displays. So it would be reasonable to predict infants to reveal a similar level of discrimination as they did in the single-item study, discriminating a twofold change in the size of the individual elements of the array. However, given that all arrays in our task are homogeneous in item size and so novel test displays not only involve changes in the size of a single element but of multiple elements simultaneously, it is conceivable that infants may perform better than in previous studies. That is, the simultaneous change in the size of multiple items may provide redundant information to the infant which could serve to facilitate their discriminations, as has been found in other studies involving sequential and numerical ordering (e.g., Bahrick and Lickliter, 2000; Lewkowicz, 2004; Suanda et al., 2008). If so, data should support the claim that infants discriminate extent cues with better precision than that with which they discriminate number (i.e., they discriminate less than a twofold change in extent), as posited by Piaget and others (Piaget, 1952; Mix et al., 2002b; Soltesz et al., 2010).

Alternatively, these early “number is harder” claims may have simply been wrong and continuous extent may not be privileged over number – data revealing infants to be poor discriminators of the extent of an array may be the rule, not the exception (Brannon et al., 2004; Cordes and Brannon, 2008a). When presented with an array, extent representations may be hindered because number is a salient property of a set and infants preferentially attend to number at the expense of area (see Cordes and Brannon, 2009b). Under this scenario, infants have trouble attending to any continuous property in an array of elements because they are distracted by enumeration of the items. If so, infants should require a significantly greater change in the size of the individual items (more than a twofold change) in order to succeed in our task.

In addition to exploring these opposing predictions regarding infant discriminations of item size within an array, the current studies also explore the role of numerical information on representations of an item’s size. In our first study we allow number to vary between arrays in an attempt to eliminate numerical cues as a basis for responding (i.e., Brannon et al., 2004; Cordes and Brannon, 2008a). The question is whether they extract the invariant item size and ignore changes in cumulative surface area and number. One possibility, however, is that providing inconsistent numerical information is detrimental to the formation of extent representations – that is, we may unduly bias the infants toward failure in our task by varying both number and cumulative area. Thus, in our second experiment, number, and cumulative area are held constant throughout habituation.

Despite strenuous controls for the intensive parameters of an array (i.e., item size) in most studies of numerical discrimination in infancy (e.g., Xu and Spelke, 2000; Xu, 2003; Brannon et al., 2004; Cordes and Brannon, 2008a), no studies have explicitly examined infants’ abilities to discriminate the size of items within a set. Thus, in two experiments, we explore infant discriminations of changes in the size of items presented within an array. These studies will serve as the first investigation into the reasoning behind the implementation of standard design controls in infant numerical cognition and also provide data to address the on-going debate regarding the relative precision with which infants discriminate number and extent of arrays.

Experiment 1

Materials and Methods

We tested whether infants could detect a four- (Experiment 1a) or a threefold (Experiment 1b) change in the size of individual elements in an array. Seven-month-old infants were habituated to homogeneous sets of dots for which dot size stayed constant from trial-to-trial, but the number of dots (and hence, the cumulative area) varied sixfold. Infants were then tested with dot arrays that contained the same size dots and arrays that contained dots with a three- or fourfold change in size.

Participants

Participants were 36 (n = 20 Experiment 1a; n = 16 Experiment 1b) healthy full-term 7-month-old infants (M = 7 months 2 days, range: 6 months 16 days – 7 months 19 days; 22 female) recruited from the Raleigh/Durham area. Data from an additional 31 babies were discarded because of failure to reach the habituation criterion (n = 14), fussiness resulting in failure to complete at least four test trials (n = 14), external noise interference (building construction: n = 1), and computer error (n = 2)¹. Data from one additional subject was excluded due to excessively long looking times on two test trials (greater than 3 SD away from the mean looking time of all infants).

Design

Infants were habituated to homogeneous arrays of red dots. Across displays, the number of dots and cumulative area in each display varied sixfold, but the size of the individual dots in each display was constant. Infants were then tested with arrays of dots in which the sizes of the individual elements were the same as in habituation (familiar) and in which the element size differed fourfold (Experiment 1a) or threefold (Experiment 1b) from that of habituation (novel).

Stimuli

Stimuli were created with Canvas software and displayed in the center of the computer monitor (Figure 1). There were six different habituation stimuli, each with a different number of red dots (6, 9, 12, 18, 25, or 36 dots). Thus, cumulative area varied sixfold throughout habituation. The size of all habituation dots was 8 cm².

FIGURE 1

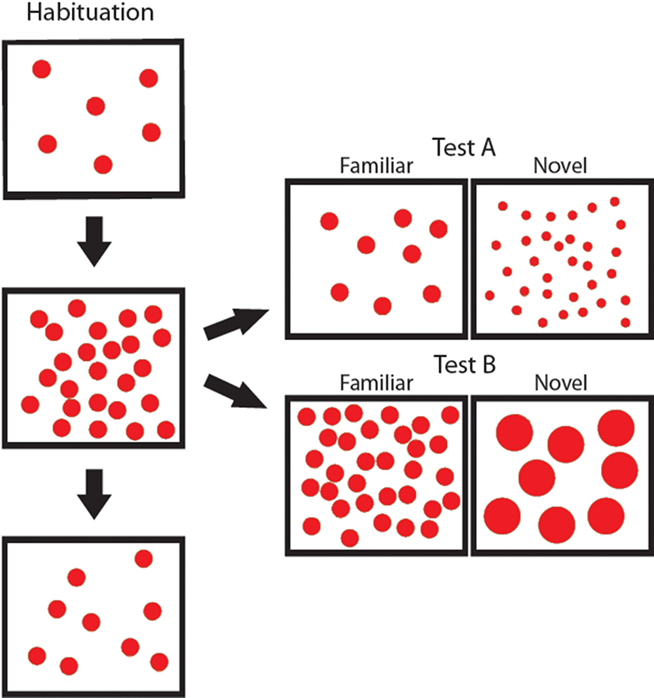
Figure 1. Sample stimuli from Experiment 1a. Throughout habituation, the number of items in each display varied sixfold, however the size of the items remained constant. In test, infants saw displays with the same item size and displays with items that changed in size fourfold from habituation (Test A – item size decrease; Test B – item size increase).

Following habituation, infants were presented with six test trials alternating between displays with the same dot size (familiar) and with a four- (Experiment 1a) or threefold (Experiment 1b) change (novel) compared to habituation. The number of dots in the test displays [8 and 32 for fourfold change (Experiment 1a), 10 and 30 for threefold change (Experiment 1b)] was chosen so as to be approximately equidistant from the mean of the number of dots in habituation, while keeping the cumulative area of the two test displays the same. Since background size was constant throughout habituation and test, item density in test was also approximately equidistant from the mean of habituation. Half of the infants saw Test Set A, in which novel displays involved dots that were smaller than that of habituation, and the other half of the infants saw Test Set B in which novel displays involved an increase in dot size. For example, in Test Set A of Experiment 1a (fourfold change), familiar test displays contained 8 dots (8 cm² each) and novel displays contained 32 dots (2 cm² each) such that cumulative area of novel and familiar displays was the same (64 cm²). On the other hand, familiar displays in Test Set B of Experiment 1a contained 32 dots (8 cm² each) and novel displays contained 8 dots (32 cm² each), such that cumulative area was again constant across test displays (at 256 cm²).

Apparatus

Infants were seated in a high-chair (or on a parent’s lap) 95 cm from a computer monitor. Parents were seated next to their infants and instructed to refrain from talking to, touching, or otherwise interacting with their infant for the duration of the experiment. If an infant became fussy, the experimenter initiated a short break and then resumed the experiment. For an infant to remain in the final sample, the break must have been less than 1 min in duration and could not have occurred between a pair of test trials. A microcamera monitoring the infant’s face and the stimulus presentation computer feed were multiplexed onto a TV monitor and a computer with digital recording software. One or two experienced experimenters blind to the experimental condition recorded the infants’ looking behavior while viewing the live video with the display occluded. The input was fed into a RealBasic program, which automatically advanced the stimulus and moved onto the test phase when the criterion was met. The program recorded infants as looking or not looking for each 100 ms interval and calculated inter-observer reliability. Reliability between two observers who coded 75% of the data live or offline (as conservatively computed based on agreement or disagreement at each 100 ms interval for each trial, averaged across trials, and then across subjects) was on average 94% (offline coding program – Libertus, 2008).

Procedure

All research reported in this paper was conducted in compliance with policies of the Duke University Institutional Review Board. Informed consent was obtained from a parent of each participant before testing. The experimenter initiated trials when the infant looked in the direction of the monitor. Each trial continued until the infant looked for a minimum of 0.5 s and ended after the infant looked for a total of 60 s or looked away for a continuous 2 s. Habituation stimuli were presented in a pseudo-random order until the infant met the habituation criterion (a 50% reduction in looking time over three consecutive trials, relative to the first three trials in which the infant looked for a total of at least 12 s) or until 16 trials were completed. After habituation the infants were tested with six test trials that alternated between familiar and novel displays. The order of novel and familiar test trials was counterbalanced across participants.

Results²

Experiment 1a

A paired-samples t-test revealed a significant reduction in looking time from the first three habituation trials (M = 10.5 s) to the last three habituation trials [M = 4.1; t(19) = 6.3, p < 0.0001] as expected given that only infants who habituated were included in the final sample. The average number of trials to habituation was 9.3.

A 2 × 2 × 2 mixed-factor ANOVA testing the between-subjects factors of test set [Test Set A (size decrease) vs. B (size increase)] and test order (novel or familiar test trial first) and the within-subjects factor of test trial type (novel or familiar) revealed a significant main effect of test trial type [F(1, 16) = 8.7, p = 0.01], a significant test set × test order interaction [F(1, 16) = 5.5, p < 0.04], and no other significant effects or interactions. The main effect of test trial type reflected the fact that infants looked longer to the novel (M = 6.0 s) as compared to the familiar (M = 4.5 s) test trials [t(19) = 3.1, p < 0.02], indicating they successfully detected the change in element size (14/20 infants looked longer to novel as compared to familiar, p = 0.058 Binomial statistics, see Figure 2).

FIGURE 2

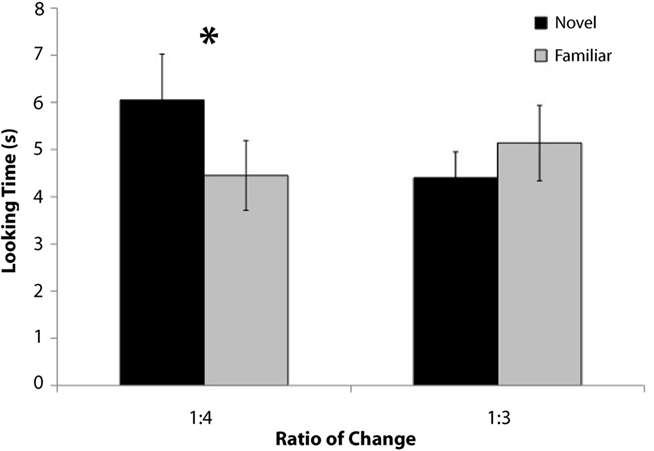
Figure 2. Mean looking times during the three familiar and three novel test trials for infants in Experiment 1 (variable number in habituation).

The test set × test order interaction indicated that infants who saw the more numerous display first in test (regardless of item size) were more likely to look longer throughout all test trials (M = 7.0 s) compared to those who saw the less numerous display first [M = 3.5 s; t(19) = 2.4, p < 0.04].

Experiment 1b

Again, a paired-samples t-test revealed a significant reduction in looking time from the first three habituation trials (M = 13.0 s) to the last three habituation trials [M = 4.4 s; t(15) = 8.0, p < 0.0001]. The average number of trials to habituation was 8.3.

A 2 × 2 × 2 mixed-factor ANOVA testing the between-subjects factors of test set [Test Set A (size decrease) vs. B (size increase)] and test order (novel or familiar test trial first) and the within-subjects factor of test trial type (novel or familiar) revealed a significant test set × test order interaction [F(1, 12) = 7.5, p < 0.02] revealing that infants who saw the more numerous display first in test (regardless of novelty) looked longer overall (in all test trials, M = 6.1 s) compared to those who saw the less numerous display first [M = 3.5 s; t(15) = 2.9, p < 0.02]. No other significant main effects or interactions were found (p > 0.2). Importantly, no main effect or interaction involving test trial type was found, and only 8 of the 16 (Binomial statistic: p > 0.5) infants looked longer to the novel displays (compared to familiar) revealing that infants did not detect the threefold change in the size of the items of the sets (Figure 2).

Experiment 1 combined analyses

An overall ANOVA looking at the between-subjects factor of ratio of change (threefold or fourfold) and the within-subjects factor of test trial type (novel or familiar) revealed a significant ratio of change × test trial type interaction [F(1, 34) = 5.6, p < 0.03] and no other significant main effects, confirming the fact that infants succeeded in detecting a fourfold, but not a threefold change in the size of items in a set.

Experiment 2

Results of Experiment 1 reveal that infants require as much as a fourfold change in the size of individual items of a display in order to detect a change in the size of the items. This result is surprising in light of previous findings indicating that 6-month-olds can detect as little as a twofold change in the size of a single item (Brannon et al., 2006). While these findings suggest that the presence of more than one item detracts from the ability to represent surface area, there is another explanation that may account for the discrepancy in discrimination precision that must first be ruled out. In the Brannon et al. (2006) study that used a single Elmo face, the number of items did not change across trials as it did in Experiment 1 here. It may be the case that infants were distracted by the changing number of items in each display and thus were less likely to attend to continuous extent cues not because set size was greater than one but because set size varied from trial-to-trial. Although it is common practice in studies of infant quantitative cognition to vary irrelevant quantitative dimensions throughout habituation while keeping the relevant quantitative dimension constant (e.g., Xu and Spelke, 2000; Xu, 2003; Brannon et al., 2004; Cordes and Brannon, 2008a, 2009a), it is also possible that variability in number hampers the cognitive procedure used to represent continuous extent. Experiment 2 tests this hypothesis by examining infant abilities to detect three- or fourfold changes in the size of items in an array when the size of the array is kept constant throughout habituation.

Materials and Methods

Participants

Participants were 40 (n = 20 Experiment 2a; n = 20 Experiment 2b) healthy full-term 7-month-old infants (mean age = 7 months 0 days, range: 6 months 16 days – 7 months 18 days; 21 female). Data from an additional 14 babies were discarded because of failure to reach the habituation criterion (n = 5), fussiness resulting in failure to complete at least four test trials (n = 5), falling asleep during the experiment (n = 1), parental interference (n = 1), external noise interference (building construction: n = 1), and computer error (n = 1). Data from one additional baby were excluded due to excessively long looks (more than 3 SD away from the mean looking time of all infants) on two or more test trials.

Design

Infants were habituated to arrays of red dots that were homogenous in size. The number of dots in each display and the size of the elements were held constant throughout habituation. Infants were subsequently tested with homogeneous arrays of dots in which dot size was the same as in habituation (familiar) and in which dot size differed fourfold (Experiment 2a) or threefold (Experiment 2b) from that of habituation (novel). Although the number of dots in test differed from that of habituation (in order to prevent cumulative surface area from being a relevant cue for discrimination), the number of dots in all test displays was held constant.

Stimuli

Stimuli were created with Canvas software and displayed in the center of the computer monitor (Figure 3). As in Experiment 1, stimuli were composed of homogeneous arrays of red circles in which each circle was 8 cm². In Experiment 2a all habituation stimuli contained 16 elements and in Experiment 2b all habituation stimuli contained 19 elements. There were six different habituation stimuli, each with a different spatial configuration of the same number of dots. Thus, both the number and cumulative area of displays were constant across habituation.

FIGURE 3

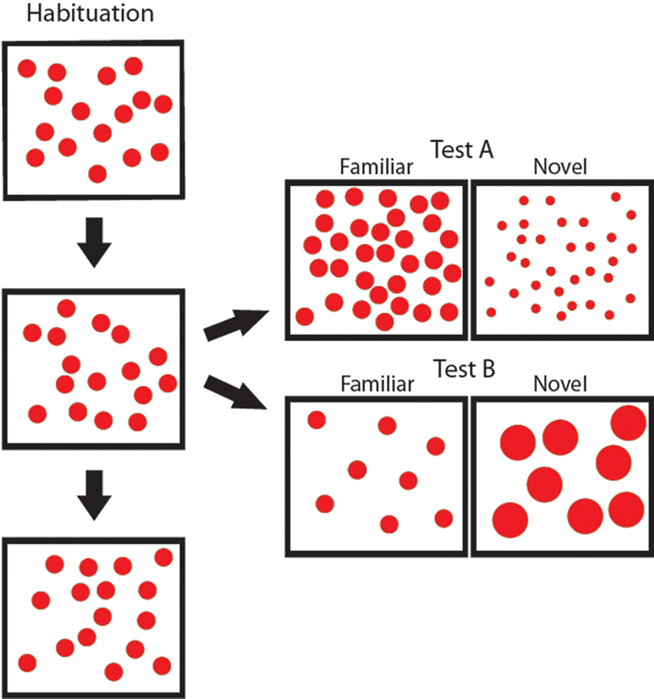
Figure 3. Sample stimuli from Experiment 2a. In habituation, the number of items in each display and the size of the items remained constant throughout habituation. In test, infants saw displays with the same item size and displays with items that changed in size fourfold from habituation.

Following habituation, infants were presented with six test trials alternating between displays with the same dot size (familiar) and with a four- (Experiment 2a) or threefold (Experiment 2b) change (novel) compared to habituation. Half of the infants saw novel displays in which the dots were smaller than that of habituation (Test Set A), and the other half of the infants saw novel displays involving an increase in dot size (Test Set B). The number of items in the novel and familiar displays of a given test set was always the same, chosen in order to make the cumulative area of the test displays equidistant from that of habituation. For example, in Experiment 2a (fourfold change) all displays in Test Set A contained 32 dots, however dots in the familiar displays were 8 cm² each while those in the novel displays were 2 cm² such that cumulative areas of novel (256 cm²) and familiar (64 cm²) displays were equidistant (on a logarithmic scale) from that of habituation (128 cm²) whereas displays in Test Set B (of the same experiment) contained only 8 dots each (dots in familiar displays were 8 cm² each and in novel displays were 32 cm² each). In Experiment 2b, set sizes in test were 11 and 33. Although the number of dots in test differed from that of habituation (in order to prevent cumulative area from being a relevant cue for discrimination), infants only saw one change in number (from habituation to test) thus reducing the possibility that numerical changes affected infant abilities to discriminate item size.

Apparatus and procedure

The apparatus and procedure for Experiment 2 were identical to those of Experiment 1. Inter-coder reliability was determined to be 93%.

Results

Experiment 2a

As expected, a paired-samples t-test revealed a significant reduction in looking time from the first three habituation trials (M = 11.5 s) to the last three habituation trials [M = 4.1 s; t(19) = 12.2, p < 0.0001]. The average number of trials to habituation was 7.7.

A 2 × 2 × 2 mixed-factor ANOVA testing the between-subjects factors of test set [Test Set A (size decrease) vs. B (size increase)] and test order (novel or familiar test trial first) and the within-subjects factor of test trial type (novel or familiar) revealed a significant main effect of test trial type [F(1, 16) = 4.9, p < 0.05] and no other significant effects or interactions. The main effect of test trial type reflected longer looking times to the novel (M = 5.5 s) as compared to the familiar (M = 4.3 s) test trials [t(19) = 2.5, p < 0.03], indicating that infants detected the change in element size (16/20 infants looked longer to novel as compared to familiar, p < 0.01 Binomial statistics; Figure 4).

FIGURE 4

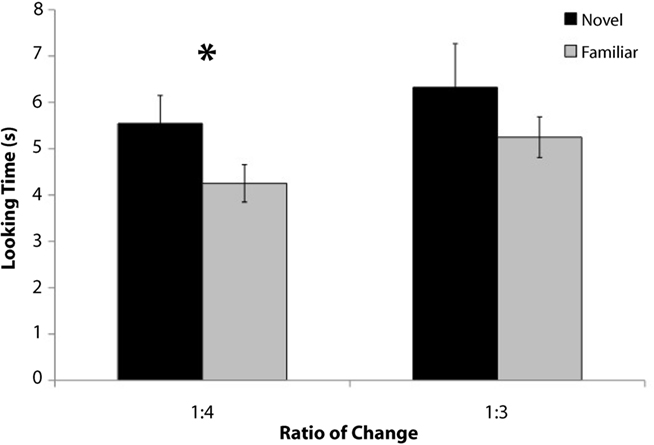
Figure 4. Mean looking times during the three familiar and three novel test trials for infants in Experiment 2 (number constant in habituation).

Experiment 2b³

Again, there was a significant reduction in looking time from the first three (M = 11.7 s) to the last three habituation trials [M = 4.0 s; t(19) = 11.8, p < 0.0001]. The average number of trials to habituation was 7.9.

A 2 × 2 × 2 mixed-factor ANOVA testing the between-subjects factors of test set [Test Set A (size decrease) vs. B (size increase)] and test order (novel or familiar test trial first) and the within-subjects factor of test trial type (novel or familiar) revealed a significant three-way interaction [F(1, 16) = 6.6, p = 0.02] and no other significant main effects or interactions. Although on average infants looked longer to novel (M = 6.3 s) as compared to familiar test trials (M = 5.2 s), the main effect of test trial type was not significant [F(1, 16) = 2.1, p > 0.16] indicating that infants did not detect the threefold change in the size of the items. In fact, only half of the infants (10 of 20; Binomial statistic p > 0.58) looked longer to the novel test trials compared to familiar again suggesting they did not detect a change in the size of the items (Figure 4).

Experiment 2 combined analyses

An overall ANOVA looking at the between-subjects factor of ratio of change (threefold or fourfold) and the within-subjects factor of test trial type (novel or familiar) revealed a significant main effect of novelty [F(1, 38) = 5.7, p < 0.03] and no other significant main effects or interactions. The interaction between ratio of change and test trial type was not significant (p > 0.8).

Experiments 1 and 2 combined analyses

An overall ANOVA examining the effects of ratio of change (three- or fourfold), habituation condition [number varying (Experiment 1) or constant (Experiment 2)], and test trial type (novel or familiar) on looking times in test across Experiments 1 and 2 was conducted. A significant effect of test trial type was found [F(1, 72) = 5.3, p < 0.03], revealing that on average, infants preferred the novel as compared to familiar test trials. In addition, a near-significant ratio of change × test trial type interaction was found [F(1, 72) = 3.3, p = 0.072] revealing that infants successfully detected the fourfold, but not the threefold change in item size. The habituation condition × test trial type was not significant [F(1, 72) = 1.1, p > 0.2], indicating that keeping the numerosity of the sets constant in Experiment 2 did not facilitate infants’ ability to track individual element size.

Discussion

Our results suggest that infants show coarse discrimination for the continuous variables of the individuals that make up a set. Specifically, in two experiments 7-month-old infants required as much as a fourfold change in the size of the individual items of a set in order to detect a change. In contrast to previous findings indicating that 6-month-olds detect as little as twofold changes in the number of items in a set (e.g., Xu and Spelke, 2000), our data reveal that when presented with similar arrays of items, infants represent surface area with remarkable imprecision. This is surprising given that the area representations required for successful discrimination in our task did not require any overt computations such as summing area over multiple elements. At a minimum, success in our task only required attention to a single item in each array whereas representations of number inherently require attention to all individuals in the set. Despite the seemingly simplified task demands in our area discrimination task, infants required twice as much of a change in element size as they did for number in order to succeed. Thus, contrary to common assumptions in the field of cognitive development (e.g., Piaget, 1952; Mix et al., 2002a,b), when presented with a set of items, infants are much more likely to detect a change in number than in continuous extent (Cordes and Brannon, 2008b, 2009a).

In addition to providing the first test of infant discriminations of the size of items in a set, results of the current study speak to the discrepancy in precision with which infants discriminate changes in the area of a single item (Brannon et al., 2006) and of the cumulative area of a set of items (Cordes and Brannon, 2008a). Despite detecting relatively small (twofold) changes in the size of an individual item, infants required a fourfold change in element size when elements were presented within an array of identical elements in order to successfully detect a change. This is somewhat surprising because, as noted above, success in our task simply required attention to a single element in each display – properties of the set as a whole were irrelevant to the discrimination. That is, infants encountered identical task demands to that of the single element area discrimination task in Brannon et al. (2006), and yet they apparently failed due to the presence of more than one item. In fact, one might have predicted that the homogeneous arrays in our experiments would facilitate area discrimination in that they provide multiple redundant cues or a “super-stimulus.” Abundant research reveals infant discriminations benefit from redundant information (e.g., Bahrick and Lickliter, 2000; Lewkowicz, 2004). This however was not the case. Instead, our data suggest that the presence of more than one item in a set may in fact detrimentally impact infant abilities to represent area. Of course a caveat is that infants may have been more interested in the red Elmo faces used by Brannon et al. (2006) compared to our red dot arrays⁴, however overall looking times in Brannon et al. (M = 6.6 s) and our study (M = 6.5 s) did not differ [t(111) = 0.1, p > 0.9]⁵ suggesting that this saliency explanation is unlikely.

One potential explanation for our results is that when infants are presented with arrays they automatically attempt to track number rather than area and that this numerical process interferes with tracking the continuous properties of the elements of the set. Prior work supports this view in that infants, children, and adults are more likely to detect changes in number than cumulative area when presented with large (>3 items) sets (e.g., Xu and Spelke, 2000; Brannon et al., 2004; Barth, 2008; Cordes and Brannon, 2008a, 2009b; Cantlon et al., 2010; see Feigenson et al., 2002a; Cordes and Brannon, 2009a; Xu et al., 2005 for discussion of small/large distinction). The claim that numerical representations interfere with continuous extent representations however is not entirely consistent with our pattern of results. Specifically, when the number of items in the set varied throughout habituation and test (Experiment 1), infants habituated to the displays at the same rate and revealed the exact same precision in discrimination of element size as when the number of items stayed the same (Experiment 2). Thus, the identical pattern of results obtained in Experiments 1 and 2 indicates that infants did not attend to changes in number at the expense of attending to changes in surface area. Instead our data suggest that these were seemingly independent processes. The presence of multiple items appeared to detract from infant abilities to represent surface area regardless of whether number was held constant or varying. This is consistent with previous findings revealing infants are poor discriminators of the continuous extent across sets (cumulative area – Cordes and Brannon, 2008a). Even though infants did not need to attend to more than one item in the set in our current study, when presented with a large set of items, infants spontaneously attended to all elements of the display and this spreading of attention detrimentally impacted the precision with which they represented continuous extent. Surprisingly, this spreading of attention does not appear to have a similar effect on their ability to represent number in other studies (e.g., Xu and Spelke, 2000), again supporting the claim that infants are better discriminators of number than of continuous extent.

Given that infants represent the size of items within a homogeneous set and the cumulative area of a set of items with the same level of precision, our data also suggest that their poor performance in representing cumulative area in previous studies was not solely due to a noisy summation process. Instead, infants are simply less sensitive to changes in element size when elements are presented within an array compared to when they are presented in isolation.

In conclusion, results of the current study provide further evidence that infants are poor discriminators of continuous extent. Despite the prevalent view in the field of cognitive development that representing number requires greater cognitive effort compared to representing size and cumulative area (e.g., Piaget, 1952; Mix et al., 2002a,b; Soltesz et al., 2010), our findings suggest otherwise. In fact, it appears that when presented with sets continuous variables are not automatically encoded in infancy and that instead infants may often fail to track seemingly large changes in the size of objects in their world.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank the members of the Brannon Cognitive Development Laboratory, in particular, we thank Emily Hopkins and Anna Beth Keith for help with data collection. We also thank Liz Heller for help with figure creation. We thank the parents and infants who donated their time to participate in the research. This material is based upon work supported by the National Science Foundation (Grant No. 0448250 and an NSF CAREER ROLE/DLS research grant to Elizabeth M. Brannon), the National Institute for Mental Health (RO1 MH066154 to Elizabeth M. Brannon), an NIH NRSA Post-Doctoral Fellowship (to Sara Cordes), and a Sloan Foundation Fellowship (to Sara Cordes). Correspondence concerning this article should be addressed to Sara Cordes (cordess@bc.edu).

Footnotes

1. ^Although many studies include infants who fail to meet the habituation criterion (e.g., Xu, 2003; Wood and Spelke, 2005), we thought it was important to have a full sample of habituated infants in order to perform a fair comparison with data from Experiment 2 that involved less complex habituation stimuli.
2. ^In all experiments, looking times longer than 3 SD away from the mean were treated as outliers and were replaced with the next longest looking time (within 3 SD, as per Cordes and Brannon, 2009b). This resulted in the replacement of 1, 3, 3, and 3 data points in Experiments 1a, 1b, 2a, and 2b respectively.
3. ^One pair of missing data points (in which the infant fussed out before the completion of all three sets of test trials) in Experiment 2b were replaced with the average looking times for those test trials (as per Brannon et al., 2004; Xu and Spelke, 2000).
4. ^However, it should be noted that one previous study of numerical discrimination in infancy employed both social and non-social (dot array) stimuli in their tasks (Cordes and Brannon, 2009a) and an identical pattern of performance was observed, suggesting that the nature of the stimuli did not affect discrimination precision.
5. ^Overall looking times did not differ, nor did looking times just during habituation, or during test. This was the case for all ratios tested, as well as a comparison between looking times during the threefold change in the size of Elmo’s face and in our threefold change conditions (Experiments 1b and 2b).

References

Bahrick, L. E., and Lickliter, R. (2000). Intersensory redundancy guides attentional selectivity and perceptual learning in infancy. Dev. Psychol. 36, 190–201.

Pubmed Abstract | Pubmed Full Text

Barth, H. C. (2008). Judgments of discrete and continuous quantity: an illusory Stroop effect. Cognition 109, 251–266.

Pubmed Abstract | Pubmed Full Text

Brannon, E. M., Abbott, S., and Lutz, D. J. (2004). Number bias for the discrimination of large visual sets in infancy. Cognition 93, B59–B68.

Pubmed Abstract | Pubmed Full Text

Brannon, E. M., Lutz, D., and Cordes, S. (2006). The development of area discrimination and its implications for numerical abilities in infancy. Dev. Sci. 9, F59–F64.

Pubmed Abstract | Pubmed Full Text

Brannon, E. M., Suanda, S., and Libertus, K. (2007). Temporal discrimination increases in precision over development and parallels the development of numerosity discrimination. Dev. Sci. 10, 770–777.

Pubmed Abstract | Pubmed Full Text

Cantlon, J. F., Safford, K. E., and Brannon, E. M. (2010). Spontaneous analog magnitude representations in 3-year-old children. Dev. Sci. 13, 289–297.

Clearfield, M. W., and Mix, K. S. (1999). Number versus contour length in infants’ discrimination of small visual sets. Psychol. Sci. 10, 408–411.

Clearfield, M. W., and Mix, K. S. (2001). Amount versus number: infants’ use of area and contour length to discriminate small sets. J. Cogn. Dev. 2, 243–260.

Cohen, L. B., and Marks, K. S. (2002). How infants process addition and subtraction events. Dev. Sci. 5, 186–201.

Cordes, S., and Brannon, E. M. (2008a). Discrimination of continuous quantities in 6-month old infants: using number is just easier. Child Dev. 79, 476–489.

Cordes, S., and Brannon, E. M. (2008b). Quantitative competencies in infancy. Dev. Sci. 11, 803–808.

Cordes, S., and Brannon, E. M. (2009a). Discrimination of small from large numbers in 7-month old infants. Dev. Psychol. 45, 1583–1594.

Cordes, S., and Brannon, E. M. (2009b). The relative salience of discrete and continuous quantities in infants. Dev. Sci. 12, 453–463.

Cordes, S., Gallistel, C. R., Gelman, R., and Latham, P. (2007). Nonverbal arithmetic in humans: light from noise. Percept. Psychophys. 69, 1185–1203.

Pubmed Abstract | Pubmed Full Text

Davis, H., and Memmott, J. (1983). Autocontingencies: rats count to three to predict safety from shock. Anim. Learn. Behav. 11, 95–100.

Feigenson, L. (2007). The equality of quantity. Trends Cogn.Sci. 11, 185–187.

Pubmed Abstract | Pubmed Full Text

Feigenson, L., Carey, S., and Hauser, M. (2002a). The representations underlying infants’ choice of more: object files versus analog magnitudes. Psychol. Sci. 13, 150–156.

Feigenson, L., Carey, S., and Spelke, E. S. (2002b). Infants’ discrimination of number vs. continuous extent. Cogn. Psychol. 44, 33–66.

Izard, V., Sann, C., Spelke, E. S., and Streri, A. (2009). Newborn infants perceive abstract numbers. Proc. Natl. Acad. Sci. U.S.A. 106, 10382–10385.

Pubmed Abstract | Pubmed Full Text

Jordan, K. E., and Brannon, E. M. (2006). The multisensory representation of number in infancy. Proc. Natl. Acad. Sci. U.S.A. 103, 3486–3489.

Pubmed Abstract | Pubmed Full Text

Kobayashi, T., Hiraki, K., and Hasegawa, T. (2005). Auditory-visual intermodal matching of small numerosities in 6-month old infants. Dev. Sci. 8, 409–419.

Pubmed Abstract | Pubmed Full Text

Lewkowicz, D. J. (2004). Perception of serial order in infants. Dev. Sci. 7, 175–184.

Pubmed Abstract | Pubmed Full Text

Libertus, K. (2008). Preferential Looking Coder. Available at: http://www.duke.edu/∼kl41

Lipton, J. S., and Spelke, E. S. (2003). Origins of number sense: large-number discrimination in human infants. Psychol. Sci. 14, 396–401.

Pubmed Abstract | Pubmed Full Text

Mix, K. S., Huttenlocher, J., and Levine, S. C. (2002a). Multiple cues for quantification in infancy: is number one of them? Psychol. Bull. 128, 278–294.

Mix, K. S., Huttenlocher, J., and Levine, S. C. (2002b). Quantitative Development in Infancy and Early Childhood. New York, NY: Oxford University Press.

Piaget, J. (1952). The Child’s Conception of Number. London: Routledge and Kegan Paul.

Soltesz, F., Szucs, D., and Szucs, L. (2010). Relationships between magnitude representation, counting and memory in 4- to 7-year-old children: a developmental study. Behav. Brain Funct. 6, 1–14.

Pubmed Abstract | Pubmed Full Text

Starkey, P., Spelke, E. S., and Gelman, R. (1983). Detection of intermodal numerical correspondences by human infants. Science 222, 179–181.

Pubmed Abstract | Pubmed Full Text

Suanda, S., Tompson, W., and Brannon, E. M. (2008). Changes in the ability to detect ordinal numerical relationships between 9 and 11 months of age. Infancy 13, 308–337.

Pubmed Abstract | Pubmed Full Text

vanMarle, K., and Wynn, K. (2006). Six-month-old infants use analog magnitudes to represent duration. Dev. Sci. 9, F41–F49.

Pubmed Abstract | Pubmed Full Text

Wood, J. N., and Spelke, E. S. (2005). Infants’ enumeration of actions: numerical discrimination and its signature limits. Dev. Sci. 8, 173–181.

Pubmed Abstract | Pubmed Full Text

Xu, F. (2003). Numerosity discrimination in infants: evidence for two systems of representations. Cognition 89, B15–B25.

Pubmed Abstract | Pubmed Full Text

Xu, F., and Spelke, E. S. (2000). Large number discrimination in 6-month-old infants. Cognition 74, B1–B11.

Pubmed Abstract | Pubmed Full Text

Xu, F., Spelke, E. S., and Goddard, S. (2005). Number sense in human infants. Dev. Sci. 8, 88–101.

Pubmed Abstract | Pubmed Full Text