- 1 Brain and Cognition, Department of Psychology, Erasmus University Rotterdam, Rotterdam, Netherlands
- 2 Amsterdam School of Communication Research, University of Amsterdam, Amsterdam, Netherlands
Numbers might be understood by grounding in spatial orientation, where small numbers are represented as low or to the left and large numbers are represented as high or to the right. We presented numbers in concrete (seven shoes in a shoe shop) or abstract (29 – 7) contexts and asked participants to make relative magnitude judgments. Following the judgment a target letter was presented at the top or bottom (Experiments 1–3) or left or right (Experiment 4) of the visual field. Participants were better at identifying letters at congruent than incongruent locations, but this effect was obtained only when numbers were presented in concrete contexts. We conclude that spatial grounding might have a smaller role for numbers in abstract than in concrete context.
Introduction
If you would ask someone whether seven pairs of shoes is a lot or a little, the person would probably respond that this depends on the context. For example, it would be a little to have in a shoe shop but a lot to bring on a weekend to Paris (at least for sensible people). In order to evaluate magnitude one needs to mentally compare the number to a reference quantity such as an approximate number of shoes in a regular shoe shop or in an overnight bag. In the present study we investigated the mental representation of number magnitude. In particular, we compared to what extent numbers in concrete contexts (e.g., seven pairs of shoes) and numbers in abstract contexts (e.g., 7) have spatial representations.
Because number meaning can vary between very concrete and very abstract, depending on the context, the representation of numbers provides an interesting case for grounded theories of cognition (Glenberg, 1997; Barsalou, 1999; Lakoff and Núñez, 2000). On one end of the continuum numbers refer to perceptible quantities of concrete stuff such as shoes and oranges, and on the other end numbers are used to refer to things that have no perceptible referents in the world such as negative numbers and square roots. Much of the empirical support for the grounded cognition framework comes from studies that showed sensory–motor grounding for representations of concrete objects and actions, but so far not many studies have shown sensory–motor grounding for abstract concepts (Pecher et al., 2011). Since abstract concepts are an essential part of cognition, explaining how abstract concepts are represented by sensory–motor simulations is a critical challenge for the grounded framework (Machery, 2007; Mahon and Caramazza, 2008; Borghi et al., 2011; Dove, 2011).
Several researchers have proposed that abstract concepts are grounded in sensory–motor simulations by metaphorical mappings between abstract concept and concrete, spatial domains (Lakoff and Johnson, 1980, 1999; Lakoff, 1987; Gibbs, 1994, 2005). On this account, mental representations of abstract concepts take their structure from concrete image schemas (but see Kranjec and Chatterjee, 2010). For example, in natural language people often use spatial terms when they talk about time (e.g., the meeting has been moved forward), which suggests that representations for space and time are partially overlapping (see also Walsh, 2003). Initially, evidence for such mappings came from linguistic expressions, but more recently results from behavioral experiments have supported the cognitive metaphor theory (Boroditsky and Ramscar, 2002; Richardson et al., 2003; Meier and Robinson, 2004; Spivey et al., 2005; Casasanto, 2008; Van Dantzig, 2009; Boot and Pecher, 2010, 2011; Zanolie et al., 2011; Sell and Kaschak, 2011).
A second proposal explaining how abstract concepts are grounded in sensory–motor simulations posits an important role for situations. Barsalou and Wiemer-Hastings (2005) argued that the specific situations in which abstract concepts occur might be mentally simulated. To investigate this idea they asked participants to list properties for concepts at varying levels of abstraction. Their results confirmed that situational properties were important for abstract concepts. On this account, numbers might get their meaning from situational information such as when the number refers to a quantity of something (seven pairs of shoes) in a relevant context (the shoe shop). Therefore, numbers should have richer representations in concrete contexts than without such a context.
The metaphor explanation for number representations is supported by the spatial numerical association of response codes (SNARC) effect. Many researchers have suggested that numbers are represented visuo-spatially on a mental number line. The best known effect is the horizontal SNARC effect (e.g., Dehaene et al., 1993) although there are a few studies that also showed a vertical SNARC effect for hand responses (Ito and Hatta, 2004; Gevers et al., 2006; Ristic et al., 2006) and eye movement responses (Schwartz and Keus, 2004). Participants respond faster with the left hand to low numbers than to high number, and faster with the right hand to high numbers than to low numbers (see Gevers et al., 2010 for similar effects with verbal responses) even when magnitude is irrelevant to the task, as in parity judgment. Such findings could be interpreted as showing that participants represent numbers along a horizontal mental number line with small numbers on the left and large numbers on the right of the continuum. On an alternative account, however, the SNARC effect could be attributed to processes that occur during response selection (Keus and Schwarz, 2005; Keus et al., 2005; Müller and Schwarz, 2007) or to polarity alignment (Proctor and Cho, 2006; Landy et al., 2008; Santens and Gevers, 2008; Bae et al., 2009). If the effect can be attributed to response selection, no underlying mental representation needs to be assumed to explain the SNARC effect. Thus, at present there is no agreement yet as to whether the SNARC effect indicates a spatial representation of numbers.
Stronger evidence for a spatial representation of numbers is provided by studies that show effects of number magnitude on spatial attention (Fischer et al., 2003; Nicholls et al., 2008; Salillas et al., 2008). Fischer et al. (2003) found that participants were faster to detect a target at the left when it was preceded by a low digit (one or two) and faster to detect a target at the right when preceded by a high digit (eight or nine). These attention effects indicate automatic activation of a spatial representation of numbers on a horizontal dimension. Unfortunately, the effect on spatial attention is not obtained very consistently (Galfano et al., 2006; Ristic et al., 2006; Lindemann et al., 2008; Zanolie and Pecher, 2011). In the attentional paradigm spatial information might be less salient than in the traditional SNARC studies because spatial information is not relevant for the response. Zanolie and Pecher (2011) showed that the effect of number magnitude on spatial attention critically depends on the relevance of magnitude in the task context. Thus, there is some evidence that number representation affects spatial attention although the effect is probably due to active rather than automatic processing of number magnitude.
The SNARC effect has been investigated mostly in the horizontal direction. Linguistic sources, however, provide very little evidence for a horizontal mental number line but much evidence for a vertical mental number line. In natural language vertical words are often used to talk about magnitude. For example, people might say prices are high, mortgage rates dropped, incomes can riseor heat is turned up or down (Johnson, 1987; Lakoff and Núñez, 2000; Bergen et al., 2007). Why would they not say that incomes are moving to the right and heat is turned left? The systematic way in which vertical but not horizontal terms are used for magnitude suggests that magnitude is represented in terms of verticality (Lakoff and Johnson, 1980). Therefore, it may be the case that in representations of magnitude vertical orientation is more important than horizontal orientation. In the present study we investigated whether thinking about magnitude directed spatial attention vertically or horizontally.
A second goal of the present study was to investigate whether spatial attention is affected differently by magnitude in concrete (e.g., seven pairs of shoes in a shop) and abstract (e.g., seven) contexts. So far, most evidence for spatial number representations has been obtained with numbers in abstract contexts. In the present study we presented numbers either in a concrete, natural context or in a more abstract context of just other numbers. On the one hand we might expect that numbers in concrete contexts are more closely associated to spatial directions, because they refer to concrete magnitudes such as a row of shoes or a stack of books that actually have spatial dimensions. A study by Bergen et al. (2007) suggests that vertical spatial representations might be restricted to situations and events that refer to concrete vertical space. They investigated the effect of described motion on spatial attention along the vertical midline. They found that sentences with concrete movements (e.g., the mule climbed) interfered with processing of an unrelated visual stimulus, but no such effect was found for sentences with abstract movements (e.g., the cost climbed). Bergen et al. (2007) argued that representations of concrete situations interfered with visual processing because they use the same resources. Abstract representations do not involve visual simulation, however, and thus do not interfere with visual processing.
On the other hand, numbers in abstract contexts may need grounding in the spatial domain precisely because they lack perceptual properties. Several studies have obtained effects of abstract representations on spatial attention, suggesting that these representations are grounded in spatial image schemas (Richardson et al., 2003; Meier and Robinson, 2004; Van Dantzig, 2009). These findings are predicted by cognitive metaphor theorists, who claim that abstract concepts are understood by metaphorical mappings between abstract and concrete domains. Whereas mental simulation of visual details interferes with perceptual processing, effects of image schemas on spatial attention should facilitate processing of visual stimuli (Estes et al., 2008).
In the present study we investigated how processing of visual stimuli at different locations is affected by numbers in concrete and abstract contexts. Because the spatial position of a number is relative to other numbers (Reynvoet and Brysbaert, 1999; Nathan et al., 2009), we asked participants to make relative magnitude judgments to numbers in either a concrete or an abstract context. To assess the activation of spatial image schemas the magnitude judgment was followed by an unrelated stimulus (the letter p or q) in a spatial location that was either congruent or incongruent with the image schematic location of the number. If spatial attention is affected by number magnitude, identification of the letter should be facilitated in congruent positions compared to incongruent positions.
The letter identification task has been used in numerous studies that investigated effects on spatial attention (e.g., Meier and Robinson, 2004; Meier et al., 2007; Estes et al., 2008; Van Dantzig, 2009). The advantage of using a secondary task is that in the experimental set-up magnitude judgment (the first task) is not related to spatial position, and letter identification (the second task) is not related to either spatial position or magnitude judgment. Proctor and Cho (2006) have suggested that congruency effects in binary tasks can be explained by polarity alignment. This effect occurs if stimulus and response dimensions have polarity, that is, can be coded as + (plus) and − (minus). Proctor and Cho (2006), but see Pecher et al., 2010 assume that in spatial dimensions, above and right are coded as +. They also assume that “yes” responses are coded as +. Therefore, the polarity principle predicts that “yes” responses will be faster when they are aligned with stimuli or response sides that are also + (i.e., above or right). In the letter identification task such alignment effects will not play a role because the “p” or “q” response does not have an obvious polarity. Even if participants would code the responses as + and −, however, this would not affect the overall results, because “p” and “q” responses are collapsed.
Experiment 1
In Experiment 1 we presented sentences in which a number was presented in a natural context. Participants decided whether the magnitude was relatively few or many(the Dutch words weinigand veel were used, which do not refer to height and can be used for both mass and count nouns). Whether the magnitude was relatively few or many depended on the situation, because the same absolute numbers appeared in both conditions (e.g., The man had two books in his bookcasevs. The man read two books a day). Thus, participants had to use the situation in order to make a magnitude judgment. Magnitude judgments were followed by identification of a letter p or q which appeared at the top or bottom of the screen (as in the study by Meier and Robinson, 2004).
If magnitude is represented by vertical position we expected that attention would shift to the top for relatively high magnitudes and to the bottom for relatively low magnitudes. This attention shift should facilitate identification of targets in the congruent position compared to targets in the incongruent position. It should be noted that we did not use quantities that explicitly referred to vertical positions (e.g., we did not use items like the tree was 6 meters tall). Neither did we use words that referred to vertical movement or direction (e.g., dropped, up). Thus, any effect on vertical attention was due to the representation of the concept magnitude rather than to the literal orientation of actions or objects mentioned in the sentence.
Methods
Participants
Thirty-two undergraduate psychology students at the Erasmus University Rotterdam received course credit for participating. All participants were fluent speakers of Dutch.
Materials
All instructions and materials were in Dutch. We created 40 sentences in the few condition containing a relatively small quantity and 40 sentences in the many condition containing a relatively large quantity (examples are shown in the Appendix). The same absolute quantities were used in the few and many conditions, so whether it was few or many depended on the sentence context and not on the absolute number. Different kinds of quantity indications were used (e.g., 100 meters, 10 minutes, 10 euro). No words were used that referred to vertical position or movement. Across participants, sentences were counterbalanced over the target letter identity, target letter position, and block order. Each combination of letter identity and letter position was used equally often in each condition and block. Twenty-one additional sentences were created for practice and instruction.
Procedure
Participants were tested individually on PCs separated by walls. Participants responded by pressing a button on a response box that had five aligned buttons. Four different response mappings were used, such that participants used two fingers of each hand to respond, and used one hand for each task so that the two fingers of the same hand were used to make the two responses in one task. Response mapping was varied between subjects. Buttons were labeled with the letter v (veel – Dutch for many), the letter w(weinig – Dutch for few), the letter p, and the letter q. Participants were instructed to make magnitude judgments by choosing few or many. A sentence was presented in the center of the screen until a response was made. Then, 200 ms after the response, the letter p or q (28 pt Garamond) was presented at the top or bottom of the screen which had to be identified as quickly and accurately as possible by pressing the corresponding button. The next trial started 500 ms after the response to the target was made or after the feedback. Feedback (fout – Dutch for error) was provided for 1500 ms after incorrect responses to the letter targets. Twenty practice trials preceded the 80 experimental trials. The experimental sentences were presented in random order in two blocks, with the restriction that sentences that contained the same quantity were presented in different blocks. Between the two blocks participants could take a break and feedback on their accuracy in the first block was provided.
Results
Four items were removed from the analysis because fewer than 60% of the participants gave the intended magnitude response (Two in the many and two in the few condition). We calculated mean reaction times and accuracy for the letter identification responses. Incorrect responses (to prime or target, 8.1%) and responses more than 2 SD from the subject’s mean (4.2%) were excluded from the reaction time analyses. Mean reaction times and error rates are presented in Figure 1. In the reaction times we obtained a significant interaction between magnitude and vertical position, F(1, 31) = 4.75, MSE = 732.6, η2 = 0.13, p < 0.05. Participants were faster to identify a letter presented at the top when they first read a sentence in which the magnitude was many compared to a few, t(31) = 5.08, SEM = 5.08, η2 = 0.24, p < 0.0001. Responses to letters at the bottom of the screen were not different between conditions, t(31) = 1.49, SEM = 5.1, η2 = 0.03, p > 0.10. Responses to letters were faster in the many than in the few condition, F(1, 31) = 4.58, MSE = 1478.7, η2 = 0.13, p < 0.05, and responses were faster to letters at the top than the bottom of the screen, F(1, 31) = 5.38, MSE = 3421, η2 = 0.15, p < 0.05.
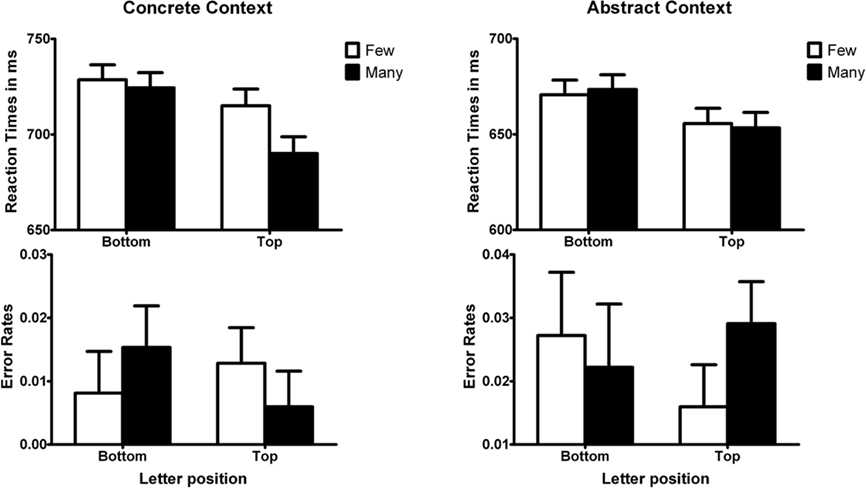
Figure 1. Reaction times and error rates for the letter identification task in Experiments 1 (Concrete Context) and 2 (Abstract Context). Error bars represent standard error of the mean difference for adjacent bars.
In the error rates we also obtained an interaction effect between position and magnitude, F(1, 31) = 5.06, MSE = 0.000, η2 = 0.14, p < 0.05. None of the other effects reached significance.
Experiment 2
Next we investigated if the magnitude-position congruency effect could be replicated with quantities in an abstract context of just other numbers. As in Experiment 1, participants made relative magnitude judgments. In Experiment 2 the numbers 0–100 were used and participants judged magnitude by comparing each number to 50.
Method
Participants
Participants were 32 students from the same pool who had not participated in Experiment 1.
Materials
The numbers 0–49 and 51–100 were used.
Procedure
The procedure was the same as in Experiment 1, except that prior to the letter identification task participants judged whether the number was a few or many compared to 50. Twenty numbers were used for practice; the remaining 80 numbers were used as experimental trials. Counterbalancing was the same as in Experiment 1, and in addition odd and even numbers were also counterbalanced across letter position.
Results
The same data analysis procedure was used as for Experiment 1. The results are displayed in Figure 1. Incorrect responses (5.3%) and remaining outliers (4.6%) were removed. In the reaction times we obtained no interaction effect between magnitude and vertical position, F < 1 nor in the error rates, F(1, 31) = 1.13, MSE = 0.001, η2 = 0.04, p > 0.25.
Experiment 3
In Experiment 1 we found that number magnitude directed spatial attention, whereas no such effect was observed in Experiment 2. The main difference between the experiments was that the numbers in Experiment 1 referred to concrete situations and in Experiment 2 to abstract situations. This suggests that the vertical representation of magnitude is activated more strongly when people represent numbers that refer to concrete situations than numbers that refer to abstract situations. Besides abstractness, however, there were a few other procedural differences between the two experiments. In order to directly compare the two types of number representation we ran an additional experiment in which we made the two tasks more similar. In particular, we controlled for two differences between Experiments 1 and 2. First, in Experiment 1 the reference point (the “normal” magnitude in that context) was implicit, whereas it was explicitly provided in Experiment 2. Second, the reference point was variable in Experiment 1 because it depended on the context. In Experiment 2, however, it was fixed (i.e., it was always 50). In Experiment 3 we presented numbers in both concrete and abstract contexts, and an explicit reference point was given for both types of stimuli. In addition, the value of the reference point varied between trials for both types of stimuli.
Method
Participants
Thirty-two students from the same pool who had not participated in Experiments 1 and 2 participated for course credits.
Materials
The same materials as in Experiments 1 and 2 were used. In addition, all prime sentences and numbers (on which the magnitude judgment was made) were now preceded by a reference sentence or reference number that provided an explicit reference point for the prime. Thus, the order of events for each trial was: reference – magnitude stimulus – letter stimulus. For each magnitude sentence from Experiment 1 we created a referent sentences which contained a different quantity in the same context (e.g., 60,000 people can be seated in the stadium) as the magnitude sentence (e.g., 80 people were seated in the stadium).
To prevent participants simply comparing the two quantities from referent and magnitude sentence without considering the situation half of the referent sentences were replaced by fillers that had the same quantity in a different context (e.g., 80 people attended the business meeting). Sentences used as experimental trials and fillers were counterbalanced between subjects. For each magnitude number from Experiment 2 we selected two different referent numbers. Referent numbers could be at large or small numerical distances from the magnitude numbers, and were chosen such that the absolute size of the referent was not predictive of the response.
In both blocks the target task was identification of the letters p and q at the top or bottom of the screen as in Experiments 1 and 2.
Procedure
The same procedures as in Experiment 1 and 2 were used. One block had the same procedure as Experiment 1 except that the magnitude sentence was preceded by a referent sentence. The other block had the same procedure as in Experiment 2 except that each magnitude number was preceded by a referent number. Participants were instructed to press the middle button (labeled sentence1/number1) after they processed the referent (sentence or number) and to use it as a comparison for the next stimulus. After making the magnitude judgment the target letter p or q was presented at the top or bottom of the screen. Assignment of sentences to experimental and filler trials was counterbalanced across participants, as was the order of sentence and number blocks. At the end of the experiment we asked participants whether they had any hypotheses about the purpose of the experiment.
Results
None of the participants guessed the purpose of the experiment correctly. The mean reaction times and error rates are displayed in Figure 2. The same data analysis procedure was used as for Experiments 1 and 2. Incorrect responses (4.4% in the sentence condition and 5.0% in the number condition) and remaining outliers (3.8% in the sentence condition and 7.0% in the number condition) were removed.
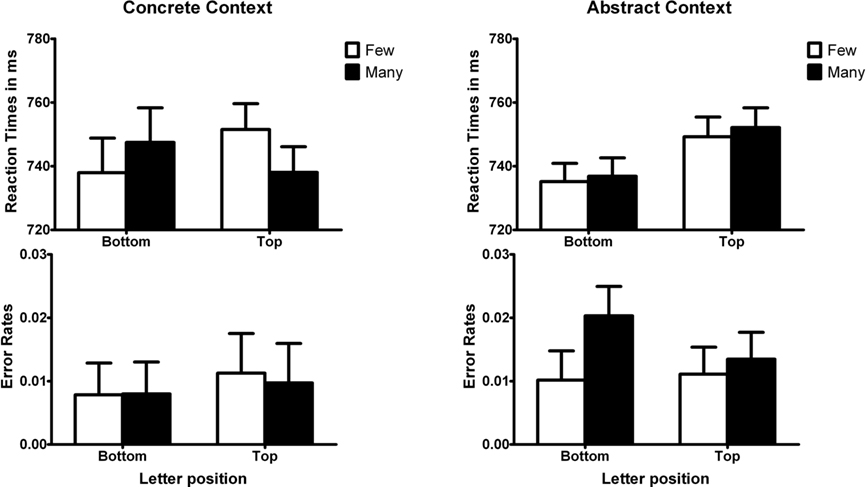
Figure 2. Reaction times and error rates for the letter identification task in Experiment 3. Error bars represent standard error of the mean difference for adjacent bars.
The results of Experiment 3 are consistent with those of Experiments 1 and 2. The three-way interaction effect (magnitude × vertical position × type of quantity) approached significance in the reaction times, F(1, 63) = 2.86, MSE = 1630.3, η2 = 0.043 p = 0.096 but not in the error rates, F < 1. This marginal interaction indicated that the interaction effect between magnitude and vertical position was different between numbers in the two types of contexts.
For trials that were preceded by numbers in concrete contexts, the interaction effect between magnitude and vertical position approached significance, F(1, 63) = 3.60, MSE = 2349.9, η2 = 0.054, p = 0.062. Participants responded faster to a letter at the top when they first read a sentence in the many condition compared to the few condition, t(63) = 2.22, SEM = 6.06, η2 = 0.042, p < 0.05, whereas participants responded faster to a letter at the bottom when they first read a sentence in the few compared to the many condition, although this difference was not statistically significant, t(63) = 1.57, SEM = 6.06, η2 = 0.012, p > 0.05. In the error rates we obtained no significant interaction effect, F < 1.
For trials that were preceded by numbers in abstract contexts, there was no significant interaction between magnitude and vertical position in the reaction times, F < 1, or in the error rates, F(1, 63) = 1.65, MSE = 0.001, η2 = 0.025, p > 0.20. A main effect of vertical position showed that participants responded faster to letters at the bottom than at the top, F(1, 63) = 8.24, MSE = 1672.8 η2 = 0.12, p < 0.01.
Experiment 4
The previous results suggest that numbers in concrete contexts direct vertical spatial attention but numbers in abstract contexts do not. A possible explanation is that numbers in concrete situations have a mainly vertical orientation, whereas numbers in abstract situations have a mainly horizontal orientation. This explanation would be consistent with the SNARC effect and with effects of number magnitude on spatial attention, which are usually obtained with numbers in abstract contexts. The effects of number on spatial attention are not very robust, however, and appear to depend on how strongly numerical magnitude information is activated by the number (Galfano et al., 2006; Ristic et al., 2006; Lindemann et al., 2008; Zanolie and Pecher, 2011). An alternative explanation is that numbers in concrete contexts activate spatial representations more strongly than numbers in abstract contexts, irrespective of the spatial orientation. To distinguish between these two explanations we used the same design as in Experiment 3 except that the letters in the letter identification task were presented at the left and right rather than top and bottom of the screen.
Method
Participants
Thirty-one students from the same pool who had not participated in any of the previous experiments participated for course credits.
Materials and procedure
The materials and procedure were the same as in Experiment 3 with two exceptions. Most important, in the target task the letters p and q were presented at the left and right on the computer screen (in the vertical center position). In addition, for the magnitude sentences we used only the same context referent sentence. Twenty additional fillers were created in which the magnitude sentence was preceded by a same number, different context referent sentence.
Results
None of the participants guessed the purpose of the experiment correctly. The mean reaction times and error rates are displayed in Figure 3. The same data analysis procedure was used as for the previous Experiments. Incorrect responses (3.1% in both sentence and number condition) and remaining outliers (9.9% in the sentence condition and 8.3% in the number condition) were removed.
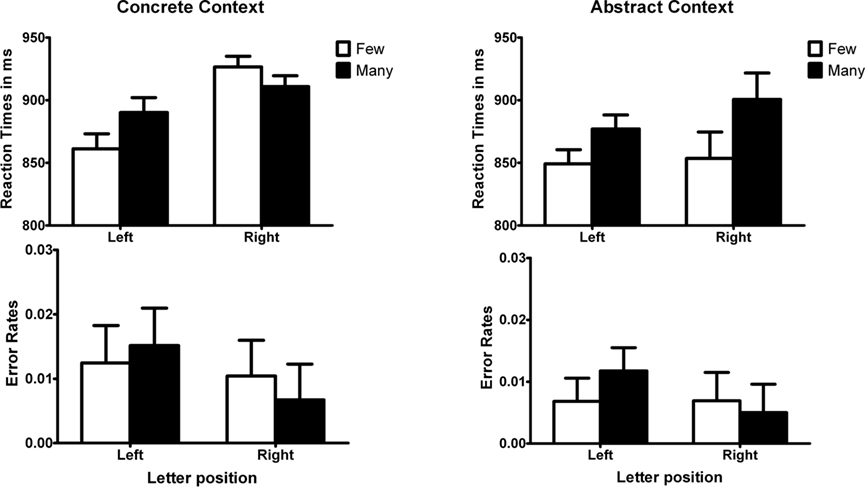
Figure 3. Reaction times and error rates for the letter identification task in Experiment 4. Error bars represent standard error of the mean difference for adjacent bars.
The results of Experiment 4 basically replicated those of Experiment 3 and showed similar effects for horizontal and vertical spatial orientation. The three-way interaction effect (magnitude × horizontal position × type of quantity) approached significance, F(1, 30) = 3.07, MSE = 5135.2, η2 = 0.093 p = 0.090 for reaction times and F(1, 30) = 2.77, MSE = 0.0001, η2 = 0.084 p = 0.011 for error rates. This interaction indicated that the interaction effect between magnitude and horizontal position was different between the two types of contexts.
For trials that were preceded by numbers in concrete contexts, the interaction effect between magnitude and horizontal position was significant, F(1, 30) = 9.02, MSE = 1699.1, η2 = 0.23, p < 0.01. Participants responded faster to a letter at the left when they first read a sentence in the few condition compared to the many condition, t(30) = 2.41, SEM = 12.00, p < 0.05, whereas participants responded faster to a letter at the right when they first read a sentence in the many compared to the few condition, t(30) = 1.80, SEM = 8.63, p = 0.08. Overall, participants responded faster to letters at the left than at the right, F(1, 30) = 10.62, MSE = 5406.9, η2 = 0.26, p < 0.01. In the error rates we obtained no significant interaction effect, F < 1.
For trials that were preceded by numbers in abstract contexts, there was no significant interaction between magnitude and horizontal position, F < 1 for reaction times and F(1, 30) = 1.17, p > 0.20 for error rates. A main effect of magnitude showed that participants responded faster to letters following a “few” decision than following a “many” decision, F(1, 30) = 11.58, MSE = 3755.3 η2 = 0.28, p < 0.01.
General Discussion
In four experiments we investigated the effect of magnitude representations on spatial attention. Participants made magnitude decisions to numbers presented in a concrete or abstract context. Subsequently, a target letter was presented at the top or bottom (Experiments 1–3) or the left or right (Experiment 4) of the computer screen. We found that identification of target letters was influenced by the magnitude decision. Lower magnitudes directed attention to the bottom or left of the screen and higher magnitudes directed attention to the top or right of the screen. This was only the case, however, when magnitude decisions were made to numbers in concrete contexts. When numbers were presented in abstract contexts no effect of magnitude on spatial attention was observed.
The interaction between magnitude and spatial position was not due to the response itself, as has been suggested for the SNARC effect (Keus and Schwarz, 2005; Keus et al., 2005; Müller and Schwarz, 2007; Landy et al., 2008; Santens and Gevers, 2008; Bae et al., 2009). In our experiments, the target response (p or q) was unrelated to letter position, magnitude decision, and the congruency between position and quantity. Even if participants had used a response mapping between the magnitude response (few or many) and response on the target (p or q) this cannot explain the results because the data in each condition are based on equal numbers of p and q responses. Thus, any positive and negative effects of such mapping would have been collapsed into one average for each condition. Therefore, the interaction between magnitude and spatial position on target identification is better explained by differences in spatial attention for low and high magnitudes.
Our finding that the effect of magnitude on spatial attention was larger in concrete than abstract contexts was surprising for two reasons. First, some researchers have argued that abstract concepts are grounded in sensory–motor processing by metaphorical mappings (Lakoff and Johnson, 1980, 1999; Lakoff, 1987; Gibbs, 1994, 2005). On this account, abstract concepts are understood by metaphorical mappings between the abstract concept and concrete, spatial domains. Such mappings should be more essential to understand numbers in abstract contexts than in concrete contexts. Abstract numbers have no grounding in sensory–motor processing whereas numbers in concrete contexts can be simulated by sensory–motor processing. Thus, abstract numbers should activate image schemas to a larger extent than concrete numbers. The present results do not support this account because we showed that numbers in concrete contexts have a larger effect on both vertical and horizontal spatial attention than numbers in abstract contexts. A possible metaphorical explanation might be that alternative mappings were used for abstract numbers. For example, magnitude might be represented as motion along a path (Lakoff and Núñez, 2000) or as values in a non-spatial sensory domain (Núñez et al., in press). Although we cannot exclude these alternatives based on the present data, the spatial number line appears to be the most “natural” grounding, at least for educated Europeans (Núñez et al., in press). Thus, it seems reasonable to assume that if participants in our study used metaphorical mappings these should most likely have been vertical or horizontal.
Second, even if the effect on spatial attention was the same for concrete and abstract magnitudes, the positive effect of concrete magnitudes should have been opposed by a negative interference effect. Spatial congruency effects might be explained by two opposing mechanisms (Estes et al., 2008). First, a representation might direct visual attention to the congruent spatial location just as arrows or verbal commands (left, up) do. As a result, target processing at the congruent location is facilitated compared to target processing at incongruent locations. Second, simulation of perceptual experiences with objects might occupy the same resources as those needed to identify the visual stimulus. This will cause interference similar to the Perky effect (Craver-Lemley and Reeves, 1992; Bergen et al., 2007) at the congruent location. For example, mental simulation of cowboy hat will interfere more with perception of stimuli in a high position than mental simulation of cowboy boot. Interference should only be expected for concrete and not for abstract concepts, because abstract concepts do not have the perceptual details that might compete for resources with visual perception. Facilitation, on the other hand, might be expected for both concrete and abstract concepts. On this account, more facilitation is expected for abstract than concrete magnitudes, because for the concrete magnitudes the effect is counteracted by perceptual interference.
Our finding of larger facilitation for concrete than abstract magnitudes seems at odds with this idea that concrete concepts cause more visual interference than abstract concepts. The contexts described by our stimuli, however, did not have a specific spatial direction. For example, seven pairs of shoes in a shoe shop might have any spatial layout. Therefore, any visual interference caused by perceptual details of the concrete contexts would not be systematically related to magnitude and thus would not affect the interaction between magnitude and letter position. Although our results thus do not necessarily contradict the interference account, it does not explain why concrete magnitude had a larger effect on spatial attention than abstract magnitude.
It is possible that magnitude judgments in concrete contexts required deeper or richer processing than those in abstract contexts. In that case, our results would be consistent with findings that spatial attention induced by number magnitude is weak and depends on the relevance and depth of number processing in the task (Galfano et al., 2006; Ristic et al., 2006; Lindemann et al., 2008; Zanolie and Pecher, 2011). Judging the magnitude of seven pairs of shoes in a shop might result in a richer representation of the relative magnitude than judging the magnitude of 7 compared to 23. With this assumption differences in depth of processing might explain the differences between abstract and concrete context. Because our paradigm differed in several ways from those used in prior studies one may ask whether previous findings have any bearing on our results. First, the response categories, few and many, are quantifiers. One could argue that quantifiers are processed differently than absolute numbers, for example because they are less exact. However, the stimuli still contained exact numbers, so it seems unlikely that participants did not process exact numerical information. Second, attention was measured in a letter identification task rather than a target detection task (i.e., present/absent decision). Although both tasks should be affected by manipulations of spatial attention, they may still differ in how they are affected by unrelated tasks. Third, in previous studies the interval between presentation of the number and that of the target was short. In our study, the target stimulus was time-locked to the magnitude decision and thus varied with decision speed. Bearing in mind these differences, we tentatively argue that the effect of magnitude on spatial attention appears to depend on the depth and relevance of number meaning activation.
The assumption that grounding in spatial representations depends on the depth of number representations leads to the question how more superficial representations can still result in good performance. We propose that experienced number users have developed shortcuts that allow them to perform certain tasks without activating a rich and grounded meaning of numbers. For example, after learning the multiplication tables students can answer multiplication questions without even fully understanding the concept of multiplication. Such associative knowledge might be sufficient to perform simple tasks (such as magnitude judgment) in abstract contexts. Barsalou et al. (2008; see also Simmons et al., 2008) have proposed a similar mechanism for language processing. They argue that in some linguistic tasks, participants do not need to fully simulate a concept but instead can base their responses on simple word associations. It is possible that experienced number users can rely on a similar set of associative links between numbers in simple number tasks. This idea is supported by findings that participants sometimes treat numbers represented by fingers as symbolic (Di Luca et al., 2010). Thus, even though the exact number is presented in an analog form processing benefits from a symbolic representation. Such findings indicate that number processing using associative shortcuts is possible and in some cases perhaps even more efficient, for example in simple or over-learned tasks. When more meaningful processing is required, however, as with numbers in a more concrete context, representations involve sensory–motor simulations, including metaphorical mappings.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research was supported by a VIDI grant from the Netherlands Organization for Scientific Research (NWO) to Diane Pecher. We would like to thank Rafael Núñez for pleasant and useful exchanges of ideas.
References
Bae, G. Y., Choi, J. M., Cho, Y. S., and Proctor, R. W. (2009). Transfer of magnitude and spatial mappings to the SNARC effect for parity judgments. J. Exp. Psychol. Learn. Mem. Cogn. 35, 1506–1521.
Barsalou, L. W., Santos, A., Simmons, W. K., and Wilson, C. D. (2008). “Language and simulation in conceptual processing,” in Symbols, Embodiment, and Meaning, eds M. De Vega, A. M. Glenberg, and A. C. Graesser (Oxford: Oxford University Press), 245–283.
Barsalou, L. W., and Wiemer-Hastings, K. (2005). “Situating abstract concepts,” in Grounding Cognition: The Role of Perception and Action in Memory, Language, and Thinking, eds D. Pecher and R. A. Zwaan (Cambridge: Cambridge University Press), 129–163.
Bergen, B. K., Lindsay, S., Matlock, T., and Narayanan, S. (2007). Spatial and linguistic aspects of visual imagery in sentence comprehension. Cogn. Sci. 31, 733–764.
Boot, I., and Pecher, D. (2010). Similarity is closeness: metaphorical mapping in a perceptual task. Q. J. Exp. Psychol. (Colchester) 63, 942–954.
Boot, I., and Pecher, D. (2011). Representation of categories: metaphorical use of the container schema. Exp. Psychol. 58, 162–170.
Borghi, A. M., Flumini, A., Cimatti, F., Marocco, D., and Scorolli, C. (2011). Manipulating objects and telling words: a study on concrete and abstract words acquisition. Front. Psychol. 2:15. doi: 10.3389/fpsyg.2011.00015
Boroditsky, L., and Ramscar, M. (2002). The roles of body and mind in abstract thought. Psychol. Sci. 13, 185–189.
Casasanto, D. (2008). Similarity and proximity: when does close in space mean close in mind? Mem. Cognit. 36, 1047–1056.
Craver-Lemley, C., and Reeves, A. (1992). How visual imagery interferes with vision. Psychol. Rev. 99, 633–649.
Dehaene, S., Bossini, S., and Giraux, P. (1993). The mental representation of parity and the number magnitude. J. Exp. Psychol. Gen. 122, 372–396.
Di Luca, S., Lefèvre, N., and Pesenti, M. (2010). Place and summation coding for canonical and non-canonical finger numeral representations. Cognition 117, 95–100.
Dove, G. (2011). On the need for embodied and dis-embodied cognition. Front. Cogn. 1:242. doi: 10.3389/fpsyg.2010.00242
Estes, Z., Verges, M., and Barsalou, L. W. (2008). Head up, foot down: object words orient attention to the objects’ typical location. Psychol. Sci. 19, 93–97.
Fischer, M. H., Castel, A. D., Dodd, M. D., and Pratt, J. (2003). Perceiving numbers causes spatial shifts of attention. Nat. Neurosci. 6, 555–556.
Galfano, G., Rusconi, E., and Umiltà, C. (2006). Number magnitude orients attention, but not against one’s will. Psychon. Bull. Rev. 13, 869–874.
Gevers, W., Lammertyn, J., Notebaert, W., Verguts, T., and Fias, W. (2006). Automatic response activation of implicit spatial information: evidence from the SNARC effect. Acta Psychol. (Amst.) 122, 221–233.
Gevers, W., Santens, S., Dhooge, E., Chen, Q., Van den Bossche, L., Fias, W., and verguts, T. (2010). Verbal-spatial and visuospatial coding of number-space interactions. J. Exp. Psychol. Gen. 139, 180–190.
Gibbs, R. W. (1994). The Poetics of Mind: Figurative Thought, Language, and Understanding. New York: Cambridge University Press.
Gibbs, R. W. J. (2005). “The psychological status of image schemas,” in From Perception to Meaning, ed. B. Hampe (Berlin: Mouton de Gruyter), 113–135.
Ito, Y., and Hatta, T. (2004). Spatial structure of quantitative representation of numbers: evidence from the SNARC effect. Mem. Cognit. 32, 662–673.
Johnson, M. (1987). The Body in the Mind: The Bodily Basis of Reason and Imagination. Chicago: University of Chicago Press.
Keus, I. M., Jenks, K. M., and Schwarz, W. (2005). Psychophysiological evidence that the SNARC effect has its functional locus in a response selection stage. Brain Res. Cogn. Brain Res. 24, 48–56.
Keus, I. M., and Schwarz, W. (2005). Searching for the functional locus of the SNARC effect: Evidence for a response-related origin. Mem. Cognit. 33, 681–695.
Kranjec, A., and Chatterjee, A. (2010). Are temporal concepts embodied? A challenge for cognitive neuroscience. Front. Psychol. 1:240. doi: 10.3389/fpsyg.2010.00240
Lakoff, G., and Johnson, M. (1999). The Philosophy in the Flesh: The Embodied Mind and its Challenge to the Western Thought. New York, NY: Basic Books.
Lakoff, G., and Núñez, R. E. (2000). Where Mathematics Comes From: How the Embodied Mind Brings Mathematics into Being. New York: Basic Books.
Landy, D. H., Jones, E. L., and Hummel, J. E. (2008). “Why spatial-numeric associations aren’t evidence for a mental number line,” in Proceedings of the 30th Annual Conference of the Cognitive Science Society, Austin, TX, 357–362.
Lindemann, O., Abolafia, J. M., Pratt, J., and Bekkering, H. (2008). Coding strategies in number space: memory requirements influence spatial-numerical associations. Q. J. Exp. Psychol. 61, 515–524.
Mahon, B. Z., and Caramazza, A. (2008). A critical look at the embodied cognition hypothesis and a new proposal for grounding conceptual content. J. Physiol. Paris 102, 59–70.
Meier, B. P., Hauser, D. J., Robinson, M. D., Friesen, C. K., and Schjeldahl, K. (2007). What’s “up” with god? Vertical space as a representation of the divine. J. Pers. Soc. Psychol. 93, 699–710.
Meier, B. P., and Robinson, M. D. (2004). Why the sunny side is up: association between affect and vertical position. Psychol. Sci. 15, 243–247.
Müller, D., and Schwarz, W. (2007). Is there an internal association of numbers to hands? The task set influences the nature of the SNARC effect. Mem. Cognit. 35, 1151–1161.
Nathan, M. B., Shaki, S., Salti, M., and Algom, D. (2009). Numbers and space: associations and dissociations. Psychon. Bull. Rev. 16, 578–582.
Nicholls, M. E. R., Loftus, A. M., and Gevers, W. (2008). Look, no hands: a perceptual task shows that number magnitude induces shift of attention. Psychon. Bull. Rev. 15, 413–418.
Núñez, R., Doan, D., and Nikoulina, A. (in press). Squeezing, (striking), and vocalizing: is number representation fundamentally spatial? Cognition.
Pecher, D., Boot, I., and van Dantzig, S. (2011). “Abstract concepts: sensory-motor grounding, metaphors, and beyond,” in The Psychology of Learning and Motivation, ed. B. Ross (Burlington: Academic Press), 217–248.
Pecher, D., Van Dantzig, S., Boot, I., Zanolie, K., and Huber, D. E. (2010). Congruency between word position and meaning is caused by task induced spatial attention. Front. Cogn. 1:30. doi: 10.3389/fpsyg.2010.00030
Proctor, R. W., and Cho, Y. S. (2006). Polarity correspondence: a general principle for performance of speeded binary classification tasks. Psychol. Bull. 132, 416–442.
Reynvoet, B., and Brysbaert, M. (1999). Single-digit and two-digit Arabic numerals address the same semantic number line. Cognition 72, 191–201.
Richardson, D. C., Spivey, M. J., Barsalou, L. W., and McRae, K. (2003). Spatial representations activated during real-time comprehension of verbs. Cogn. Sci. 27, 767–780.
Ristic, J., Wright, A., and Kingstone, A. (2006). The number line effect reflects top-down control. Psychon. Bull. Rev. 13, 862–868.
Salillas, E., El Yagoubi, R., and Semenza, C. (2008). Sensory and cognitive processes of shifts of spatial attention induced by numbers: an ERP study. Cortex 44, 406–413.
Santens, S., and Gevers, W. (2008). The SNARC effect does not imply a mental number line. Cognition 108, 263–270.
Schwartz, W., and Keus, I. M. (2004). Moving the eyes along the mental number line: comparing SNARC effects with saccadic and manual responses. Percept. Psychophys. 66, 651–664.
Sell, A. J., and Kaschak, M. P. (2011). Processing time shifts affects the execution of motor responses. Brain Lang. 117, 39–44.
Simmons, W. K., Hamann, S. B., Harenski, C. L., Hu, X. P., and Barsalou, L. W. (2008). fMRI evidence for word association and situated simulation in conceptual processing. J. Physiol. Paris 102, 106–119.
Spivey, M. J., Richardson, D. C., and Gonzalez-Marquez, M. (2005). “On the perceptual-motor and image-schematic infrastructure of language,” in Grounding Cognition: The Role of Perception and Action in Memory, Language, and Thinking, eds D. Pecher, and R. A. Zwaan (Cambridge: Cambridge University Press), 246–281.
Van Dantzig, S. (2009). Mind the Body: Grounding Conceptual Knowledge in Perception and Action. Rotterdam: Erasmus University.
Walsh, V. (2003). A theory of magnitude: common cortical metrics of time, space and quantity. Trends Cogn. Sci. (Regul. Ed.) 7, 483–488.
Keywords: numbers, quantity, context, grounded cognition, abstract concept
Citation: Pecher D and Boot I (2011) Numbers in space: differences between concrete and abstract situations. Front. Psychology 2:121. doi: 10.3389/fpsyg.2011.00121
Received: 07 July 2010;
Accepted: 27 May 2011;
Published online: 08 June 2011.
Edited by:
Anna M. Borghi, University of Bologna and Institute of Cognitive Sciences and Technologies, ItalyReviewed by:
Michael Kaschak, Florida State University, USAMariagrazia Ranzini, University of Bologna, Italy
Copyright: © 2011 Pecher and Boot. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: Diane Pecher, Department of Psychology, Erasmus University Rotterdam, T12-33, Post Box 1738, 3000 DR Rotterdam, Netherlands. e-mail:cGVjaGVyQGZzdy5ldXIubmw=

