Linking speech perception and neurophysiology: speech decoding guided by cascaded oscillators locked to the input rhythm

The premise of this study is that current models of speech perception, which are driven by acoustic features alone, are incomplete, and that the role of decoding time during memory access must be incorporated to account for the patterns of observed recognition phenomena. It is postulated that decoding time is governed by a cascade of neuronal oscillators, which guide template-matching operations at a hierarchy of temporal scales. Cascaded cortical oscillations in the theta, beta, and gamma frequency bands are argued to be crucial for speech intelligibility. Intelligibility is high so long as these oscillations remain phase locked to the auditory input rhythm. A model (Tempo) is presented which is capable of emulating recent psychophysical data on the intelligibility of speech sentences as a function of “packaging” rate (Ghitza and Greenberg, 2009). The data show that intelligibility of speech that is time-compressed by a factor of 3 (i.e., a high syllabic rate) is poor (above 50% word error rate), but is substantially restored when the information stream is re-packaged by the insertion of silent gaps in between successive compressed-signal intervals – a counterintuitive finding, difficult to explain using classical models of speech perception, but emerging naturally from the Tempo architecture.

Introduction

Neuronal oscillations are believed to play a role in various perceptual and cognitive tasks, including attention (Lakatos et al., 2008), navigation (Buzsáki, 2005), memory (Gruber et al., 2008; Palva et al., 2010), motor planning (Donoghue et al., 1998), and in the context of the present work, spoken-language comprehension (Haarman et al., 2002; Bastiaansen and Hagoort, 2006). Spatial patterns of neural activation associated with speech processing have been visualized in different regions of the auditory cortex by a variety of brain-imaging methods (PET, fMRI; e.g., Pulvermueller, 1999; Giraud et al., 2004). The specific timing of activation across the auditory cortex has been observed with electromagnetic recordings (MEG, EEG, ECoG; e.g., Canolty et al., 2007; Giraud et al., 2007; Luo and Poeppel, 2007). Modulation of oscillatory activity is typically seen in distinct frequency bands. As will be elaborated, in the context of spoken-language comprehension, frequencies of particular relevance are the delta (<3 Hz), theta (4–8 Hz), beta (15–30 Hz), and gamma (>50 Hz).

The specific computational functions of neural oscillations are uncertain. One possible function is to coordinate the activity of distinct cortical regions and integrate activity across multiple spatial and temporal scales; an oscillatory hierarchy may serve as an organizing instrument for such function (von Stein and Sarnthein, 2000; Fries, 2005). An oscillatory hierarchy may also serve as a central pacemaker, similar to the synchronization facilitator proposed by Singer and others for cortical processing (cf., review by Singer, 1999; Buzsáki, 2006). Such a hierarchy may control excitability in neuronal ensembles (Kopell and LeMasson, 1994; Hopfield, 2004; Lakatos et al., 2005; Palva et al., 2005; Schroeder and Lakatos, 2009). In the context of the present work, both possible functions may play an important role in decoding spoken language (Morillon et al., 2010).

Linking hypotheses between the acoustics of speech and neuronal structures that may be involved in recognition have recently been discussed both in speech research and cognitive neuroscience (e.g., Zatorre et al., 2002). What, however, is the relation between neuronal oscillations (on the particular scales mentioned above) and the information carried in speech signals, important for intelligibility? Importantly, there is a remarkable correspondence between average durations of speech units and the frequency ranges of cortical oscillations. Phonetic features (duration of 20–50 ms) are associated with gamma (>50 Hz) and beta (15–30 Hz) oscillations, syllables, and words (mean duration of 250 ms) with theta (4–8 Hz) oscillations, and sequences of syllables and words embedded within a prosodic phrase (500–2000 ms) with delta oscillations (<3 Hz). In line with this correspondence between cortical oscillations and critical units for the representation of speech, Poeppel (2003) proposed a multi-resolution model where speech is processed concurrently on at least two different time scales (a slow and fast rate), and then information is extracted and combined for lexical access.

Correlation between the acoustics of spoken language and EEG and MEG responses was demonstrated by showing that temporal cortical responses in the theta range and the beta range contain enough information to discriminate single words (Suppes et al., 1997), artificial simple sentences (Suppes et al., 1998), naturalistic sentences (Luo and Poeppel, 2007), audiovisual speech (Luo et al., 2010), or to correlate with intelligibility (Ahissar et al., 2001; Luo and Poeppel, 2007). Interestingly, these findings can be interpreted in two distinct ways: (1) cortical oscillations may be a key representational mechanism, in particular oscillations corresponding to modulation frequencies commensurate with intelligible speech. A decoding mechanism may be a phase pattern read-out of theta-band responses, extracted from a sliding 200-ms temporal window – a period of one theta oscillation (Luo and Poeppel, 2007); or (2) the observed cortical rhythms are merely a reflection of an underlying computational mechanism, where the brain sets time intervals for analysis of individual speech components by intrinsic oscillations pre-tuned to an expected speech rate and re-tuned during continuous speech processing by locking to the temporal envelope (Ahissar et al., 2001; Poeppel, 2003; Giraud et al., 2007). Such a computational principle is in line with the putative role of a hierarchical oscillatory array – controlling neuronal excitability and thus stimulus-related responses in neuronal ensembles (Kopell and LeMasson, 1994; Lakatos et al., 2005; Schroeder and Lakatos, 2009).

To gain further insight into the possible role played by brain rhythms in speech perception, Ghitza and Greenberg (2009) measured the intelligibility of naturally spoken, semantically unpredictable sentences (i.e., without context) time-compressed by a factor of 3, with insertions of silent gaps in between successive intervals of the compressed speech. Without insertions intelligibility was poor (about 50% word error rate) but was restored considerably by the insertion of gaps, as long as the gaps were between 20 and 120 ms. Since the duration of the acoustic interval was held constant (40 ms) the sole varying parameter was the length of the inserted gap, hence any change in intelligibility could be attributed to the length of the inserted gap per se rather than to the amount of information contained in the acoustic interval. The insertion of gaps was interpreted as the act of providing extra decoding time (a cortical factor) via “re-packaging” the information stream. Maximal perceptual restoration occurred when the gaps were 80-ms long.

These results were surprising; current models of speech perception (up through the word level) rely, almost exclusively, on the acoustics of the speech itself. Phones are identified first¹, and the ordered sequence of identified phones results in a pointer to the lexicon (e.g., Marslen-Wilson and Welsh, 1978; Marslen-Wilson, 1987; Luce and McLennan, 2005; Stevens, 2005). How could standard models account for Ghitza and Greenberg’s counterintuitive behavioral data? According to these models the speech containing gaps should be, at most, as intelligible as the continuous speech, yet intelligibility improves! The emerging conjecture, therefore, was that current models of speech perception that consider acoustic features alone are incomplete, and that an additional mechanism that incorporates the role of decoding time during memory access must be in play. A conceptual model (Tempo) was envisioned in which brain rhythms, in the form of nested oscillations, have a role in decoding speech by temporally controlling the process of matching acoustic patterns to linguistic units.

In the present study the structure of Tempo and the role of its components have been further crystallized, allowing a qualitative assessment of the degree to which the model can predict human performance. As will be demonstrated, the model is capable of emulating the behavioral results of Ghitza and Greenberg (2009) ² – a challenging data set, difficult to explain using current models of speech perception, but emerging naturally from the Tempo architecture. More specifically, the cascaded oscillatory array at the core of Tempo, which is capable of tracking the acoustic input rhythm, will turn out to be crucial for the decoding process, where intelligibility is high so long as the array remains phase locked to the input rhythm. As such, the model provides an explicit linking hypothesis between speech perception and computational neuroscience. It should be noted that the scope here is restricted to recognizing syllables in spoken sentences, with no connection to lexical structure; higher levels of linguistic abstraction (e.g., from syllable to word to prosodic phrase) are not addressed here.

The remainder of the paper is organized as follows. The architecture of Tempo is presented in Section “Tempo – Architecture.” The behavioral data of Ghitza and Greenberg (2009), to be emulated by Tempo, are summarized in Section “Intelligibility of Time-Compressed Speech with Insertions of Silence Gaps (After Ghitza and Greenberg, 2009).” In Section “Emulating Intelligibility of Time-Compressed Speech with Insertions of Gaps” the performance of the model is demonstrated by analyzing the anticipated response of the system to input waveforms used in the Ghitza and Greenberg (2009) study. The relationship between classical models of speech perception (up through the syllable level) and Tempo, and the implications of the new dimensions of the model seem necessary to account for the Ghitza and Greenberg (2009) data are discussed in Section “Discussion.” The Appendix briefly reviews a biophysically inspired model for the representation of time-varying stimuli using a network exhibiting oscillations on a faster time scale (Shamir et al., 2009), an extended version of which is exploited in Tempo.

Tempo – Architecture

In Tempo, the sensory stream (generated by a model of the auditory periphery, e.g., Chi et al., 1999; Ghitza et al., 2007) is processed by a parsing path and a decoding path, which correspond to the lower and upper parts of Figure 1. In the lower path, the temporal attributes of speech are parsed and provide features expressed in the form of an internal clock-like mechanism, realized as an array of cascaded oscillators. The frequencies and relative phases of the oscillators determine the time frames that control the decoding process, performed in the upper path, which links chunks of sensory input with stored time–frequency memory patterns.

FIGURE 1

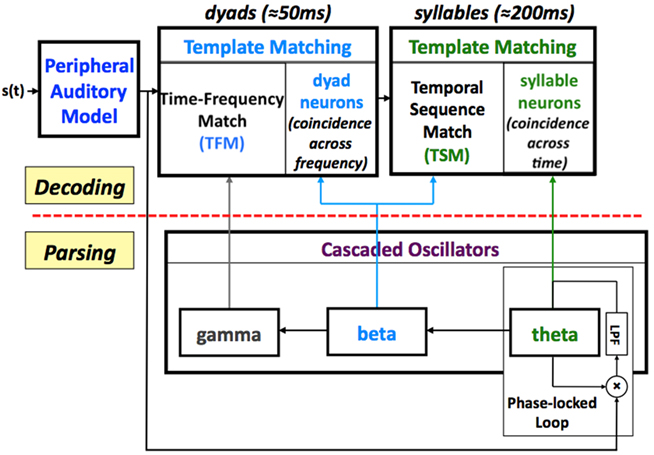
Figure 1. A block diagram of the Tempo model. It comprises lower and upper paths that process the sensory stream generated by a model of the auditory periphery. The lower path extracts parsing information, which controls the decoding process performed in the upper path. The parsing is expressed in the form of an internal clock-like mechanism, realized as an array of cascaded oscillators locked to the input syllabic rhythm; the frequencies and relative phases of the oscillations determine the processing time frames that control the decoding process. See text for details.

Parsing

Psychophysical studies on the role of temporal modulation (e.g., Dau et al., 1997) and speech modulation, in particular (e.g., Houtgast and Steeneken, 1985), demonstrates the relative importance of modulations in the range of 3–10 Hz to intelligibility. This range of modulations reflects the range of syllable rates in naturally spoken speech, on the one hand, and is similar to the frequency range of cortical theta oscillations, on the other hand. This observation, and the robust presence of these energy fluctuations in the auditory response to the speech signal (as is illustrated in Figure 2), led to the hypothesis that the theta oscillator is the master in the cascaded array, and that the other oscillators entrain to theta. The theta oscillator is assumed to be capable of tracking the input rhythm; it can be viewed, for example, as the voltage controlled oscillator (VCO) of a phase-lock loop (PLL) system (e.g., Viterbi, 1966; Ahissar et al., 1997; Zacksenhouse and Ahissar, 2006), locked to the temporal fluctuations of the cortical auditory representation of the speech signal (e.g., the modulation spectrum). In accord with neurophysiological data, the frequency of the theta oscillator is restricted to a range between 4 and 10 Hz (i.e., a theta cycle of 100- to 250-ms long). As such, the theta oscillator provides syllabic parsing.

FIGURE 2

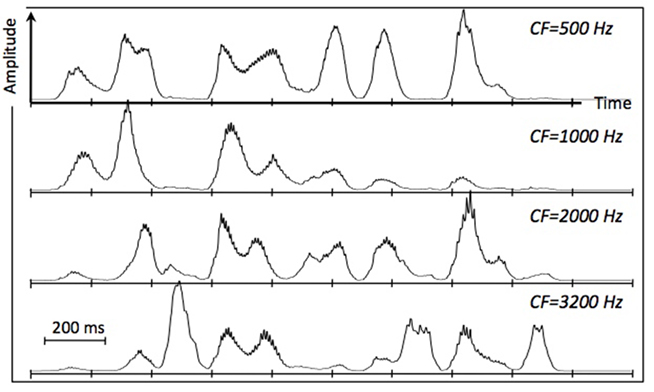
Figure 2. Cochlear envelopes in terms of a simulated inner hair cell response, low-pass filtered to 50 Hz, at four characteristic frequencies. The input is the semantically unpredictable sentence “The ripe style heard their spades,” naturally spoken by a male speaker (from Ghitza and Greenberg, 2009). The duration of the signal is roughly 2 s (ten 200-ms long frames). The rate of the envelope fluctuations is about 5 peaks per second. Low-frequency cochlear channels mainly reflect the presence of vowels and nasals, and high frequency channels mainly reflect fricatives and stop-consonants. The PLL (see Figure 1) is locked to the temporal fluctuations of the cortical auditory representation of the speech signal (e.g., the modulation spectrum), which is related to the cochlear response.

The theta oscillator sets the frequency of a beta oscillator, to be a multiple of the theta frequency; for the present demonstration of Tempo the multiple was set to 4, hence the frequency of the beta oscillator range between 16 and 40 Hz³. The phase of the beta oscillator is set to 0 at the start of the theta cycle. Hence, there are four beta cycles inside one theta cycle, all with equal duration – this is so because of the assumption that the beta oscillator remains constant within one theta cycle. The beta oscillator provides finer parsing, on dyad-long information within the syllable (i.e., about 50 ms long). It is worth recalling that a dyad is the acoustic reflection of the dynamic gesture of the articulators while moving from one phone to the next. Often, there is an “acoustic edge” (at the boundary between the phones) associated with this movement; hence the dyad may be viewed as the waveform segment “centered” at the acoustic edge. It is important to note, however, that for some diphones the exact location of an acoustic edge is not obvious.

A third oscillator is in the gamma range, with a frequency set to be a multiple (set to 4 here) of the beta frequency. The span of a gamma cycle is commensurate with the rapid spectro-temporal transitions associated with dyad elements. The phase of the gamma oscillator is set to a constant at the start of the theta cycle, so as to maintain a consistent alignment of the gamma cycles within the beta cycles.

The cascaded oscillatory array possesses three properties that will prove to be crucial for a successful account of Ghitza and Greenberg’s (2009) data. Two are inspired by solid findings of the characteristics of cortical oscillations: (1) each oscillator has a finite range of oscillation frequencies (e.g., Buzsáki, 2006); (2) oscillators in the array are related (by nesting, e.g., Schroeder and Lakatos, 2009). A third property emerges from a hypothesis, central to Tempo: (3) the oscillators are capable of remaining locked to the input rhythm as its changes (slowly) with time (Ahissar et al., 2001; Nourski et al., 2009), implying that the cycle durations of the oscillators adapt to the input. As demonstrated in Section “Emulating Intelligibility of Time-Compressed Speech with Insertions of Gaps,” performance (in terms of syllable error rate) remains high as long as locking is maintained but drops once out of lock (e.g., when the oscillators reach the boundaries of their respective frequency ranges).

Decoding

In the upper path, the acoustic stream is processed by two template-matching components running in tandem. The first, a time–frequency match (TFM) component, maps beta-cycle long speech segments (i.e., dyads) to memory neurons, termed dyad neurons, by computing coincidence in firing across auditory (i.e., tonotopic) frequency channels. At this level, time–frequency patterns are matched over relatively short time intervals (about 50 ms) and are often formant transitions associated with such phonetic features as place of articulation, which is important for distinguishing consonants (and hence words). This pattern-matching operation is performed within a beta cycle, and mapping onto a dyad neuron occurs at the end of each beta cycle. One possible realization of the TFM component is the extension of a model suggested by Shamir et al. (2009), briefly described in the Appendix. It is a model for the representation of time-varying stimuli (e.g., dyads) by a network exhibiting oscillations on a faster time scale (e.g., gamma). An important property of the extended model is the insensitivity to time-scale variations – a necessary (but not sufficient) requirement of a model capable of explaining humans’ insensitivity to phonemic variations (see last paragraph in the Appendix).

The second pattern-matching component, a temporal sequence match (TSM), maps syllabic primitives onto memory neurons termed syllable neurons, by measuring coincidence in firing activity of a sequence of dyad neurons within a theta cycle (about 200 ms). Mapping onto a syllable neuron occurs at the end of the theta cycle.

Intelligibility of Time-Compressed Speech with Insertions of Silent Gaps (After Ghitza and Greenberg, 2009)

Listening to time-compressed speech provides useful insight into how the brain decodes spoken language (e.g., Garvey, 1953; Foulke and Sticht, 1969; Dupoux and Green, 1997; Dilley and Pitt, 2010). Ghitza and Greenberg (2009) measured intelligibility (in terms of word error rate) of time-compressed speech with insertions of silent gaps. The speech material was semantically unpredictable sentences (e.g., “Where does the cost feel the low night?” and “The vast trade dealt the task”), to eliminate the role of context. Three classes of signal conditions were tested: (1) waveforms without time compression (with a syllabic rate of about 5 syllables/s), and waveforms time-compressed by a factor of 2 (i.e., with a syllabic rate of about 10 syllables/s), (2) waveforms time-compressed by a factor of 3 (a syllable rate of about 15 syllables/s), and (3) waveforms in class 2 with further distortion inflicted: the waveforms were blindly segmented into consecutive 40-ms fragments (called “packets”), each followed by a silent gap. This synthesis procedure allowed to generate stimuli with the factors of “information per packet” (i.e., the information in the speech fragment) and “packaging rate” disassociated. In Ghitza and Greenberg (2009) the amount of speech information per packet was kept constant (because no portion of the acoustic signal was discarded – only time-compressed – and because the speech intervals remained fixed throughout the experiment); the sole varying parameter was the packaging rate, controlled by the length of the inserted gap. The resulting waveforms exhibited a packaging rate ranging from 15 to 5 packets/s (0- to 160-ms of gap duration, respectively). (MP4 files are available for listening as Supplementary Materials.)

Word error rate for the stimuli in class 1 was marginal (about 2%), but the performance for the signals in class 2 was poor (>50% error rate). Surprisingly, performance for the signals in class 3 improved, with a U-shaped performance curve (Figure 3); intelligibility was restored considerably as long as the gaps were between 20 and 120 ms. Lowest word error rate (i.e., highest intelligibility) occurred when the gap was 80-ms long or, equivalently, at the rate of 8.3 packets/s, down to about 20% (the “optimal” rate). Moving from the optimal rate leftward (i.e., an increase in the packaging rate) resulted in deterioration in intelligibility; deterioration also occurs moving rightward (i.e., a decrease in the packaging rate). No (purely) auditory or articulatory model can explain this behavior. Ghitza and Greenberg (2009) interpreted the insertion of silent gaps as an act of providing “needed” decoding time and conjectured that an additional mechanism that incorporates the role of decoding time during memory access must be in play; they further hypothesized that decoding time is governed by low-frequency (quasi-periodic) brain oscillations. The manner by which decoding time is governed by the oscillatory array is discussed in paragraph Tempo and Decoding Time, in Section “Discussion.”

FIGURE 3

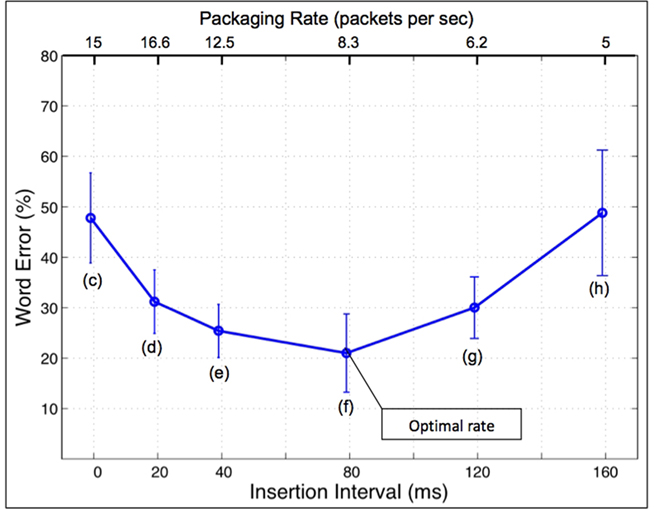
Figure 3. Intelligibility of time-compressed speech with inserted silent gaps (from Ghitza and Greenberg, 2009). The signal conditions are labeled (c–h), in correspondence with the labeling in Figure 4 and Table 1. Word error rate is plotted as a function of gap duration or, equivalently, packaging rate. Speech was time-compressed by a factor of 3. Acoustic intervals were consecutive 40-ms long speech intervals, kept the same for all conditions. Without insertions performance is poor (>50% word error rate). Counter- intuitively, the insertion of gaps improves performance, resulting in a U-shaped performance curve. The lowest word error rate (i.e., highest intelligibility) occurs when the gap was 80-ms long (or, equivalently, at the rate of 8.3 packets/s), down to ca. 20% (the “optimal” rate). (The intelligibility of uncompressed speech, and speech compressed by a factor of 2, is high, with error rate <2%.)

Emulating Intelligibility of Time-Compressed Speech with Insertions of Gaps

We start by outlining the functional requirements of Tempo, by setting up the parameters of the model, and by defining the articulated speech information (ASI) – a measure of the amount of speech information carried by a fragment of time-compressed speech; this measure will allow a comparative assessment of Tempo’s capability to decode speech material spoken at different speeds. The anticipated response of the model to speech stimuli used by Ghitza and Greenberg (2009) is analyzed in Subsections Response to Uncompressed Speech, Response to Speech Compressed by a Factor of 2, Response to Speech Compressed by a Factor of 3.

Functional Requirements

Any adequate model of speech perception must be able to predict a variety of psychophysical data. The present study is confined to the Ghitza and Greenberg (2009) data. Albeit limited, the data point to certain functional requirements any viable model must satisfy:

(1) Speech at normal speed and speech that is time-compressed by a factor of 2: word error rate must be virtually zero. One implication, for Tempo, is that the TFM component, which maps beta-cycle long dyads onto memory (dyad) neurons, should be insensitive to time-scale modifications up to a factor of 2. That is, acoustic realizations of dyads that differ in their duration up to a factor of 2 (e.g., due to time compression) should be mapped onto the same memory neuron⁴. The extension of Shamir et al. (2009), described in the Appendix, exhibits properties that satisfy this requirement.

(2) Speech that is time-compressed by a factor of 3:

(a) Without insertion of silent gaps. Word error rate should be about 50%.

(b) With insertions, at optimal rate. Word error rate should be about 20% – an improvement of 30% compared to the case of no insertions.

(c) With insertions, left of optimal rate. As packaging rate increases (with respect to optimal rate), word error rate should increase in a U-shape fashion, from 20% (at optimal rate) to 50%.

(d) With insertions, right of optimal rate. As the packaging rate decreases, word error rate should increase from 20% (at optimal rate) to 50% (at the maximum gap duration tested).

(e) We shall elaborate on the possible source of errors in Subsection Response to Speech Compressed by a Factor of 3.

Setting Up the Parameters of Tempo

In introducing Tempo (see Section “Tempo – Architecture”) few assumptions have been made: it was assumed, plausibly, that each oscillator has a finite range of frequencies, and that the oscillators are related (cascaded). A key assumption was that the master, theta oscillator (hence the entire cascade) is capable of tracking the quasi-periodic input rhythm as long as those rhythms are within the theta frequency range. For the analysis here we set the following parameters (some are re-iterated):

(1) The PLL module tracks the input rhythm perfectly (as long as they are within the theta range).

(2) The theta frequency range is bounded to 4–10 Hz.

(3) The beta frequency is an integer multiple of theta, chosen here to be 4. Consequently, there are four beta cycles (of equal length) within one theta cycle.

(4) The phase of the beta oscillator is set to zero at the start of the theta cycle.

(5) A dyad neuron is triggered at the end of a beta cycle, and only for cycles with a non-zero input.

(6) The gamma frequency is a multiple of beta, also by a factor of 4. Consequently, there are four gamma cycles within one beta cycle.

(7) The phase of the gamma oscillator is set to a constant at the start of the theta cycle, to maintain a consistent alignment of the gamma cycles within the beta cycles.

(8) Memory neurons exist for every dyad and syllable. The acquisition process by which those neurons become associated with meaning is beyond the scope of this study.

It is noteworthy that the beta to theta ratio, and the gamma to beta ratio, should be set up in accord with neurophysiological data. At present, there is a lack of a unanimous agreement on the frequency range of these oscillators; we believe that our choice is within reason.

Definition: Articulated Speech Information (ASI)

In the process of demonstrating that Tempo is capable of accounting for the U-shaped behavioral data we shall need to assess its decoding accuracy for different time-compressed versions of the original waveform. A question thus arises: what is the amount of speech information carried by a fragment of a time-compressed speech? For example, what is the amount of speech information within a 40-ms long interval of speech time-compressed by a factor of 4? We propose to measure this quantity in terms of the speech information that was intended to be conveyed by the speaker when uttered (i.e., before compression). Thus, we define the ASI within a given time window as the duration, in milliseconds, of the uncompressed speech inside that window. In our example, the ASI in a 40-ms long fragment of speech time-compressed by 4 is 4 × 40 = 160 ms, and it comprises about 3 typical 50-ms long uncompressed dyads. It is worth emphasizing that there is a distinction between the amount of information articulated by the speaker (i.e., intended to be conveyed) and the amount of information perceived by the listener. During the decoding process some of the articulated information may be lost; the amount of loss depends on the time compression ratio and is measured with respect to the ASI.

Response to Uncompressed Speech

Figure 4 elucidates the analysis. The figure comprises nine panels, Figure 4a–h, depicting one theta-cycle long window of the stimuli corresponding to each of Ghitza and Greenberg’s (2009) signal conditions. Each panel contains the Fourier-based spectrogram, and an illustration of the corresponding cascaded oscillations in the form of markers: red, blue, and magenta markers represent the theta, beta, and gamma oscillations, respectively.

FIGURE 4

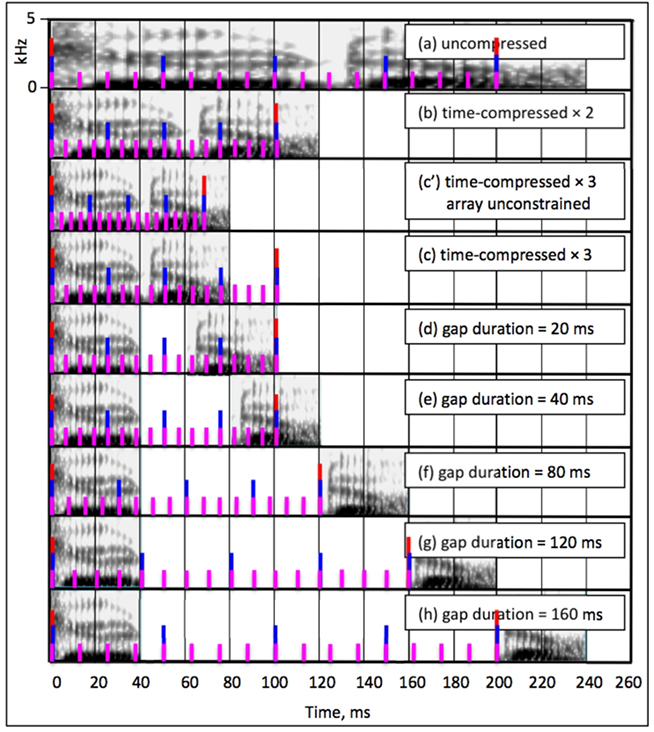
Figure 4. One theta-cycle long time window of the stimuli of Ghitza and Greenberg (2009), spectrograms in black, and a cartoon illustration of the corresponding oscillations in red, blue, and magenta (corresponding to the theta, beta, and gamma oscillations, respectively). Time is plotted along the x-axis of the spectrograms (in milliseconds), frequency is plotted along the y-axis (0–5 kHz, linear scale), and stimulus intensity is denoted by color (light- and dark gray indicate low- and high amplitude, respectively, in decibel). (a) A spectrogram of a 240-ms long segment of uncompressed speech and the corresponding oscillations. Since the input syllabic rate (assumed to be 5 syllables/s) is within the theta frequency range, theta = 5 Hz, beta = 20 Hz, and gamma = 80 Hz (see Response to Uncompressed Speech). (b) The spectrogram of (a) time-compressed by a factor of 2 (hence lasting 120 ms). The syllabic rate is 10 syllables/s, and since the theta oscillator is still within boundaries the oscillatory array stays locked to the input rhythm (with theta = 10 Hz, beta = 40 Hz, and gamma = 160 Hz). No TFM errors compared to (a) because the TFM coding window – i.e., the beta cycle – and the compressed stimulus are locked (see Response to Speech Compressed by a Factor of 2). (c′) The spectrogram of (a) time-compressed by a factor of 3 (lasting 80 ms); the syllabic rate is 15 syllables/s. Shown are oscillations of a hypothetical system, in which the frequency range of the oscillators in the array is unconstrained, hence theta = 15 Hz, beta = 60 Hz, and gamma = 240 Hz. No TFM errors compared to (a) because of the same rational as in (b); see Response to Speech Compressed by a Factor of 3). (c) Same as (c′) but with a constrained oscillatory array. The syllabic rate of the acoustics is 15 syllables/s – outside the theta range. The theta oscillator is “stuck” at its upper frequency limit (10 Hz). Compared to conditions (a) and (b) a mismatch occurs (see Stimulus Without Insertions; (d) speech compressed by a factor of 3, with insertions of 20-ms long silent gaps; packaging rate (16.6 packets/s) is outside the theta range, hence the theta frequency is 10 Hz (see Left of Optimal Rate). (e) With insertions of 40-ms long gaps; packaging rate (12.5 packets/s) is outside the theta range, hence the theta frequency is 10 Hz (see Left of Optimal Rate). (f) With insertions of 80-ms long gaps – optimal rate; packaging rate is 8.3 packets/s – inside the theta range; theta frequency at 8.3 Hz (see Optimal Rate). (g) With insertions of 120-ms long gaps; packaging rate is 6.2 packets/s, inside the theta range and the theta frequency is 6.2 Hz (see Right of Optimal Rate). (h) With insertions of 160-ms long gaps; packaging rate is 5 packets/s, inside the theta range and the theta frequency is 5 Hz (see Right of Optimal Rate).

Figure 4a shows a spectrogram of a 240-ms long segment of uncompressed speech and the corresponding oscillations. Since the input syllabic rate (assumed to be about 5 syllables/s) is within the theta frequency range, theta = 5 Hz, beta = 20 Hz, and gamma = 80 Hz. At the end of each beta cycle, the TFM component (the extension of Shamir et al., 2009 described in the Appendix) will map the beta-cycle long speech segment onto a dyad neuron. The 200-ms long theta cycle (with ASI = 1 × 200 = 200 ms) is sampled with four beta cycles, 50-ms long each, matching the number of typical dyads composing the ASI. At the end of each theta cycle the TSM component will map a sequence of 4 dyad neurons onto a syllable neuron. The resulting syllable-neuron sequence will be the baseline, reference sequence in assessing the performance of Tempo in the following Subsections.

Response to Speech Compressed by a Factor of 2

Figure 4b shows the spectrogram of Figure 4a time-compressed by a factor of 2 (hence lasting 120 ms). The syllabic rate is 10 syllables/s, and since the theta oscillator is still within its boundaries the oscillatory array stays locked to the input rhythm, with theta = 10 Hz, beta = 40 Hz, and gamma = 160 Hz. Since the TFM model is insensitive to time-scale variations (this is so as long as the TFM coding window – i.e., the beta cycle – and the compressed stimulus are locked, as is the case here), the same dyad neurons are triggered as in Subsection Response to Uncompressed Speech (i.e., no TFM errors): the 100-ms long theta cycle (with ASI = 2 × 100 = 200 ms) is sampled with four beta cycles (25-ms long each), matching the number of typical dyads composing the ASI. Because of the errorless TFM mapping, the triggered syllable-neurons sequence is same as the reference sequence defined in Subsection Response to Uncompressed Speech, i.e., no TSM errors.

Response to Speech Compressed by a Factor of 3

Figure 4c,c′ show the spectrogram of Figure 4a time-compressed by a factor of 3 (lasting 80 ms); the syllabic rate is 15 syllables/s. For a hypothetical system, in which the frequency range of the oscillators in the array is unconstrained, the oscillators and the compressed stimulus are in lock. Following the rationale of the error analysis in Subsection Response to Speech Compressed by a Factor of 2, there are no TFM or TSM errors. A constrained oscillatory array, however, introduces errors.

TFM errors

A theme common to all stimuli time-compressed by three (Figure 4c–h) is that while the syllabic rate within the time-compressed speech fragments is the same (at 15 syllables/s) the frequency of the theta oscillator, dictated by the packaging rate, varies. Thus, a mismatch occurs because the TFM coding window (i.e., the beta cycle) and the compressed stimulus inside the window are out-of-sync. The lack of a complete computational description of the TFM component prevents an estimate of the absolute number of TFM errors; however, a qualitative estimate of the error trend (i.e., the performance in one condition relative to another) can be inferred [see paragraph Tempo (Overall) Errors below].

TSM errors

Reflect the number of dyads unaccounted for due to the limited decoding capacity of the receiver. The dyad loss stems from a mismatch between the number of dyads to be decoded (i.e., the number of dyads articulated) and the number of dyad-neuron activations permitted by the Tempo. The time unit over which errors are calculated is the theta cycle: the number of dyads to be decoded is the number of uncompressed dyads composing the ASI, and the number of dyad-neuron activations is determined by the temporal attributes of the time-compressed stimulus. In Tempo there are four beta cycles per one theta cycle, and a dyad neuron is triggered at the end of a non-zero beta cycle (see Subsection Setting Up the Parameters of Tempo). Thus, the maximum number of neurons available to decode one theta-cycle long acoustic segment is four. For continuous signals the number of activated dyad neurons is four, and for a signal with silent gaps this number may be less than four (because a dyad neuron is triggered only for non-zero input, see Subsection Setting up the Parameters of Tempo). We term these neurons activated dyad neurons. Note that TSM errors indicate how the temporal aspects of speech – apart from the spectral aspects – affect intelligibility. This is so because the location and duration of the theta cycle – the time window over which TSM errors are calculated – are determined by the parsing process that takes the temporal aspects of the stimulus as input. In calculating the number of TSM errors we assume that the dyads are recognized correctly; error in dyad recognition is considered a TFM error. Thus, in our analysis, the TSM error count (associated with temporal attributes of speech) is independent from the TFM error count (associated with the spectral attributes).

Table 1 shows the average number of TSM errors for stimuli representing each of Ghitza and Greenberg’s (2009) signal conditions. The table comprises nine columns, (a–h), in correspondence with the rows of Figure 4. For calculating the number of errors we consider a generic uncompressed speech waveform 2400-ms long, with a fixed syllabic rate of 5 syllables/s; assuming that the duration of a typical dyad is 50 ms, the uncompressed stimulus comprises 48 dyads. It is further assumed that the theta oscillator tracks the input without error. The TSM errors are represented in terms of the total number of dyads, out of 48, that are lost during the decoding process (row “total number of dyads lost”). This number, denoted N_E (index E for Error), is calculated as follows. Let N_T (T for Theta) be the number of theta cycles inside the stimulus, N_U (U for Uttered) be the number of typical dyads composing the ASI of one theta cycle (see the rows shaded in light blue), and N_A (A for Activated) the number of activated dyad neurons per theta cycle (equals the number of beta cycles covering the non-zero portion within the theta cycle – see the rows shaded in light yellow, where ⌈x⌉ is the value of x, rounded up to the nearest integer). Then, N_E = N_T × (N_U − N_A). Note that N_A is an integer number, obtained by rounding up to the nearest integer the number of beta cycles covering the non-zero portion of a theta cycle: a “residual” speech fragment, which only spans a portion of a beta cycle, is regarded as one dyad. Paragraphs Stimulus Without Insertions, Optimal Rate, Left of Optimal Rate, Right of Optimal Rate below discuss the reasoning behind the entries of Table 1.

TABLE 1

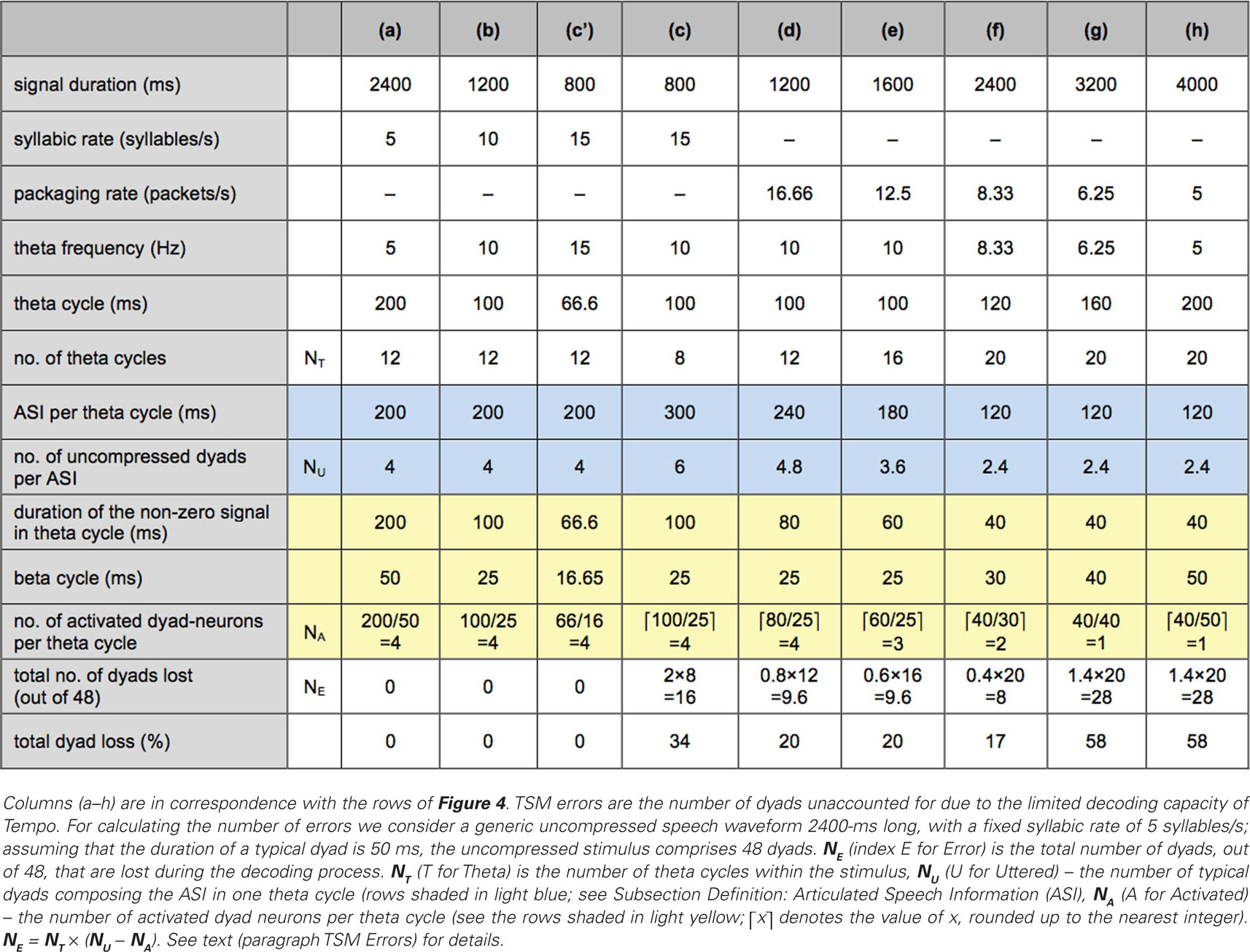
Table 1. TSM errors for the stimuli of Ghitza and Greenberg’s (2009).

Stimulus without insertions

The syllabic rate of the acoustic signal is 15 syllables/s – outside the theta range (Figure 4c). The theta oscillator is “stuck” at its upper frequency limit (10 Hz). Compared to Sections Response to Uncompressed Speech and Response to Speech Compressed by a Factor of 2 a mismatch occurs, resulting in TFM errors; a qualitative account of these errors is deferred to paragraph Tempo (Overall) Errors. The number of TSM errors is calculated in row (c) of Table 1. The duration of the time-compressed signal is 800 ms (because the duration of the uncompressed signal is 2400 ms); the theta cycle is 100-ms long, thus the number of theta cycles spanning the duration of the entire waveform is 8. The ASI in a theta cycle is ASI = 3 × 100 = 300 ms – the duration of 6 dyads (rows in light blue), while the number of activated dyad neurons is just 4 (rows in light yellow). Thus, at the end of each theta cycle the TSM component will decode 6 dyads as a sequence of only 4 dyad neurons – a loss of 2 dyads per theta cycle, i.e., an average total loss of 16 dyads (34%).

Optimal rate

Figure 4f shows a spectrogram of the signal in Figure 4c with a 40-ms long acoustic fragments and 80-ms long inserted gaps. The resulting packaging rate (the reciprocal of 80 + 40 = 120 ms) is 8.33 packets/s – inside the theta range – thus the theta frequency is 8.33 Hz (with theta and beta cycles of 120- and 30-ms long, respectively). Although the oscillatory array is locked to the rhythm imposed by the packaging process, mismatch exists between the syllabic rate of the signal inside the acoustic interval (15 syllables/s) and the theta frequency (8.33 packets/s), resulting in TFM errors; a qualitative account of these errors is deferred to paragraph Tempo (Overall) Errors. The number of TSM errors is calculated in column (f) of Table 1. The time-compressed signal, 800-ms long, contains twenty 40-ms long acoustic segments thus the stimulus duration here is 2400 ms [20 × (40 + 80) = 2400 ms]; the theta cycle is 120-ms long, and thus the number of theta cycles spanning the duration of the entire waveform is 20. The duration of the non-zero signal in a theta cycle is 40 ms, therefore the ASI in a theta cycle is ASI = 3 × 40 = 120 ms – the duration of 2.4, 50-ms long typical dyads (rows in light blue), while the number of activated dyad neurons in a theta cycle is just 2 (a 40-ms long acoustic interval and a 30-ms long beta cycle – see rows in light yellow). Thus, at the end of each theta cycle the TSM component will decode 2.4 dyads as a sequence of 2 dyad neurons – a loss of 0.4 dyads per theta cycle, i.e., an average total loss of 8 dyads (17%).

Left of optimal rate

In Figure 4d,e, the inserted gaps are 20- and 40-ms long, with a packaging rate of 16.66 and 12.5 packets/s, respectively. This rate is outside the theta range, imposing a theta frequency of 10 Hz (a theta cycle of 100 ms). A qualitative account of the TFM errors is deferred to paragraph Tempo (Overall) Errors. The number of TSM errors is calculated in columns (d) and (e) of Table 1 following the same rationale outlined in paragraph Optimal Rate, resulting in an average total dyad loss of 20% for each condition.

Right of optimal rate

In Figure 4g,h, the inserted gaps are 120- and 160-ms long, with a packaging rate of 6.25 and 5 packets/s, respectively. This rate is inside the theta range, with corresponding theta frequencies of 6.25 and 5 Hz. A qualitative account of the TFM errors is deferred to the paragraph Tempo (Overall) Errors. The number of TSM errors is calculated in columns (g) and (h) of Table 1 following the same rationale outlined in paragraph Optimal rate, resulting in an average total dyad loss of 58% for each condition.

Tempo (overall) errors

The TSM errors shown in Table 1 are U-shaped, in line with the behavioral data. Is Tempo’s overall error behavior U-shaped as well? To answer this question we need an estimate of the TFM error curve; the lack of a fully developed computational model of TFM prevents an estimate of the absolute number of these errors but we can infer the error trend. For all signal conditions left of the optimal rate (depicted in Figure 4c–e) the theta frequency is the same (10 Hz), and thus the degree of mismatch between the acoustic rhythm and the theta frequency is similar, resulting in a similar number of TFM errors. For the signal conditions right of the optimal rate (Figure 4g,h) the theta oscillator is in lock to the packet frequency, resulting in a theta frequency of 6.25 and 5 Hz, with 40- and 50-ms long beta cycles, respectively. Since the duration of the acoustic fragment is 40 ms (i.e., less than or equal to the duration of one beta cycle), the number of gamma cycles per acoustic interval is diminishing (3–4 gamma cycles per interval, to the right of optimal rate, as opposed to 6–7 cycles, to the left), resulting in a larger number of TFM errors due to a coarser sampling of the signal dynamics. The trend of the TFM errors, therefore, would exhibit a “mirrored-L” shape.

As noted in paragraph TSM Errors, the TSM error count and the TFM error count disassociate. Here, we merge the two with equal weight; adding the mirrored-L shaped TFM error curve to the U-shaped TSM error curve will result in a U-shaped Tempo error curve. Compared to the TSM error curve, the Tempo error curve would be elevated and with a different tilt. Achieving a numerical fit between the U-shaped Tempo errors and the U-shaped behavioral data probably lies in the properties of the TFM model, yet to be developed.

Discussion

Scope of Study

In the broader context, there is a body of work on the effects of time compression of speech on intelligibility (e.g., Garvey, 1953; Foulke and Sticht, 1969; Dupoux and Green, 1997), showing high word error rates (greater than 50%) under a compression factor of 3. There is also work showing rhythmic and speech rate based effects on lexical perception and word recognition accuracy (e.g., Dilley and Pitt, 2010). The focus of our study, however, is a different finding, which shows that insertion of silent gaps markedly improves the intelligibility of time-compressed speech as long as the gaps are between 20 and 120 ms (Figure 3). Conventional models of speech perception have a difficulty in accounting for this result because they assume a strict decoding of the acoustic signal of speech itself by the auditory system and higher neural centers. Tempo incorporates the role of an additional dimension, namely the decoding time during memory access, into the classical framework of speech perception. This mechanism is realized by allowing a cascaded array of oscillators to track the input rhythm⁵ thus enabling the prediction of a spectrum of data, i.e., that intelligibility of uncompressed speech, and speech compressed by a factor of 2, is high (<2% word error); that intelligibility of speech time-compressed by three is poor (greater than 50% word error); and that the insertion of silent gaps markedly improves intelligibility.

The Role of Parsing

The parsing path determines the time frames (both location and duration) that control the decoding process. This information is expressed in the form of an array of cascaded oscillators with theta as the master. The oscillatory array is driven by the temporal attributes of speech: the master oscillator is assumed to be capable of tracking the input rhythm accurately, e.g., via a PLL mechanism locked to the auditory response. Assuming perfect tracking, a theta cycle is aligned with a speech segment that is often a Vowel–Consonant-cluster–Vowel. (This is so because the prominent energy peaks across the auditory channels, to which the PLL is locked to, are associated with vowels.) Two points are noteworthy. First, the PLL module (yet to be implemented) plays a crucial role in Tempo; an inaccurate tracking of the input rhythm will result in out-of-sync theta oscillations (and therefore beta, and gamma), hence inadequate time frames (in terms of location and duration), which will severely tamper with the decoding process. Second, naturally spoken language exhibits substantial irregularity in timing, mostly in the form of hesitation and disfluency. How will such irregularity affect the performance of the tracking mechanism? Tempo provides a framework for a reasonable explanation of the manner in which the cortical receiver may handle this difficulty; when the input rhythm is unsettled (e.g., hesitation or disfluency), the theta oscillator (and hence the entire array) is idling at its core frequency (say at mid range), ready to reenter the tracking mode.

Dyad vs. Diphone

The dyad unit plays an important role in the decoding path of Tempo. The TFM component maps acoustic intervals, beta-cycle long, onto memory neurons termed dyad neurons. Note that there is a distinction between a dyad and a diphone; a diphone is the concatenation of two phones, while the dyad is the acoustic realization of the diphone. As noted in Subsection Setting Up the Parameters of Tempo, the acquisition process by which dyad neurons become associated with their respective diphonic representation is beyond the scope of this study. Hence, dyads here should be read as primitive dyads – not necessarily diphones.

Beta-Cycle Long Dyads

In Tempo, a dyad is a speech segment of beta-cycle duration. Note that (i) there are 4 dyads inside one theta cycle, all with equal duration – this is so because of the assumption that the beta frequency remains constant within one theta cycle, and (ii) being of equal length, not all 4 (beta-long) dyads within one theta cycle can be consistently “centered.”

In the case of uncompressed speech a dyad is often aligned with the acoustic realization of a diphone. As a consequence of note (ii), the “center” of two different acoustic realizations of the same diphone (i.e., two beta-long dyads) will not necessarily be located at the same position within the dyad. This represents a difficulty: to which dyad neuron should such dyads be mapped onto? A partial answer to this question probably lies in the properties of the TFM model described in the Appendix, and yet to be implemented.

Even more so is the case of the Ghitza and Greenberg (2009) stimuli with gaps, where the beta-long dyads are rarely aligned with the “canonical” acoustic realization of a diphone. Consequently, Tempo is expected to produce a considerable number of errors, as discussed in Subsection Response to Speech Compressed by a Factor of 3, a trend in line with the behavioral data.

Theta-Cycle Long Syllables

In Tempo, a segment of theta-cycle duration is mapped onto a syllable neuron. A syllable neuron is activated by a specific ordered sequence of four beta-cycle long dyads – this is the role of the TSM component. Syllables here should be read as primitive syllables – not necessarily words. The acquisition process, by which syllable neurons become associated with their respective word representation, is beyond the scope of this study.

Phonemic Variability and the TFM Component

In spite of the acoustic variation in time and frequency, e.g., across talkers (men, women, and children), listeners are able to reliably perceive the underlying phonetic units. As described in Subsection Decoding of Section “Tempo – Architecture”, the TFM component maps dyads to dyad neurons by computing coincidence across tonotopic frequency channels. Given the frequency variability in the formant space, the matching cannot be based on strict tonotopic map. Rather, a loose tonotopicity is envisioned, the degree of which psychophysical studies will tell (for example, what is the tolerable frequency shift, in terms of number of critical bands?) We adopt the stance that it is the variability of the time–frequency signature as a whole that matters. The TFM model discussed in the Appendix provides robustness against temporal variations, but has yet to address variations in frequency.

Tempo vs. Classical Framework

Conventional models of speech perception assume a strict decoding of the acoustic signal by the auditory system and higher neural centers. The decoding path of Tempo conforms to this notion; the TFM component is a neuronally inspired mechanism, which maps the acoustic time–frequency features of a dyad (beta-cycle long) onto the corresponding memory neuron. For speech rates that result in flawless human performance (e.g., uncompressed speech, speech compressed by two) the beta-long dyads, determined by the parsing path, are aligned with their diphonic representation and Tempo operates as classical models do. The parsing path plays an important role in explaining the counterintuitive U-shape performance in the case of speech uttered too fast – with or without the insertion of gaps – and is an insightful extension to traditional models. In this sense, Tempo links the classical acoustically driven perspectives with the cortically inspired timing perspective.

Tempo and Decoding Time

Ghitza and Greenberg (2009) interpreted the insertion of silent gaps as an act of providing “needed” decoding time. They hypothesized that the decoding time is governed by cortical oscillations. How so? The architecture of Tempo provides an insight into this relationship.

In Tempo, a dyad is decoded at the end of a beta cycle; a syllable is decoded at the end of the theta cycle by integrating a sequence of, at most, 4 dyads. For stimuli without gap insertions, as long as theta is locked to the input rhythm (i.e., uncompressed, time-compressed by two) the ASI within a theta cycle comprises about 4 typical dyads – compatible with the processing capacity of Tempo [columns (a) and (b), Table 1]. For a compression factor of 3 the theta is “stuck” at its upper frequency limit (10 Hz), and the ASI within the 100-ms long theta cycle comprises 6 typical dyads – greater than Tempo’s processing capacity [column (c), Table 1]. The insertion of silent gaps – the act of providing extra decoding time – should be viewed as a re-packaging process, aiming at a better synchronization between the input information flow and the capacity of the “receiver.” Best synchronization is achieved by tuning the packaging rate to the mid range of the theta oscillator. The optimal packaging rate (hence the optimal gap duration, or the “needed” decoding time) is, therefore, dictated by the properties of the oscillatory array. The U-shape curve of the behavioral data tells us that there is a range of preferred packaging rates – rather than a sweet spot – reflecting the frequency range of the theta oscillator. In particular, re-packaging with a gap duration (read: decoding time) which is too short or too long compared to an 80-ms long gap (the optimal rate) results in errors due to a mismatch between the number of uncompressed dyads composing the ASI within the theta cycle (the number of dyads to be decoded), and the number of dyad-neuron activations permitted by the receiver.

Tempo and the Role of Delta Oscillations

In the parsing path of Tempo the theta oscillator is the master. A legitimate question arises whether this choice is appropriate in the context of speech perception? Parsing is the process by which the speech signal is temporally partitioned into zones that are linked to a variety of linguistic levels of abstraction, ranging from phonetic segment to syllable to word and ultimately prosodic phrase. One could argue that the parsing process begins at the phrasal level – which spans a duration of 0.5–2 s and is commensurate with the frequency range of the delta rhythms – and then works down to shorter intervals associated with words and syllables. Therefore, when realizing the parsing process as a cascaded oscillatory array, the delta oscillator – not the theta – should be master.

The reasons for our preference to assign the theta as the master oscillator are presented in Subsection Parsing of Section “Tempo – Architecture”, namely the psychophysical evidence on the relative importance to intelligibility of modulations in the range of 3–10 Hz, and the strong presence of these energy fluctuations in the speech signal; such strong presence is crucial for a robust tracking of the input rhythm by the cascaded array. In contrast, the acoustic presence of delta-related acoustic features, e.g., intonation (or pitch) contours, is weak. In our view the delta rhythm, indeed, plays an important role in prosodic parsing, which pertains to sequences of syllables and words, hence tapping contextual effects; as such, the delta oscillator interacts with the theta, beta, and gamma oscillators in a top-down fashion. The manner by which this process is carried out cortically is beyond the scope of this study; here we focused on developing a model capable of predicting the data of Ghitza and Greenberg (2009), where the speech material comprised naturally spoken, semantically unpredictable sentences.

Summary

The critical thesis at the basis of the approach presented here is that current models of speech perception that only consider properties of the signal derived from the acoustics are incomplete, and that the role of decoding time during memory access should be incorporated. It is hypothesized that decoding time is dictated by neuronal oscillations. The emerging cortical computational principle is the notion of template-matching operations guided by an array of cascaded oscillators locked to the sensory input rhythm. This computation principle was exploited in a computational model, Tempo. A qualitative study was presented, showing that the performance of the model is in line with challenging, counterintuitive human data (Ghitza and Greenberg, 2009) that are hard to explain by current models of speech perception.

The key properties that enable such performance are the cascaded synchronization of the oscillators within the array, and the capability of the theta oscillator (and hence the entire array) to track and stay locked to the input syllabic rhythm. These properties are the reason why the performance remains high as long as the oscillators are within their intrinsic frequency range, and why performance drops once the oscillators are out of lock (e.g., hit their boundaries). When locking is maintained, the TFM model (an extension of Shamir et al., 2009) maps acoustic segments of a dyad length to memory (dyad) neurons in a manner that is insensitive to time-scale variations. Outside the locking range errors increase due to erroneous mapping of dyad-long acoustics (TFM errors) and due to difficulties in memory access, as the number of available dyad-neuron activations within a theta cycle is insufficient (TSM errors).

Since the performance data are expressed as word errors, a comprehensive, quantitative validation would require a Tempo-based word recognition system. Such a system is yet to be developed, including the components of Tempo in the parsing path, the decoding path, and beyond (i.e., how to integrate syllables into words?). Psychophysical data are required to fine-tune the model (e.g., what is the distribution of TFM and TSM errors in humans?). Finally, this study is confined to a limited (albeit challenging) data set; more tests are needed to ascertain whether Tempo is able to predict a variety of other psychophysical data.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

I thank Steven Greenberg for valuable discussions in the early stages of the project. I also thank Steven Epstein, Anne-Lise Giraud, Nancy Kopell, David Poeppel, and the three reviewers for providing detailed and constructive suggestions, which made the revised version stronger and more concise than the original. This study was funded by a research grant from the Air Force Office of Scientific Research.

Supplementary Material

The MP4 files (eight stimuli, one for each of the conditions (a) to (h) – see Figure 4) can be found online at http://www.frontiersin.org/auditory_cognitive_neuroscience/10.3389/fpsyg.2011.00130/abstract

Footnotes

1. ^The phonetic transcription may be provided, for example, by an array of phonetic feature detectors, which generate a phonetic-features vector that identifies the specific phone (e.g., Stevens, 2005).
2. ^Note that Ghitza and Greenberg’s (2009) data are in terms of word errors; therefore, a fully, quantitative validation would require a Tempo-based word recognition system, not available at present. Here we present a qualitative study, demonstrating performance in line with the behavioral data.
3. ^It is noteworthy that oscillations in the high end of this range may also be considered low-gamma oscillations.
4. ^Complying with this requirement is one (the temporal) aspect of what is considered the Holy Grail in models of speech perception. Models of speech perception capable of explaining humans’ insensitivity to phonemic variations are still under pursuit, and formulating a perception-relevant metric to measure a distance between two speech segments of different duration is still considered an unresolved problem.
5. ^The relationship between Tempo and decoding time is discussed in paragraph Tempo and Decoding Time below.

References

Ahissar, E., Haidarliu, S., and Zacksenhouse, M. (1997). Decoding temporally encoded sensory input by cortical oscillations and thalamic phase comparators. Proc. Natl. Acad. Sci. U.S.A. 94, 11633–11638.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ahissar, E., Nagarajan, S., Ahissar, M., Protopapas, A., Mahncke, H., and Merzenich, M. M. (2001). Speech comprehension is correlated with temporal response patterns recorded from auditory cortex. Proc. Natl. Acad. Sci. U.S.A. 98, 13367–13372.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bastiaansen, M., and Hagoort, P. (2006). Oscillatory neuronal dynamics during language comprehension. Prog. Brain Res. 159, 179–196.

Pubmed Abstract | Pubmed Full Text

Borgers, C., Epstein, S., and Kopell, N. J. (2005). Background gamma rhythmicity and attention in cortical local circuits: a computational study. Proc. Natl. Acad. Sci. U.S.A. 103, 7002–7007.

CrossRef Full Text

Buzsáki, G. (2005). Theta rhythm of navigation: link between path integration and landmark navigation, episodic and semantic memory. Hippocampus 15, 827–840.

CrossRef Full Text

Buzsáki, G. (2006). Rhythms of the Brain. New York: Oxford University Press.

Canolty, R. T., Soltani, M., Dalal, S. S., Edwards, E., Dronkers, N. F., Nagarajan, S. S., Kirsch, H. E., Barbaro, N. M., and Knight, R. T. (2007). Spatiotemporal dynamics of word processing in the human brain. Front. Neurosci. 1:185–196. doi: 10.3389/neuro.01/1.1.014.2007

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Chi, T., Gao, Y., Guyton, M. C., Ru, P., and Shamma, S. A. (1999). Spectro-temporal modulation transfer functions and speech intelligibility. J. Acoust. Soc. Am. 106, 2719−2732.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dau, T., Kollmeier, B., and Kohlrausch, A. (1997). Modeling auditory processing of amplitude modulation. I. Detection and masking with narrow-band carriers. J. Acoust. Soc. Am. 103, 2892–2905.

CrossRef Full Text

Dilley, L., and Pitt, M. (2010). Altering context speech rate can cause words to appear or disappear. Psychol. Sci. 21, 1664–1670.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Donoghue, J. P., Sanes, J. N., Hatsopoulos, N. G., and Gaál, G. (1998). Neural discharge and local field potential oscillations in primate motor cortex during voluntary movements. J. Neurophysiol. 79, 159–173.

Pubmed Abstract | Pubmed Full Text

Dupoux, E., and Green, K. (1997). Perceptual adjustment to highly compressed speech: effects of talker and rate changes. J. Exp. Psychol. Hum. Percept. Perform. 23, 914–927.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Foulke, E., and Sticht, T. G. (1969). Review of research on the intelligibility and comprehension of accelerated speech. Psychol. Bull. 72, 50–62.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fries, P. (2005). A mechanism for cognitive dynamics: neuronal communication through neuronal coherence. Trends Cogn. Sci. (Regul. Ed.) 9, 474–480.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Garvey, W. D. (1953). The intelligibility of speeded speech. J. Exp. Psychol. 45, 102–108.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ghitza, O., and Greenberg, S. (2009). On the possible role of brain rhythms in speech perception: intelligibility of time-compressed speech with periodic and aperiodic insertions of silence. Phonetica 66, 113–126.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ghitza, O., Messing, D., Delhorne, L., Braida, L., Bruckert, E., and Sondhi, M. M. (2007). “Towards predicting consonant confusions of degraded speech,” in Hearing – From Sensory Processing to Perception, eds B. Kollmeier, G. Klump, V. Hohmann, U. Langemann, M. Mauermann, S. Uppenkamp, and J. Verhey (Berlin: Springer-Verlag), 541–550.

Giraud, A. L., Kell, C., Thierfelder, C., Sterzer, P., Russ, M. O., Preibisch, C., and Kleinschmidt, A. (2004). Contributions of sensory input, auditory search and verbal comprehension to cortical activity during speech processing. Cereb. Cortex 14, 247–255.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Giraud, A. L., Kleinschmidt, A., Poeppel, D., Lund, T. E., Frackowiak, R. S. J., and Laufs, H. (2007). Intrinsic cortical rhythms determine cerebral specialization for speech perception and production. Neuron 56, 1–8.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gruber, T., Tsivilis, D., Giabbiconi, C. M., and Müller, M. M. (2008). Induced electroencephalogram oscillations during source memory: familiarity is reflected in the gamma band, recollection in the theta band. J. Cogn. Neurosci. 20, 1043–1053.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Haarman, H. J., Cameron, J. A., and Ruchkin, D. S. (2002). Neuronal synchronization mediates on-line sentence processing: EEG coherence evidence from filler-gap constructions. Psychophysiology 39, 820–825.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hopfield, J. J. (2004). Encoding for computation: recognizing brief dynamical patterns by exploiting effects of weak rhythms on action-potential timing. Proc. Natl. Acad. Sci. U.S.A. 101, 6255–6260.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Houtgast, T., and Steeneken, H. J. M. (1985). A review of the MTF concept in room acoustics and its use for estimating speech intelligibility in auditoria. J. Acoust. Soc. Am. 77, 1069–1077.

CrossRef Full Text

Kopell, N., and LeMasson, G. (1994). Rhythmogenesis, amplitude modulation and multiplexing in a cortical architecture. Proc. Natl. Acad. Sci. U.S.A. 91, 10586–10590.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lakatos, P., Karmos, G., Mehta, A. D., Ulbert, I., and Schroeder, C. E. (2008). Entrainment of neuronal oscillations as a mechanism of attentional selection. Science 320, 110–113.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lakatos, P., Shah, A. S., Knuth, K. H., Ulbert, I., Karmos, G., Mehta, A. D., Ulbert, I., and Schroeder, C. E. (2005). An oscillatory hierarchy controlling neuronal excitability and stimulus processing in the auditory cortex. J. Neurophysiol. 94, 1904–1911.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Luce, P. A., and McLennan, C. (2005). “Spoken word recognition: the challenge of variation,” in The Handbook of Speech Perception, eds D. B. Pisoni, and R. E. Remez (Oxford, UK: Blackwell Publishing), 591–609.

Luo, H., Liu, Z., and Poeppel, D. (2010). Auditory cortex tracks both auditory and visual stimulus dynamics using low-frequency neuronal phase modulation. PLoS Biol. 8, e1000445. doi: 10.1371/journal.pbio.1000445

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Luo, H., and Poeppel, D. (2007). Phase patterns of neuronal responses reliably discriminate speech in human auditory cortex. Neuron 54, 1001–1010.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Marslen-Wilson, W. D. (1987). Functional parallelism in spoken word-recognition. Cognition 25, 71–102.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Marslen-Wilson, W. D., and Welsh, A. (1978). Processing interactions during word recognition in continuous speech. Cognition 10, 487–509.

Morillon, B., Lehongrea, K., Frackowiak, R. S. J., Ducorps, A., Kleinschmidt, A., Poeppel, D., and Giraud, A. L. (2010). Neurophysiological origin of human brain asymmetry for speech and language. Proc. Natl. Acad. Sci. U.S.A. 107, 18688–18693.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Nourski, K. V., Reale, R. A., Oya, H., Kawasaki, H., Kovach, C. K., Chen, H., Howard, III, M. A., and Brugge, J. F. (2009). Temporal envelope of time-compressed speech represented in the human auditory cortex. J. Neurosci. 29, 15564–15574.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Palva, J. M., Monto, S., Kulashekhar, S., and Palva, S. (2010). Neuronal synchrony reveals working memory networks and predicts individual memory capacity. Proc. Natl. Acad. Sci. U.S.A. 107, 7580–7585.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Palva, J. M., Palva, S., and Kaila, K. (2005). Phase synchrony among neuronal oscillations in the human cortex. J. Neurosci. 25, 3962–3972.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Poeppel, D. (2003). The analysis of speech in different temporal integration windows: cerebral lateralization as “asymmetric sampling in time”. Speech Commun. 41, 245–255.

CrossRef Full Text

Pulvermueller, F. (1999). Words in the brain’s language. Behav. Brain Sci. 22, 253–366.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schroeder, C. E., and Lakatos, P. (2009). Low-frequency neuronal oscillations as instruments of sensory selection. Trends Neurosci. 32, 9–18.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Shamir, M., Ghitza, O., Epstein, S., and Kopell, N. (2009). Representation of time-varying stimuli by a network exhibiting oscillations on a faster time scale. PLoS Comput. Biol. 5, e1000370. doi: 10.1371/journal.pcbi.1000370

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Singer, W. (1999). Neuronal synchrony: a versatile code for the definition of relations? Neuron 24, 49–65.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Stevens, K. (2005). “Features in speech perception and lexical access,” in The Handbook of Speech Perception, eds D. B. Pisoni, and R. E. Remez (Oxford, UK: Blackwell Publishing), 125–155.

Suppes, P., Han, B., and Lu, Z. L. (1998). Brain-wave representation of sentences. Proc. Natl. Acad. Sci. U.S.A. 95, 15861–15866.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Suppes, P., Lu, Z. L., and Han, B. (1997). Brain-wave representation of words. Proc. Natl. Acad. Sci. U.S.A. 94, 14965–14969.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Viterbi, A. J. (1966). Principles of Coherent Communication. New York: McGraw-Hill.

von Stein, A., and Sarnthein, J. (2000). Different frequencies for different scales of cortical integration: from local gamma to long range alpha/theta synchronization. Int. J. Psychophysiol. 38, 301–313.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Zacksenhouse, M., and Ahissar, E. (2006). Temporal decoding by phase-locked loops: unique features of circuit-level implementations and their significance for vibrissal information processing. Neural. Comput. 18, 1611–1636.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Zatorre, R., Belin, P., and Penhume, V. (2002). Structure and function of auditory cortex: music and speech. Trends Cogn. Sci. (Regul. Ed.) 6, 37–46.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text