- 1 Department of General Psychology, University of Padova, Padova, Italy
- 2 Center for Mind/Brain Sciences, University of Trento, Rovereto (Trento), Italy
Newly hatched domestic chicks, reared with identical objects, when presented with sets of 3 vs. 2 objects disappearing one-by-one behind separate screens, spontaneously inspected the screen occluding the larger set; even when the continuous variables (area or perimeter) were controlled for (Rugani et al., 2009). Here, using a similar paradigm, we investigated the ability of chicks to perform addition on larger sets of objects. Chicks imprinted on five identical objects, were presented at test with 6 vs. 9 objects which disappeared one-by-one (Exp. 1). In Exp. 2, the same overall number of objects (15) was used, but employing an increased ratio, i.e., 5 vs. 10. In both experiments, when continuous variables were not made equal, chicks spontaneously inspected the screen occluding the larger set. However, when the size of the objects was adjusted so as to make the total surface area or perimeter equal for the two sets, chicks did not exhibit any preference. Lack of choice in the control conditions could be due to a combination of preferences; to rejoin the larger numerousness as well as the bigger objects (Rugani et al., 2010a). In Exp. 3, chicks were familiarized, during imprinting, with objects of various dimensions, in an attempt to reduce or suppress their tendency to approach objects larger than the familiar ones. Again chicks failed to choose at test between 5 vs. 10 objects when continuous variables were made equal. Results showed that chicks, after a one-by-one presentation of a large number of objects, rejoined the larger set. In order to choose the larger set, chicks estimated the objects in the two sets and then compared the outcomes. However, differently to what has been described for small numerousness, chicks succeeded only if non-numerical cues as well as numerical cues were available. This study suggests that continuous variables are computed by chicks for sets of objects that are not present at the same time and that are no longer visible at the time of choice.
Introduction
Only adult humans master symbolic mathematics (Carey, 2004), nevertheless a variety of non-human creatures possess some kinds of numerical competences (reviews in Shaun et al., 2010; Vallortigara et al., 2010). These range from numerical discrimination (mastered by salamanders, Plethodon cinereus, day-old domestic chicks, Gallus gallus, horses, Equus caballus, Uller et al., 2003; Rugani et al., 2008, 2010b; Uller and Lewis, 2009), ordinal abilities (possessed by honey bees, Apis mellifera, domestic chicks, Clark’s Nutcracker, Nucifraga columbiana, rats, Rattus norvegicus, Davis and Bradford, 1986; Chittka and Geiger, 1995; Suzuki and Kobayashi, 2000; Rugani et al., 2007, 2010, 2011; Dacke and Srinivasan, 2008), to simple arithmetic (reviews in: Gallistel, 1990; Dehaene, 1997; Spelke and Dehaene, 1999; Brannon and Roitman, 2003). Primates have been demonstrated to be able to learn summation of quantity representations. Chimpanzees (Pan troglodytes) and squirrel monkeys (Saimiri sciureus) trained to associate Arabic numerals to the correspondent number of food reinforcements, chose the option that made them earn the greater number of reinforcements, even when they were presented with sums of the Arabic numerals and not solely with a simple comparison between numerals (Rumbaugh et al., 1987, 1988; Boysen and Berntson, 1995; Olthof et al., 1997). Capuchin monkeys (Cebus apella), after learning to exchange different tokens to obtain different quantities of the same food, could use tokens as symbols to flexibly sum quantities (Addessi et al., 2007). Nevertheless summation has been also proved to be mastered by non-verbal subjects even in absence of specific training. The pioneer study that investigated spontaneous (in absence of training) arithmetic abilities in non-verbal subjects was conducted on pre-verbal humans: Wynn (1992), using violation of expectancy and looking time method, demonstrated that infants can solve simple arithmetic operations (1 + 1 = 2 and 2 − 1 + 1). For example in the 1 + 1 = 2 task, a “Mickey Mouse” doll was placed on a stage, a screen was placed in front of it, hiding the doll, and then another “Mickey Mouse” was, visibly to the subject, introduced behind the screen. Then the screen was removed revealing either a possible or an impossible sum of dolls. Infants looked longer at the “impossible” outcomes of either one doll or three dolls than at the possible outcome of two dolls. Infants behaved as if they knew that the sum hidden behind the screen should be of exactly two. Wynn’s data were replicated by subsequent studies where possible intervening variables were controlled for. Simon et al. (1995) designed two new conditions to test for the possible use of the “Impossible Identity” and the “Impossible Arithmetic,” to explain infants’ looking time preferences. Indeed Wynn’s data could be explained either by an arithmetical computation (as Wynn suggested) or by recognition of a physically impossible event, regardless of arithmetic. To clarify this, Simon et al. (1995) used two different kinds of dolls (“Elmo” and “Ernie”). “Elmo” dolls were presented in the initial trial phase and then surreptitiously replaced with “Ernie” dolls (and vice versa). Infants’ expectations were not violated by this identity switch. They looked longer only at the numerically unexpected outcome and not at the outcome identity. This indicates that, in some sense, infants represent the object numbers stripped of their non-numerical features.
Wynn’s paradigm was also adapted to test arithmetic reasoning in non-human primates, using food as attractor and requiring subjects to choose the quantity to be eaten. Subjects were presented with some food items, which were subsequently obscured by a screen. Following this, some items were visibly added or removed from behind the screen. Finally, the screen was lowered revealing an expected or unexpected object number. Cotton-top tamarins (Saguinus oedipus), lemurs (Eulemur fulvus, Eulemur mongoz, Lemur catta, and Varecia rubra), and domestic dogs (Canis familiaris), if presented with the 1 + 1 operation, looked longer at the unexpected outcome of three or one, compared to the expected value of two, demonstrating that subjects expected the exact result, and not a number different from it (Uller et al., 2001; West and Young, 2002; Santos et al., 2005).
Using a different paradigm, based on the spontaneous tendency to follow their imprinting stimulus, simple arithmetic abilities were demonstrated in young domestic chicks (G. gallus). Chicks were reared for the first 4 days of life with an imprinting stimulus, composed of five identical objects (red plastic balls). On Day 5, each bird was presented with two different sets of imprinting elements which disappeared, one-by-one, behind one of two identical opaque screens. In the comparison 2 vs. 3, chicks consistently approached the screen occluding the larger number of objects, even when the continuous variables (area and perimeter) were controlled for. In a more difficult task, in which, after the initial disappearance of the two sets, some of the objects were visibly transferred from one screen to the other, in the conditions: (4 − 2) vs. (1 + 2); (5 − 3) vs. (0 + 3); (4 − 1) vs. (1 + 1); and (5 − 2) vs. (0 + 2) chicks rejoined the larger object number, demonstrating that they were capable of performing the subsequent additions and subtractions of elements that appeared and disappeared (Rugani et al., 2009).
In most of the studies presented above, participants were able to compute the correct outcome of simple arithmetic operations solely when both sets were small (upper limit of three or four elements for each set). Nevertheless, several other studies seem to suggest that even non-language creatures can add and subtract large numerousness. Monkeys could be trained to sum different numbers of dots when large numerousness were employed. At test – consisting in a matching-to-sample task – monkeys were required to make an explicit choice about which of two arrays matched the sum of two addends each viewed separately (Cantlon and Brannon, 2007). Monkeys were firstly presented with a set of dots and, after a brief delay, with a second set. Then they were presented with either a correct or an incorrect result. Monkeys were rewarded for selecting the value that represented the correct sum of the sets previously presented. Results demonstrated that monkeys are able to mentally add numerical values together. Furthermore, their accuracy was ratio-dependent, suggesting that the task was performed by “combining” analog-magnitude representations. Using the spontaneous looking time paradigm, 9-month-old infants were shown to be able to sum and subtract large sets (5 + 5 and 10 − 5) of elements even when surface area and perimeter length, were controlled for (McCrink and Wynn, 2004). Chimpanzees were able to sum different sets of food items and to select the larger quantities in the comparisons 5 vs. 8; 5 vs. 10; and 6 vs. 10 (Beran and Beran, 2004) and 2 + 2 + 3 vs. 3 + 4 + 1 (Beran, 2001), even when continuous variables were controlled for.
This study aims at extending research on spontaneous and non-linguistic arithmetic to large numeracy in very young animals.
Experiment 1
After having been imprinted on sets comprising a different number of identical objects, chicks preferred to associate with the larger set when they were given the possibility to approach either of two sets, each comprising a different number of objects all identical to the imprinting ones (Rugani et al., 2010a). Moreover, when the imprinting objects were presented and made to disappear, one-by-one, behind either of two identical screens, in the comparison 2 vs. 3, chicks were shown capable of rejoining the larger group, even when continuous variables were controlled for (Rugani et al., 2009).
Here, we used imprinting as a tool, because it allows domestic chicks (a precocial species) a rapid learning of the features of the “mother.” By the virtue of exposure, chicks learn the overall properties of imprinting stimuli, which include both their continuous physical variables (i.e., area, volume, perimeter) as well as their numerical attributes, and they could use them for recognition of familiarity and novelty (Rugani et al., 2010a).
Chicks spontaneous (i.e., that do not require traditional conditioning procedures) learning is employed in the following experiments to investigated the ability of day-old domestic chicks to compare representations of larger sets of objects in the comparison 6 vs. 9.
Materials and Methods
Subjects and rearing conditions
Subjects were 18 female “Hybro” (a local variety derived from the White Leghorn breed) domestic chicks (G. gallus). They were obtained weekly from a local commercial hatchery (Agricola Berica, Montegalda, Vicenza, Italy) when they were only a few hours old. On arrival, they were immediately housed singly in standard metal home cages (28 cm wide × 32 cm long × 40 cm high) at controlled temperature (28–31°C) and humidity (68%), with food and water available ad libitum in transparent glass jars (5 cm in diameter, 5 cm high). The cages were constantly (24 h/day) lit by fluorescent lamps (36 W), located 45 cm above each cage. Continuous light exposure was used as a standard procedure for all subjects, as it helps the singly caged newborn chicks to feed and to identify the water in their first days of life. Each chick was placed in one cage together with an imprinting stimulus. The imprinting stimulus was identical for all chicks and consisted of a set of five identical objects, (two-dimensional, about 1 mm thick, red plastic squares measuring 2.5 cm × 2.5 cm). Previous studies have shown that this kind of object is very effective in producing social attachment through filial imprinting in this strain of chicks (Rugani et al., 2009, 2010; Fontanari et al., 2011). Each object was suspended in the center of the cage by a fine thread, at about 4–5 cm from the floor, so that it was located at about chicks’ head height. The imprinting objects were also separated by 2 cm from one another, so as to reduce the physical overlapping (see Figure 1).

Figure 1. An example of a stimulus used during imprinting phase, each stimulus was composed of five identical red bi-dimensional squares.
Chicks were reared in these conditions from the morning (11 a.m.) of the first day (i.e., Monday, the day of their arrival, which was considered as Day 1) to the morning (11 a.m.) of Day 3 (Wednesday), when each chick singly underwent training and, about 1 h later, testing. In the time between training ad test, chicks were returned to their own cage with their imprinting stimulus.
Apparatus
Training and testing took place in an experimental room, located near the rearing room. In the experimental room temperature and humidity were maintained at a constant 25°C and 70% respectively. During both training and testing the experimental room was kept dark, except for the light coming from a 40-W lamp placed about 80 cm above the center of the apparatus.
The testing apparatus was a circular arena (95 cm in diameter and 30 cm outer wall height) with the floor uniformly covered by a white plastic sheet. Within the arena, adjacent to the outer wall, there was a starting box (10 cm × 20 cm × 20 cm) made of opaque plastic sheets, with an open top allowing insertion of the bird. The side of the starting box, facing the center of the arena, consisted of a removable clear glass partition (20 cm × 10 cm), in such a way that the subject, while confined, could see the inside of the apparatus (Figure 2). The starting box was used for holding the chicks shortly before the beginning of each trial. In front of the starting box, 35 cm away from it, there was one (or two) blue opaque cardboard screen (16 cm × 8 cm). The number of screens employed depended on the experimental phase: a single screen was used during training, while two identical screens, positioned in the center of the arena, symmetrically with respect to the front of the starting box (20 cm apart from one another) were used during testing. To prevent the chicks from seeing the hidden objects before having circled almost completely around the screen, the screens were provided with 3 cm bent back edges on the two vertical sides.

Figure 2. The test apparatus employed in all of the experiments described. In the picture, a chick, confined into the starting box, and the two screens, as during the test phase, are present. The stimuli, each composed of five or 10 identical squares (as in the No Control condition of Exp. 2) are also visible.
Procedure
Training. On day 3, at around 12.30, chicks underwent training. Each chick, together with a single object (i.e., a square), identical to one of those used for imprinting, was placed within the testing arena, in front of, and 15 cm away from, the single screen. The object was held the from above, via a fine thread, between the starting box (about 10 cm far from it) and the screen, at about 5 cm from the floor of the apparatus, so that it was at chick’s height. Overall this period, the chick was left free to move around and get acquainted with the environment for about 5 min. Thereafter, the experimenter slowly moved the square toward the screen, and then behind it, until the object completely disappeared from the chick’s sight. This procedure was repeated a few times, until the chick started to follow the object behind the screen as soon as it was made to disappear. Thereafter, the chick was confined within the starting box, behind the transparent front partition, so that it could see the object being moved within the arena. As soon as the object had completely disappeared behind the screen, the chick was set free in the arena by lifting the frontal partition. Every time the chick rejoined the object, as a reward, it was allowed to spend a few seconds with it. Then, the whole procedure was restarted and repeated until the chick rapidly rejoined the object for three consecutive times. On average, about 15 min were required to complete the training for each chick.
Testing. Testing took part 2 h after the end of training and consisted, for each chick, of 20 consecutive valid trials. At the beginning of each testing trial the bird was confined to the starting box, behind the transparent partition, from where it could see the inner arena and the two screens (see Figure 2). On each trial, six elements were presented (placed at first at about 10 cm from the front of the starting box) to the chick and then made to move and disappear consecutively (i.e., one-by-one) behind one screen, thereafter nine elements were made to consecutively disappear behind the other screen. In this way, one-by-one, all elements were presented, first all those of one set (that were to disappear behind one of the two screens) and then all those of the other group (that made to disappear behind the other screens). The set (six or nine) that was made to disappear firstly, as well as the screen (i.e., the one on the left or the one on the right) behind which the set was made to disappear was scheduled before in accord with a semi random sequence. The whole procedure lasted between 204 and 210 s. Each element was kept in front of the starting box for 3 s and then it took 3 s to be moved back behind the screen (6 s overall). About 2 s elapsed from the disappearance of one object and the appearance of the next one. Three seconds after the disappearance of both sets, the transparent partition was removed and the chick was left free to move within the arena. A choice was defined as when the chick’s head had entered the area behind one of the two screens, only the choice for the first screen visited was scored and thereafter the trial was considered over. At the end of each trial, chicks were allowed to spend a few seconds with their “social companions” behind the screen chosen.
If the chick did not approach either screen within 180 s, the trial was considered null and void and it was repeated immediately afterward. Whenever the chick failed to respond also at the second attempt of performing the trial, that trial was considered as null and recorded as such, this means that chicks could score less than 20 valid trials. In the first experiment two chicks scored 19 valid trials and two other chicks scored 18 valid trials, the remaining 14 subjects scored all 20 valid trials.
After three consecutive null trials, the chick was discarded from the experiment.
Chicks’ behavior was observed on a monitor connected to a video camera; this way subjects were not distracted by direct observation. Nevertheless their behavior was entirely video-recorded to allow the experimenters to later score chicks’ performance. The two measures were always consistent with each other (100% consistency).
The number of trials in which each chick chose the screen hiding the larger number of imprinting objects (arbitrary chosen as the correct choice) was considered and percentages were computed as: Number of Correct Choices/Number of Valid Trials × 100. Parametric paired t-tests (to compare different conditions) or one-sample t-tests (to assess significant departures from chance level, i.e., 50%) were used.
Chicks were divided into three experimental groups, depending on the stimuli employed during testing. Testing stimuli consisted of red squares, identical in material and color to those used for imprinting, but differing in their dimensions depending on the experimental group. In the no control (NC) group (N = 10) the dimensions of the squares that composed the two testing sets were maintained identical to those of the squares of the imprinting stimulus. In both the same perimeter (SP, N = 4) and in the same area (SA, N = 4) control groups, the set of nine elements comprised squares of dimensions identical to those used during imprinting, while the set of six elements comprised larger sized squares. The dimensions of the squares in the set of six objects were computed to equate the overall perimeter (with squares measuring 3.75 cm × 3.75 cm each) or the overall area (with squares measuring 3.06 cm × 3.06 cm each) of the set of nine objects.
Results and Discussion
Four subjects scored 14 or more correct responses out of 20 (two tailed Binomial test, p = 0.037); two subjects scored 13 out of 20 or 12 out of 18 correct responses (two tailed Binomial test, p = 0.070); and the remaining four subjects scored 12 correct responses out of 20 or 11 out of 18 (two tailed Binomial test, p = 0.121); no chick scored less than 50% of correct responses.
A parametric one-sample t-test was done to compare the performance of the NC group with the chance level (50%). It showed as subjects preferentially chose the screen hiding nine objects over the screen hiding six objects [N = 10; Mean = 66.777, SEM = 2.693; one-sample t-test: t(9) = 7.619; p < 0.001; see Figure 3].
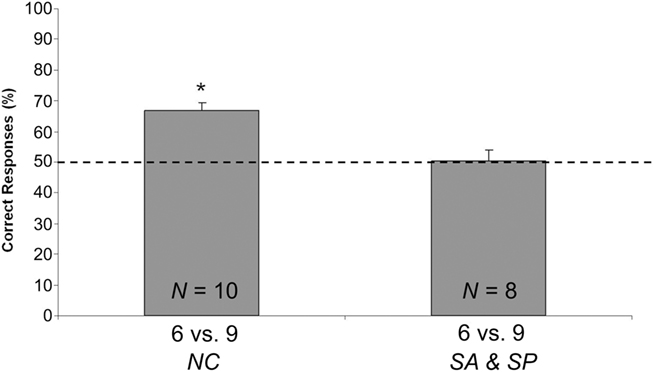
Figure 3. Results of Exp. 1. Percentages of correct responses (group means ± SEM) scored by chicks that underwent the no control test (NC) or both the control tests: same area (SA) and same perimeter (SP). The dotted line (y = 50) represents chance level.
In order to assess if the overall performance depended on learning occurring during testing, the percentage of correct responses on the first five trials was compared with chance level [N = 10; Mean = 74.666, SEM = 5.048; one-sample t-test: t(9) = 4.886; p < 0.009]. From the first trials, chicks preferentially chose the larger set. Moreover, to exclude any effect of learning overall during testing trials, a comparison between the percentage of correct responses given to the first vs. the last five trials (N = 10; Mean = 60.000, SEM = 6.667) was done. A paired t-test did not reveal any difference [t(18) = 1.754; p < 0.097], showing there was no improvement of performance during testing.
No difference [t(6) = 0.739; p = 0.488; two sample t-test] emerged when comparing the percentage of correct responses emitted by the two control groups (SP: N = 4; Mean = 53.223, SEM = 4.964; and SA: N = 4; Mean = 47.500, SEM = 5.951). Data for the two control groups were therefore merged, and the resulting mean (N = 8; Mean = 50.361, SEM = 3.747) did not differ from chance level [one-sample t-test, t(7) = 0.096; p = 0.962; see Figure 3].
Results confirmed that, in the absence of any specific training, chicks are spontaneously able to master summation of elements (Rugani et al., 2009). This means that during the one-by-one presentation of the objects, chicks were building a representation for each set, and that they could then compare the two representations stored in memory, to decide which was the larger. Differently to what happened with smaller numeracy (Rugani et al., 2009), where the discrimination was based on the actual number of the non-visible objects and not on differences in continuous variables, such as perimeter or area, here chicks mastered the task only when numerical and continuous variables were both available. This suggests that chicks used the continuous variables or a combination of numerousness and continuous extents to estimate the magnitude of the sets. This finding implies that continuous variables are computed in a representation which is updated, over time, during one-by-one object presentation. Another possible explanation could be that chicks have an intrinsic preference not only for the larger array (Rugani et al., 2010a), but even for the larger individual objects.
Experiment 2
The aim of the second experiment was to determine chicks’ ability to discriminate between larger numerousness, as described by a wider ratio (1:2).
Experiment 1 showed that when squares of identical size were used (NC group), chicks spontaneously inspected the screen occluding the larger set in the comparison 6 vs. 9. When the size of the objects was adjusted to control for the total area, or the perimeter (SP and SA groups), performance did not differ from chance level. The possibility for chicks to master this task seems to be tied to the possibility to use the continuous variables seen during object presentation, even if at the moment of choice these were no longer visible. In Exp. 2, the same overall number of objects (i.e., 15) was used, but employing a wider ratio (1:2), in the 5 vs. 10 comparison. In fact in a non-linguistic numerical task, when large numeracies were employed, their discrimination was shown to be strictly correlated with Weber’s law (Meck and Church, 1983; Boysen et al., 1996; Barth et al., 2003; Piazza et al., 2004; Pica et al., 2004; Cantlon and Brannon, 2006, 2007). According to this law, the ability to discriminate two sets is a function of the ratio between numerousness, rather than a function of the absolute difference between them. Since discrimination of large numerousness obeys Weber’s law: increasing the difference between the numerousness, discrimination’s accuracy would increase.
Materials and Methods
Subjects
Subjects were a new group of 18 female domestic chicks. Rearing conditions were identical to those described for the first experiment. Chicks were divided in three experimental groups, depending on the stimuli employed during testing.
Stimuli
Imprinting stimuli were identical for all chicks and consisted of a set of five identical, two-dimensional (about 1 mm thick), red plastic squares (2.5 cm × 2.5 cm).
Testing stimuli also consisted of red squares, but their dimensions varied in accordance with the experimental group. In the NC group (N = 10) the original dimensions of the imprinting squares (2.5 cm × 2.5 cm) were maintained, so that both sets were composed of identical squares. Both in the SP (N = 4) and in the SA (N = 4) control groups, the set of 10 elements comprised squares of dimensions identical to those used during imprinting, while the set of five elements comprised larger sized squares. The dimensions of each square in the set of five elements were computed in order to match the overall contour length (with squares measuring 5.00 cm × 5.00 cm each for the SC) or the overall area (with squares measuring 3.54 cm × 3.54 cm each for the SA) of the set of 10 elements.
Procedure
The apparatus and the experimental phases (training and testing) were identical to those described in the previous experiment, with each chick undergoing 20 test trials on Day 3.
Results and Discussion
Five subjects scored 14 or more correct responses out of 20 (two tailed Binomial test: p = 0.037); two subjects scored 13 out of 20 or 12 out of 18 correct responses (p = 0.070); and the remaining three subjects scored 12 correct responses out of 20 (p = 0.121). Therefore all chicks selected the screen hiding more objects over 50% of times.
When the performance of chicks of the NC group was compared with the chance level with a one-sample t-test, it resulted that subjects preferentially chose the screen hiding 10 squares over the screen hiding 5 squares [N = 10; Mean = 69.423, SEM = 2.693; one-sample t-test: t(9) = 7.213; p < 0.001; see Figure 4]. In order to check for learning that might have occurred during testing, chicks’ performance on the first five trials was considered. Already from the first trials, chicks preferentially chose the larger set [N = 10; Mean = 67.500, SEM = 6.021; one-sample t-test: t(9) = 2.907; p < 0.017].
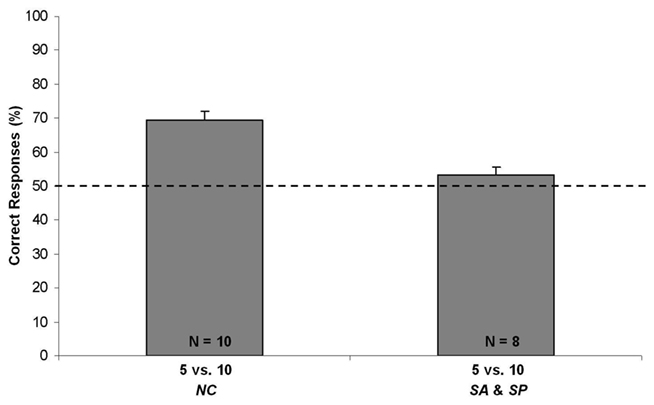
Figure 4. Results of Exp. 2. Percentages of correct responses (group means ± SEM) shown by chicks of NC, SA, and SP conditions, that underwent the 5 vs. 10 test. The dotted line (y = 50) represents chance level.
A comparison between chick’s choice for the screen hiding the larger number of objects in the first five trials and in the last five trials (N = 10; Mean = 69.000, SEM = 4.819) showed no improvement in the performance during testing trials [t(18) = 0.195; p < 0.848].
No difference [t(6) = 0.929; p = 0.389, two sample t-test] emerged when comparing the percentage of correct responses emitted by the two control groups (SP: N = 4; Mean = 52.380, SEM = 2.969; and SA: N = 4; Mean = 56.388, SEM = 3.131). Data of the two control groups were therefore merged, and the resulting mean (N = 8; Mean = 53.263, SEM = 2.320) did not differ from chance level [one-sample t-test, t(7) = 1.407; p = 0.202; see Figure 4].
Results confirmed the ability of chicks to store information about two sets of objects, consisting of up to 15 elements, and to use these representations to discriminate which set is the larger. Nevertheless this ability seems, again, to be strictly linked to the possibility to process both numerical and non-numerical cues, although this was impossible to assess during the presentation of the objects. Furthermore, the performance of chicks did not improve with an increased ratio (i.e., 1:2, in the comparison 5 vs. 10) as compared with a potentially more difficult one (2:3, in the comparison 6 vs. 9), used in Exp. 1. Indeed, even in the comparison 5 vs. 10 chicks were not able to solve the task when the continuous variables were controlled for.
Experiment 3
The previous experiments have shown that chicks presented with a total of 15 objects, disappearing one-by-one behind either of two identical screens, were able to find the larger set in the comparison 6 vs. 9 and 5 vs. 10, but this occurred only when the sets were composed of objects of the same size. When the continuous variables were controlled for, by employing sets of objects of different sizes, to equate the overall area or perimeter in the two sets, chicks failed. Results of the control conditions of the first two experiments can be accounted for in terms of a preference for the set comprising the novel sized, or bigger, objects as well as for the set comprising the larger number: in fact in the control groups of both experiments the sets of smaller numerousness comprised the larger elements. We wondered whether the use of objects of differing dimensions during imprinting (to make chicks to familiarize with elements of all sizes) would consequently improve the discrimination even in the control groups.
Materials and Methods
Subjects
Subjects were a new group of eight female domestic chicks. Rearing conditions were identical to those described for the previous experiments. Chicks were divided in two experimental groups: SP group (N = 4) and SA group (N = 4).
Stimuli and procedure
Imprinting stimuli were sets of five two-dimensional (about 1 mm thick), red plastic squares. Each imprinting stimulus was composed of five red squares of various side length (3.54; 5; 2.5 cm, that were the dimensions of the squares used respectively for the SA, SP, and NC group in the 5 vs. 10 comparison of Exp. 1). Three different sets of stimuli were used during the first three rearing days for each chick. A first set was composed of squares of 3.54 and 2.5 cm of side. A second set comprised squares of the dimension of 5 and 2.5 cm. A third set comprised a mix of all the dimensions (2.5, 3.54, and 5 cm).
To make the chicks acquainted with squares of each dimension, each set of objects was used, as imprinting stimulus, in chicks’ rearing cages for 24 h, before the test phase.
Testing stimuli consisted again of red squares. In the two experimental groups (SP and SA) a set comprised 10 squares of 2.50 cm × 2.50 cm, while the other set comprised five larger sized squares measuring respectively 3.54 cm × 3.54 cm for the SA and 5.00 cm × 5.00 cm for the SP.
Apparatus, general training, and testing procedures were the same as in the previous experiments.
Results and Discussion
No difference [t(6) = 0.540; p = 0.609; two sample t-test] emerged when comparing the percentage of correct responses emitted by the two control groups (SP: N = 4; Mean = 54.538, SEM = 5.885; and SA: N = 4; Mean = 50.658, SEM = 4.135; see Figure 5). Data were therefore merged, and the resulting mean (N = 8; Mean = 52.598, SEM = 3.409) was at chance level [one-sample t-test, t(7) = 0.762; p = 0.501].
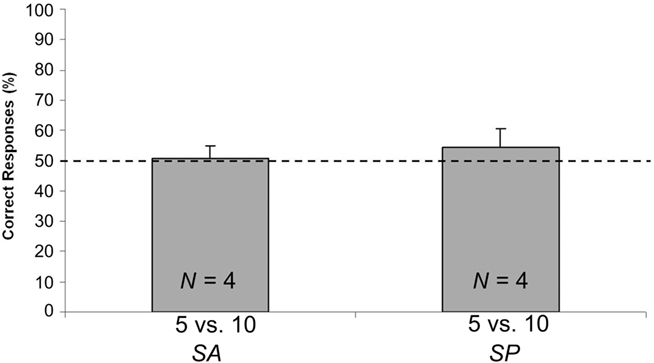
Figure 5. Results of Exp. 3. Percentages of correct responses (group means ± SEM) shown by chicks of SA and SP conditions, that underwent the 5 vs. 10 test, following familiarization with element of various dimensions. The dotted line (y = 50) represents chance level.
Familiarization with all the dimensions of the squares that were there used at test, did not result in a significant choice at test. These results seem to confirm that the ability of chicks to add large sets of elements is correlated to the availability of numerical and non-numerical cues during the presentation of the stimuli. These results seem to suggest either that the non-numerical information is important as well as the numerical one or that access to both numerical and non-numerical information is crucial to master this task.
General Discussion
Results showed that chicks are able to rejoin the larger group of objects (real or artificial social companions) after a one-by-one presentation of objects constituting either of two separate sets. Moreover, chicks seem to be able to compare the representations of the two sets so as to choose the larger one. However, differently to that which has been described for small numerousness, when large numerousness were employed, chicks succeeded only if non-numerical cues, as well as numerical, were available. An explanation for this difference may be found in the ability to discriminate small and large numerousness. Two systems usually dominate current debates on numerical competences in pre-verbal infants and non-human animals, with empirical evidence providing support for either system. One of them – the system for small numerousness – concerns enumeration of small groups of up to four objects; it is very accurate and allows the representation of exactly the numeracy of items presented, irrespective of their size (Trick and Pylyshyn, 1993; Gallistel and Gelman, 2000; Feigenson et al., 2004). The second system – the Analogue Magnitude System – operates also above these numbers, with the limit that the discrimination between two numbers decreases in accuracy as their ratio becomes smaller (Dehaene et al., 2002).
A recurring dispute about numerical competences in non-verbal subjects is the role played by continuous variables. The majority of investigations on this topic have been conducted in the domain of the number discrimination task: with the sets to be discriminated both visible at the time of choice. When small numbers were employed, infants represented total continuous extent, rather than numerousness (Clearfield and Mix, 1999; Feigenson et al., 2004); while non-human animals responded to the number of objects in the arrays, rather than to their overall continuous extent (day-old domestic chicks: Rugani et al., 2008; honey bees: Gross et al., 2009). This last finding is reversed when larger numerousness are employed, where continuous extent seems to be more important for small than large sets for infants (Xu and Spelke, 2000; Xu et al., 2005), but not for domestic chicks.
Nevertheless, in a different kind of task, in which the to be discriminated sets were no longer visible at choice time, it was demonstrated that animals can perform arithmetic calculations of a small number of objects, even when some of the intervening variables are controlled for (rhesus macaques: Hauser et al., 2000; rhesus monkeys: Hauser and Carey, 2003; Cotton-Top Tamarins: Uller et al., 2001; day-old domestic chicks: Rugani et al., 2009). Even in the domain of large numerousness non-verbal creatures are able to perform simple arithmetic. Using the expectancy violation looking time method, rhesus monkeys were proved to spontaneously (without training) compute addition operations, correctly discriminating between items of four or eight for the operations 3 + 1; 2 + 2; 4 + 4. By employing food items (lemons) of different dimension, to control for the continuous variables, it has been proved that this ability relies upon representation of numerousness and not upon the continuous amount of material (Flombaum et al., 2005).
In our experiments, the peculiarity of the species, as well as the kind of attractors employed in these experiments, allow for a good control of the continuous variables to be employed with very young animals in a summation task. Our data demonstrated that chicks are able to maintain a trace of the numerousness of hidden objects, comprising of two distinct sets, updating the representation of each set during the sequential addition of elements. This does not mean that chicks are representing the exact number of objects in each set, but rather that they have a sense of the location where the larger amount has been finally made to disappear. However, chicks’ choice remained at chance when the continuous extent was controlled for, and their performance did not improve when the ratio between the number of objects became greater, from 2:3 in the 6 vs. 9 comparison to 1:2 in the 5 vs. 10 comparison. In both comparisons, in fact, the discrimination was possible solely when numerical and non-numerical information were both available during the presentation of the stimuli. This suggests that non-numerical information is processed and remains available at the moment of choice, when the stimuli are no longer visible. One possibility is that, when large numerousness are used, individual recognition becomes increasingly difficult for chicks, that therefore prefer to rely of physical extent rather than numerical cues.
Moreover, the discrimination was based on the memory of the spatial position of the visibly disappearing objects, since any direct assessment of the sensory stimuli associated with the two sets was not possible at the time of choice.
Hence chicks’ behavior seemed to indicate an ability to combine two quantitative representations (addends) to form a new representation (i.e., the sum). Here, to test this ability we took advantage of chicks’ strong motivation to rejoin a social companion (Regolin et al., 2005) and of chicks’ preference for the larger between different numbers of imprinting objects (Rugani et al., 2010a). This capability may though not be specific of social attractors, but it could be found in other situations in which animals are motivated to rejoin the larger group of objects, being them social or non-social.
An important issue that remains open to investigation is why should chicks fail to discriminate when controls for “amount of stuff” are applied. Nonetheless, this study provides an insight on the essential role played by continuous variables in this kind of task, which seems to be both computed by animals during the presentation of stimuli (even sequential one-by-one presentation) and then memorized and processed at the time of choice.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
All procedures were in accordance with the Italian and European Community laws on animal research and treatment. The authors wish to thank Silvia Mantoni for the help provided with animal care and testing and Dr. Jonathan Niall Daisley for revising the manuscript. This work has been realized also thanks to the support from the Provincia autonoma di Trento and the Fondazione Cassa di Risparmio di Trento e Rovereto.
References
Addessi, E., Crescimbene, L., and Visalberghi, E. (2007). Do capuchin monkeys (Cebus apella) use tokens as symbols? Proc. R. Soc. Lond., B, Biol. Sci. 274, 2579–2585.
Barth, H., Kanwisher, N., and Spelke, E. (2003). The construction of large number representations in adults. Cognition 86, 201–221.
Beran, M. J. (2001). Summation and numerousness judgments of sequentially presented sets of items by chimpanzees (Pan troglodytes). J. Comp. Psychol. 115, 181–191.
Beran, M. J., and Beran, M. M. (2004). Chimpanzees remember the results of one-by-one addition of food items to sets over extended time periods. Psychol. Sci. 15, 94–99.
Boysen, S. T., and Berntson, G. G. (1995). Responses to quantity: perceptual versus cognitive mechanisms in chimpanzees (Pan troglodytes). J. Exp. Psychol. Anim. Behav. Process. 21, 82–86.
Boysen, S. T., Berntson, G. G., Hannah, M. B., and Cacioppo, J. T. (1996). Quantity-based interference and symbolic representation in chimpanzees (Pan troglodytes). J. Exp. Psychol. Anim. Behav. Process. 22, 76–86.
Brannon, E. M., and Roitman, J. D. (2003). “Nonverbal representations of time and number in animals and human infants,” in Functional and Neural Mechanism of Interval Timing, ed. W. H. Meck (New York, NY: CRC Press), 143–182.
Cantlon, J. F., and Brannon, E. M. (2006). Shared system for ordering small and large numbers in monkeys and humans. Psychol. Sci. 17, 401–406.
Cantlon, J. F., and Brannon, E. M. (2007). Basic math in monkeys and college students. PLoS Biol. 5, e328. doi: 10.1371/journal.pbio.0050328
Clearfield, M. W., and Mix, K. S. (1999). Number versus contour length in infant’s discrimination of small visual sets. Psychol. Sci. 10, 408–411.
Davis, H., and Bradford, S. A. (1986). Counting behavior by rats in a simulated natural environment. Ethology 73, 265–280.
Dehaene, S., Dehaene-Lambertz, G., and Cohen, L. (2002). Abstract representations of numbers in the animal and in the human brain. Trends Neurosci. 21, 355–361.
Feigenson, L., Dehaene, S., and Spelke, E. (2004). Core Systems of numbers. Trends Cogn. Sci. 8, 307–314.
Flombaum, J. I., Junge, J. A., and Hauser, M. D. (2005). Rhesus monkeys (Macaca mulatta) spontaneously compute addition operations over large numbers. Cognition 97, 315–325.
Fontanari, L., Rugani, R., Regolin, L., and Vallortigara, G. (2011). Object individuation in three-day old chicks: use of property and spatiotemporal information. Dev. Sci. doi: 10.1111/j.1467-7687.2011.01074.x
Gallistel, C. R., and Gelman, R. (2000). Non-verbal numerical cognition: from reals to integers. Trends Cogn. Sci. 4, 59–65.
Gross, H. J., Pahl, M., Si, A., Zhu, H., Tautz, J., and Zhang, S. (2009). Number-Based Visual Generalisation in the Honeybee. PLoS ONE 4, e4263. doi: 10.1371/journal.pone.0004263
Hauser, M. D., and Carey, S. (2003). Spontaneous representation of small numbers of objects by rhesus macaques: examinations of content and format. Cogn. Psychol. 47, 367–401.
Hauser, M. D., Carey, S., and Hauser, L. B. (2000). Spontaneous number representation in semi-free ranging rhesus monkeys. Proc. R. Soc. Lond., B, Biol. Sci. 267, 829–833.
McCrink, K., and Wynn, K. (2004). Large-number addition and subtraction by 9-month-old Infants. Psychol. Sci. 15, 776–781.
Meck, W., and Church, R. (1983). A mode control model of counting and timing processes. J. Exp. Psychol. Anim. Behav. Process. 9, 320–334.
Olthof, A., Iden, C. M., and Roberts, W. A. (1997). Judgments of ordinality and summation of number symbols by squirrel monkeys (Saimiri sciureus). J. Exp. Psychol. Anim. Behav. Process. 23, 325–333.
Piazza, E., Izard, V., Pinel, P., and Dehaene, S. (2004). Tuning curves for approximate numerosity in the human parietal cortex. Neuron 44, 547–555.
Pica, P., Lemer, C., Izard, V., and Dehaene, S. (2004). Exact and approximate arithmetic in an Amazonian indigene group. Science 306, 499–503.
Regolin, L., Rugani, R., Pagni, P., and Vallortigara, G. (2005). Delayed search for a social and a non-social goal object by the young domestic chick (Gallus gallus). Anim. Behav. 70, 855–864.
Rugani, R., Fontanari, L., Simoni, E., Regolin, L., and Vallortigara, G. (2009). Arithmetic in newborn chicks. Proc. R. Soc. Lond., B, Biol. Sci. 276, 2451–2460.
Rugani, R., Regolin, L., and Vallortigara, G. (2007). Rudimental competence in 5-day-old domestic chicks: identification of ordinal position. J. Exp. Psychol. Anim. Behav. Process. 33, 21–31.
Rugani, R., Regolin, L., and Vallortigara, G. (2008). Discrimination of small numerosities in young chicks. J. Exp. Psychol. Anim. Behav. Process. 34, 388–399.
Rugani, R., Regolin, L., and Vallortigara, G. (2010a). Imprinted numbers: newborn chicks’ sensitivity to number vs. continuous extent of objects they have been reared with. Dev. Sci. 13, 790–797.
Rugani, R., Kelly, M. D., Szelest, I., Regolin, L., and Vallortigara, G. (2010b). Is it only humans that count from left to right? Biol. Lett. 6, 290–292.
Rugani, R., Vallortigara, G., Vallini, B., and Regolin, L. (2011). Asymmetrical number-space mupping in the avian brain. Neurobiol. Learn. Mem. 95, 231–238.
Rumbaugh, D. M., Savage-Rumbaugh, E. S., and Hegel, M. T. (1987). Summation in the chimpanzee (Pan troglodytes). J. Exp. Psychol. Anim. Behav. Process. 13, 107–115.
Rumbaugh, D. M., Savage-Rumbaugh, E. S., and Pate, J. L. (1988). Addendum to “summation in the chimpanzee (Pan troglodytes),” J. Exp. Psychol. Anim. Behav. Process. 14, 118–120.
Santos, L. R., Barnes, J., and Mahajan, N. (2005). Expectations about numerical events in four lemur species (Eulemur fulvus, Eulemur mongoz, Lemur catta and Varecia rubra). Anim. Cogn. 8, 253–262.
Shaun, D. B. M., Jordan, F., Vallortigara, G., and Clayton, N. (2010). Origins of spatial, temporal and numerical cognition: insights from animal models. Trends Cogn. Sci. 14, 477–481.
Simon, T. J., Hespos, S. J., and Rochat, P. (1995). Do infants understand simple arithmetic? A replication of Wynn (1992). Cogn. Dev. 10, 253–269.
Spelke, E. S., and Dehaene, S. (1999). Biological foundations of numerical thinking. Trends Cogn. Sci. 3, 365–366.
Suzuki, K., and Kobayashi, T. (2000). Numerical Competence in Rats (Rattus norvegicus): Davis and Bradford (1986) extended. J. Comp. Psychol. 114, 73–85.
Trick, L. M., and Pylyshyn, Z. W. (1993). What enumeration studies can show us about spatial attention: evidence for limited capacity preattentive processes. J. Exp. Psychol. Hum. Percept. Perform. 19, 331–351.
Uller, C., Hauser, M. D., and Carey, S. (2001). Spontaneous representation of number in cotton-top tamarins (Saguinus oedipus). J. Comp. Psychol. 115, 248–257.
Uller, C., Jaeger, R., and Guidry, G. (2003). Salamanders (Plethodon cinereus) go for more: rudiments of number in an amphibian. Anim. Cogn. 6, 105–112.
Uller, C., and Lewis, J. (2009). Horses (Equus caballus) select the greater of two quantities in small numerical contrasts. Anim. Cogn. 12, 733–738.
Vallortigara, G., Regolin, L., Chiandetti, C., and Rugani, R. (2010). Rudiments of mind: number and space cognition in animals. Comp. Cogn. Behav. Rev. 5, 78–99.
West, R. E., and Young, R. J. (2002). Do domestic dogs show any evidence of being able to count? Anim. Cogn. 5, 183–186.
Xu, F., and Spelke, E. S. (2000). Large number discrimination in 6-month-old infants. Cognition 74, B1–B11.
Keywords: number cognition, counting, number sense, arithmetic, domestic chick, human infant, large numeracy, continuous variables
Citation: Rugani R, Regolin L and Vallortigara G (2011) Summation of large numerousness by newborn chicks. Front. Psychology 2:179. doi: 10.3389/fpsyg.2011.00179
Received: 01 March 2011; Accepted: 18 July 2011;
Published online: 07 September 2011.
Edited by:
Elizabeth M. Brannon, Duke University, USAReviewed by:
Kristy VanMarle, University of Missouri, USAClaudia Uller, University of Cambridge, UK
Copyright: © 2011 Rugani, Regolin and Vallortigara. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: Rosa Rugani, Department of General Psychology, University of Padova, Via Venezia 8, Padova, Italy. e-mail:cm9zYS5ydWdhbmlAdW5pcGQuaXQ=

