- Department of Psychology, Vanderbilt University, Nashville, TN, USA
Perhaps walking and chewing gum is effortless, but walking and tracking moving objects is not. Multiple object tracking is impaired by walking from one location to another, suggesting that updating location of the self puts demands on object tracking processes. Here, we quantified the cost of self-motion in terms of the tracking load. Participants in a virtual environment tracked a variable number of targets (1–5) among distractors while either staying in one place or moving along a path that was similar to the objects’ motion. At the end of each trial, participants decided whether a probed dot was a target or distractor. As in our previous work, self-motion significantly impaired performance in tracking multiple targets. Quantifying tracking capacity for each individual under move versus stay conditions further revealed that self-motion during tracking produced a cost to capacity of about 0.8 (±0.2) objects. Tracking your own motion is worth about one object, suggesting that updating the location of the self is similar, but perhaps slightly easier, than updating locations of objects.
Introduction
We often find ourselves in environments where we need to keep track of objects moving around us while we ourselves are also in motion, such as when we drive in traffic, play team sports, or walk down a crowded sidewalk. These common situations can be challenging – tracking moving objects and navigating through space are both demanding tasks. We use attention and memory to keep tabs on the changing locations of objects of interest as they move, a process known as object tracking (Cavanagh and Alvarez, 2005; Allen et al., 2006; Fougnie and Marois, 2006; Tombu and Seiffert, 2008). Object tracking has a limited capacity that can be measured as the number of targets that can be tracked in a given set of conditions (Pylyshyn and Storm, 1988; Scholl et al., 2001; Alvarez and Franconeri, 2007; but see Ma and Huang, 2009). As we move, we update a representation of our own changing location in space, a process known as spatial updating. Although spatial updating tends to occur obligatorily (Rieser, 1989; Farrell and Robertson, 1998; Farrell and Thomson, 1998; May and Klatzky, 2000), it requires cognitive resources (Amorim et al., 1997) and also appears to be limited in capacity (Wang et al., 2006; Wang, 2007). Research describing the limitations of these processes provides a better understanding of how people function in complex environments.
Much previous research has investigated the properties of object tracking and spatial updating abilities, but there are few details about how these processes interact. Recently, we have found that these two processes tap common spatial resources (Thomas and Seiffert, 2010). Our experiments demonstrated that when observers moved around an area in which they were tracking three targets moving amidst identical distractors, their object tracking performance suffered compared to when they remained in one location. Self-motion impaired object tracking both when observers walked around the tracking area and when they were pushed along the same path in a wheelchair. This impairment occurred both in an immersive virtual environment and a real-world analog and was robust even when observers did not receive visual feedback about their own movements. However, we also found that self-motion did not interfere when observers moved while performing a difficult feature-tracking task that did not involve changes to target locations. Taken together, these experiments strongly suggest that self-motion impairs object tracking performance because both rely on a process of updating spatial representations over time.
Our previous findings suggest spatial updating and object location tracking processes interfere with one another, indicating that they rely on common spatial resources. If object tracking and spatial updating require common resources, then perhaps we can understand one process in terms of the other – how these resources are shared and allocated across the two tasks. As our first step in achieving this goal, we asked how spatial updating could be assessed in terms of object tracking capacity. Quantifying attributes of cognitive function provides insights into the underlying structure of information processing and the relationship between different functions. For example, working memory was originally quantified as containing about seven objects (Miller, 1956), but this value was later revised to about four objects when the strategies and components of memory were better understood (see Baddeley, 1992; Cowan, 2001). Quantifying the capacity of working memory has benefited understanding of its nature in terms of representational structure of features, neural substrates, and development (Vogel et al., 2001; Ross-Sheehy et al., 2003; Alvarez and Cavanagh, 2004; Todd and Marois, 2004; Xu and Chun, 2006; Jiang et al., 2008; Oakes et al., 2010). For the current study, the goal was to understand the relationship between self-motion and object tracking. Quantification of the effect of self-motion in terms of object tracking will allow us to determine whether it makes sense to interpret the interference between the two tasks in terms of a single process, such as a mechanism for tracking changes in spatial location. When an observer needs to move through her environment while simultaneously keeping track of the things moving around her, does a location tracking mechanism treat the self as just another moving item to track? Alternatively, is spatial updating of self-position calculated in a more efficient – or even more costly – manner?
In the current experiment, we set out to quantify the load of self-motion on tracking capacity. To measure the cost of self-motion on object tracking, we asked participants to keep track of a subset of identical moving balls while walking in an immersive virtual environment. Participants either walked around the area in which the balls moved or walked in place maintaining a constant location as in previous work (Thomas and Seiffert, 2010). In the current study, we systematically varied the number of targets participants tracked in order to derive estimates of participants’ tracking capacity – that is, how many moving objects they could successfully individuate and maintain over time. By measuring tracking capacity both while participants walked around and walked in place, we quantified the cost of self-motion in terms of the number of objects tracked.
Materials and Methods
Participants
Fourteen volunteers from Vanderbilt University participated for course credit. The research was approved by the Vanderbilt University Institutional Review Board and conformed to the ethical standards for conducting research established by the American Psychological Association. Informed consent was obtained from all participants.
Apparatus
Participants viewed the virtual environment on an nVisor SX head mounted display (HMD; NVIS, Reston, VA, USA), which presented stereoscopic images in a 60° diagonal field of view at a refresh rate of 60 Hz using Vizard software (WorldViz, Santa Barbara, CA, USA) rendered graphics. A three-axis orientation sensor (InertiaCube2; Intersense, Bedford, MA, USA) tracked head orientation and an optical tracking system (PPTX4; WorldViz, Santa Barbara, CA, USA) tracked head position. The graphics displayed in the HMD were updated based on head position and orientation, leading participants’ physical movements to translate into visual movements within the virtual world.
Stimuli, Procedure, and Design
Participants saw a virtual world inside the HMD consisting of blue sky and a green ground plane. They stood approximately 4 ft from the center of a rendered 2.7 × 2.7 ft black outlined box on the ground plane. Inside this box were 10 red balls that subtended approximately 1.3° of visual angle when viewed in the center of the box. Participants performed a multiple object tracking task. At the start of each trial, each ball appeared stationary in a random starting location along its predefined path for 500 ms. One, two, three, four, or five of these balls were designated as targets, changing color from red to blue for 1700 ms before returning to red. All of the balls then moved in circular paths around the center of the box, with the radius of each path ranging randomly in 0.09 ft steps from approximately 0.2 to 1.3 ft, the speed of each dot ranging randomly in 1 deg steps from approximately 2 to 25 deg/s. At these radii and speeds, the slowest balls tended to move about a quarter of a full circle during a trial, while the fastest balls tended to move around their circular paths up to three times. Each ball had equal probability of moving clockwise or counterclockwise. Although the circles were often very close together, making it difficult to distinguish whether an individual ball was moving along a path with a radius greater or less than its neighbors, to prevent participants from encoding ball position based on radius without regard for the balls’ motion, the two innermost and two outermost balls were never designated as targets. After 4 s of movement, the balls stopped moving and one ball changed color from red to blue. Participants verbally responded “yes” if they thought that the probed blue ball was the same as one of the targets and “no” otherwise. For half of trials, the cued ball was a target; for the other half of trials it was a distractor.
While engaged in the tracking task, participants could move in two different ways. In the move condition, participants walked an arc 90° around the box, moving a quarter circle from the center of one side of the box to an adjacent side. While walking, participants remained oriented so that their bodies faced the direction in which they moved and their heads remained turned toward the box. Participants initiated this walk at the same time that the tracking balls began to move and completed the walk when the balls stopped. To ensure that participants walked appropriately, an experimenter guided them by holding one end of a 4-ft stick while the participant held the other end. In the stay condition, on the other hand, participants simply walked in place, replacing their feet in the same location that they picked them up. While walking in place, participants were oriented identically to the move condition but maintaining a constant position. At the end of each trial in which participants changed location, they turned 180° so that they could move in the opposite direction along the same arc on the next move trial.
At the beginning of a session, participants spent a few minutes observing the testing area without the HMD as they provided consent and listened to instructions. Participants then had the opportunity to look around the virtual environment with the HMD before performing eight practice trials in which they tracked one or two targets. They then performed four blocks of 60 trials each in which number of targets (1–5), movement condition (move or stay), and probe identity (target or distractor) were randomly intermixed. Before each trial began, an experimenter announced whether the trial was in the move or stay condition.
Results
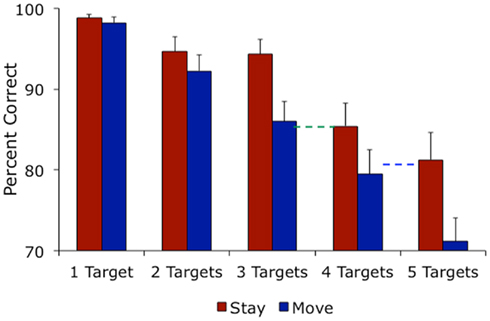
Participants made more tracking errors as tracking load increased from one to five balls and made more errors in the move condition than in the stay condition (Figure 1). A 5 × 2 ANOVA confirmed these effects, showing significant main effects of number of targets [F(4, 52) = 39.37, MSE = 56.04, p < 0.001] and self-motion [F(1,13) = 46.14, MSE = 22.76, p < 0.001]. The interaction between number of targets and self-motion approached significance [F(4,52) = 2.43, MSE = 45.43, p < 0.06]. Planned pairwise comparisons showed that this marginal interaction was driven by a lack of difference between tracking performance in the move versus stay conditions under low tracking load [t(13) = 0.99, p > 0.3 for the one-target case and t(13) = 1.39, p > 0.1 for the two-target case] but significantly better tracking in the stay condition under higher tracking load [t(13) = 3.43, p < 0.01 for tracking three targets, t(13) = 2.35, p < 0.04 for tracking four targets, and t(13) = 2.75, p < 0.02 for tracking five targets]. This pattern of results replicates and extends our previous findings, showing that self-motion impairs object tracking when tracking load is sufficiently high (Thomas and Seiffert, 2010).
To determine whether results indicate differences in sensitivity or report bias, we conducted the same analyses as reported above on d′ and beta ratio values (Macmillan and Creelman, 2005). A 5 × 2 ANOVA on d′ values showed significant effects of number of targets [F(4,52) = 43.98, partial η2 = 0.772, p < 0.001] and self-motion [F(1,13) = 43.71, partial η2 = 0.771, p < 0.001]. The interaction between number of targets and self-motion approached significance [F(4,52) = 2.43, partial η2 = 0.158, p < 0.06]. Planned pairwise comparisons on d′ values showed that this marginal interaction was driven by a lack of difference between tracking performance in the move versus stay conditions under low tracking load [t(13) = 1.05, p > 0.30 for the one-target case and t(13) = 1.41, p > 0.10 for the two-target case] but significantly better tracking in the stay condition under higher tracking load [t(13) = 3.39, p < 0.005 for tracking three targets, and t(13) = 2.92, p < 0.02 for tracking five targets; for four targets results were marginal, t(13) = 2.12, p < 0.06]. A 5 × 2 ANOVA on beta ratio values showed a marginal main effect of number of targets [F(4,52) = 2.24, partial η2 = 0.147, p < 0.08] and no effect of self-motion [F(1,13) = 2.14, partial η2 = 0.141, p > 0.10] and no interaction [F(4,52) < 1]. Taken together, this pattern of results replicates results reported as percent correct and shows that self-motion impairs tracking sensitivity and not bias (Thomas and Seiffert, 2010).
At first glance, the averaged data are suggestive about the quantitative cost of self-motion in terms of number of objects tracked. When participants tracked three balls while moving, their performance was similar to when they tracked four balls while stationary [green dashed line in Figure 1; t(13) = 0.32, p > 0.75]. Similarly, performance tracking four balls while moving was equivalent to tracking five balls while stationary [blue dashed line in Figure 1; t(13) = 0.54, p > 0.59]. In other words, the cost of adding one more target appears similar to the cost of self-motion; the decrement in performance from adding one more target in the stay condition was similar to the decrement in performance associated with moving. Overall participants’ average percent correct suggests that the cost of self-motion is about one object.
To quantify the cost of self-motion on tracking in terms of the number of objects, we estimated tracking capacity for each individual participant in both stay and move conditions. We evaluated performance in terms of the effective number of targets tracked by calculating Cowan–Pashler’s K (Pashler, 1988; Cowan, 2001) with:
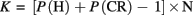
where K = estimated number of balls tracked, H = proportion of accurate “yes” responses (hits), CR = proportion of accurate “no” responses (correct rejections), and N = number of target balls. K values are a performance measure similar to percent correct, but given in terms of the number of objects that are effectively tracked (as in Scholl et al., 2001). For example, when there were three targets, if a participant had a hit rate of 0.8333 and a correct rejection rate of 0.8333, then the K value of 1.999 would indicate that participant was able to effectively track about two of the three targets on average. For each participant, we calculated K for each level of the factor that varied the number of targets, separately for the move and stay conditions. This allowed us to compare the asymptotes of the K curves as an estimate of the overall capacity costs of self-motion during tracking. Tracking capacity (C) for each individual was estimated by fitting the K values with an elbow curve that assumed perfect tracking performance for conditions with fewer targets than C and performance capped at C for conditions with more targets than C. The value of C that provided the least squared error from the data was taken as the estimated tracking capacity. This estimation of tracking capacity does not correct for guessing, nor consider the benefit to performance from known distractors (Hulleman, 2005). However, we assume that any such correction would be the same for move and stay conditions because we manipulated self-motion independently of the tracking task. While the absolute values of capacity may be overestimated here, we assume the relationship between the capacity for move and stay conditions would not be affected by such analyses. As such, we use this analysis to quantify the cost of self-motion in terms of the effective number of targets tracked.
Capacity estimates under both the move and stay conditions for each participant agreed with the estimates from the overall average. All but one participant had a smaller capacity in the move condition than the stay condition (Figure 2, points relative to blue line), showing the reliability of the effect of self-motion on tracking performance across participants. Interestingly, 9 out of the 13 participants showing a cost had a difference between capacities for stay versus move conditions that was less than one (Figure 2, points relative to the red line). Calculating difference scores – subtracting the tracking capacity for the move condition from the tracking capacity for the stay condition – revealed a self-motion cost that, averaged across participants, was 0.8 objects (SE = 0.2). This estimate for the cost of self-motion was reliably greater than zero [t(13) = 4.6, p < 0.0005], but not reliably different from one [t(13) < 1, ns]. Taken together, these analyses suggest that most individual participants experienced a cost of self-motion of about one object.
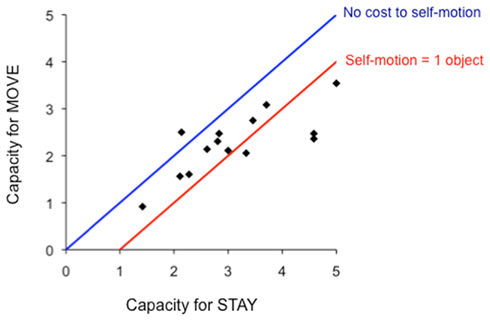
Figure 2. Estimates of tracking capacity (C) for each participant in the move and stay conditions. The blue line shows the perfect one-to-one relationship that would occur if tracking capacity was unaffected by self-motion. The red line shows a perfect cost of one object due to self-motion.
Discussion
We often find ourselves in situations where we must move through the environment while simultaneously keeping track of other objects moving around us. The results of the current study show that self-motion hampers tracking performance at a cost that is about the same as adding one more target object. Replicating and extending our previous work (Thomas and Seiffert, 2010), we found that when participants were only required to track one or two objects, self-motion did not substantially interfere with this task. However, when participants attempted to keep track of three, four, or five objects, there was a significant cost of self-motion on tracking performance. More specifically, we found that participants’ capacity data in move versus stay conditions were best described by fitting curves that differed in their asymptotes by 0.8. These results are in line with the idea that the spatial updating associated with self-motion draws upon resources that are also tapped in keeping track of multiple moving objects. We cannot help but update a representation of our own changing location in space as we move (e.g., Farrell and Robertson, 1998; May and Klatzky, 2000), but we do so at the expense of updating other objects’ changing locations as they move. Moreover, results from the majority of participants showed that keeping track of one’s own location in space may be slightly less costly than tracking another object. In other words, when an observer moves while trying to keep track of other moving objects, self-motion imposes an additional load on the tracking mechanism of a bit less than one additional external object.
The results of the current study provide the first estimate of the actual cost of self-motion on object tracking. Quantification of the effect of self-motion in terms of object tracking allows us to interpret the interference between the two tasks in terms of a single process. The observation that self-motion produces a cost to tracking performance that is very similar to adding one more target object seems to suggest that people mentally update a representation of their own location in space with the same process they use to update representations of moving objects. A mechanism that tracks the location of the self and objects could use a single spatial representation, such as an allocentric map of the room, or affect multiple representations in a similar way, such as updating egocentric coordinates of objects and a representation of the self in the room. In our experiment, we attempted to match the speed and trajectories of both observers and the targets; participants walked along a curved path that was similar to the circular paths of the moving balls. Our results therefore speak to situations in which an observer’s location changes in a very similar manner to tracking target locations. It is possible that in situations where an observer moves more quickly or along a more complicated trajectory, self-motion may reduce object tracking capacity to an even greater extent. In addition, our evidence does not allow for strong conclusions about the nature of the limitation in cognitive processing driving these effects. The concept of capacity as depicted here could be taken to suggest that the mind has slots for attending to and remembering a set number of objects (Miller, 1956; Cowan, 2001; Awh et al., 2007; Zhang and Luck, 2008). However, results are equally compatible with a more complex model of cognitive processing in which limits of performance are due to other factors, such as sampling rate, interference, or optimization of representation integrity (d’Avossa et al., 2006; Kazanovich and Borisyuk, 2006; Ma and Huang, 2009; Vul et al., 2009). Whatever the model, the results demonstrate that the cost of self-motion is approximately the same as the cost of tracking another object, suggesting that similar processing may occur for updating the memory of the location of the self and the location of objects.
In conclusion, we find that adding self-motion to a multiple object tracking task costs a little less than adding one additional target, at least in cases where self-motion mirrors target motion such as driving in traffic, playing team sports, or walking down a crowded sidewalk. Both spatial updating and object tracking call upon a common mechanism that keeps track of the changing locations of items – one’s own position as well as those of objects in the environment. This mechanism may process information about self-location somewhat more efficiently than information about other objects. Such efficiency may not be surprising. After all, we have more experience keeping track of where we are than we do for any external objects and before we can act effectively on our environment, we must first have a representation of where we are within it.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Support for this work was provided by NSF MRI Grant 0821640 and NEI Core Grant P20-EY008126. We would like to thank Nicole Jardine for her assistance with testing participants in the experiment.
References
Allen, R., McGeorge, P., Pearson, D., and Milne, A. (2006). Multiple-object tracking: a role for working memory? Q. J. Exp. Psychol. 59, 1101–1116.
Alvarez, G. A., and Cavanagh, P. (2004). The capacity of visual short-term memory is set both by visual information load and by number of objects. Psychol. Sci. 15, 106–111.
Alvarez, G. A., and Franconeri, S. L. (2007). How many objects can you track? Evidence for a resource-limited attentive tracking mechanism. J. Vis. 7, 1–10.
Amorim, M. A., Glasauer, S., Corpinot, K., and andBerthoz, A. (1997). Updating an object’s orientation and location during nonvisual navigation: a comparison between two processing modes. Percept. Psychophys. 59, 404–418.
Awh, E., Barton, B., and Vogel, E. K. (2007). Visual working memory represents a fixed number of items regardless of complexity. Psychol. Sci. 18, 622–628.
Cavanagh, P., and Alvarez, G. (2005). Tracking multiple objects with multifocal attention. Trends Cogn. Sci. (Regul. Ed.) 9, 349–354.
Cowan, N. (2001). The magical number 4 in short-term memory: a reconsideration of mental storage capacity. Behav. Brain Sci. 24, 87–114.
d’Avossa, G., Shulman, G. L., Snyder, A. Z., and Corbetta, M. (2006). Attentional selection of moving objects by a serial process. Vision Res. 46, 3403–3412.
Farrell, M. J., and Robertson, I. H. (1998). Mental rotation and the automatic updating of body-centered spatial relationships. J. Exp. Psychol. Learn. Mem. Cogn. 24, 227–233.
Farrell, M. J., and Thomson, J. A. (1998). Automatic spatial updating during locomotion without vision. Q. J. Exp. Psychol. 51A, 637–654.
Fougnie, D., and Marois, R. (2006). Distinct capacity limits for attention and working memory. Psychol. Sci. 17, 526–534.
Hulleman, J. (2005). The mathematics of multiple object tracking: from proportions correct to number of objects tracked. Vision Res. 45, 2298–2309.
Jiang, Y. V., Shim, W. M., and Makovski, T. (2008). Visual working memory for line orientations and face identities. Atten. Percept. Psychophys. 70, 1581–1591.
Kazanovich, Y., and Borisyuk, R. (2006). An oscillatory neural model of multiple object tracking. Neural Comput. 18, 1413–1440.
Ma, W. J., and Huang, W. (2009). No capacity limit in attentional tracking: evidence for probabilistic inference under a resource constraint. J. Vis. 9, 1–30.
Macmillan, N. A., and Creelman, C. D. (2005). Detection Theory: A User’s Guide, 2nd Edn. Mahwah, NJ: Lawrence Erlbaum Associates.
May, M., and Klatzky, R. L. (2000). Path integration while ignoring irrelevant movement. J. Exp. Psychol. Learn. Mem. Cogn. 26, 169–186.
Miller, G. A. (1956). The magical number seven plus or minus two: some limits on our capacity for processing information. Psychol. Rev. 63, 81–97.
Oakes, L. M., Hurley, K. B., Ross-Sheehy, S., and Luck, S. J. (2010). Developmental changes in infants’ visual short-term memory for location. Cognition 118, 293–305.
Pylyshyn, Z., and Storm, R. (1988). Tracking multiple independent targets: evidence for a parallel tracking mechanism. Spat. Vis. 3, 179–198.
Rieser, J. J. (1989). Access to knowledge of spatial structure at novel points of observation. J. Exp. Psychol. Learn. Mem. Cogn. 15, 1157–1165.
Ross-Sheehy, S., Oakes, L. M., and Luck, S. J. (2003). The development of visual short-term memory capacity in infants. Child Dev. 74, 1807–1822.
Scholl, B. J., Pylyshyn, Z. W., and Feldman, J. (2001). What is a visual object? Evidence from target merging in multiple object tracking. Cognition 80, 159–177.
Thomas, L. E., and Seiffert, A. E. (2010). Self-motion impairs multiple-object tracking. Cognition 117, 80–86.
Todd, J. J., and Marois, R. (2004). Capacity limit of visual short-term memory in human posterior parietal cortex. Nature 428, 751–754.
Tombu, M., and Seiffert, A. E. (2008). Attentional costs in multiple-object tracking. Cognition 108, 1–25.
Vogel, E. K., Woodman, G. F., and Luck, S. J. (2001). Storage of features, conjunctions, and objects in visual working memory. J. Exp. Psychol. Hum. Percept. Perform. 27, 92–114.
Vul, E., Frank, M. C., Tenenbaum, J. B., and Alvarez, G. (2009). “Explaining human multiple object tracking as resource-constrained approximate interference in a dynamic probabilistic model,” in Advances in Neural Information Processing Systems, eds Y. Bengio, D. Schuurmans, J. Lafferty, C. K. I. Williams, and A. Culotta (Cambridge, MA: MIT Press), 22.
Wang, R. F. (2007). “Spatial processing and view-dependent representations,” in Spatial Processing in Navigation, Imagery, and Perception, eds F. Mast, and L. Jancke (New York, NY: Springer Science+ Business Media Inc.), 49–65.
Wang, R. F., Crowell, J. A., Simons, D. J., Irwin, D. E., Kramer, A. F., Ambinder, M. S., Thomas, L. E., Gosney, J. L., Levinthal, B. R., and Hsieh, B. B. (2006). Spatial updating relies on an egocentric representation of space: effects of the number of objects. Psychon. Bull. Rev. 13, 281–286.
Xu, Y., and Chun, M. M. (2006). Dissociable neural mechanisms supporting visual short-term memory for objects. Nature 440, 91–95.
Keywords: multiple object tracking, spatial updating, self-motion
Citation: Thomas LE and Seiffert AE (2011) How many objects are you worth? Quantification of the self-motion load on multiple object tracking. Front. Psychology 2:245. doi: 10.3389/fpsyg.2011.00245
Received: 10 June 2011; Accepted: 06 September 2011;
Published online: 28 September 2011.
Edited by:
Anna M. Borghi, University of Bologna, ItalyReviewed by:
Costantini Marcello, University of Chieti, ItalyJessica K. Witt, Purdue University, USA
Copyright: © 2011 Thomas and Seiffert. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: Laura E. Thomas, Department of Psychology, NDSU Dept. 2765, Fargo, ND 58108, USA. e-mail:bGF1cmEuZS50aG9tYXNAbmRzdS5lZHU=