Introduction
Like number words and written numerals, fingers can be used to represent numbers. In fact, due to their ubiquitous availability, agility, and discrete quantity, they are considered the most natural tool for counting, which renders them attractive for theories of embodied (numerical) cognition (Andres et al., 2008; Di Luca and Pesenti, 2011). As they are so closely linked to the human body, finger counting sequences may appear to be universal, but both their composition (Bender and Beller, in preparation) and their existence (Butterworth et al., 2011; Crollen et al., 2011) depend on culture. In this paper we will argue that it is crucial for any (embodied) theory of numerical cognition to take this cultural variability into account. To substantiate this claim, we depict some of the cultural variability in finger counting, followed by a brief representational analysis, from which directions for future research will be derived.
Cultural Variability in Finger Counting
Even regarding the simple use of fingers for counting from 1 to 10, a great deal of variability can be observed in how precisely this is done: (a) The palm can be turned toward oneself or toward others, (b) fingers can be extended or bent, (c) counting may begin with the left or right hand, and with thumb, index, or little finger, and (d) the switch between hands may be based on anatomical symmetry or spatial continuation (Menninger, 1969; Lindemann et al., 2011).
Beyond these variations in procedural detail, however, more fundamental differences arise in terms of which parts of a hand people count with and to what other body parts they extend counting (for a non-exhaustive sample see Figure 1). In “Western” systems like A, fingers are extended serially. German Sign Language DGS B uses the dominant hand for counting 1 through 5, while the other hand indicates sub-base 5 (Iversen et al., 2006). Indian merchants from Maharashtra C are reported to employ a proper base 5, the multiples of which are counted on the second hand (Ifrah, 1985). East African Bantu languages D switch between hands to obtain two approximately equal addends (Schmidl, 1915). And body counting systems of Highland New Guinea such as the Oksapmin counting system E make use of additional parts like the wrist, elbow, shoulder, and head (Saxe, 1981). Instead of entire fingers, some systems employ finger segments, the edges between segments as in F, or the space between fingers. Finally, the Roman system G illustrates a completely different type, as it represents numbers not by accumulating tokens, but by their distinct combinations. For instance, nine different gestures consisting of the little, ring, and middle finger of the left hand denote the units 1 through 9, whereas other finger sets denote the tens, hundreds, and thousands (Williams and Williams, 1995).
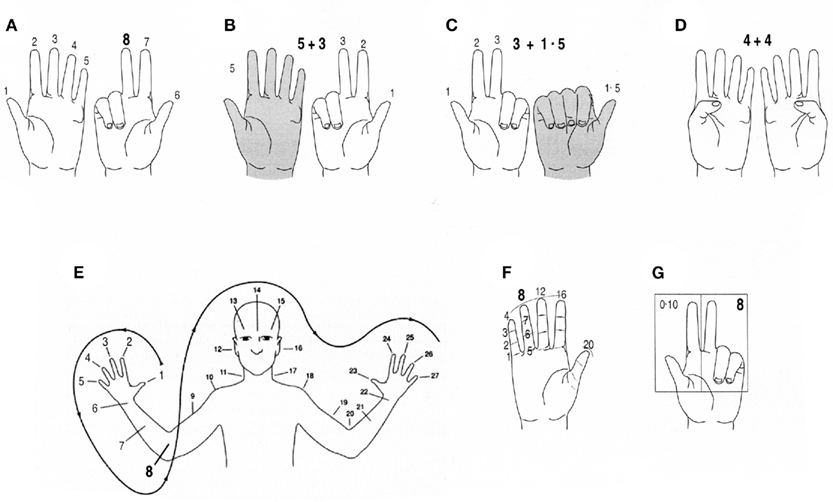
Figure 1. Variability in finger counting systems, illustrated for number eight signs [(E) downloaded from Marmasse et al, 2000].
Properties of Finger Counting Systems
Like verbal counting sequences (Bender and Beller, 2011) and numeral notations (Zhang and Norman, 1995; Chrisomalis, 2004; Widom and Schlimm, in press), each finger counting sequence constitutes a numeration system with specific properties:
(1) Dimensionality: One-dimensional (1D) systems link number symbols to numbers by one-to-one correspondence; 1 × 1D systems compose number symbols from a base and power dimension; and (1 × 1) × 1D systems additionally use a sub-base. This taxonomy, designed to categorize notational systems, can also be applied to finger counting systems: A, D, E, and F all constitute 1D systems, C and G constitute 1 × 1D systems, and B constitutes a (1 × 1) × 1D system.
(2) Dimensional representation: Basic numbers are represented either by quantity (cumulative) or shape (ciphered). In Figure 1, all but the last system are cumulative, as the number is represented by the corresponding amount of tokens. Power terms are represented in an integrated, parsed, or positional manner. Representation is integrated when the same symbol(s) denotes multiplier and power simultaneously (as in Greek κ = 20), and parsed when multiplier and power are denoted by different symbols (as in “two hundred”). Positional representation is realized, for instance, in Arabic digits. Accordingly, B is parsed, and C and G are (partly) positional.
(3) Base size: In verbal numeration systems, the most frequently used base is 10, followed by 20 and 5 (Comrie, 2005). This prevalence has been repeatedly linked to the anatomy of the human body. Yet, even if the hand is the most important model for structuring numeral systems, this need not give rise to uniformly structured numeral systems. Our survey (Bender and Beller, in preparation) also attests to (sub-)bases 4, 6, 8, and 12 in extant systems – and to various different reasons for these bases (e.g., counting the space between fingers yields base 4, while adding the wrist to the full hand yields base 6).
(4) Extent: The extent of a numeration system is defined by its limiting number L (Greenberg, 1978), which is the largest number expression regularly composed or the farthest point reached in indexing. Due to the limited number of fingers, finger counting has often been assumed to be restricted to L = 10, and this has also been regarded as one of its most severe disadvantages. However, as demonstrated in Figure 1, extending counting beyond 10 is possible, either by enlarging the number of tokens or by transforming a 1D system into 1 × 1D. The limiting numbers thus reached are 27 (in E), 30 C, 40 F, and 10,000 G.
It is evident that finger counting systems differ considerably with respect to their system properties. But how (if at all) do these differences affect the cognitive representation and processing of numbers?
Cognitive Implications
Embarrassingly little is known about the cognitive ramifications of cultural differences in finger counting. Most studies on finger counting conducted so far have restricted themselves to the type of 10 finger systems depicted in Figure 1A and its manifold variants. The most notable exception is recent work that scrutinizes possible effects of sub-base 5 inherent in DGS, as well as other 10 finger systems (Iversen et al., 2006; Domahs et al., 2010, 2011; Klein et al., 2011). The findings reveal that the specific structure of these systems has distinct consequences for cognitive processing in number comparison and parity judgment tasks, and affects both the SNARC and the MARC effects. More generally, finger counting habits modulate the markedness of numerical representations like the mental number line (overview in Andres et al., 2008; Fischer and Brugger, 2011).
However, possible effects of variations in dimensional representation, base size, or extent remain unresolved. For instance, previous research emphasized the importance of acquired number systems for exact numerosity (Wiese, 2003; Feigenson et al., 2004) and indicated that the range of accurate counting is determined by the availability of number words (Beller and Bender, 2008; Frank et al., 2008). This primacy of verbal representations is questioned by cases in which lacking number words are compensated by body tallying systems (cf. Bender and Beller, in preparation). Moreover, while availability of body parts clearly constrains finger counting systems, their plain amount is not the limiting factor. Rather, the range of counting critically depends on dimensional representation and base size.
Another factor known to affect performance in numerical tasks is dimensional representation (Zhang and Norman, 1995; Zhang and Wang, 2005): Findings from number comparison tasks indicate that numbers are represented in a distributed manner, which incorporates the external representation. The specific properties of this external representation determine how salient the different types of numerical information are. The full range of numerical information (nominal, ordinal, interval, and ratio information) is made immediately available in cumulative representations, whereas ciphered systems provide nominal information only and thus increase the cognitive load as they require retrieval of the missing information from memory. A comparison of respective finger counting systems might shed light on how deeply these differences affect cognitive processing.
The final issue considered here relates to consistency with other representational systems. Most people use more than one numeration system – typically a verbal system, a notational system, and a more or less conventionalized finger counting sequence. In English, for instance, none of these is structurally identical to any other: The verbal system is ciphered/parsed (and fraught with irregularities), the Arabic digits are ciphered/positional, and typical finger counting is 1D cumulative. Structural mismatches like these are assumed to impede learning in novices and impair processing even in advanced users (cf. Beller and Bender, 2011), but the range of implications arising from these differences is not yet fully explored.
Conclusion
Embodied theories of numerical cognition are grounded in the hybrid position of fingers as naturally available tools and as crucial components in cognitive development. However, the numerical meaning attached to fingers is also culturally encoded, and in strikingly diverse ways. Taking this diversity into account more thoroughly is a prerequisite for promoting research in this field.
References
Andres, M., Olivier, E., and Badets, A. (2008). Actions, words, and numbers: a motor contribution to semantic processing? Curr. Dir. Psychol. Sci. 17, 313–317.
Beller, S., and Bender, A. (2008). The limits of counting: numerical cognition between evolution and culture. Science 319, 213–215.
Beller, S., and Bender, A. (2011). Explicating numerical information: when and how fingers support (or hinder) number comprehension and handling. Front. Psychol. 2:214. doi: 10.3389/fpsyg.2011.00214
Bender, A., and Beller, S. (2011). “Numerical cognition and ethnomathematics,” in A Companion to Cognitive Anthropology, eds D. Kronenfeld, G. Bennardo, V. C. de Munck and M. D. Fischer (Cambridge: Wiley-Blackwell), 270–289.
Butterworth, B., Reeve, R., and Reynolds, F. (2011). Using mental representations of space when words are unavailable: studies of enumeration and arithmetic in indigenous Australia. J. Cross Cult. Psychol. 42, 630–638.
Comrie, B. (2005). “Numeral bases,” in The World Atlas of Language Structures, eds M. Haspelmath, M. S. Dryer, D. Gil, and B. Comrie (Oxford: Oxford University Press), 530–533.
Crollen, V., Seron, X., and Noël, M.-P. (2011). Is finger-counting necessary for the development of arithmetic abilities? Front. Psychol. 2:242. doi: 10.3389/fpsyg.2011.00242
Di Luca, S., and Pesenti, M. (2011). Finger numeral representations: more than just another symbolic code. Front. Psychol. 2:272. doi: 10.3389/fpsyg.2011.00272
Domahs, F., Klein, E., Moeller, K., Nuerk, H.-C., Yoon, B.-C., and Willmes, K. (2011). Multimodal semantic quantity representations: further evidence from Korean sign language. Front. Psychol. 2.
Domahs, F., Moeller, K., Huber, S., Willmes, K., and Nuerk, H.-C. (2010). Embodied numerosity: implicit hand-based representations influence symbolic number processing across cultures. Cognition 116, 251–266.
Feigenson, L., Dehaene, S., and Spelke, E. (2004). Core systems of number. Trends Cogn. Sci. (Regul. Ed.) 8, 307–314.
Fischer, M. H., and Brugger, P. (2011). When digits help digits: spatial-numerical associations point to finger counting as prime example of embodied cognition. Front. Psychol. 2:260. doi: 10.3389/fpsyg.2011.00260
Frank, M. C., Everett, D. L., Fedorenko, E., and Gibson, E. (2008). Number as a cognitive technology: evidence from Pirahã language and cognition. Cognition 108, 819–824.
Greenberg, J. H. (1978). “Generalizations about numeral systems,” in Universals of Human Language, Vol. 3, ed. J. H. Greenberg (Stanford: Stanford University Press), 249–295.
Iversen, W., Nuerk, H.-C., Jäger, L., and Willmes, K. (2006). The influence of an external symbol system on number parity representation, or what’s odd about 6? Psychon. Bull. Rev. 13, 730–736.
Klein, E., Moeller, K., Willmes, K., Nuerk, H.-C., and Domahs, F. (2011). The influence of implicit hand-based representations on mental arithmetic. Front. Psychol. 2:197. doi: 10.3389/fpsyg.2011.00197
Lindemann, O., Alipour, A., and Fischer, M. H. (2011). Finger counting habits in middle-eastern and western individuals: an online survey. J. Cross Cult. Psychol. 42, 566–578.
Marmasse, N., Bletsas, A., and Marti, S. (2000). Numerical Mechanisms and Children’s Concept of Numbers. Available at: http://web.media.mit.edu/∼/(stefanm/society/som_final.html; download: 10.5.2011 14:03
Saxe, G. B. (1981). Body parts as numerals: a developmental analysis of numeration among the Oksapmin in Papua New Guinea. Child Dev. 52, 306–316.
Schmidl, M. (1915). Zahl und Zählen in Afrika [Number and counting in Africa]. Mitt. Anthropol. G. Wien 35, 165–209.
Widom, T. R., and Schlimm, D. (in press). Methodological reflections on typologies for numeral systems. Sci. Context.
Williams, B. P., and Williams, R. S. (1995). Finger numbers in the Greco-Roman world and the early middle ages. Isis 86, 587–608.
Zhang, J., and Norman, D. A. (1995). A representational analysis of numeration systems. Cognition 57, 271–295.
Citation: Bender A and Beller S (2011) Fingers as a tool for counting – naturally fixed or culturally flexible? Front. Psychology 2:256. doi: 10.3389/fpsyg.2011.00256
Received: 19 July 2011;
Accepted: 15 September 2011;
Published online: 12 October 2011.
Copyright: © 2011 Bender and Beller. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence:YmVuZGVyQHBzeWNob2xvZ2llLnVuaS1mcmVpYnVyZy5kZQ==

