- 1 Division of Cognitive Sciences, University of Potsdam, Potsdam, Germany
- 2 Neuropsychology Unit, University Hospital, Zurich, Switzerland
Spatial–numerical associations (SNAs) are prevalent yet their origin is poorly understood. We first consider the possible prime role of reading habits in shaping SNAs and list three observations that argue against a prominent influence of this role: (1) directional reading habits for numbers may conflict with those for non-numerical symbols, (2) short-term experimental manipulations can overrule the impact of decades of reading experience, (3) SNAs predate the acquisition of reading. As a promising alternative, we discuss behavioral, neuroscientific, and neuropsychological evidence in support of finger counting as the most likely initial determinant of SNAs. Implications of this “manumerical cognition” stance for the distinction between grounded, embodied, and situated cognition are discussed.

Space and Numbers are Abundantly Associated
We all use space when dealing with quantities, both in real-life situations and in our minds. Examples include the sorting of objects into physical piles when counting them, or organizing tallies into spatially separate groups. Documenting this pervasive use of mental space, well over 100 experiments have now studied our tendency to associate small numbers (1 or 2) with left hemispace and larger numbers (8 or 9) with right hemispace, usually in parity or magnitude classification tasks (Wood et al., 2008). But spatial–numerical associations (SNAs) influence our entire behavioral repertoire, from response selection to response force, from movement initiation speed to subsequent attention allocation (Hubbard et al., 2005; Fischer, 2011). Spatial activities including drawing and gesturing help both children and mathematicians to solve numerical problems (Nunez, 2006; Goldin-Meadow et al., 2009; Lubin et al., 2010). Finally, we also think of even numbers as more “right” than odd numbers (Nuerk et al., 2004) and of addition as rightward movement and subtraction as leftward movement (McCrink et al., 2007; Pinhas and Fischer, 2008; Knops et al., 2009). Here we refer to all such relationships collectively as SNAs.
Despite the remarkable prevalence of SNAs there is currently no consensus as to how they originate. This omission hampers our understanding of numerical cognition and is incompatible with the prevalent theoretical framing of cognition as an abstract and amodal process (Barsalou, 2008). We address this omission by first reviewing the notion, prominent in current theoretical arguments, of SNAs as emerging from reading habits. Then we describe recent behavioral and neuroscientific evidence in support of an alternative origin of SNAs, namely finger counting habits. We argue that reading-related biases are only a minor contributor to SNAs, and that finger counting is an important universal factor that shapes the spatial nature of numerical representations and processing. Despite being the most conspicuous element of embodiment in the domain of numerical cognition, finger counting remains a relatively neglected issue (Figure 1). Therefore we sketch out theoretical implications of finger counting for grounded, embodied, and situated cognition more generally in a final section. We conclude that the study of “manumerical cognition,” the role of fingers in our comprehension of numbers, holds great promise for grasping the embodied nature of thought.
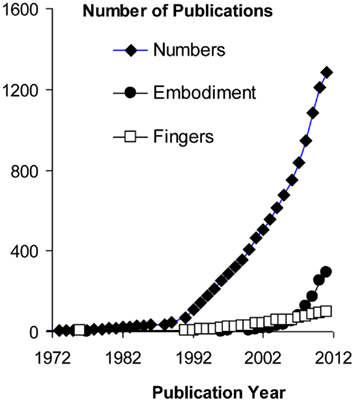
Figure 1. Cumulative number of publications found in Web of Knowledge on July 2, 2011, using as search terms (a) TS = (“embodied cognition”) or TS = (“embodied process*”); (b) TS = (“finger count*”); (c) TS = (“num* cognition” or “num* process*”).

Re-Evaluating the Role of Reading
Early studies of SNAs in Western countries proposed that a directional left-to-right scanning habit is initially acquired with reading and subsequently “spills over” into the numerical domain, thus causing horizontal SNAs (Dehaene et al., 1993; Berch et al., 1999). But at least four arguments suggest that reading habits themselves cannot fully account for the multitude of SNAs and are unlikely to be their ultimate cause.
First, even within a given culture, the notion of a well-defined one-way reading direction is an oversimplification. For instance, Hebrew readers, who read text right-to-left still read embedded numbers left-to-right. Accordingly, the absence of horizontal SNAs was demonstrated in a Hebrew population – presumably because word and number reading habits cancel each other (Shaki et al., 2009). Consistent with this observation, SNAs do obtain in Hebrew readers when the spatial associations of numbers are made consistent with the general reading direction (Fischer et al., 2010; Figure 2), or when the association is assessed orthogonally to the conflict-inducing dimensions, i.e., by using vertical response keys (Shaki and Fischer, 2011). In Chinese–English bilingual readers the presentation format of numbers (Chinese or Arabic symbols) determines their mapping along the vertical or horizontal dimension (Hung et al., 2008), again indicating the presence of multiple SNAs. In both cases it is not reading direction per se, but their spatial consistency, or their contextual association, which shapes SNAs.
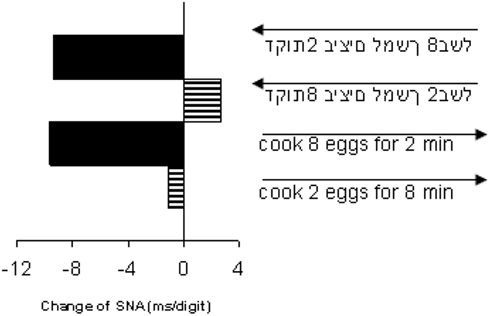
Figure 2. Change in SNAs of Hebrew and English participants reading cooking recipes with different number magnitudes at the beginning and end of each line. Change was measured per regression slopes calculated from number classification speed in the parity task before vs. after reading. In both languages only the incongruent SNA (large number at sentence start) induced a change. Arrows above text excerpts indicate reading direction. Adapted from Fischer et al. (2010).
Secondly, the assumption that years of exposure to a reading culture gradually shape a person’s SNAs runs against more recent observations. Russian–Hebrew bilinguals modify their SNA after reading a few minutes of Cyrillic or Hebrew text (Shaki and Fischer, 2008); in fact, merely reading a single Cyrillic or Hebrew word changes their SNA from 1 s to the next (Fischer et al., 2009). Even during reading, SNAs depend on the positioning of digits within a text (Fischer et al., 2010, Figure 2), clearly indicating that effects of reading are much more short-lived and fragile than originally thought. Directional reading habits provide, at best, only a small contribution to the overall SNAs.
Developmental data provide a third argument against a role of reading as the origin of SNAs. For example, 4.5-year-old children already explore objects more efficiently when they are numbered in left-to-right ascending order (Opfer and Furlong, 2011; see also Tversky et al., 1991). These observations establish the small-left association as a default in Western cultures that needs to be explained. The developmental time-line of SNAs is more fully discussed in a recent review by Göbel et al. (2011).
Finally, SNAs can emerge in the complete absence of reading. Gulledge (2006) compared students against rhesus monkeys in a magnitude classification task. Participants moved a mouse cursor to indicate the numerically larger of two dot patterns, and response latencies showed a horizontal SNA for both groups. In another animal study, newborn domestic chicks learned the positions of 10 pecking holes arranged in a radial array (extending from near to far). When later tested with the array rotated 90°, i.e., in a horizontal extension, they spontaneously translated the formerly radially ascending sequence into a left-to-right, but not a right-to-left ascending sequence (Rugani et al., 2010). Spatial exploration biases have been made responsible for this asymmetric organization of number space in the avian brain (Rugani et al., 2011). Together, these animal studies indicate that directional scanning habits in a linguistic context are not needed to explain the emergence of systematic SNAs.

Fingers Lend a Hand to Digits
Given the limited legs of the reading hypothesis, we propose that SNAs might instead originate from a different directional habit that exhibits both universality and cross-cultural variability: Finger counting. Across the world, most children initially acquire number concepts through finger counting, by either spontaneous practice, observing their parents, or direct tutoring. Finger counting has a long cultural tradition (Göbel et al., 2011) and is surprisingly prevalent today, both as an overt behavior and as a cognitive representation. A girl born without forearms and hands used her phantom fingers to solve arithmetic problems (Poeck, 1964). While this behavior could have been learned from observing other people, a scaffolding function of innate components of both a finger schema and basic calculation routines cannot be excluded. This hypothesis receives tentative support from the fact that newborns already imitate finger postures (Nagy et al., 2005). Interestingly, they prefer to do so with their left hand, which, in turn, links in with findings from an ongoing internet-based study (please visit www.counting.cognitive-psychology.eu/) which showed that adults in English-speaking countries also prefer to start counting on the fingers of their left hand (Lindemann et al., 2011). Thus, they associate small numbers with left space, and might have done so as children. It is not clear why this pattern is less biased in some Mid-European and Mediterranean cultures but the preference clearly reverses in Middle Eastern cultures, where there are more right-starters. Importantly, left-starters as a group have stronger and more consistent SNAs than right-starters (Fischer, 2008), possibly due to congruency between their individual SNAs and the population stereotype that is expressed on rulers, graphs, etc. This makes finger counting a prime candidate for the origin of directional SNAs and their cross-cultural variation. Given this potential of finger counting as a foundation of SNAs, we now review the empirical evidence for an involvement of fingers in numerical cognition, including behavioral, and neuroscientific studies.
Behavioral Evidence
Recent research has established links between hand movements and number processing, such as congruency effects between number magnitude and grasp aperture (reviewed in Andres et al., 2008; Badets and Pesenti, 2010). But several observations show that the SNA can be traced to the finger level: Finger responses are faster when the mapping of number stimuli onto fingers agrees with the direction of finger counting (Di Luca et al., 2006). Seeing canonical finger counting postures differs from seeing arbitrary finger postures: Di Luca and Pesenti (2008), Di Luca et al. (2010) documented faster naming of numerosities indicated by canonical postures, and ruled out differential familiarity or saliency as confounds. Di Luca et al. (2010) found that canonical postures selectively prime one target number whereas arbitrary finger postures prime all numbers-up to and including the target. We will return to this important observation of a modulation of grounded number representations by embodied number associations. Finally, addition is faster when canonical finger postures appear after naming the result, thus providing evidence for arithmetic outcome anticipation in terms of finger associations (Badets et al., 2010).
Early studies reporting a negative relationship of finger counting with intelligence did not control for individual differences in the ability to differentiate between the single fingers (Sauls and Beeson, 1976). In fact, this faculty of finger gnosis predicts future numerical skills (Fayol et al., 1998; Noël, 2005). Children between 7 and 9 years no longer use fingers overtly during mental calculation but make a disproportionate number of split-5 errors (deviating by 5 from the correct solution), suggesting they forgot to “keep their hand in mind” (Domahs et al., 2008). In adults, classifying the digit pairs 4–6 and 5–7 by magnitude is slower in Germans (who count up to 5 on one hand) than in Chinese (who count up to 9 on one hand), suggesting that it takes longer to compare bimanually than unimanually represented numbers (Domahs et al., 2010), presumably because the latter do not require interhemispheric communication.
Some studies that investigated finger-number associations as a function of hand posture (palm down, i.e., right thumb is left of pinkie vs. palm up, i.e., right thumb is right of pinkie) seem to weaken the case for exclusively finger-based SNAs. Brozzoli et al. (2008) found that, after seeing a small number, participants responded faster to tactile stimuli on either the thumb or the pinkie, whichever was the leftmost finger in space (see also Behrmann and Moscovitch, 1994). Likewise, in a finger-number size compatibility task the speed advantage of the index over ring finger was inverted when hand posture was changed (Leuthard et al., 2005, see also Riello and Rusconi, this issue). Similar space-based rather than hand-based finger-number associations resulted from another hand posture manipulation, arm crossing. When participants tapped their fingers repeatedly in random order, while simultaneously naming the numbers from 1 to30 in a random sequence, they named smaller random numbers when the new tap occurred to the left of the previous one in space, regardless of whether their hands were straight or crossed (Plaisier and Smets, 2011). Both hand posture manipulations (pronation/supination and midline crossing) seem to show dominance of external over hand-based space in the mapping of numbers. However, on second consideration, these findings do not diminish the impact of finger-number associations, but only show how flexible the reference frames are that allow an optimal orientation in physical as well as in number space and that guarantee rapid adjustments to a given situation. Detailed processing models that combine somatotopic and external referencing of fingers and hands, respectively (Haggard et al., 2006) are currently missing. They will have to consider that the cortical representation of hands and fingers are overlapping to a large extent, but once required by situational demands can function surprisingly independently (Heed et al., 2011).
Neuroscientific Evidence
Tang et al. (2006) showed that numerical tasks activate motor cortex in Chinese but not Western adults. This was taken to reflect arithmetic learning with an abacus in Asian cultures, indicating their embodied representation of number facts. Kaufmann et al. (2008) showed that children’s (but not adults’) brain activity during magnitude judgments reflected finger-based processing strategies. Two TMS studies showed increased corticospinal excitability specifically for the hand muscles during numerical judgments (Andres et al., 2007; Sato et al., 2007). Also, when TMS is applied to the angular gyrus (Rusconi et al., 2005) it disrupts both access to the finger schema and number magnitude processing. Evidence for a functional overlap of number and finger representations is often claimed from Gerstmann syndrome (Gerstmann, 1940), where acalculia is accompanied by finger agnosia. Although this interpretation is now unlikely (Rusconi et al., 2010), co-morbidities involving writing and left–right discrimination put the association between fingers and numbers in the larger context of symbolic action in space. The spatial–postural invariance noted by Brozzoli et al. (2008) and Plaisier and Smets (2011) may make digits as body parts ideal candidates to deal with digits as points in number space. Finally, Tschentscher et al. (2010) recently compared activation in primary hand motor cortex in adults who start finger counting on either their left or their right hand. The authors found that passively looking at small numbers or number words activated right motor cortex in left-starters but not in right-starters. This work extends the influential demonstration of a somatotopic activation of motor cortex by the reading of action verbs (Pulvermüller, 2005) to the reading of numerical concepts. Together, this behavioral, neuropsychological, and neuroscientific evidence supports the idea of a close link between number and finger knowledge.

Grounded, Embodied and Situated Magnitude Processing
The brain has developed together with the rest of the body as a way to regulate perception and bodily actions in a situation- and task-appropriate manner. This insight has recently regained attention as “embodied cognition,” often also as “grounded” or “situated cognition.” We propose a hierarchical relationship between these terms before discussing implications of this view for the origin of SNAs (Figure 3).
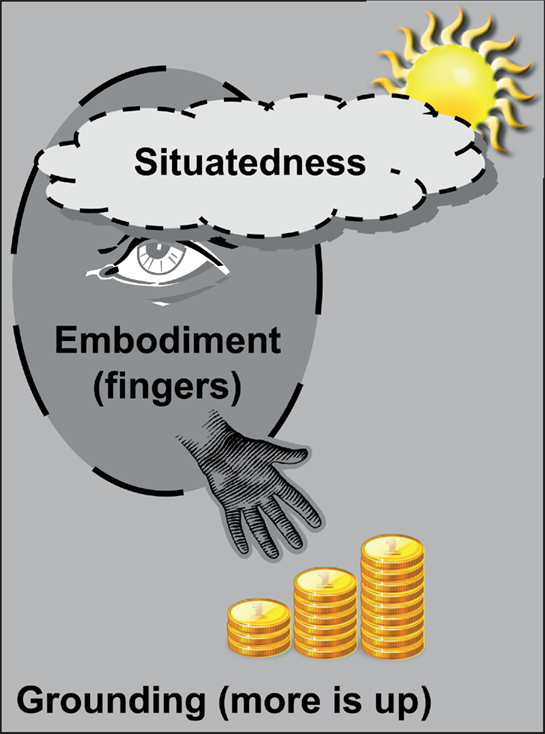
Figure 3. Illustration of the hierarchical relationship of grounded, embodied, and situated cognition in the numerical domain.
The most fundamental aspect of cognitive representations is their grounding which reflects universal properties of the world. One example is the large numbers-up and small numbers-down association that comes from accumulating objects into piles and that subsequently pervades our metaphorical use of language (Lakoff and Nunez, 2000). On top of this environment-based conceptual grounding, the sensorimotor constraints of our bodies shape embodied knowledge representations, as in grasp aperture modulation during object interactions or finger counting (De Cruz, 2008). Finally, range- and context-dependence of SNAs (Dehaene et al., 1993; Bächtold et al., 1998) reflect the flexibility of situated number concepts. This theoretical stance is orthogonal to other theoretical views such as the extended mind hypothesis (Clark, 2008) or the more general theory of magnitude representation (Bueti and Walsh, 2009). It makes several predictions about mathematical practice that can inform our search for the origins of SNAs and the nature of human thought.
First, the hierarchical priority of grounding over embodiment implies that summation coding should be more robust than place coding of numerosities, i.e., larger numerosities should experientially encompass smaller numerosities, unless a cognitively higher level of processing intervenes. This prediction is in line with empirical findings, summarized above, on place vs. summation coding as a function of canonical vs. arbitrary finger postures (Di Luca et al., 2010). By the same rationale, vertical SNAs should be more robust and harder to abolish than horizontal SNAs (Fischer, 2011; Shaki and Fischer, 2011).
Second, an embodied stance on numerical cognition predicts that different body postures, and their effects on spatial reference frames, should influence SNAs. Supporting this prediction, healthy adults generate smaller random numbers while turning their head left and larger random numbers while turning their head right (Loetscher et al., 2008). Also, both horizontal and vertical eye positions reliably predict the magnitude of a number emitted “at random” (Loetscher et al., 2010). Crossing one’s hands over lateralized response keys can eliminate SNAs (Wood et al., 2006). Furthermore, the embodiment nature of number processing predicts that sensory–motor idiosyncrasies should impact on SNAs. There is clinical evidence that this is in fact the case. Patients with right-hemisphere lesions, who fail to attend to the left side of their body and who neglect left hemispace, err toward large numbers when asked to bisect number intervals (Zorzi et al., 2002). The error in explicit number interval bisection is not correlated, however, with rightward displacements in the bisection of real lines (Doricchi et al., 2005), nor does left-sided neglect manifest itself as small number bias in random generation (Loetscher and Brugger, 2009). This indicates that, while hemispatial neglect affects orientation along a number line, the laws that govern attention in physical and number space are not identical.
A third set of predictions comes from the view of situated magnitude processing. Thus, SNAs should be differentially affected by task-dependent hemispheric deployment. Evidence for such flexibility comes from dual-task paradigms, where left-hemisphere verbal memory load abolished SNAs in parity decisions but not in magnitude comparisons, whereas the opposite interference pattern occurred for right-hemisphere visual–spatial load (van Dijck et al., 2009). Hemispheric activation paradigms can also bias healthy subjects’ preference for small or large numbers during digit randomization (Loetscher and Brugger, 2007), and individual preferences for left- vs. right-hemisphere mediated tasks bias number choices toward higher or lower magnitudes (Bachmann et al., 2010). Finally, handedness, one of the most conspicuous signs of hemispheric specialization, does not influence SNAs per se (Dehaene et al., 1993). However, considering that in most cases “more is better” (rather than worse), interactions between emotional valence and hemispace (Casasanto, 2009) are to be expected. Thus, we recently found regular SNAs as long as small numbers denoted undesirable and large numbers desirable events, but as soon as emotional connotations were reversed, no SNAs were observed (in preparation).

Manumerical Cognition: The Science of Dactylonomy
Our brief review illustrates the bewildering number of potential sources of the association between number and space. We believe that this reflects the human capacity to quickly learn to associate any symbol or abstract relation with a spatial position or relationship (Bächtold et al., 2000; Gattis, 2002). Thus, SNAs are the expression of some general cognitive rule that reflects the “placement” of an image in space (the spatialization of ideas) and the relative (in) compatibility that emerges from using lateral effectors to respond to these ideas. Studies with children and amputees are likely to further advance our understanding of this intriguing phenomenon. The embodied cognition approach is a most suitable framework for further progress along this path, and the study of “manumerical cognition” (Fischer, 2008) holds great promise for our understanding of the embodied nature of thought.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Martin H. Fischer was supported by AHRC grant Poetry Beyond Text, Peter Brugger by Swiss National Science grant 320030_127480.

References
Andres, M., Olivier, E., and Badets, A. (2008). Actions, words, and numbers: a motor contribution to semantic processing? Curr. Dir. Psychol. Sci. 17, 313–317.
Andres, M., Seron, X., and Olivier, E. (2007). Contribution of hand motor circuits to counting. J. Cogn. Neurosci. 19, 563–576.
Bachmann, V., Landolt, H.-P., Fischer, M. H., and Brugger, P. (2010). Asymmetric prefrontal cortex functions predict asymmetries in number space in healthy adults. Brain Cogn. 74, 306–311.
Bächtold, D., Baumüller, M., and Brugger, P. (1998). Stimulus-response compatibility in representational space. Neuropsychologia 36, 731–735.
Bächtold, D., Brugger, P., and Regard, M. (2000). Processing of spatial locations: hemispace effects during encoding but not recall. Neuropsychologia 38, 864–872.
Badets, A., and Pesenti, M. (2010). Creating number semantics through finger movement perception. Cognition 115, 46–53.
Badets, A., Pesenti, M., and Olivier, E. (2010). Response–effect compatibility of finger–numeral configurations in arithmetical context. Q. J. Exp. Psychol. (Colchester) 63, 16–22.
Behrmann, M., and Moscovitch, M. (1994). Object-centered neglect in patients with unilateral neglect: effects of left-right coordinates of objects. J. Cogn. Neurosci. 6, 1–16.
Berch, D. B., Foley, E. J., Hill, R. J., and Ryan, P. M. (1999). Extracting parity and magnitude from Arabic numerals: developmental changes in number processing and mental representation. J. Exp. Child Psychol. 74, 286–308.
Brozzoli, C., Ishihara, M., Goebel, S. M., Salemme, R., Rossetti, Y., and Farne, A. (2008). Touch perception reveals the dominance of spatial over digital representation of numbers. Proc. Natl. Acad. Sci. U.S.A. 105, 5644–5648.
Bueti, D., and Walsh, V. (2009). The parietal cortex and the representation of time, space, number and other magnitudes. Philos. Trans. R. Soc. Lond. B Biol. Sci. 364, 1831–1840.
Casasanto, D. (2009). Embodiment of abstract concepts: good and bad in right- and left-handers. J. Exp. Psychol. Gen. 138, 351–367.
Clark, A. (2008). Supersizing The Mind: Embodiment, Action And Cognitive Extension. Oxford: University Press.
De Cruz, H. (2008). An extended mind perspective on natural number representation. Philos. Psychol. 21, 475–490.
Dehaene, S., Bossini, S., and Giraux, P. (1993). The mental representation of parity and number magnitude. J. Exp. Psychol. Gen. 122, 371–396.
Di Luca, S., Grana, A., Semenza, C., Seron, X., and Pesenti, M. (2006). Finger-digit compatibility in Arabic numeral processing. Q. J. Exp. Psychol. (Colchester) 59, 1648–1663.
Di Luca, S., LeFèvre, N., and Pesenti, M. (2010). Place and summation coding for canonical and non-canonical finger numeral representations. Cognition 117, 95–100.
Di Luca, S., and Pesenti, M. (2008). Masked priming effect with canonical finger numeral configurations. Exp. Brain Res. 185, 27–39.
Domahs, F., Krinzinger, H., and Willmes, K. (2008). Mind the gap between both hands: evidence for internal finger-based number representations in children’s mental calculation. Cortex 44, 359–367.
Domahs, F., Moeller, K., Huber, S., Willmes, K., and Nuerk, H.-C. (2010). Embodied numerosity: implicit hand-based representations influence symbolic number processing across cultures. Cognition 116, 251–266.
Doricchi, F., Guariglia, P., Gasparini, M., and Tomaiuolo, F. (2005). Dissociation between physical and mental number line in right hemisphere brain patients. Nat. Neurosci. 8, 1663–1665.
Fayol, M., Barrouillet, P., and Marinthe, C. (1998). Predicting arithmetical achievement from neuropsychological performance: a longitudinal study. Cognition 68, B63–B70.
Fischer, M. H. (2008). Finger counting habits modulate spatial-numerical associations. Cortex 44, 386–392.
Fischer, M. H. (2011). “The spatial mapping of numbers – its origin and flexibility,” in Language and Action in Cognitive Neurosciences, eds Y. Coello, and A. Bartolo (London: Psychology Press).
Fischer, M. H., Mills, R. A., and Shaki, S. (2010). How to cook a SNARC: number placement in text rapidly changes spatial-numerical associations. Brain Cogn. 72, 333–336.
Fischer, M. H., Shaki, S., and Cruise, A. (2009). It takes only one word to quash the SNARC. Exp. Psychol. 56, 361–366.
Gerstmann, J. (1940). Syndrome of finger agnosia, disorientation for right and left, agraphia and acalculia. Arch. Neurol. Psychiatry 44, 398–407.
Göbel, S. M., Shaki, S., and Fischer, M. H. (2011). The cultural number line: a review of cultural and linguistic influences on the development of number processing. J. Cross Cult. Psychol. 42, 543–565.
Goldin-Meadow, S., Wagner Cook, S., and Mitchell, Z. A. (2009). Gesturing gives children new ideas about math. Psychol. Sci. 20, 267–272.
Gulledge, J. P. (2006). Hemispheric Differences in Numerical Cognition: A Comparative Investigation of How Primates Process Numerosity. Psychology Dissertations. Available at: http://digitalarchive.gsu.edu/psych_diss/12
Haggard, P., Kitadono, K., Press, C., and Taylor-Clarke, M. (2006). The brain’s fingers and hands. Exp. Brain Res. 172, 94–102.
Heed, T., Backhaus, J., and Roeder, B. (2011). Integration of hand and finger location in external spatial coordinates for tactile localization. J. Exp. Psychol. Hum. Percept. Perform. [Epub ahead of print].
Hubbard, E. M., Piazza, M., Pinel, P., and Dehaene, S. (2005). Interactions between numbers and space in parietal cortex. Nat. Rev. Neurosci. 6, 435–448.
Hung, Y. H., Hung, D. L., Tzeng, O. J. L., and Wu, D. H. (2008). Flexible spatial mapping of different notations of numbers in Chinese readers. Cognition 106, 1441–1450.
Kaufmann, L., Vogel, S. E., Wood, G., Kremser, C., Schocke, M., Zimmerhackl, L.-B., and Koten, J. W. (2008). A developmental fMRI study of non-symbolic numerical and spatial processing. Cortex 44, 376–385.
Knops, A., Thirion, B., Hubbards, E. M., Michel, V., and Dehaene, S. (2009). Recruitment of an area involved in eye movements during mental arithmetic. Science 324, 1583–1585.
Leuthard, J., Bächtold, D., and Brugger, P. (2005). Is “left” always where the thumb is right? Stimulus-response compatibilities as a function of posture and location of the responding hand. Cogn. Behav. Neurol. 18, 173–178.
Lindemann, O., Alipour, A., and Fischer, M. H. (2011). Finger counting habits in Middle-Eastern and Western individuals: an online survey. J. Cross Cult. Psychol. 42, 566–578.
Loetscher, T., Bockisch, C., Nicholls, M. E. R., and Brugger, P. (2010). Eye position predicts what number ypu have in mind. Curr. Biol. 20, R264–R265.
Loetscher, T., and Brugger, P. (2007). Exploring number space by random digit generation. Exp. Brain Res. 180, 655–665.
Loetscher, T., and Brugger, P. (2009). Random number generation in neglect patients reveals enhanced response stereotypy, but no neglect in number space. Neuropsychologia 47, 276–279.
Loetscher, T., Schwarz, U., Schubiger, M., and Brugger, P. (2008). Head turns bias the brain’s random number generator. Curr. Biol. 18, R60–R62.
Lubin, A., Poirel, N., Rossi, S., Lanoë, C., Pineau, A., and Houdé, O. (2010). Pedagogical effect of action on arithmetic performances in Wynn-like tasks solved by 2-year-olds. Exp. Psychol. 57, 405–411.
McCrink, K., Dehaene, S., and Dehaene-Lambertz, G. (2007). Moving along the number line: operational momentum in nonsymbolic arithmetic. Percept. Psychophys. 69, 1324–1333.
Nagy, E., Compagne, H., Orvos, H., Pal, A., Molnar, P., Janszky, I., Loveland, K. A., and Bardos, G. (2005). Index finger movement imitation by human neonates: motivation, learning, and left-hand preference. Pediatr. Res. 58, 749–753.
Noël, M.-P. (2005). Finger gnosia: a predictor of numerical abilities in children? Child Neuropsychol. 11, 413–430.
Nuerk, H. C., Iversen, W., and Willmes, K. (2004). Notational modulation of the SNARC and the MARC (linguistic markedness of response codes) effect. Q. J. Exp. Psychol. A 57A, 835–863.
Nunez, R. (2006). “Do real numbers really move?” in 18 Unconventional Essays on the Nature of Mathematics, ed. R. Hersch (New York: Springer), 160–181.
Opfer, J. E., and Furlong, E. E. (2011). How numbers bias preschoolers’ spatial search. J. Cross Cult. Psychol. 42, 682–695.
Pinhas, M., and Fischer, M. H. (2008). Mental movements without magnitude? A study of spatial biases in symbolic arithmetic. Cognition 109, 408–415.
Plaisier, M. A., and Smets, J. B. J. (2011). Number magnitude to finger mapping is disembodied and topological. Exp. Brain Res. 209, 395–400.
Poeck, K. (1964). Phantoms following amputation in early childhood and in congenital absence of limbs. Cortex 1, 269–275.
Pulvermüller, F. (2005). Brain mechanisms linking language and action. Nat. Rev. Neurosci. 6, 576–582.
Rugani, R., Kelly, D. M., Szelest, I., Regolin, L., and Vallortigara, G. (2010). Is it only humans that count from left to right? Biol. Lett. 6, 290–292.
Rugani, R., Vallortigara, G., Vallini, B., and Regolin, L. (2011). Asymmetrical number-space mapping in the avian brain. Neurobiol. Learn. Mem. 95, 231–238.
Rusconi, E., Pinel, P., Dehaene, S., and Kleinschmidt, A. (2010). The enigma of Gerstmann’s syndrome revisited: a telling tale of the vicissitudes of neuropsychology. Brain 133, 320–332.
Rusconi, E., Walsh, V., and Butterworth, B. (2005). Dexterity with numbers: rTMS over left angular gyrus disrupts finger gnosis and number processing. Neuropsychologia 43, 1609–1624.
Sato, M., Cattaneo, L., Rizzolatti, G., and Gallese, V. (2007). Numbers within our hands: modulation of corticospinal excitability of hand muscles during numerical judgement. J. Cogn. Neurosci. 19, 684–693.
Sauls, C., and Beeson, B. F. (1976). The relationship of finger counting to certain pupil factors. J. Educ. Res. 70, 81–83.
Shaki, S., and Fischer, M. H. (2008). Reading space into numbers – a cross-linguistic comparison of the SNARC effect. Cognition 108, 590–599.
Shaki, S., and Fischer, M. H. (2011). Multiple spatial mappings in numerical cognition. J. Exp. Psychol. Hum. Percept. Perform. (in press).
Shaki, S., Fischer, M. H., and Petrusic, W. M. (2009). Reading habits for both words and numbers contribute to the SNARC effect. Psychon. Bull. Rev. 16, 328–331.
Tang, Y., Zhang, W., Chen, K., Feng, S., Ji, Y., Shen, J., Reiman, E. M., and Liu, Y. (2006). Arithmetic processing in the brain shaped by cultures. Proc. Natl. Acad. Sci. U.S.A. 103, 10775–10780.
Tschentscher, N., Hauk, O., Fischer, M. H., and Pulvermüller, F. (2010). “You can count on the motor cortex: fMRI reveals embodied number processing,” in Poster Presented at the Festschrift in Honour of Brian Butterworth: “Numbers in the Brain”, Institute of Cognitive Neuroscience, University College London, London.
Tversky, B., Kugelmass, S., and Winter, A. (1991). Cross-cultural and developmental trends in graphic productions. Cogn. Psychol. 23, 515–557.
van Dijck, J.-P., Gevers, W., and Fias, W. (2009). Numbers are associated with different types of spatial information depending on the task. Cognition 113, 248–253.
Wood, G., Nuerk, H. C., Willmes, K., and Fischer, M. H. (2008). On the cognitive link between space and number: a meta-analysis of the SNARC effect. Psychol. Sci. Q. 50, 489–525.
Wood, G., Nuerk, H.-C., and Willmes, K. (2006). Crossed hands and the SNARC effect: a failure to replicate Dehaene, Bossini and Giraux 1993. Cortex 42, 1069–1079.
Keywords: embodied cognition, finger counting, numerical cognition
Citation: Fischer MH and Brugger P (2011) When digits help digits: spatial–numerical associations point to finger counting as prime example of embodied cognition. Front. Psychology 2:260. doi: 10.3389/fpsyg.2011.00260
Received: 01 August 2011; Accepted: 19 September 2011;
Published online: 17 October 2011.
Edited by:
Liane Kaufmann, Private University for Health Sciences, Medical Informatics and Technology, AustriaReviewed by:
Vincent Walsh, University College London, UKHelen De Cruz, Katholieke Universiteit Leuven, Belgium
Copyright: © 2011 Fischer and Brugger. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: Martin H. Fischer, Division of Cognitive Sciences, University of Potsdam, 14476 Potsdam, Germany. e-mail:bWFydGluZkB1bmktcG90c2RhbS5kZQ==

