- School of Social Sciences, Humanities and Arts, University of California Merced, Merced, CA, USA
I show how the dynamics of consciousness can be formally derived from the “open dynamics” of neural activity, and develop a mathematical framework for neuro-phenomenological investigation. I describe the space of possible brain states, the space of possible conscious states, and a “supervenience function” linking them. I show how this framework can be used to associate phenomenological structures with neuro-computational structures, and vice-versa. I pay special attention to the relationship between (1) the relatively fast dynamics of consciousness and neural activity, and (2) the slower dynamics of knowledge update and brain development.
Consider the following passage, written by Edmund Husserl in the early part of the twentieth century:
every entity that is valid for me [is]… an index of its systematic multiplicities. Each one indicates an ideal general set of actual and possible experiential manners of givenness… every actual concrete experience brings out, from this total multiplicity, a harmonious flow… (Husserl, 1970, p. 166)1.
Husserl emphasizes how, in experiencing things – in tasting coffee, driving through a neighborhood, or studying a mathematical theorem – we are related, in some sense, to “systematic multiplicities”: all possible ways this coffee, this neighborhood, this theorem could be experienced. Now consider a second passage, this one written by Paul Churchland in 2002:
…human cognition involves… many hundreds, perhaps even thousands, of internal cognitive “spaces,” each of which provides a proprietary canvas on which some aspect of human cognition is continually unfolding (Churchland, 2002).
Churchland is elaborating on the connectionist approach to cognitive science. According to this approach, as we taste coffee, travel through a neighborhood, or study a theorem, patterns of activity unfold in various parts of the brain, and these unfolding patterns correspond to trajectories in mathematical spaces which describe all possible patterns of activity for the relevant neural systems.
These are striking parallels, especially given the contrast between Husserl (the transcendental idealist) and Churchland (the reductive physicalist)2. Despite their philosophical differences, their methods are similar – both focus on a system’s possibilities, and represent those possibilities using mathematical structures3. Rather than simply introspecting on his actual conscious states, Husserl considers manifolds of possible conscious states. Rather than simply considering what some actual brain happens to do, Churchland considers spaces of possible brain states. Moreover, I will argue that the theories they describe have a shared mathematical form.
Parallels between cognitive science and phenomenology are by now widely recognized. With the emergence of consciousness studies in the early 1990s came “neurophenomenology” (Varela, 1996) and “naturalized phenomenology” (Petitot et al., 2000), as well as the journal Phenomenology and the Cognitive Sciences4. However, there have been few attempts to develop the parallels suggested by the Husserl/Churchland comparison: that is, to understand how the dynamics of neural activity, as described using a connectionist formalism, relates to the dynamics of consciousness, as described by Husserl5. I will argue that there is a systematic set of parallels between the two domains, which has broad relevance for the study of consciousness and its neural basis.
The plan of the paper is as follows. First, I consider the notion of a state space, and describe the main state spaces of interest in neurophenomenology: the space of possible brain states B, and the space of possible conscious states C (state spaces are denoted by upper case bold-faced letters throughout). Then, I define dynamical constraint in a state space, and show how neuroscientists and phenomenologists independently describe such constraints. To connect phenomenology and neuroscience, I describe a “supervenience function” that links B to C, and argue that dynamical constraint in phenomenology can be formally derived from dynamical constraint in neuroscience. I argue that these connections can be drawn in a way that brackets certain recalcitrant philosophical issues, e.g., the mind–body problem and the “hard problem” of consciousness. I end by showing how the abstract considerations developed in the paper can be applied to real-world research, by considering subspaces of B and C and relations between these subspaces. The overall result is a formal framework for studying the relationship between neural and phenomenological dynamics.
In discussing dynamical systems theory, and in particular connectionist dynamical systems, I make a number of simplifying assumptions, and treat certain concepts in non-standard ways. To avoid confusion I should make these simplifications and departures explicit at the outset. Dynamical systems comprise a broad class of mathematical models, encompassing iterated functions and most differential equations. Dynamical systems theory is typically used to analyze the behavior of complex systems, especially when traditional methods are difficult to apply. For example, it can be difficult to predict the motion of three or more celestial bodies using analytic techniques (the “n-body problem”), but considerable insight in to the nature of these motions can be achieved by visualizing collections of orbits using dynamical systems theory. I put dynamical systems theory to philosophical use here, emphasizing abstract features of dynamical systems (e.g., the concept of a state space, and what I call “dynamical constraint”) that help bridge neuroscience and phenomenology, but that are rarely focused on otherwise. Moreover, I do not treat dynamical systems theory as an alternative to other approaches to cognitive science (as in, e.g., Van Gelder, 1998), but rather as a mathematical framework that is neutral with respect to cognitive architectures.
Connectionist networks (or neural networks) are a specific class of dynamical systems, consisting of nodes (model neurons) connected by weights (model synapses)6. They are “brain-like” models, but they abstract away from important details of neural processing (Smolensky, 1988). For example, spikes and spike timing, axonal delays, and dendritic morphology – all thought to be essential to an understanding of the brain’s dynamics – are left out of most connectionist networks. Moreover, weights in connectionist networks are often treated as fixed parameters, which is misleading, because real synapses are constantly changing their state. Even though I focus on simple network models in this paper, I am ultimately interested in real nervous systems – and thus in the kind of model we will have in the imagined future of a perfect theoretical neuroscience7. Throughout I assume that the claims I make based on simplified connectionist models could be refined in light of more detailed neural models.
State Spaces and Their Structure
A dynamical system is a rule defined on a state space, which is a set of possible states for a system, a set of ways a system could be8. Thus, dynamical systems theory is a form of possibility analysis. In focusing on possibilities, dynamical systems theory follows a tradition extending back to Aristotle, who made the distinction between potentiality (dunamis) and actuality (entelecheia or energeia) central to his metaphysics. The distinction is familiar. In science, observations of the actual behaviors of a physical system are used to frame laws governing all possible behaviors for that system. For example, in neuroscience, laws governing all possible behaviors of a neural circuit are abstracted from observations of the actual behaviors of that circuit. The perspective is also prominent in Husserl (Yoshimi, 2007). Rather than just introspecting on consciousness and describing its contents – in the manner of a literary “stream of consciousness” (think of Molly Bloom’s train of thought at the end of Ulysses) – Husserl describes laws governing all possible conscious processes, where those possibilities exist in what he calls “manifolds” (Mannigfaltigkeiten) of possible experiences.
Formally, a state space is a set of points with some structure, a “space” in the mathematical sense, where each point in the space corresponds to one possibility for the system it represents9. Assuming a state space meaningfully represents a set of possibilities, we can reason about those possibilities using the mathematical properties of the state space. For example, state spaces are often metric spaces, which means that we can associate pairs of points with numbers (distances) which indicate how close those points are to one another, and thus how similar the possibilities they represent are. State spaces are often also vector spaces, which means (among other things) that vector addition is defined, so that we can consider some possibilities to be the result of adding other possibilities together. Vector spaces also have a dimension, which implies (for spaces with dimension ≥ 2) that we can think of the represented possibilities as being “built up” from constituents in lower dimensional spaces. A common form of state space, which combines these properties, is an n-dimensional Euclidean space (or region of such a space), the set of all possible n-tuples of real numbers together with an inner product. For example, R3 is a three-dimensional Euclidean space, the set of all triples of real numbers. R3 is a metric space (we can compute the distance between any two points in R3) and a three-dimensional vector space: it is the product of three lower dimensional spaces (three lines). If a set of possibilities is represented by R3, this implies that we can say how similar any two possibilities are, and that we can think of any possibility as a combination of three constituents, each of which can itself be represented by a point in a line.
What is the structure of the space B of possible brain states? We can begin to answer this question by considering the standard connectionist representation of a neural network with n neurons. The state space of such a network is a region of an n-dimensional Euclidean space Rn. Each point in this region corresponds to a possible pattern of firing rates over the network’s n neurons. For example, the state space for a network with 40 neurons is a region of a R40, a 40-dimensional Euclidean space. As noted above, this is a metric space, so that we can use the Euclidean metric to say how similar any two network states are to one another. We can also think of any particular network state as a combination of the states of 40 individual neurons. Since it is a vector space, we can talk about adding network states together as well. A network’s state space in this sense is sometimes called an “activation space,” because it describes a network’s fast-changing activity, as opposed to more slowly changing structural features (in particular, weight strengths, which incrementally change via a learning process). When the firing rate of each neuron is normalized to lie in the interval (0,1), a connectionist activation space has the form of a solid hypercube with 2n vertices. For example, the activation space in this sense for a brain with 100-billion neurons is a 100-billion dimensional solid hypercube, with 2100-billion vertices10.
This connectionist representation assumes a fixed number of neurons. However, we want to allow that brains gain and lose neurons over time. To address this issue, we can posit another space G of possible brain structures, where a brain structure is taken to be a weighted graph, a set of vertices (neurons) connected by labeled edges (synapses), where the edge-labels correspond to the strengths of synapses11. There are other ways of representing brain structures, but this representation is convenient for our purposes. Let G be the space of all such graphs, a brain structure space12. The activation space for each brain structure g ∈ G is a solid hypercube in Rn, where n is the number of neurons in g. B can then be defined as the union of activation spaces for all brain structures in G. It trivially follows that for each brain structure g ∈ G, there will be a subset of B containing patterns of neural activity possible for g, what I call an “accessible region” Bg ⊆ B for brain g13.
The distinction between a structure space and an activation space is important below, where we consider slow changes in the structure space G and the way these changes affect the dynamics of brain activity in B. Such a distinction also occurs in dynamical systems theory, where a parameter space is sometimes distinguished from a main state space. In dynamical systems theory, parameters are usually fixed (though they can be artificially manipulated in order to identify comparatively dramatic changes to a system’s dynamics known as “bifurcations”). This is somewhat misleading, since structural features of a brain are constantly changing, albeit at a slower rate than neural activity. To address this we could consider a combined structure–activity space – one in which both brain structure and neural activity change at the same time, but at different rates. However, the distinction between slow structural changes and more active dynamics will be useful here, because it highlights important parallels between neuroscience and phenomenology.
Now consider the space of possible human conscious states C. I take a conscious state to encompass everything a person is aware of at a moment in time. For example, I now see my computer, think about what I am writing, hear conversation in the periphery, and feel some pain in my joints. I take the totality of these phenomenal properties or “qualia” to correspond to my current conscious state14. What is the structure of C? Some (in particular mind–brain identity theorists) have simply identified C with B. In that case, the structure of C just is the structure of B. This approach is taken by, for example Zeeman (1964) who describes something like the connectionist view of an activation space qua hypercube, and then refers to it as a “thought cube.” However, multiple realization considerations suggest that B ≠ C, in which case C may have a different structure than B. What that structure is remains largely unstudied15.
Even though the exact structure of C is unknown, we can make some conjectures. C seems to be a metric space, insofar as some conscious states are more similar to one another than others are. My conscious state now (sitting and typing) feels more similar to that same conscious state with the addition of a feeling of an itch in my foot than it is to a conscious state in which I am skydiving. Perhaps C is a vector space, so that we can think of any particular conscious state as a combination of more elementary components: a sensory state (itself composed of visual, auditory, and other states), a cognitive state, etc. Perhaps scalar multiplication corresponds to an increase in the intensity of a conscious state. But none of this is obvious.
In fact, it is not even clear that certain basic properties of most state spaces – e.g., the assumption that they can be meaningfully represented using totally ordered sets like the real numbers – apply to C. It is well-known that for a broad range of psychological data – e.g., judgments of indifference with respect to pitch and tone – that transitivity fails. Stimuli s1 and s2 might sound the same, s2 and s3 might sound the same, and similarly for s3 and s4. However, s1 might not sound the same as s4: there might be a just noticeable difference or JND between s1 and s4 but not between the other pairs (this is the “intransitivity of indifference”). Such sets cannot be meaningfully represented by a totally ordered set (like the real numbers), but can be represented by “semi-orders” (Suppes and Zinnes, 1963; Narens and Luce, 1986). The upshot could be that C has some form of semi-ordered structure. Or, it could mean that human judgments about their own states have a semi-ordered structure, but C itself does not16.
Dynamical Constraint
The static structure of a state space, though interesting, is not the primary concern of dynamical systems theory. The main work of dynamical systems theory is to describe rules which constrain the way a system can evolve in time. As we will see, such constraints have been independently described in neuroscience and phenomenology. Given that my brain is structured in a particular way, and given that I exist in a structured environment, patterns of neural activity in my brain can only unfold in some ways, and not others. Similarly in phenomenology. Given the structure of my background knowledge and my sensory environment (both of these concepts are defined below) my conscious experience can only unfold in some ways, and not others.
Formally, a dynamical system is a rule which associates points in a system’s state space with future states. More precisely, a dynamical system is a map ɸ: S × T → S, where S is the state space, and T is a time space17. For any state x ∈ S at initial time t0 ∈ T (i.e., for any initial condition), ɸ says what unique state that system will be in at all times in T. Thus dynamical systems are, by definition, deterministic – initial conditions always have unique futures – though their behavior can be complex and in practice unpredictable. A dynamical system generates a set of orbits or paths in the state space, where each orbit is one possible way the system could evolve in time18. Every point in the state space is associated with a path, so that the whole state space is filled with paths. The complete set of paths of a dynamical system is its phase portrait, which describes all possible ways the system could behave, relative to all possible initial conditions19. We focus on phase portraits, because they are uniquely associated with dynamical systems, and are relatively easy to reason about, especially in this philosophical context.
An example of a phase portrait is shown in Figure 1. The phase portrait describes the possible behaviors of a simple neural network (a Hopfield network), with two neurons. (This type of system was selected for illustrative purposes, not as a model of actual brain dynamics). The state space S for this network is the set of possible patterns of activity for its two neurons, a region of R2. Choose any point in this space (any initial pattern of activity for these two neurons) and the phase portrait shows what points will follow (what patterns of activity will unfold in the network). It is immediately evident from the picture that initial states spiral in toward a single point – an “attracting fixed point” – shown as a black dot in the center of the space. If the phase portrait looked different, for example, if it were filled with concentric circles, or if the arrows pointed in the other direction, then we would have a different dynamical system, a network which behaved in a different way. (In the figure, the light gray lines are the two nullclines of the system, where the velocity in one direction is 0; their intersection is the fixed point, where the velocity in both directions is 0. The nullclines and fixed point indicate the intrinsic dynamics of the system.)
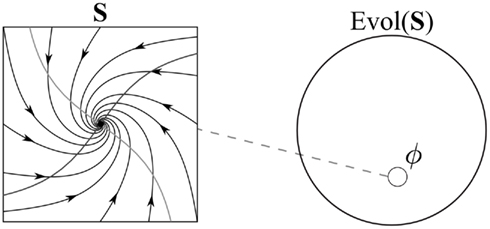
Figure 1. A phase portrait ɸ on S corresponds to a subset of Evol(S). The relative size of ɸ and Evol(S) are for illustrative purposes only (similarly for subsequent figures).
A more abstract way of thinking about phase portraits is in terms of what I call “dynamical constraint.” Of all the logically possible ways a system could change its state over time, only some of these are consistent with the rule ɸ corresponding to a dynamical system. To formalize this point, first consider the set of all possible ways states in a state space S could be instantiated over time. Each possible succession of states is what I will call a “time evolution.” Formally, an evolution in this sense is an arbitrary mapping from times in T to states in S. (Insofar as the term “evolution” suggests a process consistent with a system’s dynamics, this is non-standard terminology – an “evolution” in my sense is any arbitrary time-orderings of points in the state space). I designate the set of all such time evolutions as “Evol(S)20.” Evol(S) is a time evolution space or evolution space for S. It is a very large, abstract space. In the case where S is the plane, for example, we can think of Evol(S) as the set of all possible figures that could be drawn in the plane, given a specified amount of time. There are no limits – one can draw loops, figure eights, dot patterns, or simply keep the pen on a single point – so long as at each moment in T a point is being drawn somewhere. In the case where S is a neural network, we can imagine that a set of electrodes has been connected to all of the network’s neurons. Think of a modified Matrix machine, with electrodes stimulating every neuron in a brain, rather than just the sensory neurons21. Such a machine would be capable of overriding a network’s intrinsic dynamics, and could thereby cause a network to travel through any arbitrary sequences of states, and thereby instantiate any point in Evol(S).
The crucial point is this: a phase portrait ɸ on S is a subset (typically a proper subset) of the evolution space Evol(S). The dynamics ɸ constrain the system to evolve in some ways and not others. Of all logically possible ways the states in S could change in time – of all possible time evolutions in Evol(S) – only those in ɸ ⊆ Evol(S) are consistent with the system’s dynamics. It is in this sense that a dynamical system imposes dynamical constraint on its state space. Note that in most cases, ɸ will be much smaller than the space Evol(S) which contains it22. For example, of all the figures that could be drawn in S in Figure 1, only spiral-shaped curves like those shown in the figure are in the system’s phase portrait. The neural network’s structure constrains activity to unfold in these particular ways, and prohibits many other logically possible time evolutions.
One problem with dynamical systems theory as applied to the study of mind and brain is that dynamical systems are in a certain sense closed (Hotton and Yoshimi, 2010)23, but mind and brain are in various ways open and embodied, as numerous philosophers and cognitive scientists have shown in recent years24. In Hotton and Yoshimi(2011, 2010) the issue is addressed by defining a more complex version of a dynamical system, what we call an “open dynamical system25.” An open dynamical system is a compound system, which separately models an agent when it is isolated from any environment (its intrinsic or closed dynamics), and the same agent when it is embedded in an environment. More specifically, we separately model the intrinsic dynamics of an agent on its own, and the dynamics of that same agent in the context of a total system or environmental system e which contains that agent as a part26.
When an agent is embedded in an environment, the set of paths in its phase portrait S changes. The agent’s intrinsic dynamics, represented by a phase portrait ɸ in S, is morphed to become a more complex open phase portrait ɸe in the same state space S. Each path in this open portrait corresponds to one possible behavior for the agent when it is in this environment.
An example of an open phase portrait is shown in Figure 2. The figure shows what happens to the Hopfield network shown in Figure 1 when it is embedded in a simple environment, consisting of two objects which pass the network at regular intervals and stimulate its two nodes (for details, see Hotton and Yoshimi, 2010, 2011). Four sample paths from the network’s open phase portrait are shown. The complete open phase portrait for this embodied agent is a superposition of these paths (and a continuum of others intermediate between them) in the state space. Paths no longer spiral in to the fixed point, but are rather pulled in loops around the fixed point (the network is pulled away from the fixed point when objects come in to view, but pulled back toward it when they go out of view). However, the neural network itself, the “intrinsic dynamics” of the agent, is the same (notice that the nullclines and fixed point – which “pulls” all network states toward it – are the same in Figures 1 and 2).
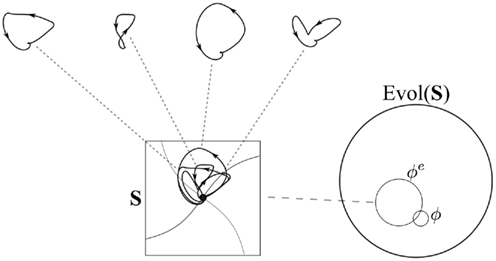
Figure 2. Open phase portrait for the network whose closed phase portrait is shown in Figure 1, when it is embedded in a simple environment e. Like the closed phase portrait ɸ, the open phase portrait ɸe corresponds to a subset of Evol(S).
An open phase portrait, like a closed phase portrait, is a set of paths, a subset of Evol(S). Thus, the concept of dynamical constraint still applies when we consider open systems. For example, the open phase portrait ɸe for the embodied neural network shown in Figure 2 contains a continuum of loop-shaped paths. Even though these paths overlap in a complex way, they still represent a substantial set of constraints on how the system can behave. The open phase portrait ɸe, like the closed phase portrait ɸ, contains a very specific set of paths in the evolution space Evol(S)27. The paths in ɸe are more complex than the paths in ɸ, but they still correspond to a proper and very small subset of the full evolution space. Of all logically possible sequences of states for this network, only a few will ever occur, given the intrinsic dynamics of the network, and, in the case of ɸe, the structure of its environmental embedding.
Having consider dynamical constraint in simple closed and open systems, let us consider how these ideas apply to our two domains of interest: neuroscience and phenomenology.
Consider first a brain g with n neurons, whose state space is a solid hypercube Bg ⊆ Rn. Recall that g is a member of a brain structure space G, and that for any brain structure g ∈ G, there will be a subset Bg ⊆ B containing patterns of neural activity possible for g. That is, any brain structure g determines an accessible regionBg of B, for a brain of type g. During development, as neurons and synapses grow and die, and as synapses change their strength, a person’s brain structure changes. This can be represented by a path g1…gn, where gi ∈ G. In fact the entire course of a brain’s development, from the emergence of the first neuron to the organism’s death, can be represented in this way. As this “life path” is traced out during a brain’s development, there is a corresponding “window” in B, a changing region of accessibility Bg1,…,B gn (see Figure 3). This captures the idea that brain states possible for me as a child are not the same as brain states possible for me as an adult, though both are subsets of an encompassing space B of all possible brain states28.
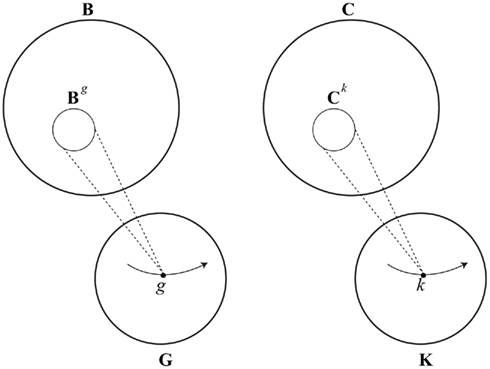
Figure 3. Space of brain structures G, states of background knowledge K, and corresponding “accessible” regions of the space of brain states B and conscious states C.
Now consider an environment for brain g, that is, a total system that contains g as a part. To do so, we first let c be a function that associates any brain g with those environmental systems e that contain it. Any environmental system in c(g) has brain structure g embedded in it. So, given a brain g, we can consider an environmental system e ∈ c(g) that embeds g, and then consider the open dynamics of this brain in this environment, that is, an open phase portrait in Bg. We can designate this phase portrait “ɸg,e.” In any realistic case, ɸg,e will be a tiny subset of Evol(Bg), containing just those brain processes compatible with brain structure g when it is embedded in environmental system e. Note the two superscripts in ɸg,e. Dynamical constraint for embodied brains can vary in two ways: with changes in underlying brain structure g, and with changes in the environmental system e in which a given brain structure is embedded. Thus we have two knobs we can turn when considering possible constraints on the activity of an embodied brain. As we turn the first knob, brain structure changes; as we turn the second knob, the environmental system changes. As we turn these two knobs we have a changing region of accessibility in B, and a changing and morphing set of paths in this region.
Summarizing: for any brain structure g ∈ G and environment e ∈ c(g), there exists:
(1) An accessible region of brain space Bg ⊆ B
(2) An open phase portrait ɸg,e ⊆ Evol(Bg)
What do phase portraits like ɸg,e – those describing brains g in environments e – actually look like? It is too early to say with much precision, but work in the area is active and promising. One of the most detailed modeling studies to date is Izhikevich and Edelman (2008), which describes a model network with a million neurons and over a billion synapses whose connectivity was determined by images of white matter connectivity as well as physiological studies of cortical microcircuits (others are pursuing similar projects, e.g., Markram, 2006). Among the dynamical features observed in the model were (1) sensitivity to initial conditions, a hallmark of chaos (adding a single spike could radically alter the state of the entire cortical network in less than a second), and (2) global oscillatory rhythms (e.g., alpha, beta, and delta waves) in the absence of inputs, which parallel those observed in humans. Other work considers specific circuits in the brain and their dynamics, in relation to various cognitive tasks.
Let us now turn to phenomenology. Though Husserl does not introduce explicit governing equations for consciousness, he clearly posits what I have called “dynamical constraint” in the space C of possible conscious states. Given who a person is (that is, given a person’s preexisting knowledge, skills, and capacities), and given the way sensory data happen to be organized for a person, only some sequences of conscious states (paths in C) will be possible, and others will not be. That is, only some subset ψ ⊆ Evol(C) will be possible for a person in a (phenomenological) environment. These ideas parallel the neural case in what I think is a remarkable way, especially insofar as they can be independently developed on phenomenological grounds.
The notion of dynamical constraint occurs in the context of Husserl’s “transcendental” phenomenology, which is a development of themes that go back at least to Kant (who famously claimed that space and time are conditions on the possibility of coherent experience, rather than features of a mind-independent reality). In Husserl, Kant’s conditions on the possibility of coherent experience correspond to “rules” (Regeln) which regulate the way experience must be organized in order for a world to appear. To explain what this means, Husserl sometimes considers what would happen if there were no such rules at all, so that any arbitrary subjective process could occur (compare the random brain processes induced by the customized Matrix machine). In such cases, Husserl says, the subjective stream could be so chaotic that the appearing world would, in effect, be “annihilated:”
Could it not be that, from one temporal moment on… the series of appearances would run into one another in such a way that no posited unity could ultimately be maintained…? Could it not happen that all fulfillment whatsoever would cease completely and the entire stream of appearance dissolve into a mere tumult of meaningless sensations?… Thus we arrive at the possibility of a phenomenological maelstrom … it would be a maelstrom so meaningless that there would be no I and no thou, as well as no physical world – in short, no reality (Husserl, 1997, pp. 249–250).
Husserl here describes two ways we could fail to have any sense of a transcendent world. In the first case, the “series of appearances would run into one another in such a way that no posited unity could ultimately be maintained.” In other words, we would have flashes of experiences – a house, a dog, a painting – but they would appear to the mind in a random, haphazard order without any internal coherence. In the other case, subjectivity at every instant is a meaningless “maelstrom;” “the entire stream of appearance dissolve(s) into a mere tumult of meaningless sensations.” In neither case does Husserl imagine “absolute nothingness” (as, one supposes, with death or pre-natal non-existence)29. Rather, Husserl imagines disruptions in the system of rules or transcendental laws that determine how conscious processes are organized so as to present or “constitute” a coherent world of things.
The concept of a phenomenological maelstrom shows how certain very general rules constrain the way consciousness must be organized in order for a coherent world to appear. We will focus on two specific forms of constraint, which parallel the forms of neural constraint described above.
A first set of constraints is associated with a person’s “background knowledge” which I take to include skills, beliefs, capacities, personality characteristics, and all the largely unconscious factors that contribute to a person’s identity30. The totality of such knowledge in some sense defines who a person is phenomenologically. Husserl refers to this as a “horizon” of “pre-knowledge” (vorwissen) informing the structure of a person’s conscious experiences over time31. Given what I have learned over the course of my life, I will experience things in a particular way from moment to moment, which is different from how someone else, with a different stock of knowledge, would experience those things.
Background knowledge imposes several kinds of constraint on experience. First, it constrains what conscious states are possible for a person or being with that background. I cannot have all the same conscious experiences as a child or a mouse, given my overall knowledge and capacities, and they cannot have the same experiences as me. I am not sure Husserl ever makes the point, but others have. Joyce for example, observes (in the voice of Stephen Daedalus), that “the minds of rats cannot understand trigonometry32.” Focusing on human conscious states, it seems clear that someone without the requisite training (an average toddler, for example) can not have an experience of understanding quantum mechanics, even if they can have many different conscious experiences. These points suggest that, in general, someone with background knowledge k will be constrained to have experiences in some subset Ck ⊆ C. These are accessible conscious states for a person with background knowledge k. As a person’s background knowledge changes, we have an unfolding path in K (the set of all possible states of background knowledge), and a changing window of accessible conscious states in C (see Figure 3).
Background knowledge not only places a person in an accessible region Ck ⊆ C, it also constrains the order in which experiences in that accessible region can be instantiated. Suppose, for example, that I have background knowledge k, and that I am standing before my house, instantiating a conscious state s ∈ Ck. I know from daily experience that the walls are painted white inside. Now I walk in to the house, and discover that all the walls have been painted orange. Given my background knowledge k, I must be surprised. A sequence of experience that begins in s and has me experiencing orange walls inside, where I am not surprised, is impossible, given k. Given my background knowledge, some paths in Ck are ruled out, and others are not – I am constrained to be in a subset ψk ⊆ Evol(Ck)33. Note that, qua a set of paths in a state space, ψk is just a phase portrait, and hence corresponds to a kind of phenomenological dynamics. So, as background knowledge changes on the basis of my ongoing experience, we have a path in K. For each point along this path we have an accessible region of C, Ck. We also have a set of possible conscious processes in that subset, that is, a changing subset ψk of Evol(Ck).
Husserl recognizes these points in a general way, noting that a person’s horizon (in the sense of background knowledge) is constantly changing, and that as it changes, one’s way of perceiving objects changes as well: “[the] horizon is constantly in motion; with every new step of intuitive apprehension, new delineations of the object result” (Husserl, 1975, p. 122). He also refers to changes in background knowledge using geological metaphors, describing an accumulation of “sediments” (Niederschlag) as we learn new things, as well as continuously varying “weightings” associated with particular items of knowledge. For example, each day I drive to work and see the same things on the road. Over time my “weighted” confidence in the presence of these things is strengthened34.
In addition to these knowledge-based constraints on experience, there are “external” constraints as well, corresponding to the organization of sensory data in the conscious field. It is a fact of experience that things appear to consciousness in certain ways, and that we only have partial control over these appearances35. Husserl captures this idea with his notion of sensory or “hyletic” data, which are (on one interpretation) “something ego-foreign that enters into our acts [experiences of things] and limits what we can experience – that is, limits the stock of noemata [specific ways a thing can be experienced] that are possible in a given situation” (Føllesdal, 1982, p. 95)36. For example, if I am standing before a house with my eyes open, I am constrained to see a house-like shape before me. I can not just “will” the house-shaped form away, or force myself by sheer volition to have a full-blooded experience of skydiving or scuba diving. Similarly over time: brute facts about how sensory data are organized during a given stretch of time constrain what kind of experiences I could have during that period. We already saw that background knowledge constrains me to be in some subset ψk of Evol(Ck) during a particular period of time. Brute sensory forms further constrain me during this time, limiting me to an even smaller subset of Evol(Ck). To formalize these idea let a “sensory system” h be a system of sensory constraints that determines what sensory forms appear to a person (with background knowledge k) over time, something like a phenomenological environmental system. We can write this as ψk,h ⊆ Evol(Ck). As with neural constraint, phenomenological constraint varies along two dimensions: we have two knobs we can turn when considering possible constraints on consciousness over time. As we turn the first knob, background knowledge changes; as we turn the second knob, a system of sensory constraints changes. As we turn the these two knobs we have a changing region of accessibility in C, and a changing and morphing set of paths in this region.
Summarizing, for a person with background knowledge k, relative to sensory system h, there exists:
(1) An accessible region of the space of conscious states Ck ⊆ C
(2) A set of possible paths ψk,h ⊆ Evol(Ck)
Neurophenomenology Via Supervenience
We have seen that phenomenology and connectionism have a similar dynamical structure. However, there is reason to believe that they do not have an identical structure. Consider the following reductio. Suppose that brain states are identical to conscious states, so that B = C. This implies that every alteration in a person’s brain, however miniscule, corresponds to a change in consciousness. But it seems that a single neuron can change its firing rate by a tiny amount, or a neuron can be lost, without changing consciousness. In fact, there is experimental evidence for this, insofar as it has been known since the 1960s that there is a threshold of cortical stimulation, above which subjects report a change in consciousness (the presence of a subjective sensation), and below which they do not (Libet et al., 1967). This in turn suggests that some changes in neural activity do not produce changes in consciousness. If that is right, the space of brain states is not the same as the space of consciousness states, B ≠ C37. The argument is a variant on Putnam’s classic critique of the identity theory (Putnam, 1967), and the upshot is similar: if the argument is sound, conscious states are “multiply realized” not just in radically different physical systems (Putnam’s emphasis), but even in different states of the same brain38.
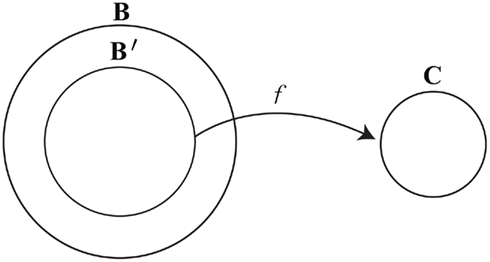
To link the dynamics of brain activity with the dynamics of consciousness, in a way that allows for a many-to-one relation between brain states and conscious states, we can draw on the philosophical concept of supervenience. Mental–neural supervenience is ontologically minimalist: it only says that people who differ in their mental states must differ in their brain states, or, equivalently, that being in the same brain state entails being in the same mental state. I have shown elsewhere (Yoshimi, 2011b) that a mental–neural supervenience relation in this sense entails a “supervenience function” f. Such a function associates brain states x with conscious states f(x), where any person in brain state x at a time will also be in conscious state f(x) at that time [in such cases I will say that x “determines” f(x)]. More precisely, assuming mental–neural supervenience, any brain state in a subset B′ ⊆ B determines a unique conscious states in C (see Figure 4; brain states in B but not B′ do not determine any conscious state – they correspond to coma, dreamless sleep, etc.)39.
It should be obvious how f can be used to link neural dynamics with conscious dynamics. Any path in B′ can be associated with a path in C using f. As my brain changes state while I am awake, a path unfolds in B′. Each state in this path has an image in C under f, and thus we have a corresponding path in C. In this way any neural evolution in B′ can be associated with a stream of consciousness in C. One problem here is that paths in B will not always stay in B′ (and thus would not always have an image in C); they weave in and out of B′, entering B′ as a person wakes up, and leaving B′ when (for example) that person goes in to a dreamless sleep. To address this issue, in the rest of the paper I will usually assume that structures in B have been restricted to B′, and thus have an image in C. For example, when discussing paths in B, I only consider the restriction of those paths to B′.
The supervenience function is largely (and, I think, usefully) neutral with respect to the mind–body problem40. Supervenience only tracks correlations between physical states and mental states, without specifying their ontological status. For example, supervenience is consistent with dualism: if dualism is true, a supervenience function could map physical brain states to non-physical mental states. If the identity theory is true, the supervenience function maps physical brain states to themselves, and the function is an identity map. If non-reductive physicalism (a form of physicalism that allows for multiple realization) is true, then the supervenience function associates neural states with the conscious states they realize, and the function is many-to-one. It is even possible to describe an idealist version of mental–physical supervenience (in fact Husserl actually does this; Yoshimi, 2010). I regard this neutrality as a virtue of the supervenience relation. Using supervenience we can make progress in our study of neuro-phenomenological dynamics, without having to resolve the difficult (and perhaps essentially intractable) metaphysical questions associated with the mind–body problem41.
If it is the case that B = C and the supervenience function is a 1–1 identity map, the dynamics of neural activity are identical to the dynamics of consciousness. If the supervenience function is many to one, the move from B to C via f involves a kind of compression or simplification, where many brain states can determine the same conscious state, and conversely, the same conscious states can be multiply realized in many brain states. This in turn implies that the dynamics of neural activity are related to but different from the dynamics of consciousness. We can imagine, for example, that a loop in B, corresponding to a neural oscillation in the brain gets mapped to a single point in C, corresponding to a particular conscious state42.
The dynamics of consciousness can now be derived from the dynamics of neural activity:
(1) Consider a brain structure g ∈ G. g determines an accessible region B′g ⊆ B′.
(2) Consider an environment e ∈ c(g). There exists an open dynamical system describing g in this environment, which in turn determines an open phase portrait ɸg,e ⊆ Evol(B′g).
(3) The image of B′g under f is Cg ⊆ C.
(4) The image of ɸg,e under f is ψg,e ⊆ Evol(Cg).
(5) So, dynamical constraint in phenomenology can be derived from dynamical constraint in the brain.
(1) says that for any brain structure g there is an “accessible” region of B′ (the domain of the supervenience function). More specifically, we begin with a brain structure g ∈ G, and we consider the accessible subset Bg ⊆ B corresponding to g. We then take the intersection of Bg and B′, and call it B′g. (This intersection may be empty – it may be that a given brain structure g cannot determine any conscious states. In that case the results below follow trivially.)
(2) says that we can describe the behavior of a brain g in an environment by an open dynamical system. Consider an environment e that contains brain g, that is, an environment e ∈ c(g). An open dynamical system for g in this environment determines an open phase portrait ɸg,e in Bg, which can be restricted to B′g. As we saw above, any phase portrait can be thought of as inducing “dynamical constraint” on its state space, i.e., as determining a subset of the set of all possible time evolutions in that space. In this case we have a phase portrait ɸg,e ⊆ Evol(B′g), which contains time evolutions in B′g consistent with the dynamics of brain g in environment e.
(3) notes that we can take the image of the set of accessible brain states B′g in C, which yields a set of accessible conscious states for g, Cg ⊆ C (see Figure 5). This can be thought of as the set of conscious states possible for a person given the structure of his or her brain.
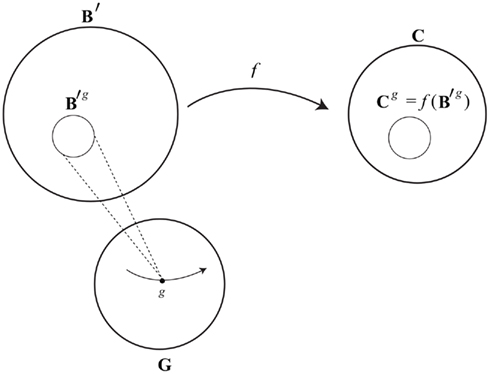
Figure 5. A brain structure g ∈ G determines an accessible region B′g ⊆ B′, which in turn has its image Cg under f in C. An open phase portrait ɸg,e (not shown) defined on B′g also has its image under f, yielding a phase portrait ψg,e in Cg. In this way phenomenological dynamics can be derived from neural dynamics.
(4) says that each path in ɸg,e can be associated with a path in Cg using f. I call the resulting set of paths ψg,e. Since paths in ψg,e are time evolutions in Cg, ψg,e ⊆ Evol(Cg). Thus we have dynamical constraint in the phenomenological domain. For a person with a brain of type g in an environment e, some conscious processes are possible (those in ψg,e), and others are not (those in Evol(Cg) but not ψg,e).
Thus, (5), the dynamics of consciousness, as specified by ψg,e ⊆ Evol(Cg), can be formally derived from the dynamics of neuroscience.
The overall picture we have is as follows. In the course of a person’s life, neurons come and go, synapses become more or less efficient in transmitting information, etc. We thus have a changing “life path” g1…gn in the brain structure space G. As this path unfolds, we have a changing window of accessibility Bg1,…,Bgn in B (different brain states become possible as the brain’s structure changes), which determines a corresponding window of accessibility in C relative to the supervenience function (different conscious states become possible as the brain’s structure changes). Within the changing window of neural accessibility we also have a changing and morphing phase portrait, which determines which neural processes are possible for this person, once we have specified an environment. This in turn determines which conscious processes are possible for this person. In this way the dynamics of consciousness can be derived from the dynamics of an embodied brain.
I have shown how various phenomenological structures like those described by Husserl can be derived from neural structures, but I have not shown them to be the same. I have not reduced Husserlian phenomenology to neuroscience. For example, are the conscious states in Ck determined on purely phenomenological grounds to be consistent with a person’s background knowledge k the same as those that are possible given the structure of that person’s brain g? That is, does Cg = Ck? Similarly, is it the case that the dynamical constraints implied by phenomenology are equivalent to those implied by neuroscience? One could address the issue by arguing that the phenomenologically grounded constructs should be eliminated as a matter of theoretical parsimony. We have seen that all the work the phenomenological constructs do can be done by the neurally derived constructs. Moreover, the neurally derived constructs are subject to more precise measurement than constructs based on introspection, which is known to be error-prone (Schwitzgebel, 2008). Another approach would be to allow that the phenomenological constructs and their neurally derived counterparts might be logically distinct (and to study that distinction philosophically), but to focus, in practice, on the neurally derived constructs, given that the neurally derived constructs are more empirically tractable.
Subspaces and Applications
We have seen how the dynamics of consciousness can be formally derived from the dynamics of neural activity, and in the process have developed a conceptual framework for neuro-phenomenological investigation. However, it is not yet clear how this framework can be applied to extant research. The problem is that I have focused on very “large” spaces – in particular, B and C – which are far removed from the concerns of working neuroscientists and phenomenologists. States in B are patterns of activity involving (for a typical human brain) billions of spiking neurons. States in C are fields of consciousness or Erlebs, totalities of phenomenal data for persons at times. How can these results inform studies of specific neural systems or phenomenological domains?
We can address the issue by considering subspaces of Bg and Cg (in the rest of this section I assume an arbitrary human brain structure g). Recall that the state space Bg for a brain g with n neurons is (on the standard connectionist representation) a solid hypercube in Rn with 2n vertices. Any subset of g’s neurons defines a subspace of Bg, a “smaller” hypercube contained within it: visual cortex space, temporal cortex space, fusiform face area space, etc. These are the “internal cognitive spaces” Churchland refers to in the opening quote. In some sense these are “part spaces”: each point in visual cortex space, for example, corresponds to a pattern of activity for g’s visual cortex, which is part of a larger pattern of activity over all that brain’s neurons.
Since it is not clear what the mathematical structure of C is, it is not clear in what sense we can meaningfully speak of “phenomenological subspaces.” However, it seems clear that can talk about part spaces of Cg, which we can take to be subspaces. For example, we can think of smell space as the set of all possible smell experiences, where each smell experience is a part of some total conscious field in Cg. In fact, Husserl himself makes use of this idea when he refers to phenomenological “spheres” – the sphere of visual experiences, the sphere of kinesthetic (bodily) sensations, the “affective sphere,” etc. (Yoshimi, 2010).
Assuming we can meaningfully speak of neural and phenomenological subspaces, the question remains of how they are related to each other. One possibility is that they are related by supervenience, so that subspaces of Cg supervene on subspaces of Bg and are thus related by supervenience functions. For example, if visual experiences supervene on states of visual cortex, we can define a subspace supervenience function which associates states of visual cortex (points in a subspace of Bg) with visual experiences (points in a subspace of Cg). Any state of g’s visual system will determine a unique visual experience relative to this function. Numerous questions arise here. For example, is it plausible to suppose, consistently with the existence of a visual cortex-to-visual experience supervenience function, that a patch of visual cortex in vitro could support visual phenomenology?43 Perhaps not. I think there are plausible ways of meeting this challenge (and related challenges), but here I will simply assume – as many others do, at least tacitly – that neural and phenomenological subspaces can be defined, and that they can be related by supervenience functions.
Using these functions, specific forms of phenomenology can be studied in relation to specific brain circuits. Subspace supervenience functions can be used to move back and forth between phenomenology and neuroscience, deriving phenomenological predictions from neural data, and generating neural predictions from phenomenological claims44. In moving from neuroscience to phenomenology, we begin with a path or other structure in Bg, project this structure down to a lower dimensional subspace (e.g., visual cortex space), and then use a subspace supervenience function to map this projected structure to a corresponding subspace of Cg – one of Husserl’s “phenomenological spheres” (e.g., the space of possible visual experiences). It should be noted that these paths and structures can be changed in the process. For example, in Figure 6, a path in a three-dimensional space is changed when it is projected to a lower dimensional space. We can also derive neural predictions from phenomenology. To do so, we can begin with a structure in Cg, project it to a phenomenological subspace, and then consider that structure’s pre-image in a subspace of Bg relative to a subspace supervenience function.
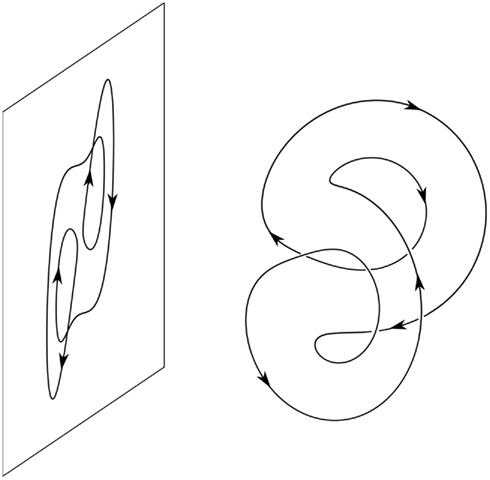
Figure 6. A loop-shaped orbit in R3 projected to a two-dimensional subspace. The loop in R3 does not cross itself, but its projection does, twice. The orbit is taken from the Lorenz equation, for a parameter value near one of its many bifurcations.
There are problems here, some of them substantial (for example, we do not actually know what these subspace supervenience functions are), and in practice various auxiliary assumptions must be made in order to perform any actual neuro-phenomenological analysis of this kind. Still, as a way of understanding how the dynamics of phenomenology and neuroscience are related, I think the approach is promising, and again, I take myself to be formalizing ideas already tacit in much of the literature.
To further develop these ideas, in the remainder of this section I describe examples of existing research that can be interpreted using this framework. The relevant hypotheses are preliminary and subject to revision or falsification, but they collectively convey a sense of how I envision neurophenomenology unfolding.
First, certain classical connectionist ideas concerning the structure of an activation space can be used to make phenomenological predictions. Activation spaces are often hierarchically organized in to subsets that correspond to psychologically significant categories45. For example, the activation space of Cottrell’s (1990) face recognition network contains subsets corresponding to faces and non-faces, male and females faces, and individual faces. These subsets were not programmed in to Cottrell’s network, but emerged in the course of training. The connectionist model can be thought of as an approximation of a biological neural network (whose state space is a subspace of Bg), perhaps a network in the fusiform face area in the temporal lobe, known to be implicated in face recognition. Assume a subspace supervenience function links states of this network with conscious perceptions of faces in a “face recognition” subspace of Cg. Relative to these assumptions, we can predict that the category structure of the neural state space is preserved under the subspace supervenience function. If that is right, then every brain state in the male-face subset of the brain network is mapped to an experience of a male-face, all the female-face brain states are mapped to experiences of female-faces, etc. So the neural category structure predicts a phenomenological category structure. Similarly in other domains, e.g., for grammatical and semantic categories, which have been studied using connectionist networks (Sejnowski and Rosenberg, 1987; Elman, 1991), and which could be used to predict our tacit phenomenological awareness of linguistic categories.
A related set of ideas is associated with the notion that memories are fixed points of attractor networks (Hopfield, 1984; Rumelhart and McClelland, 1987b). In such cases a network’s settling in to a fixed point attractor is interpreted as memory retrieval from a partial cue. The settling process can be understood in terms of the maximization of a “harmony function” defined on the activation space, where the value of this function represents the “goodness of fit” between the current sensory input and knowledge stored in the connection weights (Prince and Smolensky, 1997, p. 1607). Mangan (1991, 1993) links “goodness of fit” in this sense with a felt sense of “meaningfulness” in the field of consciousness. The degree to which inputs are consistent with stored knowledge structures is, according to Mangan, correlated with a phenomenological continuum between states where we feel confused (low levels of meaningfulness) to states that in some sense feel “right” (high levels of meaningfulness, which Mangan associates with esthetic experience and scientific discovery). To formalize this, we can begin with a subspace of Bg corresponding to an attractor network in the brain, say, a region of temporal cortex associated with semantic processing. A harmony function can be defined on this subspace, so that at any moment a degree of harmony can be associated with activity in this network. If we assume the harmony values of the neural patterns are preserved under the relevant subset supervenience function, then the degree of meaningfulness of an experience will correspond to the harmony of the neural pattern that produced it. In this way we can predict meaningfulness of experiences from neural patterns, at least in principle.
A third example comes from Churchland (2005), who predicts new forms of color phenomenology based on the color opponency theory of color vision. According to this theory, triples of retinal ganglion cells code for colors, and patterns of activity across these triples correspond to color experiences at points in the visual field. Thus we have a collection of three-dimensional subspaces of Bg, one for each point in the visual field. Since Churchland is an identity theorist, we also have a subspace supervenience function for each of these triples, which is an identity map (a pattern of activity for a relevant triple of ganglion cells is identical to a color experience at the corresponding point in the visual field). What is exciting about Churchland’s proposal is that it can be used to make specific predictions about visual phenomenology, without having to directly intervene in the brain (compare the abstract and currently untestable cases above). Churchland notes that chromatic fatigue – induced by prolonged exposure to a color stimulus – makes retinal cells change their activity, in a way that can be represented by vector addition in the three-dimensional color space. By fatiguing ourselves with respect to specific color stimuli, we can force our ganglion cells to move to points in the color space which they otherwise could not visit, resulting in unusual color experiences. In this way, Churchland predicts new forms of phenomenology, arguing that color experiences not possible in normal conditions can be induced in this way, e.g., impossibly dark blues, hyperbolic oranges, and self-luminous greens. I encourage you to try it and judge for yourself.
Finally, an example in the reverse direction, from phenomenology to neuroscience. According to Husserl, conscious experience is non-repeatable: “The same [mental state] cannot be twice, nor can it return to the same total state” (Husserl, 1990, p. 315). One reason Husserl gives is that we always experience the world against the background of our past, and since our past is always changing, we never see the world in precisely the same way. If this is true, then it corresponds to a topological claim about paths in C: no path in C can ever cross itself. However, even if this is the case for total fields of consciousness in C, a projection of a path in C to a subspace of C could cross itself (as in Figure 6). This is, moreover, phenomenologically plausible. Even if I can not have the same total experience twice, it seems possible that I can experience the same visual image twice (e.g., by blinking while standing before an unchanging scene), and it is all but guaranteed that the same color can recur in a given part of the visual field. In fact it seems that as we move from C to successively lower dimensional subspaces, that the probability of repetition increases. These claims can be used to generate neural predictions. If a path in C does not cross itself, this suggests that its pre-image in B would not cross itself either. Moreover, if paths in successively lower dimensional subspaces of C are increasingly likely to cross themselves, this suggests that the same is true of successively lower dimensional subspaces of B. Again this seems intuitively plausible. The same total state of a person’s brain may never recur, and recurrence is unlikely even for states of the entire visual system, but by the time we consider the one-dimensional activation space of a single neuron, repetition is all but guaranteed.
Conclusion
We have seen that from a few relatively uncontroversial assumptions (e.g., mental–physical supervenience, which brackets the mind–body problem and the hard problem of consciousness), a framework for integrating phenomenology and neuroscience can be developed. I have tried to convey some of the excitement associated, at least for me, with this enterprise. Husserl describes a complex set of rules governing the evolution of consciousness in various domains, and these rules can be derived from dynamical laws governing neural activity in embodied brains. Among other things, this suggests that conscious processes – paths in C – have shapes, which can be visualized via their pre-images in B. Some have begun to look at such paths in animal brains (Gervasoni et al., 2004), and it is also possible to study these paths in simulations of embodied neural network agents (Phattanasri et al., 2007; Hotton and Yoshimi, 2010). By interpreting studies like these in a neuro-phenomenological framework, we can begin to understand the actual topology and geometry of “manifolds,” “horizons,” and other structures Husserl only describes in a qualitative way.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
I am grateful to Tomer Fekete, Scott Hotton, Rolf Johansson, Matthew Lloyd, Wayne Martin, David Noelle, Eric Thomson, Jonathan Vickrey, an anonymous referee, and an audience of faculty and graduate students at UC Merced, for valuable feedback on earlier versions of this paper.
Footnotes
- ^The passage is from The crisis of European sciences and transcendental phenomenology, written between 1934 and 1937, just before Husserl’s death. On the history of this text see the editor’s introduction to Husserl (1970).
- ^Though Husserl himself was open to a kind of naturalistic investigation (Yoshimi, 2010).
- ^This is perhaps more surprising in Husserl. However, his Ph.D. was in mathematics, under Weierstrass, and mathematical themes run throughout his work (Yoshimi, 2007).
- ^On the history of the scientific study of consciousness prior to the 1990s, see Mangan (1991), Yoshimi (2001).
- ^However, there have been some studies along these lines, including Petitot (2000) and Lloyd (2004). Churchland (2002) and Palmer (2008) consider the relationship between neuroscience and Kant’s transcendental philosophy. Spivey (2007) considers similar ideas from the standpoint of psychology and cognitive science. There is also an important line of research integrating dynamical systems theory, phenomenology, and cognitive science, with an emphasis on Heideggerean phenomenology (Wrathall and Malpas, 2000; Dreyfus, 2007; Thompson, 2007). On the relationship between this kind of account and my own, see Yoshimi (2009).
- ^For an overview of the connectionist standpoint, see Rumelhart and McClelland(1987a, Vol. 1, Chap. 1–4).
- ^Compare O’Brien and Opie (1999). For an overview of theoretical/computational neuroscience (as opposed to connectionism), see Dayan and Abbott (2001).
- ^I treat states as properties insofar as they can be instantiated by numerically distinct things. I also assume that states apply to objects at instantaneous moments (or durations), and that only one state in a state space can be instantiated by an object at a time. The states of interest here are complex properties (sometimes called “structural universals”), e.g., the property of having 100-billion neurons firing in a particular way, or the state of experiencing a complex visual scene in a particular way. Some of these points are developed in Yoshimi (2011b).
- ^The points in the state space and the possibilities they represent are, strictly speaking, distinct. Following standard practice, however, I (largely) suppress the distinction and allow “state” to refer either to points in the mathematical representation or to possibilities for the real system they represent. The concept of a meaningful representation of an empirical structure by a numerical structure is studied in measurement theory (Narens and Luce, 1986).
- ^See Smolensky (1987). Other discussions of the use of state space representations in cognitive science include Edelman (1998) and Gärdenfors (2004).
- ^This is a generalization of a connectionist “weight space,” the set of all n x n matrices, where each matrix describes a pattern of synaptic connectivity over the n nodes of a neural network. In such a representation, the values of ith row and jth column of the matrix correspond to the strength of the weight connecting neuron i to neuron j. Absent connections are represented by zeros.
- ^There are a number of problems with G. Some network structures in G will not correspond to human brains, or perhaps not to any biologically possible brain at all. Moreover, different graphs can have the same state space on this account. For these and other reasons a more nuanced representation of brain structure space will ultimately be needed.
- ^A similar but subtly different approach to modeling brain states in relation to conscious states is in Tononi (2008), Balduzzi and Tononi (2009). Like me, Balduzzi and Tononi approach neurophenomenology by emphasizing the possibilities of a system and the mathematical structure of those possibilities. For example they refer to a “a mathematical dictionary relating neurophysiology to the geometry of the quale and the geometry to phenomenology” (Balduzzi and Tononi, 2009, p. 2). However, I assume that an instantaneous state of a brain (a state in Bg) is sufficient to determine a person’s instantaneous conscious state. This is sometimes called a “synchronous supervenience” thesis, since the idea is that the base state of a system at a time is sufficient to determine the supervenient state of that system at that time. Balduzzi and Tononi deny this (“it does not make sense to ask about the quale generated by a state (firing pattern) in isolation” p. 11), focusing instead on information relationships between probability distributions defined on (something like) activation spaces in my sense. Fully developing the relationship between the ideas presented here and Balduzzi and Tononi’s important work is beyond the scope of this paper, but it is worth noting the difference. In this regard also see Fekete (2010).
- ^On the concept of a “total” conscious state, cf. Gurwitsch (1964), who described “fields of consciousness” as “totalities of co-present data” (p. 3). Also see Carnap, who based his foundationalist program on Erlebs, “experiences themselves in their totality and undivided unity” (Carnap, 2003, Sec. 67).
- ^Stanley has studied “qualia space” and concluded that it is a “closed pointed cone in an infinite dimensional separable real topological vector space” (Stanley, 1999, p. 11).
- ^This is not as exotic as it may sound. It is often the case that measurement errors create a semi-ordered structure. For example, judgments of length using a ruler have some margin of error, so that “sameness” of judged lengths is intransitive. But despite this intransitivity in sameness of judged lengths, the underlying space of “true lengths” can still be meaningfully represented by a totally ordered set like the real numbers. For discussion of these issues see Suppes et al. (1989, p. 300).
- ^Subject to several additional conditions; on the formal definition of a dynamical system, see Katok and Hasselblatt (1996), Hotton and Yoshimi (2011). Note that this abstract definition covers more familiar types of mathematical models as special cases. For example, iterated functions and most forms of differential equation satisfy this abstract definition, and are thus dynamical systems.
- ^The term “orbit” is standard in dynamical systems theory. The term “path” is neutral between classical dynamical systems and open dynamical systems, and so I will prefer that term here. When a differential equation is a dynamical system, its solutions are its orbits.
- ^“Phase portrait” usually refers to a visual depiction of a sample of a dynamical system’s orbits. I use the term to refer to a complete collection of orbits for a system, whether they are depicted in an image or not (what is sometimes called an “orbit space”).
- ^Evol(S) is a function space, the set of all possible functions from T to S. In set-theoretic notation, Evol(S) = ST. When discussing Evol(S) in relation to a dynamical system on S, I assume the time set T is the same for both.
- ^I am referring to the production of simulated experiences via artificial sensory stimulation, as described in the movie The Matrix.
- ^To make the notion of relative size precise – so that we could meaningfully talk about one set being “smaller than” another – measures would have to be defined on both spaces.
- ^Classical dynamical systems must either assume a system is isolated from any environment, or consider a higher dimensional system which incorporates the environment (we take the latter strategy, but then provide tools for considering what happens inside an “agent system”).
- ^For an overview of the embodiment literature, see Yoshimi (2011a).
- ^In doing so we formalize ideas that are present in various forms in earlier studies. See Yoshimi (2011a) for more on precedent and references to earlier sources.
- ^I refer equivalently to “total systems” “environmental systems” and “environments,” even though strictly speaking an environmental system is that part of a total system distinct from an agent.
- ^Note that in the figure, I show ɸ and ɸe as intersecting, because they can have paths in common, though in many cases they will not have paths in common.
- ^A background assumption is that there is another dynamical system on G, which describes how an organism’s brain structure develops over time. It is, presumably, an open system, insofar as organisms are reciprocally coupled to their environments.
- ^“… a mere maelstrom of sensations, I say, is indeed not absolute nothingness. It is only nothing that can in itself constitute a world of things” (Husserl, 1997, p. 250).
- ^Compare what Searle (1983) calls the “background of intentionality.”
- ^This is one of several distinct senses of “horizon” in Husserl.
- ^Cf. the discussion of “cognitive closure” in McGinn (1989), which includes references to earlier discussions of this idea in the philosophy of mind.
- ^The generation and update of expectations relative to background knowledge is a prominent feature of Husserl’s account. Husserl describes these relations in mathematical terms, as an “interplay of independent and dependent variables” (Husserl, 2001, p. 52), where body movements are the independent variables and expected perceptions are the dependent variables. For a provisional formalization see Yoshimi (2009).
- ^See Husserl (1975, p. 119) and Husserl (1982, p. 332).
- ^This idea has a long history: it is present in various ways in (for example) Heidegger, Fichte, and the Stoics.
- ^It should be noted that Føllesdal’s reading of hyletic data as constraining perceptual interpretations is controversial in Husserl scholarship.
- ^This denies a highly specific form of the type identity theory, since the relevant types are states (brain states and conscious states), and states are here taken to be complex properties (see note 8) – e.g., the property of having 100-billion neurons firing in a particular way.
- ^“Multiple realization” canonically refers to the fact that the same mental state can be realized in different kinds of physical systems; e.g., a human, an alien, and a computer. However, multiple realization can also apply to different brain states for a particular species, or to different states of a single person’s brain, given its structure at a time (Shagrir, 1998; Bickle, 2006). It is this last, most narrowly scoped sense of “multiple realization” that I focus on here. Also note that a view that allows multiple realization can still be physicalist. In fact, non-reductive physicalism – according to which the mind is physical even though psychology can not be reduced to neuroscience or physics – is a standard position in contemporary philosophy of mind, largely because of multiple realization arguments (Stoljar, 2009).
- ^Many interesting and open questions are raised by this formulation. Is B′ connected, as the figure suggests? What is the relative size of B′ with respect to B? What are the properties of f? Is it 1–1? Is it continuous? Is it differentiable?
- ^Note that I only say that supervenience is “consistent” with these positions. Some positions on the mind–body problem are also consistent with the denial of supervenience. For example, dualism is consistent with failure of supervenience: an unstable pineal gland could break supervenience in the case of classical Cartesian dualism, allowing that the same brain state gives rise to different conscious states at different times.
- ^The idea that the mind–body problem might be essentially unsolvable is associated with explanatory gap arguments (Levine, 1983) and “mysterian” arguments in the philosophy of mind (McGinn, 1989), as well as the “hard problem” of consciousness (Chalmers, 1995).
- ^Of course, a pressing question in this case is what the supervenience function is. I am aware of no current investigation in to this question. Libet’s work suggests the supervenience function partitions brain space into a collection of relatively uniform classes (the pre-images of f), each of which occupies more or less the same amount of brain space, but more work is needed.
- ^There has been very little work in these areas, to my knowledge, but see Wilson (2001) and Mandik (2011) for tools that could be helpful. For example, it could be that activity in visual cortex determines a specific visual experience, so long as suitable activity occurs in the rest of the brain (this is what Wilson calls a “background condition” of realization).
- ^A prediction about a person’s phenomenology is less obviously testable than a prediction about neuroscience is, though there are methods for assessing the coherence of phenomenological claims, e.g., via convergence with other sources of data (Mangan, 1991).
- ^The philosophical implications of these ideas are also developed by Smolensky (1988), Lloyd (1995), and Churchland (1996), among others.
References
Balduzzi, D., and Tononi, G. (2009). Qualia: the geometry of integrated information. PLoS Comput. Biol. 5, e1000462. doi: 10.1371/journal.pcbi.1000462
Bickle, J. (2006). Multiple Realizability. Available at: http://plato.stanford.edu/entries/multiple-realizability/
Carnap, R. (2003). The Logical Structure of the World and Pseudoproblems in Philosophy. Chicago, IL: Open Court Publishing.
Churchland, P. (1996). The Engine of Reason, the Seat of the Soul: A Philosophical Journey into the Brain. Cambridge, MA: The MIT Press.
Churchland, P. (2002). Outer space and inner space: the new epistemology. Proc. Addresses Am. Philos. Assoc. 76, 25–48.
Churchland, P. (2005). Chimerical colors: some phenomenological predictions from cognitive neuroscience. Philos. Psychol. 18, 527–560.
Cottrell, G. W. (1990). “Extracting features from faces using compression networks: face identity emotion and gender recognition using holons,” in Connectionist Models: Proceedings of the 1990 Summer School, Waltham, MA, 328–337.
Dreyfus, H. L. (2007). Why Heideggerian AI failed and how fixing it would require making it more Heideggerian. Philos. Psychol. 20, 247–268.
Edelman, S. (1998). Representation is representation of similarities. Behav. Brain Sci. 21, 449–467.
Elman, J. L. (1991). Distributed representations, simple recurrent networks, and grammatical structure. Mach. Learn. 7, 195–225.
Føllesdal, D. (1982). “Husserl’s theory of perception,” in Husserl, Intentionality and Cognitive Science, eds H. L. Dreyfus, and H. Hall (Cambridge, MA: MIT Press), 93–96.
Gervasoni, D., Lin, S. C., Ribeiro, S., Soares, E. S., Pantoja, J., and Nicolelis, M. A. L. (2004). Global forebrain dynamics predict rat behavioral states and their transitions. J. Neurosci. 24, 11137.
Hopfield, J. J. (1984). Neurons with graded response have collective computational properties like those of two-state neurons. Proc. Natl. Acad. Sci. U.S.A. 81, 3088.
Hotton, S., and Yoshimi, J. (2011). Extending dynamical systems theory to model embodied cognition. Cogn. Sci. 35, 1–36.
Hotton, S., and Yoshimi, J. (2010). The dynamics of embodied cognition. Int. J. Bifurcat. Chaos 20, 1–30.
Husserl, E. (1970). Crisis of European Sciences and Transcendental Phenomenology, 1st Edn. Evanston, IL: Northwestern University Press.
Husserl, E. (1982). Ideas Pertaining to a Pure Phenomenology and to a Phenomenological Philosophy: First Book: General Introduction to a Pure Phenomenology. The Hague: Martinus Nijhoff.
Husserl, E. (1990). Ideas Pertaining to a Pure Phenomenology and to a Phenomenological Philosophy: Second Book: Studies in the Phenomenology of Constitution. Dordrecht: Kluwer Academic Publisher.
Husserl, E. (2001). Analyses Concerning Passive and Active Synthesis: Lectures on Transcendental Logic. Dordrecht: Springer.
Izhikevich, E. M., and Edelman, G. M. (2008). Large-scale model of mammalian thalamocortical systems. Proc. Natl. Acad. Sci. U.S.A. 105, 3593.
Katok, A., and Hasselblatt, B. (1996). Introduction to the Modern Theory of Dynamical Systems. Cambridge: Cambridge University Press.
Libet, B., Alberts, W. W., Wright, E. W., and Feinstein, B. (1967). Responses of human somatosensory cortex to stimuli below threshold for conscious sensation. Science 158, 1597.
Mangan, B. (1991). Meaning and the Structure of Consciousness: An Essay in Psycho-Aesthetics. Berkeley, CA: University of California Berkeley.
Mangan, B. (1993). Taking phenomenology seriously: the “fringe” and its implications for cognitive research. Conscious. Cogn. 2, 89–108.
Narens, L., and Luce, R. D. (1986). Measurement: the theory of numerical assignments. Psychol. Bull. 99, 166–180.
O’Brien, G., and Opie, J. (1999). A connectionist theory of phenomenal experience. Behav. Brain Sci. 22, 127–148.
Petitot, J. (2000). “Morphological eidetics for phenomenology of perception,” in Naturalizing Phenomenology: Issues in Contemporary Phenomenology and Cognitive Science, eds J. Petitot, F. Varela, B. Pachoud, and J.-M. Roy (Stanford, CA: Stanford University Press), 330–371.
Petitot, J., Varela, F., Pachoud, B., and Roy, J. (2000). Naturalizing Phenomenology Issues in Contemporary Phenomenology and Cognitive Science, eds J. Petitot, F. Varela, B. Pachoud, and J.-M. Roy (Stanford, CA: Stanford University Press).
Phattanasri, P., Chiel, H. J., and Beer, R. D. (2007). The dynamics of associative learning in evolved model circuits. Adapt. Behav. 15, 377–396.
Prince, A., and Smolensky, P. (1997). Optimality: from neural networks to universal grammar. Science 275, 1604.
Putnam, H. (1967). “The nature of mental states,” in Readings in the Philosophy of Psychology, ed. N. Block (Cambridge, MA: Harvard University Press), Vol. 1, 222–231.
Rumelhart, D. E., and McClelland, J. L. (1987a). Parallel Distributed Processing: Explorations in the Microstructure of Cognition: Foundations, Vol. 1. Cambridge, MA: MIT Press.
Rumelhart, D. E., and McClelland, J. L. (1987b). Parallel Distributed Processing: Explorations in the Microstructure of Cognition: Psychological and Biological Models, Vol. 2. Cambridge, MA: MIT Press.
Searle, J. R. (1983). Intentionality, an Essay in the Philosophy of Mind. Cambridge: Cambridge University Press.
Sejnowski, T. J., and Rosenberg, C. R. (1987). Parallel networks that learn to pronounce English text. Complex Syst. 1, 145–168.
Shagrir, O. (1998). Multiple realization, computation and the taxonomy of psychological states. Synthese 114, 445–461.
Smolensky, P. (1987). “Neural and conceptual interpretations of PDP models,” in Parallel Distributed Processing: Explorations in the Microstructure of Cognition-Vol. 2: Psychological and Biological Models, eds J. McClelland, D. Rumelhart, and the PDP Research Group, Cambridge, MA: The MIT Press.
Stoljar, D. (2009). Physicalism. Available at: http://plato.stanford.edu/entries/physicalism/
Suppes, P., Krantz, D. M., Luce, R. D., and Tversky, A. (1989). Foundations of Measurement, Vol. 2: Geometrical, Threshold, and Probabilistic Representations. New York, NY: Academic Press.
Suppes, P., and Zinnes, J. L. (1963). “Basic measurement theory,” in Handbook of Mathematical Psychology, Vol. 1, eds R. D. Luce, R. R. Bush, and E. Galanter (Hoboken, NJ: Wiley and Sons).
Thompson, E. (2007). Mind in Life: Biology, Phenomenology, and the Sciences of Mind. Cambridge, MA: Harvard University Press.
Tononi, G. (2008). Consciousness as integrated information: a provisional manifesto. Biol. Bull. 215, 216.
Van Gelder, T. (1998). The dynamical hypothesis in cognitive science. Behav. Brain Sci. 21, 615–628.
Varela, F. J. (1996). Neurophenomenology: a methodological remedy for the hard problem. J. Conscious. Stud. 3, 330–349.
Wrathall, M., and Malpas, J. (2000). Heidegger, Coping, and Cognitive Science. Cambridge, MA: MIT Press.
Yoshimi, J. (2001). Dynamics of Consciousness: Phenomenology, Neuroscience, and Dynamical Systems Theory. Dissertation, University of California, Irvine.
Yoshimi, J. (2009). Husserl’s theory of belief and the Heideggerean critique. Husserl Stud. 25, 121–140.
Yoshimi, J. (2010). “Husserl on Psycho-Physical Laws,” in New Yearbook for Phenomenology and Phenomenological Philosophy X 25–42.
Keywords: phenomenology, connectionism, dynamical systems theory, supervenience, neural networks, Husserl
Citation: Yoshimi J (2011) Phenomenology and connectionism. Front. Psychology 2:288. doi: 10.3389/fpsyg.2011.00288
Received: 30 September 2010; Paper pending published: 16 January 2011;
Accepted: 10 October 2011; Published online: 15 November 2011.
Edited by:
Matthew R. Broome, University of Warwick, UKCopyright: © 2011 Yoshimi. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: Jeff Yoshimi, School of Social Sciences, Humanities and Arts, University of California, Merced, 5200 North Lake Road, Merced, CA, USA. e-mail:anlvc2hpbWlAdWNtZXJjZWQuZWR1