- 1 Psychology Human Sciences, Swansea University, Swansea, UK
- 2 Department of Psychological and Brain Sciences, Indiana University, Bloomington, IN, USA
One of the most influential research programs in psychology is that of Tversky and Kahneman’s (1973, 1983) on heuristics and biases in decision-making. Two characteristics of this program are, first, compelling empirical demonstrations that in some decision-making situations naïve observers violate the rules of classic probability (CP) theory and, second, that corresponding behavior can be explained with simple heuristics. Tversky and Kahneman’s work has led to a vast literature on what is the basis for psychological process in decision-making. Note that their work, however impactful, has not settled the debate of whether CP theory is suitable for modeling cognition or not. CP models have attracted enormous interest and they often do provide excellent coverage of cognitive processes (e.g., Oaksford and Chater, 2007; Griffiths et al., 2010; Tenenbaum et al., 2011).
The idea of heuristics is appealing. First, they are simple. The assumption that human cognition is based on heuristics partly avoids the computational intractability problems which plague some formal approaches (cf. Sanborn et al., 2010). Second, they often allow an understanding of one process in terms of theory developed for other cognitive processes. Consider the representativeness and availability heuristics. According to the representativeness heuristic, judgments of frequency are driven by similarity and according to the availability heuristic by the ease of identifying related instances in memory. Thus, with these heuristics, an explanation for decision-making becomes one of similarity or memory. Third, heuristics often have strong empirical support. Tversky and Kahneman’s approach has been to motivate explanations based on heuristics by providing compelling demonstrations for violations of the standard approaches (in decision-making, CP theory). Other proponents of heuristic approaches have argued that heuristic schemes lead to better results (e.g., Gigerenzer and Todd, 1999).
There is nothing wrong with heuristic approaches. But, there is a sense in which theoreticians have a bias for cognitive models based on formal frameworks, whether it is Bayesian probability, formal logic, or the quantum probability (QP) theory, which we discuss (cf. Elqayam and Evans, 2011). The properties of formal frameworks are interconnected. For example, all expressions in classical probability theory are based on a handful of axioms. Thus, one cannot accept the psychological relevance of one expression, but reject another: they are all related to each other. By contrast, heuristics, however successful, are somewhat interchangeable. Postulating the relevance of the representativeness heuristic does not necessitate the relevance of the availability heuristic (Pothos and Busemeyer, 2009a).
The QP research program in psychology partly originated as an attempt to reconcile people’s violations of CP theory in decision-making situations with formal theory and examine whether it is possible to express formally some of the key heuristics in decision-making. QP theory is a theory for assigning probabilities to observables (Isham, 1989). Physicists are happy to employ CP theory in most cases but they believe that, ultimately, QP theory is the more appropriate choice. CP theory works by defining a sample space and expressing probabilities in terms of subsets of this space. A key property of this approach is the commutative nature of events and subsequent order independence for probabilities assigned to the joint events. QP is a geometric approach to probability. Events correspond to different subspaces and probabilities are computed by projections to these subspaces (note that projections have been discussed before in psychology; Sloman, 1993). Crucially, this makes probability assessment potentially order and context dependent and, e.g. (a suitable definition of), conjunction can fail commutativity. This and related interference effects lead to interesting predictions from QP theory.
In the famous Linda experiment (Tversky and Kahneman, 1983), participants are told about Linda, who sounds like a feminist and are then asked to judge the probability of statements about her. The important comparison concerns the statements “Linda is a bank teller” and “Linda is a feminist and a bank teller.” The first statement is extremely unlikely. The second statement is a conjunction of the first statement and another one. Thus, according to CP theory, P(bank teller) ≥ (bank teller feminist). But, results violate CP theory, as most participants consider the statement “Linda is a bank teller and a feminist” as the more probable one (this is called the conjunction fallacy). Tversky and Kahneman’s explanation was that cognitive process is not based on CP theory, rather, participants employ a representativeness heuristic. They consider Linda as a very typical feminist, so that the characterization “bank teller and feminist” is probable, regardless of the bank teller part. One could also invoke an availability heuristic (as Tversky and Koehler, 1994 later did), whereby the statement “bank teller and feminist” activates memory instances similar to Linda.
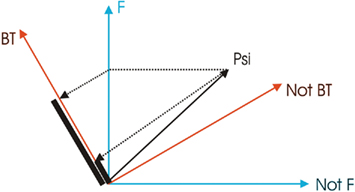
Figure 1 illustrates the QP theory explanation of the conjunction fallacy. The state vector is labeled as Psi and corresponds to what participants learn about Linda from the story. One 1D subspace corresponds to Linda being a feminist and another to a bank teller. We compute the probability for each possibility by projecting the state vector onto the corresponding subspace and squaring the length of the projection. If participants are asked to evaluate the probability that Linda is a just bank teller or just a feminist this is very unlikely and likely respectively. In QP theory, conjunction has to be typically defined as a sequential operation, i.e., Prob(A ∧ B) ≡ Prob(A ∧ then B). Assume that in decision-making the more probable statement is evaluated first (this means that more probable statements are more likely to be included in the decision-making process; cf. Gigerenzer and Todd, 1999). Then, the probability computation involves projecting first to the feminist ray and then to the bank teller ray. The first projection is fairly large, we knew this already. The critical point is that from the feminist ray, there is now a sizeable projection onto the bank teller ray. Thus, whereas the direct projection to the bank teller one was small, the indirect projection (via the feminist ray) is much larger. Such a scheme can account for violations of the conjunction fallacy (and many other related empirical results; Busemeyer et al., 2011).
What is the implication about psychological process implied in the quantum theory model? In classical probability theory it has to be the case that Prob(bank teller ∧ feminist) = Prob(feminist ∧ bank teller) ≤ Prob(bank teller). But in QP theory, when considering possibilities which are represented by subspaces at oblique angles as in Figure 1, the assessment of any possibility is dependent on the assessment of previous possibilities. In the case of the conjunctive statement in the Linda problem, assessing the possibility that Linda is a bank teller depends on the previous consideration that Linda is a feminist. Clearly, the Linda story makes it very unlikely that Linda is a bank teller. But, feminists can have all kinds of different professions and, even though being a bank teller is perhaps not the most likely one, it is still a plausible profession. Therefore, once a participant has accepted that Linda is a feminist, it becomes easier to think of various professions for Linda, including that of a bank teller. That is, according to the quantum model, accepting Linda as a feminist, allows the system to establish a similarity between the initial representation (the initial information about Linda) and the representation for a bank teller. From a quantum theory perspective, representativeness, being a similarity process, is subject to chain and context effects, and this is exactly what happens in the Linda example. An alternative perspective is that seeing Linda as a feminist increases availability for other related information about Linda, such that Linda might be a bank teller. Briefly, this is the quantum theory explanation for the conjunction fallacy (Busemeyer et al., 2011).
Quantum probability theory has been applied in other decision-making situations (e.g., Trueblood and Busemeyer, 1992; Atmanspacher et al., 2004; Khrennikov, 2004; Aerts, 2009). We next consider an application which illustrates a different aspect of the theory. According to the sure-thing principle, if you intend to do A when B is true and you intend to do A when B is not true, then you should still intend to do A if you do not know if B is true or not. The sure-thing principle follows from the law of total probability in CP theory, P(A) = P(A ∧ B) + P(A ∧ not B). Surprisingly, Shafir and Tversky (1992) reported violations of the sure-thing principle in a prisoner’s dilemma task. In their experiment, the matrix of payoffs was set up so that participants preferred to defect, knowing that the other person had already defected and knowing that the other person had cooperated. However, many participants reversed their judgment and decided to cooperate, when they did not know the other player’s action. Such a finding can be partly explained with cognitive dissonance theory (e.g., Festinger, 1957), according to which people change their beliefs to be consistent with their actions. Thus, if participants have a cooperative bias, in the “unknown” condition, they might be cooperating because they imagine the other person is willing to cooperate as well (Shafir and Tversky, 1992, called this idea wishful thinking). One could also apply Tversky and Shafir’s (1992) suggestion that violations of the sure-thing principle can arise from a failure of consequential reasoning (this idea was put forward for the two-stage gambling task). In the known-defect situation there is a good reason to defect and likewise for the known – cooperate situation. But, in the unknown conditions it is as if the (separate) good reasons for defecting under each known condition cancel out (Busemeyer and Bruza, 2011, Chapter 9)!
Pothos and Busemeyer (2009a,b) created a quantum and classical model for violations of the sure-thing principle. Both models assumed that the state vector in the unknown case is a convex combination of the states in the known-defect and known-cooperate cases. Then, there is a process of evolving the state according to the relative payoff for different options and the cognitive dissonance principle. In both the QP and the CP case, the probability of defecting is determined by this evolved state. But, in the classic case, whatever the process of evolution, the evolved representation (vector) is still a convex combination of the known-defect, known-cooperate cases, which means that the CP model is always constrained by the law of total probability. By contrast, in the QP case probabilities are determined from the state vector by a squaring operation. For example, |a+b|2 = a2 + b2 + a*b + b *a The last two terms are interference terms and they can be negative, so that |a + b|2 < a2 + b2, violating the law of total probability. Thus, the QP model allows an expression of the idea that individually perfectly good reasons or causes (high a2, high b2) can partly cancel each other out. Note, further, that although the utility representation in the quantum model is simple (there is a utility parameter, analogous to that in more standard decision models, like Kahneman and Tversky’s, 1979, prospect theory), the possibility of interference effects would allow, e.g., a consistent preference for a risky option, over the sure-thing (i.e., a stable risk preference).
These are promising results for QP theory. Its features which make us optimistic are that probability assessment is context- and order-dependent, so that earlier components in a process can affect later ones. In fact, such features are implied in some powerful heuristics, such as representativeness and availability. Quantum theory provides a promise that the intuitions for such heuristics could be described in a formal framework.
References
Atmanspacher, H., Filk, T., and Romer, H. (2004). Quantum zero features of bistable perception. Biol. Cybern. 90, 33–40.
Busemeyer, J. R., and Bruza, P. (2011). Quantum Models of Cognition and Decision Making. Cambridge: Cambridge University Press.
Busemeyer, J. R., Pothos, E. M., Franco, R., and Trueblood, J. (2011). A quantum theoretical explanation for probability judgment errors. Psychol. Rev. 118, 193–218.
Elqayam, S., and Evans, J. S. (2011). Subtracting “ought” from “is”: descriptivism versus normativism in the study of the human thinking. Behav. Brain Sci. 233–248.
Gigerenzer, G., and Todd, P. M. (1999). Simple Heuristics that Make us Smart. New York: Oxford University Press.
Griffiths, T. L., Chater, N., Kemp, C., Perfors, A., and Tenenbaum, J. B. (2010). Probabilistic models of cognition: exploring representations and inductive biases. Trends Cogn. Sci. 14, 357–364.
Kahneman, D., and Tversky, A. (1979). Prospect theory: an analysis of decision under risk. Econometrica 47, 263–291.
Khrennikov, A. Y. (2004). Information Dynamics in Cognitive, Psychological, Social and Anomalous Phenomena. Kluwer Academic.
Oaksford, M., and Chater, N. (2007). Bayesian Rationality: The Probabilistic Approach to Human Reasoning. Oxford: Oxford University Press.
Pothos, E. M., and Busemeyer, J. R. (2009a). The fallacy of normativism: falling in love with ourselves. A case for limited prescriptive normativism. Behav. Brain Sci.
Pothos, E. M., and Busemeyer, J. R. (2009b). A quantum probability explanation for violations of “rational” decision theory. Proc. R. Soc. B 276, 2171–2178.
Sanborn, A. N., Griffiths, T. L., and Navarro, D. J. (2010). Rational approximations to rational models: alternative algorithms for category learning. Psychol. Rev. 117, 1144–1167.
Shafir, E., and Tversky, A. (1992). Thinking through uncertainty: nonconsequential reasoning and choice. Cogn. Psychol. 24, 449–474.
Tenenbaum, J. B., Kemp, C., Griffiths, T. L., and Goodman, N. (2011). How to grow a mind: statistics, structure, and abstraction. Science 331, 1279–1285.
Trueblood, J. S., and Busemeyer, J. R. (1992). A comparison of the belief-adjustment model and the quantum inference model as explanations of order effects in human inference. Cogn. Sci.1166–1171.
Tversky, A., and Kahneman, D. (1973). Availability: a heuristic for judging frequency and probability. Cogn. Psychol. 5, 207–232.
Tversky, A., and Kahneman, D. (1983). Extensional versus intuitive reasoning: the conjuctive fallacy in probability judgment. Psychol. Rev. 90, 293–315.
Tversky, A., and Koehler, D. J. (1994). Support theory: a nonextensional representation of subjective probability. Psychol. Rev. 101, 547–567.
Citation: Pothos EM and Busemeyer JR (2011) Formalizing heuristics in decision-making: a quantum probability perspective. Front. Psychology 2:289. doi: 10.3389/fpsyg.2011.00289
Received: 09 May 2011;
Accepted: 11 October 2011;
Published online: 15 November 2011.
Copyright: © 2011 Pothos and Busemeyer. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence:ZS5tLnBvdGhvc0Bzd2Fuc2VhLmFjLnVr