- 1 Department of Psychology, University of Basel, Basel, Switzerland
- 2 Max Planck Institute for Human Development, Berlin, Germany
We have been here before. In psychology and philosophy, character traits have been invoked time and again to argue that people should be disposed to behave consistently across a wide range of trait-relevant scenarios. Take moral behavior. In frameworks ranging from Aristotelian moral psychology, virtue ethics, and Kohlberg’s (1984) developmental stage theory of moral reasoning to contemporary economic theories of fairness (e.g., Fehr and Schmidt, 1999), the same premise applies: The virtues, traits, and social preferences a person possesses and the developmental stages she has passed through supposedly imply consistency in how she will behave in morally relevant situations (see Doris, 2002). But it just isn’t so.
Seemingly inconsequential situational changes can give rise to consequential behavioral inconsistencies. In a classic study by Darley and Batson (1973), for instance, students at the Princeton Theological Seminary – whose current mission statement lists “compassion” among its training objectives – failed to show exactly this quality in the face of a minor contextual change. The experiment required students to walk from one building to another. On the way, and believing that they were running late, merely 10% of the students offered help to a (confederate) person slumped in a doorway. When time was of little concern, however, 63% of them did so. This inconsistency in compassionate behavior is striking given the seemingly minor situational change. Although examples of such inconsistencies abound (Fleischhut and Gigerenzer, in press), the notion of stable virtues remains “deeply compelling” to most of us – notwithstanding the fact that “much of this lore rests on psychological theory that is some 2,500 years old” (Doris, 2002, p. ix).
The lore of stable and domain-general risk preferences arose in the twentieth century (for a canonical reference, see Samuelson, 1938), and it is at least as seductive as theories of robust and context-invariant moral traits and virtues. Without the assumption of stable preferences standard utility models in many fields of economics simply would not work. Yet evidence against this assumption has been mounting for decades (see Friedman and Sunder, 2011). Let us give just two recent examples. Contrary to expected utility theory, Tversky and Kahneman (1992) and Tversky and Fox (1995) showed that, depending on domain (loss versus gain) and probability (low versus high), people behave in both a risk-averse and a risk-seeking way. Specifically, they are risk-averse when the probability of winning is high but risk-seeking when it is low. In the loss domain, in contrast, people are risk-averse when the probability of losing is low but risk-seeking when it is high (Table 1). This “fourfold pattern” runs counter to the assumption of risk aversion as a domain-general trait. It has been shown to arise in decisions from description (Hertwig et al., 2004), where – as is common in choices between monetary gambles such as those used by Kahneman and Tversky (1979) – people are able to peruse descriptions of probability and outcome distributions. Outside the laboratory, however, outcomes and probabilities are rarely known with certainty and served up to the decision-maker on a platter. Consequently, people must often choose between options without having a convenient description of possible choice outcomes, let alone their probabilities. One strategy for overcoming such uncertainty is to sample the payoff distributions to learn about the options’ attractiveness and, based on the experienced information, to come to a decision. In such decisions from experience (Hertwig and Erev, 2009) the fourfold pattern is reversed (Table 1; see also Hertwig, 2011). In other words, inferred risk preferences vary as a function of the mode of decision making (description versus experience) as well as domain (gain versus loss) and probability (low versus high).
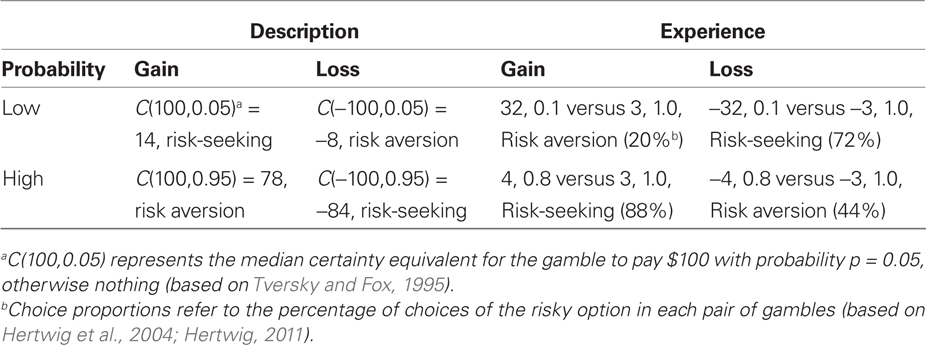
Table 1. Fourfold pattern in decisions from description and reversed pattern in decisions from experience (Hertwig, 2011).
Instability in risk preferences has also been found in real-world data. Starting with the assumption that people are expected utility maximizers, Barseghyan et al. (2011) examined whether the choice of insurance cover in a sample of U.S. households can be modeled by the same coefficient of absolute risk aversion. It could not. Households’ inferred risk preferences proved to be unstable across highly related decision contexts, differing not only between auto insurance and home insurance but also between two different types of auto insurance (collision versus comprehensive).
How to Model Inconsistencies in Behavior
Perhaps the most common response to these demonstrations of unstable risk preferences has been to increase the flexibility of expected utility theory while retaining its original scaffolding. Flexibility comes in the form of additional adjustable parameters. To take one prominent example, cumulative prospect theory (Tversky and Kahneman, 1992) has five adjustable parameters, which allow both for separate value functions for losses and gains and for a probability-weighting function to accommodate the fourfold pattern. In this approach, any further inconsistencies in risk preferences (e.g., Barseghyan et al., 2011) would require additional adjustable parameters – for instance, a parameter that accommodates risk aversion as a function of different insurance domains. Similar attempts to “repair” expected utility theory (Selten, 2001) in light of contrary evidence include introducing error terms into utility models (e.g., Hey and Orme, 1994) and assuming stochastic preferences (e.g., the random preference model; Loomes and Sugden, 1995). The problems with this approach have become obvious. Parameterized repair models, which already assume complex computations, become even more opaque as-if models that cannot describe the underlying decision process.
It is time to move out of this theoretical cul-de-sac. The alternative we propose is to replace the concept of preferences by that of heuristics or, more generally, of cognitive strategies that give rise to diverse behavioral patterns. By “heuristic” we mean a strategy that ignores part of the information in order to make decisions faster and more accurately (Gigerenzer and Gaissmaier, 2011). Although inconsistent behavior presents a problem for the notion of stable preferences, for the framework of heuristics it does not. On the contrary, heuristics imply what looks like inconsistent behavior and can even predict when it will occur. A person who consistently relies on the same heuristic can behave in a seemingly inconsistent way. The inconsistency does not reside, however, in the person; it arises from looking at behavior through the lenses of a theory that assumes stable preferences.
How Lexicographic Heuristics Imply Inconsistencies
Heuristics enable one to model choices indicative of inconsistent risk preferences in terms of the sequential processing steps and the interactions between the heuristic and the choice environment. For illustration, consider the priority heuristic (Brandstätter et al., 2006, 2008), which belongs to the class of lexicographic rules. The heuristic is composed of the following steps (for generalization to loss gambles and multiple outcomes, see Brandstätter et al., 2006):
Search rule. Go through the considerations in the following order: minimum gain, probability of minimum gain, maximum gain.
Stopping rule. Stop examination if the minimum gains differ by 1/10 (or more) of the maximum gain; otherwise, stop examination if probabilities differ by 1/10 (or more) of the probability scale.
Decision rule. Choose the gamble with the more attractive gain (probability). The more attractive gamble is that with the higher (minimum or maximum) gain and the lower probability of leading to the minimum gain.
To demonstrate how the heuristic works, let us return to the fourfold pattern. Table 1 (left panel) reports certainty equivalents C, which represent the amount of money for which a person proves to be indifferent between a risky gamble and the certain amount C. Consider, for instance, the upper-left cell. The median C of $14 exceeds the expected value of the risky gamble ($5,100 with a probability of 5%). People are thus interpreted to be risk-seeking because of their preference for the risky gamble over the sure gain of $5. This information thus lends itself to the construction of choice problems such as the following:
A: 100 with p = 0.05
0 with p = 0.95
B: 5 with p = 1
To predict the majority choice in this gamble, the priority heuristic starts by comparing the minimum gains (0 and 5). The difference in the minimum gain, $5, does not reach the aspiration level of 10 (1/10 of 100) and so fails to discriminate between the options. Consequently, the probabilities of the minimum gains are examined next. These do not discriminate either (1.0–0.95 < 0.10). Therefore, the heuristic turns to the maximum gains (100 and 5) and predicts that the option that offers the higher gain (the risky option) is chosen. This choice, which accords with the certainty equivalent of $14 (Table 1), implies risk-seeking.
Without resorting to non-linear transformations of quantities or to other adjustable parameters, the priority heuristic can correctly predict the entire fourfold pattern of risk preferences in decisions from description and in fact logically implies it (Katsikopoulos and Gigerenzer, 2008). The key to its predictive power is the sequential activation of several classic heuristics. Specifically, in the domain of gains, the heuristic’s first consideration is the only one examined by the minimax heuristic, which embodies risk aversion through its policy of always selecting the option with the highest minimum payoff. Unlike minimax, however, the priority heuristic bases its choice on the minimum outcomes only when the difference between them exceeds an aspiration level. If this aspiration level is not reached, then only the second consideration, the probability of the minimum outcome, is attended to. This consideration captures the policy of the least likely heuristic, which embodies risk aversion by identifying each gamble’s worst outcome and selecting the gamble with the lowest probability of leading to the lowest payoff. Again, the priority heuristic takes advantage of an aspiration level to “evaluate” whether this policy is reasonable. If not, it shifts gears and consults the last consideration, the maximum outcomes. This is the home turf of the maximax heuristic, which chooses the gamble with the highest monetary payoff, thus implementing unconditional risk-seeking.
The priority heuristic thus integrates three classic heuristics into one and works through them sequentially. As a result, it can produce risk-averse or risk-seeking choices, depending on the number of considerations that a particular choice problem requires the heuristic to examine. Moreover, depending on the specific sequence of successive choice problems, a user of the heuristic may seem to act risk-averse one minute and risk-seeking the next only to switch back to what appears to be aversion again. This pattern of behavior does not reflect unstable risk preferences, however, but rather follows directly from the interaction of the heuristic’s architecture with the choice environment. Admittedly, one could still defend the notion of a general risk disposition by arguing that risk-averse or risk-seeking people choose different heuristics from their adaptive toolbox. But if that were true, then risk-averse people should consistently use minimax and risk-prone people maximax – not the priority heuristic. The evidence does not support this conjecture (Brandstätter et al., 2006). Finally, note that the priority heuristic, like any heuristic, is not a domain-general strategy. It operates on explicitly stated (described) probabilities, and thus cannot explain the reversed fourfold pattern in decisions from experience (Table 1; for a psychological account of this class of decisions see, for instance, Gonzalez and Dutt, 2011).
How Heuristics in the Social World Imply Behavioral Inconsistencies
The interaction between a heuristic and the environment may also be the key to understanding apparent behavioral inconsistencies in morally relevant situations. For illustration, consider the equity heuristic (Hertwig et al., 2002), according to which parents divide their resources among their n children equally in any given investment interval. The heuristic can produce both equal and unequal cumulative distributions of parental resources and thus a fairer or less fair outcome. It does not, however, create both equality and inequality through inconsistent preferences. Instead, depending on the environment – specifically, the number of children, their birth order, and the size of interbirth intervals – the equity heuristic implies equal or unequal investments across children. The case of organ donation illustrates how another simple strategy, the default heuristic, can produce predominantly altruistic behavior in “opt-out” countries such as France and Austria and predominantly non-altruistic behavior in Germany and the Netherlands, where people must “opt in” to be donors. Again, the drastically different hypothetical organ donation rates are not a reflection of inconsistent preferences or traits in neighboring societies but rather the product of the interaction between an environment (here, the legal default) and the heuristic (which accepts the default; Fleischhut and Gigerenzer, in press).
Conclusion
Inconsistencies in observed behavior have been interpreted as conflicting with assumed stable preferences or traits. According to our analysis, the problem lies not in the inconsistent behavior but in the assumed existence of preferences, whether stable, probabilistic, or of another kind. We show that a theoretical analysis that explains behavior as a function of heuristics’ interactions with the environment can do more than describe seeming behavioral inconsistencies post hoc; it can predict precisely when such inconsistencies will occur.
Acknowledgments
We thank Laura Wiles and Valerie M. Chase for editing the manuscript. The first author was supported by the Swiss National Science Foundation (Grant 10014-126558).
References
Barseghyan, L., Prince, J., and Teitelbaum, J. C. (2011). Are risk preferences stable across contexts? Evidence from insurance data. Am. Econ. Rev. 101, 591–631.
Brandstätter, E., Gigerenzer, G., and Hertwig, R. (2006). The priority heuristic: Making choices without trade-offs. Psychol. Rev. 113, 409–432.
Brandstätter, E., Gigerenzer, G., and Hertwig, R. (2008). Risky choice with heuristics: reply to Birnbaum (2008), Johnson, Schulte-Mecklenbeck, and Willemsen (2008) and Rieger and Wang (2008). Psychol. Rev. 115, 281–290.
Darley, J. M., and Batson, C. D. (1973). From Jerusalem to Jericho: a study of situational and dispositional variables in helping behavior. J. Pers. Soc. Psychol. 27, 100–108.
Doris, J. M. (2002). Lack of Character: Personality and Moral Behavior. New York: Cambridge University Press.
Fehr, E., and Schmidt, K. M. (1999). A theory of fairness, competition, and cooperation. The Quarterly Journal of Economics 114, 817–868.
Fleischhut, N., and Gigerenzer, G. (in press). “Beyond character: social heuristics explain moral behavior,” in Simple Heuristics in a Social World, eds R. Hertwig, U. Hoffrage, and the ABC Research Group (New York: Oxford University Press).
Friedman, D., and Sunder, S. (2011). Risk Curves: From Unobservable Utility to Observable Opportunity Sets (June 6, 2011). Yale Economics Department Working Paper. Available at: http://ssrn.com/abstract=1858769
Gigerenzer, G., and Gaissmaier, W. (2011). Heuristic decision making. Ann. Rev. Psychol. 62, 451–482.
Gonzalez, C., and Dutt, V. (2011). Instance-based learning: integrating sampling and repeated decisions from experience. Psychol. Rev. 118, 523–551.
Hertwig, R. (2011). The psychology and rationality of decisions from experience. Synthese. doi: 10.1007/s11229-011-0024-4
Hertwig, R., Barron, G., Weber, E. U., and Erev, I. (2004). Decisions from experience and the effect of rare events in risky choice. Psychol. Sci. 15, 534–539.
Hertwig, R., Davis, J. N., and Sulloway, F. J. (2002). Parental investment: how an equity motive can produce inequality. Psychol. Bull. 128, 728–745.
Hertwig, R., and Erev, I. (2009). The description-experience gap in risky choice. Trends Cogn. Sci. 13, 517–523.
Hey, J. D., and Orme, C. (1994). Investigating generalizations of expected utility theory using experimental data. Econometrica 62, 1291–1326.
Kahneman, D., and Tversky, A. (1979). Prospect theory: an analysis of decision under risk. Econometrica 47, 263–292.
Katsikopoulos, K. V., and Gigerenzer, G. (2008). One-reason decision-making: Modeling violations of expected utility theory. J. Risk Uncertain. 37, 35–56.
Kohlberg, L. (1984). Essays in Moral Development: The Psychology of Moral Development, Vol. 2. New York: Harper & Row.
Loomes, G., and Sugden, R. (1995). Incorporating a stochastic element into decision theories. Eur. Econ. Rev. 39, 641–648.
Selten, R. (2001). “What is bounded rationality?” in Bounded Rationality: The Adaptive Toolbox, eds G. Gigerenzer and R. Selten (Cambridge, MA: MIT Press), 13–36.
Citation: Hertwig R and Gigerenzer G (2011) Behavioral inconsistencies do not imply inconsistent strategies. Front. Psychology 2:292. doi: 10.3389/fpsyg.2011.00292
Received: 01 July 2011;
Accepted: 11 October 2011;
Published online: 15 November 2011.
Copyright: © 2011 Hertwig and Gigerenzer. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence:cmFscGguaGVydHdpZ0B1bmliYXMuY2g=

