1 Who Knows a Utility Representation
Repeatedly it is alleged that this or that theory concerns a decision maker maximizing some utility function. But, as I have been at pains to discuss, the representation is not a creature of the decision maker but of the scientist studying the decision maker’s behavior “The representation theorems go in only one direction: from behavioral and structural properties to numerical representations. The behavioral properties embody the scientific information that we, as scientists, have about the decision maker. It is the scientist, not the decision maker, who formulates both the properties (axioms) and the representation. The decision maker exhibits the behavior which, presumably, arises from some fairly complex neuronal processes…” (Luce, 2000, p. 25). This observation holds far more broadly than just in decision making.
2 Uniqueness of the Representation
Uniqueness of representations is, of course, a very well trodden topic. The gist is that in addition to proving a representation theorem, one must also formulate a uniqueness theorem – how do the several representations relate? In most of the popular measurement theories, the uniqueness falls into one of Stevens’ (1946, 1951) well known classification: nominal, ordinal, interval, log-interval, ratio, and absolute scales (see Krantz et al., 1971; Luce et al., 1990).
As I recently came to realize, when we are dealing with a preference weak order ≥ and a binary operation ⊕, such as the concatenation of two sums of money, for which 0 money is an identity of ⊕ and ⊕ is commutative, associative, and monotonic in ≥, things are not really quite as simple as has been long believed.
Recall that Hölder (1901) proved in this context the existence of an additive representation
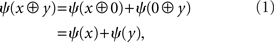
which is unique up to a ratio scale.
A century later it was recognized that, in the context of utility theory, we also have the interplay between value and risk, which means that multiplication as well as addition is in play. See, e.g., (3) below. So the mapping should be into 〈ℝ, ≥, +, ×〉, in which case the full set of polynomial (p-additive) representations are (see Luce, 2000, p.151, § 4.4.6)
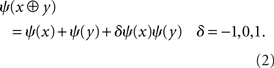
Of course, δ = 0 is Hölder’s original solution. The other two are quite different in that they are absolute scales (see Luce, 2010a). Here is the reason: when δ ≠ 0, (2) is equivalent to
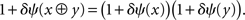
But this expression is not invariant under any transformation of ψ other than the identity. The fact they are absolute scales has several important implications.
3 Some Implications of the p-Additive Representation
3.1 Three Types of People
There are three inherently different types of people corresponding to their values of δ. The following simple behavioral criterion to decide a particular person’s type was reported by Luce (2010a).
Let (x, p; y, 1 − p) denote the gamble where x occurs with probability p and y with probability 1 − p and suppose, as is true in a great many theories of utility, that
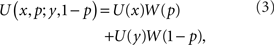
where ψ has been replaced in this context by U for utility, W is a strictly increasing subjective probability function, and W(0) = 0. Further, assume that
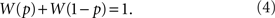
Find the probability p1/2 with subjective probability 1/2, i.e., such that for the representation (3) and for all x > y
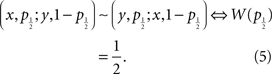
I assume that W(p) = p is satisfied for p = 0, p = p1/2, possibly for p = 1, but not elsewhere. Note that it follows that relative to the line f(p) = p, the weighting function W must be either S-shaped or inverse S-shaped. See Section 3.4 of Luce (2000) for a summary of empirical estimates which seem to agree with this prediction.
Then the criterion for δ is that for all x > x′ > y > y′
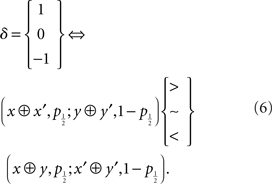
Observe that under the ordering constraint on the consequences, the gamble on the left has a greater variance than the one on the right. For that reason, the three δ types are called, respectively, risk-seeking (δ = 1), risk-neutral (δ = 0), and risk-averse (δ = −1). It would not surprise me that in the academic population, which is the source of many experimental respondents, risk-averse types will predominate except, perhaps, in schools of business.
It has yet to be shown empirically that this classification holds up in the population. But should it, one simply should not average data over people without, at the least, dealing with the three classes separately. Indeed, really only the δ = 0 types should ever be averaged. Individual differences are important. This has significant implications – e.g., many behavioral economic experiments should be redone taking into account individual types (Luce, 2010b).
3.2 Utility Forms of Risk Types
Three forms of utility follow from (2) and (6): there exist positive constants α, κ, and λ such that
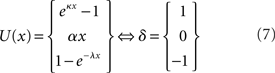
(Luce, 2010a). Note that for δ = 1, this function is bounded from below by −1 and unbounded from above, whereas for δ = −1 it is unbounded from below and bounded by 1 from above.
3.3 Interpersonal Comparisons of Utility
Because the δ ≠ 0 scales are absolute, interpersonal comparisons become meaningful, although for a mix of −1 and 1 types, only in the common interval (−1,1) (Luce, 2010a). No such comparisons can be made involving risk-neutral types of people. If correct, this makes sense of the fact that classical utility theorists have found interpersonal comparisons impossible (e.g., Robbins, 1938; Harsanyi, 1977; Elster and Roemer, 1991; Hammond, 1991; Binmore, 2009) although most of us intuit that we regularly make such comparisons. And just how many of us are risk-neutral?
3.4 Psychophysical Scaling in General
As I have thought more about subjective intensity scales, I have come to realize that many other attributes of subjective intensity closely resemble the utility theory of risk except that most are defined only on the non-negative real numbers (Luce, under review). Indeed, the only exceptions that I know of involve what can be called binary senses that involve the close interaction of the two ears and of the two eyes. The binary theory coupled with certain loudness and brightness data simply rule out the two δ ≠ 0 cases.
Thus, when we ask a respondent to match subjective intensities of one modality to those of another modality, then, because of the three values of δ arise for all but the binary attributes, we get a complex of predicted results (Luce, under review, Table 1). This fact suggests an extensive experimental program to be done.
4 Closing Remarks
I have made a strong claim here, namely, that a slight mathematical oversight – mapping just into addition when, for other theoretical reasons, multiplication is also involved – has put us on a misguided course for over a century. And that course may, in a number of ways, have been scientifically misleading.
Acknowledgments
This research was supported in part by the U. S. Air Force Office of Research grant FA9550-08-1-0468 – any opinion, finding, and conclusions or recommendations expressed in this material are those of the author and do not necessarily reflect the views of the Air Force. I thank Dr. Ragnar Steingrimsson, my empirical collaborator, for detailed and helpful comments on a draft version of this opinion piece.
References
Binmore, K. (2009). “Interpersonal comparison of utility,” in Oxford Handbook of the Philosophy of Economics, Chapter 20, eds H. Kincaid and D. Ross (New York, NY: Oxford University Press), 540–559.
Elster, J., and Roemer, J. (eds).(1991). Interpersonal Comparisons of Well-Being. London: Cambridge University Press.
Hammond, P. (1991). “Interpersonal comparisons of utility: why and how they are and should be made,” in Interpersonal Comparisons of Well-Being, eds J. Elster and J. Roemer (London: Cambridge University Press), 200–254.
Harsanyi, J. (1977). Rational Behavior and Bargaining Equilibrium in Games and Social Situations. Cambridge: Cambridge University Press.
Hölder, O. (1901). Die Axiome der Quantität und die Lehre vom Mass. Ber. Verh. Kgl. Sächsis. Ges. Wiss. Leipzig Math.-Phys. Classe. 53, 1–64.
Krantz, D. H., Luce, R. D., Suppes, P., and Tversky, A. (1971). Foundations of Measurement, Vol. I, Reprinted 2007. New York: Academic Press.
Luce, R. D. (2010a). Interpersonal comparisons of utility for 2 of 3 types of people. Theory Decis. 68, 5–24.
Luce, R. D. (2010b). Behavioral assumptions for a class of utility theories: a program of experiments. J. Risk Uncertain. 41, 19–27.
Luce, R. D., Krantz, D. H., Suppes, P., and Tversky, A. (1990). Foundations of Measurement: Vol.III. Representations, Axiomatization, and Invariance, Reprinted 2007. San Diego: Academic Press.
Citation: Luce RD (2011) Inherent individual differences in utility. Front. Psychology 2:297. doi: 10.3389/fpsyg.2011.00297
Received: 06 August 2011;
Accepted: 11 October 2011;
Published online: 15 November 2011.
Copyright: © 2011 Luce. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with
*Correspondence:cmRsdWNlQHVjaS5lZHU=
