- 1 Department of Psychology, University of Warwick, Coventry, UK
- 2 Department of Psychology, University of Essex, Colchester, UK
To what extent are preferences for risk – and for other economic quantities – stable, and to what extent are they malleable and context-dependent? Judgments and choices are strongly influenced by the context of available options in both the laboratory and the real world (e.g., Parducci, 1995; Sharpe et al., 2008), and this applies both to choices between risky options and more generally (Stewart et al., 2003). What cognitive processes underpin these contextual influences? According to the decision by sampling model (DbS: Stewart et al., 2006), judgments of a stimulus in a context depend solely on the relative ranked position of the stimulus within the remembered or experienced context of judgment. The claim that only relative ranked position matters appears, however, to contradict both empirical data and an earlier model of judgment, range frequency theory (RFT: Parducci, 1965, 1995), according to which the position of a stimulus with respect to the highest and lowest stimuli in the context (its range position) also matters. Here we show that a purely rank-based approach can account for apparent range effects when the relative memorability of contextual items, as independently determined by a memory model (Brown et al., 2007), is taken into account.
Such a demonstration is important for several reasons. In particular, it is important to understand whether the skew of a distribution (e.g., the degree of inequality of an income distribution) influences the judgments of items (e.g., individuals’ own incomes) within that distribution. If judgments are based solely on relative rank (as DbS claims), there should be no effects of distribution skewness – yet such effects are frequently observed. For example, there is a tension between the claim that income inequality within a society influences various indices of societal well-being (e.g., Wilkinson and Pickett, 2009) and the claim that individuals are primarily or solely concerned with the ranked position of their income (Boyce et al., 2010). Here we address this tension directly.
The Decision by Sampling model assumes that, when making a judgment, people draw a sample from memory, the choice environment, or both. They then compare, ordinally, the to-be-judged stimulus with each sample item. Consider the problem of determining one’s wage satisfaction. According to DbS, one might call to mind two individuals who get paid less (Nlower = 2), and three individuals who get paid more (Nhigher = 3). That is, one is the i’th most highly paid person out of n, where i = 3 and n = 6. The resulting estimate of one’s relative ranked position, Fi, is according to DbS simply:
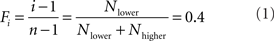
Crucially, such a judgment can be based on cognitively basic ordinal binary comparisons.
The rank-based process in DbS explains how changes in the distribution of contextual items will influence judgment. Consider for example a positively skewed set of wages, with many relatively low earners and few relatively high earners. Such a distribution is illustrated in Figure 1A, along with a range-matched negatively skewed distribution. If satisfaction comes from a wage’s relative ranked position in its context, the function relating satisfaction to wage will be concave for a positively skewed distribution, because relative ranked position will rise faster with income at the lower part of the distribution. As one moves higher up the positively skewed distribution, it becomes progressively more expensive to buy each additional increment in relative rank. And indeed, participants’ judgments are described by just such a concave function, with a corresponding convex function being associated with a negatively skewed distribution (Figure 1C). The judgments are taken from Brown et al. (2008) and are here normalized to lie between 0 and 1. Figure 1B shows a second pair of distributions designed to examine relative rank effects – the highlighted item pairs have the same absolute value, are located in distributions matched for mean and endpoints, and hence differ only in their relative rank within their respective contexts. Again, the satisfaction associated with each hypothetical wage is influenced by its relative rank (Figure 1D). More generally, DbS has been used to explain why apparent utility curves have the shape they do (e.g., the concave relationship between utility and money arises because of the positively skewed distribution of financial gains in the environment) and more specifically to give a process-level account of why models such as Prospect Theory (Kahneman and Tversky, 1979), work well descriptively (Stewart et al., 2006; Stewart, 2009).
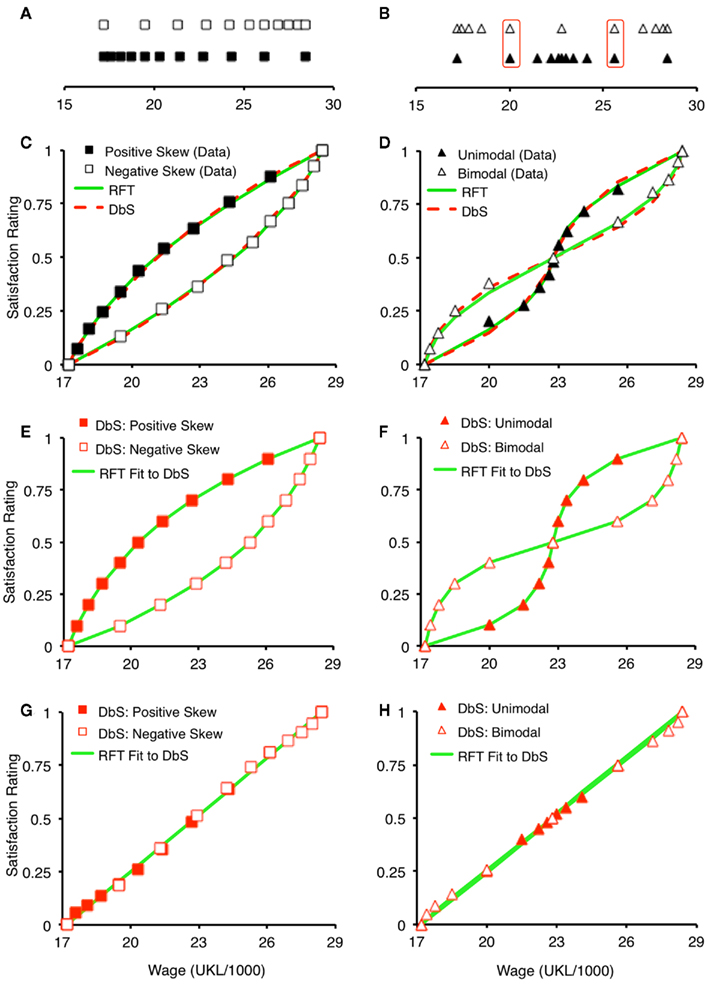
Figure 1. Comparison of the predictions of RFT and the combined DbS-SIMPLE model (see text for details). (A) Positively and negatively skewed wage distributions. (B) Bimodal and unimodal wage distributions. (C,D) Fit of RFT and DbS-SIMPLE to wage satisfaction judgments. (E,F) Predictions of DbS-SIMPLE model with high memory discriminability, and fit of RFT to those predictions. (G,H) Predictions of DbS-SIMPLE model with low memory discriminability, and fit of RFT to those predictions.
Although numerous studies appear consistent with the relative rank principle in DbS, additional effects of the range position of stimuli are often observed. DbS was motivated partly by, and inherits much of the support for, an earlier – and highly influential – account of contextual judgment: RFT. Although less oriented toward providing a process-level account, and focused more on experimental rather than remembered contexts, RFT shares with DbS the assumption that the relative ranked position of an item within its context will affect its judgment. However, unlike DbS, RFT predicts that the position of an item with respect to the highest and lowest stimuli will also affect its judgment. Here we aim to reconcile the apparent presence of range effects (as postulated by RFT) with the purely rank-based processes of DbS. In RFT, Mi, the subjective psychological magnitude of xi, (where xi is the ith largest in a set of n stimuli) will be given by:

where Ri is the range value of xi:

and Fi is the relative ranked ordinal position (or “frequency value”) of the item in the ordered set, as used in DbS and given by Eq. 1 above (although DbS assumes a retrieved rather than experimentally provided context).
Thus (according to RFT), the subjective magnitude of a stimulus in a context will depend on (a) the position of the stimulus along a line joining the lowest and highest points in the set and (b) the rank ordered position of the stimulus. In Eq. 2, w is a weighting parameter which is often estimated at approximately 0.5 for physical judgments.
Range frequency theory has been highly successful as a descriptive account of judgments in context (Parducci, 1995). However, an important part of RFT’s success comes from its inclusion of a range-based as well as a rank-based component. For example, the solid green lines in Figures 1C,D show the fit of RFT to the wage satisfaction judgments. The estimated values of w that led to this fit were 0.32 (C) and 0.43 (D), suggesting that both range and rank affect judgment (see Eq. 2).
It might therefore appear to be a serious limitation of DbS that it predicts only effects of relative rank and not additional effects of range (and hence, as noted earlier, of skew). Here, however, we argue that apparent range effects could reflect the reduced psychophysical discriminability of items in relatively crowded regions of psychological space, as predicted by models of memory. For example, the SIMPLE model of memory (Brown et al., 2007) views memory retrieval as a discrimination task. An important dimension along which discrimination occurs is assumed to be temporal (Brown et al., 2009), as is needed to explain forgetting, but here we focus on the dimension along which judgment must be made (e.g., the amount of a wage). Central to the model is the notion of distinctiveness (intuitively: items are viewed as distinctive, and hence discriminable in and retrievable from memory, to the extent that they occupy relatively isolated locations in multidimensional psychological space).
We first provide an intuitive example. Consider the median wage (20) highlighted in the following context of wages: [5 10 15 20 23 24 25]. If all contextual items are included in the sample, the relative ranked position of 20 will be 0.5 [Nlower/(Nhigher + Nlower) = 3/6]. Suppose however that the three wages above the median are less distinctive in memory (because they are close to one another), and that each has a probability of being included in the sample of just 0.5. The judgment of the median wage will then be (Nlower)/(Nhigher + Nlower) = 3/4.5 = 0.67. This falls between the relative ranked position of 20 (which was 0.5) and the range position of 20 (which, by Eq. 3, is 0.75). Thus, a purely rank-based account such as DbS may be able to account for apparent range effects when the distinctiveness and hence availability in memory of contextual items is incorporated. We illustrate with a basic implemented model.
According to the SIMPLE model, the confusability of any two items in memory will be a reducing exponential function of the distance between them in psychological space:

where ηi,j is the similarity between items i and j and di,j the distance between them (here, the distance along the dimension of judgment that separates the two items – e.g., a difference in wages). We assume that the probability of an item being included in a sample used for judgment will depend on its retrievability. In SIMPLE, the retrievability of an item will depend on its discriminability, where the discriminability of item i is inversely proportional to its summed similarity to every other potentially available stimulus. Specifically, the discriminability of the trace for item i, Di, is given by:

where n is the number of available response alternatives (this will be just the number of available potential comparison stimuli). Discriminability is converted into predicted recall probability by taking into account the possibility of omissions. If Di is the discriminability given by the preceding equation, the recall probability Pi is given by:

where t is the threshold (such that if discriminability is below a threshold an item cannot be retrieved) and s determines the slope of the transforming function (effectively, how noisy the omission threshold is).
We now illustrate, using the wage satisfaction data, how a DbS model can give rise to apparent range effects when supplemented by this model of memory distinctiveness and retrieval. The model assumes that the probability of each item being included in the sample that determines judgment is predictable from the SIMPLE model (Eqs 5–7 above). The satisfaction with each wage was assumed to be based purely on the relative rank of each wage within its context (as in Eq. 1), but with each item weighted by the probability of it being included in the sample.
The fit of the model to the wage satisfaction data (Figures 1C,D) is shown as a dashed red line. Parameter values were c = 2.11, t = 0.47, s = 4.24 for all four (positive, negative, unimodal and bimodal) distributions. Despite not including any range-based component, the model fits the data as well as does RFT (solid green line) – fits were not statistically distinguishable on the illustrative data, although we note that the combined model has additional parameters. The reason for the combined model’s behavior is as stated above – the items in relatively crowded regions of stimulus space are less distinctive and hence contribute less to the rank-based comparison process in DbS than they would if they were equally likely to enter (or carried equal weight within) the sample.
To explore the combined (SIMPLE + DbS) model, we derived its predictions under various assumptions about memory discriminability, then examined how well RFT would fit the model’s behavior. We first set c to a large number, with the result that all items could be perfectly discriminated and all contributed to the rank-based judgment. Results are shown in Figures 1E,F, where it is evident that strong rank effects are produced – as expected, because items are equally discriminable and all contribute to judgment. The solid lines show the SSE-minimizing fit of RFT to the data generated from the model; the estimated value of w was 0 (i.e., RFT accommodated the fact that only rank-based comparison occurred).
Figures 1G,H show the predictions of the model when c = 1.8 (left column) and 1.6 (right column). Parameters t and s were set at 0.8 and 5 respectively for both pairs of distributions. The best-fitting version of RFT estimated w = 0.95, indicating that the output of the rank-based model was interpreted by RFT as a predominantly range-based model.
In summary, apparent range effects can emerge from a purely rank-based judgment model when item discriminability is accommodated. Thus apparent range effects need not support RFT over purely rank-based accounts. Moreover, effects of distribution skew (e.g., income inequality) need not be inconsistent with the operation of purely rank-based judgments. Finally, we note that although the SIMPLE + DbS model behaves similarly to RFT under the conditions described above, the models are not formally identical and can make different predictions.
Acknowledgment
This research was supported by grant RES-062-23-2462 from the Economic and Social Research Council (UK).
References
Boyce, C. J., Brown, G. D. A., and Moore, S. C. (2010). Money and happiness: rank of income, not income, affects life satisfaction. Psychol. Sci. 21, 471–475.
Brown, G. D. A., Gardner, J., Oswald, A. J., and Qian, J. (2008). Does wage rank affect employees’ well-being? Ind. Relat. 47, 355–389.
Brown, G. D. A., Neath, I., and Chater, N. (2007). A temporal ratio model of memory. Psychol. Rev. 114, 539–576.
Brown, G. D. A., Vousden, J. I., and McCormack, T. (2009). Memory retrieval as temporal discrimination. J. Mem. Lang. 60, 194–208.
Kahneman, D., and Tversky, A. (1979). Prospect theory: an analysis of decision under risk. Econometrica 47, 263–291.
Parducci, A. (1995). Happiness, Pleasure and Judgment: The Contextual Theory and its Applications. Mahwah, NJ: Lawrence Erlbaum Associates.
Sharpe, K. M., Staelin, R., and Huber, J. (2008). Using extremeness aversion to fight obesity: policy implications of context dependent demand. J. Consum. Res. 35, 406–422.
Stewart, N. (2009). Decision by sampling: the role of the decision environment in risky choice. Q. J. Exp. Psychol. 62, 1041–1062.
Citation: Brown GDA and Matthews WJ (2011) Decision by sampling and memory distinctiveness: range effects from rank-based models of judgment and choice. Front. Psychology 2:299. doi: 10.3389/fpsyg.2011.00299
Received: 30 July 2011;
Accepted: 11 October 2011;
Published online: 15 November 2011.
Copyright: © 2011 Brown and Matthews. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence:Zy5kLmEuYnJvd25Ad2Fyd2ljay5hYy51aw==

