- 1 Knowledge Media Research Center, Tuebingen, Germany
- 2 Department of Psychology, Eberhard-Karls University, Tuebingen, Germany
- 3 Institute of Mathematics and Computing, Ludwigsburg University of Education, Ludwigsburg, Germany
Children typically learn basic numerical and arithmetic principles using finger-based representations. However, whether or not reliance on finger-based representations is beneficial or detrimental is the subject of an ongoing debate between researchers in neurocognition and mathematics education. From the neurocognitive perspective, finger counting provides multisensory input, which conveys both cardinal and ordinal aspects of numbers. Recent data indicate that children with good finger-based numerical representations show better arithmetic skills and that training finger gnosis, or “finger sense,” enhances mathematical skills. Therefore neurocognitive researchers conclude that elaborate finger-based numerical representations are beneficial for later numerical development. However, research in mathematics education recommends fostering mentally based numerical representations so as to induce children to abandon finger counting. More precisely, mathematics education recommends first using finger counting, then concrete structured representations and, finally, mental representations of numbers to perform numerical operations. Taken together, these results reveal an important debate between neurocognitive and mathematics education research concerning the benefits and detriments of finger-based strategies for numerical development. In the present review, the rationale of both lines of evidence will be discussed.
At an early stage of development, children learn the basic principles of numbers and arithmetic with the help of external finger-based representations of numerical quantity (e.g., Butterworth, 1999). Indeed, accumulated evidence suggests that such early finger-based representations have a considerable influence on children’s manipulation of symbolic Arabic digits, as well as on the development of both basic numerical competencies (e.g., understanding of numerical magnitude) and arithmetical competencies (e.g., successful performance of the carry operation in addition later on), hereafter referred to by the acronym numerical/arithmetical competencies. However, the question as to whether reliance on finger-based representations remains beneficial or whether it becomes detrimental is subject of an ongoing debate between researchers in neurocognitive science and mathematics education. In the present article, the state of the art in neurocognitive and mathematics education literature shall be reviewed. In a second step, we ask important questions relevant to an integrated view of finger-based strategies in numerical/arithmetical development in neurocognitive and mathematics education research.
Neurocognitive Perspective
From a neurocognitive perspective, finger counting provides multisensory input that conveys information on both cardinal and ordinal aspects of numbers. Here, the number of fingers and their arrangement on both hands plays a fundamental role in first applications of externalized representations of numerical magnitude in initial counting and calculation. The importance of such embodied finger-based representations of number magnitude is further illustrated by findings suggesting that blind children (Crollen et al., 2011) and even children with amputated hands and forearms (Poeck, 1964) use their (phantom) hands and fingers as external quantifiers.
In line with such findings, recent neurocognitive data indicate that finger gnosis is associated with children’s numerical/arithmetical competencies, including computational skills (e.g., Noël, 2005; Penner-Wilger et al., 2007a,b). Even in adults, recent evidence suggests that the link between finger (counting) patterns and semantic cardinal number magnitudes is stronger for canonical (e.g., 7 represented by 5 and 2 fingers) as compared to non-canonical finger patterns (e.g., 7 represented by 4 and 3 fingers; Di Luca and Pesenti, 2008; Di Luca et al., 2010). This suggests a close link between finger counting and the representation of abstract number magnitude in healthy adults (Di Luca et al., 2006; Di Luca and Pesenti, 2010). However, the exact origin of this link is still debated. On the one hand, Brozzoli et al. (2008) showed that the association of numbers and fingers is modulated by palm orientation. This suggests a more general association of relatively smaller and larger numbers with “left” and “right,” respectively, independent of specific fingers (e.g., see also Ishihara et al., 2006). On the other hand, Di Luca et al. (2006, 2010; see also Di Luca and Pesenti, 2008, 2010) have presented converging evidence indicating a direct association of specific numbers embodied as specific fingers/finger patterns.
Finally, recent neuroimaging data suggest that the neural correlates of finger and number representations are located in neighboring or even overlapping cortex areas (see e.g., Kaufmann et al., 2008). From a neurocognitive view, this link seems to be functional and not exclusively correlational. For instance, Gracia-Bafalluy and Noël (2008) observed that systematic training of finger gnosis led to an improvement of numerical performance. Moreover, Badets and Pesenti (2011) showed that learning to associate certain finger movements with meaningless syllables automatically associated certain magnitudes with the same syllables (see also Andres et al., 2008b for a review on finger-based numerical associations).
Yet, recent research not only investigated associations between finger-based representations and numerical/arithmetical competencies but also specified the importance of mode and structure in the interrelation of finger and number representations, with space and base being particularly relevant in this context.
In terms of space, recent studies indicate a reliable influence of finger-based representations on the spatial representation of number magnitude. For individuals (Fischer, 2008) and cultures (Lindemann et al., 2011) that start counting predominantly with their left hand – that is, associating small numbers with the left – indications of a left-to-right-oriented mental number line dominate. A successful and functioning spatial representation of numbers in children is associated with more elaborate calculation skills (e.g., Bachot et al., 2005; Booth and Siegler, 2008). Thus, an indirect influence of embodied finger-based representations of numbers on general numerical/arithmetical competencies can be expected (Gracia-Bafalluy and Noël, 2008, see also Fischer and Brugger, 2011 for a review).
Second, with respect to the representation of base the German and many other, but not all, finger counting systems are so-called sub-base 5 systems. In sub-base 5 systems, numbers such as 7 are always coded as 5 + 2 (i.e., one whole hand and two more fingers), but never as, for instance, 4 + 3 (e.g., Brissiaud, 1992). Moreover, the finger symbol for 2 within the finger symbol for 7 is identical to the finger symbol for the number 2. Interestingly, this structural ambiguity seems to influence the processing of symbolic Arabic digits: specific sub-base 5 effects have been observed for deaf signers (Iversen et al., 2004, 2006; Domahs et al., 2010), children (Domahs et al., 2008), and even healthy adult participants (Domahs et al., 2010). In the latter study, sub-base 5 effects in a magnitude comparison task were found to be more pronounced for German as compared to Chinese adults. Importantly, the German, not the Chinese, finger counting system involves a sub-base of 5. In the Chinese system numbers between 6 and 10 are coded symbolically using only one rather than two hands. Finally, in the study by Domahs et al. (2008), primary school children were required to solve simple (sum < 10) or complex (sum > 10) addition problems. Importantly, the probability that numbers differing from the correct result by 5, and thus by one hand, were produced as erroneous responses was reliably higher than expected on the basis of their distance to the correct result. This increased probability of wrong-by-5 errors is interpreted as a direct influence of the structure of finger-based representations on mental arithmetic involving symbolic Arabic digits (see also Klein et al., 2011 for sub-base 5 effects in addition in adults).
In summary, the above-reviewed evidence indicates that there is a functional link between both the spatial layout as well as the base structure of finger counting systems and numerical/arithmetical competencies. Therefore, neurocognitive researchers conclude that successful finger counting and finger-based arithmetic serve as building blocks for later numerical/arithmetical development and thus should be taught early in kindergarten and primary school.
Nevertheless, the study of Domahs et al. (2008) is also relevant to the direction of embodied finger-based influences. Generally proficient finger gnosis and finger counting/calculation abilities are regarded as beneficial for numerical/arithmetic development in the neurocognitive literature (see above). However, the data of Domahs et al. (2008) suggest that this may only be part of the story: Driven by the sub-base 5 structure of the finger counting system, the probability of specific split-5 errors is increased and finger-based representations are seen as the reasons for these errors. Thus, in this specific case finger-based representations are not beneficial but detrimental instead – a view held prominently in the literature of mathematics education research presented in the following section.
Mathematics Education Perspective
Research in mathematics education assumes that young children begin performing calculations by counting, mostly using their fingers (Schipper, 2005). Nevertheless, a problem may arise when first elements of numeracy anchored on finger counting are perpetuated to the point of hindering the necessary passage to an understanding of numerosity, of operations, and of computational strategies. Krauthausen and Scherer(2001, see also Padberg and Benz, 2011) report several findings that reveal the tension between the relevance of counting on the one hand and the problems this may cause on the other:
• Counting is a fundamental competency. However, persistent use of this strategy alone may lead to severe problems with computational tasks.
• Weaker children have trouble generating computational strategies from finger counting. In the long run, children who only use counting strategies tend to obtain fewer correct results than those who also use other computational strategies.
Mathematics education research recommends fostering mental numerical representations so as to induce children to abandon finger counting at the end of first or beginning of second grade, at the latest. More precisely, this entails shifting from finger counting to performing computations with the help of concrete structured representations and finally, to base computations on abstract mental representations of numbers (e.g., Floer, 1995; Kaufmann and Wesselowski, 2006). At the end of these phases numbers should no longer be represented as sequences of single units (e.g., fingers), but as decomposable into larger entities. In fact, the failure to abandon finger-based representations is seen as one possible reason for children’s computing errors in second grade.
The goal in current mathematics education is to ensure that children understand their computations and acquire computational flexibility. One priority is that early counting should implicitly convey mathematical features, such as the associative and commutative properties of addition and multiplication. For example:
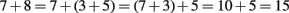
or
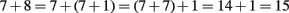
or
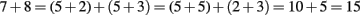
These examples illustrate that adequate decompositions and compositions of numbers become a basis for flexible calculation, where, for example, 8 can be seen as 3 + 5, 7 + 1, or as 5 + 3. Making conscious use of these decompositions requires that these become automatic in children’s minds. This automatism should not be acquired through memorization but rather emerge through children’s handling of representations both enactively and mentally (Wessolowski, 2010).
Most frameworks for early arithmetic in mathematics education are characterized by a debate between the positions of different representation methodologies (Maier, 1990; Butterworth et al., 2011). Accordingly, it is questioned whether such decompositions can be developed through mere use of one’s fingers? Most authors agree that fingers should be treated as belonging to possible representational devices. Some mathematics educators do propose using fingers not only for sequential counting but also for representing numbers (Lorenz and Radatz, 1993). Schipper (2005, 2009) describes exercises with fingers for subitizing and quasi-subitizing numbers up to 10 (see also Eckstein, 2011 for finger-based strategies for numbers up to 1,000). However, comparable to neurocognitive research it has been observed that the use of fingers for counting and performing numerical operations stresses a cognitive anchoring on 5 and 10, that is, on sequential strategies that do not foster representations of numbers as cardinal entities (Moser Opitz, 2009; Gaidoschik, 2010).
In the end, flexibility with regard to representational changes is considered a core component of performing successful arithmetical operations. Yet, in the first phase of this debate methodologies strictly based on counting had a strong impetus (Eckstein, 2011) and were practiced for more than four decades. The birth of the “New Math” era in the 1960s led educators to promote a methodology whereby counting with fingers was to be exclusively used at an early stage. The New Math era stressed the importance of developing a feeling for both cardinality and ordinality rather than for just ordinality. An interest in finger counting re-emerged in the 1990s, especially in connection with dyscalculia.
Recent studies on early arithmetic, in particular those that bridge mathematics education with cognitive psychology and neuroscience, indicate that the brain contains a special device for making sense of numbers (e.g., Dehaene, 1997; Butterworth, 1999). Children begin to enumerate objects at an early age, just as they begin to differentiate between colors (e.g., Wynn, 1998; Feigenson et al., 2002). Nevertheless, instruction in numerical operations is indispensible for acquiring the basic competency called numeracy (e.g., Floer, 1995).
Successful primary school children acquire flexibility for juggling between different types of representations when counting and operating with numbers; this is not true of dyscalculic children. To foster elementary numeracy in dyscalculic children, educators propose working mainly with one central representational framework, namely, number imaging, both enactively (i.e., using their hands to operate with structured materials, such as blocks and cubes) and iconically (i.e., looking at pictorial representations, like dots or icons). A typical symptom of dyscalculic children is firmly consolidated sequential counting, often anchored on finger counting. Adequate treatment with structured, enactive materials that foster number images, number decompositions and the cardinal aspect of numbers can enhance the understanding of numbers, so that decompositions like 8 = 7 + 1 = 5 + 3 = 3 + 5 are handled more easily.
Furthermore, the participation of parents is crucial in fostering their children’s early computational abilities and in motivating them to successfully implement the aforementioned representational changes (e.g., Mehlhuish et al., 2008). It is known, for instance, that boys tend to abandon finger counting earlier than girls (Pawelec and Kurz-Milcke, 2009), apparently because parents are somewhat stricter with boys. The feminist literature tends to view this unequal treatment and corresponding effects as disadvantageous for girls (Carr and Jessup, 1997; Martignon, 2010).
Dissociations, Limitations, and Integration of Educational and Neurocognitive Approaches
There is obviously some discrepancy between neurocognitive and mathematics education communities concerning the beneficial and/or detrimental influences of finger-based counting/calculation strategies on numerical development. On the one hand, much of the neurocognitive literature indicates a functional and beneficial interrelation between finger-based numerical representations and numerical/arithmetical development in terms of an embodied numerosity representation (e.g., Domahs et al., 2010). On the other hand, mathematics education research sees finger-based strategies in counting and calculation as a starting point that should be overcome in favor of more elaborate and abstract representations upon which numerical cognition is assumed to operate.
Basically, the rationale behind the neurocognitive argument is based on correlational associations between different cognitive measures or different brain activations of numerical/arithmetical competencies and indicators of finger-based representations. To our knowledge, in the neuorocognitive literature, there is only one intervention study that has trained finger gnosis and showed transfer effects (Gracia-Bafalluy and Noël, 2008). In contrast, the view held by mathematics education researchers is often falsely drawn on the observation that children using finger-based back-up strategies show poor numerical/arithmetical performance. Both views are problematic: in first case causal conclusions may be drawn on correlational data, while in the latter case it is unknown whether children exhibit poor numerical/arithmetical competencies because they still use their fingers or whether they use their fingers because this is their only available cognitive strategy.
Despite such methodological constraints, the current state of the art in both neurocognitive as well as mathematics education research suggests that the question whether or not finger-based counting and/or calculation strategies are beneficial may be too broad to be answered definitively at the moment. For instance, the effects of age and individual differences must be considered. Moreover, differences may arise with the differing presuppositions employed by neurocognitive and mathematics education researchers. Consider, for instance, the role of age. Mathematics education research suggests that reliance on finger-based representations should be overcome and replaced by more abstract numerical representations by the end of first grade to prevent detrimental influences. Neurocognitive research, however, predicts that finger-based representations influence number processing and arithmetic even in numerate adults as an additional, and sometimes helpful, embodied representation (i.e., without excluding the role of other representations, such as place-value representation) in arithmetic development.
Moreover, in contrast to mathematics education research, the neurocognitive perspective does not consider fingers as just another external material for learning to count and/or to calculate (like blocks or marbles, for example). Instead, based on the concept of embodied cognition, finger-based representations are considered to be a natural numerical representation, which is firmly grounded on sensory-bodily experience, and prevails even when more abstract or conceptual representations are built up.
Finally, there may also be task- and individual-related differences. Finger-based representations may be more beneficial for some subgroups of children, for instance less skilled children, as a multisensory experience that helps build abstract mental representations. Furthermore, finger-based representations may be particularly useful for specific tasks but not for others. For example, finger-based representations may be more beneficial in operations involving addition than multiplication, as even most single-digit multiplications exceed the number range possible to code easily by two hands. However, considering that multidigit numbers are processed decomposed into the single digits of units, tens, hundreds, etc. (see Nuerk et al., 2011 for a review), which can be represented by fingers, and considering that the same representations of these digits are recruited in single- as well as in multidigit number processing (e.g., Verguts and De Moor, 2005), it is conceivable that influences of finger-based representations may not only be limited to numbers up to 10.
Even though neurocognitive and mathematics education research agrees that children make use of finger-based numerical representations, they disagree on the consequences of reliance on such numerical representations. On the one hand, the neurocognitive literature suggests that embodied numerical representations, including finger-based ones, are important in numerical cognition in general (even present in educated adults, see Domahs et al., 2010). On the other hand, mathematics education research recommends the reliance on external representations, including finger-based ones, only as an aid in the transition to mental representations of numbers. These are then assumed to underlie adult numerical cognition (see also Rips et al., 2008, for the development of number concepts). In sum, the different views clearly show that there is a lack of systematic communication between the two disciplines. Further, the theoretical postulates and assumptions arising from the two different fields need to be addressed. To remedy this situation, interdisciplinary discourse between neurocognitive science and mathematics education is urgently needed.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Andres, M., DiLuca, S., and Pesenti, M. (2008a). Finger counting: the missing tool? Behav. Brain Sci. 31, 642–643.
Andres, M., Olivier, E., and Badets, A. (2008b). Actions, words, and numbers: a motor contribution to semantic processing. Curr. Dir. Psychol. Sci. 17, 313–317.
Bachot, J., Gevers, W., Fias, W., and Roeyers, H. (2005). Number sense in children with visuospatial disabilities: orientation of the mental number line. Psychol. Sci. 47, 172–183.
Booth, J. L., and Siegler, R. S. (2008). Numerical magnitude representations influence arithmetic learning. Child Dev. 79, 1016–1031.
Brissiaud, R. (1992). “A toll for number construction: finger symbol sets,” in Pathways to Number: Children’s Developing Numerical Abilities, eds J. Bideaud, C. Meljac, and J. P. Fischer (Hillsdale: Lawrence Erlbaum), 99–126.
Brozzoli, C., Ishihara, M., Goebel, S. M., Salemme, R., Rossetti, Y., and Farne, A. (2008). Touch perception reveals the dominance of spatial over digital representation of numbers. Proc. Natl. Acad. Sci. 105, 5644–5648.
Butterworth, B., Varma, S., and Laurillard, D. (2011). Dyscalculia: from brain to education. Science 332, 1049–1053.
Carr, M., and Jessup, D. (1997). Gender differences in first-grade mathematics strategy use: social and metacognitive influences. J. Educ. Psychol. 89, 318–328.
Crollen, V., Mahe, R., Colligon, O., and Seron, X. (2011). The role of vision in the development of finger-number interactions: finger-counting and finger-monitoring in blind children. J. Exp. Child. Psychol. 109, 525–539.
Dehaene, S. (1997). The Number Sense: How the Mind Creates Mathematics. New York: Oxford University Press.
Di Luca, S., Grana, A., Semenza, C., Seron, X., and Pesenti, M. (2006). Finger-digit compatibility in Arabic numeral processing. Q. J. Exp. Psychol. 59, 1648–1663.
Di Luca, S., LeFèvre, N., and Pesenti, M. (2010). Place and summation coding for canonical and non-canonical finger numeral representations. Cognition 117, 95–100.
Di Luca, S., and Pesenti, M. (2008). Masked priming effect with canonical finger numeral configurations. Exp. Brain Res. 185, 27–39.
Di Luca, S., and Pesenti, M. (2010). Absence of low-level visual differences between canonical and noncanonical finger–numerical configurations. Exp. Psychol. 57, 202–207.
Domahs, F., Krinzinger, H., and Willmes, K. (2008). Mind the gap between both hands: evidence for internal finger-based number representations in children’s mental calculation. Cortex 44, 359–367.
Domahs, F., Moeller, K., Huber, S., Willmes, K., and Nuerk, H.-C. (2010). Embodied numerosity: implicit hand-based representations influence symbolic number processing across cultures. Cognition 116, 251–266.
Eckstein, B. (2011). Mit 10 Fingern zum Zahlverständnis [Understanding Numbers Using 10 Fingers]. Göttingen: Vandenhoeck & Ruprecht.
Feigenson, L., Carey, S., and Spelke, E. (2002). Infants’ discrimination of number vs. continuous extent. Cogn. Psychol. 44, 33–66.
Fischer, M. H. (2008). Finger counting habits modulate spatial-numerical associations. Cortex 44, 386–392.
Fischer, M. H., and Brugger, P. (2011). When digits help digits: spatial–numerical associations point to finger counting as prime example of embodied cognition. Front. Psychology 2:260. doi: 10.3389/fpsyg.2011.00260
Floer, J. (1995). Wie kommt das Rechnen in den Kopf? Veranschaulichen und Handeln im Mathematikunterricht [How calculations enter the head]. Die Grundschulzeitschrift 82, 20–39.
Gaidoschik, M. (2010). Wie Kinder rechnen lernen – oder auch nicht. Eine empirische Studie zur Entwicklung von Rechenstrategien im ersten Schuljahr [How Children Do or Do Not Learn to Calculate]. Bern: Peter Lang Verlagsgruppe.
Gracia-Bafalluy, M., and Noël, M. P. (2008). Does finger training increase young children’s numerical performance? Cortex 44, 368–375.
Ishihara, M., Jacquin-Courtois, S., Flory, V., Salemme, R., Imanaka, K., and Rossetti, Y. (2006). Interaction between space and number representations during motor preparation in manual aiming. Neuropsychologia 44, 1009–1016.
Iversen, W., Nuerk, H. C., Jager, L., and Willmes, K. (2006). The influence of an external symbol system on number parity representation, or what’s odd about 6? Psychon. Bull. Rev. 13, 730–736.
Iversen, W., Nuerk, H.-C., and Willmes, K. (2004). Do signers think differently? The processing of number parity in deaf participants. Cortex 40, 176–178.
Kaufmann, L., Vogel, S. E., Wood, G., Kremser, C., Schocke, M., and Zimmerhackl, L. B. (2008). A developmental fMRI study of nonsymbolic numerical and spatial processing. Cortex 44, 376–385.
Kaufmann, S., and Wesselowski, S. (2006). Rechenstörungen – Diagnose und Förderbausteine [Mathematics Disabilities – Diagnosis and Remediation Steps]. Seelze: Friedrich Verlag.
Klein, E., Moeller, K., Willmes, K., Nuerk, H.-C., and Domahs, F. (2011). The influence of implicit hand-based representations on mental arithmetic. Front. Psychol. 2:197. doi:10.3389/fpsyg.2011.00197
Krauthausen, G., and Scherer, P. (2001). Einführung in die Mathematikdidaktik [Introduction to Didactics of Mathematics]. Heidelberg: Spektrum.
Lindemann, O., Alipour, A., and Fischer, M. H. (2011). Finger counting habits in Middle Eastern and Western individuals: an online survey. J. Cross Cult. Psychol. 42, 566–578.
Lorenz, J. H., and Radatz, H. (1993). Handbuch des Förderns im Mathematikunterricht [Handbook of Special Needs in Mathematics Instruction]. Hannover: Schroedel.
Martignon, L. (2010). “Mädchen und Mathematik [Girls and Mathematics],” in Handbuch Mädchenpädagogik [Handbook of Pedagogy for Girls], eds A. Matzner and I. Wyrobnik (Weinheim: Betz Verlag), 220–232.
Mehlhuish, E. C., Sylva, K., Sammons, P., Siraj-Blatchford, I., Taggart, B., Phan, M. B., and Malin, A. (2008). Preschool influences on mathematics achievement. Science 321, 1161–1162.
Moser Opitz, E. (2009). Zählen, Zahlbegriff, Rechnen. Theoretische Grundlagen und eine empirische Untersuchung zum mathematischen Erstunterricht in Sonderklassen [Counting, number concepts, calculation]. Bern: Haupt.
Noël, M.-P. (2005). Finger gnosia: a predictor of numerical abilities in children? Child Neuropsychol. 11, 413–430.
Nuerk, H.-C., Moeller, K., Klein, E., Willmes, K., and Fischer, M. H. (2011). Extending the mental number line – A review of multi-digit number processing. J. Psychol. 219, 3–22.
Padberg, F., and Benz, C. (2011). Didaktik der Arithmetik [Didactics of Arithmetic]. Heidelberg: Spektrum.
Pawelec, B., and Kurz-Milcke, E. (2009). “Gender differences in early mathematics strategy use,” in Proceedings of the XIV European Conference of the ESDM, Vilnius.
Penner-Wilger, M., Fast, L., LeFevre, J.-A., Smith-Chant, B. L., Skwarchuk, S. L., Kamawar, D., and Bisanz, J. (2007a). “Putting your finger on it: how neuropsychological tests predict children’s math ability,” in Poster session at the Biennial Meeting of the Society for Research in Child Development, Boston.
Penner-Wilger, M., Fast, L., LeFevre, J.-A., Smith-Chant, B. L., Skwarchuk, S. L., Kamawar, D., and Bisanz, J. (2007b). “The foundations of numeracy: subitizing, finger gnosia, and fine motor ability,” in Poster session at 29th Annual Conference of the Cognitive Science Society, Nashville.
Poeck, K. (1964). Phantoms following amputation in early childhood and in congenital absence of limbs. Cortex 1, 269–275.
Rips, L. J., Bloomfield, A., and Asmuth, J. (2008). From numerical concepts to concepts of number. Behav. Brain Sci. 31, 623–642.
Schipper, W. (2005). Modul G 4: Lernschwierigkeiten erkennen – verständnisvolles Lernen fördern [Recognizing Learning Difficulties – Promoting Comprehensive Learning]. Kiel: SINUS-Transfer Grundschule.
Schipper, W. (2009). Handbuch für den Mathematikunterricht an Grundschulen [Handbook for Mathematics Instruction in Primary School]. Braunschweig: Schroedel.
Verguts, T., and De Moor, W. (2005). Two-digit comparison: decomposed, holistic or hybrid? Exp. Psychol. 52, 195–200.
Keywords: finger counting, numerical development, neurocognitive, mathematics education
Citation: Moeller K, Martignon L, Wessolowski S, Engel J and Nuerk H-C (2011) Effects of finger counting on numerical development – the opposing views of neurocognition and mathematics education. Front. Psychology 2:328. doi: 10.3389/fpsyg.2011.00328
Received: 28 July 2011;
Accepted: 24 October 2011;
Published online: 29 November 2011.
Edited by:
Martin H. Fischer, University of Dundee, UKReviewed by:
Martin H. Fischer, University of Dundee, UKEvelyn Kroesbergen, Utrecht University, Netherlands
Christophe Mussolin, Université Libre de Bruxelles, Belgium
Copyright: © 2011 Moeller, Martignon, Wessolowski, Engel and Nuerk. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Korbinian Moeller, Knowledge Media Research Center, Schleichstrasse 6, 72076 Tuebingen, Germany. e-mail:a29yYmluaWFuLm1vZWxsZXJAdW5pLXR1ZWJpbmdlbi5kZQ==


 Silvia Wessolowski3
Silvia Wessolowski3
