- 1 Cognitive and Information Sciences, University of California Merced, Merced, CA, USA
- 2 Centre for Brain and Cognitive Development, Birkbeck University of London, London, UK
- 3 Cognitive, Perceptual and Brain Sciences, University College London, London, UK
In the tangram task, two participants are presented with the same set of abstract shapes portrayed in different orders. One participant must instruct the other to arrange their shapes so that the orders match. To do this, they must find a way to refer to the abstract shapes. In the current experiment, the eye movements of pairs of participants were tracked while they were engaged in a computerized version of the task. Results revealed the canonical tangram effect: participants became faster at completing the task from round 1 to round 3. Also, their eye-movements synchronized over time. Cross-recurrence analysis was used to quantify this coordination, and showed that as participants’ words coalesced, their actions approximated a single coordinated system.
Introduction
I would even say that the alterity of the other inscribes in this relationship that which in no case can be “posed”
(Derrida, 1981/2004, p. 77; Translated by Bass).
To most readers, this sentence from Derrida is void of meaning. Granted it is presented without a broader context, but such words as “alterity” and “posed” are among a network of expressions that have been critiqued as lacking any clarity or substance (e.g., Putnam, 2004). Thousands of scholars carefully train to interpret these words, and use them in their own literary studies (e.g., Norris, 2002). The postmodernist vocabulary is a stark example of the process of fixing a set of shared expressions that can confuse and even frustrate those outside the clique.
This fixing process is not particular to postmodernism, however. It can be found within and across many cliques and cultures and is integral to the use and development of language. Across families and regions of England, for example, there are at least 57 words that are systematically used to refer to a television remote control, from “doofla” to “melly” (The English Project, 2008). If you do not know what “afterclap” and “manther” refer to, you can seek out an online source of modern slang. Such normative agreement can even invert the meaning of a word. “Egregious,” for example, used to mean “standing out because of great virtue,” but a gradual accrual of, perhaps ironic, usage has fixed its meaning as wholly negative. The fixing process can also be very rapid, taking place during the events of a single day of a small group of people with common interests.
In the present work, we aim to elucidate the behavioral microstructure of the emergence of referential vocabulary by analyzing the eye movements and computer-mouse movements of pairs of people coordinating novel expressions for unfamiliar objects. Previous studies have analyzed these emerging expressions and how long it takes for them to arise. In the current paper, we focus exclusively on what happens in the perceptuo-motor coupling dynamics between people during this emergence. Our results suggest that the gradual construction of a shared vocabulary synchronizes two people in the fine-grained dynamics of the eyes and hand.
Cognitive science has most often been in the business of studying processes of individual cognizers (Miller, 1984). But over the past 20 years the study of cognition has moved beyond individuals and into pairs or small groups of people and the environment in which they are embedded (e.g., Turvey et al., 1981; Hutchins, 1995; Clark, 1996; Hollan et al., 2000; Knoblich and Sebanz, 2006). Pairs or groups are probably, after all, the most common context of our species’ behavior. Recently, detailed experimental investigation of joint activities has generated its own literature (see the collection in Galantucci and Sebanz, 2009; see also Sebanz et al., 2006). These results align with previous work arguing that groups of people in their task environment may function, in many respects, like one single cognitive system (e.g., Hutchins, 1995). One characteristic of our species that permits such fluid, multi-person functioning is our powerful communication system. People who speak the same language have a vast shared vocabulary permitting its users to help each other orient appropriately to objects in the world (e.g., see Galantucci, 2005). Whether on the hunt in the Sahara or in a restaurant with a deep menu, a shared reference scheme can organize multi-person behaviors in efficient ways.
Our results add to this view of language as a tool to organize the microstructure of cognition and action during interaction. We employed a task in which a shared reference system emerges, and examined how it transforms the behavior of those using it. Ostensibly, it permits its users to perform reference tasks much more efficiently. If you and I both know what “the jingly one” refers to, each time one of us employs it, the other can sharply orient to the appropriate referent. This skill is most often measured by completion time of these reference tasks. Here we show that something else occurs, more fundamental than simply pace of success: an emerging referential scheme induces partners in a reference task to become coupled in their visual attentional system. To show this, we focus our analysis on the eyes and hand during a well-understood joint task used extensively in previous work: the tangram task (Krauss and Weinheimer, 1964). Previous work has studied language use and completion times in the tangram task. In our study, we do not analyze the linguistic content of the task, as it is well-understood what occurs and has been widely replicated. Instead, we go underneath those levels of analysis, and quantify the coupling between eye-movement patterns. We show that the signature of attentional coupling changes across rounds as a referential scheme is agreed upon by two task partners.
In the tangram task, pairs of participants work with a set of six unfamiliar, abstract shapes (Krauss and Weinheimer, 1964; Krauss and Glucksberg, 1969; see Figure 1). They see the same shapes, but arranged in a different order. One, the “matcher,” must arrange her shapes to match the order of the “director.” The director must use careful description in order for the matcher to succeed. Once all six shapes are re-ordered, they repeat the task. A robust pattern of change occurs as the same set of shapes are used again and again. Participants take less time to solve the task, require fewer words to do so, and end up with a jointly constructed scheme of shorthand descriptions for the shapes (Clark and Wilkes-Gibbs, 1986; see Clark, 1996, Chapter 3, for a detailed review). Once multiple rounds have been performed, the pair are capable of effectively identifying tangrams and completing the task quite rapidly. In this sense, the two people have become a coherent, functional unit (Hutchins, 1995).

Figure 1. Split screen view of an example tangram trial used in this task. The director, looking at the screen on the left, seeks a description to help the matcher select the same shape on his or her screen. Across rounds, referential language changes from detailed descriptions, such as “the guy kind of carrying the triangle,” (highlighted here with a box) to simplified, entrained expressions, such as “carrying guy.”
The tangram task is a carefully controlled experimental context to measure this “soft-assembly” of a two-person joint system (see Shockley et al., 2009 and Marsh et al., 2009, for theoretical discussion). Because it is well known what happens at the word level in this task, here we focus exclusively on the perceptuo-motor machinery of this system1. We track participants in the tangram task, and analyze the eye and mouse movements across three rounds of tangram identification. Through cross-recurrence analysis, a method based on the study of coupled dynamical systems, it is possible to obtain real-time quantification of behavioral coupling as it unfolds over rounds of tangram communication (Dale and Spivey, 2005; Richardson and Dale, 2005; see Dale et al., 2011, for a comparison to other lag-based methods). These analyses show that there is extremely tight visual and motor coordination occurring in the pair, and how this coordination changes across rounds. We conclude that these properties of the tangram identification “device” are highly similar to those properties that have been identified in individual cognitive systems. With Hutchins (1995) and Sebanz et al. (2003) we argue that two-person systems exhibit the same loose-coupling under task constraints that a single cognitive processor exhibits, further demonstrating that pairs of people or beyond may serve as coherent units of analysis themselves (Tollefsen, 2002, 2006).
What does it take for two people to form “one system”? One definition, according to Hutchins (1995), is that they are part of a set of goals or functions that cannot be understood through any one person alone (e.g., a speed-controlling cockpit). At a finer-grained level, another way of understanding how two people come to form a functional unit is that their perceptuo-motor behavior literally takes the same shape. For example, eye movements in our task, as we show below, become more coupled from round to round, until the lag between director and matcher is not significantly different from 0 s. Their eye movements come to approximate one another. Because the tangram task is also rendering a novel referential scheme, it is both linguistic and perceptuo-motor channels that are becoming tightly aligned in order for the participants to achieve the task. In short, their various behavioral channels go from slowly achieving the task, to a loosely coupled cognitive and perceptuo-motor network: they are no longer separate individuals achieving the task, but in some sense share the same cognitive and perceptuo-motor “state space.”
This outcome is not obvious given current debate in the study of discourse and psycholinguistics. Though previous work has shown a tight coupling of visual attention during dialog (Richardson et al., 2007), and has shown systematic coupling of gaze to reference (Griffin, 2001), it is unclear how this tight coupling emerges. In Richardson et al.’s (2007) work, the coupling of visual attention is based on a well-established set of words and events that interlocutors recognize and discuss (e.g., of Simpsons television characters). But it requires years to establish that level of expertise with language, and also requires considerable common ground. In the current study, an entrained vocabulary is assumed to emerge in just minutes, in a referential domain (tangram shapes) that is completely unfamiliar to the participants.
We thus recognized two possibilities. First, a pair may speed up in their performance as they progress through the task, but exhibit only weak and unchanging perceptuo-motor coupling characteristics. For example, the director’s attention might consistently lead the matcher’s all the way through each round of the task, with the maximal overlap in their eye-movements unchanging. In such a circumstance, language is speeding up only their choice performance, and not organizing their perceptuo-motor channels. A second possibility is that the two participants in this task will change flexibly together as the task unfolds, and the director and matcher come to exhibit tighter coupling dynamics. If so, the director’s lead will be diminished (if not obliterated), and the two people in the task, director, and matcher, will come to have more and more locked visual attention under a referential scheme that emerges in just minutes.
Experiment
Methods
Participants
Twenty pairs of participants were recruited from the Stanford University subject pool, and performed the tangram task for class credit. One participant in a pair was randomly assigned to the director role, and the other was assigned to matcher. Eight of these pairs did not provide mouse-movement data due to technical problems. The remaining 12 pairs formed the basis of eye-mouse analyses (see below).
Apparatus
Two eye-tracking labs on different floors of a building were used. In one of the labs an ASL 504 remote eye-tracking camera was positioned at the base of a 17″ LCD display. Participants sat unrestrained approximately 30″ from the screen. The display subtended a visual angle of approximately 26° × 19°. The camera detected pupil and corneal reflection position from the right eye, and the eye-tracking PC calculated point-of-gaze in terms of coordinates on the stimulus display. A PowerMac G4 received this information at 33 ms intervals, and controlled the stimulus presentation and collected looking time data. The second lab used the same apparatus with one difference: the display was a 48′′ × 36′′ back projected screen and participants sat 80″ away (this lab was designed for infants under a year old). A slightly larger visual angle of approximately 33° × 25° was subtended in this second lab. Participants communicated through the intercom feature on 2.4 GHz wireless, hands-free phones.
Stimuli
Six tangram shapes were used, similar to those used in previous work. These shapes derive from combinations of common geometric objects (squares, triangles, etc.), and many appear to be humanoid-like forms with subtle distinctions among them. These were projected in a randomized fashion in a 2 × 3 grid to both director and matcher.
Procedure
Each participant in the pair was told if s/he was a director or a matcher, and kept that roles for the duration of the experiment. They performed three rounds of the tangram task. In each, the order of the shapes was randomized for both participants. The director described each shape in turn. Whereas in the classic task, the matcher re-ordered the shapes, in our computerized version the matcher used a mouse to select the shapes in order that they appeared for the director. When the matcher identified the sixth and last shape the round ended.
Data and analysis
We extracted three behavioral signals at a sampling rate of approximately 30 Hz: (Deye) the tangram fixated by the director, (Meye) the tangram fixated by the matcher, and (Mmouse) the tangram “fixated” by the matcher’s mouse cursor. For any given participant pair and communication round, three time series were thus produced: two sequences of eye movements and one sequence of mouse movements. For each round, separate analyses were conducted on the three possible alignment pairings: director’s and matcher’s eye movements (Deye–Meye), matcher’s mouse and eye movements (Mmouse–Meye), and director’s eyes/matcher’s mouse (Deye–Mmouse). To explore the patterns of coordination in these pairings, we conducted a version of cross-recurrence analysis. This simply compared all time points of two time series, and generated a lag-based percentage of how much matching or “cross-recurring” (i.e., tangram fixation) took place at each lag. By plotting this percentage match, known as percentage recurrence or %REC, across all lags, we generated a diagonal-wise recurrence lag profile reflecting the pattern of coordination between the two time series (akin to a “categorical” cross-correlation function; see Dale et al., 2011; also see Jermann and Nuessli, 2011, for an elegant explanation).
When the %REC is largely distributed to the right or left of such a plot, it has direct bearing on the leading/following patterns of the systems producing those time series. For example, consider the top-right recurrence profile shown in Figure 2. This is the eye-movement %REC profile for Deye–Meye on round 1 for a particular dyad. The largest proportion of recurrent looks occurs at negative lags. This shows that at this early stage of the task, the director’s eye movements are leading the matcher’s (see Richardson and Dale, 2005, for more methodological detail).
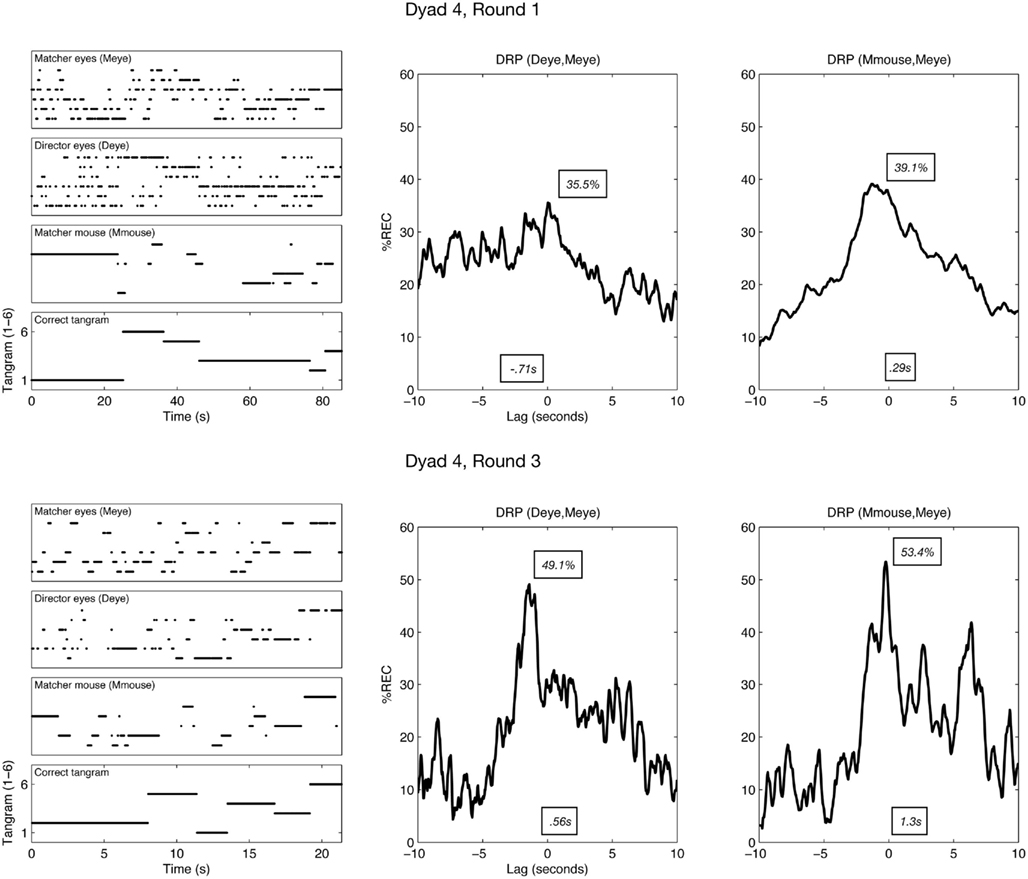
Figure 2. Left column: example time series from one dyad in rounds 1 and 3. The bottom row shows, across time, the correct tangram (expressed as numeric code) that the director is attempting to get the matcher to find. Above this correct tangram is the time series for each of the analyzed channels. For example, Deye (director eyes) shows the time series of which tangram is fixated at a given moment (expressed again as a consistent code from 1 to 6). Middle/right columns: the recurrence lag profiles of pairs of these time series, with mean (s) and maximum (%) shown as examples of quantifying the profiles as a distribution (DRP = diagonal-wise recurrence profile). The profile is constructed by finding how much each time series matches (expressed as percentage recurrence, %REC) when they are lagged relative to one another. The maximum would reflect, for example, the relative point in time at which the channels are maximally aligned. See main text for more details.
Examples of time series and construction of the recurrence lag profiles are shown in Figure 2. To quantify how these profiles changed their position and shape across rounds, we treated the recurrence profiles as distributions of temporal data. The mean lag will be the central tendency of the overall coordination pattern, kurtosis will reflect how pointed the coordination is, and so on. Such a distribution analysis of the recurrence profile permitted us to describe quantitatively the changes in shape and position that can be seen, for example, in Figure 2.
For each dyad, round, and modality combination we extracted five characteristics of the recurrence lag profiles. First, we measured the overall mean recurrence across the whole profile (avg. %REC). This would be akin to measuring the mean density of a probability distribution (mean of y-axis values). This simply reflects, in a ±lag window, how much overall cross-recurrence is occurring between two time series. Second, we measured the maximum %REC occurring in the profile. In analysis of distributions, this is equivalent to finding the value of the maximum density (maximum y-axis value). This measure would reflect the maximum recurrence, achieved at one of the lags. Third, kurtosis and dispersion (SD) of the profiles were produced. The first of these measures reflects the pointedness of the coordination. A high kurtosis would indicate the presence of coordination within a small lag window, occurring for a shorter, pointed period of time; lower kurtosis would reflect a broad lag window during which states are recurrent. Dispersion (SD) has the inverse interpretation, and is calculated by treating the profile as a distribution of lags and finding the SD of the sample. Finally, we measured the central tendency (mean) of the profile. In simple distribution analyses, this is equivalent to finding the point along the x-axis (here, a lag in seconds) that reflects the center of the distribution. This would measure the overall weighted center of the recurrence profile. A positive or negative mean (different from 0) would be indicative of leading or following by one of the time series (see Obtaining Distributions from Lag Profiles in Appendix for more detail).
We chose a lag window of ±10 s to explore matching between modalities. In previous work, we have found that crucial peaking of recurrence between two people is at approximately ±3 s (Richardson and Dale, 2005; Richardson et al., 2007, 2009b). We chose a wider window to ensure that our analyses both contain the key coordination region and the broader shape of the distribution.
Results
Below, we first present the canonical tangram effect: participants became faster at completing the task from round 1 to round 3. Following this, we conducted a baseline analysis to show that overall coordination across the three modality pairings (Deye–Meye, Mmouse–Meye, and Deye–Mmouse) is above shuffled baseline comparisons. Finally, in a test of the profile distribution characteristics, results reveal two systems that are becoming one: eye-movements synchronize, the matcher’s eyes, and mouse are lagged relative to each other but more pointedly over rounds, and the director’s eyes and the matcher’s hand exhibit a distinct temporal lag. In short, the two participants, director and matcher, approximate a single coordinated system. In analyses presented below, to analyze individual distribution values across the 20 pairs, we used a linear mixed-effects model (lmer in R) treating subject as a random factor, and tangram round as the sole fixed effect. In a manner described in Baayen et al. (2008), we report p-values derived from Markov chain Monte Carlo (MCMC) methods calculated from p-values fnc in R. This analysis was chosen because it allows use of round as a continuous variable to estimate change from round to round. Where reported, approximate degrees of freedom are estimated using a Kenward–Roger correction technique described in Kenward and Roger (1997) using KRmodcomp in R (it is important to note that the MCMC significance levels are established based on simulation of the data, and not on the approximate degrees of freedom. These estimates are shown for convenience).
Completion time
As in previous tangram experiments (see Clark, 1996), dyads became increasingly effective at performing the task. Participants required an average of 141.5 s in the first round, 57.8 s in the second, and only 34.8 in the third. The last two rounds were significantly faster than round 1, ts > 10, ps < 0.0001. Round 3 was also carried out faster than round 2, t(19) = 5.6, p < 0.0001.
Shuffled vs. non-shuffled lag profile
We first conducted a shuffled baseline analysis for all measures. This was done by performing the same lag profile analysis but with shuffled versions of our time series, so that the temporal structure is removed. As would be expected, the total recurrence in all analyses within the ±10 s window was substantially higher in the non-shuffled vs. shuffled conditions, ts > 7, ps < 0.0001. This main effect of shuffling held in each round when analyzed separately. In short, coordination is significant across all rounds compared to baseline, across all analyses: Deye–Meye, Deye–Mmouse, and Mmouse–Meye. The question we explore in distribution analyses below is how that coordination is organized. (Please see Which Baseline to Use? in Appendix for a discussion of use of shuffling as a reasonably conservative baseline for a data set of this size, and a comparison to other methods.)
Director–matcher eye-movement synchronization (Deye–Meye)
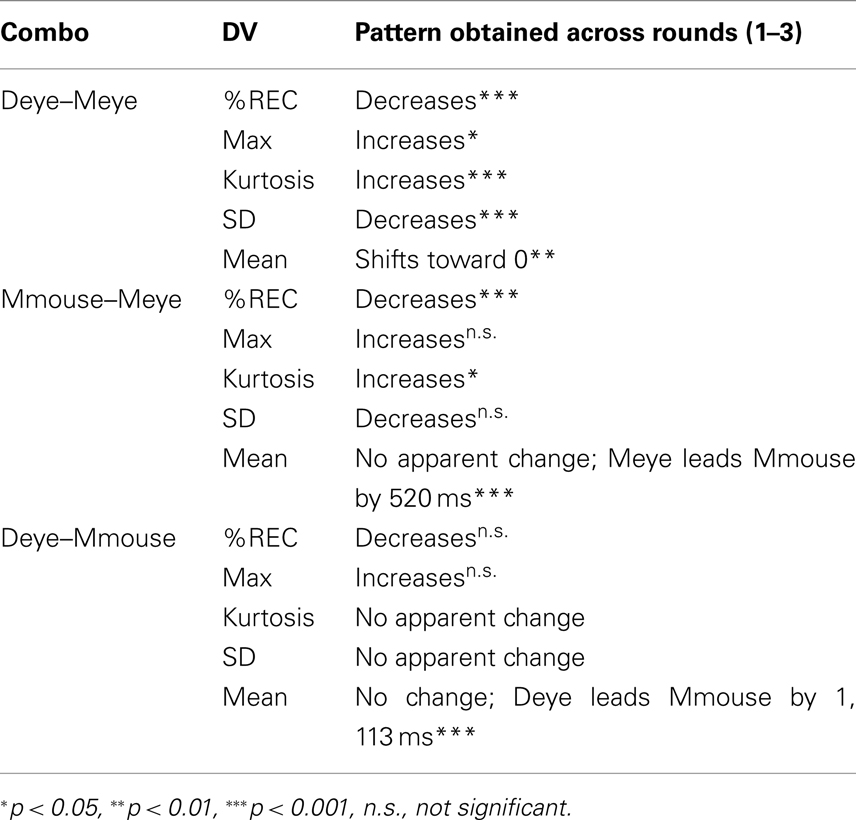
The recurrence lag profiles for the alignment between director’s eye movements and matcher’s eye movements is shown in Figure 3A. It revealed several significant effects across rounds. First, the overall recurrence (mean %REC) drops from round to round, t(39) = 4.9, p < 0.0001, with overall recurrence higher in round 1 (30.3%) than rounds 2 (24.5%) and 3 (21.1%; ps < 0.005). Second, there is also a main effect of round for the maximum %REC achieved, t(39) = 2.9, p < 0.05. Round 1 (39.3%) has a lower maximum %REC value than round 3 (45.0%; p < 0.05), with round 2 (42.1%) in between (but not significantly differing from these). It is important to note that this maximum difference may not be visible in Figure 2, because the maximum of the averaged profiles is not necessarily the same as the averaged of the maximum of the profiles (e.g., consider two non-overlapping normal distributions have higher average maximum, than the maximum of their average). Third, kurtosis if these distributions increases across rounds, as is indeed visible in the average profiles, t(39) = 5.4, p < 0.001. Rounds 3 (2.4) and 2 (2.1) had higher kurtosis than round 1 (1.9; ps < 0.05). Likewise, dispersion in terms of the SD (in seconds) of the profiles is decreasing from round 1 (5.5 s) to 2 (5.2 s) to 3 [4.8 s; t(39) = 6.5, p < 0.001]. Finally, the mean of this lag profile (in seconds) is changed from round to round, t(39) = 3.0, p < 0.005. The center of these profiles is shifting toward 0 s, with round 1 (−0.7 s) and round 2 (−0.8 s) significantly lower than 0 s, ts > 4, p < 0.001. By round 3, however, the recurrence lag profiles have an average center of 0.3 s, which is not significantly different from 0, t(19) = 0.9, p = 0.4.
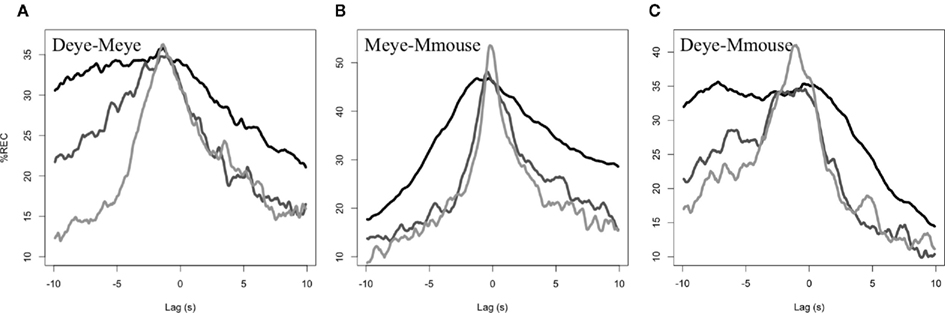
Figure 3. Mean lag profiles across dyads. Round (A) is black, round (B) mid grey, and round (C) light grey.
Overall, the recurrence lag profiles between the eye movements of director and matcher, are becoming more sharply (higher kurtosis, lower dispersion) synchronous (center near 0) across rounds of communication. Though average %REC of the whole distribution is higher in the earlier rounds of communication, it achieves a smaller maximum, and has a distribution that is shifted away from that center of 0. By later rounds, the referential scheme synchronizes the eyes near a lag of 0 and does so without requiring long stretches of time. In short, the director and matcher are coming to exhibit highly coordinated patterns of visual attention as the referential system is emerging in the task.
Matcher mouse-movement/matcher eye-movement synchronization (Mmouse–Meye)
As noted above, eight of the pairs did not supply matcher mouse tracking due to technical errors. We used the time series (Mmouse and Meye) from the remaining 12 to conduct the same linear mixed-effects analyses on the recurrence lag profile characteristics. Parallel to the statistics reported in the previous section, we obtained the following results.
Overall recurrence is again diminishing across rounds 1–3 (34, 24.7–22.3%, respectively), t(23) = 4.2, p < 0.001. Maximum recurrence is changing over rounds, with the direction of the effect exhibiting the same pattern (49.9, 52.0, and 57.9%, across rounds), t(23) = 2.6, p < 0.05. In individual comparisons, round 3 did have significantly higher recurrence than round 1 (p < 0.05). Kurtosis did significantly change over rounds, t(23) = 2.6, p < 0.05 (2.1, 2.4, and 2.5 from rounds 1 to 3), though dispersion did not seem to change, but is again in the same direction as seen in the previous analysis (5.1, 4.8, and 4.7 s), t(23) = 1.6, p = 0.11. The mean of the lag profile did not change, t(23) = 0.16, p = 0.9. Interestingly, however, the mean seemed highly stable from round to round (0.5,0.6,0.5 s)2 and this mean value was significantly greater than 0, one-sample t(35) = 4.0, p < 0.001. This suggests that there is a stable leading by the eyes by approximately 520 ms overall. Figure 3B shows average recurrence profiles.
Though the pattern of significance is different, likely due to lessened power given lost data, the same general patterns held. The drop in average %REC and increase in kurtosis suggests that the eyes and hand are becoming more sharply coordinated in time. In addition, the stability in the mean value, and significant deviation from 0, suggests a structural limitation of the matcher’s hand–eye coordination: there is consistent leading of the hand by the eye.
Direct eye-movement/matcher mouse-movement synchronization (Deye–Mmouse)
In analysis of the 12 pairs that provided Mmouse data, the following results held. First, there appears to be a drop again in mean density of %REC (29.4, 22.5, 22.1%), but this is only marginally significant, t(23) = 1.6, p = 0.08. Maximum %REC value is significantly increasing from round to round (42.9, 47.8, and 54.6%), t(23) = 2.2, p < 0.05. Kurtosis (2.1, 3.1, and 2.5) and dispersion (5.2, 4.5, and 4.6 s) did not achieve significance. Interestingly, the mean was again relatively stable in these profiles (−1.0, −1.4, and −0.9 s) indicating that the director’s eyes lead the hand of the matcher by approximately 1 s, one-sample t(35) = −3.8, p < 0.001. In general, these results lack the robustness of those in Section “Director–Matcher Eye-Movement Synchronization (Deye–Meye),” but argue for an invariant of matcher’s hand following the director’s eyes that is perhaps predictably greater than the delay on the matcher’s own eyes (see Figure 3C for average profiles).
Mouse serving as spatial index?
In the previous analysis, it appears that the mouse–cursor time series maintain a kind of invariant temporal relationship with Deye and Meye – it is lagged by a certain time signature, and does not appear to change from round to round. One reason for this may be that the mouse remains stable over candidate choices, and only moves once the tangram choice has been established (e.g., clicking on the current shape it is hovering over, or moving to a new selection). This possibility is suggested in Figure 2, in which it can be seen that the mouse–cursor time series are relatively more stable than the eyes, and tend to remain on top of particular possible choices.
In order to test this idea quantitatively, we compared the eye-movement time series (Deye/Meye) with the matcher’s mouse (Mmouse): if the mouse is serving as a kind of “holding place,” then it should exhibit longer stretches of one particular event than the eyes, which are sampling the tangram visual array more freely. To do this, we measured the number of times the tangram fixated (by the eyes and “fixated” by the mouse) changes from t − 1 to t. We then divide this count score by the length of a given time series to obtain a percentage score for the proportion of changes occurring in the time series. When we do this, Mmouse time series change considerably less often (2.07%) than Deye (6.06%) and Meye (7.08%), ts > 7, ps < 0.0001.
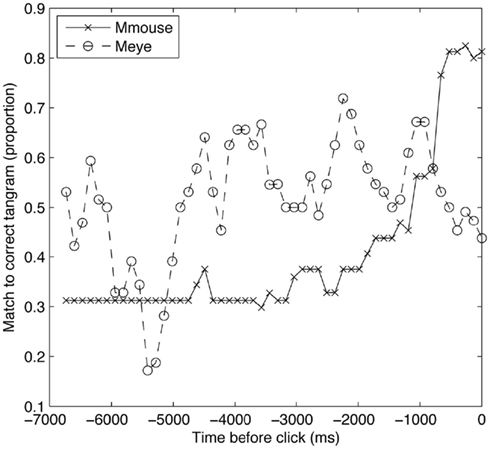
One problem with this analysis, however, is that we cannot know the baseline stability of manual movements compared to eye movements under any other circumstance. It may be expected that the mouse will move less than the eyes. In order to further test the notion that the mouse is serving as a stable spatial index, we carried out an additional analysis. Figure 4 shows trials of a given length (>15 s), averaged across all participants and trials, and plots the probability that Meye and Mmouse are on the correct tangram during the last few seconds before it is selected. The matchers’ eyes are more likely to be looking at the correct tangram for most of this period, as the matcher first locates the tangram and then moves the mouse to it.
Interestingly, in the last moments of the trial, Meye drops rapidly, below Mmouse. The matcher looks away from the correct tangram while their mouse remains. After listening to some of the conversations, we observed that often during the final moments of the trial, after having successfully identified a tangram, participants would look around at close competitors and confirm that they were onto the intended shape (e.g., “Ok so not the runner, the walker”). This pattern of converging upon the correct shape and then double checking other candidates can be seen in the dynamics of the eyes and hand. In particular, the use of the mouse pointer as a marker has the hallmarks of what Kirsch and Maglio (1994) called an “epistemic action”: an external physical action that serves an internal cognitive function. In experiments on “spatial indexing” (Richardson and Spivey, 2000; Richardson and Kirkham, 2004) external location plays a similar role supporting cognition.
General Discussion
At the beginning of the tangram task, when director and matcher have not yet become coordinated through referential expressions, the director’s eyes lead the matcher’s eyes. We demonstrated this through quantifying the alignment between eye movements of both people with cross-recurrence analysis. After generating a diagonal-wise recurrence lag profile, we treated it as a distribution, and quantified its characteristics. At the start of the experiment, the overall recurrence between director and matcher eye movements reflects a significant lead by the director: the profiles are shifted to the left. We asked how this coupling changes over rounds of the tangram task. This can be expressed as a test of how the profile’s shape is changing, using the distribution characteristics extracted from the recurrence profile as a quantification of this change. By the final round, systematic cross-modal coordination emerged. Importantly, the recurrence profiles of director/matcher eye movements were centered at 0 s, suggesting that, on average, the director is no longer so sharply leading the matcher. It is not simply that the director and matcher achieve the task faster, but they are strongly synchronized in their perceptuo-motor activity. With the emerging interplay among multiple behavioral channels, the two participants are therefore acting as a single, coordinated “tangram recognition system.” Table 1 summarizes our basic findings.
Though the eyes synchronize, the hand’s behavior may serve a separate purpose. We found in analysis of the time series that the matcher’s hand remains relatively more stable than the eyes, and that it maintains a stable temporal lag relationship to the director’s and matcher’s eyes. The matcher’s hand remains lagged, likely due to an “anchoring” to spatial indices in the visual workspace (see also Ballard et al., 1995; Brennan, 2005; Richardson et al., 2009a). As the eyes of director and matcher sample the world to be potentially responded to, the hand stays steady above candidate decisions.
This characterization of the pair as a single “system” can be understood on the backdrop of recent work on the coordination of reference domains during interaction. For example, participants in interactive tasks are subtly influenced by shared and unshared information (Richardson et al., 2007, 2009b), suggesting that coordination is a central component of naturalistic interactive tasks (Tanenhaus and Brown-Schmidt, 2008). Attention and comprehension are coordinated tightly as participants become accustomed to a complex referential domain (Brown-Schmidt et al., 2005, 2008). Sebanz et al. (2003) have argued that the very representations and processes used by partners in a task come to overlap simply by being co-present, and particularly by being jointly involved and aware of each other’s roles during the task (see also Knoblich and Jordan, 2003; Richardson et al., 2008, 2010). Indeed, the language-as-action tradition (as described in Tanenhaus and Brown-Schmidt, 2008 and Clark, 1996), which sees one person’s communication system as largely doing things to or with others, encourages a view consistent with recent perspectives on cognition as “soft-assembling” (e.g., Kugler et al., 1980) into loosely coupled functional systems during interactive tasks (Shockley et al., 2009).
The emergence of rich connections between low-level perceptual systems and high-level conceptual systems has been predicted by a number of theories (e.g., Barsalou, 1999). For example, Garrod and Pickering (2004) argue that a process of alignment cascades across all levels during interaction, and the data we present has quantified the manner in which the perceptuo-motor systems of conversants become coupled through the cascading influence of lexical entrainment (Brennan and Clark, 1996). Recent basic experimental work on individuals provides evidence that linguistic elements, such as shorthand phrases or novel labels for objects, come to organize a range of cognitive and perceptual functions, even in basic visual psychophysical tasks (e.g., Lupyan and Spivey, 2008; Huettig and Altmann, 2011). Similarly, at the level of dyads, what we have shown in the current paper is that changes in behavior during the tangram task are much deeper than a simple increase in the speed with which the task is performed. The emerging reference scheme organizes the perceptual and motor dynamics of interlocutors. Their visual attention becomes tightly coupled, while the matcher’s hand maintains an invariant temporal relationship between these two eye-movement channels – in a manner that resembles the offloading of memory during other hand–eye tasks in individuals (Ballard et al., 1995). The tight bridge between language and broader cognition is therefore a fundamental character of the fine-grained dynamics of each as they mutually influence each other during communication.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Footnotes
- ^For recent investigation of speech and perceptual channels in a related problem-solving task see Kuriyama et al. (2011) and Terai et al. (2011).
- ^NB: the sign on the mean reflects the direction of leading/following by a given time series. Here, positive values indicate the matcher’s eyes are leading. Negative values would have the opposite interpretation. This interpretation is simply determined by the order in which the time series are entered into analysis.
References
Baayen, R. H., Davidson, D. J., and Bates, D. M. (2008). Mixed-effects modeling with crossed random effects for subjects and items. J. Mem. Lang. 59, 390–412.
Bakeman, R., Robinson, B. F., and Quera, V. (1996). Testing sequential association: estimating exact p values using sampled permutations. Psychol. Methods 1, 4–15.
Ballard, D. H., Hayhoe, M. M., and Pelz, J. B. (1995). Memory representations in natural tasks. J. Cogn. Neurosci. 7, 66–80.
Boker, S. M., Xu, M., Rotondo, J. L., and King, K. (2002). Windowed cross-correlation and peak picking for the analysis of variability in the association between behavioral time series. Psychol. Methods 7, 338–355.
Brennan, S. E. (2005). “How conversation is shaped by visual and spoken evidence,” in Approaches to Studying World-Situated Language Use: Bridging the Language-as-Product and Language-as-Action Traditions, eds J. C. Trueswell, and M. K. Tanenhaus (Cambridge, MA: MIT Press), 95–129.
Brennan, S. E., and Clark, H. H. (1996). Conceptual pacts and lexical choice in conversation. J. Exp. Psychol. Learn. Mem. Cogn. 22, 1482–1493.
Brown-Schmidt, S., Campana, E., and Tanenhaus, M. K. (2005). “Real-time reference resolution by naive participants during a task-based unscripted conversation,” in Approaches to Studying World-Situated Language Use: Bridging the Language-as-Product and Language-as-Action Traditions, eds J. C. Trueswell, and M. K. Tanenhaus (Cambridge, MA: MIT Press), 153–171.
Brown-Schmidt, S., Gunlogson, C., and Tanenhaus, M. K. (2008). Addressees distinguish shared from private information when interpreting questions during interactive conversation. Cognition 107, 1122–1134.
Clark, H. H., and Wilkes-Gibbs, D. (1986). Referring as a collaborative process. Cognition 22, 1–39.
Dale, R., and Spivey, M. J. (2005). “Categorical recurrence analysis of child language,” in Proceedings of the 27th Annual Meeting of the Cognitive Science Society (Mahwah, NJ: Lawrence Erlbaum), 530–535.
Dale, R., Warlaumont, A. S., and Richardson, D. C. (2011). Nominal cross recurrence as a generalized lag sequential analysis for behavioral streams. Int. J. Bifurcat. Chaos 21, 1153–1161.
Galantucci, B. (2005). An experimental study of the emergence of human communication systems. Cogn. Sci. 29, 737–767.
Galantucci, B., and Sebanz, N. (2009). Joint action: current perspectives. Top. Cogn. Sci. 1, 255–259.
Griffin, Z. M. (2001). Gaze durations during speech reflect word selection and phonological encoding. Cognition 82, B1–B14.
Hollan, J., Hutchins, E., and Kirsh, D. (2000). Distributed cognition: toward a new foundation for human-computer interaction research. ACM Trans. Comput. Hum. Interact. 7, 174–196.
Huettig, F., and Altmann, G. T. M. (2011). Looking at anything that is green when hearing “frog”: how object surface colour and stored object colour knowledge influence language-mediated overt attention. Q. J. Exp. Psychol. 64, 122–145.
Jermann, P., and Nuessli, M.-A. (2011). “Unravelling cross-recurrence: coupling across timescales,” in Proceedings of International Workshop on Dual Eye Tracking in CSCW (DUET 2011), Aarhus.
Kenward, M. G., and Roger, J. H. (1997). Small sample inference for fixed effects from restricted maximum likelihood. Biometrics 53, 983–997.
Kirsh, D., and Maglio, P. (1994). On distinguishing epistemic from pragmatic action. Cognit. Sci. 18, 513–549.
Knoblich, G., and Jordan, J. S. (2003). Action coordination in groups and individuals: learning anticipatory control. J. Exp. Psychol. Learn. Mem. Cogn. 29, 1006.
Knoblich, G., and Sebanz, N. (2006). The social nature of perception and action. Curr. Direct. Psychol. Sci. 15, 99.
Krauss, R. M., and Glucksberg, S. (1969). The development of communication: competence as a function of age. Child Dev. 255–266.
Krauss, R. M., and Weinheimer, S. (1964). Changes in reference phrases as a function of frequency of usage in social interaction: a preliminary study. Psychon. Sci. 113–114.
Kugler, P. N., Kelso, J. A. S., and Turvey, M. T. (1980). On the concept of coordinative structures as dissipative structures: I. Theoretical lines of convergence. Tutorials Motor Behav. 3–47.
Kuriyama, N., Terai, A., Yasuhara, M., Tokunaga, T., Yamagishi, K., and Kusumi, T. (2011). “Gaze matching of referring expressions in collaborative problem solving,” in Proceedings of International Workshop on Dual Eye Tracking in CSCW (DUET 2011), Aarhus.
Lupyan, G., and Spivey, M. J. (2008). Perceptual processing is facilitated by ascribing meaning to novel stimuli. Curr. Biol. 18, R410–R412.
Marsh, K. L., Richardson, M. J., and Schmidt, R. C. (2009). Social connection through joint action and interpersonal coordination. Top. Cognit. Sci. 1, 320–339.
Miller, G. A. (1984). “Informavores,” in The Study of Information: Interdisciplinary Messages, eds F. Machlup, and U. Mansfield (New York, NY: Wiley), 111–113.
Richardson, D. C., Altmann, G. T. M., Spivey, M. J., and Hoover, M. A. (2009a). Much ado about eye movements to nothing: a response to Ferreira et al.: taking a new look at looking at nothing. Trends Cogn. Sci. 13, 235–236.
Richardson, D. C., Dale, R., and Tomlinson, J. M. (2009b). Conversation, gaze coordination, and beliefs about visual context. Cogn. Sci. 33, 1468–1482.
Richardson, D. C., and Dale, R. (2005). Looking to understand: the coupling between speakers and listeners eye movements and its relationship to discourse comprehension. Cogn. Sci. 29, 1045–1060.
Richardson, D. C., Dale, R., and Kirkham, N. Z. (2007). The art of conversation is coordination: common ground and the coupling of eye movements during dialogue. Psychol. Sci. 18, 407–413.
Richardson, D. C., Hoover, M. A., and Ghane, A. (2008). “Joint perception: gaze and the presence of others,” in Proceedings of the 30th Annual Conference of the Cognitive Science Society, Austin, TX, 309–314.
Richardson, D. C., and Kirkham, N. Z. (2004). Multimodal events and moving locations: eye movements of adults and 6-month-olds reveal dynamic spatial indexing. J. Exp. Psychol. Gen. 133, 46–62.
Richardson, D. C., and Spivey, M. J. (2000). Representation, space and Hollywood Squares: looking at things that aren’t there anymore. Cognition 76, 269–295.
Richardson, D. C., Street, C. N. H., and Tan, J. (2010). “Joint perception: gaze and beliefs about social context,” in Proceedings of the 32nd Annual Conference of the Cognitive Science Society, Austin, TX.
Sebanz, N., Bekkering, H., and Knoblich, G. (2006). Joint action: bodies and minds moving together. Trends Cogn. Sci. (Regul. Ed.) 10, 70–76.
Sebanz, N., Knoblich, G., and Prinz, W. (2003). Representing others’ actions: just like one’s own? Cognition 88, B11–B21.
Shockley, K., Baker, A. A., Richardson, M. J., and Fowler, C. A. (2007). Articulatory constraints on interpersonal postural coordination. J. Exp. Psychol. Hum. Percept. Perform. 33, 201–208.
Shockley, K., Richardson, D. C., and Dale, R. (2009). Conversation and coordinative structures. Top. Cogn. Sci. 1, 305–319.
Tanenhaus, M. K., and Brown-Schmidt, S. (2008). Language processing in the natural world. Philos. Trans. R. Soc. B Biol. Sci. 363, 1105.
Terai, A., Kuriyama, N., Yasuhara, M., Tokunaga, T., Yamagishi, K., and Kusumi, T. (2011). “Using metaphors in collaborative problem solving: an eye-movement analysis.” in Proceedings of International Workshop on Dual Eye Tracking in CSCW (DUET 2011), Aarhus.
Tollefsen, D. P. (2002). Collective intentionality and the social sciences. Philos. Soc. Sci. 32, 25.
Turvey, M. T., Shaw, R. E., Reed, E. S., and Mace, W. M. (1981). Ecological laws of perceiving and acting. Cognition 9, 237–304.
Appendix
Obtaining Distributions from Lag Profiles
Previous work has subjected cross-correlation functions to analysis (e.g., Boker et al., 2002), and the measures in this paper require a derived sample from which measures like kurtosis can be calculated. In order to treat a lag profile as a distribution, and subject it to distribution analyses, we carried out a simple translation procedure. For each time slice along the x-axis of a lag profile, we repeated that time slice’s corresponding time value (e.g., in milliseconds) into a set of observations equal to some multiple (mt) of the y-axis %REC value. In order to ensure that all lag profiles had the same sample size when subjected to distribution analyses, we used a procedure that translated the profile into N ≅ 10,000 observations:
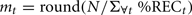
where %RECt is the percentage recurrence at a give time lag t. In order to obtain the number of samples for that time value t, we simply multiply it by mt, and the sample becomes the following collection:
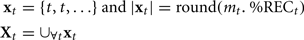
with xt as a set of observations for some time lag t, and Xt as the total set of observations (the union of all observations across time lags). This results in a set of observations the histogram of which resembles the original lag profile, and is composed of approximately 10,000 observations.
Which Baseline to Use?
There has been discussion of using permutation to construct baselines for these kinds of lag analyses (e.g., Bakeman et al., 1996). One recent approach is that cross-lag baselines should be assembled by “virtual pairs”: Random pairs of dyads should be produced by similar analysis of time series from participants combined from separate dyads. This is important for continuous time series, for which shuffling obliterates the spectral structure of the signal (e.g., Shockley et al., 2007). However, for nominal behavior sequences of this kind, shuffling serves only to create time series the events of which occur with a probability reflecting baseline occurrence of those events (in other words, the first-order probability of looking at tangram two in a shuffled time series, at any point in time, is simply proportional to the overall frequency with which it occurs in the series).
Whether this is more or less conservative than virtual pairing, however, is not a simple question to answer. In order to test this, we developed a simple probabilistic model that produces nominal time series of the kind we analyze here. This permits large-scale exploration of the statistical impact of different baselines. We had pairs of agents (N = 20) take “turns” and produce 500-element nominal time series with 6 event codes (similar to the current experiment). These agents were coupled according to a simple procedure shown in Table A1 below. The stronger the bias parameter, the stronger the connection between nominal sequences of agent A and B, and the greater the %REC measures.
We used a range of bias parameters, and generated 50 simulated “conversations” for each agent pair. We then did exactly the same cross-recurrence analysis over these simulations as above; we also carried out two baselines: simple shuffling and virtual pairing. The results are shown in Figure A1 below. An average recurrence was calculated from averaging a range of ±10 elements from the lag profile (analogous to the range ±10 s used in the real data above, as this element range captures the coordination between agents in their lag profile). For 50 conversations (per bias value), the baselines were compared by assessing which would estimate a higher baseline recurrence average.
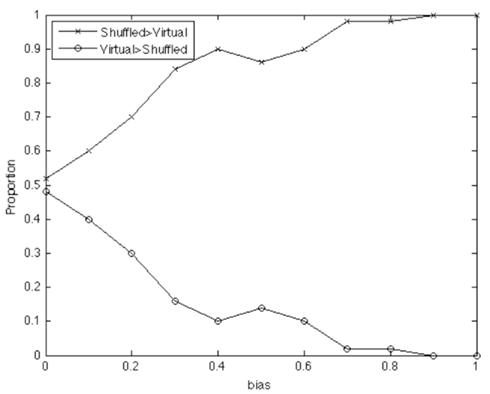
Figure A1. Simple shuffling tends to produce a higher proportion of simulated baselines than the virtual pair method, especially as the ‘true’ coupling between systems strengthens.
As seen in Figure A1, virtual pairing produces less conservative baseline scores because it estimates base-rate recurrence as lower than the shuffled baseline (conversely, shuffled baselines are more commonly greater in magnitude). And in fact this pattern holds the more likely there is to be an effect (i.e., with greater bias values, causing more tightly coupled agents). In other words, the simple shuffled baseline reflecting the base-rate probability of a particular event’s occurrence provides a test that is less likely to produce a Type I error. The reason for this can be explained intuitively: Sequences of events that hold in the original data are much less likely to overlap in virtual pairings than when shuffling occurs, because shuffling allows the individual occurrences to be distributed evenly over the time series. While the virtual pairing is more “real” in the sense that the pairs are based on the original data – the simple statistical baseline serves as a more conservative statistical basis for testing the presence of coordination. We therefore use it in this paper, as in previous papers.
Keywords: language, reference, vision, attention, coordination, synchrony, interaction, communication
Citation: Dale R, Kirkham NZ and Richardson DC (2011) The dynamics of reference and shared visual attention. Front. Psychology 2:355. doi: 10.3389/fpsyg.2011.00355
Received: 01 September 2011; Accepted: 10 November 2011;
Published online: 30 November 2011.
Edited by:
Andriy Myachykov, University of Glasgow, UKReviewed by:
Markus Janczyk, University of Würzburg, GermanyMichael Kaschak, Florida State University, USA
Copyright: © 2011 Dale, Kirkham and Richardson. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Rick Dale, Cognitive and Information Sciences, University of California Merced, Merced, CA 95343, USA. e-mail:cmRhbGVAdWNtZXJjZWQuZWR1