- Department of Psychological Sciences, University of Melbourne, Parkville, VIC, Australia
The research examined the relationship between 65 5- to 7-year-olds’ finger gnosia, visuo-spatial working memory, and finger-use in solving single-digit addition problems. Their non-verbal IQ and basic reaction time were also assessed. Previous research has found significant changes in children’s representational abilities between 5 and 7 years. One aim of the research was to determine whether changes in finger representational abilities (finger gnosia) occur across these ages and whether they are associated with finger-use in computation. A second aim was to determine whether visuo-spatial working memory is associated with finger gnosia and computation abilities. We used latent class profile analysis to identify patterns of similarities and differences in finger gnosia and computation/finger-use abilities. The analysis yielded four finger gnosia subgroups that differed in finger representation ability. It also yielded four finger/computation subgroups that differed in the relationship between finger-use and computation success. Analysis revealed associations between computation finger-use/success subgroups, finger gnosia subgroups, and visuo-spatial working memory. A multinomial logistic regression analysis showed that finger gnosia subgroup membership and visuo-spatial working memory uniquely contribute to a model predicting finger-use in computation group membership. The results show that finger gnosia abilities change in the early school years, and that these changes are associated with the ability to use fingers to aid computation.
Introduction
Fingers have long been thought to play an important role in the development of counting and computation abilities (Butterworth, 2005). Many preschool children spontaneously use fingers to support their initial counting behaviors (Gelman and Gallistel, 1978; Fuson, 1998), and school-aged children often use fingers when executing arithmetic operations [e.g., single-digit addition (SDA): see Geary, 2004, 2007; Geary and Hoard, 2005]. Although fingers provide a seemingly natural way of instantiating counting principles (e.g., one-to-one, stable order and cardinality principles) as well as different aspect of computation knowledge (e.g., base-10 knowledge; Di Luca et al., 2006; Domahs et al., 2008), little is known about developmental constraints that may affect the role of fingers in the acquisition of computation abilities. Indeed, Crollen et al. (this issue) review the question of whether finger counting is part of a necessary stage for the development of numerical cognition and whether its use is spontaneous in every child. We suggest that at least two factors may constrain the development of finger-use in computation: namely, (1) developmental limitations in children’s ability to manipulate cognitive representations; and (2) individual differences in spatial processing capacities.
Fifty years ago White (1965) described 21 changes in cognitive capacities between 5- and 7-years of age (often referred to as the 5- to 7-shift: see Sameroff and Haith, 1996). While the 5- to 7-year shift was originally conceptualized in Piagetian terms (i.e., the transition from inflexible, pre-operational thought to more flexible concrete operational thought), it has recently been reconceptualized in terms of developmental changes in the integration and/or coordination of cognitive capacities (Siegler and Chen, 2008; Sameroff, 2010). The claim is that young children’s reasoning is limited by an inability to coordinate cognitive representations because of limited processing capacities. Although little work has investigated finger gnosia and its applications in terms of the 5- to 7-shift, at least two developmental stages may be proposed: (1) the acquisition of a flexible representation of fingers; and (2) a flexible ability to use fingers as a cognitive tool in the service of number cognition. It is unlikely that children who are yet to acquire a flexible representation of fingers will be able to use them effectively as computation aids.
It is possible that finger–number representation is associated with a pre-existing spatial, non-symbolic magnitude system (de Hevia and Spelke, 2009, 2010; Mundy and Gilmore, 2009). The symbolic system for representing numbers is thought to be mapped onto the pre-existing non-symbolic, spatial magnitude system (Fias and Fischer, 2005; Brozzoli et al., 2008; Holloway and Ansari, 2009; Mundy and Gilmore, 2009). Some researchers claim that it is too simplistic to assume that the symbolic system spontaneously maps onto the non-symbolic magnitude system, and suggest that fingers may serve an intermediate role in the mapping processes (Fayol and Seron, 2005).
The possibility that finger, number, and spatial representations are linked was first raised by Gerstmann in the 1920s who observed that finger agnosia (the inability to distinguish among fingers) and difficulties in left-to-right orientation are often associated with acalculia (see Benton, 1987, 1992; Miller and Hynd, 2004). More recently, it has been suggested that they are likely to be linked because they are associated with neighboring neuroanatomical regions of the intraparietal cortex (Dehaene et al., 2003; Butterworth, 2005). The parietal cortex, and specifically the intraparietal sulcus (IPS) and left angular gyrus, are implicated in number representation (Pesenti et al., 2000; Fias et al., 2003; Feigenson et al., 2004; Pinel et al., 2004; Hubbard et al., 2005; Nieder and Dehaene, 2009), while finger agnosia is associated with left parietal damage (Rusconi et al., 2009). The parietal lobe contains regions responsible for representing number (Hubbard et al., 2005; Nieder and Dehaene, 2009), but fMRI indicates that it is also involved with hand movements (Sato et al., 2007), particularly regions surrounding the IPS (Hubbard et al., 2005). Sato et al. (2007) demonstrated that transcranial magnetic stimulation (TMS) to the left angular gyrus disrupts the ability to perform tasks that require access to finger representations, as well as interfering with the capacity to make number judgments. This extensive body of findings support claims for an association between finger and number representations; however, it is silent about how these representations emerge in the course of development.
The precise mediating role fingers serve in numerical cognition is a matter of debate (Sato and Lalain, 2008; Wood and Fischer, 2008). Some claim that habitual finger counting practices influence the long-term associations between number and fingers and, ipso facto, how number is represented cognitively (Di Luca et al., 2006; Domahs et al., 2008, 2010). For example, finger counting strategies can modify the SNARC effect: individuals who start counting on their right hand exhibit a reduced SNARC effect (Fischer, 2008). However, neuropsychological research that shows number, finger, and spatial representations are related caution against a purely “practice” account of finger–number associations (Fias and Fischer, 2005; Hubbard et al., 2005). It should be noted that adherents of the so-called neurological and cultural-practice views emphasize the importance of spatial properties of fingers/hands, even though they may disagree on the reasons for their importance (see Bender and Beller, this issue; Klein et al., this issue, for detailed discussion of these issues). Nevertheless, neither approach has much to say about the reasons for, or implications of, developmental differences in finger gnosia abilities.
Poor finger gnosia is associated with poor arithmetic performance (Fayol et al., 1998; Fayol and Seron, 2005; Noël, 2005; Gracia-Bafalluy and Noël, 2008). Noël (2005), for example, found that finger gnosia predicts calculation errors, but not general abilities (e.g., reading abilities). Fayol et al. (1998) reported that performance on perceptuo-tactile tasks was a better predictor of maths performance than general developmental tests (see also Gracia-Bafalluy and Noël, 2008). In these studies finger gnosia was assessed by an interviewer touching a child’s finger; the child either pointed to a fingers/hand diagram to indicate the touched finger or recalled a number assigned to a finger (Fayol et al., 1998; Noël, 2005; Gracia-Bafalluy and Noël, 2008). Like many finger gnosia tasks, these tasks comprised both a motor and a finger representation component, making it difficult to identify which of them is associated with arithmetic difficulties. Indeed, psychomotor difficulties are often associated with developmental disorders (Holsti et al., 2002). It has long been known that some school-related difficulties (arithmetic and writing) are associated with motor and psychomotor difficulties (Rourke and Strang, 1978; Ozols and Rourke, 1988; Rourke, 1995). It is possible that the association between poor finger gnosia and arithmetic difficulty observed in previous research reflects psychomotor difficulties, rather than difficulties associated with finger–number relationships per se. Indeed, the visual-motor structure and movement of fingers is thought to support the creation of an internal representation of number (Pesenti et al., 2000). In the present research we minimize the potential impact of motor difficulties by employing a finger gnosia task that eliminates the motor component, and which focuses explicitly on finger–hand knowledge.
One difficulty interpreting previous research findings on the relationship between finger gnosia and arithmetic abilities is that they have tended to focus on general arithmetic performance, rather than finger-use in specific arithmetic problem solving. Research examining the acquisition of SDA abilities may provide a framework for remedying this oversight. The acquisition of SDA problem solving abilities has been well described (Geary et al., 2004, 2007; Kaufmann and Nuerk, 2005), and most models of SDA development assume finger-use is an integral part of problem solving development (Geary and Hoard, 2005; Geary et al., 2007). Although fingers may be analogous to external computation aids, developmental constraints may affect their use as tools in numerical cognition. In particular, flexible finger gnosia representations and spatial capacities may affect finger-use in computation.
In summary, given the mediating role attributed to fingers in numerical cognition, at least three questions require answers. First, how should finger representation (finger gnosia) be assessed? Most finger gnosia tests conflate motor movement (e.g., pointing) and finger representation. Since a link between developmental motor disorders and arithmetic ability has been found (Holsti et al., 2002), it is important to minimize the motor component in finger gnosia assessments. Second, what is the relationship between 5- to 7-year-olds’ finger gnosia and finger-use in computation? Third, are finger gnosia and spatial ability associated; and to what degree do finger gnosia and spatial ability separately predict finger-use in computation ability?
The Current Study
We examined the relationship between 5- to 7-year-olds finger representations on a non-motoric finger gnosia task and finger-use/success solving SDA problems. We also assessed their performances on a visuo-spatial working memory task (Corsi, 1972), the Ravens Colored Progressive Matrices task (Raven et al., 1986: hereafter referred to as Ravens) and on a basic reaction time (RT) task.
The relationship between visuo-spatial working memory and math abilities has been observed in several studies in older elementary school children (i.e., older than 7 years; Bull et al., 2008; Holmes et al., 2008; Lonnemann et al., 2008; Passolunghi and Cornoldi, 2008). However, relatively little is known about the association between visuo-spatial working memory and enumeration abilities in younger children. Further, since finger representations are thought to provide links between non-symbolic quantities and symbolic numbers, it is important to determine whether finger gnosia per se is associated with visuo-spatial ability and finger-use in computation.
Processing speed is considered an index of IQ (Kail, 2007), and is related to math abilities in older students (Bull and Johnston, 1997; Floyd et al., 2003). A processing speed measure is important for two reasons. First, it is important to determine whether processing speed is an important determinant of SDA problem solving ability; and second, whether it is associated with speed of making finger gnosia judgments. The Ravens is a standardized measure of non-verbal reasoning ability, which has long been regarded as a measure of general intelligence (Spearman, 1946).
On the basis of previous SDA research findings, we expect age-related changes, as well as individual differences, in 5- to 7-year-olds’ SDA abilities (Canobi et al., 1998, 2003; Geary, 2007). Insofar as finger-use is associated with the acquisition of SDA ability, we expect that finger gnosia would be associated with finger-use and success in SDA across age. (It should be noted that mature SDA ability is associated with an absence of finger-use since children are able to retrieve answers to problem from memory without having to resort to effortful computational process – see Geary, 2007.) Also on the basis of previous research, which has found a relationship between visuo-spatial work memory and math ability (Lonnemann et al., 2008), we expect that a similar relationship would be observed in the present research. However, we make no explicit predictions about the relationships between finger gnosia and visuo-spatial working memory and their impact on age-related changes in SDA abilities. Further, we make no explicit predictions about the moderating impact of Ravens and RT.
Materials and Methods
Participants
Thirty Kindergarten (M = 5 years 10 months, SD = 3.30 months) and 35 Year One (M = 6 years 11 months, SD = 4.14 months) children, comprising approximately equal numbers of males and females from a non-government school in a middle-class suburb of a large Australian city, participated. These children were selected to approximately represent a 5- to 7-year-olds shift sample. All children had normal or corrected to normal vision. According to their teachers, no child had known learning difficulties. The study was conducted in accordance with the authors’ University’s Human Ethics Committee requirements.
Materials and Procedure
Children were interviewed individually in a quiet room at their school. They completed five tasks on four successive days; namely: (1) a Non-motoric Finger Gnosia (Finger Gnosia) test; (2) a SDA test; (3) the Corsi Blocks (Corsi) visual spatial working memory test; (4) the Ravens Colored Progressive Matrices (Ravens) test; and (5) a basic RT task. The Corsi and RT tasks were completed on day one; and the Finger Gnosia, SDA, and Ravens tests were presented on the subsequent 3 days (task order was randomized). Children’s handedness was also determined on day one. Each test/day sessions lasted between 10 and 20 min. Stimuli for the SDA and RT tasks were presented on 15½″ laptop computer screen in which presentation was controlled using DMDX (Version 2) software (Forster and Forster, 2001).
Handedness was assessed in three ways: (1) teacher’s report; (2) the hand children used to pick-up and pass an object to the interviewer; and (3) the hand with which children used to write. The three indices were 100% consistent; on the basis of which 60 children were deemed right-handed and five left-handed. A formal handedness assessment was not used (e.g., Edinburgh Handedness Inventory-Oldfield, 1971) because pilot work revealed children had difficulty understanding the test language.
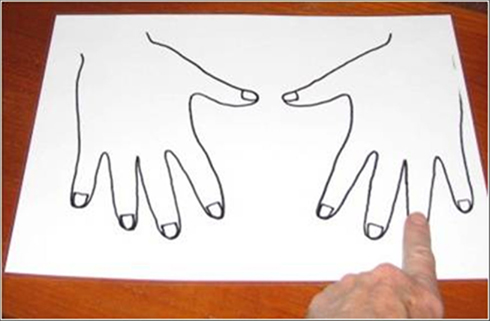
The Finger Gnosia test apparatus comprised (1) a 34-cm × 25.5-cm × 16-cm box that had a 17-cm × 6-cm opening on one side and open on the opposite side, and (2) a schematic outline of a palms-down pair of hands (Figure 1 is a photo of the Finger Gnosia apparatus). The 17-cm × 6-cm opening was large enough for children to put their hands through. Children placed their hands, palm down, through the 17-cm × 6-cm opening so that the examiner could see them from the opposite side of the box, but the child could not see them. The examiner touched one of the children’s fingers and simultaneously pointed to a finger on the schematic drawing of the hands (which was placed to left of the box; see Figures 1 and 2). Children were instructed to indicate as quickly and as accurately as possible whether the “touched” finger and the finger pointed to on the diagram were the same by saying “yes” or “no.”
Only four of the eight fingers and two thumbs were used in the Finger Gnosia test; namely, the left and right ring finger (fingers 2 and 9 respectively), and the left and right index finger (fingers 4 and 7 respectively). These fingers were selected to avoid the anchoring properties of the outside digits, as well as the saliency of the middle finger, and to require discrimination among the fingers on each of the hands. The Finger Gnosia test sequence involved four practice, and 72 test trials. The test trials comprised one correct and three incorrect finger–hand correspondence categories: (1) Correct Finger, Correct Hand – CFCH (e.g., touched finger 2-pointed to finger 2); (2) Incorrect Finger, Correct Hand – IFCH (e.g., touched finger 2-pointed to finger 4); (3) Correct Finger, Incorrect Hand – CFIH (e.g., touched finger 2-pointed to finger 7); and (4) Incorrect Finger, Incorrect Hand – IFIH (e.g., touched finger 2-pointed to finger 9). Thirty-six of the Finger Gnosia judgment trials comprised correct finger–correct hand relations, and 36 trials comprised instances of the three incorrect finger–hand relationships. The purpose of the practice trials was to familiarize children with judgment procedures and to emphasize that judgment were to be made about finger relations when hands were palm down. All children were able to describe the procedure and successfully completed the practice trials. Of interest were the number of correct judgments and response times for the four finger–hand judgment categories. As the interviewer touched/pointed to fingers, she said “this one,” the sound of which activated an audio timing mechanism, and response times were measured from this point to children responding either “yes” or “no.”
Single-digit addition competence was assessed by the ability to solve 30 two-term SDA problems of the form “a + b” = ? Children encounter SDA problems as part of their school curricula, and thus were familiar with the problem format. Addends comprised the numbers “2” to “7” presented in both orders (e.g., 2 + 7 and 7 + 2) and excluded tied pairs (e.g., 2 + 2). SDA problems were present via the laptop computer screen. When a child gave an answer to a problem, the interviewer (1) pressed a response key to record the time taken to solve problems, (2) recorded the answer to the problem, and (3) noted whether the child used fingers to aid problem solving.
Corsi Blocks (Corsi, 1972) is a measure of visuo-spatial working memory, performance, which is associated with math performance in older children (Kyttala and Lehto, 2008). It comprises nine 2.5 cm × 2.5 cm × 2.5 cm blocks fixed in random arrangement on a 25-cm × 25-cm board. The interviewer taps a sequence of blocks, one per second, and children attempt to repeat the tap sequence in the same (forward span) or reversed (backward span). In two practice trials, children were encouraged to wait for 5 s before acting, to limit impetuous responding and to instantiate task requirements. In the actual test, children responded immediately after the interviewer said “now.” Within a trial, a tap sequence begins with the interviewer tapping two blocks. The two-block tap sequence is repeated and if one or both sequences have been successfully completed, the sequence is increased in length by one block. Two sequences are presented before increasing again by one block. A trial is discontinued after the child fails to correctly reproduce both tap sequences of the same length. There has been considerable inconsistency in the administration and scoring of the Corsi Blocks test (Berch et al., 1998). We adopt the Corsi administrative methodology used by Kessels et al. (2000). Consistent with Kessels et al. (2000), we report the raw span score.
Ravens Colored Progressive Matrices (Raven et al., 1986) is a standardized measure of non-verbal reasoning ability which has long been regarded as a measure of general intelligence (Spearman, 1946). It comprises 36 stimuli in which a section of a colored pattern is missing and participants attempt to complete the pattern by selecting from among six possible options. The 1998 test guidelines and age norms were used to administer and calculate Ravens scores.
Basic RT task
A black target dot appears on the laptop screen between 500 and 1000 ms after the appearance of a fixation point. Children pressed the computer shift key using their dominant hand as soon as the dot appeared. Basic processing speed was based on the average time taken to respond to the target dot on nine trials. Different ISIs were included to prevent target prediction effects.
Analytic Approach
To identify possible Finger Gnosia and SDA subgroups, we used Latent Gold’s latent profile analysis to determine whether different data structures (different subgroups) are embedded within the overall Finger Gnosia and SDA data structures (see Vermunt and Magidson, 2000, 2003; Notelaers et al., 2006). We used latent profile analysis for two reasons. First, it makes no assumptions about the measurement properties of stimuli (e.g., it does not assume that measures are continuous in nature). Second, Latent Gold’s latent profile model technique has advantages over traditional clustering techniques in that it does not rely on traditional modeling assumptions (i.e., linear relationships, normal distributions, homogeneity). The technique identifies subgroups by grouping people who share similar characteristics via probability-based classification. Further, replication analyses select the best start seed to insure groups are unaffected by local maxima. This analytic approach stands in contrast to more traditional methods in which age is treated as a factor. Nevertheless, given the occurrence of large within-age individual differences in young children’s numerical cognition (Canobi et al., 1998, 2003), we suggest latent profile analysis has much to recommend it to those interesting in characterizing developmental changes in math ability.
Finger Gnosia subgroups were determined by including in the analysis correct responses for the four finger judgment categories (i.e., CFCH; IFCH; CFIH; and IFIH judgments). SDA subgroups were determined by including problem solving accuracy and finger-use in calculating answers. Kindergarten and Year 1 children were included in the same analyses to determine the degree to which age was associated with subgroup membership. However, this approach does not obviate examining age-related changes.
Results
No relationship was found between handedness or gender or any of the other factors in the study; consequently, neither handedness nor gender were considered further.
Although no significant grade-related differences were observed in the cognitive indices (Corsi: Kindergarten M = 4.00, SD = 0.12; Year 1 M = 4.07, SD = 0.10; Ravens: Kindergarten M = 58.50, SD = 27.01; Year 1 M = 59.14, SD = 23.50; RT: Kindergarten M = 717.83, SD = 100.12; Year 1 M = 698.69, SD = 97.56), possibly because of within-age variability in the measures, age-related trends were observed across the measures.
Finger Gnosia Profiles
Inspection of the four Finger Gnosia measures (see Materials and Methods for a description of these measures) revealed substantial variability in correct judgments in each of the four judgment categories: CFCH (M = 86.54, SD = 12.5); IFCH (M = 74.03, SD = 30.0); CFIH (M = 80.8, SD = 23.4); and IFIH (M = 80.8, SD = 19.1).
To explore the significance of variability among the four Finger Gnosia measures, Latent profile analysis was conducted and revealed a four group solution, which accounted for 71% of the variance in the pattern of correct judgments. The four group solution was selected on the basis of the Bayesian information criterion (BIC) representing a significant model fit [BIC (LL) = 206; p > 0.05].
The correctness patterns of the four groups are presented in Figure 3. These correctness patterns can be characterized as: (1) a finger/hand confusion (FHC) subgroup (n = 13), (2) a finger confusion (FC) subgroup (n = 9), (3) a good finger gnosia (GFG) subgroup (n = 24), and (4) a high finger gnosia (HFG) subgroup (n = 19).
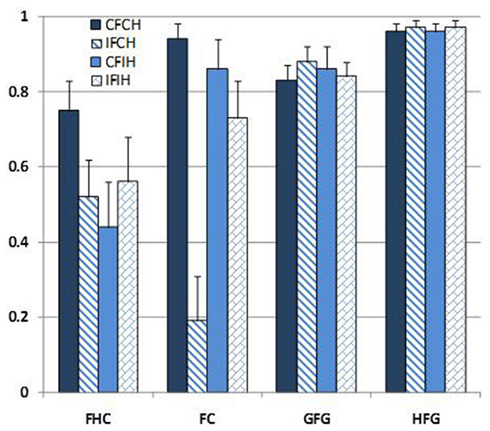
Figure 3. Proportion CFCH, IFCH, CFIH, and IFIH judgments correct as a function of NMFG subgroup membership.
One-way ANOVAs showed that the four subgroups differed from each other on each of the four Finger Gnosia judgment measures. Specifically, for CFCH judgments: F (3, 61) = 14.87, p < 0.001; η2 = 0.42; for IFCH: F (3, 61) = 106.55, p < 0.001; η2 = 0.84; for CFIH: F (3, 61) = 43.12, p < 0.001; η2 = 0.68; for IFIH: F (3, 61) = 27.55, p < 0.001; η2 = 0.58. Moreover, there was an interaction between judgment condition and subgroup [F (9, 183) = 22.26, p < 0.001; η2 = 0.52]. The HFG subgroup was more successful than other subgroups for all conditions (ps < 0.05). For the IFCH measure, the FC subgroup performed significantly worse than FHC subgroup, which in turn performed worse than the GFG subgroup (ps < 0.05). For CFIH measure, the FHC subgroup performed worse than the FC and GFG subgroups (ps < 0.05); and for IFIH measure, the four subgroups were different from each other (ps < 0.05). These patterns of findings support the use of the FHC, FC, GFG, HFG subgroup labels.
Table 1 reports the relationship between finger gnosia subgroups and grade, which revealed a significant association between the two factors (χ2 (3, N = 65) = 22.41, p < 0.001; γ = 0.74, p < 0.001). Although Kindergarten and Year 1 children were present in all subgroups, age-related changes in finger gnosia abilities are evident.
Finger Gnosia Judgment Measure and Subgroup Response Times
The speed of making correct and incorrect judgments for the four Finger Gnosia subgroups (averaged across finger gnosia measures) is presented in Table 2. Initial analysis revealed no differences in judgment decision times for the three incorrect judgment measures (i.e., IFCH, CFIH, and IFIH measures). As a consequence, the data for these three judgment conditions were combined into one error judgment condition (i.e., time taken to make a decision).
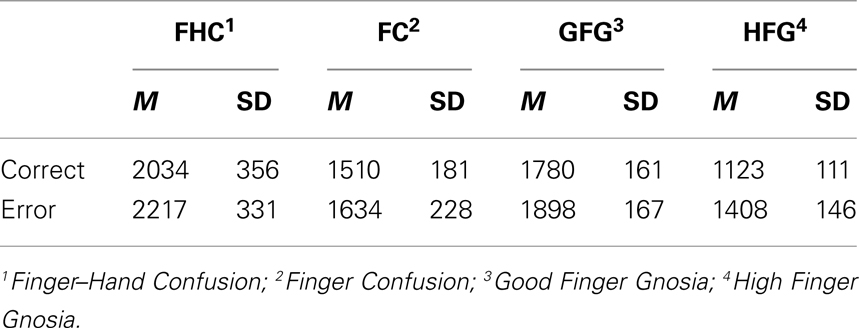
Table 2. Average judgment times for finger gnosia correct and error conditions as a function of subgroup membership.
With the exception of the HFG subgroup, subgroups did not differ in the time taken to make error and correct judgments, suggesting that judgment error was not due to children making judgments quickly [t (18) = 3.57, p < 0.01 for the HFG subgroup].
Profiles of SDA Finger-Use
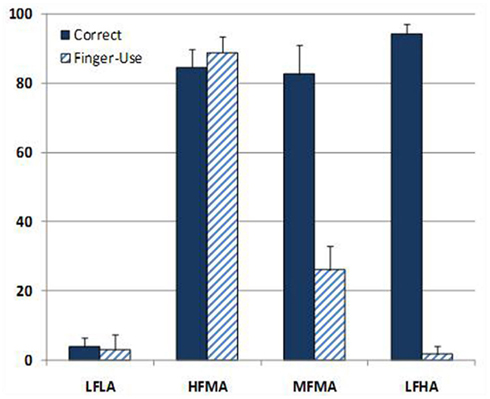
The number of SDA problems children solved correctly and the percentage of occasions on which they used fingers to compute answers was subjected to Latent Gold’s latent profile analysis. (It should be noted that students were always successful in solving SDA problems when they used their fingers.) The analysis yielded four subgroups (n = 15, 24, 11, 15), which accounted for 94% of the variance in the pattern of responses in the data. The four subgroup solution was selected on the basis of a significant model fit [BIC (LL) = 1183; p > 0.05]. The four subgroups showed that SDA problem solving and finger-use varied orthogonally (Hi/Lo finger-use × Hi/Lo SDA problem solving success; see Figure 4 for the SDA, Finger-use subgroups). Two subgroups were characterized by low finger-use, one of which had low accuracy (LFLA), and the other showed successful performance (LFHA). The other two subgroups showed moderate accuracy, one with high finger-use (HFMA), the other with moderate finger-use (MFMA).
The SDA Finger-use subgroups differed from each other in accuracy and computational finger-use [Accuracy: F (3, 61) = 245.29, p < 0.001; η2 = 0.92; Finger-Use: F (3, 61) = 378.37, p < 0.001; η2 = 0.95]. Further, there was an interaction effect between success and finger-use [F (3, 61) = 175.03, p < 0.001; η2 = 0.90]. Post hoc analysis revealed that the LFLA subgroup performed significantly worse in solving SDA problems than the other subgroups (ps < 0.05); the LFHA subgroup solved more SDA problems correctly than the other three subgroups (ps < 0.05); however, the two finger-use subgroups did not differ in SDA problem solving ability.
Of interest is whether there is an aged-based relationship between grade and SDA finger-use subgroups (see Table 3). The LFLA subgroup comprises Kindergarten children only, but both grades are represented in the other three subgroups. As expected, a relationship was found between the SDA finger-use subgroup and age [χ2 (3, N = 65) = 29.29, p < 0.001; γ = 0.77, p < 0.001]. The presence of Kindergarten children in all four subgroups, and of Year 1 children in three of the four subgroups, highlights SDA variability.
In what follows we focus only on the SDA and Finger Gnosia subgroups.
Relationship between Finger Gnosia and SDA Subgroups and Cognitive Ability
One-way ANOVAs examined Finger Gnosia and SDA subgroup differences in RT, Ravens, and Corsi abilities (see Tables 4 and 5 for means and SDs for all measures).
Analyses showed that neither the Finger Gnosia subgroups nor the SDA finger-use subgroups differed in RT or Raven’s performance. However, both the Finger Gnosia and SDA subgroups differed in Corsi span [Finger Gnosia: F (3, 61) = 2.88, p < 0.05; η2 = 0.13; SDA Finger-use: F (3, 61) = 6.89, p < 0.001; η2 = 0.25]. Post hoc tests showed that the HFG subgroup had a longer Corsi span than the two subgroups exhibiting finger representation difficulties (i.e., FHC and FC). Similarly, the Low Finger-use, High Ability SDA subgroup had a longer span than the other three subgroups (ps < 0.05), which did not differ from each other.
Relationships between Finger Gnosia and SDA Subgroups
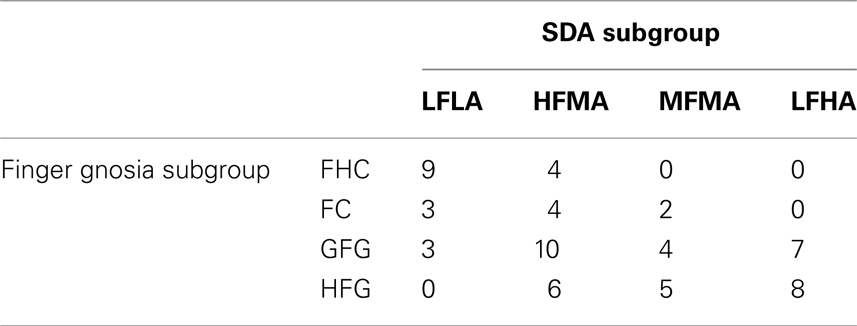
Table 6 reports the cross tabulation between Finger Gnosia and SDA finger-use subgroup memberships. Analyses showed a significant relationship between subgroup membership for the two measures [χ2 (9, N = 65) = 30.31, p < 0.001; γ = 0.70, p < 0.001]. The findings provide support for the hypothesis that differences in children’s finger gnosia are associated with their use of fingers as computational aids in solving simple addition problems.
Predicting SDA Finger-Use from Finger Gnosia and Corsi Span
Results show that SDA Finger-use subgroups were associated with the Finger Gnosia subgroups and Corsi span. To further investigate the relationships between the three measures, a multinomial logistic regression analysis was conducted in which SDA Finger-use subgroup membership was predicted from Finger Gnosia subgroup membership and Corsi span. The results showed that the goodness of fit for the overall model was very good [Pearson χ2 (174, N = 65) = 134.17, p = 0.98; pseudo r2 (Cox and Snell) = 0.55]. Overall, 58.5% of the children were correctly assigned to SDA finger-use subgroups. More specifically, Corsi span and Finger Gnosia subgroup membership made significant unique contributions to the overall model [χ2 (3, N = 65) = 14.07, p < 0.01 and χ2 (9, N = 65) = 37.99, p < 0.001 respectively].
Discussion
The research was designed to investigate the developmental relationship between differences in finger gnosia representations, visuo-spatial working memory, and finger-use in SDA problem solving. The results demonstrate a strong relationship between finger gnosia subgroup membership and SDA finger-use/problem solving success subgroups. Even though visuo-spatial working memory was associated with finger gnosia and SDA subgroup membership, finger gnosia subgroup membership predicted SDA finger-use subgroups over and above the contribution of visuo-spatial working memory. These findings demonstrate for the first time that finger gnosia representations change between 5- and 7-years, and these changes are related to finger-use in computation. Furthermore, visuo-spatial abilities and finger gnosia are independently associated with computation abilities.
Measuring Finger Gnosia
The results suggest that the non-motoric finger gnosia measure provided a good characterization of individual differences in finger representation. Moreover, given the association between psychomotor difficulties, developmental disorders, and problems in number processing (Rourke, 1995; Holsti et al., 2002), our findings provide direct evidence for the importance of a measure of finger gnosia, uncontaminated by motor activity, in predicting arithmetic abilities. Furthermore, the results show that within the 5- to 7-age range, there is substantial improvement in finger representation. Kindergarten children initially exhibit problems discriminating fingers within and between hands. In contrast, most of the Year 1 students exhibited good or very good finger representation.
Performance Profiles
Our findings revealed the existence of individual differences in finger gnosia judgment ability. Specifically, four distinctly different profiles of finger gnosia judgment were identified. The subgroups were characterized by the differential ability to accurately judge the four finger gnosia measures (i.e., relationships between the touched finger and the indicated diagram finger). It should be noted that all subgroups were slightly slower in making incorrect than correct judgments, which suggests that error judgment per se did not reflect impulsive responding. Although, as expected, there was a significant association between finger gnosia subgroup membership and age, children from both age groups were represented across all the subgroups. This finding highlights the importance of taking into account of the wide range of difference in young children’s abilities in addition to age-related changes. It also suggests that subgroups provided a detailed characterization of children’s finger representation development.
Four SDA finger-use profiles were identified, which varied orthogonally as a function of problem solving ability and finger-use. These subgroups were also associated with age, but children from both ages were represented in three of the four groups, suggesting that subgroup membership is more informative about SDA finger-use than age alone. It is evident that even within a narrow age range, large individual differences exist in computation ability and finger-use.
Relationships between Finger Gnosia, SDA Finger-Use, and Cognitive Abilities
The findings showed that the non-motoric finger gnosia and computational finger-use subgroups were systematically associated with each other. Specifically, children who showed poor finger gnosia, characterized by FHC or FC, were largely assigned to the low finger-use, low ability SDA subgroup. Moreover, all children in the high computational ability subgroup were classified in the good and HFG subgroups.
These findings support previous research, which show that poor finger gnosia is associated with poor arithmetic performance (Fayol et al., 1998; Fayol and Seron, 2005; Noël, 2005; Gracia-Bafalluy and Noël, 2008). However, our findings add to previous research in two ways. First, prior research did not investigate the relationship between the finger gnosia and finger-use in computation. Second, by partitioning finger gnosia performance data, we identified profiles of finger representation that were systematically associated with SDA finger-use and success. In particular, the association was not confined to the relationship between poor finger gnosia and a lack of arithmetic problem solving success; it also showed that children with HFG exhibited high calculation ability.
We found no association between subgroup membership on either of the tasks and basic RT or performance on the Ravens test. This finding is important because it shows that the response speed differences between the finger gnosia subgroups were not an artifact of basic RT, but of finger representation ability. Furthermore, although some research has shown that differences in arithmetic success are related to overall processing speed (Geary and Brown, 1991; Kail, 2007), our findings are consistent with research that found little relationship between general measures of ability and numerical cognition in young children (Butterworth, 2005).
However, for both the Finger Gnosia and SDA finger-use subgroups, there was an association with visuo-spatial working memory performance. This result is not unexpected, and is consistent with previous research showing that Corsi span is associated with computational ability (Landerl et al., 2009). Nevertheless, this particular finding provides additional important information about the relationship between spatial ability and number competence: it showed that visuo-spatial working memory was systematically associated with SDA abilities in young children.
Although visuo-spatial working memory was associated with performance profiles on both the finger gnosia and SDA tasks, finger gnosia subgroup membership predicted SDA subgroup membership over and above the contribution of visuo-spatial working memory. This suggests that the finger gnosia and visuo-spatial working memory are independently related to computation ability.
Overall, the findings suggest an important relationship between both age-related and individual differences in children’s finger representations, and the ways in which they use fingers in computation. They also suggest that finger representations become more precise with age, which in turn, is related to the way in which fingers are used to solve computation problems. Furthermore, they provide more detailed information about the nature of finger representation and its unique contribution to computational finger-use.
Finger Representation, Spatial Ability, and Arithmetic Competence
Previous research has considered the relationship between computational finger-use and arithmetic ability (Di Luca et al., 2006; Domahs et al., 2008), finger gnosia and number ability (Fayol et al., 1998; Gracia-Bafalluy and Noël, 2008), and the relationship between visuo-spatial working memory and arithmetic competence (Lonnemann et al., 2008; Landerl et al., 2009). However, with the exception of our research, no study has examined the three-way relationship between finger representation, computational finger-use, and spatial working memory. Indeed, our research suggests that finger gnosia is partially independent of spatial working memory.
While many studies have found an association between finger representation, finger-use, and enumeration, there is debate about how fingers instantiate numerical knowledge. As noted earlier some claim that the properties of number are acquired through habitual hand/finger counting practice (Di Luca et al., 2006; Domahs et al., 2008, 2010; Sato and Lalain, 2008). Others claim that hand/finger representations facilitate mapping numerical concepts onto a pre-existing spatial, mental number line. Whatever side one takes in this debate, our findings suggest that the development of finger representation per se cannot be ignored, nor can the relationship between finger gnosia and the use of fingers as computational tools.
Future Research
The performance profiles identified herein suggest developmental trajectories for finger representation and finger-use in arithmetic problem solving. We suggest that a longitudinal analysis of young children’s finger gnosia and finger-use in enumeration would help to establish a development model of the relationship between the two components. Indeed, developmental changes in the relationship between spatial ability, finger gnosia, and arithmetic performance would help identify the precise contribution of each component to the acquisition of number knowledge. Furthermore, we need to better understand the developmental interrelationship between early learning environments and the emergence of cognitive representations (Sameroff, 2010). In the present study, we showed that finger representation ability changed between 5- and 7-years. However, we are unable to say why this change occurred. It is possible that calculation practices may facilitate finger representation, which in turn may facilitate more sophisticated calculation practices.
Improving finger gnosia is assumed to mediate the spatial representations that support numerical development. Further research that investigates finger gnosia training would help determine whether spatial representations of number can be targeted directly. This is consistent with Lonnemann et al.’s (2008) suggestion that visuo-spatial strategies may assist number processing when they coincide with spatial representations.
Conclusion
We investigated the developmental role fingers play in the acquisition of computation abilities, in particular, whether non-motoric finger gnosia predicts finger-use in computation. We show for the first time that non-motoric finger gnosia is a good measure of motoric finger-use in simple addition. Moreover, we also show that both finger gnosia (possibly, the spatial properties of finger/hand arrangements) and spatial working memory independently predict finger-use in computation. This suggests that different kinds of spatial processes support the development of numerical cognition. It is also evident that general cognitive measures (processing speed and non-verbal reasoning in the present context) do not predict arithmetic competence, at least in young children.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Benton, A. L. (1987). “Mathematical disability and the Gerstmann syndrome,” in Mathematical Disabilities: A Cognitive Neuropsychological Perspective, eds G. Deloche and X. Seron (New Jersey: Lawrence Erlbaum Associates, Inc.), 111–120.
Berch, D. B., Krikorian, R., and Huha, E. M. (1998). The Corsi blocktapping task: methodological and theoretical considerations. Brain Cogn. 38, 317–338.
Brozzoli, C., Ishihara, M., Göbel, S. M., Salemme, R., Rossetti, Y., and Farnè, A. (2008). Touch perception reveals the dominance of spatial over digital representation of numbers. Proc. Natl. Acad. Sci. U.S.A. 105, 5644–5648.
Bull, R., Espy, K. A., and Wiebe, S. A. (2008). Short-term memory, working memory, and executive functioning in preschoolers: longitudinal predictors of mathematical achievement at 7 years. Dev. Neuropsychol. 33, 205–228.
Bull, R., and Johnston, R. S. (1997). Children’s arithmetical difficulties: contributions from processing speed, item identification, and short term memory. J. Exp. Child. Psychol. 65, 1–24.
Butterworth, B. (2005). The development of arithmetical abilities. J. Child Psychol. Psychiatry 46, 3–18.
Canobi, K. H., Reeve, R. A., and Pattison, P. (1998). The role of conceptual understanding in children’s addition problem solving. Dev. Psychol. 34, 882–891.
Canobi, K. H., Reeve, R. A., and Pattison, P. E. (2003). Patterns of knowledge in children’s addition. Dev. Psychol. 39, 521–534.
Corsi, P. M. (1972). Human Memory and the Medial Temporal Region of the Brain. Dissertation Abstracts International, 34, 819B, McGill University Microfilms No. AA105-77717, Montreal, QC.
de Hevia, M.-D., and Spelke, E. S. (2009). Spontaneous mapping of number and space in adults and young children. Cognition 110, 198–207.
de Hevia, M.-D., and Spelke, E. S. (2010). Number-space mapping in human infants. Psychol. Sci. 21, 653–660.
Dehaene, S., Piazza, M., Pinel, P., and Cohen, L. (2003). Three parietal circuits for number processing. Cogn. Neuropsychol. 20, 487–506.
Di Luca, S., Granà, A., Semenza, C., Seron, X., and Pesenti, M. (2006). Finger-digit compatibility in Arabic numeral processing. Q. J. Exp. Psychol. 59, 1648–1663.
Domahs, F., Krinziger, H., and Willmes, K. (2008). Mind the gap between both hands: evidence for internal finger-based number representations in children’s mental calculation. Cortex 44, 359–367.
Domahs, F., Moeller, K., Huber, S., Willmes, K., and Nuerk, H.-C. (2010). Embodied numerosity: implicit hand-based representations influence symbolic number processing across cultures. Cognition 116, 251–266.
Fayol, M., Barrouillet, P., and Marinthe, X. (1998). Predicting arithmetical achievement from neuropsychological performance: a longitudinal study. Cognition 68, B63–B70.
Fayol, M., and Seron, X. (2005). “About numerical representations: insights from neuropsychological, experimental, and developmental studies,” in Handbook of Mathematical Cognition ed. J. I. D. Campbell (New York: Psychology Press), 3–22.
Feigenson, L., Dehaene, S., and Spelke, E. S. (2004). Core systems of number. Trends Cogn. Sci. (Regul. Ed.) 8, 307–314.
Fias, W., and Fischer, M. H. (2005). “Spatial representation of numbers,” in Handbook of Mathematical Cognition, ed. J. I. D. Campbell (New York: Psychology Press), 43–54.
Fias, W., Lammertyn, J., Reynvoet, B., Dupont, P., and Orban, G. A. (2003). Parietal representation of symbolic and nonsymbolic magnitude. J. Cogn. Neurosci. 15, 47–56.
Fischer, M. H. (2008). Finger counting habits modulate spatial-numerical associations. Cortex 44, 386–392.
Floyd, R. G., Evans, J. J., and McGrew, K. S. (2003). Relations between measures of Cattell–Horn–Carroll (CHC) cognitive abilities and mathematics achievement across the school-age years. Psychol. Sch. 40, 155–171.
Forster, K. I., and Forster, J. C. (2001). DMDX Version 2.9.01. Available at: http://www.u.arisona.edu/(jforster/dmdx.htm. 30/05/2010
Geary, D. C. (2007). An evolutionary perspective on learning disability in mathematics. Dev. Neuropsychol. 32, 471–519.
Geary, D. C., and Brown, S. C. (1991). Cognitive addition: strategy choice and speed of processing differences in gifted, normal, and mathematically disabled children. Develop. Psychol. 27, 398–406.
Geary, D. C., and Hoard, M. K. (2005). “Learning disabilities in arithmetic and mathematics,” in Handbook of Mathematical Cognition, ed. J. I. D. Campbell (New York: Psychology Press), 253–268.
Geary, D. C., Hoard, M. K., Byrd-Craven, J., and Desoto, M. C. (2004). Strategy choices in simple and complex addition: contributions of working memory and counting knowledge for children with mathematical disability. J. Exp. Child. Psychol. 88, 121–151.
Geary, D. C., Hoard, M. K., Byrd-Craven, J., Nugent, L., and Numtee, C. (2007). Cognitive mechanisms underlying achievement deficits in children with mathematical learning disability. Child Dev. 78, 1343–1359.
Gelman, R., and Gallistel, C. R. (1978). The Child’s Understanding of Number. Cambridge, MA: Harvard University Press.
Gracia-Bafalluy, M., and Noël, M.-P. (2008). Does finger training increase young children’s numerical performance? Cortex 44, 368–375.
Holloway, I. D., and Ansari, D. (2009). Mapping numerical magnitudes onto symbols: the numerical distance effect and individual differences in children’s mathematics achievement. J. Exp. Child. Psychol. 103, 17–29.
Holmes, J., Adams, J. W., and Hamilton, C. J. (2008). The relationship between visuospatial sketchpad capacity and children’s mathematical skills. Eur. J. Cogn. Psychol. 20, 272–289.
Holsti, L., Grunau, R. V. E., and Whitfield, M. F. (2002). Developmental coordination disorder in extremely low birth weight children at nine years. Dev. Behav. Pediatr. 23, 9–15.
Hubbard, E. M., Piazza, M., Pinel, P., and Dehaene, S. (2005). Interactions between number and space in parietal cortex. Nat. Rev. Neurosci. 6, 435–448.
Kail, R. V. (2007). Longitudinal evidence that increases in processing speed and working memory enhance children’s reasoning. Psychol. Sci. 18, 312–313.
Kaufmann, L., and Nuerk, H.-C. (2005). Numerical development: current issues and future perspectives. Psychol. Sci. 47, 142–170.
Kessels, R. P. C., Van Zandvoort, M. J. E., Postma, A., Kappelle, L. J., and De Haan, E. H. F. (2000). The Corsi block-tapping task: standardization and normative data. Appl. Neuropsychol. 7, 252–258.
Kyttala, M., and Lehto, J. E. (2008). Some factors underlying mathematical performance: the role of visuospatial working memory and non-verbal intelligence. Eur. J. Psychol. Edu. 23, 77–94.
Landerl, K., Fussenegger, B., Moll, K., and Willburger, E. (2009). Dyslexia and dyscalculia: two learning disorders with different cognitive profiles. J. Exp. Child. Psychol. 103, 309–324
Lonnemann, J., Krinzinger, H., Knops, A., and Willmes, K. (2008). Spatial representations of numbers in children, and their connection with calculation abilities. Cortex 44, 420–428.
Miller, C. J., and Hynd, G. W. (2004). What ever happened to developmental Gerstmann’s syndrome? Links to other pediatric, genetic, and neurodevelopmental syndromes. J. Child Neurol. 19, 282–289.
Mundy, E., and Gilmore, C. K. (2009). Children’s mapping between symbolic and nonsymbolic representations of number. J. Exp. Child. Psychol. 103, 490–502.
Nieder, A., and Dehaene, S. (2009). Representation of number in the brain. Annu. Rev. Neurosci. 32, 185–208.
Noël, M.-P. (2005). Finger gnosia: a predictor of numerical abilities in children? Child Neuropsychol. 11, 413–430.
Notelaers, G., Einarsen, S., De Witte, H., and Vermunt, J. (2006). Measuring exposure to bullying at work: the validity and advantages of the latent class cluster approach. Work Stress 20, 288–301.
Oldfield, R. C. (1971). The assessment and analysis of handedness:the Edinburgh inventory. Neuropsychologia 9, 97–113.
Ozols, E. J., and Rourke, B. P. (1988). Characteristics of young learning disabled children classified according to patterns of academic achievement: auditory-perceptual and visual-perceptual disabilities. J. Clin. Child Psychol. 17, 44–52.
Passolunghi, M. C., and Cornoldi, C. (2008). Working memory failures in children with arithmetical difficulties. Child Neuropsychol. 14, 1–14.
Pesenti, M., Thioux, M., Seron, X., and De Volder, A. (2000). Neuroanatomical substrates of Arabic number processing, numerical comparison and simple addition: a PET study. J. Cogn. Neurosci. 12, 461–479.
Pinel, P., Piazza, M., Le Bihan, D., and Dehaene, S. (2004). Distributed and overlapping cerebral representations of number, size, and luminance during comparative judgments. Neuron 41, 983–993.
Raven, J. C., Court, J. H., and Raven, J. (1986). Manual for Raven’s Progressive Matrices and Vocabulary Scales. London: Lewis.
Rourke, B. P. (ed.). (1995). Syndrome of Nonverbal Learning Disabilities: Neurodevelopmental Manifestations. New York: Guilford Press.
Rourke, B. P., and Strang, J. D. (1978). Neuropsychological significance of variations in patterns of academic performance: motor, psychomotor, and tactile-perceptual abilities. J. Pediatr. Psychol. 3, 62–66.
Rusconi, E., Gonzaga, M., Adriani, M., Braun, C., and Haggard, P. (2009). Know thyself: behavioural evidence for a structural representation of the human body. PLoS ONE 4, e5418. doi:10.1371/journal.pone.0005418
Sameroff, A. (2010). A unifi ed theory of development: a dialectic integration of nature and nurture. Child Dev. 81, 6–22.
Sameroff, A. J., and Haith, M. M. (1996). The Five to Seven Year Shift: The Age of Reason and Responsibility. Chicago: The University of Chicago press.
Sato, M., Cattaneo, L., Rizzolatti, G., and Gallese, V. (2007). Numbers within our hands: modulation of corticospinal excitability of hand muscles during numerical judgment. J. Cogn. Neurosci. 19, 684–693.
Sato, M., and Lalain, M. (2008). On the relationship between handedness and hand-digit mapping in finger counting. Cortex 44, 393–399.
Siegler, R. S., and Chen, Z. (2008). Differentiation and integration: guiding principles for analyzing cognitive change. Dev. Sci. 11, 433–448.
Vermunt, J. K., and Magidson, J. (2000). Latent GOLD 2.0 User’s Guide 29 [Software Manual]. Belmont, MA: Statistical Innovations.
Vermunt, J. K., and Magidson, J. (2003). Addendum to the Latent GOLD User’s Guide: Upgrade Manual for Version 3.0 [Software Manual]. Belmont, MA: Statistical Innovations.
White, S. H. (1965). Evidence for a hierarchical arrangement of learning processes. Adv. Child Dev. Behav. 2, 187–220.
Keywords: finger gnosia, computational finger-use, spatial processes, individual differences, young children
Citation: Reeve R and Humberstone J (2011) Five- to 7-year-olds’ finger gnosia and calculation abilities. Front. Psychology 2:359. doi: 10.3389/fpsyg.2011.00359
Received: 08 August 2011;
Accepted: 15 November 2011;
Published online: 08 December 2011.
Edited by:
Liane Kaufmann, Private University for Health Sciences, Medical Informatics and Technology, AustriaReviewed by:
Martin H. Fischer, University of Potsdam, GermanyLuisa Girelli, Università degli Studi Milano Bicocca, Italy
Copyright: © 2011 Reeve and Humberstone. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Robert Reeve, Department of Psychological Sciences, University of Melbourne, Parkville, VIC 3010, Australia. e-mail:ci5yZWV2ZUB1bmltZWxiLmVkdS5hdQ==