- 1 Institute of Cognitive Neuroscience, University College London, London, UK
- 2 Department of Psychology, City University, London, UK
To test whether atypical number development may affect other types of quantity processing, we investigated temporal discrimination in adults with developmental dyscalculia (DD). This also allowed us to test whether number and time may be sub-served by a common quantity system or decision mechanisms: if they do, both should be impaired in dyscalculia, but if number and time are distinct they should dissociate. Participants judged which of two successively presented horizontal lines was longer in duration, the first line being preceded by either a small or a large number prime (“1” or “9”) or by a neutral symbol (“#”), or in a third task participants decided which of two Arabic numbers (either “1,” “5,” “9”) lasted longer. Results showed that (i) DD’s temporal discriminability was normal as long as numbers were not part of the experimental design, even as task-irrelevant stimuli; however (ii) task-irrelevant numbers dramatically disrupted DD’s temporal discriminability the more their salience increased, though the actual magnitude of the numbers had no effect; in contrast (iii) controls’ time perception was robust to the presence of numbers but modulated by numerical quantity: therefore small number primes or numerical stimuli seemed to make durations appear shorter than veridical, but longer for larger numerical prime or numerical stimuli. This study is the first to show spared temporal discrimination – a dimension of continuous quantity – in a population with a congenital number impairment. Our data reinforce the idea of a partially shared quantity system across numerical and temporal dimensions, which supports both dissociations and interactions among dimensions; however, they suggest that impaired number in DD is unlikely to originate from systems initially dedicated to continuous quantity processing like time.
Introduction
Developmental dyscalculia (DD) is a congenital and specific learning disability affecting the understanding of numerical concepts and arithmetical information in the context of normal intelligence (American Psychiatric Association, 1994), and affecting 4–7% of the population (Shalev et al., 2005; Shalev, 2007). Most research on DD has focused on the ability to process numbers represented symbolically or non-symbolically and on arithmetical skills (e.g., Butterworth et al., 2011). However, to date, it is still unknown whether dyscalculia affects solely number quantity processing or whether it extends to other non-numerical quantity dimensions such as luminance, physical size, or time. Anecdotally, DD subjects frequently report poor ability to appreciate time which is often exemplified by their unreliable punctuality at appointments or by their inability to plan activities. However, it is unclear whether these self-reports reflect a genuine disability in time perception and cognition, or whether they are more related to a difficulty in performing numerical operations relating to time, for instance in calculating how much time is needed to get to an appointment. In this study we aimed to explore the relation between time and numbers from the perspective of atypical number development in dyscalculia. Specifically, we aimed to test whether congenitally malfunctioning number processing may extend to time processing.
Suggestive evidence that dyscalculia may impair continuous dimensions as well as processing of numbers comes from the observation that DD children are slower than controls in comparing the physical size of Arabic numerals (Rousselle and Noël, 2007; but see Landerl et al., 2004). Moreover, in numerical Stroop-like tasks, where trials of congruent physical and numerical magnitude typically result in faster and more accurate responses, no facilitation is reported in both adults and children with DD (Rubinsten and Henik, 2005; Landerl and Kölle, 2009). To date, no studies have explored the continuous dimension of time in DD.
Investigating time processing in DD could also clarify the relation between numbers and time. Specifically, it may elucidate whether these magnitude dimensions are processed through (1) a single accumulator that can operate in either the time or the numerosity mode (Meck and Church, 1983), an idea recently reformulated in terms of an approximation system (e.g., Feingenson, 2007; Cantlon et al., 2009), or a “metric” system for action (Walsh, 2003, see Figure 1A); or (2) via dimension-specific mechanisms, whereby magnitude information is processed independently for each dimension (e.g., Agrillo et al., 2010; Dehaene and Brannon, 2011, see Figure 1B). A third possibility is that time and number share the same operational mechanisms, for instance comparison mechanisms or decision components (Cohen Kadosh and Walsh, 2008). This hypothesis has so far been tested in the case of space and number whereby decision rather than representational systems seem to be in common between these magnitude dimensions (Tang et al., 2006; Santens and Gevers, 2008; Santens and Verguts, 2011).
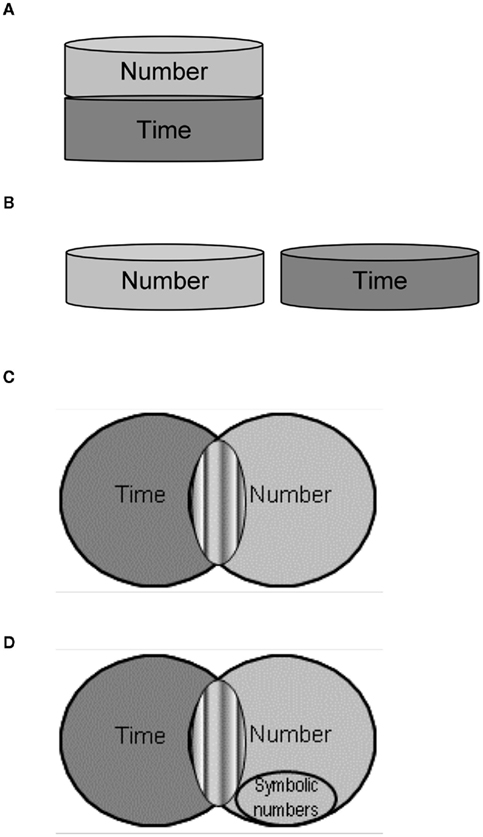
Figure 1. Possible links between number and time. (A) Number and time fully share a single magnitude system, initially hypothesized as an “internal accumulator” representing information about either the numerosity or the duration of events/objects at one given time (e.g., Meck and Church, 1983); a single magnitude system would predict no dissociations between number and time and no interactions between them. (B) Number and time are fully independent, such that magnitude information is analyzed according to metrics unique to each dimension and therefore dissociations but no interactions are expected between dimensions (e.g., Murphy, 1996, 1997; Agrillo et al., 2010; Dehaene and Brannon, 2011). (C) Number and Time partly share a magnitude system (or possibly operational mechanisms depicted in gray stripes) and are also implemented by dimension-specific processes, such that interactions are possible as well as dissociation among dimensions if the dimension-specific processes are selectively impaired (ATOM, Walsh, 2003; Cantlon et al., 2009; Cappelletti et al., 2009, 2011). (D) Symbolic numbers may recycle systems dedicated to number or numerosity processing but are unlikely to recycle systems dedicated to continuous quantity processing like time.
In the present study we reasoned that if number and time are both impaired in DD, this might suggest that they share a magnitude representation or operational mechanisms; on the other hand, if time processing is spared in DD – who by diagnosis have impaired number processing – then either these magnitude dimensions are implemented by distinct magnitude systems or they only partly share a common magnitude system or operational mechanisms. Secondly, we aimed to test whether time processing could nevertheless be modulated by numerical magnitude. Such modulation of numbers on time has been previously found in healthy participants as well as in patients (Dormal et al., 2006; Xuan et al., 2007; Cappelletti et al., 2009, 2011), but not studied in congenital impairments of numbers. We therefore tested possible interactions between numbers and time, which would be expected given a fully or partly shared magnitude or operational system. Conversely, no influence of numbers on time processing might be expected if these dimensions are implemented by fully independent systems which do not interact with each other.
Materials and Methods
Participants
All participants were neurologically normal, with normal or corrected to normal vision. They were all naïve to the purpose of the study and all gave informed consent to participate and were paid for their participation. The study was approved by the Local Ethics Committee.
Adults with developmental dyscalculia
Twelve right-handed English-speaking DD adults took part in the study (one male; mean age: 43.8 years). They were diagnosed with dyscalculia on the basis of the Dyscalculia Screener (Butterworth, 2003) and of additional standardized numerical tasks (see below). DD participants also undertook cognitive assessment to test general intelligence.
All 12 participants obtained a standardized score below the cut-off point in the Dyscalculia Screener (see below); they were also impaired in two standardized calculation tests (the Graded Difficulty Arithmetical test, Jackson and Warrington, 1986; the subtest of the WAIS, Wechsler, 1986), and in number comparison, a key test to reveal intact number processing. In this task, DD revealed an abnormally large distance effect (Moyer and Landauer, 1967) such that the time required to discriminate between stimuli numerically close was abnormally long relative to controls, consistent with some previous studies (e.g., Rousselle and Noël, 2007). In contrast, they obtained an average or high average IQ suggesting preserved intellectual functioning (see Table 1).
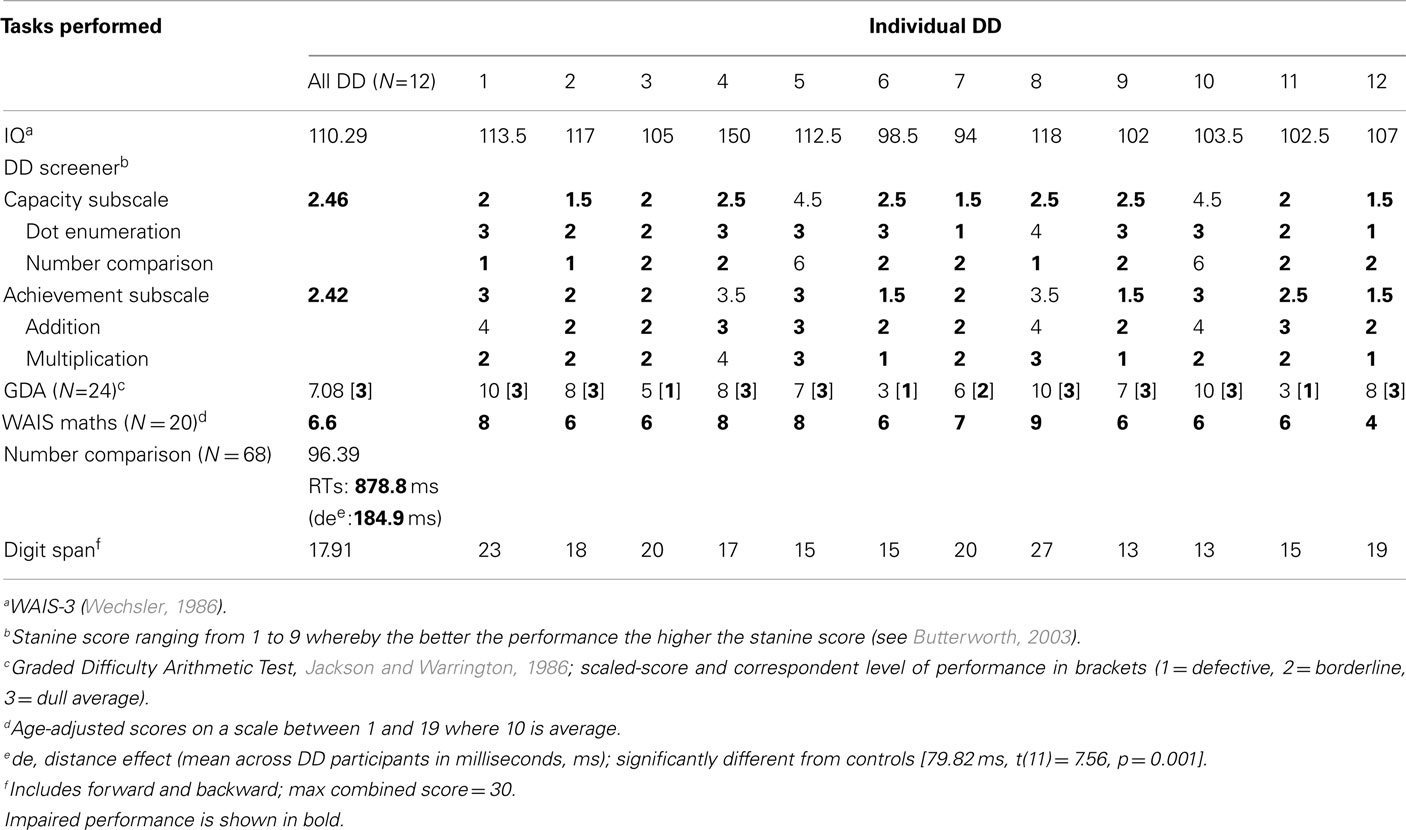
Table 1. Dyscalculic participants’ performance in the Dyscalculia Screener and in other background tasks. Percent correct or scaled-scores.
Control subjects
Overall 22 right-handed adults participated in the study (6 males and 16 females, mean age: 43.2 years, range 25–70).
The Dyscalculia Screener
The Dyscalculia Screener (Butterworth, 2003) is a standardized computer-based test that comprises four item-timed tasks. These four tasks are divided into two subscales: a “capacity subscale,” which involves a dot enumeration task and a number comparison task, and an “achievement subscale,” which involves two maths verification tasks (Butterworth, 2003; Iuculano et al., 2008). The software diagnoses DD on the basis of norms derived from performance expressed as an inverse efficiency score (median reaction times multiplied by error-rate) which is known to be important in the diagnosis of arithmetical learning disabilities (Jordan et al., 2002; Landerl et al., 2004; Butterworth, 2005).
To be classified as dyscalculic, participants had to obtain: (1) a standardized score below 81 on at least one of the two tasks of the “capacity subscale” of the Dyscalculia Screener (test average of the nationally standardized score = 100, SD = 15); (2) an IQ score within the normal range (full-scale IQ not below 80); and (3) impaired performance in two additional standardized tests of maths (the Graded Difficulty Arithmetic Task, Jackson and Warrington, 1986 and the subtest of the WAIS-R, Wechsler, 1986, see Table 1).
Preliminary Investigation
Since dyscalculic participants often claim that their time processing is inaccurate, we first aimed to provide a preliminary measure of time performance. We used four tasks that resembled as much as possible everyday situations requiring either an estimate or a more precise calculation of time. The “time estimation” task required participants to estimate the time needed to perform familiar actions (e.g., making a cup of tea) or the duration of events (e.g., flying from London to New York). The “time calculation” task required participants to perform calculation on numbers indicating time (e.g., If the time is now 10.35 p.m., what time will it be in 2 h and 50 min?). The “knowledge of exact temporal facts” task required participants to answer questions about precise temporal facts (e.g., how many hours in a day?). The “time comparison” task required participants to indicate the later time among two expressed as 24-h clock (e.g., “11.45” or “15.30”). All problems were orally presented for un-speeded, oral responses. For these preliminary tasks, DD participants were compared to a group of 12 age-matched controls which were part of a larger sample and differed from those that took part in the experimental tasks (mean age = 51.2; range: 25–70).
Dyscalculic participants were accurate at estimating the duration of events or actions [no difference from controls, t(11) = 0.64, p = 0.51 ns] as well as at comparing times [t(11) = 0.12, p = 0.38 ns]; their knowledge of exact temporal facts was also preserved [t(11) = 0.85, p = 0.2 ns]. However, they were significantly worse than controls when performing the time calculation task [t(11) = 2.54, p = 0.03]. This seems consistent with dyscalculics’ self-report of their time processing not being accurate. The experimental investigation aimed to further explore time processing in DD.
Experimental Investigation
There were three different experimental conditions assessing duration discrimination in the presence of irrelevant symbolic or numerical stimuli. All these experimental conditions have been previously validated in both control participants and in neurological patients and are known to engage time processing in the range of sub-second durations (see Cappelletti et al., 2009, 2011). These durations were chosen as most theories and research on time processing are based on sub-second durations (e.g., Ivry and Spencer, 2004; Karmarkar and Buonomano, 2007); therefore choosing short durations allowed us to interpret the findings with respect to these theories. Participants performed the three conditions in counterbalanced order. All experimental conditions required participants to judge which of two temporal intervals lasted longer using a two-interval forced-choice paradigm. Numerical stimuli were always task-irrelevant but the three conditions differed in terms of the degree of indirect involvement of these numerical stimuli (see below).
Stimuli
Stimulus presentation and data collection were controlled using the Cogent Graphics toolbox (http://www.vislab.ucl.ac.uk/Cogent/) and Matlab7.0 software on a Sony S2VP laptop computer. Stimuli were viewed on the computer’s built-in liquid-crystal screen, which subtended a visual angle of 20.8° horizontal by 15.83° vertical from a viewing distance of about 50 cm. A chin-rest was used to stabilize head position. Video mode was 640 × 480 pixels, with 60 Hz refresh rate.
Symbol and number prime conditions
High-contrast white horizontal lines (length 10.29° of visual angle, width 0.17°) were presented on a black background. The two lines were centered on the vertical meridian and presented sequentially in a two-interval discrimination paradigm, one line 5.07° above the horizontal meridian and the other 5.07° below (see Figure 2). The first of the lines in the two-interval sequence (Reference line) had always a duration of 600 ms. The second line (Test line) could vary in duration according to the Method of Constant Stimuli. Test durations spanned a range of −240 to 240 ms (i.e., from 360 to 840 ms in steps of 60 ms) including the Reference duration of 600 ms.
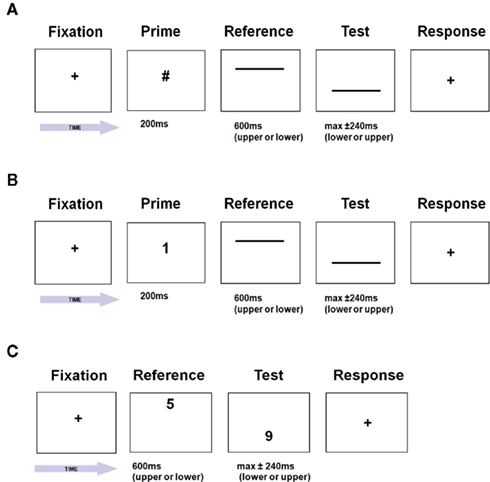
Figure 2. Experimental design in the (A) symbol and (B) the number prime conditions, participants judged which of two horizontal lines lasted longer, with the reference line preceded respectively by a non-numerical (“#,” Symbol Prime Condition) or a numerical prime (“1” or “9,” Number Prime Condition). In the “1–5–9” Condition (C), participants judged temporal durations directly on Arabic numbers.
Two types of prime were used: the symbol “#” (Symbol Prime Condition, see Figure 2A) or two Arabic numbers, i.e., “1” or “9” (Number Prime Condition, see Figure 2B). Both types of prime subtended 0.87° vertically and between 0.25° and 0.65° horizontally and were presented in white Helvetica font at the center of the display.
“1–5–9” condition
This was adapted from an existing paradigm (Oliveri et al., 2008) and previously used to assess time processing in a neurological patient (Cappelletti et al., 2009). The stimuli consisted of sequential pairs among three possible Arabic numbers (“1,” “5,” “9”) subtending 1.72° of visual angle and presented in a two-interval discrimination paradigm, one number 5.07° above the horizontal meridian and the other 5.07° below in randomized order (see Figure 2C).
Experimental Design
Symbol and number prime conditions
Each trial began with a centrally displayed fixation spot, which remained visible until a key press from the participant. The prime was then immediately displayed centrally for 200 ms. A blank interval of 100 ms preceded the first line display (Reference line) appearing at the top (or bottom) of the computer screen, followed after an inter-stimulus-interval of 100 ms by the second line display (Test line) appearing at the bottom (or top) of the computer monitor. The screen then remained blank with a white cross in the middle until a response from the subject. As our interest was primarily in the accuracy of temporal discrimination rather than speed of information processing, there was no time-pressure to respond and no measure of response times. The next trial immediately followed the response. In the Symbol and Number Prime Conditions, Test values were randomly sampled without replacement from a set of equally spaced values bracketing the Reference value with equal frequency. Nine values were used to improve reliability of psychometric curve-fitting; in each experimental block of the Number Prime Condition, number primes were randomly sampled from the two possible values with equal frequency. In the Symbol Prime Condition, there were 40 observations for each test duration, yielding a total of 360 trials, presented over 4 blocks of 90 trials. In Number Prime Condition, there were 40 observations for each cell of the design (9 levels × 2 primes), yielding a total of 720 trials, presented over 8 blocks of 90 trials.
“1–5–9” condition
Trials began with a central fixation point that remained visible until a key press from the participants. The first number then appeared on the top (or bottom) part of the computer screen for 600 ms followed by an ISI of 200 ms and by the second number, appearing on the bottom (or top) part of the computer screen. The first number was a 600 ms fixed-duration reference number (“5”) while the second number could be either “1,” “5,” or “9,” and was either of a shorter or longer duration relative to the reference. A range of durations between 360 and 840 ms was used in steps of 60 ms, with four shorter and four longer durations plus the reference, presented in equal proportion in 450 trials. These durations were chosen on the basis of previous studies with neurological patients (Harrington et al., 2004; Cappelletti et al., 2009). Only Test numbers “1,” “5,” and “9” rather than the whole range from 1 to 9 was used. This is because we aimed to keep the task’s overall length adequate to be administered to our participants while maximizing the chance to observe any effect of numerical magnitude on time perception. Therefore, only numbers at the extreme of the single-digit range, i.e., the smallest and the largest were used. After the disappearance of the second digit the screen remained blank until a response was made. There was no time-pressure to respond.
Procedure
Participants were seated comfortably in a quiet room with their head in a chin-rest, facing the computer screen under normal fluorescent room lighting. In each experiment, at the end of each trial participants were instructed to indicate whether the top or the bottom horizontal line or number lasted longer using the top or bottom-arrow keys on the laptop keyboard. For each experimental condition, participants had at least 20 practice trials prior to the first experimental block, although an additional practice block was run where necessary to ensure familiarity with the task. Practice trials were not included in analysis.
Data Analysis
Accuracy
A general measure of accuracy was computed for each subject as the proportion of all trials in which the subject correctly indicated the location of the line or the number that lasted longer. A higher accuracy score indicates that the subject found it overall easier to discriminate the reference from the test durations.
Point of subjective equality (PSE)
For each subject, experimental condition and prime type, we first constructed a psychometric function relating the proportion of trials in which the subject’s response (whether correctly or incorrectly) identified the Test stimulus as longer than the Reference. We then interpolated the psychometric function with a logistic curve, using a least-squares algorithm provided by the PSIGNIFIT toolbox for Matlab (Wichmann and Hill, 2001). To find the point of subjective equality (PSE) we then read off the Test duration at which “Test longer” responses are 50% (i.e., the Test is perceptually indistinguishable in duration from the Reference). In the Number Prime and the “1–5–9” Conditions we also compared performance with the two numerical primes to test any possible interactions between time and numbers.
Just noticeable difference (JND)
Using the fitting procedure described above, we also obtained the just noticeable difference (JNDs) for each participant. This measures the minimal difference in duration between Test and Reference line or number that could be discriminated with reliable accuracy. The JND was computed by reading off from the fitted psychometric function the Test durations at which 25 and 75% of the responses indicated “Test longer,” then dividing the difference between these two durations by two (Coren et al., 1999; Cousineau, 2005).
In all experimental conditions, accuracy, PSEs, and JNDs were entered into separate Analyses of Variance (ANOVA), with experimental condition and group as factors. Moreover, performance in the different primes (“1,” “9,” and “#”) and numerical stimuli (“1,” “5,” “9”) was compared in planned t-tests as described in the Result sessions below.
Results
Accuracy
There was a significant effect of experimental condition [F(2, 44) = 4.9, p < 0.01], of group [F(1, 22) = 5.1, p = 0.03], and a significant condition by group interaction [F(2, 44) = 5.0, p < 0.01]. Specifically, accuracy did not differ between DD and controls in the Symbol Prime condition [t(22) = 1.3, p = 0.2, ns], but strikingly in the identical time discrimination task with number primes (Number Prime Condition), DD, and controls’ performance differed significantly [t(22) = 2.4, p < 0.03]. Likewise, controls and DD’s accuracy differed significantly in the “1–5–9” Condition [t(22) = 2.3, p = 0.04].
Just Noticeable Difference
There was a significant main effect of experimental condition [F(2, 44) = 4.9, p = 0.012], of group [F(1, 22) = 7.7, p = 0.03], and a significant condition by group interaction [F(2, 44) = 4.99, p = 0.01]. Specifically, DD and controls differed significantly only when numbers were part of the experimental paradigm, i.e., in the Number Prime Condition [t(22) = 2.1, p = 0.04] and the “1–5–9” Condition [t(22) = 2.2, p = 0.03], but not in the Symbol Prime Condition [t(22) = 0.76, p = 0.4, ns, see Figure 3].
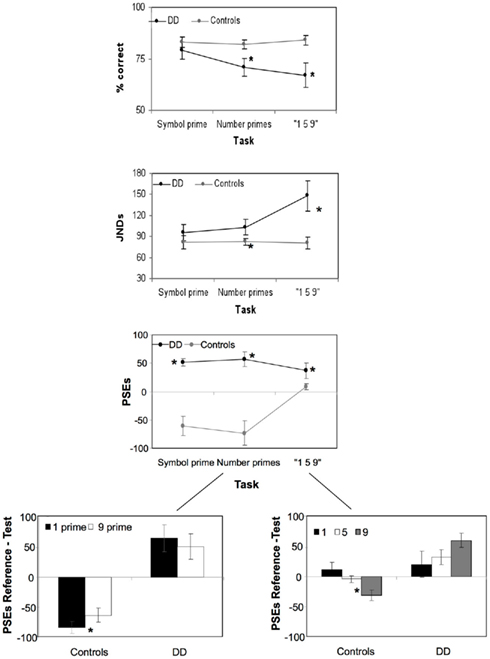
Figure 3. Performance in all experimental conditions and modulation of numerical stimuli in the number prime and the “1–5–9” conditions. Performance in the three time discrimination conditions is described in terms of accuracy, just noticeable difference (JNDs), and point of subjective equality (PSE) for DD and control participants. Asterisk indicate statistical significance for the difference between the two groups of participants or between stimuli (i.e., “1” vs. “9” prime conditions). Values on the y-axis indicate how much longer (positive) or shorter (negative) a stimulus had to be displayed in order to be perceived as different from the reference stimulus (JNDs) or of the same duration of the reference stimulus (PSEs).
Point of Subjective Equality
There was a significant main effect of experimental condition [F(2, 44) = 7.6, p = 0.001], of group [F(2, 22) = 52.3, p < 0.001] and a significant interaction of experimental condition and group [F(2, 44) = 15.3, p < 0.001]. DD and controls differed significantly in all experimental conditions, such that DD over-estimated the duration of the first stimulus [Symbol Prime Condition: t(22) = 7.0, p < 0.001, Number Prime Condition: t(22) = 4.8, p < 0.001; “1–5–9” Condition: t(22) = 2.3, p = 0.03, see Figure 3].
A further analysis of the primes used showed that in the Number Prime Condition, DD showed no difference between priming conditions [t(11) = 0.79, p = 0.44, ns], such that numerical quantity did not modulate their performance. In contrast, in controls PSE’s for both primes were significantly shorter in duration than the Reference of 600 ms [“1” prime: t(11) = 5.02, p < 0.001; “9” prime: t(11) = 3.92, p = 0.004]. The difference between the priming conditions in controls was highly significant [t(11) = 3.4, p = 0.005], consistent with the Reference duration being perceived as approximately 20 ms shorter when preceded by a low-valued prime compared to a high-valued prime.
In the “1–5–9” Condition, an analysis on the values indicating proportion of test “longer” responses for each number indicated that DD’s performance was not modulated by the quantity expressed by numbers stimuli [F(2, 22) = 1.5, p = 0.24, ns]. In contrast, quantity modulated controls’ responses [F(2, 22) = 3.2, p = 0.05]. The results of fitting PSE’s to the controls’ data revealed that relative to the test value “5,” the duration of the test value of “9” had to be about 30 ms shorter [t(11) = 3.22, p = 0.008] in order to be perceived as equal to the reference stimulus “5” whereas the duration of the test value “1” had to be only 12 ms shorter [t(11) = 1.9, p = 0.05]. DD participants’ PSE’s indicated a significant over-estimation relative to controls for the numerical values “5” and “9” but not “1” [number “1”: t(22) = 0.8, p = 0.9, ns; number “5”: t(22) = 2.2, p = 0.03; number “9”: t(22) = 2.2, p = 0.04, see Figure 3].
Comparison of Experimental Conditions
We directly compared performance within each group in the three experimental conditions. Performance expressed as JNDs showed that DD differed in the Symbol Prime Condition relative to the Number Prime and the “1–5–9” Conditions [t(11) = 3.2, p = 0.009 and t(11) = 2.5, p < 0.02 respectively] and only marginally in the Number Prime Condition relative to “1–5–9” Condition [t(11) = 2.0, p = 0.06]. In contrast, control participants’ performance did not differ in any of these experimental Conditions [Symbol vs. Number Prime: t(11) = 0.3, p = 0.7, ns; Symbol Prime vs. “1–5–9”: t(11) = 0.2, p = 0.8, ns; Number Prime vs. “1–5–9”: t(11) = 0.29, p = 0.77, ns].
Correlations between Time Performance and Numerical Skills
In DD participants, the degree of numerical impairment expressed by the Dyscalculia Screener (Butterworth, 2003) negatively correlated with performance in time discrimination irrespective of the prime or the stimuli used (Symbol Prime Condition: R2 = 0.68, p < 0.001; Number Prime Condition: R2 = 0.41, p < 0.03; “1–5–9” Condition: R2 = 0.31, p = 0.05). Since this correlation is based on JNDs, whereby the smaller the value the better the performance, the relation between numerical impairment and time discrimination is actually positive. This therefore suggests that the more severe the degree of dyscalculia, the more impaired time discrimination was (see Figure 4). Note that we did not measure control participants with the Dyscalculia Screener, so it remains to be tested whether such correlation may exist in the numerically normal population as well or whether it may be specific to dyscalculics. However performance in time discrimination did not correlate with any other mathematical tasks.
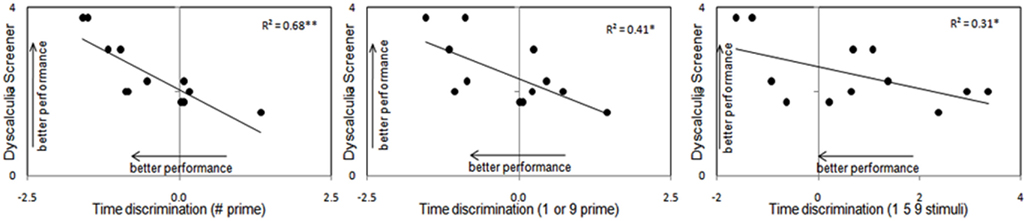
Figure 4. Correlations between the degree of dyscalculia expressed by the Dyscalculia Screener (Butterworth, 2003) and proficiency in time discrimination in all the experimental conditions in dyscalculic participants only.
Discussion
In this study, we undertook a detailed investigation of number and time processing in adults with DD and in control participants. Consistent with their diagnosis, our DD participants were impaired in numerical processing as indicated by an abnormally large distance effect when comparing Arabic numerals, by their poor performance in arithmetic tasks and in numerosity estimation. There were three principle findings: (i) in contrast to their numerical impairment, DD’s temporal discrimination showed comparable acuity to controls, with reliable discrimination between two lines differing in duration (in the presence of symbol primes); (ii) in DD discrimination became abnormally poor when the identical line stimuli were preceded by numerical primes, even though these were task-irrelevant, or when durations were judged on numerical stimuli directly; (iii) there were distinct interactions between time and numbers for controls vs DDs: for controls, but not DD, the perception of duration appeared to be modulated by the value of task-irrelevant numbers. For example, durations were reported as shorter than veridical in the presence of smaller numbers compared to large numbers, consistent with previous findings (Dormal et al., 2006; Cappelletti et al., 2009, 2011). However, the absence of such numerical modulation in DD could be explained by their impaired number processing.
Temporal discriminability in DD degraded further with increasing salience of the task-irrelevant numerical stimuli. For instance, when temporal discrimination was performed directly on numerical stimuli (“1–5–9” Condition), DDs were more impaired relative to the task where numbers only appeared as primes (Number Prime Condition). DDs’ impaired temporal discrimination is unlikely to be due to task difficulty as at least two of our time tasks (Symbol and Number Prime Condition) were identical except from the type of prime used, and yet DD’s performed significantly differently. Moreover, these tasks were not intrinsically dissimilar in their difficulty level as there was no difference in control participants’ performance whose discriminability remained stable across these conditions. Likewise, DDs’ impaired time discrimination is unlikely to be caused by attention or working memory deficits, which are sometimes associated with dyscalculia (Rubinsten and Henik, 2005; Ashkenazi et al., 2009), as these deficits would have affected the three experiments equally.
A Partly Shared Magnitude System or Decision Component
The dissociation between time and numbers, and their interaction are problematic for the proposal of a fully shared magnitude mechanism similar to Meck and Church’s (1983) mode-control model (see Figure (1A), which would predict equal impairment of different magnitude dimensions. Furthermore, the interaction between time and numbers observed in control participants and the impaired time discrimination in the presence of numerical stimuli in DDs challenge the notion of fully independent magnitude dimensions which would not predict any influence of one dimension on another (see Figure 1B, e.g., Murphy, 1996, 1997; Dehaene and Brannon, 2011).
Instead, we suggest that the dissociation between time and numbers observed in DD participants is best explained by the proposal of a magnitude system partly shared among dimensions. This is the idea that besides sharing a magnitude system or possibly decision-level components (Huntley-Fenner et al., 2002; McCrink and Wynn, 2004; Cohen Kadosh et al., 2007), number and time are also implemented by dimension-specific processes (e.g., Walsh, 2003; Cantlon et al., 2009; Cappelletti et al., 2009, 2011; Dehaene and Brannon, 2011, see also Figure 1C). Critically, a partly shared mechanism would account for correlations and interactions as well as dissociations among dimensions. A positive correlation such as that observed between DD’s numerical ability and JND in temporal discrimination can be explained by shared mechanisms where performance of both magnitude dimensions depends on how efficiently the common mechanism is functioning, which can vary between individuals; interactions can be explained by assuming cross-talk between the dimensions processed by the same shared mechanisms. Conversely dissociation can be explained by selective impairments of the non-overlapping dimension-specific processes. Therefore, this would account for the dissociation between number and time in DD as well as for the interaction of number magnitude on time performance. The proposal of a partly shared magnitude system would concur with findings of two recent neuropsychological studies showing that time and numbers doubly dissociate, even while numbers interacted with time perception in one of the patients (Cappelletti et al., 2009, 2011).
Whether time and number only share decision mechanisms rather than a magnitude system is difficult to address with the current data. These decision components have recently been shown to account – at least partially – for interactions between space and number (e.g., Tang et al., 2006; Santens and Gevers, 2008; Santens and Verguts, 2011), but no studies have yet looked at whether this may also be the case for time and number.
Numbers Do not Originate from Temporal Mechanisms
Besides supporting the possibility that number and time processes a partly share magnitude system, our data allow us to make a suggestion on the origin of these processes. We propose that number symbols are unlikely to develop from mechanisms originally dedicated to more primitive continuous quantity dimension such as time. The hypothesis that some recent cognitive abilities such as symbolic numbers, maths, or reading may have re-used mechanisms initially devoted to evolutionarily relevant skills is referred to as “recycling” or “redeployment” (e.g., Gould and Vrba, 1982; Dehaene and Cohen, 2007; Anderson, 2010). For instance, it has been suggested that symbolic numbers originate from a pre-verbal system for quantification, i.e., the approximate number system (“ANS,” Feigenson et al., 2004; Halberda et al., 2008) as indicated for example by the children’s initial use of analog criteria to make magnitude judgments then followed by discrete ones (e.g., Feigenson et al., 2002; Hurewitz et al., 2006, see Figure 1D). The recycling idea has recently been expanded to suggest that some mechanisms initially representing time and space are subsequently used to represent numbers (Cohen Kadosh and Walsh, 2008; Bueti and Walsh, 2009). Following this suggestion, congenital disorders with numbers could either be due to: (i) some aspects of the recycling process that failed, or (ii) symbolic numbers originating from an impaired primordial system. This latter possibility has been suggested for symbolic numbers relative to the ANS, as a link between impaired symbolic numbers and ANS has recently been shown in dyscalculia (e.g., Gilmore et al., 2010; Piazza et al., 2010). However, it has been argued by Butterworth (2010) that neither continuous quantity nor approximate numerosities can be foundational for understanding symbolic numbers or arithmetic.
At present our data do not allow us to establish whether impaired symbolic numbers may be due to a dysfunction in the recycling process of a continuous quantity dimension into numbers. However, concerning the second possibility, it seems unlikely that impaired symbolic numbers originated from impaired time processing as this was spared in our participants. This evidence converges with recent results challenging the idea that symbolic numbers may originate from continuous dimensions. For instance, single cell recording in monkeys’ IPS regions failed to show the expected correlation between neurons independently coding for continuous and numerical quantities (Tudusciuc and Nieder, 2007). Such correlations would be expected if these neurons had been recycled to represent different types of quantity. In line with this evidence, we have also recently found that symbolic numbers and continuous quantities such as time and space do not correlate and that they are each associated with structural differences in distinct regions of the brain (Cappelletti et al., under review), also consistent with a previous imaging study (Castelli et al., 2006). Taken together these findings concur to suggest that continuous quantities like time and space are unlikely to be predecessors of symbolic numbers.
It remains to be explained how numbers worsen time discrimination which was otherwise intact in DD. One possibility is that numbers might generally exert an influence on the perception of time but in DD the influence from impaired numbers was unsystematic. The resulting inconsistency of temporal judgments could explain why in DD we observed increased JNDs for temporal discrimination but no systematic bias of number value on our measure of subjective duration. In controls, by contrast, preserved numbers would influence time processing systematically, leading to consistent biases in estimation of temporal intervals (with low numbers decreasing subjective duration and high number increasing it), while leaving their JNDs unaffected. We suggest that numbers exert such an effect on time because this is a “weak” magnitude dimension, which can be more readily disrupted by several factors for instance the Triesman clicks (Treisman and Brogan, 1992), the presentation of “filled” or “empty” stimuli (Rammsayer and Lima, 1991), dual tasks (e.g., Casini and Macar, 1997), and manipulations of dopamine and acetylcholine (Meck, 1996). Therefore the combination of impaired numbers and of weak time may explain the impairment of temporal discrimination in the presence of numbers in DD.
Time Processing and Theories of Dyscalculia
To the best of our knowledge time processing has not previously been investigated in dyscalculic participants, and the current theories of dyscalculia are silent about the possible interactions between dyscalculia and the processing of time and other continuous dimensions. These theories focus mainly on the possible origin of dyscalculia. One of them claims that dyscalculia is likely to be due to impaired ANS, the system that maps approximate numerosities onto an analog magnitude and that is thought to be a precursor of symbolic number processing and maths (Gilmore et al., 2010). Based on this idea, dyscalculics are impaired in number processing because the Weber fraction (essentially their JND) of the analog representations is large and they are poor at discriminating these magnitudes (Gilmore et al., 2010; Piazza et al., 2010). However, it has also been argued that dyscalculia is due to defective “number module” that represents small numerosities discretely and not as analog magnitudes (Butterworth, 2010; Butterworth et al., 2011). Such impairment would lead to further difficulties in processing numbers symbolically and in maths. A third set of theories have suggested that dyscalculia is due to a failure in linking preserved numerical concepts to their symbols, therefore implying that impairments should mainly occur when symbolic processing of numbers is required (e.g., Rubinsten and Henik, 2005; Rousselle and Noël, 2007). None of these theories offer an explicit account of how dyscalculics may process continuous quantity, though a possible extrapolation from the ANS account would be that any stimulus represented in terms of analog magnitudes would be affected including time.
Prior to this study, a very few investigations that have focused on DDs’ processing of the continuous dimension of space and in one case of luminance, using Stroop-like paradigms. These showed lack of facilitation in congruent trials in DD relative to controls (Rubinsten and Henik, 2005; Rousselle and Noël, 2007; Landerl and Kölle, 2009; but see Landerl et al., 2004). At first glance, our results may appear different from these previous studies. However, continuous dimensions in DD have so far always been tested directly on numerical stimuli – such as selecting the numerically greater of 3 and 7 – and that there is no evidence on how these dimensions would be processed in a neutral context with no symbolic numbers. Indeed, our results suggest that the mere presence of number stimuli distorts time processing. Moreover, finer details of the participants’ performance such as the PSEs or JNDs have not previously been looked at, although they have been crucial to characterize DDs’ performance as shown in the present study. Here we suggest that the current theories of dyscalculia need to be expanded to account for processing of continuous quantity.
Conclusion
The present study provides evidence that in adults with dyscalculia continuous quantity such as time processing is not affected by atypical number development, although numbers can interact or even disrupt time processing. This suggests that time and numbers are at least partially independent, with some cross-talk between these dimensions. Moreover, these results endorse the proposal that numbers are unlikely to have “recycled” some cognitive resources otherwise used by other more ancient magnitude dimensions such as time.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was supported by grants from the Wellcome Trust and The Royal Society Dorothy Hodgkin Fellowship to Marinella Cappelletti.
References
Agrillo, C., Ranpura, A., and Butterworth, B. (2010). Time and numerosity estimation are independent: behavioral evidence for two different systems using a conflict paradigm. Cogn. Neurosci. 1, 96–101.
American Psychiatric Association. (1994). Diagnostic and Statistical Manual of Mental Disorders, 4th Edn. Washington: American Psychiatric Association.
Anderson, M. (2010). Neural re-use as a fundamental organizational principle of the brain. Behav. Brain Sci. 33, 245–313.
Ashkenazi, S., Rubinsten, O., and Henik, A. (2009). Attention, automaticity, and developmental dyscalculia. Neuropsychology 23, 535–540.
Bueti, D., and Walsh, V. (2009). The parietal cortex and the representation of time, space, number and other magnitudes. Philos. Trans. R. Soc. Lond. B Biol. Sci. 364, 1831–1840.
Butterworth, B. (2005). “Developmental dyscalculia,” in Handbook of Mathematical Cognition, ed. J. I. D. Campbell (Hove: Psychology Press), 455–467.
Butterworth, B. (2010). Foundational numerical capacities and the origins of dyscalculia. Trends Cogn. Sci. (Regul. Ed.) 14, 534–541.
Butterworth, B., Varma, S., and Laurillard, D. (2011). Dyscalculia: from brain to education. Science 332, 1049.
Cantlon, J. F., Platt, M. L., and Brannon, E. M. (2009). Beyond the number domain. Trends Cogn. Sci. (Regul. Ed.) 13, 83–91.
Cappelletti, M., Freeman, E. D., and Cipolotti, L. (2009). Dissociations and interactions between time, numerosity and space processing. Neuropsychologia 47, 2732–2748.
Cappelletti, M., Freeman, E. D., and Cipolotti, L. (2011). Numbers and time doubly dissociate. Neuropsychologia 49, 3078–3092.
Casini, L., and Macar, F. (1997). Effects of attention manipulation on perceived duration and intensity in the visual modality. Mem. Cognit. 25, 812–818.
Castelli, F., Glaser, D. E., and Butterworth, B. (2006). Discrete and analogue quantity processing in the parietal lobe: a functional MRI study. Proc. Natl. Acad. Sci. U.S.A. 103, 4693–4698.
Cohen Kadosh, R., Cohen Kadosh, K., Linden, D. E., Gevers, W., Berger, A., and Henik, A. (2007). The brain locus of interaction between number and size: a combined functional magnetic resonance imaging and event-related potential study. J. Cogn. Neurosci. 19, 957–970.
Cohen Kadosh, R., and Walsh, V. (2008). From magnitude to natural numbers: a developmental neurocognitive perspective. Behav. Brain Sci. 31, 647–648.
Coren, S., Ward, L. M., and Enns, J. T. (1999). Sensation and Perception. Fort Worth, TX: Hartcourt Brace College Publishers.
Cousineau, D. (2005). Confidence intervals in within-subject designs: a simpler solution to Loftus and Masson’s method. Tutorial Quant. Methods Psychol. 1, 42–45.
Dehaene, S., and Brannon, E. M. (eds). (2011). Space, Time, and Number in the Brain: Searching for the Foundations of Mathematical Thought. Elsevier, London.
Dormal, V., Seron, X., and Pesenti, M. (2006). Numerosity-duration interference: a Stroop experiment. Acta Psychol. (Amst.) 121, 109–124.
Feigenson, L., Dehaene, S., and Spelke, E. (2004). Core systems of number. Trends Cogn. Sci. (Regul. Ed.) 8, 307–314.
Feigenson, L., Carey, S., and Spelke, E. (2002). Infants’ discrimination of number vs continuous extent. Cogn. Psychol. 44, 33–66.
Gilmore, C. K., McCarthy, S. E., and Spelke, E. S. (2010). Non-symbolic arithmetic abilities and achievement in the first year of formal schooling in mathematics. Cognition 115, 394–406.
Gould, S. J., and Vrba, E. S. (1982). Exaptation- a missing term in the science of form. Paleobiology 8, 4–15.
Halberda, J., Mazzocco, M. M. M., and Feigenson, L. (2008). Individual differences in nonverbal number acuity predict maths achievement. Nature 455, 665–668.
Harrington, D. L., Lee, R. R., Boyd, L. A., Rapcsak, S. Z., and Knight, R. T. (2004). Does the representation of time depend on the cerebellum? Effect of cerebellar stroke. Brain 127, 561–574.
Huntley-Fenner, G., Carey, S., and Solimando, A. (2002). Objects are individuals but stuff doesn’t count: perceived rigidity and cohesiveness influence infants’ representations of small groups of discrete entities. Cognition 85, 203–221.
Hurewitz, F., Gelman, R., and Schnitzer, B. (2006). Sometimes area counts more than number. Proc. Natl. Acad. Sci. U.S.A. 103, 19 599–519.
Iuculano, T., Tang, J., and Butterworth, B. (2008). Core information processing deficits in developmental dyscalculia and low numeracy. Dev. Sci. 11, 669–680.
Ivry, R. B., and Spencer, R. (2004). The neural representation of time. Curr. Opin. Neurobiol. 14, 225–232.
Jackson, M., and Warrington, E. K. (1986). Arithmetic skills in patients with unilateral cerebral lesions. Cortex 22, 611–620.
Jordan, N. C., Kaplan, D., and Hanich, L. B. (2002). Achievement growth in children with learning difficulties in mathematics: findings of a two-year longitudinal study. J. Educ. Psychol. 94, 586–597.
Karmarkar, U. R., and Buonomano, D. V. (2007). Timing in the absence of clocks: encoding time in neural network states. Neuron 53, 427–438.
Landerl, K., Bevan, A., and Butterworth, B. (2004). Developmental dyscalculia and basic numerical capacities: a study of 8–9-year-old students. Cognition 93, 99–125.
Landerl, K., and Kölle, C. (2009). Typical and atypical development of basic numerical skills in elementary school. J. Exp. Child Psychol. 103, 544–563.
McCrink, K., and Wynn, K. (2004). Large-number addition and subtraction by 9-month-old infants. Psychol. Sci. 15, 776–781.
Meck, W. H., and Church, R. M. (1983). A mode control model of counting and timing processes. J. Exp. Psychol. Anim. Behav. Process. 9, 320–334.
Moyer, R. S., and Landauer, T. K. (1967). The time required for judgments of numerical inequality. Nature 215, 1519–1520.
Murphy, G. L. (1997). Reasons to doubt the present evidence for metaphoric representation. Cognition 62, 99–108.
Oliveri, M., Vicario, C. M., Salerno, S., Koch, G., Turriziani, P., Mangano, R., Chillemi, G., and Caltagirone, C. (2008). Perceiving numbers alters time perception. Neurosci. Lett. 438, 308–311.
Piazza, M., Facoetti, A., Trussardi, A. N., Berteletti, I., Conte, S., Lucangeli, D., Dehaene, S., and Zorzi, M. (2010). Developmental trajectory of number acuity reveals a severe impairment in developmental dyscalculia. Cognition 116, 33–41.
Rammsayer, T. H., and Lima, S. D. (1991). Duration discrimination of filled and empty auditory intervals: cognitive and perceptual factors. Percept. Psychophys. 50, 565–574.
Rousselle, L., and Noël, M. P. (2007). Basic numerical skills inchildren with mathematics learning disabilities: a comparison of symbolic vs. non-symbolic number magnitude processing. Cognition 102, 361–395
Rubinsten, O., and Henik, A. (2005). Automatic activation of internal magnitudes: a study of developmental dyscalculia. Neuropsychology 19, 641–648.
Santens, S., and Gevers, W. (2008). The SNARC effect does not imply a mental number line. Cognition 108, 263–270.
Santens, S., and Verguts, T. (2011). The size congruity effect: is bigger always more? Cognition 118, 97–113.
Shalev, R., Manor, O., and Gross-Tsur, V. (2005). Developmental dyscalculia: a prospective six-year follow-up. Dev. Med. Child Neurol. 47, 121–125.
Shalev, R.S. (2007). “Prevalence of developmental dyscalculia,” in Why is Math So Hard for Some Children? The Nature and Origins of Mathematical Learning Difficulties and Disabilities, eds. D. B. Berch, and M. M. M. Mazzocco (Baltimore, MD: Paul H. Brookes Publishing, Co.), 49–60.
Tang, J., Critchley, H. D., Glaser, D., Dolan, R. J., and Butterworth, B. (2006). Imaging informational conflict: an fMRI study of numerical Stroop. J. Cogn. Neurosci. 18, 2049–2062.
Treisman, M., and Brogan, D. (1992). Time perception and the internal clock: effects of visual flicker on the temporal oscillator. Eur. J. Cogn. Psychol. 4, 41–70.
Tudusciuc, O., and Nieder, A. (2007). Neuronal population coding of continuous and discrete quantity in the primate posterior parietal cortex. Proc. Natl. Acad. Sci. U.S.A. 104, 513–514.
Walsh, V. (2003). A theory of magnitude: common cortical metrics of time, space and quantity. Trends Cogn. Sci. (Regul. Ed.) 7, 483–488.
Wechsler, D. (1986). Wechsler Adult Intelligence Scale-Revised. New York: The Psychological Corporation.
Wichmann, F. A., and Hill, N. J. (2001). The psychometric function: I. Fitting, sampling and goodness-of-fit. Percept. Psychophys. 63, 1293–1313.
Keywords: developmental dyscalculia, time, magnitude, numerosity, number cognition
Citation: Cappelletti M, Freeman ED and Butterworth BL (2011) Time processing in dyscalculia. Front. Psychology 2:364. doi: 10.3389/fpsyg.2011.00364
Received: 16 August 2011; Accepted: 21 November 2011;
Published online: 20 December 2011.
Edited by:
Tom Hartley, University of York, UKReviewed by:
Ingmar Visser, Universiteit van Amsterdam, NetherlandsDomenica Bueti, Centre Hospitalier Universitaire Vaudois and Université de Lausanne, Switzerland
Copyright: © 2011 Cappelletti, Freeman and Butterworth. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Marinella Cappelletti, Institute of Cognitive Neuroscience, University College London, 17 Queen Square, London WC1N 3AR, UK. e-mail:bS5jYXBwZWxsZXR0aUB1Y2wuYWMudWs=


