Unimanual SNARC Effect: Hand Matters

A structural representation of the hand embedding information about the identity and relative position of fingers is necessary to counting routines. It may also support associations between numbers and allocentric spatial codes that predictably interact with other known numerical spatial representations, such as the mental number line (MNL). In this study, 48 Western participants whose typical counting routine proceeded from thumb-to-little on both hands performed magnitude and parity binary judgments. Response keys were pressed either with the right index and middle fingers or with the left index and middle fingers in separate blocks. 24 participants responded with either hands in prone posture (i.e., palm down) and 24 participants responded with either hands in supine (i.e., palm up) posture. When hands were in prone posture, the counting direction of the left hand conflicted with the direction of the left–right MNL, whereas the counting direction of the right hand was consistent with it. When hands were in supine posture, the opposite was true. If systematic associations existed between relative number magnitude and an allocentric spatial representation of the finger series within each hand, as predicted on the basis of counting habits, interactions would be expected between hand posture and a unimanual version of the spatial–numerical association of response codes (SNARC) effect. Data revealed that with hands in prone posture a unimanual SNARC effect was present for the right hand, and with hands in supine posture a unimanual SNARC effect was present for the left hand. We propose that a posture-invariant body structural representation of the finger series provides a relevant frame of reference, a within-hand directional vector, that is associated to simple number processing. Such frame of reference can significantly interact with stimulus–response correspondence effects, like the SNARC, that have been typically attributed to the mapping of numbers on a left-to-right mental line.

Introduction

The relation between spatial and numerical cognition was first assumed by Galton (1880) at the end of the nineteenth century. Taking into account introspective reports he proposed that magnitude information might be analogically arranged through the location of numbers along a spatial axis oriented from left to right. The concept of a mental number line (MNL), where smaller numbers occupy leftward locations and larger numbers rightward locations, later found consistent evidence in the spatial–numerical association of response codes (SNARC) effect. The effect was first named by Dehaene et al. (1993), in a seminal study where participants were asked to decide if a centrally presented number was even or odd by pressing one of two lateralized keys. They reported that large numbers were responded to faster with the right than with the left key and small numbers were responded to faster with the left than with the right key. Such preferential mapping effect (see, e.g., Kornblum et al., 1990) between the magnitude of a target number and the location of a correct response in external space would thus corroborate the idea of the existence of a mental representation linking numbers to space. Even if magnitude information is irrelevant to the task of parity judgment, the display and subsequent processing of an Arabic number was thus assumed to obligatorily activate its numerical magnitude code (i.e., cardinality; see, e.g., Santens and Gevers, 2008; Fitousi et al., 2009 for more recent proposals with a different emphasis). The SNARC effect is nowadays an established finding (see Fischer, 2006, for reservations) and it has been consistently found across different tasks, materials, response modalities, and populations (Fias and Fischer, 2005; Wood et al., 2008).

Dehaene et al. (1993) found that the SNARC effect does not reverse in left handed individuals or when participants are asked to respond with their hands crossed (but see Wood et al., 2006a). They found weaker SNARC effects in subjects who were originally educated in a right to left writing system, such as Iranian immigrants; and the longer their Iranian participants had dealt with a left-to-right writing system (i.e., the longer they had been living in France), the more likely they were to show the typical Western SNARC effect. Later on Zebian (2005) provided more direct evidence, by showing a significant reverse SNARC effect in monoliterate Arabic readers. These findings are interesting as they highlight the possibility that the association between number and space is the byproduct of educational factors rather than some biologically determined connection (see also Núñez, 2011). Other sources have pointed to finger counting habits, in alternative or in addition to reading direction, as a crucial component of the mental representation of number from which spatial attributes could originate (e.g., Butterworth, 1999; Fias and Fischer, 2005; Rusconi et al., 2005; Fischer and Brugger, 2011). In many cultures the use of fingers develops spontaneously in childhood, and tends to precede the use of more abstract numerical codes (Butterworth, 1999). Accordingly, influences from finger representations and counting habits have been recently shown both in children and in adult numerical cognition (see, e.g., Noël, 2005; Di Luca et al., 2006, 2010; Di Luca and Pesenti, 2010; Domahs et al., 2008, 2010; Di Luca and Pesenti, 2011). Finger counting habits appear to influence also the SNARC effect as measured in a parity judgment task with bimanual responses (Fischer, 2008). Fischer (2008) suggests that a systematic relation exists between the hand one starts counting with and the strength of the preferential mapping of numbers on bimanual lateralized responses. More precisely, the SNARC effect is weaker in right-starters compared to left-starters because their counting routine consistently associates smaller numbers to their right hand and larger numbers to their left hand, in contrast with the MNL-based correspondence effect (Fischer, 2008). Predominance of a counting- over a MNL-based representation was reported by Di Luca et al. (2006), who directly tested number–finger associations. They asked participants to respond to Arabic digits by pressing 1 of 10 keys with all 10 fingers and with their hands in prone and in supine posture. Consistent with their participants being right-starters, performance was better when small numbers were associated to the right hand and large numbers to the left hand (with modulations). Such advantage was present in either postures and top performance was achieved when the specific number-to-finger mapping was also congruent with the prototypical direction of counting within a hand, which therefore can be said to influence the way numerical information is projected into physical space via hand motor outputs (see also Sato et al., 2007 for neurophysiological evidence). In conclusion, part of the available evidence suggests that finger counting habits modulate the association between numbers and space as measured via manual responses.

On the other hand, Dehaene et al. (1993) obtained a significant SNARC effect also with an incongruent hand-to-response key mapping, that is having participants respond with their hands crossed. They thus concluded that the SNARC effect is not driven by the association between number magnitude and any lateralized effectors but it rather depends on response location. Wood et al. (2006a) later failed to replicate Dehaene et al.’s (1993) result, as the SNARC effect disappeared when their participants responded with their hands crossed. Fischer (2006) suggested that, although it is true that several spatial frames of reference may exist that either conflict with or boost each other, it is also possible that one single number to space association (which does not necessarily reflect any long-term representation) is strategically instantiated by working memory, depending on contingent task requirements and settings. In agreement with Fischer’s (2006) proposal, Bächtold et al. (1998) have shown that the classical (and supposedly MNL-related) SNARC effect can be easily “overwritten” by a reverse SNARC effect when asking participants to perform simple tasks with numbers while imagining them as hours on a clock face (whereby small numbers are on the right hand side, large numbers on the left hand side). Thus different long-term associated frames of reference and/or working memory strategic representations can contribute to the resulting behavioral SNARC effect. Finally, Wood et al. (2006b) convincingly argued that the presence (absence) of a SNARC effect in their study may not only reflect the activation (or lack of activation) of the MNL but it may also represent the end result of an interaction between different, and at times conflicting, spatial frames of reference evoked by numbers. More recently, Gevers et al. (2010) have also advanced the proposal that different mechanisms (categorical vs. coordinate spatial reference frames) may be at the origin of “endogenous” SNARC effects as detected in parity vs. magnitude judgment tasks. The proposal is especially interesting, considered that it would see these mechanisms naturally mapped on different macro-anatomical substrates (e.g., left vs. right hemisphere; Kosslyn, 2006; Gevers et al., 2010) and thus predict a specific role for the language dominant hemisphere in the SNARC effect from parity judgment and for the non-dominant hemisphere in the SNARC effect from magnitude judgment tasks (Gevers et al., 2010; see, e.g., Rusconi et al., 2011a, for consistent neuro-functional evidence).

Data from left-sided visuo-spatial neglect patients and studies with transcranial magnetic stimulation (TMS) applied on the right (non-dominant) hemisphere of healthy participants (e.g., Zorzi et al., 2002; Oliveri et al., 2004; Doricchi et al., 2005; Göbel et al., 2006; see Sandrini and Rusconi, 2009; Umiltà et al., 2009; Sandrini et al., 2011 for related reviews) reported a systematic bias toward larger numbers in numerical bisection tasks analogous to the bias that is produced by actual or virtual lesions to the right hemisphere in physical space processing. Neglect patients have also been reported to show a rightward bias in binary-choice magnitude judgment tasks on Arabic digits (Vuilleumier et al., 2004) but an intact SNARC effect in parity judgments (Priftis et al., 2006), and TMS on the right anterior hemisphere eliminates the SNARC effect in magnitude judgments but not in parity judgments (Rusconi et al., 2011a,b).

While the right hemisphere is generally considered dominant for space processing, the left hemisphere has been historically recognized as dominant for the skilled use of hands and their coordination (Liepmann, 1905; Binkofski et al., 1999). It has also been indicated as the site of body-related schemas (Kinsbourne and Warrington, 1962; Sirigu et al., 1991; Guariglia et al., 2002), in addition to hosting a language-related categorical space reference system (Kosslyn, 2006). Furthermore, left hemisphere lesions often produce spurious (i.e., either incomplete or with additional deficits) and sometimes pure Gerstmann’s syndrome, a cluster of neuropsychological symptoms characterized by left–right confusion, agraphia, acalculia, and finger agnosia (Gerstmann, 1940; see Rusconi et al., 2010 for a recent review). Likewise, TMS studies have identified contiguous neural substrates with causal effects on numerical processing, finger gnosis, and categorical left–right discrimination (Rusconi et al., 2005; Hirnstein et al., 2011). If there is any cross-talk between a supposed embodied spatial reference frame and the SNARC effect, it thus appears more likely to occur by virtue of left hemisphere fronto-parietal networks.

Building on neuropsychological insights (e.g., Gerstmann, 1940; Kinsbourne and Warrington, 1962) and on current knowledge of somatosensory stimulus processing we have recently identified an abstract structural representation of the hand and fingers that is posture-invariant (Rusconi et al., 2009). Such body structural representation would constitute a very basic form of self-awareness, and is thought to embed long-term information about the identity and the relative position of fingers rather than their current position in egocentric space (which would instead be continuously updated via proprioceptive input and be functional to action systems). As counting consists of an overlearnt sequence of movements that is essentially rooted in the invariant structure of the hand, the fixed order of fingers and their identity (e.g., Butterworth, 1999) we hypothesize the existence of a long-term association between small digits and the internal structure of the hand (i.e., the relative position of fingers) that, in addition to the side of the starting hand (Fischer, 2008), may influence the behavioral effects of number–space associations in a predictable way. The issue of a relation between hands and number has been so far tackled from two complementary perspectives: an action-related and a representational perspective (Sandrini and Rusconi, 2009). As the possible mechanism linking counting routines to the MNL is still underspecified and far from definitively established (Fischer, 2008), we propose that the posture-invariant body structural representation referred above may provide a relevant frame of reference (a within-hand directional vector) involved in the cross-talk between numbers, bodily representations, and the MNL.

In the present study we thus address the relation between number, mental space, and finger representations by investigating whether the intrinsic directionality of the finger schema, which may lie behind the widespread use of “anatomical” counting routines (see Lindemann et al., 2011), will exert any measurable effects in unimanual parity and magnitude judgment tasks – that is simple numerical tasks that are known to reliably produce spatial stimulus–response (S–R) correspondence effects with bimanual response (Umiltà and Nicoletti, 1990; Wood et al., 2008) but to the best of our knowledge have never been systematically studied in unimanual version and with posture manipulation (one notable exception being Leuthard et al., 2005, who thoroughly investigated clock-related SNARC effects for different postures of the dominant hand, in a person’s front and back space). In certain experimental and clinical settings, however, bimanual responses are best avoided, impractical, or impossible (e.g., some TMS experiments, studies with hemineglect or hemiplegic patients), and the possibility to probe number–space associations by measuring the SNARC effect with unimanual responses should not be given for granted.

In order to minimize potential carry over effects in the mapping of stimuli to responses from one posture to the other and mental rotation strategies (see, e.g., Leuthard et al., 2005) we manipulated hand posture between rather than within participants. Since the mechanisms of implicit and explicit access to number magnitude may be supported by different neuro-functional networks or even by different hemispheres (see, e.g., Priftis et al., 2006; Gevers et al., 2010; Rusconi et al., 2011a), all of our participants engaged both in a number magnitude judgment and in a parity judgment task for exploratory reasons. In particular we were interested in detecting whether hand posture may affect the SNARC effect in a different way, when probed in the context of a number parity or a number magnitude judgment task. We thus measured unimanual SNARC effects from either hands in two different postures and with two classical numerical tasks. Typically, the SNARC effect emerges in settings requiring bimanual key-press responses, with response keys aligned along the horizontal dimension and therefore being defined one as left key and the other as right key (Dehaene et al., 1993). Although the right hand typically operates the right response key, and the left hand operates the left response key, Dehaene et al. (1993) manipulated also the hand-to-key assignment in their seminal study and reported that the SNARC effect follows the laterality of response keys rather than that of the response effectors (but see Wood et al., 2006a). Later studies adopted a unimanual response version of the same task, to produce an equivalent measure of the SNARC effect for left hemispatial neglect patients who could only respond with their ipsilesional effector (i.e., the right hand only; e.g., Priftis et al., 2006). Rather than operating a left and a right response key with their left and right hands, participants operated a left and a right response key with a left and a right finger of their right hand (see Leuthard et al., 2005 for extensive background information and rationale of the unimanual variant). In the current study we will maintain the typical definition of the SNARC effect, as a preferential association of small numbers to a left response key and large numbers to a right response key. When present, the SNARC effect will be signaled by a significant interaction between number magnitude and response side (e.g., Bächtold et al., 1998), and by a negative linear regression slope for the difference between right and left response latencies having number (1–9, 5 excluded) as a regressor (e.g., Fias et al., 1996).

Unlike the usual SNARC effect, unimanual SNARC is characterized by the preferential mapping of numerical stimuli to lateralized responses operated by different fingers of the same hand rather than homologous fingers on different hands. Our participants showed anatomical finger counting routines whereby, within each hand, counting starts from the thumb and ends with the little finger, thus invariably associating small numbers (in relative terms) to the thumb and large numbers to the little finger. We thus predicted instances of conflict between the direction of an active hand spatial framework and the MNL, while processing single-digit numbers. A responding right hand in prone posture will see the two frames of reference aligned, a responding right hand in supine posture will see the two frames run in opposite directions. A responding left hand in prone posture will have its intrinsic hand direction misaligned with the MNL, whereas its supination will have them aligned (see Figure 1). If the MNL dominates over the within-hand reference frame in a unimanual context, the SNARC effect when present should remain unaffected by posture manipulations. If the hand reference frame dominates over the MNL, the SNARC effect should be significant in either aligned posture and of reverse sign in the posture with a misalignment between hand direction and MNL. If both frames of reference contribute about equally to the mapping of numbers onto response space, then it is possible that the SNARC effect is significant when they are aligned and reduced or eliminated when they are misaligned. With this manipulation it is thus possible to investigate the influence of multiple competing spatial representations in numerical cognition. An alternative view could maintain that the absence of an effect in the misaligned condition indicates the absence of any spatial frames of reference (see, e.g., Fischer, 2006; but see Wood et al., 2006b). This position however, based on a view of the SNARC effect as byproduct of working memory strategies, would require the ad hoc assumptions that posture but not responding hand in one group (right hand in supine posture) and responding hand but not posture (left hand in prone posture) in the other group make the use of MNL too taxing or task-inefficient, while being instead useful when responding with the left hand in prone posture or with the right hand in supine posture. Following previous studies (e.g., Leuthard et al., 2005; Wood et al., 2006b), we will propose that the coexistence of two conflicting frames of reference may be indicated by the lack of an overall SNARC effect in the misaligned condition due to increased variability in the leading frame of reference between participants rather than to the reciprocal neutralization of coexisting frames within individuals. If this was true, two comparable groups having significant but opposite SNARC effects should be found in the misaligned condition. Absence of both frames of reference in the misaligned condition would instead be signaled by the lack of an overall SNARC effect in concomitance with low inter-individual variability in the SNARC effect (expected to be close to null for most of the participants, with occasional deviations due to random error; Wood et al., 2006b). In the aligned condition, variability of the SNARC effect would depend in any case on random error plus inter-individual differences in the overall strength of number–space associations, with most of the participants showing a SNARC effect in one direction.

FIGURE 1

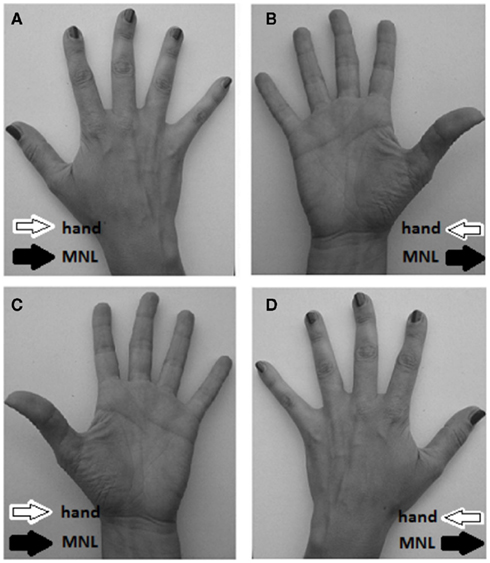
Figure 1. Schematic showing the study main rationale. (A,B) Show a right hand in prone and supine posture respectively. (C,D) Show a left hand in prone and supine posture respectively. In (A,C), within-hand counting direction (white arrow) is aligned with the mental number line direction (MNL, black arrow); in (B,D), within-hand counting direction is misaligned with the direction of the mental number line. When unimanual responses are required with index and middle fingers, a regular SNARC effect should be present in condition (A,C), whereas its presence in condition (B,D) may depend on the relative weight of the within-hand counting direction and the mental number line spatial frame.

Materials and Methods

Participants

Forty-eight healthy participants (26 females; 45 right-handed) took part in the investigation, all of whom were naïve to its purpose and were born and educated in a Western country (left-to-right reading direction). They had a mean age of 26 (SD = 5) years. The study was approved by the ethical committee for experiments on humans at the University of Trento and participants gave informed written consent before taking part in the experiment. Two independent groups were formed by random assignment of participants. One of the groups (11 females, 22 right-handed, mean age = 25, SD = 4) responded with either hands in prone posture, the other (14 females, 23 right-handed, mean age = 27, SD = 5) responded with either hands in supine posture. To avoid priming or carry-over effects in the experimental session, only at the end of the task participants were asked to show the experimenter how they count with their fingers when both their hands are free. Most participants (44 out of 48, more precisely 22 in each group) reported using the conventional Italian and French counting sequence starting from the right thumb, except for four participants who were reportedly left-starters. All of them, however, counted the smallest number on the thumb and the largest on the little finger of the opposite hand, and therefore switched from one hand to the other by following an “anatomical” (as opposed to “spatial”) sequence (see, e.g., Lindemann et al., 2011).

Apparatus, Stimuli, and Procedure

On each trial, participants fixated the center of a computer display where a white digit (range: 1–9, 5 excluded; font and size: Arial 48 Bold) subtending horizontally about 1.2° and vertically about 1.9° of visual angle was shown on black background for 1,300 ms (see Figure 2). In one of the two tasks, digits were to be classified as smaller/larger than 5, in the other digits were to be classified as even/odd. In the prone posture condition, participants kept their hands with their palms down throughout the experiment. While the responding hand was placed on the keyboard, the non-responding hand was resting comfortably on the ipsilateral knee. For half the trials participant responded with their right hand by pressing a left key with their index finger and a right key with their middle finger (see Figure 3A), and for the other half with their left hand by pressing a left key with their middle finger and a right key with their index finger. Response keys were aligned on participants’ vertical meridian, with the left key (corresponding to V on a QWERTY keyboard) in left hemispace and the right key (corresponding to N) in right hemispace. In the supine posture condition, participants kept their hands with their palms up throughout the experiment. While the responding hand was placed on the keyboard, the non-responding hand was resting comfortably on the ipsilateral knee. For half the trials participants responded with their right hand by pressing a left key with their middle finger and a right key with their index finger (see Figure 3B), and for the other half with their left hand by pressing a left key with their index finger and a right key with their middle finger. Response keys were aligned on participants’ vertical meridian, with the left key (corresponding to N, as the keyboard was reversed) in left hemispace and the right key (corresponding to V, as the keyboard was reversed) in right hemispace. In either postures they were instructed to keep their non-responding hand comfortably resting on their ipsilateral knee in the same posture as their responding hand (e.g., see Figure 3B). Their compliance was visually monitored by the experimenter throughout the entire session.

FIGURE 2

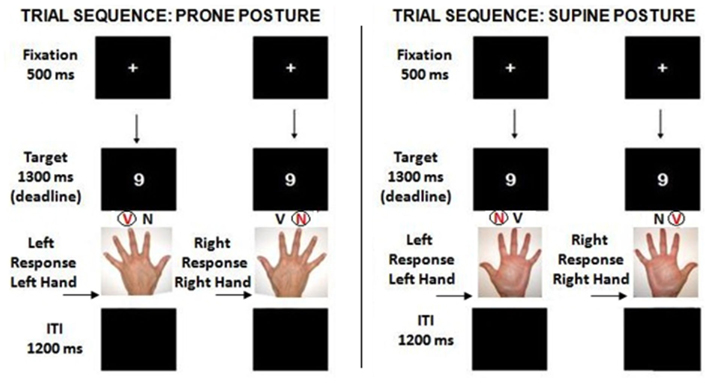
Figure 2. On each trial, participants fixated the centre of a display where a digit (1–9, 5 excluded) appeared for 1,300 ms. In half the blocks, digits were classified as smaller/larger than five in the other half as even/odd. Participants responded with either their right index and middle finger or their left index and middle finger, and the experiment was divided in two main parts according to which hand was used to respond. Since nine is large in the experimental range, the right-side key is compatible with a left-to-right representation of the numbers 1–9, and the left-side key is incompatible.

FIGURE 3

Figure 3. (A) In the prone posture, participants’ fingers (index and middle of the same hand) were placed on the V and N keys of an upright QWERTY keyboard. The response keys were centered on the participant’s vertical meridian while the other hand rested comfortably on the ipsilateral knee in the same posture as the responding hand. (B) In the supine posture, participants’ fingers (index and middle of the same hand) were placed on the V and N keys of a reverse QWERTY keyboard that was firmly attached to the table with its two bottom rows of keys (including V and N) protruding from the edge. As in the prone posture condition, the non-responding hand rested comfortably on the ipsilateral knee in the same posture as the responding hand.

Each main task (magnitude or parity judgment) included four blocks presented in ABBA order: two blocks with a S–R mapping (block-type A, e.g., “respond to small – or odd – with the left key, to large – or even – with the right key”) and two with the alternative mapping (i.e., block-type B, “respond to large – or even – with the left key, to small – or odd – with the right key”). For this reason, subjects were instructed to carefully read the instructions preceding each block and containing precise indications about the required S–R mapping. In order to avoid confounding the effects of interest with switching/remapping costs, the first eight trials of each block were considered as practice and excluded from subsequent analyses (see Rusconi et al., 2011a, for a similar procedure).

A 800-ms visual feedback (“Error” in case of incorrect or “Too Slow” in case of missing response) or blank screen (in case of correct response) followed, and was then replaced by another 1,200 ms blank screen before the start of a new trial. Since the experimental set comprised numbers ranging from 1 to 9, numbers from 1 to 4 were considered small and numbers from 6 to 9 were considered large in either task (Dehaene et al., 1993). We therefore expected, in the baseline, to find an advantage for left key responses to 1–4 and for right key responses to 6–9. The experiment was divided in two parts: one in which participants responded with index and middle fingers of their left hand, and one in which they responded with index and middle fingers of their right hand. Order of parts was counterbalanced between participants. Order of tasks was kept constant for each participant both within and between sessions. Half participants responded with their hands in a prone posture, half with their hands in a supine posture. In total, the experiment comprised 384 experimental and 128 practice trials and was completed in a single session. Each cell of the design response hand (left, right) × task (magnitude, parity) × magnitude (small, large) × response key (left, right) contained 24 observations per each individual.

Data Analysis

Response latency (mean RTs) and accuracy (arcsin-transformed percentages of correct responses) were entered in an exploratory mixed design ANOVA having one between participant factor (hand posture) with two levels and four within participant factors (responding hand, task, number magnitude, and response side) having two levels each (see below). Follow-up F- or t-tests were then carried out to disambiguate interactions. Whenever left unspecified, all of the reported follow-up tests remain significant with a family-wise Bonferroni-corrected threshold equal to 0.05/(number of comparisons in a cluster). The presence of a significant SNARC effect was then investigated more specifically by performing directional t-tests on individual β weights, as obtained from linear regressions on the RT differences between right and left responses for each target number (Lorch and Myers, 1990), in the critical posture by response hand combination for either tasks. Proportion of participants showing negative β weights are also provided for conditions in which the SNARC effect was significant, as well as the proportion of participants whose β values were higher when MNL and hand-related frames of reference were misaligned. Finally, proportions of participants having negative vs. positive βs are reported for the aligned and the misaligned condition across experiments. Relevant measures of effect size are provided throughout (Rosenthal, 1991; Field, 2007).

Results

Total error rate averaged 3.9% and both latency and accuracy data were analyzed. A mixed design 2 × 2 × 2 × 2 × 2 ANOVA having hand posture (prone, supine) as between subject factor and response hand (left, right), task (magnitude, parity), magnitude (small, large), and response key (left, right) as within subject factors was performed on mean reaction times (RTs) for correct responses. Significant main effects of task [F_(1,46) = 126.11, MSE = 4300; P < 0.001, η² = 0.73], magnitude comparison being 53 ms faster than parity judgment (magnitude: M = 512, SE = 8; parity: M = 565, SE = 8), and magnitude [F_(1,46) = 14.65, MSE = 788; P < 0.001, η² = 0.24], smaller numbers being responded to 8 ms faster than larger numbers (small: M = 534, SE = 8; large: M = 542, SE = 8) were found. The significant two-way interaction between hand and response key [F_(1,46) = 21.28, MSE = 2091; P < 0.001] indicated that left-side responses were faster than right-side responses with the left hand (left: M = 531 ms, SE = 9; right: M = 544 ms, SE = 9), and viceversa for the right hand (left: M = 548 ms, SE = 9; right: M = 531 ms, SE = 7) [T₍₄₆₎ = 3.23, P = 0.0023, r = 0.43; and T₍₄₆₎ = 3.68, P = 0.0006, r = 0.48, respectively]. A two-way interaction between magnitude and response key [F_(1,46) = 11.81, MSE = 1665; P < 0.002, η² = 0.20] was also present showing a 10.5-ms SNARC effect, further qualified by the four-way interaction between posture, hand, magnitude, and response key [F_(1,46) = 7.06, MSE = 1368; P < 0.02, η² = 0.13]. With a prone posture, a 16.5-ms SNARC effect was present and significant when responses were given with the right hand [F_(1,46) = 8.93, P < 0.005, r = 0.40] but not when they were given with the left hand (1.5 ms; F < 1; see Figure 4A). With a supine posture, a 18.5-ms SNARC effect was present and significant when responses were given with the left hand (F_(1,46) = 9.82, P < 0.004, r = 0.42) but not when they were given with the right hand (4.5 ms; F < 1; see Figure 4C). Finally, a significant three-way interaction was also found between task, magnitude, and response key [F_(1,46) = 6.480, MSE = 1029; P < 0.02; η² = 0.12] pointing to the presence of a fully significant SNARC effect in the parity task [16 ms; F_(1,46) = 20.84, P < 0.0001, r = 0.56] which fell instead far from significance in the magnitude task [4 ms; F_(1,46) = 1.131, P > 0.10].

FIGURE 4

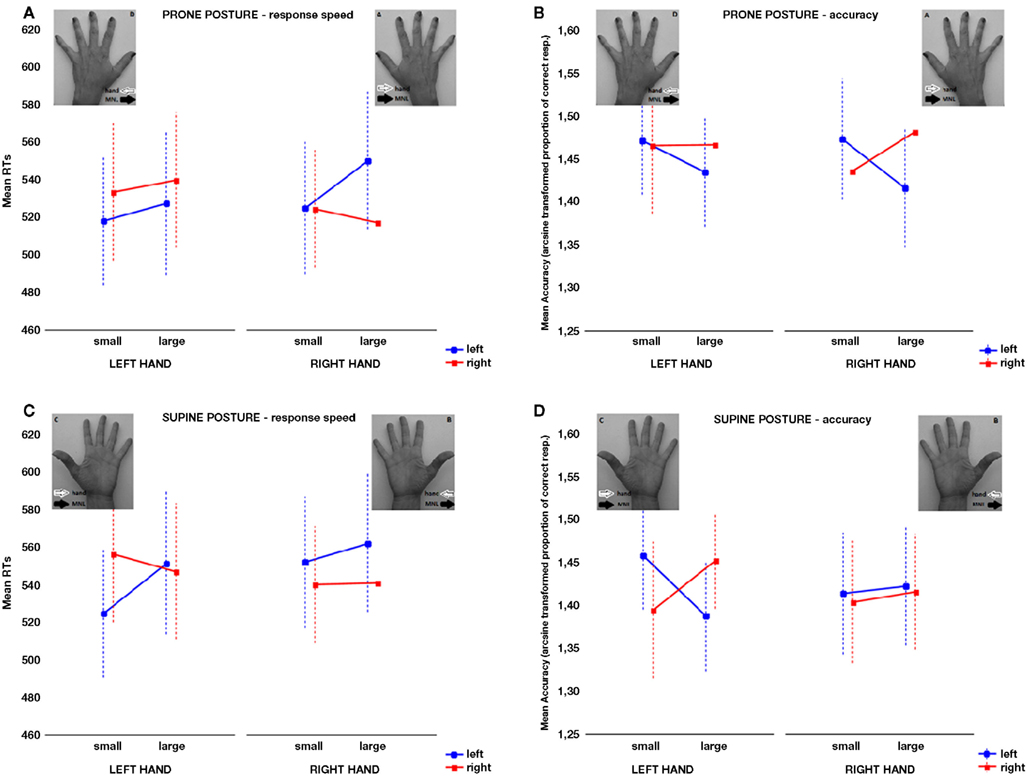
Figure 4. The four-way interaction between posture, responding hand, magnitude, and response key on mean RTs is depicted. Vertical bars denote 95% confidence intervals. (A,B) When participants kept their hands in a prone posture, the SNARC effect was significant for the right hand only (and likely driven by the difference between left and right key for large numbers). (C,D) When participants kept their hands in a supine posture, the SNARC effect was significant for the left hand only (and likely driven by the difference between left and right key for small numbers).

The same design 2 × 2 × 2 × 2 × 2 ANOVA performed on arcsin-transformed proportions of accurate responses detected a significant main effect of task [F_(1,46) = 55.92, MSE = 0.026; P < 0.001, η² = 0.55], magnitude comparison being more accurate than parity judgment (M = 1.48, SE = 0.01 and M = 1.39, SE = 0.01, respectively). Moreover, a significant two-way interaction between magnitude and response key [F_(1,46) = 10.42, MSE = 0.021, P < 0.003; η² = 0.18] indicating a regular SNARC effect was qualified by a four-way interaction between posture, hand, magnitude, and response key [F_(1,46) = 6.77, P < 0.02; η² = 0.13]. Consistently with the latency analysis, the SNARC effect was present and significant when responses were given with the right hand [F_(1,46) = 7.43, P < 0.009, r = 0.37] but not when they were given with the left hand in a prone posture (F < 1; see Figure 4B). The SNARC effect was present and significant when responses were given with the left hand [F_(1,46) = 9.71, P < 0.004, r = 0.42] but not when they were given with the right hand in a supine posture (F < 1; see Figure 4D).

The significant interactions between magnitude and response, for participants responding with their right hand in prone posture and participants responding with their left hand in supine posture, signals the presence of a classical SNARC effect. Differential RTs (or dRTs; RTs of right responses minus RTs of left responses) were thus computed for all target numbers in each of the critical experimental conditions for every participant: if a classical SNARC effect was present, it should be possible to fit dRTs with a line having negative slope (i.e., modeling faster left responses to smaller numbers and faster right responses for large numbers). Directional single-sample t-tests on individual regression slopes (see Lorch and Myers, 1990; Fias et al., 1996) showed that β weights were significantly smaller than zero [prone posture, right hand: magnitude comparison, T₍₂₃₎ = 2.72, P = 0.006, r = 0.49; M = −0.25, SE = 0.10; parity judgment: T₍₂₃₎ = 4.01, P = 0.006, r = 0.64, M = −0.30, SE = 0.07; supine posture, left hand: magnitude comparison, T₍₂₃₎ = 1.80, P = 0.042, r = 0.35; M = −0.18, SE = 0.10; parity comparison, T₍₂₃₎ = 4.54, P < 0.0001, r = 0.71; M = −0.35, SE = 0.08]. Finally, in the presence of a significant SNARC effect, 17 out of 24 participants had negative β weights in the magnitude task and 18/24 in the parity task for the prone posture condition. In the presence of a significant SNARC effect, 15/24 had negative β weights in the magnitude task, and 19/24 in the parity task, for the supine posture condition. Overall, the experimental manipulation within participants (i.e., misalignment of the spatial frames of reference by changing the responding hand) caused a significant increase in the β weights, by pushing them toward 0, of 0.21 units [T₍₄₇₎ = 3.27, P = 0.001, r = 0.43; M = −0.21, SE = 0.06], with two-thirds of the participants (i.e., 32 out of 48) showing a change in the expected direction [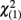 = 5.33, P = 0.021]. Finally, two separate groups of participants could be identified based on the sign of individual β weights in the misaligned condition across experiments, showing opposite SNARC effects of large size in each group [negative: N = 27, M = −0.31, SE = 0.04, T₍₂₆₎ = 8.29, P < 0.0001, r = 0.85; positive: N = 21, M = 0.26, SE = 0.04, single-sample T₍₂₀₎ = 6.62, P < 0.0001, r = 0.83]. In the aligned condition, the proportion of participants having negative vs. positive βs appeared much more unbalanced in favor of negative βs; effect sizes were in the large range for either group [negative: N = 39, M = −0.38, SE = 0.04, single-sample T₍₃₈₎ = 10.05, P < 0.0001, r = 0.85; positive: N = 9, M = 0.19, SE = 0.04, single-sample T₍₈₎ = 4.46, P < 0.01, r = 0.84]. A McNemar’s test for dichotomous variables in paired samples detected a significant difference between the misaligned and the aligned conditions (P = 0.017).

Discussion

In this study, we have used a unimanual version of the SNARC effect to test for the possible presence of an hand-related allocentric frame of reference (see, e.g., Kinsbourne and Warrington, 1962; Rusconi et al., 2009) that may be evoked by number processing. The directional vector of such representation was predicted to run from thumb-to-little based on our participants’ counting habits. By introducing conflict between the hand-related and MNL-related vectors, we predicted opposite modulations of the SNARC effect for the two hands, depending on their posture. More precisely, when the right hand is pronated (see Figure 1A) or the left hand is supinated (see Figure 1C), the direction of either hand is aligned with the direction of the MNL as their thumb-to-little axis runs from left-to-right. When the right hand is supinated (as in Figure 1B) or the left hand is pronated (as in Figure 1D), the direction of either hand is opposite to the direction of the MNL because their thumb-to-little axis run from right to left. In the former cases, a regular SNARC effect was found, in the latter cases no SNARC effect was found. Unimanual SNARC effects where thus obtained from both hands. However, for each hand the SNARC effect was found in just one of the tested postures. We showed that our manipulation acts at a group level by increasing inter-individual variability in the misaligned condition, rather than by neutralizing individual SNARC effects in the misaligned condition. This is more compatible with the coexistence, in the misaligned condition, of two vectors having similar force but opposing direction, of which only one takes the lead and influence individual performance, rather than with the absence of any frames of reference. A much less clearcut, because found in the RTs ANOVA only and the smallest in size, finding was the different reliability of the unimanual SNARC effect in parity judgment and the unimanual SNARC effect in magnitude judgment. Task, however, was not involved in any significant interactions with posture and response hand.

The above results prompt interesting speculations about the cognitive mechanisms underlying interactions between numerical magnitude and representational space. First of all, they make it implausible that the unimanual SNARC effect originates in a long-term MNL that is indiscriminately activated by number magnitude processing, because the SNARC effect was involved in an interaction with response hand and hand posture. Had it been the byproduct of MNL processing, the SNARC effect might have interacted with task but in the opposite direction than the one we reported here (i.e., stronger SNARC effect when number magnitude is relevant to the task). The fact that unimanual SNARC effects, when present, were particularly strong in the parity judgment task, seem to corroborate the idea that a within-hand frame of reference, if present, may be more active in concomitance with the activation of categorical spatial representations from the dominant hemisphere (provided that Gevers et al., 2010 perspective about the origin of the SNARC effect in parity judgments is tenable; see Introduction). On the other hand, if the SNARC was solely determined by finger identity, a reverse SNARC effect would have been found for either hand in the misaligned condition (i.e., right hand in the supine posture, Figure 1B, and left hand in prone posture, Figure 1D) since the assignment of finger to response key was reversed. The fact that this systematic association (index-small and middle-large) was not present in the aligned conditions at the group level, suggests that a fully embodied model of the mental number-space is unsatisfactory as well.

Our data could be best accommodated by assuming that, in unimanual two-choice tasks involving numbers, at least two pre-existing frames of reference may simultaneously influence performance. In particular, with a supine posture, the thumb-to-little preferential mapping of the right hand could have competed with the left–right oriented response vector deriving from the MNL. Viceversa, with a prone posture the thumb-to-little preferential mapping of the left hand could have competed with the left–right oriented response vector from the MNL. Since the non-responding hand was always kept in the same posture as the responding hand, it is unlikely that our results could be explained by conflict between active vs. inactive hand frames of reference, because this was kept constant across all conditions. Alternatively, one should postulate that a group of participants was strategically evoking a number spatial representation when responding with their right hand but not with their left hand in a prone posture, and another group was strategically evoking a numerical spatial representation when responding with their left hand but not with their right hand in supine position, which would not be theoretically parsimonious. The concomitant presence of two frames of reference fits better than the absence of any frames of reference in the misaligned condition with the proportion of participants showing negative vs. positive β weights and the detection of large and significant but reverse SNARC effects (see also Leuthard et al., 2005; Wood et al., 2006b for similar arguments).

A few other studies had previously introduced postural manipulations in simple numerical tasks (e.g., Leuthard et al., 2005; Di Luca et al., 2006; Brozzoli et al., 2008). Brozzoli et al. (2008), for example, had their participants perform a tactile detection task by foot pedal responses. The tactile stimulus could be delivered either on their right thumb or on their right little finger following the appearance of a digit on a computer display. Participants performed the test with their right hand both in supine and in prone posture, and results indicated faster detection whenever a stimulus was delivered to the left-side after the appearance of a small than a large digit and viceversa with a right-side stimulus, irrespective of hand posture. Thus Brozzoli et al. (2008) rightly concluded that Arabic digits may evoke an extrapersonal spatial frame of reference that remains active and influences behavior even when attention is focused on the hand and on tactile stimuli to individual fingers. However, Brozzoli et al.’s set-up required no motor response selection stage as the spatial effects of number magnitude processing were measured in simple reaction times. No competition between MNL and hand-related frames of reference could be detected, if their interaction becomes manifest only when a response selection stage is involved. Foot responses, moreover, may be relatively unaffected from correspondence effects arising from hand-structural representations (it would be probably different if responses required toes differentiation; see, e.g., Tucha et al., 1997). Finally, the task did not require fine finger discrimination and only the most external fingers (thumb and little), which are usually told apart even in the presence of an acquired deficit in the structural representation of the hand (see, e.g., Kinsbourne and Warrington, 1962) received stimulation. In our study, on the contrary, participants were to continuously discriminate and select between two internal fingers (index and middle) and we employed a more demanding two-choice task. Note that a study requiring discrimination between all the 10 fingers (Di Luca et al., 2006; see below) reported a striking predominance of hand-related counting associations over MNL-related associations, that is diametrically opposite to Brozzoli et al.’s conclusions.

Systematic posture manipulations for the dominant hand were adopted by Leuthard et al. (2005), who investigated spatial S–R compatibility effects in a unimanual two-choice task. Their participants had to imagine numbers as they appear on a clock face, and were to answer whether a centrally presented number came earlier or later than six o’clock. With similar instructions but bimanual responses, participants typically present a reverse SNARC effect (i.e., a spatial S–R compatibility effect consistent with the clock representation having smaller numbers on its right hand side, larger numbers on its left hand side; Bächtold et al., 1998). By originally adopting a unimanual response modality, with keys operated by the index and ring fingers of the dominant hand, Leuthard et al. (2005) reported a similar effect. Moreover, the typical reverse SNARC effect was found to follow the relative position of response keys rather than finger identity (i.e., the preferential association between finger and side of the clock interacted with posture) when participants responded in peripersonal front space (i.e., in a condition very similar to ours, except they had the same participants doing both postures and with their dominant hand only). An opposite effect of posture was found instead when participants responded with their right hand in back space. In that condition, a reverse SNARC effect was present for the supine posture only whereas it was absent for the prone posture. Absence was due to increasing variability in mental imagery strategies between participants rather than elimination of any S–R effects at the individual level. In other words, the pattern of results that we found here for right hand responses look very similar to the pattern of results that Leuthard et al. (2005) found with responses in back space. Notably, that was also the condition in which participants were left free to choose their own frame of reference (i.e., they could choose to imagine a clock in front space or a clock in back space) and lack of a reliable S–R correspondence effect in the group analysis was not taken as evidence for the absence of any spatial frames of reference. Since Leuthard et al.’s participants were actively engaged in a mental imagery task, those claims could be verified against individual strategy self-reports. Thus, unlike in our present study, a spatial frame of reference was intentionally used by participants throughout the experimental session. A task-relevant allocentric spatial representation might thus have been superimposed and given precedence over other pre-existing frames of reference (either MNL or hand-related), and consequently have overridden their potential effects (see also Bächtold et al., 1998).

Our results appear consistent with the interplay between finger counting habits and MNL-related effects as reported by Fischer (2008), who showed a reliable SNARC effect for left-starters (associating small numbers with left space via counting routines, similarly to the MNL) and a weaker SNARC effect for right-starters (associating small numbers with right space via counting routines, opposite to the MNL) with bimanual responses. Whether the direction of counting routines may exert a causal influence on the direction of MNL, however, is still an open question and not a simple one to solve. Here we adopted a complementary approach by zooming in on the within-hand directional vector that may be identical for either hand, rather than focusing on the between hands counting sequence. We reported reliable unimanual SNARC effects within either the dominant or the non-dominant hand of a group of participants that was mainly composed by right-starters (results did not change when the same analyses were performed without the four left-starters who participated in our study) and, based on Fischer (2008), would therefore be expected to show relatively weak bimanual SNARC effects. The interaction between SNARC, hand and posture, and the pattern of inter-individual variability here described suggest that counting may affect number to space mappings at multiple levels and all possible frames of reference should be taken into account when attempting to model the possible effects counting routines on MNL representations.

Like Fischer’s (2008) study, our study is in partial agreement with Di Luca et al.’s (2006), as for the supremacy of finger counting routines over MNL in numerical cognition. Di Luca et al.’s (2006) participants were are asked to respond to Arabic digits by pressing a key with one of their 10 fingers. Performance was significantly faster when the mapping of digits to fingers matched individual finger counting habits rather than MNL. Hand posture, moreover, did not modulate the finger–digit correspondence effect. Unlike in Leuthard et al. (2005) and Brozzoli et al. (2008), however, here the association between number and finger identity is largely unaffected by a change in the spatial position, and not viceversa. We could however speculate that, since Di Luca et al. (2006) employed a bimanual response modality where discrimination between the 10 fingers was necessary to the task, the counting-based frame of reference as opposed to the MNL-based frame was highly emphasized by the task. Our set-up, like Leuthard et al.’s, still required finger discrimination, however only two response alternatives were provided and two fingers (or their homologous on the other hand) were actively engaged throughout the session. Emphasis was thus not so heavily posed on the finger series and other available mental frames of references may have been activated with equal strength.

In conclusion, with the current study we provide novel evidence against a uni-dimensional model of number–space associations. In particular we propose that a posture-invariant structural representation of the hand should be taken in consideration, in addition to the side of the hand where counting starts, when investigating the relation between individual counting routines and the MNL. In addition to the distinction of concepts such as bodily left and right, finger gnosis can reliably predict numerical abilities in developmental age (Noël, 2005). Typical counting routines integrate both abilities (e.g., Butterworth, 1999). Such combination of functions and their habitual use to manipulate and represent numerosities may be rooted in and facilitated by the contiguity of left parietal circuits in which they reside (see, e.g., Rusconi et al., 2005, 2010). Left-lateralized embodied representations, however, although important, may be only one of the cross-domain support systems that are available to the adult number processing system. Visuo-spatial representations from a right-lateralized attentional system may also play an equally important role in number processing (see Sandrini et al., 2011 for a review on relevant studies). Clarifying how these separate but interacting systems can influence basic number processing will enable us to better understand both potentiality and limitations of human numerical cognition, as well as to identify new rehabilitative and educational paths toward facilitation and improvement in number skills.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors would like thank the editor and all three reviewers for their constructive comments. This study was funded by grants from the European Commission/MIUR (MERG-CT-2007-046511) to Elena Rusconi.

References

Bächtold, D., Baumüller, M., and Brugger, P. (1998). Stimulus–response compatibility in representational space. Neuropsychologia 36, 731–735.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Binkofski, F., Buccino, G., Posse, S., Seitz, R. J., Rizzolatti, G., and Freund, H. (1999). A frontoparietal circuit for object manipulation in man: evidence from an fMRI-study. Eur. J. Neurosci. 11, 3276–3286.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Brozzoli, C., Ishihara, M., Göbel, S. M., Salemme, R., Rossetti, Y., and Farnè, A. (2008). Touch perception reveals the dominance of spatial over digital representation of numbers. Proc. Natl. Acad. Sci. U.S.A. 105, 5644–5648.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Butterworth, B. (1999). The Mathematical Brain. London: Macmillan.

Dehaene, S., Bossini, S., and Giraux, P. (1993). The mental representation of parity and number magnitude. J. Exp. Psychol. Gen. 122, 371–396.

CrossRef Full Text

Di Luca, S., Granà, A., Semenza, C., Seron, X., and Pesenti, M. (2006). Finger digit compatibility in Arabic numerical processing. Q. J. Exp. Psychol. 59, 1648–1663.

CrossRef Full Text

Di Luca, S., Lefèvre, N., and Pesenti, M. (2010). Place and summation coding for canonical and non-canonical finger numerals representations. Cognition 117, 95–100.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Di Luca, S., and Pesenti, M. (2010). Absence of low-level visual difference between canonical and noncanonical finger-numeral configurations. Exp. Psychol. 57, 202–207.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Di Luca, S., and Pesenti, M. (2011). Finger numeral representations: more than just another symbolic code. Front. Psychol. 2:272. doi:10.3389/fpsyg.2011.00272

CrossRef Full Text

Domahs, F., Krinzinger, H., and Willmes, K. (2008). Mind the gap between both hands: evidence for internal finger-based number representations in children’s mental calculation. Cortex 44, 359–367.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Domahs, F., Moeller, K., Huber, S., Willmes, K., and Nuerk, H. C. (2010). Embodied numerosity: implicit hand-based representations influence symbolic number processing across cultures. Cognition 116, 251–266.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Doricchi, F., Guariglia, P., Gasparini, M., and Tomaiuolo, F. (2005). Dissociation between physical and mental number line bisection in right hemisphere brain damage. Nat. Neurosci. 8, 1663–1665.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fias, W., Brysbaert, M., Geypens, F., and d’Ydewalle, G. (1996). The importance of magnitude information in numerical processing: evidence from the SNARC effect. Mathematical Cognition 2, 95–110.

CrossRef Full Text

Fias, W., and Fischer, M. H. (2005). “Spatial representation of numbers” in Handbook of Mathematical Cognition, ed. J. I. Campbell (New York: Psychology Press), 43–54.

Field, A. (2007). Discovering Statistics Using SPSS. London: Sage.

Fischer, M. H. (2006). The future for SNARC could be stark. Cortex 42, 1066–1068.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fischer, M. H. (2008). Finger counting habits modulate spatial-numerical associations. Cortex 44, 386–392.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fischer, M. H., and Brugger, P. (2011). When digits help digits: spatial-numerical associations point to finger counting as prime example of embodied cognition. Front. Psychol. 2:260. doi:10.3389/fpsyg.2011.00260

CrossRef Full Text

Fitousi, D., Shaki, S., and Algom, D. (2009). The role of parity, physical size, and magnitude in numerical cognition: the SNARC effect revisited. Atten. Percept. Psychophys. 71, 143–155.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Galton, F. (1880). Visualised numerals. Nature 21, 252–256.

CrossRef Full Text

Gerstmann, J. (1940). Syndrome of finger agnosia disorientation for right and left agraphia and acalculia. Arch. Neurol. Psychiatry 44, 398–408.

Gevers, W., Santens, S., D’Hooge, E., Chen, Q., Van den Bossche, L., Fias, W., and Verguts, T. (2010). Verbal-spatial and visuo-spatial coding of number-space interactions. J. Exp. Psychol. Gen. 139, 180–190.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Göbel, S. M., Calabria, M., Farne‘, A., and Rossetti, Y. (2006). Parietal rTMS distorts the mental number line: simulating ‘spatial’ neglect in healthy subjects. Neuropsychologia 44, 860–868.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Guariglia, C., Piccardi, L., Puglisi Allegra, M. C., and Traballesi, M. (2002). Is atutotopoagnosia real? EC says yes. A case study. Neuropsychologia 40, 1744–1749.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hirnstein, M., Bayer, U., Ellison, A., and Hausmann, M. (2011). TMS over the left angular gyrus impairs the ability to discriminate left from right. Neuropsychologia 49, 29–33.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kinsbourne, M., and Warrington, E. K. (1962). A variety of reading disability associated with right hemisphere lesions. J. Neurol. Neurosurg. Psychiatry 25, 339–344.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kornblum, S., Hasbroucq, T., and Osman, A. (1990). Dimensional overlap: cognitive basis for stimulus–response compatibility – a model and taxonomy. Psychol. Rev. 97, 253–270.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kosslyn, S. M. (2006). You can play 20 questions with nature and win: categorical versus coordinate spatial relations as a case study. Neuropsychologia 44, 1519–1523.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Leuthard, J., Bächtold, D., and Brugger, P. (2005). Is left always where the thumb is right? Stimulus–response compatibilities as a function of posture and location of the responding hand. Cogn. Behav. Neurol. 18, 173–178.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Liepmann, H. (1905). Die linke Hemisphäre und das Handeln. Münch. Med. Wochenschr. 49, 2322–2326.

Lindemann, O., Alipour, A., and Fischer, M. H. (2011). Finger counting habits in middle-Eastern and Western individuals: an online survey. J. Cross Cult. Psychol. 42, 566–578.

CrossRef Full Text

Lorch, R., and Myers, J. (1990). Regression analyses of repeated measures data in cognitive research. J. Exp. Psychol. Learn. Mem. Cogn. 16, 149–157.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Noël, M. P. (2005). Finger gnosia: a predictor of numerical abilities in children? Child Neuropsychol. 11, 413–430.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Núñez, R. (2011). No innate number line in the human brain. J. Cross Cult. Psychol. 42, 651–668.

CrossRef Full Text

Oliveri, M., Rausei, V., Koch, G., Torriero, S., Turriziani, P., and Caltagirone, C. (2004). Overestimation of numerical distances in the left side of space. Neurology 63, 2139–2141.

Pubmed Abstract | Pubmed Full Text

Priftis, K., Zorzi, M., Meneghello, F., Marenzi, R., and Umilta, C. (2006). Explicit versus implicit processing of representational space in neglect: dissociations in accessing the mental number line. J. Cogn. Neurosci. 18, 680–688.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rosenthal, R. (1991). Meta-Analytic Procedures for Social Research, 2nd Edn. Newbury Park, CA: Sage.

Rusconi, E., Bueti, D., Walsh, V., and Butterworth, B. (2011a). Contribution of frontal cortex to the spatial representation of number. Cortex 47, 2–13.

CrossRef Full Text

Rusconi, E., Verbruggen, F., Dervinis, M., and Chambers, C. D. (2011b). “Temporal and functional specification of right parieto-frontal contribution to number space processing,” in 14th European Congress on Clinical Neurophysiology, 21–25 June 2011, Rome.

Rusconi, E., Gonzaga, M., Adriani, M., Braun, C., and Haggard, P. (2009). Know thyself: behavioural evidence for a structural representation of the human body. PLoS ONE 4, 5418–5418. doi:10.1371/journal.pone.0005418

CrossRef Full Text

Rusconi, E., Pinel, P., Dehaene, S., and Kleinschmidt, A. (2010). The enigma of Gerstmann’s syndrome revisited: a telling tale of the vicissitudes of neuropsychology. Brain 133, 320–332.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rusconi, E., Walsh, V., and Butterworth, B. (2005). Dexterity with numbers: rTMS over left angular gyrus disrupts finger gnosis and number processing. Neuropsychologia 43, 1609–1624.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sandrini, M., and Rusconi, E. (2009). A brain for numbers. Cortex 45, 796–803.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sandrini, M., Umilta, C., and Rusconi, E. (2011). The use of transcranial magnetic stimulation in Cognitive neuroscience: a new synthesis of methodological issues. Neurosci. Biobehav. Rev. 5, 516–536.

CrossRef Full Text

Santens, S., and Gevers, W. (2008). The SNARC effect does not imply a mental number line. Cognition 108, 263–270.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sato, M., Cattaneo, L., Rizzolatti, G., and Gallese, V. (2007). Numbers within our hands: modulation of corticospinal excitability of hand muscles during numerical judgment. J. Cogn. Neurosci. 19, 684–693.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sirigu, A., Grafman, J., Bressler, K., and Sunderland, T. (1991). Multiple representations contribute to body knowledge processing. Evidence from a case of autotopagnosia. Brain 114(Pt 1B), 629–642.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Tucha, O., Steup, A., Smely, C., and Lange, K. W. (1997). Toe agnosia in Gerstmann syndrome. J. Neurol. Neurosurg. Psychiatry 63, 399–403.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Umiltà, C., and Nicoletti, R. (1990). “Spatial stimulus-response compatibility,” in Stimulus-Response Compatibility: An Integrated Perspective, eds R. W. Proctor and T. G. Reeve (Amsterdam: North-Holland), 86–116.

Umiltà, C., Priftis, K., and Zorzi, M. (2009). The spatial representation of numbers: evidence from neglect and pseudoneglect. Exp. Brain Res. 192, 561–569.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Vuilleumier, P., Ortigue, S., and Brugger, P. (2004). The number space and neglect. Cortex 40, 399–410.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wood, G., Nuerk, H. C., and Willmes, K. (2006a). Crossed hands and the SNARC effect: a failure to replicate Dehaene, Bossini and Giraux (1993). Cortex 42, 1078–1088.

CrossRef Full Text

Wood, G., Nuerk, H. C., and Willmes, K. (2006b). Variability of the SNARC effect: systematic interindividual differences or just random error? Cortex 42, 1119–1123.

CrossRef Full Text

Wood, G., Willmes, K., Nuerk, H. C., and Fischer, M. H. (2008). On the cognitive link between space and number: a meta-analysis of the SNARC effect. Psychol. Sci. Q. 50, 489–525.

Zebian, S. (2005). Linkages between number concepts, spatial thinking, and directionality of writing: the SNARC effect and the reverse SNARC effect in English and Arabic monoliterates, biliterates, and illiterate Arabic speakers. J. Cogn. Cult. 5, 166–190.

CrossRef Full Text

Zorzi, M., Priftis, K., and Umiltà, C. (2002). Brain damage: neglect disrupts the mental number line. Nature 417, 138–139.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text