- 1 Section Neuropsychology, Department of Neurology, University Hospital, RWTH Aachen University, Aachen, Germany
- 2 Department of Neurology, Section Clinical Cognition Research, University Hospital, RWTH Aachen University, Aachen, Germany
- 3 Institute of Germanic Linguistics, University of Marburg, Marburg, Germany
- 4 Department of Psychology, Eberhard Karls University, Tübingen, Germany
- 5 Institut für Wissensmedien-Knowledge Media Research Center, Tübingen, Germany
- 6 Department of Korean Sign Language Interpretation, Korea Nazarene University, Cheonan, Korea
Korean deaf signers performed a number comparison task on pairs of Arabic digits. In their response times profiles, the expected magnitude effect was systematically modified by properties of number signs in Korean sign language in a culture-specific way (not observed in hearing and deaf Germans or hearing Chinese). We conclude that finger-based quantity representations are automatically activated even in simple tasks with symbolic input although this may be irrelevant and even detrimental for task performance. These finger-based numerical representations are accessed in addition to another, more basic quantity system which is evidenced by the magnitude effect. In sum, these results are inconsistent with models assuming only one single amodal representation of numerical quantity.
Introduction
Numerical cognition can be conceived as a distributed cognitive function, meaning that it requires interactive processing of information gained from both internal and external representations (Zhang and Norman, 1995; Zhang and Wang, 2005). For instance, when we have to compare two numbers regarding their numerical magnitude, we not only need to process information from internal representations (e.g., knowledge about the magnitude of the numbers), but also information from external representations (e.g., visuo-spatial properties of the symbols). In the present paper we explore the possibility that internal (i.e., mental) quantity representations are multimodal such that innate analog representations are complemented by representations based on different cultural tools (e.g., number words, Arabic numbers, finger-counting habits) which may affect performance even in simple numerical tasks. In the following, we will first shortly summarize evidence for innate analog quantity representations. Afterward, evidence for effects of culturally developed representations on numerical tasks will be reviewed. Finally, we will outline the rationale of the present study.
Innate Analog Quantity Representation
There is widespread agreement that humans share a basic internal representation of numerical quantity with higher vertebrates (Feigenson et al., 2004; Beran, 2007; Cantlon and Brannon, 2007; Agrillo et al., 2011). Using this representation, animals as well as human infants are able to decide which of two sets of objects is the numerically larger one (i.e., contains more elements) in a magnitude comparison task. Usually, performance in this kind of task is affected by the ubiquitous magnitude effect, i.e., response times (RT) and error rates increase with the numerical size of the operands involved (Restle, 1970; Brysbaert, 2005; Verguts et al., 2005; Dehaene, 2007). It has been suggested that the magnitude effect can be traced back to the spiking characteristics of specific number-sensitive neurons in prefrontal and parietal cortices, which respond increasingly diffuse to increasing numerical magnitude (Nieder, 2005). A related psychological effect is the so-called distance effect, which describes the observation that discriminating between two numbers gets easier (reflected by decreasing RT and error rates) as the numerical distance between the numbers increases. Both the magnitude and the distance effect have become hallmark effects associated with quantity processing and are addressed by virtually every model of numerical cognition. Although found in humans as well as non-human animals, it has been shown that both the effects of numerical magnitude and numerical distance decrease with education (Pica et al., 2004; Halberda and Feigenson, 2008). Decreasing magnitude and distance effects during the course of education have been attributed to an increasing degree of precision of the internal magnitude representation.
Cultural Tools of Quantity Representation
Improving precision of the human analog quantity representation during development is accompanied by the acquisition and use of culturally bequeathed number notations such as number words, Arabic digits, and finger-counting gestures (Pica et al., 2004; Halberda and Feigenson, 2008). How does the use of culturally developed number systems influence the innate analog quantity representation? The exact nature of this interaction is still under debate. Three different scenarios seem possible: first, the internal analog quantity representation, which is often described by the metaphor of a mental number line (Dehaene and Cohen, 1995; Dehaene, 2003), may be influenced by external representations such that it increases its acuity (Verguts and Fias, 2004; Dehaene, 2007) and/or adopts the base-10 structure of the Arabic number system (Nuerk et al., 2001, 2004a; Nuerk and Willmes, 2005; Verguts and De Moor, 2005; Moeller et al., 2011). Second, the inherited analog quantity representation may be replaced by a symbolic quantity representation. One proposal of this type assumes that the internal quantity representation is abstract and similar to the place-value system of the Arabic number system and most number word systems (McCloskey and Macaruso, 1995). Unfortunately, this model is silent about the nature of the transition from analog to symbolic representation and about the fate of the innate analog quantity representation.
Note that both accounts of semantic quantity representation mentioned so far (i.e., the analog mental number line and the abstract place-value system) assume that there is only one amodal representation of quantity employed across all types of stimuli and tasks (e.g., Libertus et al., 2007; Santens et al., 2009). With respect to the first account by Dehaene and Cohen (1995) it is true that the Triple-Code model proposes three different representational codes. However, only one of these three codes (i.e., the analog magnitude code) reflects a semantic representation of quantity. Input from the other two codes (i.e., visual Arabic or verbal) needs to be transcoded to the analog magnitude code to access quantity information. Even more evident is this central amodal quantity representation in the model by McCloskey (1992). The so-called Abstract Code model (McCloskey, 1992; McCloskey and Macaruso, 1995) proposes that its subsystems (comprehension, calculation, and response production) communicate through a single abstract semantic quantity code. The comprehension subsystem transforms different numerical inputs into the abstract code on which calculation and response generation subsequently operate. Access to this abstract code is necessarily required before any other numerical process is possible. In particular, the calculation subsystem operates only on this code. Finally, the production subsystem transcodes the abstract code into Arabic, written, or spoken verbal number formats again as required by the task at hand. Taken together both the Triple-Code model and the Abstract Code model assume a single amodal representation of quantity. In line with this, the dominant view in numerical cognition research claims that “robust evidence demonstrates that with or without language, number is represented abstractly – independently of perceptual features, dimensions, modality, and notation [as] in fact, this is the very definition of number.” (italics added, Cantlon et al., 2009, p. 332; see also Cohen Kadosh and Walsh, 2009 and invited commentaries for a comprehensive discussion of this point).
Nevertheless, this view is in contrast to a third type of models which assert that there is a multitude of semantic number representations, including internal analog and symbolic quantity representations, which are used depending on the type of stimuli and task at hand (Campbell and Clark, 1992; Campbell, 1994; Cohen Kadosh and Walsh, 2009). Typically, these models are rather vague, both in terms of developmental aspects and in specifying the exact interactions of the different internal representations assumed for a given task (although attempts have been made to address both issues, e.g., Cohen Kadosh and Walsh, 2009; Kucian and Kaufmann, 2009). Nevertheless, they seem easily ready to integrate finger-based quantity representations. Such finger-based representations have been assumed to play an important role at least for small quantities (Di Luca and Pesenti, 2011).
The behavioral impact of symbolic representations in numerical tasks has been described repeatedly. For instance, the base-10 structure of the Arabic number system and most number word systems (i.e., the most frequently used symbolic representations) is reflected in several numerical effects:
(i) The carry effect in mental addition: the influence of a carry operation on task performance is probably one of the most robust findings in multi-digit addition. Arithmetic problems requiring a carry operation, because the sum of the units is equal or larger than 10 (e.g., 47 + 18 = 65; unit sum 7 + 8 = 15), are usually associated with decreased performance (mirrored by larger RT and error rates) than addition problems not requiring a carry (e.g., 52 + 13 = 65; Ashcraft and Stazyk, 1981; Fürst and Hitch, 2000; Deschuyteneer et al., 2005; Kong et al., 2005; Imbo et al., 2007; Klein et al., 2010a,b).
(ii) The decade consistency effect in multiplication: multiplication errors are influenced by positional consistency, where consistency means that the error and the correct result share the same digit at the same place-value position (Campbell, 1994; Verguts and Fias, 2005a,b). For instance, the error 7 × 3 = 28 will be more likely than the error 7 × 3 = 14, because 28 and the correct result 21 share the same decade digit. Verguts and Fias(2005a,b) termed this finding neighborhood consistency: consistent neighbors share their decade digit with each other. Neighborhood consistency provides an alternative way to explain multiplication effects that were previously not associated with multi-digit structures, namely problem size-, five-, and tie-effects (see Verguts and Fias, 2005a,b, for details). The theoretically postulated consistency effect was demonstrated by Domahs et al. (2006) in a reanalysis of multiplication production data reported by Campbell (1997). Multiplication problems with many consistent neighbors tended to be less error-prone, but whenever an error occurred, it was more likely to be a consistent neighbor than an inconsistent one (see also Campbell et al., 2011). The consistency effect was replicated by Domahs et al. (2007) in an ERP study using a verification paradigm. Obviously, consistency effects cannot exist for single-digit numbers. Thus, these effects show that multiplication fact retrieval performance cannot be fully understood without taking into account structural properties of the symbolic format of input, output, and/or internal representation (i.e., multi-digit Arabic numbers or number words).
(iii) The unit-decade compatibility effect describes an aspect of multi-digit number magnitude processing performance in a magnitude comparison task. The effect is driven by the place-value structure of to-be-compared numbers. A number pair is termed unit-decade compatible whenever separate decade and unit digit comparisons lead to the same decision (as for the pair 42_57, 4 < 5, and 2 < 7) and incompatible when unit and decade comparisons lead to different decisions (47_62; 4 < 6, but 7 > 2). Since its discovery by Nuerk et al. (2001), several studies in children and adults have shown that incompatible number pairs are processed slower and with more errors than compatible pairs (Nuerk et al., 2002, 2004b, 2005).
In sum, in all the examples mentioned, behavioral traces have been observed which suggest that numerical representations are not perfectly smooth, but that there are decade breaks in the quantity representation. However, in all these cases, the base-10 structure was part of the external, i.e., stimulus representation (Arabic digits or number words) and potentially also of the putative internal quantity representation (which could be an abstract base-10 system as proposed by McCloskey and Macaruso, 1995), such that it is impossible to disentangle external from internal representational effects.
The Present Study
The present study aimed at investigating whether there is only one single amodal (analog or symbolic) internal quantity representation or rather several different, interacting internal quantity representations (Campbell and Clark, 1992; Campbell, 1994; Cohen Kadosh and Walsh, 2009). To address this question, we made use of peculiarities of culturally developed number representations (i.e., canonical finger-counting patterns) which are not part of the external stimulus representation employed in the task (Arabic numbers). It is important to note that finger-counting was not required in the current task neither for processing the stimuli nor for providing the response. With regard to finger-counting habits two things are important to the present study. First, canonical numeral finger configurations are shown to have a special status compared to non-canonical ones (Di Luca and Pesenti, 2008). Second, canonical configurations are highly diverse across cultures (Bender and Beller, 2011).
The present investigation is based on an approach successfully adopted by Domahs et al. (2010). In a number comparison task employing Arabic digits as input format, the authors found the magnitude effect (reflecting the analog quantity representation) to be modified by the number of Arabic digits, i.e., number pairs with different number of digits (8_10 and 9_11) were responded to faster than pairs with the same number of digits. Crucially, the magnitude effect was also modified by the number of hands involved in number signs, such that Arabic numbers associated with two-handed number signs yielded relatively long RTs. While the number of Arabic digits effect can in principle be related to properties of both external and internal representations, the number of hands effect can only be driven by internal representations as it is no feature of the input format (Arabic digits). Furthermore, the fact that the number of hands effect was only present in those cultural groups using two-handed number signs (hearing Germans and deaf German signers) but not in hearing Chinese, who use one-handed number signs in the relevant number range from 6 to 9 (see Figure 2), further supported the interpretation that hand-based internal number representations were activated, even though they were irrelevant and even detrimental to the task. Given that the analysis indicated specific slowing associated with two-handed number signs, Domahs et al. (2010) argued for an interpretation in terms of motor imagery involved to represent quantity in addition to some other (probably analog) quantity representation.
In the current study, we examined users of a different finger-counting system – Korean sign language (KSL). KSL involves some interesting properties which are neither part of the finger-counting systems previously investigated nor included in the Arabic digit system (see Figure 1):
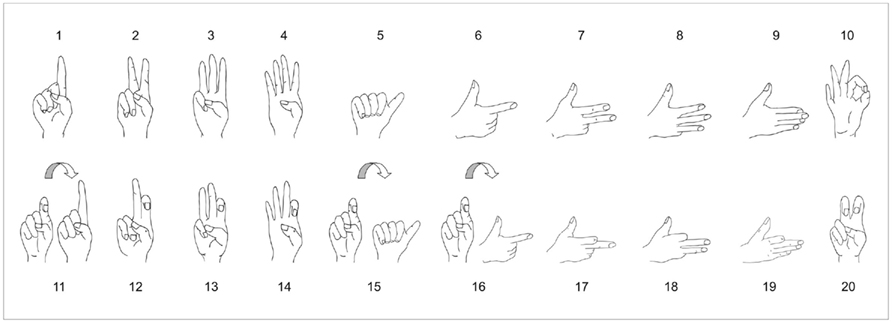
Figure 1. Finger-counting system in Korean Sign Language from the viewer’s perspective. Note that numbers 11, 15, and 16 are signed in a sequential movement of the same hand.
a) Similar to other finger-counting systems in which only one hand is used to represent numbers larger than 5, there is a break between transparent and symbolic quantity representation. This means that only representations of small numbers allow for a one-to-one correspondence between the fingers raised and the objects to be counted. However, in contrast to most of these systems, the transparency limit does not appear between 5 and 6 (see Figure 2 for the example of Chinese), but already between 4 and 5 in KSL number signs. Domahs et al. (2010) suggested that number comparison crossing this transparency limit may lead to a small but significant relative RT increase. Thus, we hypothesize that it may be more demanding to compare a pair of numbers, in which one number is represented transparently and one symbolically (i.e., 3_5 or 4_6 in KSL) than a pair of numbers where both items are either transparently or symbolically signed (i.e., all remaining number pairs).
b) In KSL numbers are signed with different hand orientations, i.e., the observer sees either the palm or the back of the hand. We hypothesized that the comparison of number pairs, where both numbers are signed in a different orientation (e.g., 4_6 or 18_20), may lead to prolonged RT as compared to the comparison of pairs with same hand orientation (e.g., 2_4 or 7_9).
c) Finally, some signs in KSL (11, 15, and 16) require a sequential movement of the same hand. This may lead to a relative RT increase for all comparisons between pairs which contain such a number.
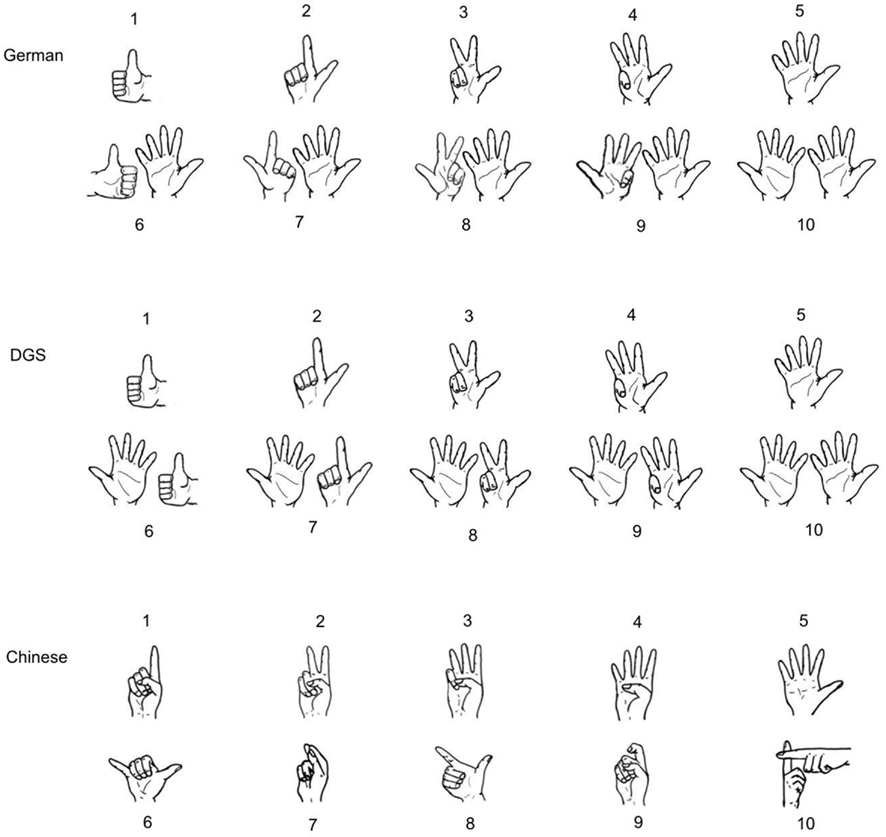
Figure 2. Finger-counting systems in German, German Sign Language (DGS), and Chinese (Domahs et al., 2010). Reprinted with permission.
In sum, using a simple number comparison task with pairs of Arabic digits, we expected to find (i) the standard magnitude effect, associated with the internal analog quantity representation. In line with findings reported by Domahs et al. (2010) we also expected (ii) a number of digits effect such that number pairs in which one number was represented by a single Arabic digit and the other by two Arabic digits (i.e., 8_10 and 9_11) should be responded to significantly faster than to be expected on the basis of their magnitude. This could be interpreted as an effect of the external stimulus representation. Crucially, we also expected to find (iii) influences of characteristic properties of the KSL number sign system (transparency limit effect, hand orientation effect, or sequential movement effect), which are not predicted by models assuming an amodal semantic quantity representation. Therefore, if such effects were observed in a culture-specific way, they would witness the multimodal nature of internal quantity representations.
Materials and Methods
Participants
Twenty-five Korean deaf signers, enrolled as undergraduate students at the Korea Nazarene University, Cheonan, took part in the experiment. Data sets of two participants had to be excluded from analyses due to failure in data recording. Mean age of the remaining 23 (11 females) participants was 22.1 years (SD = 1.6). On average, they have received 14.4 (1.1) years of formal education. All were right-handed according to their own disclosure, had normal or corrected-to normal vision and reported no mathematical deficits. All participants used KSL as their primary language although mean age of acquisition of KSL was relatively late (mean = 9.0, SD = 4.4). Nevertheless, participants’ counting habits were evaluated prior to the experiment confirming that all used the KGS finger-counting system depicted in Figure 1. All participants gave their informed consent to take part in the study.
Stimuli
The same stimulus set was used as described by Domahs et al. (2010). All number pairs with a distance of 2 within the number range from 1 to 20 were shown in both orders (i.e., 1_3 to 18_20 and 3_1 to 20_18, respectively). Stimuli were presented in central position as Arabic digits in black Arial 60 pt font against a white background. Both numbers were presented in the same line separated by seven blanks.
Procedure
Instructions were given in written Korean (Hangul) and, additionally, in KSL. Participants were instructed to answer as fast and accurately as possible. Half of the participants started with the instruction to indicate the smaller number by a corresponding button press while the other half was instructed to indicate the larger number. Response keys were the “S” key and the “L” key on a standard keyboard. After the first half of the experiment, response assignments were reversed. For each response assignment, each number pair was presented five times per order (i.e., five times 4_6 and five times 6_4). Thus, the presentation of 36 number pairs × 5 repetitions × 2 response assignments led to a total of 360 experimental trials separated in five blocks per response assignment, each block including all 36 number pairs in randomized order. Each response assignment was preceded by an additional training block of all 36 number pairs. Training results were not included in the analyses.
Each trial started with a blank screen (500 ms), followed by the presentation of a fixation cross in central position (200 ms) and another blank screen (200 ms). Then, the number pair was presented until one of the response buttons was pressed or the time limit of 2000 ms was reached. Trials were initiated in a self-paced manner, i.e., participants pressed the space-bar on the keyboard to proceed to the next trial.
Analyses
There was no speed–accuracy trade-off as indicated by a non-reliable negative correlation between mean RT and error rate (r = −0.14, p = 0.54). Incorrect responses or RT falling outside the interval of ±2.5 SD from the individual mean were excluded from the analyses. This resulted in a loss of 7.5% of data points.
The influence of the structure of different external and hypothesized internal representations on symbolic number processing was assessed by a linear mixed-effects regression analysis on mean RT per number pair. The following measures of external and internal representations were entered: first, a variable coding the presence or absence of a different number of Arabic digits (coded as −1 for pairs 8_10 and 9_11 and +1 for other pairs) was included to represent characteristics of the Arabic stimulus format. Second, numerical magnitude [i.e., the natural logarithm (ln) of the mean of each number pair] and parity (coded as +1 for odd and −1 for even pairs) were used as predictors reflecting basic semantic number representations. Finally, the following predictors were included, representing potential hand-based internal representations: transparency limit (coded +1 for pairs where one number is represented transparently and one number symbolically in KSL, i.e., 3_5 and 4_6, and coded −1 for other pairs), hand orientation (coded +1 for pairs with different hand orientation in KSL, i.e., 4_6, 5_7, 8_10, 9_11, 14_16, 15_17, 18_20, and −1 for other pairs), and movement sequence (coded +1 for pairs where at least one number is signed in a one-handed movement sequence in KSL, i.e., 9_11, 11_13, 13_15, 14_16, 15_17, 16_18, and −1 for other pairs). The contribution of these variables to the goodness of fit of the model was evaluated within the linear-mixed-effects model (lme) framework, using the lme4 package (Bates, 2007) in the R system for statistical computing (R Development Core Team, 2006). Both participants and number pairs were treated as random factors.
Moreover, intergroup differences comparing our present data of deaf Korean signers with data from participant groups (hearing Germans, deaf German signers, and hearing Chinese participants) previously reported by Domahs et al. (2010) were evaluated using one-way ANOVAs.
Finally, a stepwise discriminant analysis was conducted over mean RTs for all number pairs (1_3 to 18_20) to investigate how well the four groups of participants could be differentiated. Using the leave-one-out procedure as a cross-validation method to prevent underestimation of error classification probabilities, the best discriminating number pairs were used to classify individual RT-profiles into one of the four cultural groups.
Results
Variables Influencing Symbolic Number Comparison in KSL Participants
The resulting final model of the linear mixed-effects regression analysis is presented in Table 1. Individual participants varied substantially, as did individual number pairs, which was confirmed by log-likelihood tests for both random effects. As can be seen in Table 1, the differing number of Arabic digits, numerical magnitude as well as hand orientation turned out as significant predictors (t > 2), while all other effects (parity, transparency limit, and movement sequence failed to explain significant amounts of additional variance. Specifically, the comparison of two Arabic numbers became relatively slower with increasing numerical magnitude and when KSL hand orientation differed for the to-be-compared numbers, whereas RT became relatively faster when a one-digit Arabic number had to-be-compared with a two-digit Arabic number (see Figure 3).
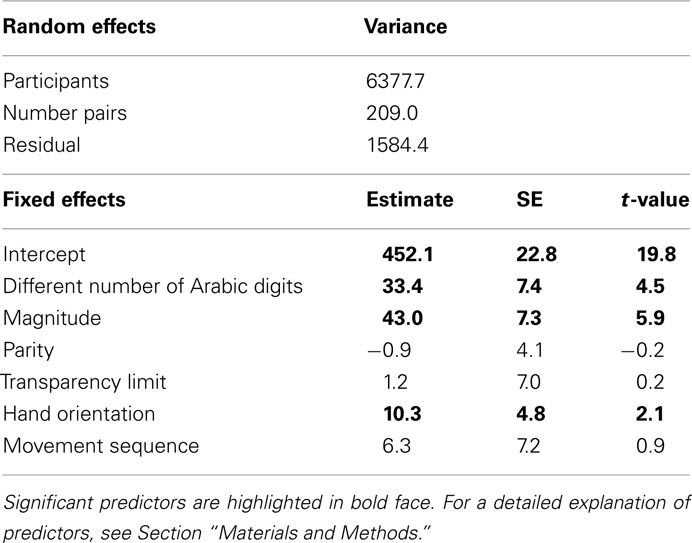
Table 1. Regression coefficients with associated SE and t-values from the analysis of mean RTs from Korean deaf signers.
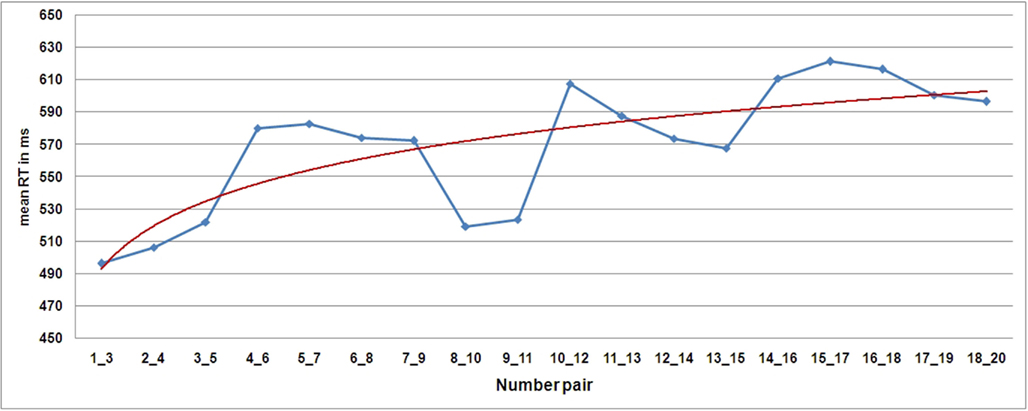
Figure 3. Mean reaction times per number pair (blue line) and logarithmic fitting (red line) of KSL participants (n = 23). For a description of the fitting procedure see Domahs et al. (2010).
Cross-Cultural Comparisons
With respect to global mean RT and RT increase (slope of a logarithmic fitting curve), KSL participants did not differ significantly from hearing Germans, deaf German signers, and hearing Chinese participants as reported by Domahs et al. (2010): mean RT was 566 ms (SD = 79 ms) for Korean deaf signers, 617 ms (104 ms) for hearing Germans, 594 ms (99 ms) for German deaf signers, and 569 ms (80 ms) for hearing Chinese participants [F(3, 95) = 1.69, p = 0.17]. Mean slope was 0.081 (SD = 0.044) for Korean deaf signers, 0.085 (0.034) for hearing Germans, 0.085 (0.026) for German deaf signers, and 0.094 (0.025) for hearing Chinese participants [F(3, 95) < 1].
However, these globally similar RT patterns were modulated differentially by local effects, as evidenced by different patterns of residuals from individual logarithmic fittings (see Figure 4; fitting procedure described in detail in Domahs et al., 2010). These local effects seem to be culture-specific. Interestingly, different hand orientation, a variable significantly contributing to the variance explained by the mixed-effects regression model on mean RTs per number pair and KSL participant (see above), did not improve regression models for hearing Germans, deaf German signers, or hearing Chinese. Note that this is the expected result in case this variable indeed reflects specific properties of KSL finger-counting (not present in the other systems) rather than some artifact (which may also be existent in the other cultural groups).
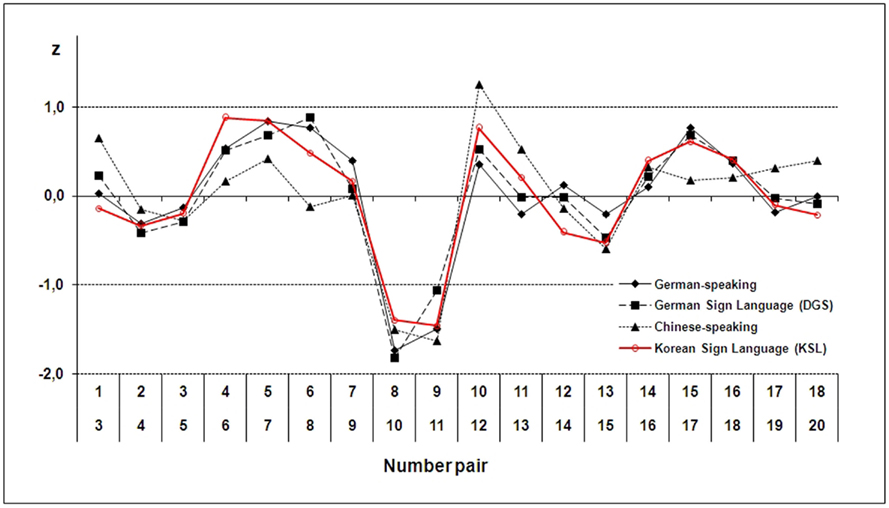
Figure 4. Standardized residuals for Korean deaf signers (red line) and three different participant groups performing the same task. Details on hearing German, deaf German, and hearing Chinese participants and the standardization procedure are reported by Domahs et al. (2010).
Finally, in a stepwise linear discriminant analysis a two-dimensional discriminant function space allowed for the significant differentiation of the four groups of participants (see Table 2; Figure 5). The variables selected for inclusion in the discriminant function space were mean RTs for the four number pairs 10_12, 8_10, 6_8, and 11_13. Using these four best discriminating number pairs, it was possible to classify a total of 57.6% of all cases correctly into one of the four cultural groups (using the leave-one-out procedure as a cross-validation procedure to prevent underestimation of error classification probabilities). Performance was best for deaf Korean signers (91.3% correctly classified) and Chinese participants (74.1% correctly classified), while RT-profiles of both German groups of participants lead to a large degree of overlap between the latter two groups (see Table 2).

Table 2. Classification of cases based on the stepwise linear discriminant function analysis using a leaving-one-out cross-validation procedure (see also Figure 5).
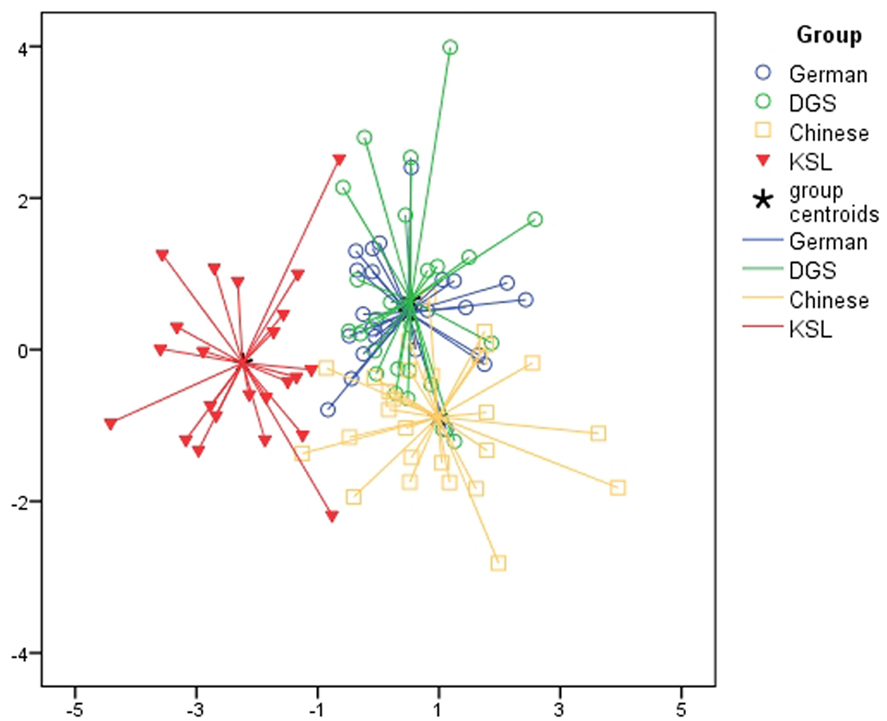
Figure 5. Combined groups plot of the results from a stepwise linear discriminant analysis on mean RT per number pair and participant (see also Table 2) using the first two dimensions of the discriminant functions space. Note that hearing Germans and deaf German signers, who have the least discriminable RT-profiles in a magnitude comparison task with Arabic digits, also have very similar finger-counting systems (see Figure 2).
We can only speculate why these four number pairs are able to discriminate between the four cultural groups. For instance, the residuals for number pair 6_8 diverge between both German groups on the one hand and Korean as well as Chinese participants on the other – possibly because for Germans 6 and 8 require two-handed finger patterns while for Korean signers both numbers are represented in the same orientation and both Asian groups can represent the individual numbers of these pairs on one hand, respectively. With respect to number pair 8_10 all four groups showed a strong effect of different number of Arabic digits, resulting in large negative residuals. However, this effect seems to be somewhat less pronounced for Chinese and Korean participants, but possibly for different reasons: for Chinese, the number sign for 10 is motorically complex, requiring a coordinated movement of both hands. For Korean signers, the signs representing 8 and 10 have different hand orientation, also causing some additional representational costs. As can be seen in the latter example, the interpretation of residuals may become particularly difficult, if different effects interfere.
Discussion
In a simple number comparison task performed by educated adult participants, we replicated the standard numerical magnitude effect, probably reflecting properties of the analog quantity representation. In line with previous findings (Domahs et al., 2010), we also observed a number of Arabic digits effect, i.e., a relative RT advantage for those number pairs comparing a single-digit and a two-digit number (8_10 and 9_11). Obviously, this effect reflects properties of the external stimulus representation (Arabic digits) on mental number processing. Both the magnitude effect and the number of digits effect have already been described for other groups of participants and do not seem to be culture-specific (e.g., Domahs et al., 2010). This is not unexpected as it is plausible to assume that both the internal analog magnitude representation and the processing of externally presented Arabic digits should in general not be modulated by culture. Crucially, we also found evidence for an influence of the specific properties of the finger-counting system used by deaf Korean signers reflecting culture-specific differences in number processing. In particular, the coding based on KSL hand orientation was a significant predictor of performance for KSL participants. Importantly, this indication of culture-specificity was further corroborated by the fact that the predictor hand orientation did not explain any additional variance when included in regression models for the other three groups (hearing and deaf Germans, hearing Chinese).
We used a simple number comparison task. This task does not involve any overt finger-counting. Furthermore, Arabic digits were used as input, which do not show characteristic properties of KSL finger-counting. Nevertheless, using the RT-profiles we were able to discriminate between cultural groups with different finger-counting habits (deaf Korean signers vs. hearing Chinese vs. German signers and hearing Germans), but failed to discriminate between groups with similar finger-counting systems (hearing Germans vs. deaf German signers).
Taken together, these results are inconsistent with theoretical approaches assuming only one single amodal semantic representation of number magnitude. Although models of this type might in principle be adapted to account for hand-based effects in numerical cognition, at present it seems unclear, how characteristic properties of finger-counting habits could be integrated in an analog quantity representation (Dehaene and Cohen, 1995; Dehaene, 2003) or an abstract base-10 based quantity representation as proposed by McCloskey and Macaruso (1995). Approaches which assume multimodal semantic representations (Campbell and Clark, 1992; Campbell, 1994; Cohen Kadosh and Walsh, 2009), on the other hand, could easily integrate a hand-based representation of quantity, although typically, this has not been included yet (e.g., Campbell and Epp, 2004). However, at present these models are grossly underspecified. It still remains to be explored which representation has to be activated in which task and to which extend. However, recent evidence suggests that finger-based representations are not only used in simple number processing but also in calculation – in children (Domahs et al., 2008) or in cases of persisting dyscalculia (Kaufmann et al., 2011) as well as in healthy adult participants (Klein et al., 2011). Thus, models of numerical cognition should incorporate the option that finger-based representations are accessed – at least concomitantly – in simple number processing and calculation tasks even if the input is in a different format and finger-based representations are not the dominant input modality for the task at hand. This has previously been suggested by Di Luca and Pesenti (2011) who proposed to consider finger-numeral representations as a fourth type of representation in the Triple-Code model originally proposed by Dehaene and Cohen (1995).
It should be noted that we do not claim that all of the systematic variance can be explained by finger-based numerical representations. Rather, it seems likely that other internal representations may be involved as well. These may include number word systems, representations based on calculation machines (e.g., abacus), regular dot patterns as found on dice, and others. However, finger-counting habits seem to be an important predictor in our data as they can predict locus (i.e., affected number pairs) and direction (RT increase or decrease) of the residuals in a culture-specific way (i.e., corresponding to the respective finger-counting habits). The fact that we observed a relative RT increase for number pairs associated with different hand orientations further supports the motor generation hypothesis proposed by Domahs et al. (2010): motor imagery for motorically more complex number signs (e.g., two-handed signs in German and DGS or reorientation of hand posture in KSL signs) leads to increased cognitive processing costs even for abstract symbolic input (Arabic digits). In contrast, we did not find evidence for the assumption that a break between transparent and symbolic finger-counting patterns affects behavior in the same task. This seems to be in line with the assumption that – at least during acquisition – number gestures are not analyzed according to their transparency (Nicoladis et al., 2011). Moreover, one could speculate whether motorical effects (like hand orientation) have more behavioral impact than purely semantic effects (like transparency limit). Yet, at the present state, a detailed account of what kind of motor complexity should affect performance to which extent is still lacking. Thus, further research is needed to disentangle why the motorical effect of hand orientation was significant in the current data while another motorical effect, i.e., the effect of movement sequence, was not.
In sum, our results support the assumption that educated adults activate some kind of internal finger-or hand-based numerical representation even in a simple task with purely symbolic input. This representation seems to be evoked automatically, even though it can have detrimental effects on the task to be solved. Consequently, our results corroborate the idea of embodied numerosity representations and are inconsistent with amodal models of quantity representation.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was supported by funding from the German Federal Ministry of Education and Research (BMBF grant KOR 10/A06). We thank Seri Min for her valuable help in organization and translation, Stefan Huber for his help with the fitting procedure, as well as Stefanie Jung for creating the line drawings.
References
Agrillo, C., Piffer, L., and Bisazza, A. (2011). Number versus continuous quantity in numerosity judgments by fish. Cognition 119, 281–287.
Ashcraft, M. H., and Stazyk, E. H. (1981). Mental addition: a test of three verification models. Mem. Cognit. 9, 185–196.
Bender, A., and Beller, S. (2011). Fingers as a tool for counting – naturally fixed or culturally flexible? Front. Psychol. 2:256. doi: 10.3389/fpsyg.2011.00256
Beran, M. J. (2007). Capuchin monkeys (Cebus apella) succeed in a test of quantity conservation. Anim. Cogn. 11, 109–116.
Brysbaert, M. (2005). “Number recognition in different formats,” in Handbook of Mathematical Cognition, ed. J. I. D. Campbell (New York, NY: Taylor & Francis), 23–42.
Campbell, J. I. D. (1997). On the relation between skilled performance of simple division and multiplication. J. Exp. Psychol. Learn. Mem. Cogn. 23, 1140–1159.
Campbell, J. I. D., and Clark, J. M. (1992). “Cognitive number processing: an encoding-complex perspective,” in The Nature and Origins of Mathematical Skills, ed. J. I. D. Campbell (Amsterdam: Elsevier Science), 457–491.
Campbell, J. I. D., Dowd, R. R., Frick, J. M., McCallum, K. N., and Metcalfe, A. W. S. (2011). Neighborhood consistency and memory for number facts. Mem. Cognit. 39, 884–893.
Campbell, J. I. D., and Epp, L. J. (2004). An encoding-complex approach to numerical cognition in Chinese-English bilinguals. Can. J. Exp. Psychol. 58, 229–244.
Cantlon, J. F., and Brannon, E. M. (2007). Basic math in monkeys and college students. PLoS Biol. 5, e328. doi: 10.1371/journal.pbio.0050328
Cantlon, J. F., Cordes, S., Libertus, M. E., and Brannon, E. M. (2009). Numerical abstraction: it ain’t broke. Behav. Brain Sci. 32, 331–332.
Cohen Kadosh, R., and Walsh, V. (2009). Numerical representation in the parietal lobes: abstract or not abstract? Behav. Brain Sci. 32, 313–328.
Dehaene, S. (2003). The neural basis of the Weber-Fechner law: a logarithmic mental number line. Trends Cogn. Sci. 7, 145–147.
Dehaene, S. (2007). “Symbols and quantities in parietal cortex: elements of a mathematical theory of number representation and manipulation,” in Sensorimotor Foundations of Higher Cognition. Attention and performance, Vol. XXII, eds P. Haggard, Y. Rossetti, and M. Kawato (Cambridge: Harvard University Press).
Dehaene, S., and Cohen, L. (1995). Towards an anatomical and functional model of number processing. Math. Cogn. 1, 83–120.
Deschuyteneer, M., De Rammelaere, S., and Fias, W. (2005). The addition of two-digit numbers: exploring carry vs. no-carry problems. Psychol. Sci. 47, 74–83.
Di Luca, S., and Pesenti, M. (2008). Masked priming effect with canonical finger numeral configurations. Exp. Brain Res. 185, 27–39.
Di Luca, S., and Pesenti, M. (2011). Finger numeral representations: more than just another symbolic code. Front. Psychol. 2:272. doi: 10.3389/fpsyg.2011.00272
Domahs, F., Delazer, M., and Nuerk, H.-C. (2006). What makes multiplication facts difficult – problem size or neighborhood consistency? Exp. Psychol. 53, 275–282.
Domahs, F., Domahs, U., Schlesewsky, M., Ratinckx, E., Verguts, T., Willmes, K., and Nuerk, H.-C. (2007). Neighborhood consistency in mental arithmetic: behavioral and ERP evidence. Behav. Brain Funct. 3, 66.
Domahs, F., Krinzinger, H., and Willmes, K. (2008). Mind the gap between both hands: evidence for internal finger-based number representations in children’s mental calculation. Cortex 44, 359–367.
Domahs, F., Moeller, K., Huber, S., Willmes, K., and Nuerk, H.-C. (2010). Embodied numerosity: implicit hand-based representations influence symbolic number processing across cultures. Cognition 116, 251–266.
Feigenson, L., Dehaene, S., and Spelke, E. (2004). Core systems of number. Trends Cogn. Sci. (Regul. Ed.) 8, 307–314.
Fürst, A. J., and Hitch, G. J. (2000). Separate roles for executive and phonological components of working memory in mental arithmetic. Mem. Cognit. 28, 774–782.
Halberda, J., and Feigenson, L. (2008). Developmental change in the acuity of the “number sense”: the approximate number system in 3-, 4-, 5-, and 6-year-olds and adults. Dev. Psychol. 44, 1457–1465.
Imbo, I., Vandierendonck, A., and De Rammelaere, S. (2007). The role of working memory in the carry operation of mental arithmetic: Number and value of the carry. Q. J. Exp. Psychol. 60, 708–731.
Kaufmann, L., Pixner, S., and Göbel, S. M. (2011). Finger usage and arithmetic in adults with math difficulties: evidence from a case report. Front. Psychol. 2:254. doi: 10.3389/fpsyg.2011.00254
Klein, E., Moeller, K., Dressel, K., Domahs, F., Wood, G., Willmes, K., and Nuerk, H.-C. (2010a). To carry or not to carry – is this the question? Disentangling the carry effect in multi-digit addition. Acta Psychol. (Amst) 135, 67–76.
Klein, E., Willmes, K., Dressel, K., Domahs, F., Wood, G., Nuerk, H.-C., and Moeller, K. (2010b). Categorical and continuous – disentangling the neural correlates of the carry effect in multi-digit addition. Behav. Brain Funct. 6, 70.
Klein, E., Moeller, K., Willmes, K., Nuerk, H.-C., and Domahs, F. (2011). The influence of implicit hand-based representations on mental arithmetic. Front. Psychol. 2:197. doi: 10.3389/fpsyg.2011.00197
Kong, J., Wang, C., Kwong, K., Vangel, M., Chua, E., and Gollub, R. (2005). The neural substrate of arithmetic operations and procedure complexity. Cogn. Brain Res. 22, 397–405.
Kucian, K., and Kaufmann, L. (2009). A developmental model of number representation. Behav. Brain Sci. 32, 340–341.
Libertus, M., Woldorff, M., and Brannon, E. M. (2007). Electrophysiological evidence for notation independence in numerical processing. Behav. Brain Funct. 3, 1.
McCloskey, M. (1992). Cognitive mechanisms in numerical processing: evidence from acquired dyscalculia. Cognition 44, 107–157.
McCloskey, M., and Macaruso, P. (1995). Representing and using numerical information. Am. Psychol. 50, 351–363.
Moeller, K., Huber, S., Nuerk, H.-C., and Willmes, K. (2011). Two-digit number processing: holistic, decomposed or hybrid? A computational modelling approach. Psychol. Res. 75, 290–306.
Nicoladis, E., Pika, S., and Marentette, P. (2011). Are number gestures easier than number words for preschoolers? Cogn. Dev. 25, 247–261.
Nieder, A. (2005). Counting on neurons: the neurobiology of numerical competence. Nat. Rev. Neurosci. 6, 177–190.
Nuerk, H.-C., Kaufmann, L., Zoppoth, S., and Willmes, K. (2004a). On the development of the mental number line: more, less, or never holistic with increasing age? Dev. Psychol. 40, 1199–1211.
Nuerk, H.-C., Weger, U., and Willmes, K. (2004b). On the perceptual generality of the unit-decadecompatibility effect. Exp. Psychol. 51, 72–79.
Nuerk, H.-C., Weger, U., and Willmes, K. (2001). Decade breaks in the mental number line? Putting the tens and units back in different bins. Cognition 82, B25–B33.
Nuerk, H.-C., Weger, U., and Willmes, K. (2005). Language effects in magnitude comparison: small, but not irrelevant. Brain Lang. 92, 262–277.
Nuerk, H.-C., Weger, U., and Willmes, K. (2002). A unit-decade compatibility effect in German number words. Curr. Psychol. Lett. Behav. Brain Cogn. 7, 19–38.
Nuerk, H.-C., and Willmes, K. (2005). On the magnitude representation of two-digit numbers. Psychol. Sci. 47, 52–72.
Pica, P., Lemer, C., Izard, W., and Dehaene, S. (2004). Exact and approximate arithmetic in an Amazonian indigene group. Science 306, 499–503.
R Development Core Team. (2006). R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing.
Santens, S., Fias, W., and Verguts, T. (2009). Abstract representations of number: what interactions with number form do not prove and priming effects do. Behav. Brain Sci. 32, 351–352.
Verguts, T., and Fias, W. (2004). Representation of number in animals and humans: a neural model. J. Cogn. Neurosci. 16, 1493–1504.
Verguts, T., and Fias, W. (2005a). Neighborhood effects in mental arithmetic. Psychol. Sci. 47, 133–140.
Verguts, T., and Fias, W. (2005b). Interacting neighbors: a connectionist model of retrieval in single-digit multiplication. Mem. Cognit. 33, 1–16.
Verguts, T., Fias, W., and Stevens, M. (2005). A model of exact small-number representation. Psychon. Bull. Rev. 12, 66–80.
Zhang, J., and Norman, D. A. (1995). A representational analysis of numeration systems. Cognition 57, 271–295.
Keywords: finger-counting, number comparison, magnitude effect, numerical size, Arabic digits, embodiment, hand posture orientation, motor imagery
Citation: Domahs F, Klein E, Moeller K, Nuerk H-C, Yoon B-C and Willmes K (2012) Multimodal semantic quantity representations: further evidence from Korean sign language. Front. Psychology 2:389. doi: 10.3389/fpsyg.2011.00389
Received: 28 July 2011; Accepted: 11 December 2011;
Published online: 04 January 2012.
Edited by:
Liane Kaufmann, Private University for Health Sciences, AustriaReviewed by:
Max Louwerse, University of Memphis, USARoi Cohen Kadosh, University College London, UK
Oliver Lindemann, Donders Institute for Brain, Cognition and Behaviour, Netherlands
Copyright: © 2012 Domahs, Klein, Moeller, Nuerk, Yoon and Willmes. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Frank Domahs, Lehr und Forschungsgebiet Neuropsychologie, Universitätsklinikum der RWTH Aachen, Pauwelsstr. 30, D-52074 Aachen, Germany. e-mail:ZG9tYWhzQG5ldXJvcHN5Y2gucnd0aC1hYWNoZW4uZGU=





