- 1 Faculty of Social Sciences, Radboud University Nijmegen, Nijmegen, Netherlands
- 2 Department of Methods and Statistics, Utrecht University, Utrecht, Netherlands
- 3 Optentia Research Program, Faculty of Humanities, North-West University, Vanderbijlpark, South Africa
- 4 Department of Methodology and Statistics, Tilburg University, Tilburg, Netherlands
In the present article we illustrate a Bayesian method of evaluating informative hypotheses for regression models. Our main aim is to make this method accessible to psychological researchers without a mathematical or Bayesian background. The use of informative hypotheses is illustrated using two datasets from psychological research. In addition, we analyze generated datasets with manipulated differences in effect size to investigate how Bayesian hypothesis evaluation performs when the magnitude of an effect changes. After reading this article the reader is able to evaluate his or her own informative hypotheses.
The data-analysis in most psychological research has been dominated by null hypothesis testing for decades. The evaluation of null hypotheses is usually combined with p-values that give a point-probability of obtaining a certain test statistic under the null distribution. For example, the probability of finding a difference in sample means when μ1 − μ2 is zero in the population. Despite the popularity of null hypothesis testing there have been some objections to the use of null hypotheses (Berger, 1985; Cohen, 1994; Krueger, 2001; Wagenmakers, 2007; Van de Schoot and Strohmeier, 2011; Van de Schoot et al., 2011a).
One often encountered objection is that the amount of information that one null hypothesis provides is usually nil (Cohen, 1994). Imagine that a researcher wants to predict adult IQ-scores by height, age and IQ-score as a child. H0 would state that βheight = βage = βIQ child = 0. Rejection of this H0 would tell us that something is going on at best. It does not tell us which predictors are related to IQ-score, nor does it indicate the magnitude or direction of the effect(s). As a consequence the researcher needs follow-up tests to establish a solid predictor model.
An issue in this example is that the null hypothesis is not the scenario that the researcher was interested in to begin with. From a theoretical point of view, a person’s height is an absurd predictor for adult IQ-score. Put more scientifically, there is no previous research or body of knowledge that would lead us to expect a meaningful relation between height and IQ-score. Before having seen any data, we already know that height is less likely to be a predictor of IQ-score than age and child IQ are. Unfortunately this background knowledge can not be included in a null hypothesis.
The researcher might have even more specific expectations which are reflected by inequality constraints between the parameters of interest. For example, the researcher may expect that child IQ is the strongest predictor of IQ-score in adult life: βheight = 0 < βage < βchild IQ. We call this inequality constrained hypothesis an informative hypothesis and it is denoted by the abbreviation Hi. Hi is the hypothesis that the researcher truly wants to test and it clearly does not resemble the null hypothesis. Klugkist et al. (2011) showed that null hypotheses often do not reflect what the social scientist really wants to test (Van de Schoot et al., 2011c). Instead, they argue, the researcher is interested in hypotheses that impose constraints upon parameters such as Hi. From now on we will call these informative hypotheses (Hoijtink, 2012).
There are various advantages to the use of informative hypotheses. First, it allows researchers to include background knowledge in the hypothesis and directly confront this background knowledge with empirical data. The use of inequality constraints makes hypotheses sophisticated and specific, unlike the null hypothesis which has a fixed form for every research endeavor. Using background knowledge will also add to the cumulative character of science; one can build upon previous research by including earlier empirical findings in new hypotheses. The use of informative hypotheses largely eliminates the multiple testing problem that occurs when one needs follow-up tests to unravel an omnibus effect. Taken together, informative hypotheses provide a solution to many of the limitations and problems that are inherent to null hypothesis testing.
The reader may have noted that some forms of informative hypotheses can be tested by use of contrasts. For example Rosenthal et al. (2000) illustrated several ways of formulating different types of contrasts reflecting background knowledge. Silvapulle et al. (2002) developed a two-step procedure for using null hypothesis testing to test one single informative hypothesis for an analysis of variance, see also Silvapulle and Sen (2004). In the first step the informative hypothesis serves the role as the alternative hypothesis and in the second step it serves the role as the null hypothesis. Van de Schoot and Strohmeier, 2011; see also, Van de Schoot et al., 2010) extended their procedure for structural equation modeling. To conclude, if one wishes to evaluate one single informative hypothesis, contrast testing can easily be used.
We acknowledge that contrast testing is a flexible way to evaluate directed expectations and that it can partly eliminate multiple testing problems as well. However, contrast testing still relies on the classical frequentist philosophy and the (ritualistic) use of p-values, against which many cases have been made (Cohen, 1994; Krueger, 2001; Wagenmakers, 2007; Van de Schoot et al., 2011a,c). Moreover, contrast testing only allows the evaluation of one single hypothesis at a time (Van de Schoot et al., 2011a). This may prove problematic when a researcher is interested in a set of hypotheses or wants to engage in model selection. For example, the adult-IQ researcher from the previous example might have a competing hypothesis which states that not child IQ but age is the strongest predictor of adult IQ. The researcher, then, does not want to assess the hypotheses one by one but intends to compare them in order to select the one that best fits the data. We get back to the topic of contrast testing in the discussion when the reader has gained familiarity with Bayesian hypothesis evaluation.
In the present article we introduce the reader to a method for the Bayesian evaluation of informative hypotheses. This method abandons point-probability estimates and null distributions entirely and is both computationally and philosophically distinct from the frequentist framework (Klugkist et al., 2005; Hoijtink et al., 2008; Van de Schoot et al., 2011a; Hoijtink, 2012). Our main aim is to make the Bayesian evaluation of informative hypotheses insightful and accessible to the reader. We do not expect the reader to have any mathematical or Bayesian background and avoid formulas and technicalities as much as possible. Instead, we provide the reader with textual and intuitive illustrations of Bayesian hypothesis evaluation and demonstrate the use of a free software package that performs Bayesian calculations without going into detail1, where many other resources are available for the interested reader as well.
The outline of the present article is as follows. We will first introduce two datasets from existing psychological research and formulate informative hypotheses. The purpose of these examples is to illustrate the application of the proposed method. After having introduced the datasets we provide a brief intermezzo where we explain the key concepts of Bayesian statistics intuitively. When the reader has gained some familiarity with those key concepts we move on to the Bayesian analyses of the datasets and spend some time interpreting the output. We will then move on to seven generated datasets where we manipulated the effect size to demonstrate how the Bayesian output is affected by differences in effect size. We will introduce these datasets, evaluate informative hypotheses for every dataset and discuss what we have learned about the influence of effect size. We conclude with a discussion of the merits and pitfalls of Bayesian hypothesis evaluation and discuss the value of our method for psychological researchers.
Introducing the Datasets
We believe applying our technique to existing psychological research is a convenient way to illustrate the method. Before doing so we introduce the datasets2 by explaining the variables and formulating informative hypotheses3.
Dataset 1: Predicting Overconsumption from Eating Behavior
The first research example stems from research on overconsumption by Van Strien et al. (2009). Amongst many other variables, Van Strien et al. (2009) assessed emotional and restrained eating behavior with two sub-scales of the DEBQ, short for Dutch Eating Behavior Questionnaire. An item used to assess emotional eating was: “Do you have a desire to eat when you are irritated?” while “Do you try to eat less at mealtimes than you would like to?” was used to measure restrained eating. The scales had a Cronbach’s alpha of 0.96 and 0.92 respectively (Cronbach, 1951).
Both types of eating behavior were expected to be related to overconsumption, which was assessed by asking participants to what degree they eat too much. The development of a model for overconsumption can help psychologists understand how emotion and self-imposed restraints affect people’s eating habits and health. The regression equation for such a model is given by
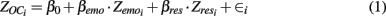
where βemo and βres are the regression weight of emotional and restrained eating on overconsumption. The i-subscript indicates the subject number and implies that participants can have different scores on the predictors, overconsumption, and the error in prediction. Z indicates that all variables were standardized. This standardization delivers β weights instead of b weights, making the regression coefficients independent of the scale of the predictor. This allows us to compare the beta weights of emotional and restrained eating even if they have different ranges.
The researchers’ expectations revolved around the beta weights in equation (1). First, they expected

stating that both emotional and restrained eating are positively related to overconsumption, Further, the researchers expected that

stating that emotional eating is the strongest predictor of the two. The rationale behind this is that emotional eating directly leads to overconsumption. Restrained eating first inhibits food intake and only then rebounds, causing overconsumption. Adding hypotheses H1 and H2 together leads to the more specific hypothesis that

The researchers evaluated null hypotheses of the form H0 = βemo = βres = 0 in a multiple hierarchical regression together with many more variables and complex paths not discussed here. They found that both types of eating behavior were indeed related to overconsumption and rejected H04. In the current paper we show how the hypotheses stated above could have been evaluated directly. We will also compare the three informative hypotheses to determine which one fits the data best.
Dataset 2: Work-Family Interference
The second example we use comes from the field of occupational psychology. Geurts et al. (2009) investigated the effects of employes’ contractual hours and overtime hours on family life. Contractual hours (contr) and overtime hours (over) were assessed by asking participants to give an average estimate of working hours. Work-family interference (WFI) was assessed with a single-item Likert-scale assessed “To what degree do you neglect family activities because of your job?”. A model surrounding work-family interference could be interesting to a variety of experts ranging from family oriented psychologists to employer advisors and has the form
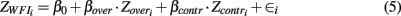
with the notation being comparable to that of equation (1). Again, the researchers had expectations about the parameter values and direction of effects. The following hypotheses accompany the original research expectations:

which states that both predictors are related to WFI because time spent on the work-floor cannot be spent at home. More specifically, the researcher expected that

stating that overtime hours are more important in predicting work-family interference than contractual hours are. The argument here is that overtime hours are quite an uncertain factor in an employes’ life and thus tend to interfere with planned family events to a higher degree than scheduled contractual hours do. Putting together H1 and H2 provides us with the more constrained hypothesis

Again the original researchers used null hypothesis testing and found that both predictors were significantly related to work-family interference. We will illustrate how the three hypotheses can be evaluated directly and compared them to one another by means of Bayesian statistics.
We will describe the analysis of both datasets after a brief intermezzo where we introduce the key concepts of Bayesian hypothesis evaluation.
Intermezzo: An Explanation of the Bayes Factor
In this intermezzo we explain the necessary concepts of Bayesian hypothesis evaluation without diving into the mathematical details. For a detailed introduction see Van de Schoot et al. (2011b) and Hoijtink (2012). For an in-depth discussion of the Bayes factor and its properties we refer the interested reader to Kass and Raftery (1995) or Lynch (2007). For more technical details about Bayesian evaluation of informative hypotheses see Mulder et al. (2010), Mulder et al. (2009), or Hoijtink et al. (2008).
In Bayesian hypothesis evaluation one may compute a Bayes factor that expresses the relative support for one hypothesis versus another hypothesis given the data. Whereas the frequentist framework expresses hypothesis support as the probability of obtaining data given the null hypothesis P(D | H0), the Bayesian framework revolves around determining the support for any hypothesis given the data P(H | D). It is important to stress that a Bayes factor is never tied to one individual hypothesis, rather, it is the relative support for that specific hypothesis compared to another specific hypothesis. For example, BF12 = 5 means H1 is five times as likely as H2. This makes the Bayes factor an interesting tool for model selection. As stated earlier we are interested in model selection, specifically, we wish to compare H1, H2, or H3 for all datasets introduced above.
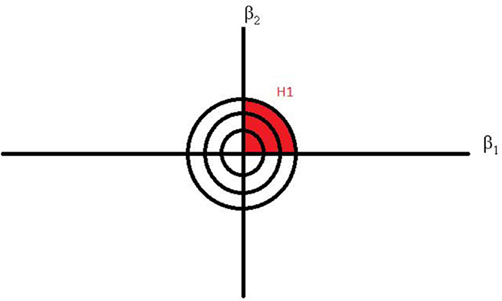
In the introduction we announced that our approach abandons the null distribution. We also abandon the assumption that a null hypothesis is true. Instead, we think of the population parameters as being distributed in a parameter space. Figure 1 provides an illustration of the entire parameter space for our examples. The two β weights could take on any value from minus to plus infinity, creating a large 2D plane. This entire plane is described by an empty or unconstrained hypothesis of the form Hu: β1, β2.
Because we can only determine a Bayes factor for our three informative hypotheses in comparison to another hypothesis, we will use this Hu as the opponent. The Bayes factor can then be interpreted as a support measure for our hypotheses versus an empty model and is defined as follows:
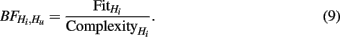
From equation (9) it follows that two ingredients are needed to compute the Bayes factor: complexity and fit. We will discuss the two separately and then show how they are combined to determine the Bayes factor.
Complexity can be perceived as the quantification of background knowledge. Let us determine the complexity of H1 to make the reader familiar with this quantification process. H1 states that both β1 and β2 should be greater than zero. Earlier we established that this expectation counts as background knowledge about the parameters β1 and β2. Because complexity only depends on this background knowledge we can compute it without having collected any data. To determine the complexity of H1 we should ask ourselves which proportion of the entire parameter space in Figure 1 is allowed by the constraints of H1. As can directly be seen from the hypothesis, only the right-upper quadrant of the parameter space satisfies the condition that both βs are positive. The right-upper quadrant is defined as one fourth of the total parameter space, and thus the complexity of H1 is 1/4 = 0.25. This proportion corresponds to the redly marked area in Figure 15. The higher the complexity, the more vague the hypothesis is because high complexity indicates a large proportion of allowed parameter space.
With complexity defined we can now look at fit, which is the second ingredient of a Bayes factor. Unlike complexity, the fit of an hypothesis depends on the data and hence can be seen as posterior information (i.e., our state of knowledge after having seen the data). Fit can be conceptualized as the proportion of parameter space that the prior distribution and the distribution of the data have in common. The higher the fit, the better the hypothesis describes the data. A fit value of one, for example, would occur of the distribution of β1 and β2 falls entirely within the redly marked area of Figure 1.
Now that an intuitive definition of complexity and fit is established, we look at the formula for the Bayes factor in equation (9) again. Suppose two researchers compare their informative hypotheses to the same unconstrained alternative. They both observe a fit of 0.80 but the hypothesis of researcher 1 had a complexity of 0.20 whereas researcher 2 was more vague about his a priori expectations and had a complexity of 0.70. Researcher 1 will then find a Bayes factor of 4 whereas researcher 2 finds a Bayes factor of 1.14. The higher the Bayes factor, the stronger the support for the informative hypothesis against the unconstrained, empty model. This implies that researcher 1 is rewarded for having been more specific than the other researcher. This reward for low complexity only holds when the hypothesis indeed fits the data well. If the a priori expectation of researcher 1 had been inaccurate, his prior distribution would show little overlap with the distribution of the data and his Bayes factor would be considerably lower than that of researcher 2.
When we know the Bayes factor for two informative hypotheses against their unconstrained models, such as the Bayes factors of 4 and 1.14 in the previous example, we can obtain the Bayes factor for their comparison by dividing the two Bayes factors. This yields a Bayes factor of 4/1.14 = 3.51. This means that there is about three and a half times more support for the hypothesis of researcher 1 than that of researcher 2.
We choose to refrain from defining when a Bayes factor is high or low. Instead, we leave this to the interpretation and judgment of the researcher. One question the reader may be left with is “But how do I know if my Bayes factor is of 1.05 is significantly different from 1.00?”, to which we would reply “Do you think this difference is meaningful?”. We want to make it abundantly clear that the Bayes factor is computationally and philosophically different from the frequentists’ p-values. A Bayes factor cannot be interpreted as a measure of significance. Even if one would rescale it into a probability – which is possible but beyond the scope of this paper – it would still have an entirely different meaning than the p-value does. We want to avoid a situation where readers try to interpret Bayesian statistics in the light of frequentist philosophy, or where cut-off values determine which hypothesis is best. Rather, we believe in the judgment and interpretation of experienced researchers as a key determinant in selecting the best hypothesis. We realize that the ability to interpret a Bayes factor takes time and that interpreting Bayesian output may be difficult for the novice reader at this point.
What we can say about Bayes factor interpretation is that the value 1 is important. A Bayes factor of exactly 1 indicates no preference for either of two hypotheses. A Bayes factor above 1 indicates preference for the first hypothesis in the comparison. In equation 9 that would be the informative hypothesis. A Bayes factor below 1 indicates preference for the other hypothesis, which would be the unconstrained hypothesis.
Now that the reader gained some familiarity with the Bayes factor and its (philosophical) properties it is time to look at the analyses and output of the real-world research examples.
Analyzing the Datasets
To analyze our data we used a free software package called BIEMS (see Mulder et al., 2009; Mulder et al., 2010) which can be obtained through http://www.tinyurl.com/informativehypotheses. We provide a step-by-step explanation of the analysis procedure and provide screenshots of BIEMS. We have chosen to stick to the default options in the software program. For a more detailed and technical explanation of all the options and steps in BIEMS, please consult Mulder et al., in press, but included in the BIEMS software package folder). The analysis of the first dataset (predicting overconsumption from emotional and restrained eating) is thoroughly illustrated and explained. The analysis of the second dataset is discussed more briefly.
Analyzing the Overconsumption Data
Recall from the example by Van Strien et al. (2009) that we formulated three informative hypotheses for predicting overconsumption from emotional and restrained eating behavior:
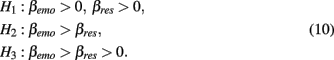
BIEMS Input
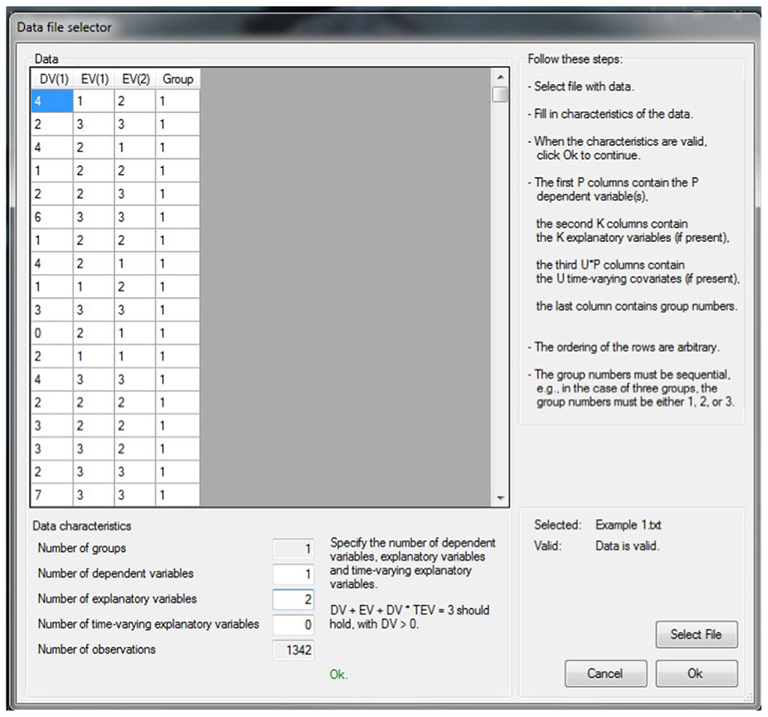
Once the informative hypotheses have been formulated and the data has been gathered, it is time to prepare the data for BIEMS. A few specific requirements are useful for the reader. First, the datafile has to be of .txt format with variables in the columns (no headers) and cases in the rows. Second, the dataset has to be complete. Third, the columns should be in a specific order. The dependent variable(s) has to be in the first column(s), followed by predictor(s), then by time-varying variables and finally there should be a grouping variable (which is mandatory). If there are no groups a column consisting of only ones will suffice. Make sure to exclude all variables which are not part of your hypotheses. BIEMS will use all the variables in your .txt file.
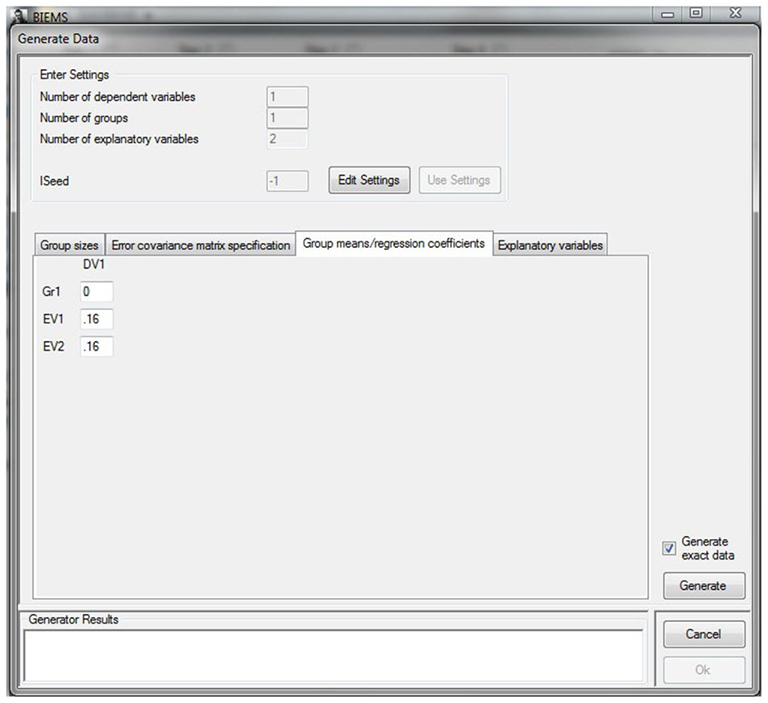
Once the datafile meets the mentioned requirements, it can be imported into BIEMS. This is the first of four steps. Figure 2 provides a screenshot of the imported overconsumption dataset. Be sure to specify the number of dependent, independent, and time-varying variables, which in our case are 1, 2, and 0 respectively. The number of groups will be determined automatically, based on the values occurring in the last column.
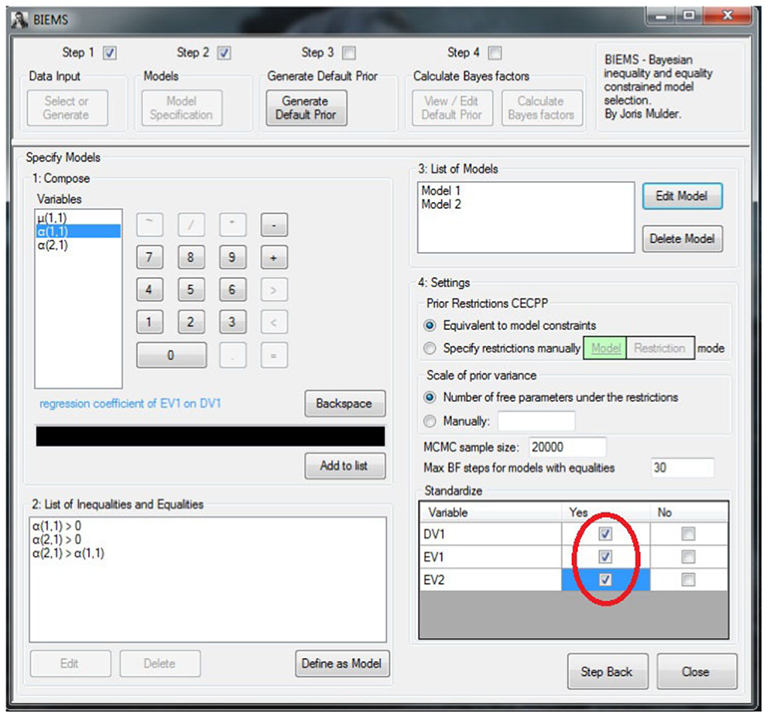
Once the dataset has been imported the hypotheses can be specified as models in the second step of the procedure. Figure 3 illustrates this model specification phase where we define the hypotheses from equations (2–4). Note that in BIEMS, hypotheses are called models. Hypotheses 1 (βemo > 0, βres > 0) and 2 (βemo > βres) have already been specified in the figure. Hypothesis 3 (βemo > βres > 0) is being specified at the moment the screenshot was taken. Note that we ask BIEMS to standardize all variables.
BIEMS Output
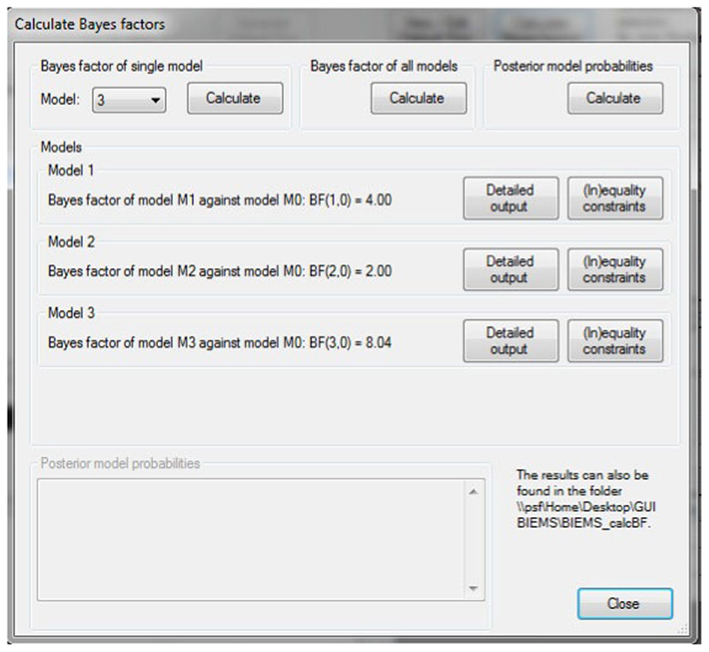
After specifying the three models we ask BIEMS to generate a default prior. Once the prior is specified, step 4 becomes available where a Bayes factor will be calculated for each model versus its unconstrained alternative. This step does not require further input from the user. Figure 4 displays the output screen of BIEMS. The Bayes factor for every model against its unconstrained alternative is displayed. For every hypothesis a more detailed output file can be obtained where, among many other statistics, the fit, and complexity can be found.
For H1 – which stated that both predictors were positively related to overconsumption – we find a complexity of 0.250, a fit of 1, and a resulting Bayes factor of 4.00. This means that the hypothesis in equation (2) receives four times more support from the data than an unconstrained (empty) model does. H2 – stating that emotional eating is more important for predicting overconsumption than restrained eating – has a complexity of 0.500, a fit of 1 as well, and consequently receives a Bayes factor of 2.00. This indicates that H2 is still a better model for the data than its unconstrained alternative. Finally, H3 – which stated that βemo > βres > 0 has a complexity of 0.125, a fit of 0.96, and a Bayes factor of 8.04. This indicates that H3 is eight times more likely than the empty model it was compared to.
Recall that we were not merely interested in the hypotheses themselves; we wanted to compare them and select the most optimal hypothesis for the data. As discussed in the intermezzo we can obtain Bayes factors for the comparison of two hypotheses by dividing the Bayes factors of those hypotheses against an unconstrained alternative. For example, comparing the Bayes factor of H3 with that of H2 gives a Bayes factor of 8.04/2.00 = 4.02 and H3 versus H1 results in a Bayes factor of 8.04/4.00 = 2.01. This indicates that H3 receives most support from the data, either when it is being compared to an empty model or another informative hypothesis. To conclude, we would say that both emotional and restrained eating are related to overconsumption with emotional eating being the strongest predictor of the two.
Analyzing the Work-Family Interference Data
For the second analysis – predicting work-family interference from contractual hours and overtime hours – we again prepared the data file and obtained Bayes factors for all three models. Recall our informative hypotheses from the introduction:
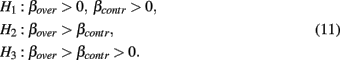
The Bayes factor for H1 against the unconstrained hypothesis is 4.05. For H2 it is 1.73 and for H3 it is 6.95. Although all informative hypotheses receive more support from the data than their unconstrained alternatives do, H3 fits the data best. Our conclusion would be that contractual hours and overtime hours are both related to work-family interference, but the relation is stronger for overtime hours. A causal interpretation of the results remains complicated because this research project was not a controlled experiment.
Generated Datasets: Various Effect Sizes
As mentioned earlier we also want to demonstrate how the Bayesian output is affected by differences in effect size. The purpose is to gather insight into the effect R2 has on the Bayes factor (a concept that will be discussed in the next section). This influence has never been studied before in regression models. Although our study is not extensive enough to serve as a full overview, it does give the reader a feeling of how effect size affects the statistical output. In contrast to the real-world datasets, the generated datasets consist of 100 observations each. This makes them more comparable to certain areas of psychological research where smaller datasets are common, such as experimental psychology.
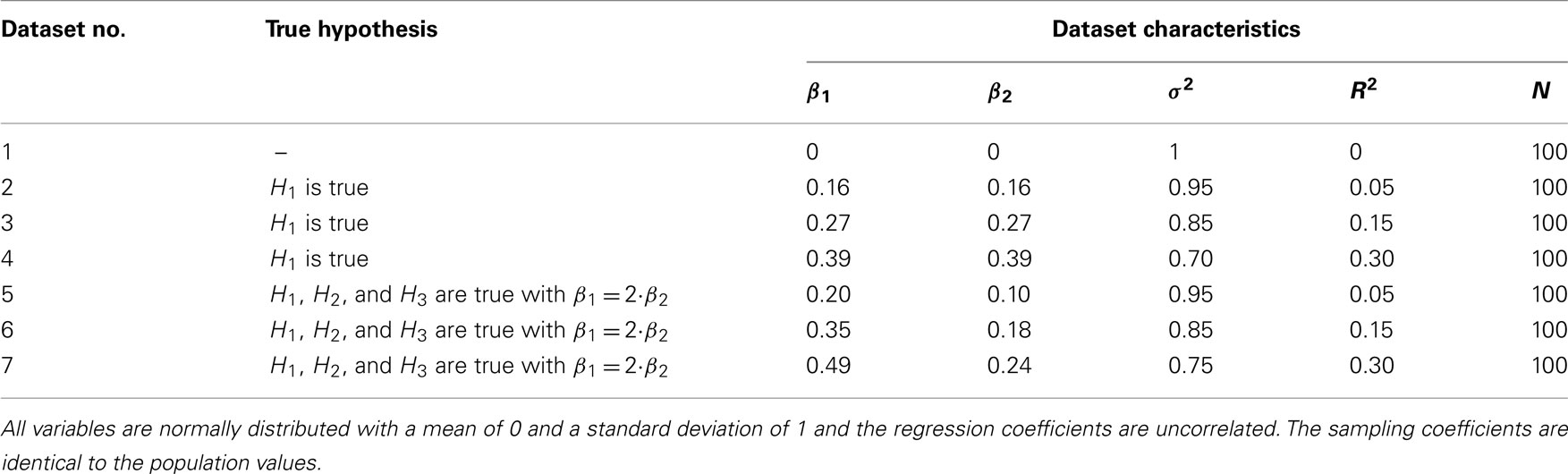
We determine the influence of R2 by generating seven datasets that have different β values and therefore different values for R2. Table 1 displays the exact design of the seven datasets. All datasets were generated with the DataGen function of the software package BIEMS. Figure 5 provides a screenshot of the generation of dataset 2 (see Table 1 for the corresponding βs).
The hypotheses we want to evaluate for these seven datasets are a generalized form of the hypotheses outlined in the real-world examples:

Because we exerted full control over the parameter values we know which hypothesis describes which dataset best (see Table 1). For example, we know that if β1 > β2 then H1 is not the best hypothesis for the data. We also know that in the first dataset, where both βs are zero, none of our informative hypotheses describe the data well. This helps us judge the performance of our Bayesian method.
We evaluated the three informative hypotheses in equation (10) in the same way as the screenshots for the overconsumption data illustrate. The fit, complexity, and Bayes factor for each hypothesis against an unconstrained hypothesis are reported in Table 2. Note that BIEMS estimates the complexity and due to the estimation process, the complexity for the three hypotheses will not be exactly the same in every analysis. For example, in Table 2 the complexities for H1 vary around 0.250 (with values being 0.247, 0.251, and so on). We know from the intermezzo that the complexity of H1 should be exactly 0.250, which corresponds to 25% of the parameter space (see Figure 1). Averaged across many iterations BIEMS would give us that exact value for the complexity, but the results displayed in Table 2 are only an estimate of that complexity based on one calculation. The reason for estimation is that in more complex hypotheses it would not be possible to determine the complexity based on calculations (Van de Schoot et al., 2012).
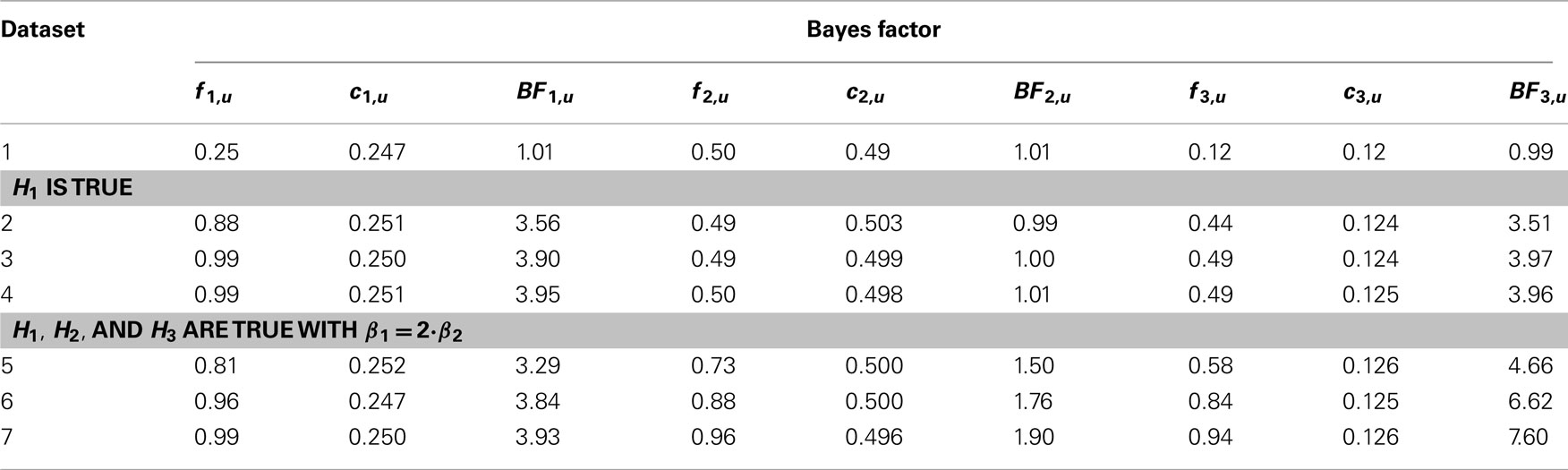
Table 2. Results corresponding to the generated datasets: Bayes factors for each informative hypothesis against its unconstrained alternative.
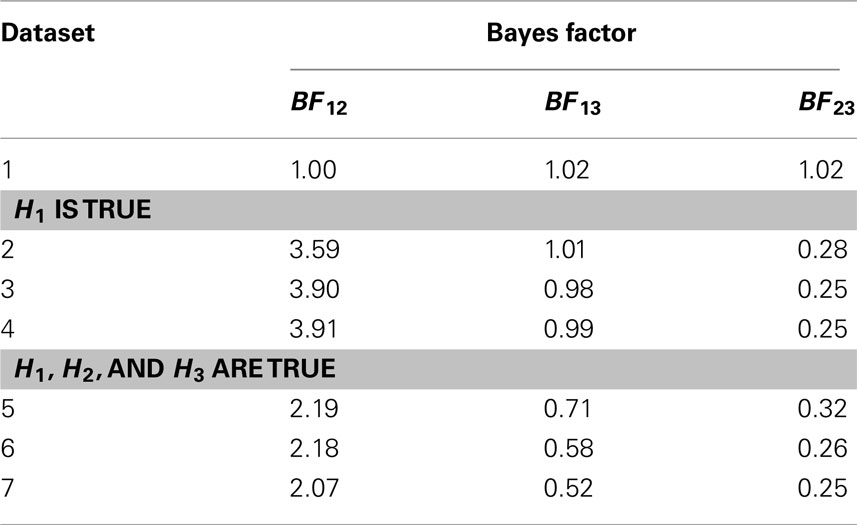
The Bayes factors for the comparison of the three informative hypotheses with each other were computed manually by dividing the Bayes factors in Table 2. The resulting Bayes factors and are displayed in Table 3. Note that BF12 denotes the Bayes factor for the comparison of H1 versus H2 and indicates the relative support for H1 in this comparison.
Recall from the intermezzo that the complexity of an hypothesis is not influenced by the data. The complexity of H1, H2, and H3 can be found in Table 2. Here we see that the hypotheses indeed have the same complexity no matter for which dataset it was computed. We also observe that the complexity of H1 is indeed 0.25, something we graphically illustrated before in Figure 1. In addition Table 2 reveals that the average complexity is largely determined by the amount of constraints: one constraint in H2 (c = 0.500), two constraints in H1 (c = 0.250), and three constraints in H3 (c = 0.125). As for the fit values, we know from the intermezzo that they are influenced by the data. Indeed, we see that the fit increases as the effect size increases. For the computation of the Bayes factor this means that a larger and larger fit value is divided by a constant complexity, implying that the Bayes factor will increase as well. This is exactly what we see in Table 2.
Let us now look at some individual cells from Table 2. We see that for dataset 1, when R2 = 0 and none of the hypotheses fit the data, the Bayes factors for all three hypotheses are around 1. This indicates that there is about equal support for the informative hypotheses as there is for the unconstrained hypothesis. Of course a researcher could still choose to prefer the informative hypothesis in this case, but his decision would be hard to sell. Instead we conclude that none of our hypotheses provides an accurate description of the data in dataset 1. Note that this corresponds to the prediction we made when we introduced the generated datasets.
Recall that the higher the Bayes factor is, the more support we have for our hypothesis versus an empty hypothesis. In datasets 2–4 we see a clear preference for H1 and H3. Note that the fit for H3 is lower than that for H1, but because H3 has a lower complexity it receives roughly the same Bayes factor as H1 does. This can be understood when we see H1 (β1 > 0, β2 > 0) as a subset of H3 (β1 > β2 > 0). Thus, when H1 is accurate, H3 is at least partly accurate as well. When we compare H1 and H3 for datasets 2–4 in Table 3 we see that we end up with roughly equal support for both hypotheses. Looking at Table 2 again we see that H2 does not receive support from the data, nor does it receive counter-evidence. The BF for this hypothesis remains stable around 1. When we compare H2 to either H1 or H3 in Table 3 we see a clear preference for the other hypotheses. We would conclude that in datasets 2–4, where the βs are equal, we do not find support for the claim that β1 > β2. Note that this conclusion is the same whether we look at dataset 2 (where R2 = 0.05) or dataset 4 (where R2 = 0.30).
When we look at datasets 5–7 in Table 2 we see that the support for H1 remains the same as it was in datasets 2–4, but the support for H2 and H3 increases. This is because there is now an actual difference between the two βs in the data (see Table 1). Note that the fit of H2 is a bit higher than that of H3, but because H2 imposes less constraints it has a higher complexity which results in lower Bayes factors. This is another example where the researcher is rewarded for having been specific when H3 was formulated.
Because in datasets 5–7 we receive support for all informative hypotheses versus the unconstrained model, it becomes especially interesting to see which of the three fits the data best. This can be deduced from Table 3 where we see that H3 receives most support. We would conclude that in datasets 5–7 both βs are bigger than zero and β1 is bigger than β2. Again we achieve this conclusion whether we look at dataset 5 (where R2 = 0.05) or dataset 7 (where R2 = 0.30).
The generated datasets were designed to demonstrate how R2 influences the results of Bayesian statistics. After having seen these results we would say that even when effect size is zero or relatively low the Bayes factor helps us choose an accurate model for the data. We conclude that the Bayes factor can be used even when the researcher expects a small effect.
Discussion and Conclusion
In this paper we have illustrated how informative hypotheses can be evaluated by means of Bayesian statistics. We applied the method to existing psychological research, where we showed the reader the process of formulating informative hypotheses, evaluating them in light of the data, and interpreting the outcomes. In addition to this application we generated and analyzed datasets with manipulated differences in effect size. This endeavor demonstrated how the Bayes factor was or was not affected by the magnitude of an effect. We now review our findings and discuss the practical value of Bayesian hypothesis evaluation for psychological researchers.
In the introduction we claimed that the null hypothesis is often not the expectation that a psychological researcher wishes to evaluate. Instead we argued that researchers often have very specific prior expectations about parameter values. In the real-world examples for overconsumption and work-family interference we saw that this was indeed the case: researchers had prior expectations about the direction and magnitude of the effects. We formulated these prior expectations and put them in the form of informative hypotheses. We then pursued to evaluate these hypotheses and express support for or against them. We were able to point out which hypothesis fit the data best without having used any null hypothesis. Moreover, we provided the reader with a step-by-step guide to enable him to do the same.
From the generated datasets we saw that the Bayes factor helps us select one of three models even when effect sizes are relatively low. We also saw that the Bayes factor increased when effect size did, reflecting more and more certainty about the parameter values as the magnitude of the effect increased. The tables in which we summarized the statistics will help the reader decide whether the approach is appealing enough for the effect sizes he/she is expecting.
In sum, we have provided the reader with a non-technical introduction to Bayesian hypothesis evaluation while avoiding technical or mathematical language. Unfortunately there are some limitations to this paper. For example, we have chosen artificially simple designs with only two predictors and one criterion each. We acknowledge that the reader will likely be confronted with more complex designs in practice. For informative hypothesis testing in structural equation modeling, for example, please consult Van de Schoot et al. (2012). Second, our generated datasets were nowhere near exhaustive. It would have been more thorough to also vary sample size. Third, we made a conscious choice to omit mathematical formulas or calculations. This means that the reader should either trust our intuitive explanations or read further into the method. For technical details of our proposed methodology we refer the interested reader to Mulder et al. (2010). Fourth, we deliberately chose not to make this paper a comparison between null hypothesis testing and the Bayesian evaluation of informative hypotheses. For such comparisons we refer the reader to Kuiper and Hoijtink (2010) or Van de Schoot et al. (2011a). Moreover, we chose not to provide the reader with any guidelines or cut-off values to interpret the Bayesian output. This may seem unfriendly, especially because we expect the reader to be a novice. Although we had good reasons to exclude comparisons and cook-book rules, we acknowledge that the lack of both may have been hard on the reader. For more details on interpreting the Bayes factor see Kass and Raftery (1995).
In the introduction we promised to get back to the subject of contrast testing. We then acknowledged that contrast testing is a flexible tool to evaluate one informative hypothesis. Nevertheless we still maintain that there are two important reasons for switching to Bayesian hypothesis evaluation.
First, contrast testing only allow the evaluation of one single informative hypothesis. It does not provide an option for comparing competing hypotheses, which is essentially what model selection is about. The Bayesian evaluation of informative hypothesis does allow the simultaneous evaluation of multiple informative hypothesis and, as we have demonstrated, assists the researcher in selecting one hypothesis from a set of hypotheses.
Second, although there is nothing wrong with null hypothesis testing, the philosophy behind Bayesian hypothesis evaluation may simply be more interesting to some researchers. In Bayesian statistics the focus is on updating the state of knowledge: we quantified what we knew about parameters before we saw any data and we updated this quantity after having seen the data. The knowledge one gathers from one Bayesian analysis may serve as background knowledge for the next, creating an accumulative science. In addition, Bayesian statistics focus on the support for a model rather than on p-values. This brings with it an entirely different line of interpreting and thinking about statistics.
Of course there are certain situations in which the evaluation of informative hypotheses is not optimal. For example, a researcher may find himself truly interested in the null hypothesis (Wainer, 1999). Note that in this situation the researcher may still choose between Bayesian and frequentist statistics as both frameworks can handle null hypotheses. The choice will then likely be determined by which framework’s philosophy is most appealing to the researcher.
To conclude, we hope to have awakened some interest and awareness in the reader. We would advise the curious reader to become acquainted with informative hypotheses and their Bayesian evaluation through experimentation and literature. The Bayesian hypothesis evaluation we illustrated may not replace null hypothesis testing entirely, but it may be a welcome addition to a researcher’s toolbox.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank our reviewers for their inspiring and constructive comments. Supported by a grant from the Dutch organization for scientific research: NWO-VICI-453-05-002.
Footnotes
- ^Throughout the paper we will use a software package called BIEMS (Mulder et al., in press). The software can be obtained through http://www.tinyurl.com/informativehypotheses
- ^Both datasets 1 and 2 were obtained from the covariance matrix that was found in the original papers with N = 1342 and N = 2242 respectively.
- ^Note that the researchers used Likert-scale variables instead of interval scales. In psychology it is common practice to use ordinal Likert scales in regression models and therefore we will adopt this approach.
- ^The exact pattern was slightly more complex, involving mediator and moderator effects that are outside the scope of this paper.
- ^BIEMS asks the user to determine the hypotheses and then computes a distribution of the parameters for each hypothesis. It is important to note that this prior parameter distribution is not subjective, even though the hypothesis itself may be. The prior distribution is chosen with desirable frequency properties, see Hoijtink (2012).
References
Berger, J. (1985). Statistical Decision Theory and Bayesian Analysis, 2nd Edn. New York: Springer-Verlag.
Cronbach, L. J. (1951). Coefficient alpha and the internal structure of tests. Psychometrika 16, 297–334.
Geurts, S., Beckers, D., Taris, T., Kompier, M., and Smulders, P. (2009). Worktime demands and work-family interference: does worktime control buffer the adverse effects of high demands? J. Bus. Ethics 84, 229–241.
Hoijtink, H. (2012). Informative Hypotheses: Theory and Practice for the Behavioral and Social Scientists. New York: CRC-press.
Hoijtink, H., Klugkist, I., and Boelen, P. A. (2008). Bayesian Evaluation of Informative Hypotheses. New York: Springer.
Klugkist, I., Laudy, O., and Hoijtink, H. (2005). Inequality constrained analysis of variance: a Bayesian approach. Psychol. Methods 10, 477–493.
Klugkist, I., Van Wesel, F., and Bullens, J. (2011). Do we know what we test and do we test what we want to know? Int. J. Behav. Dev. 35, 550–560.
Krueger, J. I. (2001). Null hypothesis significance testing: on the survival of a flawed method. Am. Psychol. 56, 16–26.
Kuiper, R. M., and Hoijtink, H. (2010). Comparisons of means using exploratory and confirmatory approaches. Psychol. Methods 15, 69–86.
Lynch, S. (2007). Introduction to Applied Bayesian Statistics and Estimation for Social Scientists. New York: Springer.
Mulder, J., Hoijtink, H., and de Leeuw, C. (in press). BIEMS: a fortran 90 program for calculating Bayes factor for inequality and equality constrained models. J. Stat. Softw.
Mulder, J., Hoijtink, H., and Klugkist, I. (2010). Equality and inequality constrained multivariate linear models: objective model selection using constrained posterior priors. J. Stat. Plan. Inference 4, 887–906.
Mulder, J., Klugkist, I., Van de Schoot, R., Meeus, W., Selfhout, M., and Hoijtink, H. (2009). Bayesian model selection of informative hypotheses for repeated measurements. J. Math. Psychol. 53, 530–546.
Rosenthal, R., Rosnow, R., and Rubin, D. (2000). Contrasts and Effect Sizes in Behavioral Research: A Correlational Approach. Cambridge: Cambridge University Press.
Silvapulle, M. J., and Sen, P. K. (2004). Constrained Statistical Inference: Order, Inequality, and Shape Constraints. Series in Probability and Statistics. London: John Wiley Sons.
Silvapulle, M. J., Silvapulle, P., and Basawa, I. V. (2002). Tests against inequality constraints in semiparametric models. J. Stat. Plan. Inference 107, 307–320.
Van de Schoot, R., Hoijtink, H., and Dekovic, M. (2010). Testing inequality constrained hypotheses in SEM models. Struct. Equ. Modeling 17, 443–463.
Van de Schoot, R., Hoijtink, H., Hallquist, M. N., and Boelen, P. A. (2012). Bayesian evaluation of inequality-constrained hypotheses in SEM models using Mplus. Struct. Equ. Modeling (in press).
Van de Schoot, R., Hoijtink, H., Mulder, J., van Aken, M., Orobio de Castro, B., Meeus, W., and Romeijn, J. (2011a). Evaluating expectations about negative emotional states of aggressive boys using Bayesian model selection. Dev. Psychol. 47, 203–212.
Van de Schoot, R., Mulder, J., Hoijtink, H., van Aken, M. A. G., Dubas, J. S., de Castro, B. O., Meeus, W., and Romeijn, J.-W. (2011b). Psychological functioning, personality and support from family: an introduction Bayesian model selection. Eur. J. Dev. Psychol. 8, 713–729.
Van de Schoot, R., Romeijn, J.-W., and Hoijtink, H. (2011c). Moving beyond traditional null hypothesis testing: evaluating expectations directly. Front. Psychol. 2:24. doi:10.3389/fpsyg.2011.00024
Van de Schoot, R., and Strohmeier, D. (2011). Testing informative hypotheses in SEM increases power: an illustration contrasting classical hypothesis testing with a parametric bootstrap approach. Int. J. Behav. Dev. 35, 180–190.
Van Strien, T., Herman, C. P., and Verheijden, M. W. (2009). Eating style, overeating, and overweight in a representative Dutch sample. Does external eating play a role? Appetite 52, 380–387.
Wagenmakers, E.-J. (2007). A practical solution to the pervasive problems of p values. Psychon. Bull. Rev. 14, 779–804.
Keywords: informative hypotheses, Bayes factor, effect size, BIEMS, multiple regression, Bayesian hypothesis evaluation
Citation: Kluytmans A, van de Schoot R, Mulder J and Hoijtink H (2012) Illustrating Bayesian evaluation of informative hypotheses for regression models. Front. Psychology 3:2. doi: 10.3389/fpsyg.2012.00002
Received: 02 June 2011;
Accepted: 04 January 2012;
Published online: 20 January 2012.
Edited by:
Joshua A. McGrane, University of Western Australia, AustraliaReviewed by:
Ben Colagiuri, University of New South Wales, AustraliaAndrew Stuart Kyngdon, MetaMetrics, Inc., Australia
Denny Borsboom, University of Amsterdam, Netherlands
Daniel Saverio John Costa, University of Sydney, Australia
Copyright: © 2012 Kluytmans, van de Schoot, Mulder and Hoijtink. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Anouck Kluytmans, Department of Methodology and Statistics, Utrecht University, P.O. Box 80.140, 3508TC Utrecht, Netherlands. e-mail:YW5vdWNrLmtsdXl0bWFuc0BnbWFpbC5jb20=


 Joris Mulder4 and Herbert Hoijtink2
Joris Mulder4 and Herbert Hoijtink2