- Technion – Israel Institute of Technology, Haifa, Israel
The leading models of human and animal learning rest on the assumption that individuals tend to select the alternatives that led to the best recent outcomes. The current research highlights three boundaries of this “recency” assumption. Analysis of the stock market and simple laboratory experiments suggests that positively surprising obtained payoffs, and negatively surprising forgone payoffs reduce the rate of repeating the previous choice. In addition, all previous trails outcomes, except the latest outcome (most recent), have similar effect on future choices. We show that these results, and other robust properties of decisions from experience, can be captured with a simple addition to the leading models: the assumption that surprise triggers change.
Analyses of financial markets reveal that the volume of trade tends to increase after sharp price increase, and also after sharp price decline (Karpoff, 1988). Higher volume of trade implies that owners are more likely to sell, and potential buyers are more likely to buy. Thus, the data suggest a fourfold response pattern to recent outcomes: Owners appear to exhibit negative recency after obtained gains (behave as if they expect a price decrease after a large price increase), but positive recency after a loss (expect another decrease after a large decrease). Potential buyers appear to exhibit the opposite pattern: positive recency after a large forgone gain (expect another increase after a large gain that they missed), and a negative recency after a forgone loss (expect a price increase after a price decrease).
Previous studies of decisions from experience appear to reflect a simpler effect of recent outcomes. Most studies document a robust positive recency effect (Estes, 1976; Barron and Erev, 2003; Barron and Yechiam, 2009; Biele et al., 2009): People tend to select the alternative that led to the best outcome in the previous trials1. This pattern is consistent with the law of effect (Thorndike, 1898), brain activity (Schultz, 1998), and is assumed by most learning models (e.g., Bush and Mosteller, 1955; Rescorla and Wagner, 1972; Erev and Roth, 1998; Fudenberg and Levine, 1998; Selten and Buchta, 1998; Camerer and Ho, 1999; Dayan and Niv, 2008; Marchiori and Warglien, 2008; Erev and Haruvy, in press).
The natural explanation for this apparent inconsistency between the stock market pattern and previous studies would be that many factors affect the behavior in the stock market, and the basic properties of human learning are only a small part of these factors. This explanation is consistent with the leading models of the stock market data. According to these models the effect of price change on the volume of trade is a product of an interaction between asymmetric traders (e.g., different interests, different knowledge etc.).
The current analysis focuses on a less natural explanation of the inconsistency. It considers the possibility that the financial data reflect an important behavioral regularity that was ignored by basic learning research. Our interest in this possibility was triggered by the recent demonstration that the insights obtained in basic learning research could be used to justify the prediction of the 2008 sub-prime crises in the financial markets (Taleb, 2007; Hertwig and Erev, 2009). Yet, the goal here is different. Rather than trying to predict the behavior of the stock market, we try to build on the robust stock market pattern in order to improve our understanding of basic learning processes. The attempt to achieve this goal led us to focus on the role of surprising outcomes. Specifically, we hypothesize that “surprise-trigger-change”2. Our definition of surprise is similar to the definition implied by the classical Rescorla–Wagner model: Surprise is assumed to increase with the gap between the expected and the observed outcomes. The surprise-trigger-change hypothesis is consistent with the stock market data: Large price changes are surprising, and for that reason they increase trade (change implies trade).
In addition, the surprise-trigger-change hypothesis can explain the fact that most learning studies document positive recency: These studies focus on the main effect of the recent payoff over the different outcomes, and do not examine this effect contingent on the level of surprise3. Thus, their results are consistent with a natural abstraction of the surprise-trigger-change hypothesis that implies a positive recency effect in most cases, and allows for the possibility of a negative recency effect after surprising outcomes.
Another nice feature of the surprise-trigger-change hypothesis involves its consistency with brain research. Analysis of the neural activation in the dopaminergic system reveals correlation between activation level and prediction error (Schultz, 1998). The current hypothesis suggests that the detection of prediction error, implies surprise, and increases the probability of a change.
The first part of the current paper tests the surprises-trigger-change hypothesis in simple binary choice experiments. The analysis continues with an exploration of the implications of the current results to the modeling of learning.
Experiment 1: The Surprise-Trigger-Change Hypothesis
Methods
Experiment 1 focuses on repeated play of the two problems presented in Table 1. The experiment used the “clicking paradigm” described in Figure 1.

Figure 1. The instructions, and the screens in a study that uses the basic clicking paradigm. In the example the participant chose Right, won 1; and the forgone payoff was 0. The exact payoffs were determined by the game’s payoff rule. Each of the games considered here focused on one of the problems listed in Tables, 1,2, or 3, and included 100 trials. Each key was associated with one of the prospects. The assignment of prospects to buttons and the order of the problems were randomly determined for each participant.
The participants were 48 Technion students. Each participant faced each problem (“game”) in a block of 100 trials. The order of the two problems was balanced over participants. The participants received a show-up fee of 30 Shekels (about $8) and could win more, or lose part of this amount in the experiment. The exact addition to the show-up fee was the outcome (in Shekels) in one randomly selected trial.
The experiment was run on personal computers. The experimental instructions (see left-hand side of Figure 1) were presented on printed sheet of paper and the participants could read them at all times. As the instructions indicate, the participants did not receive a description of the incentive structure. They were simply told that the experiment includes several multi-trial games, and their task (in each trial, in each game) is to select between the two keys. It was explained that their choices will determine their trial’s payoff, and that they will receive immediate feedback after each trial. In addition, the instructions explain that the different games involve different payoffs, and that the subjects will be informed when a new game starts.
Notice that both problems involve a choice between the status quo (payoff of 0 with certainty), and a two-outcome risky prospect. The more surprising (less likely) outcome is the best outcome (+10) in Problem 1, and the worst outcome (−10) in Problem 2.
Results of Experiment 1
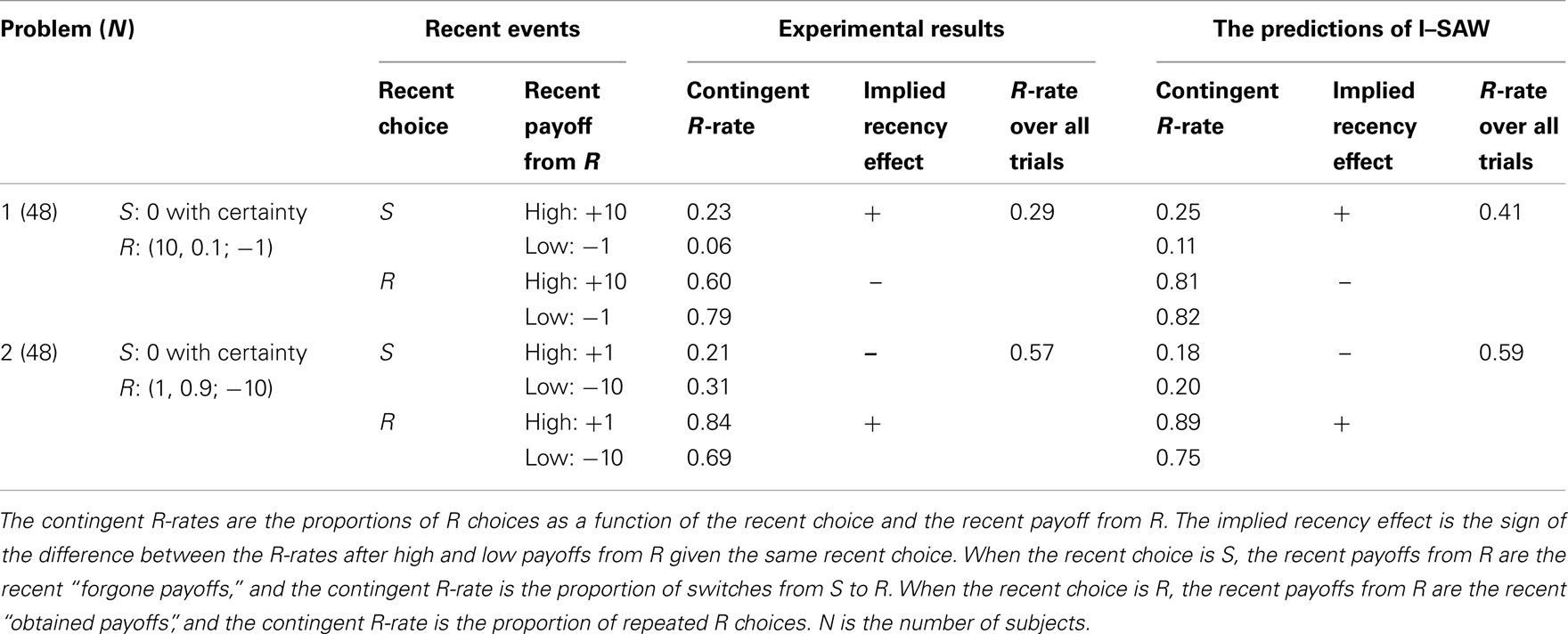
The results (c.f. Table 1) reveal the fourfold pattern predicted by the surprise-triggers-change hypothesis. In problem 1 (when the high payoff, +10, is rare and surprising) the participants exhibited positive recency after an S choice, but negative recency after an R choice. The positive recency effect is reflected by a higher rate of switches to R after high forgone payoff (23%) than after low forgone payoff (6%). The negative recency effect is reflected by a lower rate of repeated R choices after high obtained payoff (60%) than after low obtained payoff (79%).
In problem 2 (when the low payoff, −10, is rare and surprising) the participants exhibited negative recency after an S choice, but positive recency after an R choice. The negative recency effect is reflected by a lower rate of switches to R after high forgone payoff (21%) than after low forgone payoff (31%). The positive recency effect is reflected by higher rate of repeated R choices after high obtained payoff (84%) than after low obtained payoff (69%).
Analysis of individual participants reveals that this pattern is robust: 24 of the 36 participants that were faced with all eight “recent outcomes by recent choice” contingencies4 are better described by the fourfold hypothesis than by the positive recency hypothesis. This ratio (24/36) is significant larger than half (p < 0.05 in a sign test).
The aggregate R-rates were only 29% in Problem 1 when the expected value of R is positive, and 57% in Problem 2 when the expected value of Option R is negative. This result is consistent with the assertion that decisions from experience reflect underweighting of rare events (Barron and Erev, 2003).
Figure 2 presents the mean R-rates as a function of time. It reveals robustness of the main results over time.
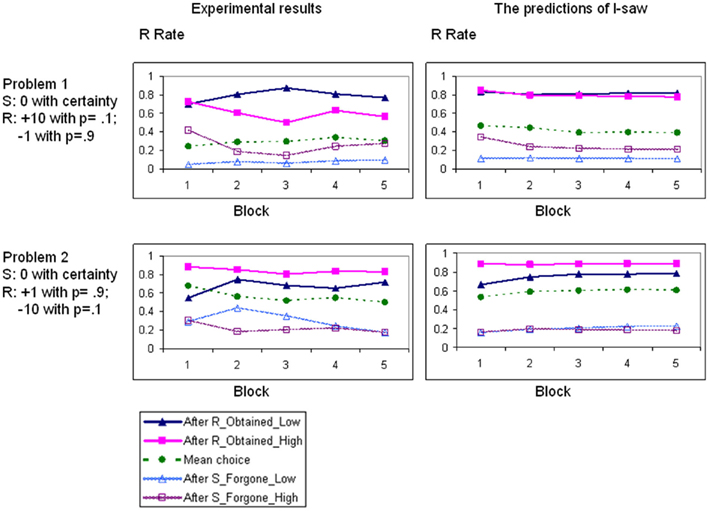
Figure 2. The mean choice rates (over the 48 participants) in five blocks of 20 trials in Experiment 1. The left-hand graphs show the experimental results, the right-hand graphs show the predictions of the model. The R curve shows the aggregate R-rate (the mean choice rate of the risky option). The other four curves show the R-rate as a function of the choice and the outcome in the previous trial.
Reanalysis of Previous Studies
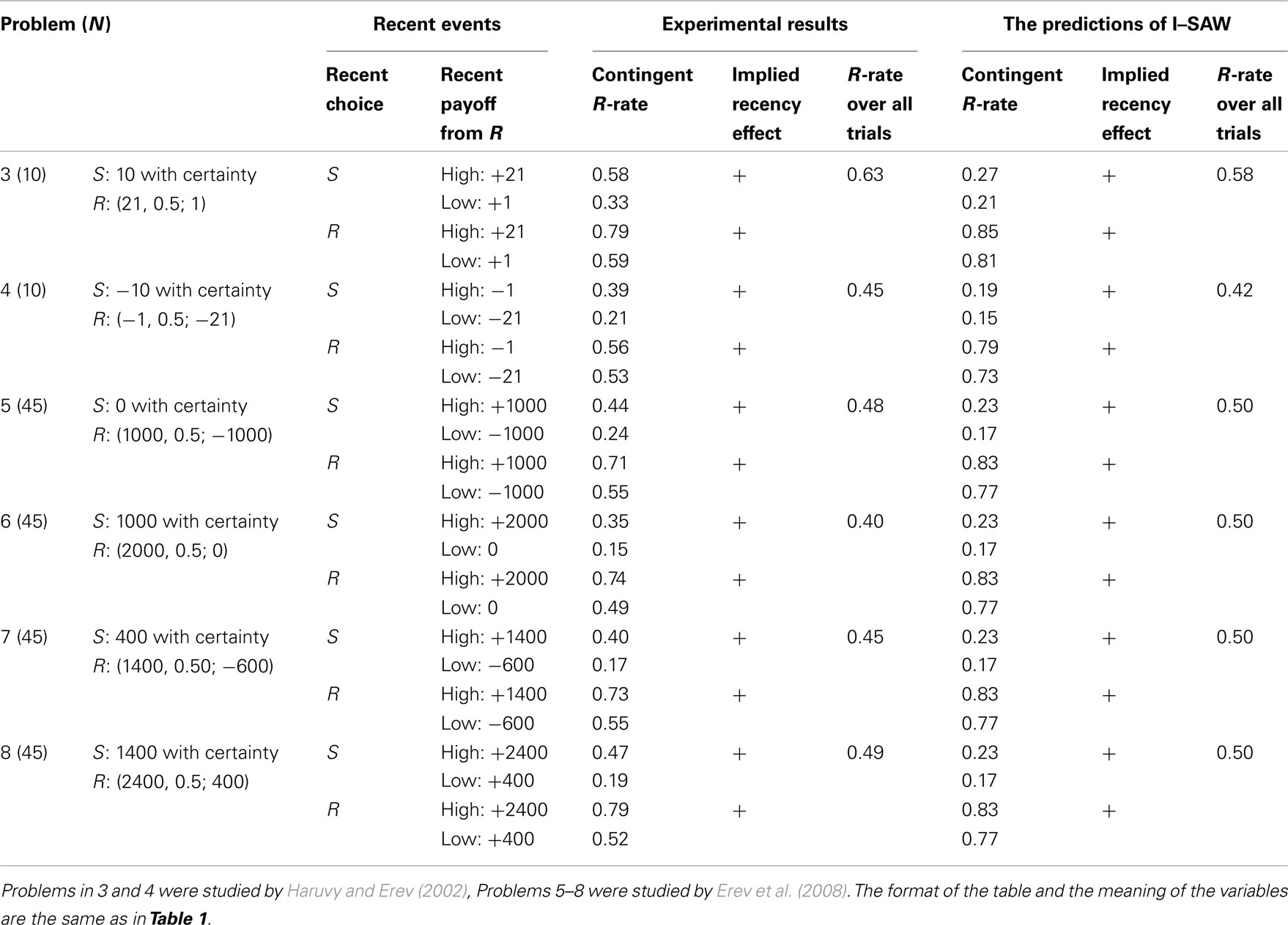
The surprise-trigger-change hypothesis implies an important boundary for the fourfold recency pattern documented above. It suggests that this pattern will not emerge when the possible outcomes are equally likely; when the outcomes are equally likely, they are equally surprising, and the probability of a change is expected to be independent of the relative attractiveness of the recent payoff. In order to evaluate this prediction we reanalyzed data from previous studies that used the current paradigm to examine repeated choices between a safe prospect and a gamble that yields two equally likely outcomes. Table 2 summarizes the contingent choice proportions documented in the study of six “50–50” problems. Problems 3 and 4 were studied in Haruvy and Erev (2002) and Grosskopf et al. (2006). Problems 5–8 were studied in Erev et al. (2008). The results are consistent with the current hypothesis. A strong positive recency effect was documented in all six problems (Problems 3–8). On average, the rate of risky choices is 58% after high payoff, and 38% after low payoff.
The Very Recent Effect
Additional analysis of the positive recency effect documented in Problems 3–8 reveals that it is limited to the very recent outcome: The choice rate of the alternative that led to the best payoff in the most recent trial is 60%, and the choice rate of the alternative that led to the best payoff in the trial before the most recent is only 50% (the rate expected under the assumption of “no recency effect”).
Experiment 2: A Robustness Test
Methods
Experiment 2 was designed to evaluate the robustness of the current results. It uses Experiment 1’s procedure with the exception that each participant was presented with 12 different problems. The participants were 28 Technion students. The 12 problems are presented in Table 3. These problems were randomly selected and studied in Erev et al. (2010a) under distinct information conditions.
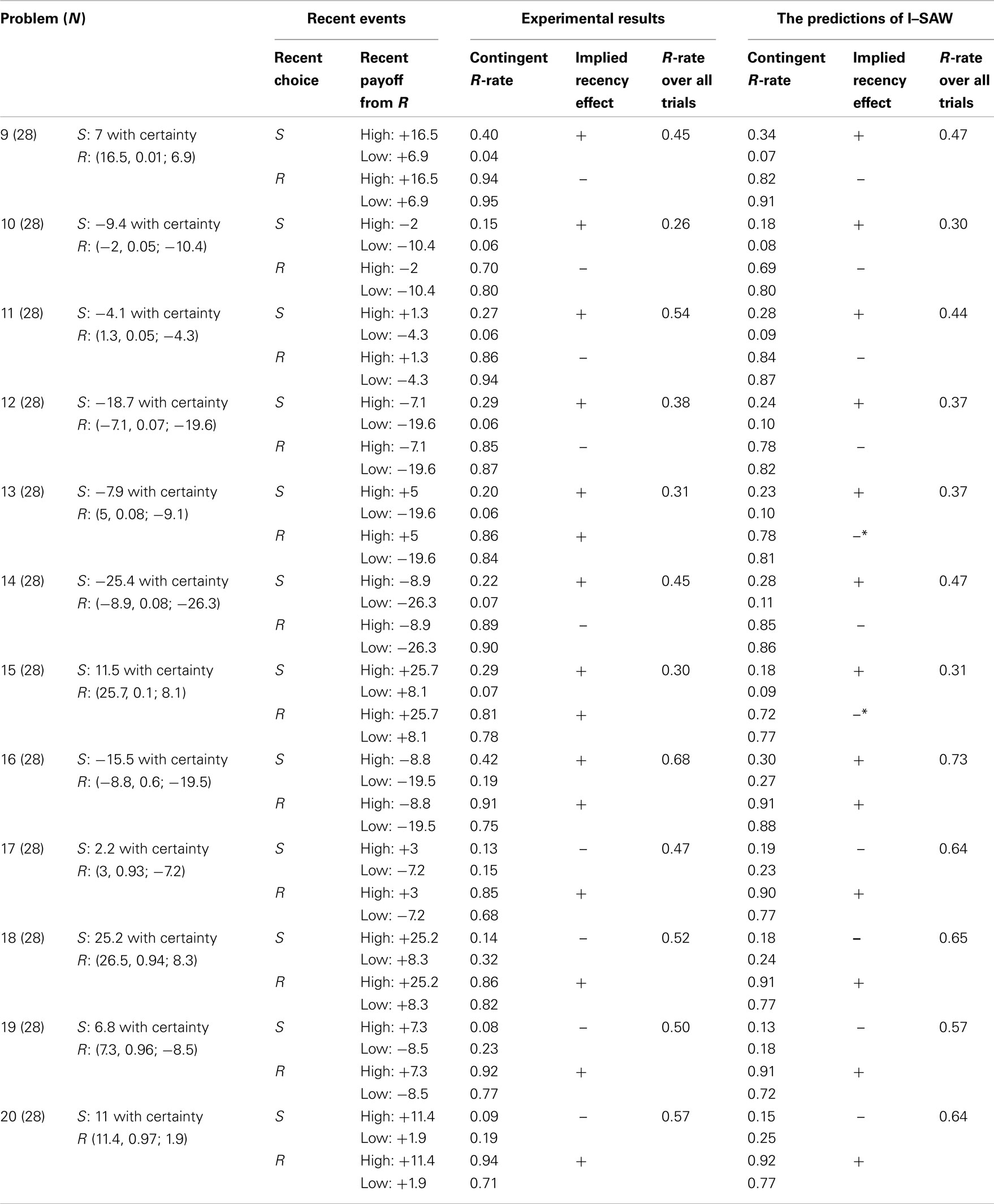
Table 3. The 12 problems studied in Experiment 2. The format of the table and the meaning of the variables are the same as in Table 1.
Results of Experiment 2
The results, summarized in Table 3, replicate the surprise-trigger-change pattern documented in Experiment 1. Problems 9–15 in which the high payoff occurs with small probability (0.1 or less) are similar to Problem 1: The participants exhibited positive recency after an S choice, but negative recency after an R choice. The positive recency effect is reflected by the observation that the mean switch rate from S to R over these seven problems was higher after the high forgone payoff (26%) than after low forgone payoff (6%). The negative recency effect is reflected by the observation that the mean rate of repeated R choice over these seven problems was lower after the high obtained payoff (84%) than after low obtained payoff (87%).
Problems 17–20 in which the low payoffs occur with small probability (0.1 or less) are similar to Problem 2: The participants exhibited negative recency after an S choice, and positive recency after an R choice. The negative recency effect is reflected by the observation that the mean switch rate from S to R over these four problems was lower after the high forgone payoff (11%) than after low forgone payoff (22%). The positive recency effect is reflected by the observation that the mean rate of repeated R choice over these four problems was higher after the high obtained payoff (89%) than after low obtained payoff (75%).
Finally, Problem 16 is which the high and low outcomes occur with moderate probability is similar to Problems 3–8: The participants exhibit positive recency after R and after S choices.
A Quantitative Summary
In order to clarify the implications of the surprise-trigger-change hypothesis we chose to quantify it within a simplified variant of the explorative sampler model that provides the best predictions of the results in the first Technion choice prediction competition (Erev et al., 2010a). The model is described below.
The Inertia Sampling and Weighting Model5
The model distinguishes between three response modes: exploration, exploitation, and inertia. Exploration implies random choice. The probability of exploration, by individual i, is 1 in the first trial, and εi (a trait of i) in all other trials.
During exploitation trials, individual i selects the alternative with the highest estimated subjective value (ESV). The ESV of alternative j at trial t > 1 is:
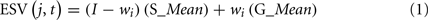
where S_Mean (sample mean) is the average payoff from Alternative j in a small sample of μi similar previous experiences (trials), G_Mean (grand mean) is the average payoff from j over all (t − 1) previous trials, and μi and wi are traits. The assumed reliance on small samples was introduced to capture the observed tendency to underweight rare events (Barron and Erev, 2003). The similarity based sampling rule was added to capture discrimination between different states of nature (Gonzalez et al., 2003)6.
The μi draws are assumed to be independent (sampling with replacement) and biased toward the most recent experience (Trial t − 1). A bias occurs with probability ρi (a trait) and implies draw of Trial t − 1. When a bias does not occur (probability 1 − ρi) all previous trials are equally likely to be sampled7. The motivation behind this assumption is the “very recent effect.”
Inertia is added with the assumption that the individuals tend to repeat their last choice. The exact probability of inertia at trial t + 1 is assumed to decrease when the recent outcomes are surprising. Specifically, if the exploration mode was not selected, the probability of inertia is:
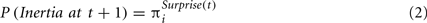
where 0 < πi < 1 is a trait that captures the tendency for inertia. As in Rescorla and Wagner (1972) we assume that surprise increases with the gap between the expected and the realized outcomes. The exact value of the gap is computed under the assumption the agents compare the realized outcomes to two estimates (or expectations): One estimate is based on the most recent outcome, and one is based on the mean payoff. Thus, the gap is the mean of four differences:

where Obtainedj(t) is the payoff obtained from j at trial t, and G_meanj(t) is the average payoff obtained from j in the first t − 1 trials (the grand mean). The surprise at t is normalized by the mean gap (in the first t − 1 trials):
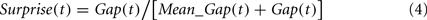
The mean gap at t is a running average of the gap in the previous trials [with Mean_Gap(1) = 0.00001]. Specifically,
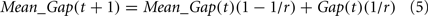
where r is the expected number of trials in the experiment (100 in the current study).
Notice that the normalization (Eq. 4) is necessary to capture the intuition that a multiplication of all the nominal payoffs by a positive constant will not increase surprise in the long term. In addition, normalization keeps the value of Surprise(t) between 0 and 1, and the probability if inertia between πi [when Surprise(t) = 1] and 1 [when Surprise(t) = 0].
An interesting justification for this gap-based abstraction comes from the observation that dopamine neurons activation increases with prediction error (Schultz, 1992, 1998; Montague et al., 1996, 2004; Caplin and Dean, 2007). The current abstraction of surprise is a quantification of this observation; in the current context, the present quantification outperforms all the other quantifications that we have considered (the choice prediction competition described below suggest that it is not easy to find a better quantification).
The traits are assumed to be independently drawn from a uniform distribution between the minimal possible value (allowed by the model) and a higher point. Thus, the estimation focused on estimating the upper points (five free parameters). The estimation used a grid search procedure. Best fit implies the following trait distribution: εi∼U[0,0.24], wi∼U[0,1], ρi∼U[0,0.12], πi∼U[0,1], and μi = 1, 2, 3, or 4.
The right-hand columns in Tables 1– 3 and Figure 2 present the predictions of inertia sampling and weighting (I–SAW) with these distributions. These exhibits reveal that I–SAW reproduces the main behavioral tendencies. For example, I–SAW correctly captures the direction (sign) of the recency effect in 38 of the 40 contingencies (20 games × 2 possible recent choices). The correlation between the 20 observed and predicted mean choice rates is 0.85, and the correlation between the 80 observed and predicted contingent choice rates is 0.94.
We believe that the most important contribution of I–SAW is the demonstration that the surprise-trigger-change assumption is sufficient to capture direction of the recency effect in the current setting. It is not necessary to assume expectations concerning specific sequential dependencies (e.g., the expectation that +10 in Problem 1 is more likely after −1); nor is it necessary to relax the assumption that good outcomes increases the tendency to choose the reinforced alternative again.
Comparison with the Explorative Sampler Model
Inertia sampling and weighting differs from the explorative sampler model that motivates it in four ways; the changes include two simplification assumptions, and two additions. The first simplification involves the probability of exploration. The explorative sampler assumes a continuous decrease in the probability of exploration with time. Specifically, 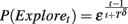 where T is the expected length of the experiment, and δ is a free parameter that captures the sensitivity to the length of the experiment. This assumption is simplified in I–SAW with the assertion that P(Exploret) = 1 if t = 1, and εi otherwise. The main motivation for the simplification is the current focus on learning with complete feedback that reduces the importance of exploration (the explorative sampler, in contrast, was designed to address learning when the feedback in limited to the obtained payoff). A second motivation is the observation that the simplification assumption saves a parameter, and does not reduce the fit of the current data.
where T is the expected length of the experiment, and δ is a free parameter that captures the sensitivity to the length of the experiment. This assumption is simplified in I–SAW with the assertion that P(Exploret) = 1 if t = 1, and εi otherwise. The main motivation for the simplification is the current focus on learning with complete feedback that reduces the importance of exploration (the explorative sampler, in contrast, was designed to address learning when the feedback in limited to the obtained payoff). A second motivation is the observation that the simplification assumption saves a parameter, and does not reduce the fit of the current data.
A second simplification concerns with the recalled subjective value of the objective outcomes. The explorative sampler allows for the possibility of a non-linear function in the spirit of prospect theory (Kahneman and Tversky, 1979) that implies diminishing sensitivity. This assumption is simplified in I–SAW with the implicit assumption that the recalled values are the objective payoffs. This simplification assumption saves a parameter, and does not reduce the fit.
The main addition, introduced in I–SAW, is the surprise-trigger-change assumption. In order to evaluate the significance of this assumption we evaluated a simplified variant of I–SAW that does not include this addition (the inertia trait, πi, is set to zero). The results reveal that with this constraint, I–SAW predicts positive recency in all 40 cases (and for that reason in capture the direction of the recency effect in only 31 of the 40 cases). In addition, this constraint reduces the correlation between the observed and predicted contingent R-rates from 0.94 to 0.77.
The second addition is the individual differences assumed in I–SAW. This addition does not increase the number of free parameters and was introduced to capture the consistent individual differences documented in recent learning studies (see Yechiam et al., 2005). Elimination of this addition has limited effect on the fit of the statistics discussed above.
Potential Generality and Alternative Models
Recall that the current paper is based on the assertion that similar learning processes drive behavior in simple laboratory experiments and in the stock market. This assertion has directed our choice of model. That is, I–SAW is meant to be more than an ad hoc summary of the current results; it tries to summarize the basic properties of decisions from experience, and should be able to provide useful prediction of behavior in a wide set of situations. In order to evaluate this optimistic “generality hypothesis” it is constructive to consider the results of a recent choice prediction competition that was organized by Erev et al. (2010b).
The competition was conducted after the completion of the first draft of the current paper (which included the data and the presentation of I–SAW), and focused on the prediction of behavior in four-person two-alternative Market Entry games. In each trial of these games, each player has to decide between a safe option and risky entry to a market in which the payoff can decrease with the number of entrants. Notice that the set of individual decision tasks considered above is a subset of the class of market entry games (the subset in which the payoffs from risky choice do not decrease with the number of other entrants).
The competition was based on two studies. Each study examined 40 games (randomly selected from the same population of games). Each game was played for 50 trials with immediate feedback concerning the obtained and the forgone payoffs. After the completion of the first study the organizers published the “introduction to the competition paper” (Erev et al., 2010b). This paper presents the results, and the best fit of these results with nine baseline models. The baseline models included the most popular models proposed to capture behavior in games (including: several versions of reinforcement learning, Erev and Roth, 1998; stochastic fictitious play, Fudenberg and Levine, 1998; EWA, Camerer and Ho, 1999) and I–SAW. The analysis of the fit of these models revealed a large advantage of I–SAW over the other models.
Immediately after the publication of the introduction paper, and before running the second study, the competition organizers challenged other researchers to participate in a competition that focuses on the prediction of the results of the second study. The call for participation in the competition was published in leading Email lists in psychology of decision making, cognitive psychology, behavioral economics, game theory, and reinforcement learning. To participate in the competition the potential competitors had to submit a model implemented in a computer program model that reads the parameters of the games as input, and derives the results as an output. The models were ranked based on their mean squared error. The participants were allowed to use improved versions of the baseline models.
Twenty-five teams participated in the competition. The submitted models included reinforcement learning, neural networks, ACT-R, and I–SAW like sampling models. The results reveal large advantage of sampling models that assume reliance on small samples and the current surprise-triggers-change rule. Indeed, all the 10 leading submissions belong to this class of models. The winner of the competition (Chen et al., 2011) is a variant of I–SAW that adds the assumption of bounded memory. The runner up (Gonzalez et al., 2011) quantifies the same assumptions in a refinement of the instance based learning model (Gonzalez et al., 2003).
It is important to emphasize that the advantage of I–SAW over the reinforcement learning models that were examined in the competition does not question that value of the reinforcement learning approach. Rather, this observation suggests that it is not easy to outperform I–SAW with the natural extensions of the popular reinforcement learning models. We hope that the publication of the competition and the current results will facilitate the exploration of the assumptions that have to be added to basic reinforcement learning models in order to capture decisions from experience. It seems that these assumptions will include sensitivity to recent choices (see similar observation in Lau and Glimcher, 2005).
In summary, the results clarify potential of simple learning models that assume reliance on small samples and surprise-trigger-change. Models of this type can be used to provide useful ex ante prediction in a wide set of situations. In addition, the competition suggests that additional research is needed to improve our understanding of the best quantification of these assumptions.
Relationship to Models of Pavlovian Conditioning
Comparison of I–SAW to the leading models of Pavlovian conditioning (including Rescorla and Wagner, 1972; Pearce and Hall, 1980) reveals one similarity, and one difference. The similarity involves the quantification of surprise by the difference between the expected and obtained outcomes. The difference involves the implication of surprise. The Rescorla–Wagner and similar models suggest that “surprise triggers learning,” and the current analysis suggests that “surprise triggers change.” This difference, however, does not imply an inconsistency: the Rescorla–Wagner model focuses on associative strength and do not have clear predictions for choice behavior. Our favorite interpretation of the effect of associative strength on choice behavior is based on Rescorla and Solomon (1967) two-process learning theory; this interpretation implies that the associative strength determines the similarity function that affects the sampling in I–SAW and similar models. We hope to address this and alternative explanations of the relationship between the current results and Pavlovian conditioning in future research.
Conclusion
The main implications of the current results are related to two of the main assumptions of basic learning research. The first assumption states that learning processes are extremely general and robust. They are common to different species (Shafir et al., 2008), underlay behavior in wide sets of situations (Skinner, 1938), and reflect basic properties of the brain (Schultz, 1998). The current analysis demonstrates the value this assumption. It shows that the apparent inconsistency between the recency effects documented in financial data and in basic learning research does not imply distinct behavioral tendencies. Examination of the sequential dependencies reveals that the fourfold recency pattern, suggested by the financial data, is a robust property of basic learning processes.
The second assumption involves the abstraction of the robust properties of learning. Most leading models assume a general positive recency effect. The current results highlight three boundaries of this effect. Two boundaries are the negative recency parts of fourfold recency pattern: Positively surprising outcomes were found to reduce the likelihood of repeated choice of the reinforcing prospect, and surprising unattractive forgone payoffs were found to increase the tendency of a switch to the prospect that led to the worst payoffs. A third boundary is suggested by the very recent effect. The current results suggest that the most recent trial has larger effect than previous experiences, but all previous experiences have an approximately the same effect independently of their recency.
The current analysis suggests that the distinct effects of recent outcomes can be captured with simple models that share two main assumptions: reliance on small samples of past experiences, and surprise-triggers-change. I–SAW, the model proposed above, is one abstraction of these assumptions. One explanation for the success of I–SAW and similar models here and in the choice prediction competition (Erev et al., 2010b), is related to the dynamic features of natural environments. The positive recency assumption is useful (likely to be selected by consequences) when the recent outcomes are best predictors of the next outcomes. But positive recency is not likely to be effective if the outcomes are determined by a Markov process with small number of distinguishable states. The reliance on the outcomes obtained in similar (and not necessarily recent) experiences, and high sensitivity to surprises, can be more effective in these settings. Thus, it is possible that the success of sampling based models reflects the ecological importance of learning in environments with relatively small number of distinguishable states.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research was supported by a grant from the Israel Science Foundation.
Footnotes
- ^Several studies highlight interesting exceptions to this regularity. One example is the evidence for negative recency in prediction tasks (Barron and Yechiam, 2009). Ayton and Fischer (2004) show that negative recency is more likely to emerge in expectations of sequences of natural events.
- ^Previous studies of the effect of surprise (Mellers et al., 1997) show that surprising outcomes are overweighted. The main additions of the current hypothesis are the assertions that (1) surprising outcome have the same effect on the implicit decision of whether to think again during learning, and that (2) without this overweighting the common implicit decision is “not to think again.”
- ^One contributor to the tendency to focus on the main effect and ignore the level of surprise is the fact that most basic learning studies focus on situations in which the feedback was limited to the obtained payoffs (and the computation of the net effect of surprise is difficult), and/or situations that do not involve low probability outcomes. Another contributor is the fact that the assumption that surprise triggers change dramatically complicates parameter estimation with the leading statistical methods.
- ^The remaining 12 participants did not face one or more of the eight contingencies. For example, 10 of them never experienced the payoff “+10” after selecting R (because they tended to select S and/or were unlucky).
- ^Computer programs (in SAS and Matlab) that derive the predictions of the current model can be downloaded from http://sites.google.com/site/gpredcomp/7-baseline-models.
- ^The current implementation of the model is simplified with the assumption that all previous trials are equally similar. The simplification assumption has to be modified to address learning in dynamic settings.
- ^This assumption implies that the sampling probability is independent of the outcome (of the sampled experiences). The assumed independence implies underweighting of rare events, and distinguishes the current models from the “representativeness heuristic” that can lead to overweighting of rare (low base rate) events (see Erev et al., 2008).
References
Ayton, P., and Fischer, I. (2004). The hot hand fallacy and the gambler’s fallacy: two faces of subjective randomness? Mem. Cognit. 32, 1369–1378.
Barron, G., and Erev, I. (2003). Small feedback-based decisions and their limited correspondence to description based decisions. J. Behav. Decis. Mak. 16, 215–233.
Barron, G., and Yechiam, E. (2009). The coexistence of over estimation and underweighting of rare events and the contingent recency effect. Judgm. Decis. Mak. 4, 447–460.
Biele, G., Erev, I., and Ert, E. (2009). Learning, risk attitude and hot stoves in restless bandit problems. J. Math. Psychol. 53, 155–167.
Camerer, C., and Ho, T. (1999). Experience weighted attraction learning normal form games. Econometrica 67, 827–874.
Chen, W., Liu, S., Chen, C.-H., and Lee, Y.-S. (2011). Bounded memory, inertia, sampling and weighting model for market entry games. Games 2, 187–199.
Dayan, P., and Niv, Y. (2008). Reinforcement learning: the good, the bad and the ugly current opinion in neurobiology. 18, 185–196.
Erev, I., Ert, E., and Yechiam, E. (2008). Loss aversion, diminishing sensitivity, and the effect of experience on repeated decisions. J. Behav. Decis. Mak. 21, 575–597.
Erev, I., Ert, E., Roth, A. E., Haruvy, E., Herzog, S., Hau, R., Hertwig, R., Stewart, T., West, R., and Lebiere, C. (2010a). A choice prediction competition, for choices from experience and from description. J. Behav. Decis. Mak. 23, 15–47.
Erev, I., Ert, E., and Roth, A. E. (2010b). A choice prediction competition for market entry games: an introduction. Games 1, 117–136.
Erev, I., and Haruvy, E. (in press). “Learning and the economics of small decisions,” in The Handbook of Experimental Economics, eds J. H. Kagel and A. E. Roth (Princeton University Press).
Erev, I., and Roth, A. E. (1998). Prediction how people play games: reinforcement learning in games with unique strategy equilibrium. Am. Econ. Rev. 88, 848–881.
Gonzalez, C., Dutt, V., and Lejarraga, T. (2011). A loser can be a winner: comparison of two instance-based learning models in a market entry competition. Games 2, 136–162.
Gonzalez, C., Lerch, J. F., and Lebiere, C. (2003). Instance-based learning in dynamic decision making. Cogn. Sci. 27, 591–635.
Grosskopf, B., Erev, I., and Yechiam, E. (2006). Foregone with the wind: indirect payoff information and its implications for choice. Int. J. Game Theory 34, 285–302.
Haruvy, E., and Erev, I. (2002). On the application and interpretation of learning models,” in Experimental Business Research, eds R. Zwick and A. Rapoport (Boston: Kluwer Academic Publishers), 285–300.
Hertwig, R., and Erev, I. (2009). The description–experience gap in risky choice. Trends Cogn. Sci. (Regul. Ed.) 13, 517–523.
Kahneman, D., and Tversky, A. (1979). Prospect theory: an analysis of decision under risk. Econometrica 47, 263–291.
Karpoff, J. M. (1988). Costly short sales and the correlation of returns with volume. J. Financ. Res. 11, 173–188.
Lau, B., and Glimcher, P. W. (2005). Dynamic response-by-response models of matching behavior in rhesus monkeys. J. Exp. Anal. Behav. 84, 555–579.
Marchiori, D., and Warglien, M. (2008). Predicting human interactive learning by regret driven neural networks. Science 319, 1111–1113.
Mellers, B., Schwartz, A., Ho, K., and Ritov, I. (1997). Elation and disappointment: emotional responses to risky options. Psychol. Sci. 8, 423–429.
Montague, P. R., Dayan, P., and Sejnowski, T. J. (1996). A framework for mesencephalic dopamine systems based on predictive Hebbian learning. J. Neurosci. 16, 1936–1947.
Montague, P. R., Hyman, S. E., and Cohen, J. D. (2004). Computational roles for dopamine in behavioural control. Nature 431, 760–767.
Pearce, J. M., and Hall, G. (1980). A model for Pavlovian learning: variations in the effectiveness of conditioned but not unconditioned stimuli. Psychol. Rev. 87, 532–552.
Rescorla, R. A., and Solomon, R. L. (1967). Two-process learning theory: relationships between Pavlovian conditioning and instrumental learning. Psychol. Rev. 74, 151–182.
Rescorla, R. A., and Wagner, A. R. (1972). “A theory of Pavlovian conditioning: variations in the effectiveness of reinforcement and nonreinforcement,” in Classical Conditioning II: Current Research and Theory, eds A. H. Black and W. F. Prokasy (New York: Appleton-Century-Crofts), 64–99.
Schultz, W. (1992). Activity of dopamine neurons in the behaving primate. Semin. Neurosci. 4, 129–138.
Selten, R., and Buchta, J. (1998). “Experimental sealed bid first price auctions with directly observed bid functions,” in Games and Human Behaviour, eds D. Budescu, I. Erev, and R. Zwick (Mahwah, NJ: Lawrence Erlbaum Associates), 79–102.
Shafir, S., Reich, T., Tsur, E., Erev, I., and Lotem, A. (2008). Perceptual accuracy and conflicting effects of certainty on risk-taking behavior. Nature 453, 917–920.
Thorndike, E. L. (1898). Animal intelligence: an experimental study of the associative processes in animals. Psychol. Rev. Monogr. Suppl. 2, 1–8.
Keywords: fourfold response pattern to recent outcomes, positive and negative recency, the very recent effect, I-SAW, volume of trade
Citation: Nevo I and Erev I (2012) On surprise, change, and the effect of recent outcomes. Front. Psychology 3:24. doi: 10.3389/fpsyg.2012.00024
Received: 05 October 2011;
Paper pending published: 24 October 2011;
Accepted: 19 January 2012;
Published online: 21 February 2012.
Edited by:
Eldad Yechiam, Technion – Israel Institute of Technology, IsraelReviewed by:
Eldad Yechiam, Technion – Israel Institute of Technology, IsraelItzhak Aharon, The Interdisciplinary Center, Israel
Copyright: © 2012 Nevo and Erev. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Ido Erev, The Max Wertheimer Minerva Center for Cognitive Studies, Faculty of Industrial Engineering and Management, Technion – Israel Institute of Technology, Haifa, Israel. e-mail:ZXJldkB0eC50ZWNobmlvbi5hYy5pbA==
 Iris Nevo
Iris Nevo