Yanyan Sheng1* Zhaohui Sheng2
- 1 Department of Educational Psychology and Special Education, Southern Illinois University, Carbondale, IL, USA
- 2 Department of Educational Leadership, Western Illinois University, Macomb, IL, USA
Coefficient alpha has been a widely used measure by which internal consistency reliability is assessed. In addition to essential tau-equivalence and uncorrelated errors, normality has been noted as another important assumption for alpha. Earlier work on evaluating this assumption considered either exclusively non-normal error score distributions, or limited conditions. In view of this and the availability of advanced methods for generating univariate non-normal data, Monte Carlo simulations were conducted to show that non-normal distributions for true or error scores do create problems for using alpha to estimate the internal consistency reliability. The sample coefficient alpha is affected by leptokurtic true score distributions, or skewed and/or kurtotic error score distributions. Increased sample sizes, not test lengths, help improve the accuracy, bias, or precision of using it with non-normal data.
Introduction
Coefficient alpha (Guttman, 1945; Cronbach, 1951) has been one of the most commonly used measures today to assess internal consistency reliability despite criticisms of its use (e.g., Raykov, 1998; Green and Hershberger, 2000; Green and Yang, 2009; Sijtsma, 2009). The derivation of the coefficient is based on classical test theory (CTT; Lord and Novick, 1968), which posits that a person’s observed score is a linear function of his/her unobserved true score (or underlying construct) and error score. In the theory, measures can be parallel (essential) tau-equivalent, or congeneric, depending on the assumptions on the units of measurement, degrees of precision, and/or error variances. When two tests are designed to measure the same latent construct, they are parallel if they measure it with identical units of measurement, the same precision, and the same amounts of error; tau-equivalent if they measure it with the same units, the same precision, but have possibly different error variance; essentially tau-equivalent if they assess it using the same units, but with possibly different precision and different amounts of error; or congeneric if they assess it with possibly different units of measurement, precision, and amounts of error (Lord and Novick, 1968; Graham, 2006). From parallel to congeneric, tests are requiring less strict assumptions and hence are becoming more general. Studies (Lord and Novick, 1968, pp. 87–91; see also Novick and Lewis, 1967, pp. 6–7) have shown formally that the population coefficient alpha equals internal consistency reliability for tests that are tau-equivalent or at least essential tau-equivalent. It underestimates the actual reliability for the more general congeneric test. Apart from essential tau-equivalence, coefficient alpha requires two additional assumptions: uncorrelated errors (Guttman, 1945; Novick and Lewis, 1967) and normality (e.g., Zumbo, 1999). Over the past decades, studies have well documented the effects of violations of essential tau-equivalence and uncorrelated errors (e.g., Zimmerman et al., 1993; Miller, 1995; Raykov, 1998; Green and Hershberger, 2000; Zumbo and Rupp, 2004; Graham, 2006; Green and Yang, 2009), which have been considered as two major assumptions for alpha. The normality assumption, however, has received little attention. This could be a concern in typical applications where the population coefficient is an unknown parameter and has to be estimated using the sample coefficient. When data are normally distributed, sample coefficient alpha has been shown to be an unbiased estimate of the population coefficient alpha (Kristof, 1963; van Zyl et al., 2000); however, less is known about situations when data are non-normal.
Over the past decades, the effect of departure from normality on the sample coefficient alpha has been evaluated by Bay (1973), Shultz (1993), and Zimmerman et al. (1993) using Monte Carlo simulations. They reached different conclusions on the effect of non-normal data. In particular, Bay (1973) concluded that a leptokurtic true score distribution could cause coefficient alpha to seriously underestimate internal consistency reliability. Zimmerman et al. (1993) and Shultz (1993), on the other hand, found that the sample coefficient alpha was fairly robust to departure from the normality assumption. The three studies differed in the design, in the factors manipulated and in the non-normal distributions considered, but each is limited in certain ways. For example, Zimmerman et al. (1993) and Shultz (1993) only evaluated the effect of non-normal error score distributions. Bay (1973), while looked at the effect of non-normal true score or error score distributions, only studied conditions of 30 subjects and 8 test items. Moreover, these studies have considered only two or three scenarios when it comes to non-normal distributions. Specifically, Bay (1973) employed uniform (symmetric platykurtic) and exponential (non-symmetric leptokurtic with positive skew) distributions for both true and error scores. Zimmerman et al. (1993) generated error scores from uniform, exponential, and mixed normal (symmetric leptokurtic) distributions, while Shultz (1993) generated them using exponential, mixed normal, and negative exponential (non-symmetric leptokurtic with negative skew) distributions. Since the presence of skew and/or kurtosis determines whether and how a distribution departs from the normal pattern, it is desirable to consider distributions with varying levels of skew and kurtosis so that a set of guidelines can be provided. Generating univariate non-normal data with specified moments can be achieved via the use of power method polynomials (Fleishman, 1978), and its current developments (e.g., Headrick, 2010) make it possible to consider more combinations of skew and kurtosis.
Further, in the actual design of a reliability study, sample size determination is frequently an important and difficult aspect. The literature offers widely different recommendations, ranging from 15 to 20 (Fleiss, 1986), a minimum of 30 (Johanson and Brooks, 2010) to a minimum of 300 (Nunnally and Bernstein, 1994). Although Bay (1973) has used analytical derivations to suggest that coefficient alpha shall be robust against the violation of the normality assumption if sample size is large, or the number of items is large and the true score kurtosis is close to zero, it is never clear how many subjects and/or items are desirable in such situations.
In view of the above, the purpose of this study is to investigate the effect of non-normality (especially the presence of skew and/or kurtosis) on reliability estimation and how sample sizes and test lengths affect the estimation with non-normal data. It is believed that the results will not only shed insights on how non-normality affects coefficient alpha, but also provide a set of guidelines for researchers when specifying the numbers of subjects and items in a reliability study.
Materials and Methods
This section starts with a brief review of the CTT model for coefficient alpha. Then the procedures for simulating observed scores used in the Monte Carlo study are described, followed by measures that were used to evaluate the performance of the sample alpha in each simulated situation.
Preliminaries
Coefficient alpha is typically associated with true score theory (Guttman, 1945; Cronbach, 1951; Lord and Novick, 1968), where the test score for person i on item j, denoted as Xij, is assumed to be a linear function of a true score (tij) and an error score (eij):
i = 1, …, n and j = 1, …, k, where E(eij) = 0, ρte= 0, and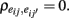 
Here, eij denotes random error that reflects unpredictable trial-by-trial fluctuations. It has to be differentiated from systematic error that reflects situational or individual effects that may be specified. In the theory, items are usually assumed to be tau-equivalent, where true scores are restricted to be the same across items, or essentially tau-equivalent, where they are allowed to differ from item to item by a constant (υj). Under these conditions (1) becomes
i = 1, …, n and j = 1, …, k, where E(eij) = 0, ρte= 0, and 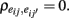Here, eij denotes random error that reflects unpredictable trial-by-trial fluctuations. It has to be differentiated from systematic error that reflects situational or individual effects that may be specified. In the theory, items are usually assumed to be tau-equivalent, where true scores are restricted to be the same across items, or essentially tau-equivalent, where they are allowed to differ from item to item by a constant (υj). Under these conditions (1) becomes
for tau-equivalence, and
where Σjυj= 0, for essential tau-equivalence.
Summing across k items, we obtain a composite score (Xi+) and a scale error score (ei+). The variance of the composite scores is then the summation of true score and scale error score variances:
The reliability coefficient, ρXX′, is defined as the proportion of composite score variance that is due to true score variance:
Under (essential) tau-equivalence, that is, for models in (2) and (3), the population coefficient alpha, defined as
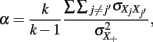
or
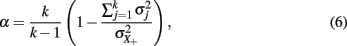
is equal to the reliability as defined in (5). As was noted, ρXX′ and α focus on the amount of random error and do not evaluate error that may be systematic.
Although the derivation of coefficient alpha based on Lord and Novick (1968) does not require distributional assumptions for ti and eij, its estimation does (see Shultz, 1993; Zumbo, 1999), as the sample coefficient alpha estimated using sample variances s2,
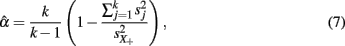
is shown to be the maximum likelihood estimator of the population alpha assuming normal distributions (Kristof, 1963; van Zyl et al., 2000). Typically, we assume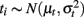 
and 
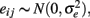where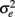 
has to be differentiated from the scale error score variance 
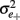defined in (4).
Study Design
To evaluate the performance of the sample alpha as defined in (7) in situations where true score or error score distributions depart from normality, a Monte Carlo simulation study was carried out, where test scores of n persons (n = 30, 50, 100, 1000) for k items (k = 5, 10, 30) were generated assuming tau-equivalence and where the population reliability coefficient (ρXX′) was specified to be 0.3, 0.6, or 0.8 to correspond to unacceptable, acceptable, or very good reliability (Caplan et al., 1984, p. 306; DeVellis, 1991, p. 85; Nunnally, 1967, p. 226). These are referred to as small, moderate, and high reliabilities in subsequent discussions. Specifically, true scores (ti) and error scores (eij) were simulated from their respective distributions with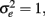 
μt= 5 and 
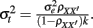The observed scores (Xij) were subsequently obtained using Eq. (2).
In addition, true score or error score distributions were manipulated to be symmetric (so that skew, γ1, is 0) or non-symmetric (γ1 > 0) with kurtosis (γ2) being 0, negative or positive. It is noted that only positively skewed distributions were considered in the study because due to the symmetric property, negative skew should have the same effect as positive skew. Generating non-normal distributions in this study involves the use of power method polynomials. Fleishman (1978) introduced this popular moment matching technique for generating univariate non-normal distributions. Headrick (2002, 2010) further extended from third-order to fifth-order polynomials to lower the skew and kurtosis boundary. As is pointed out by Headrick (2010, p. 26), for distributions with a mean of 0 and a variance of 1, the skew and kurtosis have to satisfy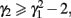 
and hence it is not plausible to consider all possible combinations of skew and kurtosis using power method polynomials. Given this, six distributions with the following combinations of skew and kurtosis were considered:
1. γ1 = 0, γ2 = 0 (normal distribution);
2. γ1 = 0, γ2 = − 1.385 (symmetric platykurtic distribution);
3. γ1 = 0, γ2 = 25 (symmetric leptokurtic distribution);
4. γ1 = 0.96, γ2 = 0.13 (non-symmetric distribution);
5. γ1 = 0.48, γ2 = − 0.92 (non-symmetric platykurtic distribution);
6. γ1 = 2.5, γ2 = 25 (non-symmetric leptokurtic distribution).
A normal distribution was included so that it could be used as a baseline against which the non-normal distributions could be compared. To actually generate univariate distributions using the fifth-order polynomial transformation, a random variate Z is first generated from a standard normal distribution, Z ∼ N(0,1). Then the following polynomial,
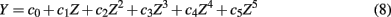
is used to obtain Y. With appropriate coefficients (c0, …, c5), Y would follow a distribution with a mean of 0, a variance of 1, and the desired levels of skew and kurtosis (see Headrick, 2002, for a detailed description of the procedure). A subsequent linear transformation would rescale the distribution to have a desired location or scale parameter. In this study, Y could be the true score (ti) or the error score (eij). For the six distributions considered for ti or eij herein, the corresponding coefficients are:
1. c0 = 0, c1 = 1, c2 = 0, c3 = 0, c4 = 0, c5 = 0;
2. c0 = 0, c1 = 1.643377, c2 = 0, c3 = −0.319988, c4 = 0, c5 = 0.011344;
3. c0 = 0, c1 = 0.262543, c2 = 0, c3 = 0.201036, c4 = 0, c5 = 0.000162;
4. c0 = −0.446924, c1 = 1.242521, c2 = 0.500764, c3 = −0.184710, c4 = −0.017947, c5 = 0.003159;
5. c0 = −0.276330, c1 = 1.506715, c2 = 0.311114, c3 = −0.274078, c4 = −0.011595, c5 = 0.007683;
6. c0 = −0.304852, c1 = 0.381063, c2 = 0.356941, c3 = 0.132688, c4 = −0.017363, c5 = 0.003570.
It is noted that the effect of the true score or error score distribution was investigated independently, holding the other constant by assuming it to be normal.
Hence, a total of 4 (sample sizes) × 3 (test lengths) × 3 (levels of population reliability) × 6 (distributions) × 2 (true or error score) = 432 conditions were considered in the simulation study. Each condition involved 100,000 replications, where coefficient alpha was estimated using Eq. (7) for simulated test scores (Xij). The 100,000 estimates of α can be considered as random samples from the sampling distribution of 
and its summary statistics including the observed mean, SD, and 95% interval provide information about this distribution. In particular, the observed mean indicates whether the sample coefficient is biased. If it equals α,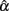 
is unbiased; otherwise, it is biased either positively or negatively depending on whether it is larger or smaller than α. The SD of the sampling distribution is what we usually call the SE. It reflects the uncertainty in estimating α, with a smaller SE suggesting more precision and hence less uncertainty in the estimation. The SE is directly related to the 95% observed interval, as the larger it is, the more spread the distribution is and the wider the interval will be. With respect to the observed interval, it contains about 95% of 
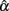around its center location from its empirical sampling distribution. If α falls inside the interval, 
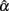is not significantly different from α even though it is not unbiased. On the other hand, if α falls outside of the interval, which means that 95% of the estimates differ from α, we can consider 
to be significantly different from α.
In addition to these summary statistics, the accuracy of the estimate was evaluated by the root mean square error (RMSE) and bias, which are defined as
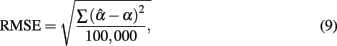
and
respectively. The larger the RMSE is, the less accurate the sample coefficient is in estimating the population coefficient. Similarly, the larger the absolute value of the bias is, the more bias the sample coefficient involves. As the equations suggest, RMSE is always positive, with values close to zero reflecting less error in estimating the actual reliability. On the other hand, bias can be negative or positive. A positive bias suggests that the sample coefficient tends to overestimate the reliability, and a negative bias suggests that it tends to underestimate the reliability. In effect, bias provides similar information as the observed mean of the sampling distribution of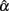 
.
Results
The simulations were carried out using MATLAB (MathWorks, 2010), with the source code being provided in the Section “Appendix.” Simulation results are summarized in Tables 1–3 for conditions where true scores follow one of the six distributions specified in the previous section. Here, results from the five non-normal distributions were mainly compared with those from the normal distribution to determine if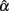 
was affected by non-normality in true scores. Take the condition where a test of 5 items with the actual reliability being 0.3 was given to 30 persons as an example. A normal distribution resulted in an observed mean of 0.230 and a SE of 0.241 for the sampling distribution of 
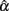(see Table 1). Compared with it, a symmetric platykurtic distribution, with an observed mean of 0.234 and a SE of 0.235, did not differ much. On the other hand, a symmetric leptokurtic distribution resulted in a much smaller mean (0.198) and a larger SE (0.290), indicating that the center location of the sampling distribution of 
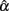was further away from the actual value (0.3) and more uncertainty was involved in estimating α. With respect to the accuracy of the estimate, Table 2 shows that the normal distribution had a RMSE of 0.251 and a bias value of −0.070. The platykurtic distribution gave rise to smaller but very similar values: 0.244 for RMSE and −0.066 for bias, whereas the leptokurtic distribution had a relatively larger RMSE value (0.308) and a smaller bias value (−0.102), indicating that it involved more error and negative bias in estimating α. Hence, under this condition, positive kurtosis affected (the location and scale of) the sampling distribution of 
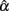as well as the accuracy of using it to estimate α whereas negative kurtosis did not. Similar interpretations are used for the 95% interval shown in Table 3, except that one can also use the intervals to determine whether the sample coefficient was significantly different from α as described in the previous section.
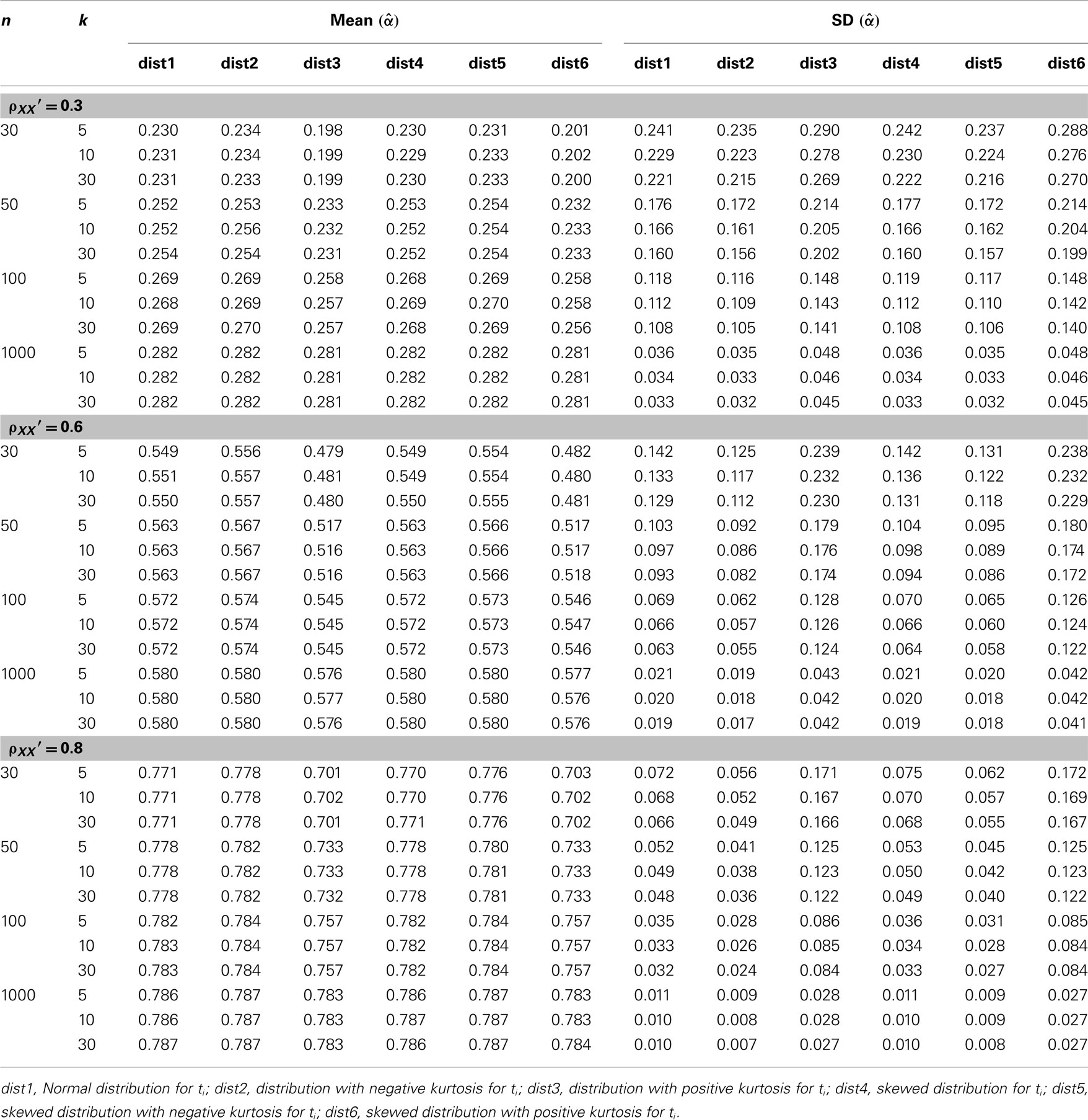
Table 1. Observed mean and SD of the sample alpha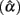 
for the simulated situations where the true score (ti) distribution is normal or non-normal.
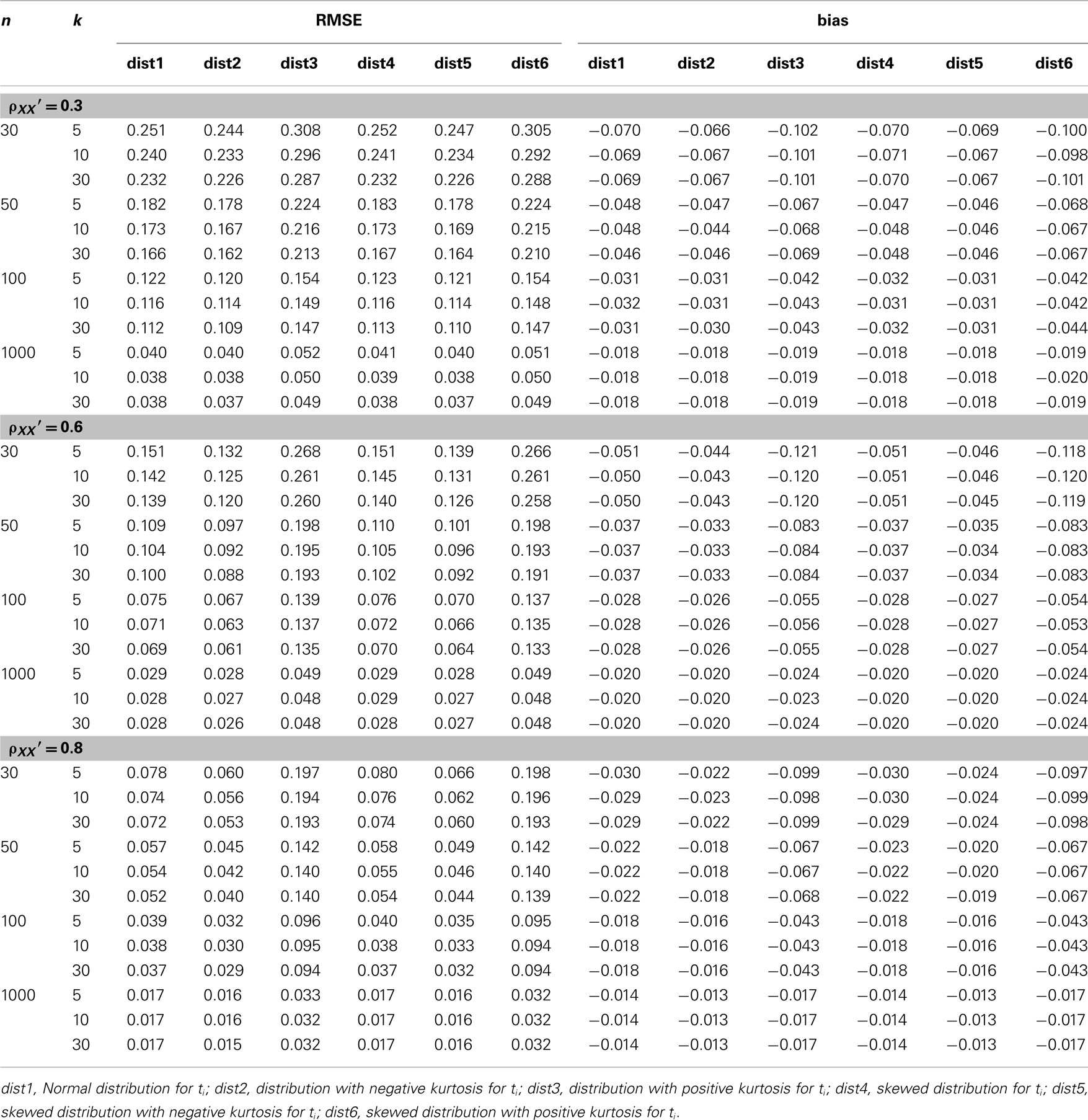
Table 2. Root mean square error and bias for estimating α for the simulated situations where the true score (t i) distribution is normal or non-normal.
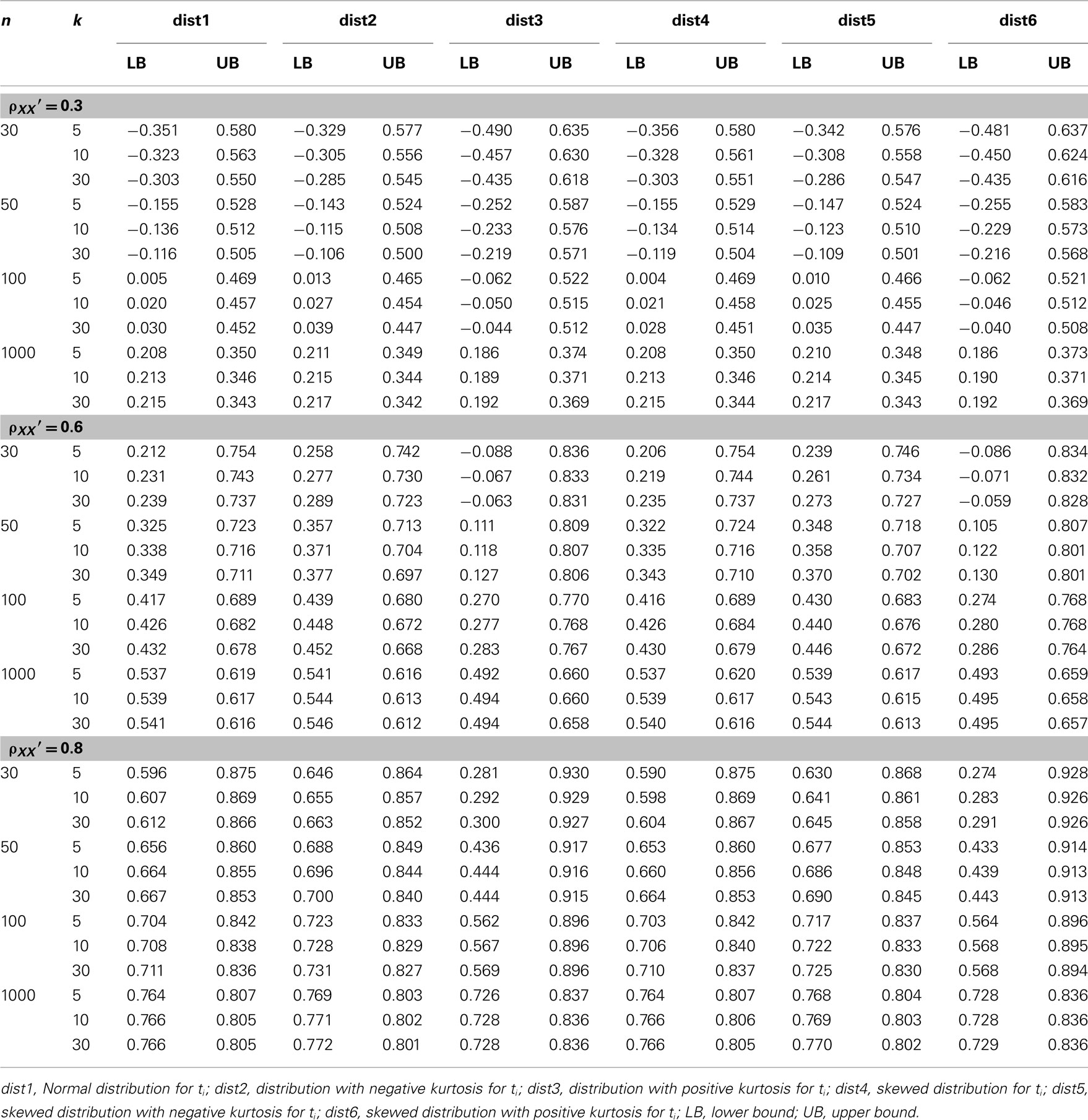
Table 3. Observed 95% interval of the sample alpha 
for the simulated situations where the true score (t i) distribution is normal or non-normal.
Guided by these interpretations, one can make the following observations:
1. Among the five non-normal distributions considered for ti, skewed or platykurtic distributions do not affect the mean or the SE for 
(see Table 1). They do not affect the accuracy or bias in estimating α, either (see Table 2). On the other hand, symmetric or non-symmetric distributions with positive kurtosis tend to result in a much smaller average of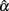 
with a larger SE (see Table 1), which in turn makes the 95% observed interval wider compared with the normal distribution (see Table 3). In addition, positive kurtosis tends to involve more bias in underestimating α with a reduced accuracy (see Table 2).
2. Sample size (n) and test length (k) play important roles for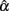 
and its sampling distribution, as increased n or k tends to result in the mean of 
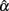that is closer to the specified population reliability (ρXX′) with a smaller SE. We note that n has a larger and more apparent effect than k. Sample size further helps offset the effect of non-normality on the sampling distribution of 
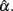In particular, when sample size gets large, e.g., n = 1000, departure from normal distributions (due to positive kurtosis) does not result in much different mean of 
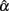although the SE is still slightly larger compared with normal distributions (see Table 1).
3. Increased n or k tends to increase the accuracy in estimating α while reducing bias. However, the effect of non-normality (due to positive kurtosis) on resulting in a larger estimating error and bias remains even with increased n and/or k (see Table 2). It is also noted that for all the conditions considered,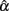 
has a consistently negative bias regardless of the shape of the distribution for ti.
4. The 95% observed interval shown in Table 3 agrees with the corresponding mean and SE shown in Table 1. It is noted that regardless of the population distribution for ti, when n or k gets larger,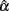 
has a smaller SE, and hence a narrower 95% interval, as the precision in estimating α increases. Given this, and that all intervals in the table, especially those for n = 1000, cover the specified population reliability (ρXX′), one should note that although departure from normality affects the accuracy, bias, and precision in estimating α, it does not result in systematically different 
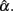In addition, when the actual reliability is small (i.e., ρXX′ = 0.3), the use of large n is suggested, as when n < 1000, the 95% interval covers negative values of 
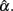This is especially the case for the (symmetric or non-symmetric) distributions with positive kurtosis. For these distributions, at least 100 subjects are needed for 
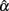to avoid relatively large estimation error when the actual reliability is moderate to large. For the other distributions, including the normal distribution, a minimum of 50 subjects is suggested for tests with a moderate reliability (i.e., ρXX′ = 0.6), and 30 or more subjects are needed for tests with a high reliability (i.e., ρXX′ = 0.8; see Table 2).
In addition, results for conditions where error scores depart from normal distributions are summarized in Tables 4–6. Given the design of the study, the results for the condition where eij followed a normal distribution are the same as those for the condition where the distribution for ti was normal. For the purpose of comparisons, they are displayed in the tables again. Inspections of these tables result in the following findings, some of which are quite different from what are observed from Tables 1–3:
1. Symmetric platykurtic distributions or non-symmetric leptokurtic distributions consistently resulted in a larger mean but not a larger SE of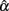 
than normal distributions (see Table 4). Some of the means, and especially those for non-symmetric leptokurtic distributions, are larger than the specified population reliability (ρXX′). This is consistent with the positive bias values in Table 5. On the other hand, symmetric leptokurtic, non-symmetric, or non-symmetric platykurtic distributions tend to have larger SE of 
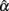than the normal distribution (see Table 4).
2. Sample size (n) and test length (k) have different effects on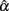 
and its sampling distribution. Increased n consistently results in a larger mean of 
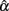with a reduced SE. However, increased k may result in a reduced SE, but it has a negative effect on the mean in pushing it away from the specified population reliability (ρXX′), especially when ρXX′ is not large. In particular, with larger k, the mean of 
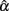decreases to be much smaller for the non-normal distributions that are leptokurtic, non-symmetric, or non-symmetric platykurtic; but it increases to exceed ρXX′ for symmetric platykurtic or non-symmetric leptokurtic distributions. It is further observed that with increased n, the difference between non-normal and normal distributions of eij on the mean and SE of 
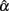reduces. This is, however, not observed for increased k (see Table 4).
3. The RMSE and bias values presented in Table 5 indicate that non-normal distributions for eij, especially leptokurtic, non-symmetric, or non-symmetric platykurtic distributions tend to involve larger error, if not bias, in estimating α. In addition, when k increases, RMSE or bias does not necessarily reduce. On the other hand, when n increases, RMSE decreases while bias increases. Hence, with larger sample sizes, there is more accuracy in estimating α, but bias is not necessarily reduced for symmetric platykurtic or non-symmetric leptokurtic distributions, as some of the negative bias values increase to become positive and non-negligible.
4. The effect of test length on the sample coefficient is more apparent in Table 6. From the 95% observed intervals for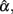 
and particularly those obtained when the actual reliability is small to moderate (i.e., ρXX′ ≤ 0.6) with large sample sizes (i.e., n = 1000), one can see that when test length gets larger (e.g., k = 30), the intervals start to fail to cover the specified population reliability (ρXX′) regardless of the degree of the departure from the normality for eij. Given the fact that larger sample sizes result in less dispersion (i.e., smaller SE) in the sampling distribution of 
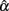and hence a narrower 95% interval, and the fact that increased k pushes the mean of 
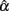away from the specified reliability, this finding suggests that larger k amplifies the effect of non-normality of eij on 
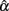in resulting in systematically biased estimates of α, and hence has to be avoided when the actual reliability is not large. With respect to sample sizes, similar patterns arise. That is, the use of large n is suggested when the actual reliability is small (i.e., ρXX′ = 0.3), especially for tests with 30 items, whereas for tests with a high reliability (i.e., ρXX′ = 0.8), a sample size of 30 may be sufficient. In addition, when the actual reliability is moderate, a minimum of 50 subjects is needed for 
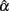to be fairly accurate for short tests (k ≤ 10), and at least 100 are suggested for longer tests (k = 30; see Table 5).
Table 4. Observed mean and SD of the sample alpha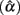 
for the simulated situations where the error score (eij) distribution is normal or non−normal.
Table 5. Root mean square error and bias for estimating α for the simulated situations where the error score (eij) distribution is normal or non−normal.
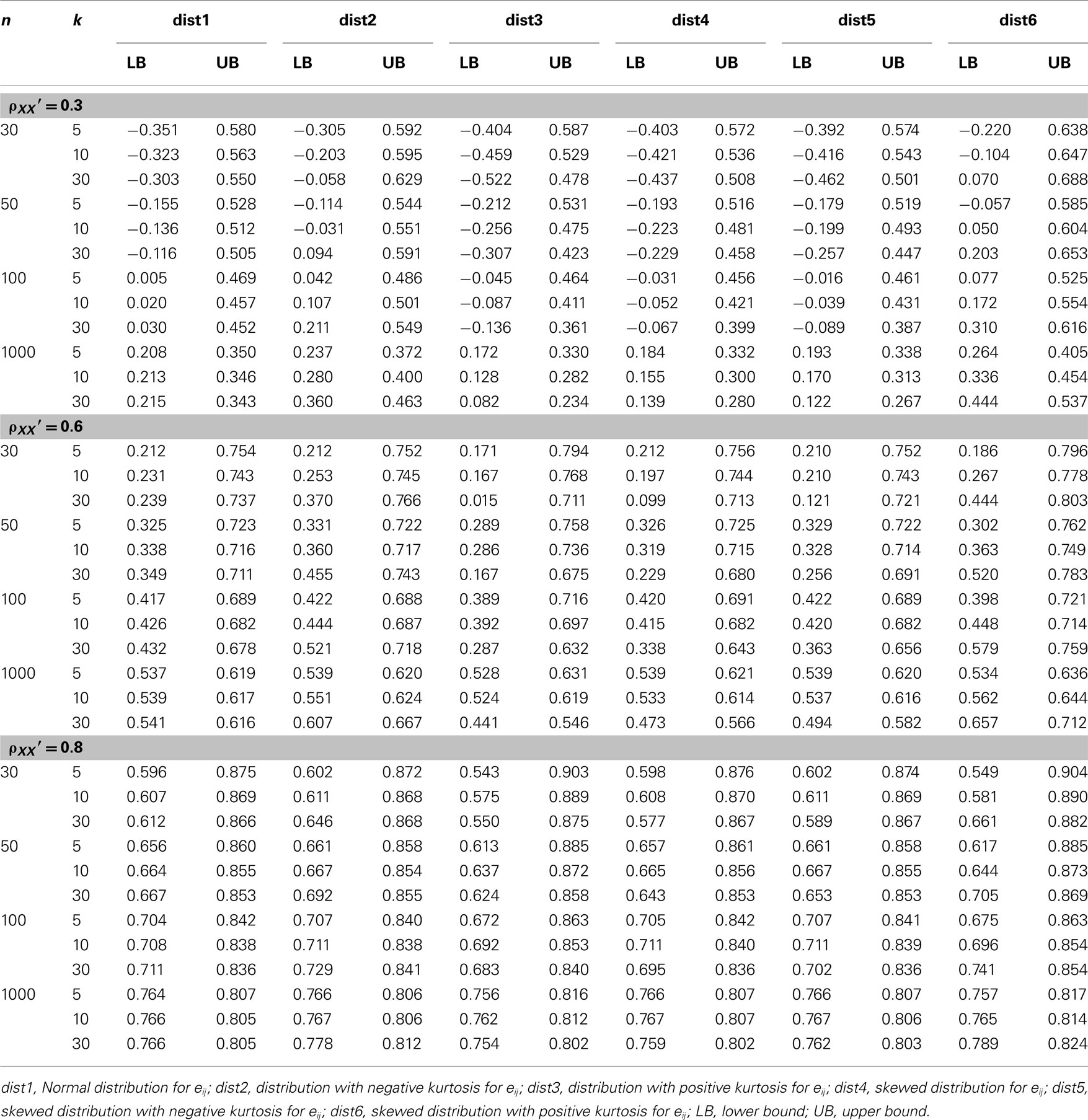
Table 6. Observed 95% interval of the sample alpha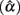 
for the simulated situations where the error score (eij) distribution is normal or non-normal.
Given the above results, we see that non-normal distributions for true or error scores do create problems for using coefficient alpha to estimate the internal consistency reliability. In particular, leptokurtic true score distributions that are either symmetric or skewed result in larger error and negative bias in estimating population α with less precision. This is similar to Bay’s (1973) finding, and we see in this study that the problem remains even after increasing sample size to 1000 or test length to 30, although the effect is getting smaller. With respect to error score distributions, unlike conclusions from previous studies, departure from normality does create problems in the sample coefficient alpha and its sampling distribution. Specifically, leptokurtic, skewed, or non-symmetric platykurtic error score distributions tend to result in larger error and negative bias in estimating population α with less precision, whereas platykurtic or non-symmetric leptokurtic error score distributions tend to have increased positive bias when sample size, test length, and/or the actual reliability increases. In addition, different from conclusions made by Bay (1973) and Shultz (1993), an increase in test length does have an effect on the accuracy and bias in estimating reliability with the sample coefficient alpha when error scores are not normal, but it is in an undesirable manner. In particular, as is noted earlier, increased test length pushes the mean of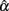 
away from the actual reliability, and hence causes the sample coefficient alpha to be significantly different from the population coefficient when the actual reliability is not high (e.g., ρXX′ ≤ 0.6) and the sample size is large (e.g., n = 1000). This could be due to the fact that eij is involved in each item, and hence an increase in the number of items would add up the effect of non-normality on the sample coefficient.
Discussion
In practice, coefficient alpha is often used to estimate reliability with little consideration of the assumptions required for the sample coefficient to be accurate. As noted by Graham (2006, p. 942), students and researchers in education and psychology are often unaware of many assumptions for a statistical procedure, and this situation is much worse when it comes to measurement issues such as reliability. In actual applications, it is vital to not only evaluate the assumptions for coefficient alpha, but also understand them and the consequences of any violations.
Normality is not commonly considered as a major assumption for coefficient alpha and hence has not been well investigated. This study takes the advantage of recently developed techniques in generating univariate non-normal data to suggest that different from conclusions made by Bay (1973), Zimmerman et al. (1993), and Shultz (1993), coefficient alpha is not robust to the violation of the normal assumption (for either true or error scores). Non-normal data tend to result in additional error or bias in estimating internal consistency reliability. A larger error makes the sample coefficient less accurate, whereas more bias causes it to further under- or overestimate the actual reliability. We note that compared with normal data, leptokurtic true or error score distributions tend to result in additional negative bias, whereas platykurtic error score distributions tend to result in a positive bias. Neither case is desired in a reliability study, as the sample coefficient would paint an incorrect picture of the test’s internal consistency by either estimating it with a larger value or a much smaller value and hence is not a valid indicator. For example, for a test with reliability being 0.6, one may calculate the sample alpha to be 0.4 because the true score distribution has a positive kurtosis, and conclude that the test is not reliable at all. On the other hand, one may have a test with actual reliability being 0.4. But because the error score distribution has a negative kurtosis, the sample coefficient is calculated to be 0.7 and hence the test is concluded to be reliable. In either scenario, the conclusion on the test reliability is completely the opposite of the true situation, which may lead to an overlook of a reliable measure or an adoption of an unreliable instrument. Consequently, coefficient alpha is not suggested for estimating internal consistency reliability with non-normal data. Given this, it is important to make sure that in addition to satisfying the assumptions of (essential) tau-equivalence and uncorrelated errors, the sample data conform to normal distributions before one uses alpha in a reliability study.
Further, it is generally said that increased data sizes help approximate non-normal distributions to be normal. This is the case with sample sizes, not necessarily test lengths, in helping improve the accuracy, bias and/or precision of using the sample coefficient in reliability studies with non-normal data. Given the results of the study, we suggest that in order for the sample coefficient alpha to be fairly accurate and in a reasonable range, a minimum of 1000 subjects is needed for a small reliability, and a minimum of 100 is needed for a moderate reliability when the sample data depart from normality. It has to be noted that for the four sample size conditions considered in the study, the sample coefficient alpha consistently underestimates the population reliability even when normality is assumed (see Table 2). However, the degree of bias becomes negligible when sample size increases to 1000 or beyond.
In the study, we considered tests of 5, 10, or 30 items administered to 30, 50, 100, or 1000 persons with the actual reliability being 0.3, 0.6, or 0.8. These values were selected to reflect levels ranging from small to large in the sample size, test length, and population reliability considerations. When using the results, one should note that they pertain to these simulated conditions and may not generalize to other conditions. In addition, we evaluated the assumption of normality alone. That is, in the simulations, data were generated assuming the other assumptions, namely (essential) tau-equivalence and uncorrelated error terms, were satisfied. In practice, it is common for observed data to violate more than one assumption. Hence, it would also be interesting to see how non-normal data affect the sample coefficient when other violations are present. Further, this study looked at the sample coefficient alpha and its empirical sampling distribution without considering its sampling theory (e.g., Kristof, 1963; Feldt, 1965). One may focus on its theoretical SE (e.g., Bay, 1973; Barchard and Hakstian, 1997a,b; Duhachek and Iacobucci, 2004) and compare them with the empirical ones to evaluate the robustness of an interval estimation of the reliability for non-normal data.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Barchard, K. A., and Hakstian, R. (1997a). The effects of sampling model on inference with coefficient alpha. Educ. Psychol. Meas. 57, 893–905.
Barchard, K. A., and Hakstian, R. (1997b). The robustness of confidence intervals for coefficient alpha under violation of the assumption of essential parallelism. Multivariate Behav. Res. 32, 169–191.
Bay, K. S. (1973). The effect of non-normality on the sampling distribution and standard error of reliability coefficient estimates under an analysis of variance model. Br. J. Math. Stat. Psychol. 26, 45–57.
Caplan, R. D., Naidu, R. K., and Tripathi, R. C. (1984). Coping and defense: constellations vs. components. J. Health Soc. Behav. 25, 303–320.
Cronbach, L. J. (1951). Coefficient alpha and the internal structure of tests. Psychometrika 16, 297–334.
Duhachek, A., and Iacobucci, D. (2004). Alpha’s standard error (ASE): an accurate and precise confidence interval estimate. J. Appl. Psychol. 89, 792–808.
Feldt, L. S. (1965). The approximate sampling distribution of Kuder-Richardson reliability coefficient twenty. Psychometrika 30, 357–370.
Fleishman, A. I. (1978). A method for simulating non-normal distributions. Psychometrika 43, 521–532.
Graham, J. M. (2006). Congeneric and (essential) tau-equivalent estimates of score reliability. Educ. Psychol. Meas. 66, 930–944.
Green, S. B., and Hershberger, S. L. (2000). Correlated errors in true score models and their effect on coefficient alpha. Struct. Equation Model. 7, 251–270.
Green, S. B., and Yang, Y. (2009). Commentary on coefficient alpha: a cautionary tale. Psychometrika 74, 121–135.
Headrick, T. C. (2002). Fast fifth-order polynomial transforms for generating univariate and multivariate nonnormal distributions. Comput. Stat. Data Anal. 40, 685–711.
Headrick, T. C. (2010). Statistical Simulation: Power Method Polynomials and Other Transformations. Boca Raton, FL: Chapman & Hall.
Johanson, G. A., and Brooks, G. (2010). Initial scale development: sample size for pilot studies. Educ. Psychol. Meas. 70, 394–400.
Kristof, W. (1963). The statistical theory of stepped-up reliability coefficients when a test has been divided into several equivalent parts. Psychometrika 28, 221–238.
Lord, F. M., and Novick, M. R. (1968). Statistical Theories of Mental Test Scores. Reading: Addison-Wesley.
Miller, M. B. (1995). Coefficient alpha: a basic introduction from the perspectives of classical test theory and structural equation modeling. Struct. Equation Model. 2, 255–273.
Novick, M. R., and Lewis, C. (1967). Coefficient alpha and the reliability of composite measurements. Psychometrika 32, 1–13.
Raykov, T. (1998). Coefficient alpha and composite reliability with interrelated nonhomogeneous items. Appl. Psychol. Meas. 22, 69–76.
Shultz, G. S. (1993). A Monte Carlo study of the robustness of coefficient alpha. Masters thesis, University of Ottawa, Ottawa.
Sijtsma, K. (2009). On the use, the misuse, and the very limited usefulness of Cronbach’s alpha. Psychometrika 74, 107–120.
van Zyl, J. M., Neudecker, H., and Nel, D. G. (2000). On the distribution of the maximum likelihood estimator for Cronbach’s alpha. Psychometrika 65, 271–280.
Zimmerman, D. W., Zumbo, B. D., and Lalonde, C. (1993). Coefficient alpha as an estimate of test reliability under violation of two assumptions. Educ. Psychol. Meas. 53, 33–49.
Zumbo, B. D. (1999). A Glance at Coefficient Alpha With an Eye Towards Robustness Studies: Some Mathematical Notes and a Simulation Model (Paper No. ESQBS-99-1). Prince George, BC: Edgeworth Laboratory for Quantitative Behavioral Science, University of Northern British Columbia.
Zumbo, B. D., and Rupp, A. A. (2004). “Responsible modeling of measurement data for appropriate inferences: important advances in reliability and validity theory,” in The SAGE Handbook of Quantitative Methodology for the Social Sciences, ed. D. Kaplan (Thousand Oaks: Sage), 73–92.
Appendix
Code in MATLAB
function result=mcalpha(n,k,evar,rho,rep)
%
% mcalpha - obtain summary statistics for sample alphas
%
% result=mcalpha(n,k,evar,rho,rep)
%
% returns the observed mean, standard deviation, and 95% interval (qtalpha)
% for sample alphas as well as the root mean square error (rmse) and bias for
% estimating the population alpha.
%
% The INPUT arguments:
% n - sample size
% k - test length
% evar - error variance
% rho - population reliability
% rep - number of replications
%
alphav=zeros(rep,1);
tbcd=[0,1,0,0,0,0];
ebcd=[0,1,0,0,0,0];
%
% note: tbcd and ebcd are vectors containing the six coefficients, c0,…,c5,
% used in equation (8) for true scores and error scores, respectively. Each
% of them can be set as:
% 1. [0,1,0,0,0,0] (normal)
% 2. [0,1.643377,0,-.319988,0,.011344] (platykurtic)
% 3. [0,0.262543,0,.201036,0,.000162] (leptokurtic)
% 4. [-0.446924 1.242521 0.500764 -0.184710 -0.017947,0.003159] (skewed)
% 5. [-.276330,1.506715,.311114,-.274078,-.011595,.007683] (skewed platykurtic)
% 6. [-.304852,.381063,.356941,.132688,-.017363,.003570] (skewed leptokurtic)
%
for i=1:rep
alphav(i)=alpha(n,k,evar,rho,tbcd,ebcd);
end
rmse=sqrt(mean((alphav-rho).^2));
bias=mean(alphav-rho);
qtalpha=quantile(alphav,[.025,.975]);
result=[mean(alphav),std(alphav),qtalpha,rmse,bias];
function A=alpha(n,k,evar,rho,tbcd,ebcd)
%
% alpha - calculate sample alpha
%
% alp=alpha(n,k,evar,rho,tbcd,ebcd)
%
% returns the sample alpha.
%
% The INPUT arguments:
% n - sample size
% k - test length
% evar - error variance
% rho - population reliability
% rep - number of replications
% tbcd - coefficients for generating normal/nonnormal true score
% distributions using power method polynomials
% ebcd - coefficients for generating normal/nonnormal error score
% distributions using power method polynomials
%
tvar=evar*rho/((1-rho)*k);
t=rfsimu(tbcd,n,1,5,tvar);
e=rfsimu(ebcd,n,k,0,evar);
xn=t*ones(1,k)+e;
x=round(xn);
alp=k/(k-1)*(1-sum(var(x,1))/var(sum(x,2),1));
function X=rfsimu(bcd,n,k,mean,var)
%
% rfsimu - generate normal/nonnormal distributions using 5-th order power
% method polynomials
%
% X=rfsimu(bcd,n,k,mean,var)
%
% returns samples of size n by k drawn from a distribution with the desired
% moments.
%
% The INPUT arguments:
% bcd - coefficients for generating normal/nonnormal distributions using
% the 5-th order polynomials
% k - test length
% evar - error variance
% rho - population reliability
% rep - number of replications
% tbcd - coefficients for generating normal/nonnormal true score
% distributions using power method polynomials
% ebcd - coefficients for generating normal/nonnormal error score
% distributions using power method polynomials
%
Z=randn(n,k);
Y=bcd(1)+bcd(2)*Z+bcd(3)*Z.^2+bcd(4)*Z.^3+bcd(5)*Z.^4
+bcd(6)*Z.^5;
X=mean+sqrt(var)*Y;
Keywords: coefficient alpha, true score distribution, error score distribution, non-normality, skew, kurtosis, Monte Carlo, power method polynomials
Citation: Sheng Y and Sheng Z (2012) Is coefficient alpha robust to non-normal data? Front. Psychology 3:34. doi: 10.3389/fpsyg.2012.00034
Received: 29 October 2011;
Paper pending published: 22 November 2011;
Accepted: 30 January 2012;
Published online: 15 February 2012.
Edited by:
Jason W. Osborne, Old Dominion University, USACopyright: © 2012 Sheng and Sheng. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Yanyan Sheng, Department of Educational Psychology and Special Education, Southern Illinois University, Wham 223, MC 4618, Carbondale, IL 62901-4618, USA. e-mail: ysheng@siu.edu