- 1 Department of Psychology, Memorial University of Newfoundland, St. John’s, NL, Canada
- 2 Department of Psychology, University of Warwick, Coventry, UK
Does decay cause forgetting? For memory over the long-term, the answer is generally agreed to be “no” (e.g., McGeoch, 1932). For memory over shorter time-periods, however, debate continues (e.g., Altmann and Gray, 2008; Lewandowsky et al., 2009). The issue has important theoretical implications, as the claim that forgetting differs over timescales is central to arguments against models of memory that deny the utility of distinguishing between short-term and long-term memory (e.g., Brown et al., 2007). Here we address two remaining issues. The first concerns empirical data. Although many results taken as evidence for decay have been accounted for by alternative accounts (e.g., in terms of interference: Neath and Brown, 2006; Brown et al., 2007), it has been argued that forgetting demonstrated by Baddeley and Scott (1971) cannot be explained without recourse to trace decay. Indeed, Nairne (2003, p. 429) stated that “the conclusions reached by Baddeley and Scott (1971) have largely dominated the field for the past three decades.” Here, we argue that an interference-based explanation originally dismissed by Baddeley and Scott can in fact account for their data. The second issue is conceptual, and concerns the possible equivalence of decay and non-decay memory models.
The Findings of Baddeley and Scott (1971)
In a typical Brown–Peterson task (Brown, 1958; Peterson and Peterson, 1959), subjects view three items (usually consonants) and, after a 3- to 30-s delay, attempt to recall them in order. Rehearsal is prevented during retention, and forgetting over time occurs. Keppel and Underwood (1962), however, observed no difference in performance in the various delay conditions on the first trial of a Brown–Peterson task. For example, in their Experiment 2, performance on the first trial was identical regardless of whether the distractor period lasted 3, 9, or 18 s (for a review, see Surprenant and Neath, 2009a). They concluded that interference, rather than trace decay, was responsible for forgetting over the short-term. Consistent with the interference view, performance decreased over trials.
Baddeley and Scott (1971), however, suggested that the Keppel and Underwood (1962) data suffered from ceiling effects which might have masked forgetting. They therefore addressed first trial forgetting when ceiling effects were absent. In Experiment 1, 152 subjects heard a single five-item list of digits in random order which they recalled after 3, 30, 60, or 120 s. During the delay, subjects wrote down letters that were read aloud by the experimenter. Results (data points, left panel of Figure 1) included clear evidence of forgetting between 3 and 30 s on the first (i.e., only) trial.
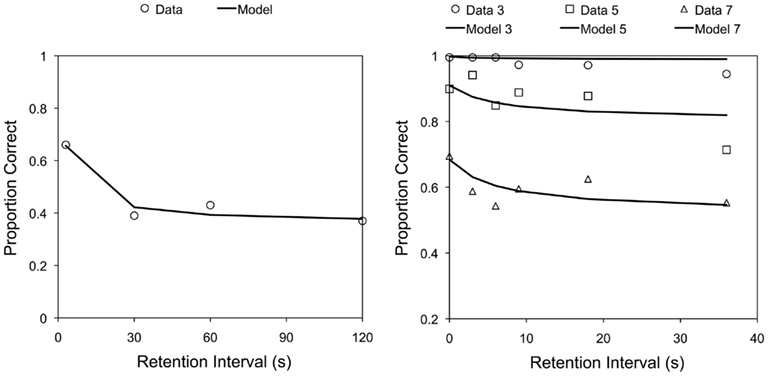
Figure 1. The data points show the proportion of items correctly recalled in Baddeley and Scott’s (1971) Experiment 1 (left panel) and the proportion of items correctly recalled from three-, five-, and seven-item lists in Experiment 2 (right panel) as a function of delay. The solid lines show the fit of SIMPLE (see text for details).
Experiment 2 further explored single trial forgetting. Four hundred twenty-four subjects recalled three-, five-, or seven-item lists of digits after 0, 3, 6, 9, 18, or 36 s. The distractor task was again writing letters. The results are shown (as data points) in the right panel of Figure 1. Baddeley and Scott(1971, p. 282) included in their analysis data from other studies and noted that over all of the studies, including their own, “forgetting approaches asymptote within approximately 5 s.”
Subjects received only a single trial, preventing proactive interference, yet forgetting occurred. Other possible sources of interference were considered and discounted. First, retroactive interference from the distractor task was thought unlikely because of the lack of evidence that letters and digits mutually interfere (Wickens et al., 1963). Second, intrasequence interference – items in the list interfering with each other – was ruled out because such interference should lead to faster forgetting for longer lists (see Melton, 1963) and this was not observed. Baddeley and Scott (1971) therefore took their results as evidence for a primary memory component which decays within about 5 s. Since its publication, the study has been cited extensively as evidence against an interference account of the data and as evidence for decay; there are few alternate accounts of these particular data and no systematic attempts to model the data1. Can a model without trace decay explain the data? Here we apply a temporal distinctiveness model, scale independent memory, perception, and learning (SIMPLE; Neath and Brown, 2006; Brown et al., 2007), to the results reported by Baddeley and Scott.
Evidence for Interference
SIMPLE – scale independent memory, perception, and learning has been described in detail elsewhere (e.g., Neath and Brown, 2006; Brown et al., 2007); here, we focus on those aspects relevant to the current simulation. Memory is conceived as a discrimination task: items are represented as locations along one or more dimensions in psychological space and in general, those items with fewer close neighbors on the relevant dimensions at the time of retrieval will be more likely to be recalled than items with more close neighbors. According to SIMPLE, unrelated items in episodic memory tasks are represented primarily or solely along a temporal dimension2. The zero point is the time the item is retrieved, and each item’s value is the time since presentation, relative to the time of retrieval.
In Experiment 1 of Baddeley and Scott (1971), the presentation rate was one item per second, and therefore, initial temporal values at the end of presentation will be 5, 4, 3, 2, and 1 for items 1–5, respectively. To these values are added the duration of the retention interval (3, 30, 60, or 120 s, depending on condition). It is assumed that recall takes time; we assumed each item takes 1 s to recall. The resulting values are logarithmically transformed, and recall probability of a particular item depends on its local distinctiveness.
The similarity, ηi,j, between two log-transformed temporal memory representations, LTi and LTj, is given by Eq. 1:

The main free parameter in SIMPLE is c: higher values of c correspond to greater distinctiveness and therefore less influence of more distant items.
The discriminability of item i, Di, when given the cue (temporal location) for stimulus j, Cj, is given by Eq. 2, in which n is the number of items in the set:
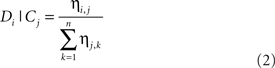
Omission errors are possible through Eq. 3, which shows recall probability, Ri, based on discriminability:

Parameter t is the threshold and parameter s can be interpreted as the noisiness of the threshold. The above is the same way SIMPLE has been applied to serial recall data in past demonstrations (see Neath and Brown, 2006; Brown et al., 2007).
There are thus three free parameters. With c = 3.248, s = 8.253, and t = 0.269, SIMPLE shows clear forgetting (the lines in the left panel of Figure 1) and adequately produces the same pattern observed by Baddeley and Scott (1971) in their Experiment 1 (R2 = 0.954). Thus, despite not incorporating trace decay, SIMPLE accounts for the data from Experiment 1 of Baddeley and Scott in exactly the same way as it does for immediate serial recall in general.
Why does performance in the model decrease between 3 and 30 s, but then effectively asymptote? The key is what Brown et al. (2007) term Weberian compression. The original temporal values undergo a logarithmic transformation, which condenses large values more than small values. Therefore, there is less of a difference when comparing the distinctiveness of items after a 30 and 60-s delay than when comparing the distinctiveness of items after a 0 and 30-s delay.
The same basic procedure was followed to fit the data from Experiment 2 of Baddeley and Scott (1971). Parameters were set to c = 0.547, s = 23.131, and t = 0.139 for all three list lengths and all six delays. Results are shown as lines in the right panel of Figure 1 (R2 = 0.937). The differential forgetting between the three-, five-, and seven-item lists is explained entirely by the presence of additional items in the list, so-called intrasequence interference.
Discussion
The dominant account of the Baddeley and Scott (1971) data is that it offers support for a multi-system account of memory in which primary (or short-term or working) memory decays within a few seconds and longer-term recollection is supported by a second memory system (see Nairne, 2003). The underlying logic was that because all sources of interference were minimized or eliminated, any observed forgetting must be due to decay.
Baddeley and Scott (1971) ruled out intrasequence interference as an explanation because they focused on Melton’s (1963) account of intrasequence interference, which does indeed predict faster forgetting for longer lists. In contrast, SIMPLE does not make this prediction because it is a local distinctiveness model: the amount of interference for a given item is most affected by near neighbors, and therefore extending the list length does not necessarily guarantee faster forgetting. Thus it is possible to account for the data reported by Baddeley and Scott without invoking either decay or two separate memory systems, and instead, by invoking the same interference account used to explain data from other paradigms (see Surprenant and Neath, 2009b).
Equivalence between Decay and Interference Models?
We have demonstrated that a model without decay accommodates empirical results that have long been taken as evidence for decay. It could be argued, however, that the SIMPLE model can be interpreted as a high level model that does not specify the key underlying processes (i.e., decay vs. interference)3. Essentially, this charge argues that the concept of “relative distinctiveness,” which is central to SIMPLE’s behavior, could be implemented through trace decay mechanisms. We consider this within the context of a time-based decay model of Anderson et al. (1998), which uses the ACT-R framework.
In the ABLM model, the baseline activation of a single occurrence of a chunk in memory decays as a logarithmic function of elapsed time. Thus the baseline activations of items stand in the same relations to each other as do the logarithmically transformed temporal distances used by SIMPLE and could, at least algebraically, be used for the same purpose, in much the same way dimensions other than time have been used with SIMPLE (see Chapter 8 of Surprenant and Neath, 2009b). Specifically, if the confusability of items in memory were related to the differences in their levels of decayed baseline activations, and the probability of recalling a given item was inversely related to its summed confusability with all other items, then a trace decay mechanism could be used to implement the same temporal distinctiveness computations as SIMPLE assumes4.
The psychological interpretation of this type of account, however, appears somewhat counterintuitive. The decay theory interpretation claims that what makes a temporally distant item hard to remember is not its low level of activation, but rather the fact that there are many other items with similarly low levels of activation. Indeed, in such a model there would be no direct relation at all between the level of activation of an item and the probability of recalling that item; instead, all that would matter is how similar the level of activation of the item was to the levels of activation of other items. It would be unnatural, then, to say that forgetting occurs due to decay.
We assume that a plausible mechanism of decay-based forgetting makes at least two claims: first, that activations reduce over time, and, second, that retrieval probability in some way reflects absolute level of activation. Once it is assumed that items which have decayed more can nonetheless be better retrieved, the model ceases to be a trace decay model in any commonsense usage. Thus although the SIMPLE account is couched at a high level of description and could be implemented in more than one way, we suggest that an interpretation in terms of trace decay stretches the meaning of “trace decay” beyond normal usage.
In summary, we have argued that classic data from Baddeley and Scott (1971), which have frequently been taken as evidence for decay, are more naturally explained in terms of temporal distinctiveness.
Acknowledgments
This work was supported, in part, by a grant from NSERC to Ian Neath and by the Economic and Social Research Council (UK) grant RES-062-23-2462 to Gordon D. A. Brown. MATLAB code for the simulations is available at http://memory.psych.mun.ca/models/simple/misc/baddeley_1971.shtml or from the first author.
Footnotes
- ^Evans and Havens (1978) suggested an explanation based on discriminability of temporal cues, but this paper has not, to our knowledge, been cited. Henson (1998, Demonstration 6) tried to fit his Start–End model to just the seven-item condition from Baddeley and Scott’s second experiment, but found the model’s rate of forgetting was too slow and could not fit the data well.
- ^We note versions of SIMPLE exist in which a position dimension, rather than a temporal dimension, is used; for a direct comparison of the two versions, see Surprenant et al. (2006).
- ^We thank E. M. Altmann and M. P. A. Page for suggestions along these lines.
- ^We note that this is not how the ABLM model works: in that model the probability of recalling one chunk rather than another depends on the chunk’s match score relative to other chunks’ match scores, where match score depends on similarity as well as baseline and other activations.
References
Altmann, E. M., and Gray, W. D. (2008). An integrated model of cognitive control in task switching. Psychol. Rev. 115, 602–639.
Anderson, J. R., Bothell, D., Lebiere, C., and Matessa, M. (1998). An integrated theory of list memory. J. Mem. Lang. 38, 341.
Baddeley, A. D., and Scott, D. (1971). Short term forgetting in the absence of proactive interference. Q. J. Exp. Psychol. 23, 275–283.
Brown, G. D. A., Neath, I., and Chater, N. (2007). A temporal ratio model of memory. Psychol. Rev. 114, 539–576.
Brown, J. (1958). Some tests of the decay theory of immediate memory. Q. J. Exp. Psychol. 10, 12–21.
Evans, T., and Havens, C. (1978). Auditory-verbal short-term-memory effects of retention interval on proactive-inhibition when interpolated interference is eliminated. Can. J. Psychol. 32, 262–269.
Henson, R. N. A. (1998). Short-term memory for serial order: the Start-End model. Cogn. Psychol. 36, 73–137.
Keppel, G., and Underwood, B. J. (1962). Proactive inhibition in short-term retention of ingle items. J. Verbal Learn. Verbal Behav. 1, 153–161.
Lewandowsky, S., Oberauer, K., and Brown, G. D. A. (2009). No temporal decay in verbal short-term memory. Trends Cogn. Sci. (Regul. Ed.) 13, 120–126.
Melton, A. W. (1963). Implications of short-term memory for a general theory of memory. J. Verbal Learn. Verbal Behav. 2, 1–21.
Nairne, J. S. (2003). “Sensory and working memory,” in Comprehensive Handbook of Psychology, Vol. 4: Experimental Psychology, eds A. F. Healy and R. W. Proctor (New York: Wiley), 423–444.
Neath, I., and Brown, G. D. A. (2006). “SIMPLE: further applications of a local distinctiveness model of memory,” in The Psychology of Learning and Motivation, ed. B. H. Ross (San Diego, CA: Academic Press), 201–243.
Peterson, L. R., and Peterson, M. G. (1959). Short-term retention of individual verbal items. J. Exp. Psychol. 58, 193–198.
Surprenant, A. M., and Neath, I. (2009a). “The 9 lives of short-term memory,” in Interactions Between Short-Term and Long-Term Memory in the Verbal Domain, eds A. Thorn and M. Page (Hove: Psychology Press), 16–43.
Surprenant, A. M., Neath, I., and Brown, G. D. A. (2006). Modeling age-related differences in immediate memory using SIMPLE. J. Mem. Lang. 55, 572–586.
Citation: Neath I and Brown GDA (2012) Arguments against memory trace decay: a SIMPLE account of Baddeley and Scott. Front. Psychology 3:35. doi: 10.3389/fpsyg.2012.00035
Received: 28 January 2012; Accepted: 30 January 2012;
Published online: 14 February 2012.
Copyright: © 2012 Neath and Brown. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence:aW5lYXRoQG11bi5jYQ==

