- 1 Department of Psychology, California State University Los Angeles, Los Angeles, CA, USA
- 2 Department of Psychological and Brain Sciences, Indiana University, Bloomington, IN, USA
- 3 School of Psychological Sciences, University of Indianapolis, Indianapolis, IN, USA
Although young children typically have trouble reasoning relationally, they are aided by the presence of “relational” words (e.g., Gentner and Rattermann, 1991). They also reason well about commonly experienced event structures (e.g., Fivush, 1984). To explore what makes a word “relational” and therefore helpful in relational reasoning, we hypothesized that these words activate well-understood event structures. Furthermore, the activated schema must be open enough (without too much specificity) that it can be applied analogically to novel problems. Four experiments examine this hypothesis by exploring: how training with a label influence the schematic interpretation of a scene, what kinds of scenes are conducive to schematic interpretation, and whether children must figure out the interpretation themselves to benefit from the act of interpreting a scene as an event. Experiment 1 shows the superiority of schema-evoking words over words that do not connect to schematized experiences. Experiments 2 and 3 further reveal that these words must be applied to perceptual instances that require cognitive effort to connect to a label rather than unrelated or concretely related instances in order to draw attention to relational structure. Experiment 4 provides evidence that even when children do not work out an interpretation for themselves, just the act of interpreting an ambiguous scene is potent for relational generalization. The present results suggest that relational words (and in particular their meanings) are created from the act of interpreting a perceptual situation in the context of a word.
Introduction
The importance of language to higher cognition is undisputed: words help learners connect previously acquired ideas (Herbert and Hayne, 2000) and move from concrete to more abstract representations (Kotovsky and Gentner, 1996; Loewenstein and Gentner, 2005). Effects of language on children’s cognition have been demonstrated in several domains in cognitive development (e.g., Miura and Okamoto, 1989; Choi and Bowerman, 1991; Levine et al., 1992; Sinha et al., 1994) and appear particularly potent in tasks that require more abstract encodings (Gelman, 1988; Waxman and Markow, 1995; Bloom and Keil, 2001) or relational reasoning (Kotovsky and Gentner, 1996; Loewenstein and Gentner, 2005; Gentner et al., 2011).
Three metaphors are often used to discuss the effect of language on cognition: (1) language as a lens, (2) language as an anchor or guide, and (3) language as a cognitive tool. The lens metaphor is related to classic Whorfian ideas, and captures the idea that the words one knows influences the information that is detected and how it is represented (Winawer et al., 2007; Boroditsky et al., 2011). The anchor (Clark, 1998; Lupyan, 2005) or guide (Plunkett et al., 2008) metaphor suggests that language aids category formation by explicitly connecting related instances or by defining boundaries, as when, for example, three dogs are all given the same label (e.g., Xu and Tenenbaum, 2007; Perry et al., 2010). The third, referred to as the tool metaphor, captures how language leverages other cognitive processes, for example, the comparison or alignment of elements (Kotovsky and Gentner, 1996; Loewenstein and Gentner, 2005; Gentner et al., 2011) such that similarity-based and analogical processes may act on these newly encoded representations. These perspectives on language suggest two broad types of words that may foster relational reasoning: novel words that can be helpful despite the lack of associations and known words that are helpful because of their rich semantic associations. The purpose here is to explore what types of words facilitate thinking and which situations benefit from the presence of those words.
The specific research questions are motivated by findings about the difficulty of relational reasoning tasks for young children and novices. Preschool children, in particular, have difficulty picking out relevant relational information when there are other more salient object features (e.g., Keil and Batterman, 1984; Gentner and Rattermann, 1991). The literature on relational reasoning in young children has repeatedly shown that words help children notice, comprehend, and make use of relations (Gelman, 1988; Gentner and Rattermann, 1991; Kotovsky and Gentner, 1996; Loewenstein and Gentner, 2005). Many of these tasks make use of novel or arbitrary relational reasoning problems. For instance, in Rattermann et al. (1990) work, they showed that labeling a series of objects varying in size as “daddy, mother, and baby” helped preschoolers reason about size relations. The child might need to discover that the “winner” in a choice task is always the middle-sized object regardless of the specific objects or their absolute sizes. Thus, words might help in these tasks because they help the child relate the novel task to known relational structures (e.g., size differences in families, Rattermann et al., 1990) or because words, even novel words, help children discover the relational structure (Gentner et al., 2011).
However, there is another context in which young children have been shown to reason relationally and with relative ease: well-understood events, such as buying fast food or going to the movies. The research in that literature suggests that children’s relational reasoning derives from their schema-like representations of event structure (Fivush, 1984; Gobbo and Chi, 1986; Bauer and Mandler, 1989; Hudson et al., 1992). Schemas are “abstract” or “variable-ized” cognitive entities (Schank and Abelson, 1995). For example, buying fast food has a common structure that is captured in a “fast food restaurant schema” across the variety of specific fast food experiences in a young child’s life but each visit also has unique features. In brief, schemas are theoretical constructs that can be roughly defined as structured representations that bring order to emotions, perceptions, and experiences (Rumelhart, 1975; Rumelhart and Ortony, 1977). Schemas and closely related notions of frames (Minsky, 1975) and scripts (Schank and Abelson, 1977, 1995) are organized slots filled by different units of knowledge suitably representing information required for responding to structurally similar situations.
Given these contexts in which children are able to reason relationally (in the presence of words or with well-understood “schematized” events), these experimental questions emerge: do words benefit children’s performances in situations such as arbitrary relational tasks used in laboratory studies because they foster schema-like interpretations? If so, is there, a “sweet spot” in the knowledge structures that words might activate – not so empty (as might be the case with novel words), that the word provides no relational structure, but also not so specific that the knowledge is of a rich and detailed experience rather than a variable-ized and therefore generalizable relational structure?
To answer the first question, we propose the Schema hypothesis: words that draw upon rich past experiences evoke schemas, well-understood, structure-sensitive event structures, and these enable relational thinking. Standard relational tasks used with young children are (particularly so from the child’s point of view) ambiguous. Words, through their meanings and through their associations with previously experienced relational structures, might invite particular interpretations that resolve the ambiguity in some meaningful way. These interpretations – if properly structured in terms of their relations – may then enable children to reason analogically about structural similarities despite surface differences.
If the Schema Hypothesis holds, one might expect that calling upon a highly familiar event structure would be most helpful in promoting relational interpretations. However, if children recall a highly fixed and specified narrative rather than a story-schema with slots in its structure, they may be unable to apply it to the present relational problem and thus less likely to respond according to relational similarity (Brown et al., 1986). More generally, for any evoked relational structure to benefit reasoning, it may have to have open slots and not be so specific that the slots are already filled in. Accordingly, there might be a need for optimal openness in the activated schema in order to support relational reasoning: children must know enough about the event structure to make inferential use about it but without too much specificity so that it can be applied analogically to novel problems. This idea fits with recent findings showing that children have difficulty attending to relations when they are distracted by more vivid concrete information (Kaminski et al., 2008; Son et al., 2008, 2011; McNeil et al., 2009). Thus, the experiments test what we call the Optimal Vagueness hypothesis: the key prediction is that less specified, less concrete, and sparsely detailed schemas may better direct attention to relational structure than richly detailed concrete situations.
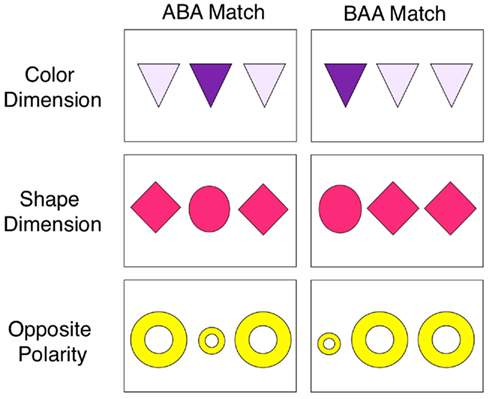
The four experiments that follow tested the Schema hypothesis and the Optimal Vagueness hypothesis by examining 4- and 5-year-old children’s relational reasoning in a task that has been commonly used to study relational reasoning in children. Our version is based on a prior study by Kotovsky and Gentner (1996). In that study, 4-year-olds were presented with a triad of cards, a standard and two answer choices – the relational match and a non-relational foil. The standard presented a relation among a set of three objects (e.g., a symmetry relation as in oOo). The elements in the answer choices were similar to each other (e.g., xXx and xxX) but differed from the standard to ensure that the only commonality shared by the standard and the relational answer was a relation. When the relational answer was in the same dimension (i.e. size symmetry, oOo and xXx), they found that 4-year-olds succeeded in responding to relations such as symmetry. However when the relational dimension changed (i.e., oOo and light blue-dark blue-light blue) or the relational polarity changed (i.e., oOo and XxX), children’s performance did not statistically differ from chance. In order to help these children respond relationally on these more difficult cross-dimensional triads, Kotovsky and Gentner introduced the task by categorizing triads using linguistic labels (e.g., “even” to indicate symmetry). They found that children who succeeded on the labeling task were then more likely to make relational choices on the difficult cross-dimension triads. The relational patterns in the studies that follow are made from three objects and are, like those of Kotovsky and Gentner, abstract – a symmetrical arrangement (ABA) or an asymmetrical arrangement (BAA). In contrast to the Kotovsky and Gentner methods, we used a lexical generalization task, first teaching children names for one instance of a pattern and then asking how they generalized that name to new instances. Across experiments, we manipulate the kinds of words used to understand how words might evoke schemas that aid in the interpretation of these relations structures.
Experiment 1: Labels that Provide Schemas
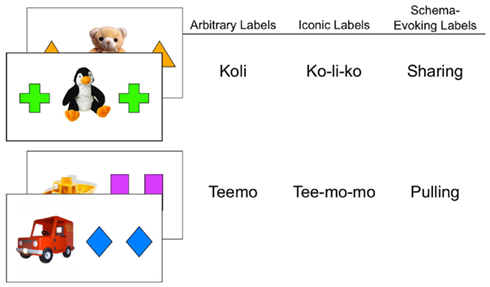
Experiment 1 tested the Schema hypothesis by labeling the cards with words whose meaning and associated referents might evoke the proper relational interpretation and comparing the effects of these potentially meaningful labels to the effects of two kinds of novel words. The schema-evoking labels were chosen to be words that (1) refer to well-organized events for young children and (2) have potentially relevant relational meanings that might help children interpret the stimulus arrays in an appropriate way. The ABA pattern, as shown in Figure 1, is made of two matching objects on either side of a unique center object. We conceptualized this center object as a toy potentially worthy of sharing. For the symmetric pattern, the word chosen to evoke the relevant relational interpretation was “sharing” because sharing events are well-understood by children in terms of balance, fairness, and the sameness of two compared entities. This may have been the intuition that led Kotovsky and Gentner (1996) to use the term “even” (for their ABA figures) which evokes a similar set of concepts. The asymmetric BAA pattern, as shown in Figure 1, always includes one item on the left that is different from the rest. We conceptualized this unique object to be a vehicle that might be pulling the other two objects. Thus to support this relational interpretation, we chose the word “pulling” because this word (perhaps especially to young children) might evoke ideas of a lead object and followers such as an engine pulling freight cars. Note that these words (like “daddy, mommy, baby” in previous studies of labels and relational learning, Rattermann et al., 1990) are merely evocative. The relational displays do not actually show an object being shared or an engine being engaged in pulling. However, if children possess schemas that are sufficiently abstract concerning these kinds of events, then the words “sharing” and “pulling” might elicit the relevant relational interpretations.
The two control conditions used novel words that might be expected to help relational reasoning by the guide or tool metaphors. In the Arbitrary Word condition, two novel nonsense words were used (i.e., “koli” for ABA; “teemo” for BAA); this condition serves as a control for any general effects of naming. Because the arbitrary words could be hard to learn and to link to the relations (which is presumably not the case for “pulling” and “sharing”), the second control condition provided iconic words that were mimetically related to the relations they labeled (Imai et al., 2008; Yoshida, in press) in terms of their phonetic form. That is, “ko-li-ko” was used for ABA patterns and “tee-mo-mo” for BAA. These words, however, are not expected to evoke relational events that are well-known to children.
Method
Participants and design
Forty-four children, average age 57 months (range 46–68 months) from daycares in a Midwest community participated in this experiment. Three additional children were tested but two were excluded from analysis due to unfavorable testing conditions (fire alarms) and the other child had difficulty during the label training (described in the procedures section). Children were randomly assigned to one of the label conditions: Arbitrary (n = 15), Iconic (n = 16), or Schema-evoking (n = 13). In this experiment (as well as the studies that follow), informed parental consent was obtained before data collection and all protocols were approved by local institutional review boards.
Materials and procedure
Training consisted simply of naming cards that were constructed to encourage a schematic construal (e.g., sharing or pulling). All participants were shown the training instances, two unique cards for each relation for a total of four training instances. The ABA relation cards were cross–penguin–cross and triangle–bear–triangle; the BAA cards were boat–rectangle–rectangle and car–diamond–diamond as shown in Figure 1. ABA cards were labeled with the same word/phrase, either “koli,” “ko-li-ko,” or “sharing” depending on the condition, and BAA cards were labeled with another word/phrase, either “teemo,” “tee-mo-mo,” or “pulling.”
Experimenters showed each training card separately and said, for example, “This is a koli card. See, this card is koli. Can you say koli?” Note that all of the words were used in the adjective form so that the same grammatical frame could be used in all conditions. After waiting for the child to repeat the word or phrase, the card was put away and the next card was named. The labels and cards were not counterbalanced because the schema-evoking and iconic words were specific to the particular relation that the children were being shown (Experiment 4 will further address this issue). Because we could not counterbalance the words in some of the conditions without changing the intent of the experiment, we also did not do so for the arbitrary labels.
After children were trained in both types of relations, the experimenter began the testing phase of the study. Testing trials asked children to find a matching card to a given linguistic label (e.g., “Can you give me the sharing card?”). There were two kinds of testing trials: memorization and generalization. All trials involved a two-alternative forced choice.
Memorization trials were made up of the same objects as the training instances (e.g., bears and triangles, penguins and crosses). A memory trial consisted of two answer choices: a card that was identical to the original learning instance and a distracter that contained the same objects in a different pattern (e.g., respectively, cross–penguin–cross and penguin–cross–cross). On memory trials, children were always asked to retrieve the card that was identical to its taught label. When children were taught that the card depicting cross–penguin–cross was “koli/ko-li-ko/sharing,” they were correct when they chose that card over the distracter (i.e., penguin–cross–cross). The memory trials were designed to test whether children were simply able to learn the association between words and their referents from the brief training segment.
Generalization cards consisted of three simple geometric shapes, as in Kotovsky and Gentner’s (1996) tasks, that re-created the ABA and BAA relations with variations on color, shape, or size dimensions (see Figure 2). The size dimension cards will be referred to as “opposite polarity” cards because they had two large objects and one small one, while all training instances were made up of two small objects and one large one. All generalization cards were novel to the participants because they were not named or shown during training. Pilot testing with generalization materials showed that children did not systematically prefer the appropriate relational example when asked for “sharing” and “pulling” cards without training (n = 7, M = 0.48, SD = 0.33).
After the brief four-card training (labeling of the exemplars), children completed 8 memory trials and 12 lexical generalization trials with the testing cards. On half of all of these trials, children were asked to get the ABA card (“Can you get the koli/ko-li-ko/sharing card?”) and shown two answer choices, an ABA (relational match) and BAA card (distracter) made of the same objects. Children were asked for the BAA card on the other trials.
The testing order started off with four memory trials to make the goal of the task clear, that is, to retrieve the object corresponding to a particular name. Then they received three blocks of generalization trials interspersed with two memory trials. Color, shape, and opposite polarity trials were not blocked but instead presented in two pseudo-random orders.
Results and Discussion
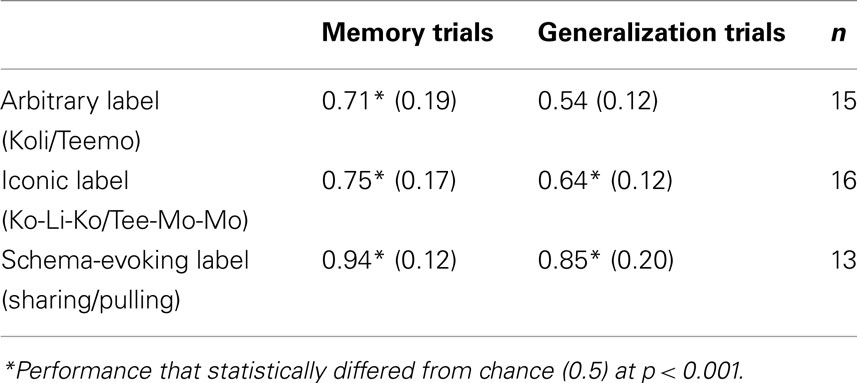
Children’s memory and generalization performances are shown in Table 1. A 2 (test: memory, generalization) × 3 (label condition: Arbitrary, Iconic, Schema-evoking) repeated-measures ANOVA, revealed a main effect of test, F(1, 41) = 20.69, p < 0.001, partial η2 = 0.34, and label condition, F(2, 41) = 18.22, p < 0.001, partial η2 = 0.47, but no interaction, F(2, 41) = 0.62. As with most tests of learning, memorization performance exceeded novel generalization.
Bonferroni corrected post hoc comparisons revealed that children trained with Schema-evoking labels showed significantly better memorization than children in either the Iconic, t(28) = 11.68, p < 0.05, or Arbitrary conditions, t(27) = 14.91, p < 0.01. These two conditions did not differ significantly, t(30) = 0.42. Performance in each of the three conditions exceeded chance levels on the memorization test, ts > 4.31, ps < 0.001.
The analyses of generalization trials also revealed that children in the Schema-evoking condition made significantly more relational matches than children in either the Iconic, t(28) = 12.20, p < 0.01, or Arbitrary conditions, t(27) = 28.82, p < 0.001. These results support the schema hypothesis that words have their effect by evoking relationally relevant interpretations. Additionally, children in the Iconic label condition chose relational matches to the given label more often than those with Arbitrary label training, t(30) = 6.34, p < 0.05. Although the Iconic and Schema-evoking generalization performances reliably differed from chance, ts > 5.86, ps < 0.001, the Arbitrary condition did not, t(14) = 1.7. This pattern suggests some benefit to Iconic labels, that is, a sensitivity by the children to the correspondence of the sound to visual patterns.
The advantage of the Schema-evoking condition on generalization test could, as hypothesized, be due to increased relational interpretations; however, because children in the Schema condition also performed better on the memory trials, better generalization performance could simply reflect more robust memory for the trained label. To examine this issue, the following analyses on generalization performance included memory performance as a covariate. Memory performance was only a marginally significant covariate, F(1, 40) = 3.34, p < 0.10, and there was still a significant effect of label condition even when memory performance was included first in a stepwise linear regression, F(2, 40) = 8.75, p < 0.01, partial η2 = 0.30.
The superior generalization performance by children who heard meaningful event-related words supports the hypothesis that schema-evoking words enhance children’s ability to apprehend the common relational structure across novel instances. The choice of schema-evoking words such as “sharing” and “pulling” to refer to ABA and BAA patterns is similar to Gentner and Rattermann’s (1991) and Rattermann et al.’s (1990) use of the word “daddy” and “baby” to help young children respond to size relations. Words like “sharing” or “daddy” may foster analogical reasoning by reminding children of relevant event structures. These words conveniently emphasize relations because the schemas they activate are both well-known and consist of well-structured relations that have been applied to multiple individual instances in the past, though never to such abstract displays as used in this experiment. Nonetheless, evoking these relational frames may facilitate processes such as alignment and comparison and thereby provide an interpretive context within which to understand even novel or perceptually ambiguous information.
Children’s poor performance in the arbitrary and iconic conditions suggests that word meaning does matter. However, the comparison in Experiment 1 was between familiar words with some meaning and novel made up words with none. The schema hypothesis, however, implies that the meaning should be relationally relevant, not just familiar. Accordingly, Experiment 2 compared schema-evoking words with other meaningful, known English words (also gerunds) that provide no obvious schematic interpretation of the relational structures displayed in the stimulus cards.
Experiment 2: Meaningful yet Unrelated Words vs. Schema-Evoking Words
This experiment replicates the Schema-evoking condition of Experiment 1 and compares performance to a new control group. In this new condition, the labels were known English words that were unrelated to the situation depicted on the card. Children saw the training cards from Experiment 1 labeled as “boiling” for ABA cards and “eating” for BAA cards.
Method
Participants and design
Forty children, average age 60.5 months (range 51–68 months) from daycares in a Midwest community participated in this experiment. None of the children had participated in Experiment 1. Five additional children were tested but three were excluded from analysis because they exclusively chose an option on one side and two for unfavorable testing conditions. Children were randomly assigned to one of the label conditions: Unrelated (n = 20) or Schema-evoking (n = 20).
Materials and procedure
The Schema-evoking condition was a replication of Experiment 1. In the Unrelated condition, ABA cards were labeled as “boiling” and BAA cards were labeled as “eating.”
Label training, memory, and generalization testing procedures were similar to Experiment 1 with a few minor changes. There were two pseudo-random orders for label training, half of the children learning ABA cards first (order: bear, penguin, boat, car) and the other half learning BAA cards first (order: boat, car, bear, penguin). After the brief four-card training (labeling of the exemplars), children began the testing trials which consisted of 8 memory trials and 12 lexical generalization trials with the testing cards. On half of all of these trials, children were asked to get the ABA card (“Can you get the boiling/sharing card?”). Children were asked for the BAA card on the other trials (“Can you get the eating/pulling card?”). The testing order began with four memory trials. Then each child received three blocks of generalization trials interspersed with two blocks of memory trials. Generalization trials were blocked into dimension-specific groups (color, shape, and opposite polarity) and were presented in one of three orders (color–shape–polarity, shape–polarity–color, and polarity–color–shape).
Results and Discussion
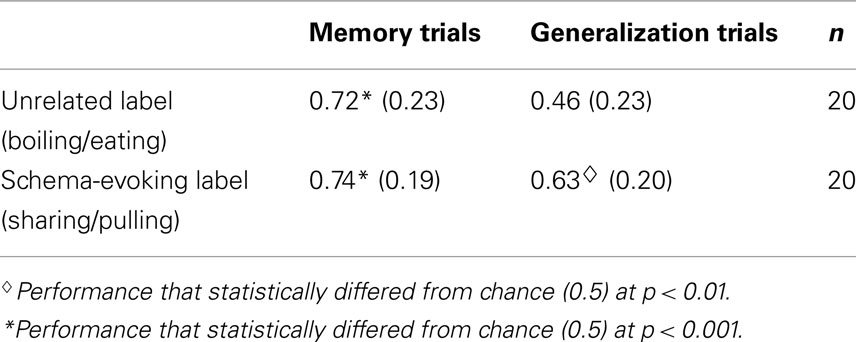
A 2 (test: memory, generalization) × 2 (label condition: Unrelated, Schema-evoking) repeated-measures ANOVA revealed a main effect of test, F(1, 38) = 30.94, p < 0.001, partial η2 = 0.45, as well as a significant interaction, F(1, 38) = 5.30, p < 0.05, partial η2 = 0.12. Although, label conditions showed no differences on memory test trials (see Table 2 for group means), there were significant differences in generalization performance, t(38) = 2.55, Bonferroni corrected p < 0.05. Comparisons to chance performance supported this analysis: generalization performance in the Schema condition exceeded chance, t(19) = 3.12, p < 0.01, while generalization by the Unrelated condition did not, t(19) = 0.48.
Typically, developmental studies of analogy and language examine the effect of particular labels on structural sensitivity (e.g., Loewenstein and Gentner, 2005, see Gentner and Rattermann, 1991 for a review). The results here demonstrate that it is not the mere use of a known word that cues relational judgments but that words foster relational interpretations by dint of their meanings. However, the question of the schematized meaning is still open – must the use of the word evoke a schema-like representation, that is a representation that is variable-ized, with slots, and thus not too specific? Or can any related meaning, including highly concrete and specific meanings, also foster relational generalization? This is the crux of the Optimal Vagueness hypothesis tested in Experiment 3. Additionally, Experiment 3 implemented an alternative method for controlling for meaningfulness by applying the labels “sharing” and “pulling” to unrelated training cards.
Experiment 3: Optimally Vague Schemas?
By the Schema hypothesis, providing the words “pulling” and “sharing” helped children because they activated relevant knowledge about events with the relevant relational properties. Although we used a central toy for “sharing” and a right-most vehicle for “pulling” to foster a relational interpretation, the geometric forms on the training instances are not actually good illustrations of either “sharing” or “pulling” situations. Further, we know from the performance of the children in the previous unrelated-control conditions that the stimulus cards alone apparently are not sufficient to evoke the relevant schemas without the schema-evoking labels. The relations that are presented by these cards, at best, vaguely resemble – or could be seen as roughly similar to – pulling or sharing events. Although these scenes can be interpreted as sharing or pulling, this act of interpretation requires prompting – for instance, by the provision of a relationally applicable label. The Optimal Vagueness hypothesis suggests that the vagueness of the resemblance – being evocative rather than highly similar – is a virtue. The idea is that a well-specified example might emphasize the objects in the example causing children not to see the schema as having open slots and thus minimizing generalization. That is, although the label “sharing” may evoke a familiar event context to young children, the perceptual situation that receives the label can lead to a vague and general idea of sharing or to a specified instantiation of sharing. A vague and schematic understanding of sharing might be multiple parties equally wanting or distributing something. Such a vague conceptualization might be better for emphasizing relations rather than the specific objects in the example. A more specific interpretation, for example, that Sally and Susie want to share a teddy bear, might not help generalization. Alternatively, one might argue that more specific (and better understood) narratives might benefit learning because it would better activate the relevant underlying knowledge. Experiment 3 tests these alternatives by training all children with the schema-evoking labels (“sharing” and “pulling”) but applying them to instances that richly, vaguely, or poorly, fit with these labels.
Method
Participants
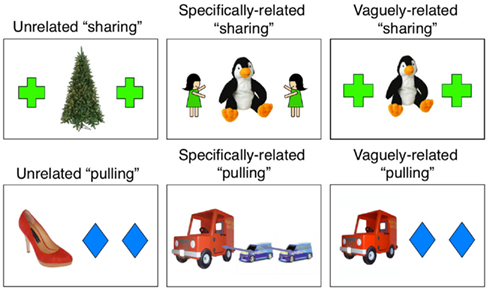
Thirty-eight children, average age 57 months (range 50–68 months) from local daycares in a Midwestern town participated in this experiment. Five additional children were excluded (three for unfavorable testing conditions; one reported by the teacher to have developmental delays; one who exclusively chose cards presented on one side). Children were randomly assigned to one of three training card conditions: Unrelated (controls, n = 12), Specifically related (n = 14), or Vaguely related (n = 13).
Materials and procedure
In this experiment, the children were shown cards labeled as either “sharing” or “pulling.” If these words (and whatever representations are activated) are powerful enough to promote relational generalization, children in all three conditions should perform equally well in the tasks. The difference among the conditions is that there were three different types of cards that were labeled. If the perceptual situation that receives the label contributes to the interpretation of the activated schema, then there should be differences in performance. Examples of the three types of training cards are shown in Figure 3.
In the Specifically related condition, the training cards were designed to concretely support children’s notions of “sharing” (or “pulling”), with attention drawn to the specific entities participating in the relation. “Sharing” cards portrayed scenes with two children flanking a stuffed animal in the middle. Instead of vaguely being interpretable as a sharing situation, this perceptual scene depicts a specific interpretation of sharing, namely that the two children must be sharing the toy in the middle. However, the training cards shown in the Vaguely related condition only evoke an ambiguous sense of “sharing” because two geometric shapes are flanking a toy in the middle. This scene could be interpretable in a number of ways, from the two shapes sharing the toy to more generally activating notions of balance or dividing evenly. Unrelated training cards were similarly vague (two geometric shapes flanking an object in the center) but contained objects that would be less interpretable by the label. For instance, an unrelated “sharing” card depicted a cross–tree–cross. Presumably, this scene is less related to “sharing” than cross–toy–cross because young children probably think about sharing toys more often than sharing trees.
Label training, memory, and generalization testing procedures were similar to Experiment 2 with one major change. During memory trials, each participant chose between condition-specific cards (e.g., Specifically related participants chose between girl–penguin–girl and penguin–girl–girl while Vaguely related participants chose between cross–penguin–cross and penguin–cross–cross cards). All children were asked for either “sharing” or “pulling” cards in both memory and generalization trials because they were all trained with these labels.
Results and Discussion
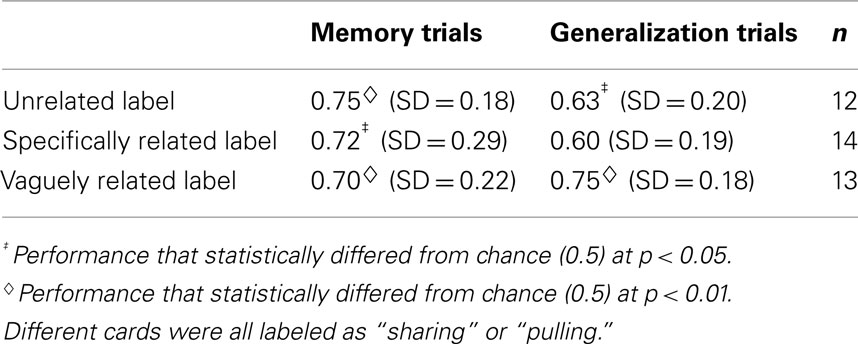
A 2 (test: memory, generalization) × 3 (training card condition) repeated-measures ANOVA revealed no main effect of test, F(1, 36) = 2.18, nor condition, F(2, 36) = 0.6, but a significant interaction, F(2, 36) = 4.64, p < 0.05, partial η2 = 0.21. A series of Bonferroni corrected post hoc comparisons were conducted to examine this interaction (see Table 3 for all group means). Although, the three training conditions showed no differences on memory test trials, they were significantly different in generalization. Vaguely related participants made significantly more relational generalizations than those in both Unrelated, t(24) = 4.83, p < 0.05, and Specifically related conditions, t(26) = 7.12, p < 0.05. This provides direct support for the Optimal Vagueness hypothesis.
Like Experiment 2, when known words are used, children are able to remember the associated instances. Performance on memory trials showed that children were just as willing to attach “sharing” and “pulling” to cards that were not quite obviously related (the Unrelated and Vaguely related training instances) as to cards that exemplified these labels (Specifically related instances). The same words were used in all three conditions so the difference in generalization scores suggests that the interpretive match between the words and instances is critical. Thus, we can conclude that relational generalization is not solely fostered by the use of a particularly apt word. Words associated with familiar, structurally organized schemas are only part of the story; how those words interact with the displays is also critical.
Relational generalization depends on the schematic interpretations that join words and referents. Perceptual instances that are appropriately vague, ones that can be interpreted in terms of those familiar schemas but require effort to do so, allow children to attend to relations within the schema. Displays that match the well-known schema too well do not lead to relational generalizations; and neither do displays that are not interpretable in terms of the schema. Thus, the match between a known schema and a sufficiently ambiguous instance reflects optimal vagueness, a “sweet spot” for transfer, because there is enough similarity between label and referent to evoke relevant past instances but enough abstractness to enable generalization to future instances.
Thus the problem with Specifically related training instances may be this: what is interpretable using an obvious and literal meaning of a word activates only a narrow understanding. Applying the word “sharing” to a specifically related instance may have activated a concrete and specific notion of “sharing” such that children did not engage in the act of adapting and interpreting, and instead simply adopted the narrow construal. This conservative strategy may simply be a prudent strategy because this is also the least assumptive understanding (see also Medin and Ross, 1989). The Vaguely related training instances may have fostered generalization by engaging children in broadening their own understanding of sharing, one that would also encompass future instances.
Another possible benefit of vagueness may be that it requires interpretive work and optimal vagueness allows this additional processing to yield a relational schematic perspective that can be applied to future instances (McQuarrie and Mick, 1999). The vaguely related situation (the combination of the word and visual stimulus) may engage children in figuring out why the cross–penguin–cross situation is a sharing situation. In the Specifically related condition, the flanking girls are readily interpreted as sharing the penguin, so relatively little cognitive gain is achieved by using the “sharing” terminology. Consistent with this idea, researchers have found shallow learning when children (Martin and Schwartz, 2005; Martin, 2009) and adults (Ross and Kennedy, 1990; Chi et al., 1994) are not given the opportunity to do the work of re-interpreting something as something else. Text comprehension research has also found that poorly written text that forces knowledgeable readers to cognitively work to find coherence promotes comprehension (McNamara et al., 1996). Perhaps a too literal instantiation of a schema may not necessitate adequate cognitive work.
Experiment 4 further explores the issue of how much interpretive work is necessary: are schematic interpretations effective only when children form one for themselves or even when children are simply told how to interpret a scene? How much cognitive work is necessary to foster future relational generalization? Perhaps simply the act of interpreting an ambiguous scene is cognitive work enough.
Experiment 4
When the label “sharing” is applied to these scenes, children may be interpreting the scene based on their past experiences with sharing and the scenes in the Vaguely related condition have enough components to foster a relevant interpretation. In Experiment 4, we made it highly difficult for children to interpret scenes according to the labels themselves. This was done by switching the meaningful labels (used in previous experiments) and scenes such that the word “sharing” was applied to the pulling cards and the word “pulling” used with the sharing cards. To examine whether schematic interpretations are effective when children are simply told how to interpret a scene, in one condition (the Story-Schema condition), we provided an appropriate interpretation for the children. For each training card, the experimenter briefly told a “story” that explained the fit between the label and the perceptual situation. As a control to this condition, in the Unrelated condition, children were given the same switched labels and cards as the Story-Schema condition, but critically were not provided with a relevant interpretation.
Method
Participants
Twenty-four children, average age 59 months (range 49–67 months) from Indiana daycares participated in this experiment. Children were randomly assigned to either the Unrelated (control, n = 12) or Story-Schema condition (n = 12). Two additional children were tested but presented a side bias, only choosing cards presented on one side.
Materials and procedure
The training cards were the same cards used Experiments 1 and 2 as well as the Vaguely related condition of Experiment 3. In contrast to previous studies, the symmetrical cards picturing stuffed animals (e.g., cross–penguin–cross) were now labeled “pulling” while the asymmetrical cards depicting vehicles were labeled “sharing” in both conditions of the current experiment. In the Unrelated-control condition, experimenters labeled these cards with the same procedure as previous studies. In the Story-Schema condition, experimenters gave a one-sentence story to go along with the label. For example, an experimenter would hold up the asymmetrical car–diamond–diamond card and say, “This is a sharing card. See, this card is sharing. Look, the diamonds are going to share the car.” For a symmetrical card, such as the cross–penguin–cross card, the experimenter would say, “This is a pulling card. See, this card is pulling. Look, the penguin is pulling the crosses closer.”
After the training sequence, the testing phase of the study began. The memory and generalization trials were similar to previous experiments. Participants in both conditions were presented with the same cards and asked the same questions. As in the previous experiments, generalization trials were blocked into dimension-specific groups and were presented in one of three pseudo-random orders. The critical difference in this study was that the relationally matching “sharing” cards are all asymmetrical and “pulling” cards are symmetrical.
Results and Discussion
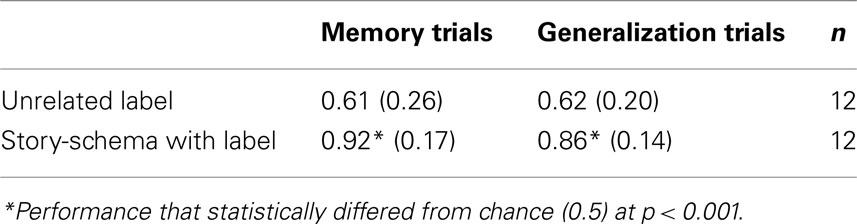
A 2 (test: memory, generalization) × 2 (training: Unrelated, Story-schema) repeated-measures ANOVA revealed no main effect of test, F(1, 22) = 0.32, nor an interaction, F(1, 22) = 0.51, but there was a significant main effect of condition, F(1, 22) = 18.99, p < 0.001, partial η2 = 0.46. Children performed significantly better in the Story-schema condition (see Table 4).
Less than half of the children in the Unrelated condition (n = 5) were able to answer more than 0.75 (6 out of 8) of memory trials correctly compared to 11 out of 12 children in the Story-schema condition, χ2(1, n = 24) = 4.11, p < 0.05. Like Experiment 1, these significant differences in memorization could be driving differences in generalization. An ANCOVA revealed that memory performance was not a significant covariate, F(1, 21) = 1.13, and training condition was a marginally significant factor, F(1, 21) = 4.23, p < 0.06, partial η2 = 0.16. The Schema-story training facilitated both children’s memorization of the initial instances and their generalization of the learned pattern.
The Schema-story apparently enabled these children to interpret the pictured events in new ways and to generalize those interpretations, a result that provides support for both the Schema Hypothesis and the Optimal Vagueness hypothesis. Children in the Schema-story condition were told how to interpret the cards rather than having to form an interpretation themselves (although applying this interpretation most likely did require some mental work) and they exhibited superior performance to children who simply received the labels. This result strongly suggests that the key is having an interpretation that makes sense. One of the difficulties for the Unrelated condition may be that it was too difficult to interpret a car–diamond–diamond scene as a “sharing” scene without some additional information. So, the insight of the Schema hypothesis still holds, that children need some background information (either from their own experiences or provided by an external source) to interpret a scene relationally. Although applying the given interpretation to the perceptual situation at hand may be slightly odd (diamonds sharing a car?), it may be that the oddness provides some opportunity for the child to work out how this perceptual situation instantiates sharing. Therein lies the contribution of the Optimal Vagueness hypothesis: perhaps to appropriately make use of a schema, the fit between the story and the situation may be better left vague and unexplained in order to promote interpretation and thus generalization. This experiment suggests that the benefit of work may not be the sheer effort exerted in finding an interpretation but simply the mental work of interpreting a scene, even if that interpretation is provided by someone else.
General Discussion
The studies in this paper used lexical generalization as a measure of how much young children represent the deep structural similarities present in an array when learning how words relate to these arrays. The key hypothesis was that words promote the discovery of relations by evoking well-known event structures, thereby relating this phenomena in relational reasoning to children’s flexible reasoning about well-known events. However, the key for relational generalization is to represent the relation in a variable-ized way such that very different kinds of entities can be seen as standing in the same relational role. This suggests that an event structure that fits too well with the depicted situation, with stereotypic entities in the relational roles, does not promote generalization. The present results provide support for both the Schema-evoking hypothesis and the Optimal Vagueness corollary. By using words and scenes that vaguely evoke event structures familiar to young children, label training boosted attention to relations and fostered relational generalization.
Two aspects of schemas motivated the design of these experiments: using words to activate schematic interpretations and using scenes conducive to schematic interpretation. The connection between language, schemas, and generalization is an old one but the direction of application in these experiments is new. Originally in the 1970s, schemas (and scripts and frames) were hypothesized as constructs to explain language comprehension (e.g., Minsky, 1975; Rumelhart, 1975; Schank and Abelson, 1977; Charniak, 1978). Individuals could interpret ambiguous language in the context of these schemas that represented events in terms of actors, actions, and objects in highly likely spatial or temporal relations. These classic ideas motivated the Schema hypothesis, which was supported by our results showing how the use of well-known words with structured meanings can bring about generalizable interpretations of ambiguous situations.
In their original conception, schemas were generalizable because of the presence of mental variables or slots that could be filled in by a set of options. Developmental researchers have found that children’s knowledge for familiar events are often formulated in such ways, highlighting relational structure and including optional and variable information (i.e. Nelson and Gruendel, 1981; Mandler, 1983; Hudson and Nelson, 1986). For well-understood events such as birthday parties, children provide general knowledge, such as expectancy that games will be played, and provide specific options, such as pin-the-tail-on-the-donkey as filler for the “games” slot. This was the motivation for the Optimal Vagueness hypothesis; that schemas were useful because they were meaningful but at the same time, not fixed nor too specific. In the present experiments, we used arrays with simple abstract elements in the roles. The benefit of these arrays – over richer ones – for children’s relational reasoning supports the idea that too much emphasis on specific fillers draws attention away from the schematic structure. Thus, less vibrant and loosely fitting fillers seems to leave more attentional resources available for processing relational structure.
The Schema and Optimal Vagueness hypotheses, when considered together, suggest a “sweet spot” for generalization. The Optimal Vagueness perspective suggests that there should not be too many particulars or concrete details involved in the labeling experience else generalization may suffer. But the Schema hypothesis shows a need for enough cues to activate relevant background information to provide appropriate interpretation and facilitate learning. The following discussion explores these two ends and their implications.
When Learning Instances are Too Specific
Generally, concrete and rich representations have more information than sparse ones and the natural consequence is that only some of this information gets learned. Concreteness is relevant to Experiment 3, in which a perceptually more detailed depiction of an event called “sharing” (or “pulling”) results in less transfer than a more schematic depiction. Although learning from concrete representations can be beneficial, it can also be problematic for three reasons. First, learners may not understand that these details are optional, creating a characterization of the situation that is unnecessarily tied to its originating context (Goldstone and Sakamoto, 2003). The second reason, related to the first, in that specific interesting details may compete against, and often overwhelm, subtle relational information (Uttal et al., 1997; DeLoache, 2000). Lastly, even relevant details may affect the appreciation of similarity to other isomorphic instances (Sloutsky et al., 2005; Kaminski et al., 2008).
Children and other learners do not a priori realize what they are supposed to learn from an experience. Given that concrete details of objects are typically more salient than relational information, particularly for young children (Gentner and Rattermann, 1991), when these details are available, they are encoded more readily. Young children’s immediate recall memory for specific details is better than recall of general structure (Slackman and Nelson, 1984; Sloutsky and Fisher, 2004). Studies of young children’s attention, such as the often used card sort task devised by Zelazo et al. (1995, 1996), show that when attention is already directed toward some feature or dimension, it is difficult for children to overcome this “attentional inertia” (Kirkham et al., 2003) when they are required to switch to another dimension. In the card sort task, the dimensions (typically color and shape) are initially fairly equal in saliency. If information is unequal in saliency, as in the case of concrete details versus relations, it is reasonable to think that young children will have an even harder time focusing their attention on the less salient relations. In the case of highly detailed training cards, children may not have even noticed the perceptual symmetry portrayed in the situation in lieu of more salient object details. The mere presence of many features in the Specifically related girl–penguin–girl scene that overlapped with the label “sharing” may have made it difficult for children to notice the symmetrical structure also in the scene. Thus, picking out and responding to relational information is often easier with sparser instances (Rattermann et al., 1990; Gentner and Rattermann, 1991). Conflating concrete details and abstract relations makes relational reasoning difficult even for adults (Goldstone and Sakamoto, 2003; Son and Goldstone, 2009).
DeLoache and colleagues (DeLoache, 1995, 2000; Uttal et al., 1999) have stressed the importance of competing concrete and symbolic construals. Concrete objects can be considered as interesting objects in their own right or as symbolic stand-ins for something else, and when concrete properties are intensified, then symbolic construals suffer. In schema terms, this symbolic “stands-for” insight is the idea of a slot to be filled in by something else. This representational insight may be the key step to generalization, with learners’ appreciation that many fillers can be placed in a slot. A particularly relevant example of this competition between interesting details and relational information is in the domain of math manipulatives. Although educators are generally in favor of concrete manipulatives (Ball, 1992; Moyer, 2001; Kennedy et al., 2007), some researchers suggest that this growing enthusiasm should be paralleled with a better understanding of what children actually learn and generalize from manipulatives (Uttal et al., 1997). Stevenson and Stigler (1994) observe that American math teachers will use anything interesting, from “marbles, Cheerios, M&Ms, checkers, poker chips, or plastic animals,” sometimes even in a single lesson. The general attitude seems to be that more information, more detailed examples, and more interest in math activities (i.e., counting M&Ms matters to children more so than counting notches on paper) are important. However, if the goal of math education is to direct attention to structure, perhaps less interesting and less concrete learning examples may serve better. The Optimal Vagueness hypothesis is more consistent with the simple tiles used by Japanese teachers (Stevenson and Stigler, 1994). The tiles are concrete and familiar in that they are physical manipulatives and used repeatedly, however they are not vivid or particularly interesting objects.
One might object to these criticisms of concrete details, claiming that the reason richly interesting items, such as M&Ms, do not benefit learning is that what is interesting about these items is irrelevant to the structure of the learning situation. This criticism, however, cannot account for the findings from Experiment 3 (see also Kaminski et al., 2008). In that experiment, the relations between the rich objects were highly relevant to understanding the schema and could have even fostered a better understanding of the balance or asymmetry in the situation. That is, the Specifically related training cards were designed to be more accurate instances of “sharing” and “pulling” than the other training cards. The Specifically related training cards, having three objects concretely related to “sharing,” provided an excellent example of sharing, yet did not allow the label to generalize to sparser versions of the same relation such as diamond–circle–diamond.
One of the fundamental problems with specificity may be that the presence of specific details changes the similarity relations between the learning cards and the generalization cards. In this study, the dissimilarity was obvious: there were no simple shapes on the Specifically related training cards and all generalization cards consisted of three simple shapes; all other training cards had at least two simple shapes. But more generally, the addition of details introduces more dissimilarity to future instances. The simplicity of abstract formalisms or simplified representations, only expressing sparse structure, allows them to be equally similar to (and equally far from) many instances (Son and Goldstone, 2009). Because abstractions have less information, and in particular less contrasting dissimilarities (Tversky, 1977; Bassok and Holyoak, 1989), they capture a prototype-like representation that anchors many instances, which may be dissimilar from each other but equally similar to the prototype (see Son et al., 2008 for a test of this hypothesis in children’s shape generalization). The central role of vague, simplified representations for learning may also explain why heavy reliance on specific examples often leads to poor understanding (Chi et al., 1989).
When Learning Instances are too Vague
After listing the disadvantages of highly specific learning scenarios, one might conclude that for generalization, the more abstract, the better. However, the present results as well as other studies clearly document children’s (and adults’) difficulties with abstract formalisms (e.g., Lave, 1988; Nunes et al., 1993). After all, merely including two simple shapes in the training cards was not enough to foster generalization to cards with simple shapes (the Arbitrary and Iconic label conditions from Experiment 1, and the Unrelated conditions from Experiments 2–4). The notion of optimal vagueness offered here suggests that learning instances can be too vague. For example, future studies should address whether applying “sharing” to simple shapes such as diamond–circle–diamond would be effective for generalization. After all, if generalization is merely a case of similarity, then such training should produce the best levels of generalization to new cards with triples of simple shapes. If such training is ineffective, it may be that such a situation is difficult to organize according to relational information because it does not sufficiently evoke richly relevant information. One immediate advantage of having toys in “sharing” scenes and vehicles in “pulling” scenes is that they provide scaffolding that partly overlaps with children’s past experiences with these actions. Exactly because the structural information conveyed to the young participants is hidden among these details, children could have simply remembered that the label “sharing” goes with the toy cards and “pulling” with vehicle ones. However, that alone could not have resulted in better generalization to scenarios that do involve toys or vehicles.
An additional disadvantage of “too much vagueness” is demonstrated by Experiment 1’s iconic label condition. As useful as a slot-like variable representation of a situation might be, a highly impoverished one, such as the “ko-li-ko” label, did not foster as much generalization as a meaningful label. The iconic labels made use of syllabic isomorphism for things that are the same on the ends (“ko”) and something different in the middle (“li”). But perhaps the relation is not even noticed, as seems likely in the present case (that is, that children did not even notice the parallel relational structure of the mimetic forms). This notion of too much vagueness might similarly explain Gick and Holyoak’s (1983) results showing less analogical generalization when participants were provided with an explicit (but abstract) statement of the underlying principle of a story than from exposure to multiple analogs. This abstract principle for these adults and “ko-li-ko” for children may just be too vague to activate relevant knowledge. Thus, the key to relational insights more generally may be building up or activating relevant past knowledge with slot-like schemas. Consistent with this idea, Gick and Holyoak found that when learners produced their own statement of the underlying principle after exposure to multiple analogs, this schema was highly predictive of subsequent transfer. Thus, in their study, a general schema created from more specific instances produced transfer. Perhaps in the current studies, the use of “sharing” allowed multiple past instances to be activated and thus aided the formation of a relationally appropriate interpretation.
The real advantage of initial concreteness may be this: that schemas can be created from them. The process of forming a schema may be important to benefits in generalization. If this is the case, the advantages of concreteness may be particularly critical early in learning. Goldstone and Son (2005) have proposed a pedagogical method of “concreteness fading” where initial instances are highly concrete but are gradually idealized over time. By initially presenting easily understood concrete ideas along with more abstract ideas, and then fading away those concrete details, this method eases a learner into a more abstract construal. This may be an effective teaching methodology because it instantiates a schematization process. Initially, during label training, our participants may have been more reliant on the concrete details but taking away the toy in the middle during the impoverished generalization trials may have fostered a “faded” understanding of the learning instances.
A related idea is “progressive alignment” by Gentner and colleagues (Kotovsky and Gentner, 1996; Gentner and Medina, 1998) which uses alignment of concretely similar situations to foster comparison, a process shown to highlight commonalities, discard deviations, and result in schema-like representations (Markman and Gentner, 1993). Presumably, if children have experiences sharing desirable toys, they may be able to effectively align their past experiences with the ambiguous one in front of them in order to create a schematic interpretation. However, if alignment of parts is critical for schematic interpretation, the relational construal created here may not be flexible enough to generalize to less alignable instances. For example, if lining up objects is critical to understanding ABA relations, then “sharing” as applied to ABA instances may not extend to instances such as AABAA or even ABBA or ABCBA. If alignment is not critical, optimally vague learning may be less “slot-like” and instead more like an image. In such a case, perhaps any instance with something vaguely different in the middle, such as a single large isosceles triangle, could be considered “sharing.”
Conclusion
The present studies, in addition to expanding on the role of words and schemas in fostering relational construals, are potentially important to a fundamental understanding of the meaning of words. In other studies where words benefit relational reasoning (i.e., “Daddy” from Gentner and Rattermann, 1991; “Even” from Kotovsky and Gentner, 1996; “Top/Middle/Bottom” from Loewenstein and Gentner, 2005), it might be tempting to think that the meaning of particular words is the source of the facilitation. The present results suggest that while meaning matters, the relevant meaning for generalizing relational concepts may be an “interpretation” that can be bent to fit multiple instances. Words that are related to well-ordered schemas allow children to take on a relational perspective – but that perspective must be applied to a situation that is conducive to developing relational meaning. As accounts of language can contribute to a better understanding of analogical reasoning, so also can an account of creating relational similarity contribute to better accounts of language.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank Stacy Einikis, Jennifer Dold, and Elizabeth Hannibal for their invaluable assistance in collecting data. We also want to express our gratitude to the participating daycares (including the children, teachers, and parents). This work was funded by National Science Foundation REESE grant 0910218 and NIH grants, HD007475 and HD28675.
References
Ball, D. L. (1992). Magical hopes: manipulatives and the reform of math education. Am. Educ. 16, 14–18.
Bassok, M., and Holyoak, K. J. (1989). Interdomain transfer between isomorphic topics in algebra and physics. J. Exp. Psychol. Learn. Mem. Cogn. 15, 153–166.
Bauer, P. J., and Mandler, J. M. (1989). One thing follows another: effects of temporal structure on 1- to 2-year-olds’ recall of events. Dev. Psychol. 25, 197–206.
Boroditsky, L., Fuhrman, O., and McCormick, K. (2011). Do English and Mandarin speakers think about time differently? Cognition 118, 123–129.
Brown, A. L., Kane, M. J., and Echols, C. H. (1986). Young children’s mental models determine analogical transfer across problems with a common goal structure. Cogn. Dev. 1, 103–121.
Charniak, E. (1978). On the use of framed knowledge in language comprehension. Artif. Intel. 11, 225–265.
Chi, M. T. H., Bassok, M., Lewis, M. W., Reimann, P., and Glaser, R. (1989). Self-explanations: how students study and use examples in learning to solve problems. Cogn. Sci. 13, 145–182.
Chi, M. T. H., De Leeuw, N., Chiu, M.-H., and Lavancher, C. (1994). Eliciting self-explanations improves understanding. Cogn. Sci. 18, 439–477.
Choi, S., and Bowerman, M. (1991). Learning to express motion events in English and Korean: the influence of language-specific lexicalization patterns. Cognition 41, 83–121.
Clark, A. (1998). Being There: Putting Brain, Body, and World Together Again (First Paper Back Edition.). Cambridge: A Bradford Book.
DeLoache, J. S. (1995). Early understanding and use of symbols: the model model. Curr. Dir. Psychol. Sci. 4, 109–113.
DeLoache, J. S. (2000). Dual representation and young children’s use of scale models. Child Dev. 71, 329–338.
Fivush, R. (1984). Learning about school: the development of kindergartners’ school scripts. Child Dev. 55, 1697.
Gelman, S. A. (1988). The development of induction within natural kind and artifact categories. Cogn. Psychol. 20, 65–95.
Gentner, D., Anggoro, F. K., and Klibanoff, R. S. (2011). Structure mapping and relational language support children’s learning of relational categories. Child Dev. 82, 1173–1188.
Gentner, D., and Rattermann, M. J. (1991). “Language and the career of similarity,” in Perspectives on Thought and Language: Interrelations in Development, eds S. A. Gelman and J. P. Byrnes (London: Cambridge University Press), 225–277.
Gick, M. L., and Holyoak, K. J. (1983). Schema induction and analogical transfer. Cogn. Psychol. 15, 1–38.
Gobbo, C., and Chi, M. (1986). How knowledge is structured and used by expert and novice children. Cogn. Dev. 1, 221–237.
Goldstone, R., and Sakamoto, Y. (2003). The transfer of abstract principles governing complex adaptive systems. Cogn. Psychol. 46, 414–466.
Goldstone, R. L., and Son, J. Y. (2005). The transfer of scientific principles using concrete and idealized simulations. J. Learn. Sci. 14, 69–110.
Herbert, J., and Hayne, H. (2000). Memory retrieval by 18-30-month-olds: age-related changes in representational flexibility. Dev. Psychol. 36, 473–484.
Hudson, J., and Nelson, K. (1986). Repeated encounters of a similar kind: effects of familiarity on children’s autobiographic memory. Cogn. Dev. 1, 253–271.
Hudson, J. A., Fivush, R., and Kuebli, J. (1992). Scripts and episodes: the development of event memory. Appl. Cogn. Psychol. 6, 483–505.
Imai, M., Kita, S., Nagumo, M., and Okada, H. (2008). Sound symbolism facilitates early verb learning. Cognition 109, 54–65.
Kaminski, J. A., Sloutsky, V. M., and Heckler, A. F. (2008). The advantage of abstract examples in learning math. Science 320, 454–455.
Keil, F. C., and Batterman, N. (1984). A characteristic-to-defining shift in the development of word meaning. J. Verb. Learn. Verb. Behav. 23, 221–236.
Kennedy, L. M., Tipps, S., and Johnson, A. (2007). Guiding Children’s Learning of Mathematics. Belmont, CA: Wadsworth Publishing.
Kirkham, N. Z., Cruess, L., and Diamond, A. (2003). Helping children apply their knowledge to their behavior on a dimension-switching task. Dev. Sci. 6, 449–467.
Kotovsky, L., and Gentner, D. (1996). Comparison and categorization in the development of relational similarity. Child Dev. 67, 2797–2822.
Lave, J. (1988). Cognition in Practice: Mind, Mathematics and Culture in Everyday Life. Cambridge: Cambridge University Press.
Levine, S. C., Jordan, N. C., and Huttenlocher, J. (1992). Development of calculation abilities in young children. J. Exp. Child. Psychol. 53, 72–103.
Loewenstein, J., and Gentner, D. (2005). Relational language and the development of relational mapping. Cogn. Psychol. 50, 315–353.
Lupyan, G. (2005). “Carving nature at its joints and carving joints into nature: how labels augment category representations,” in Modelling Language, Cognition and Action: Proceedings of the 9th Neural Computation and Psychology Workshop, eds A. Cangelosi, G. Bugmann, and R. Borisyuk (Singapore: World Scientific Publishing Co. Pte. Ltd), 87–96.
Mandler, J. (1983). “Representation,” in Manual of Child Psychology, ed. P. Mwssen (New York: Wiley), 420–494.
Markman, A., and Gentner, D. (1993). Structural alignment during similarity comparisons. Cogn. Psychol. 25, 431–467.
Martin, T. (2009). A theory of physically distributed learning: how external environments and internal states interact in mathematics learning. Child Dev. Perspect. 3, 140–144.
Martin, T., and Schwartz, D. L. (2005). Physically distributed learning: adapting and reinterpreting physical environments in the development of fraction concepts. Cogn. Sci. 29, 587–625.
McNamara, D., Kintsch, E., Songer, N. B., and Kintsch, W. (1996). Are good texts always better? Interactions of text coherence, background knowledge, and levels of understanding in learning from text. Cogn. Instr. 14, 1–43.
McNeil, N., Uttal, D., Jarvin, L., and Sternberg, R. (2009). Should you show me the money? Concrete objects both hurt and help performance on mathematics problems. Learn. Instruct. 19, 171–184.
McQuarrie, E. F., and Mick, D. G. (1999). Visual rhetoric in advertising: text interpretive, experimental, and reader response analyses. J. Consum. Res. 26, 37–54.
Medin, D. L., and Ross, B. H. (1989). “The specific character of abstract thought: categorization, problem solving, and induction,” in Advances in the Psychology of Human Intelligence, Vol. 5, ed. R. J. Sternberg (Hillsdale, NJ: Lawrence Erlbaum Associates), 189–223.
Minsky, M. (1975). “A framework for representing knowledge,” in The Psychology of Computer Vision, ed. P. H. Winston (New York: McGraw-Hill), 211–277.
Miura, I. T., and Okamoto, Y. (1989). Comparisons of U.S. and Japanese first graders’ cognitive representation of number and understanding of place value. J. Educ. Psychol. 81, 109–114.
Moyer, P. S. (2001). Are we having fun yet? How teachers use manipulatives to teach mathematics. Educ. Stud. Math. 47, 175–197.
Nelson, K., and Gruendel, J. M. (1981). “Generalized event representations: basic building blocks of cognitive development,” in Advances in Developmental Psychology, Vol. 1, eds A. Brown and M. Lamb (Hillsdale, NJ: Erlbaum), 131–158.
Nunes, T., Carraher, D. W., and Schliemann, A. D. (1993). Street Mathematics and School Mathematics. Cambridge: Cambridge University Press.
Perry, L. K., Samuelson, L. K., Malloy, L. M., and Schiffer, R. N. (2010). Learn locally, think globally. Psychol. Sci. 21, 1894–1902.
Plunkett, K., Hu, J.-F., and Cohen, L. B. (2008). Labels can override perceptual categories in early infancy. Cognition 106, 665–681.
Rattermann, M. J., Gentner, D., and DeLoache, J. (1990). “The effects of familiar labels on young children’s performance in an analogical mapping task,” in Proceedings of the Twelfth Annual Conference of the Cognitive Science Society (Hillsdale, NJ: Lawrence Erlbaum Associates), 22–29.
Ross, B. H., and Kennedy, P. T. (1990). Generalizing from the use of earlier examples in problem solving. J. Exp. Psychol. Learn. Mem. Cogn. 16, 42–55.
Rumelhart, D. E. (1975). Notes on a schema for stories,” in Representation and Understanding: Studies in Cognitive Science, eds D. G. Bobrow and A. Collins (New York: Academic Press), 211–236.
Rumelhart, D. E., and Ortony, A. (1977). “The representation of knowledge in memory,” in Schooling and the Acquisition of Knowledge, eds R. C. Anderson, R. J. Spiro, and W. E. Montague (Hillsdale, NJ: Erlbaum), 99–135.
Schank, R. C., and Abelson, R. P. (1977). Scripts, Plans, Goals, and Understanding: An Inquiry into Human Knowledge Structures. Hillsdale, NJ: Lawrence Erlbaum.
Schank, R. C., and Abelson, R. P. (1995). “Knowledge and memory: the real story,” in Knowledge and Memory: The Real Story, ed. R. S. Jr. Wyer (Hillsdale, NJ: Lawrence Erlbaum Associates), 1–85.
Sinha, C., Thorseng, L. A., Hayashi, M., and Plunkett, K. (1994). Comparative spatial semantics and language acquisition: evidence from Danish, English, and Japanese. J. Semant. 11, 253–287.
Slackman, E., and Nelson, K. (1984). Acquisition of an unfamiliar script in story form by young children. Child Dev. 55, 329.
Sloutsky, V. M., and Fisher, A. V. (2004). Induction and categorization in young children: a similarity-based model. J. Exp. Psychol. Gen. 133, 166–188.
Sloutsky, V. M., Kaminski, J. A., and Heckler, A. F. (2005). The advantage of simple symbols for learning and transfer. Psychon. Bull. Rev. 12, 508–513.
Son, J. Y., and Goldstone, R. L. (2009). Fostering general transfer with specific simulations. Pragmatics Cogn. 17, 1–42.
Son, J., Smith, L., and Goldstone, R. (2008). Simplicity and generalization: short-cutting abstraction in children’s object categorizations. Cognition 108, 626–638.
Son, J. Y., Smith, L. B., and Goldstone, R. L. (2011). Connecting instances to promote children’s relational reasoning. J. Exp. Child Psychol. 108, 260–277.
Stevenson, H., and Stigler, J. W. (1994). Learning Gap: Why Our Schools Are Failing and What We Can Learn from Japanese and Chinese Education, 1st Edn. New York: Simon & Schuster.
Uttal, D. H., Liu, L. L., and DeLoache, J. S. (1999). “Taking a hard look at concreteness: do concrete objects help young children learn symbolic relations?” in Child Psychology: A Handbook of Contemporary Issues, eds L. Balter and C. Tamis-LeMonda (Philadelphia, PA: Psychology Press), 177–192.
Uttal, D. H., Scudder, K. V., and DeLoache, J. S. (1997). Manipulatives as symbols: a new perspective on the use of concrete objects to teach mathematics. J. Appl. Dev. Psychol. 18, 37–54.
Waxman, S. R., and Markow, D. B. (1995). Words as invitations to form categories: evidence from 12- to 13-month-old infants. Cogn. Psychol. 29, 257–302.
Winawer, J., Witthoft, N., Frank, M. C., Wu, L., Wade, A. R., and Boroditsky, L. (2007). Russian blues reveal effects of language on color discrimination. Proc. Natl. Acad. Sci. U.S.A. 104, 7780–7785.
Xu, F., and Tenenbaum, J. B. (2007). Word learning as Bayesian inference. Psychol. Rev. 114, 245–272.
Yoshida, H. (in press). A cross-linguistic study of iconicity in children’s verb learning. J. Cogn. Dev.
Zelazo, P. D., Frye, D., and Rapus, T. (1996). An age-related dissociation between knowing rules and using them. Cogn. Dev. 11, 37–63.
Keywords: schemas, analogy, labels, relational reasoning, cognitive development
Citation: Son JY, Smith LB, Goldstone RL and Leslie M (2012) The importance of being interpreted: grounded words and children’s relational reasoning. Front. Psychology 3:45. doi: 10.3389/fpsyg.2012.00045
Received: 31 October 2011;
Accepted: 07 February 2012;
Published online: 07 March 2012.
Edited by:
Haley Vlach, University of California Los Angeles, USAReviewed by:
Elizabeth Goldenberg, University of California Los Angeles, USAStella Christie, University of British Columbia, Canada
Copyright: © 2012 Son, Smith, Goldstone and Leslie. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Ji Y. Son, Department of Psychology, California State University Los Angeles, 5151 State University Dr., Los Angeles, CA 90032, USA. e-mail:anNvbjJAY2Fsc3RhdGVsYS5lZHU=