- 1 Biological and Experimental Psychology Centre, School of Biological and Chemical Sciences, Queen Mary College, University of London, London, UK
- 2 Cognitive, Perceptual and Brain Sciences, Division of Psychology and Language Sciences, University College London, London, UK
The present study compared the accuracy of cue-outcome knowledge gained during prediction-based and control-based learning in stable and unstable dynamic environments. Participants either learnt to make cue-interventions in order to control an outcome, or learnt to predict the outcome from observing changes to the cue values. Study 1 (N = 60) revealed that in tests of control, after a short period of familiarization, performance of Predictors was equivalent to Controllers. Study 2 (N = 28) showed that Controllers showed equivalent task knowledge when to compared to Predictors. Though both Controllers and Predictors showed good performance at test, overall Controllers showed an advantage. The cue-outcome knowledge acquired during learning was sufficiently flexible to enable successful transfer to tests of control and prediction.
Introduction
Imagine a scenario in which after a visit to your doctor, you are told that your blood pressure is too high. Following the doctor’s recommendation, you have decided to take up more exercise by jogging, and to change your diet by reducing your salt intake. In addition you have bought the latest mobile phone application which is a self monitoring device that can help you track and analyze your blood pressure. By steadily increasing exercise and reducing intake of salty foods (interventions), and measuring your blood pressure at regular intervals, the idea is to track the relationship between exercise and salt intake (cues) and blood pressure (outcome) to assess how effective the new healthy regime is. You notice that your blood pressure recordings fluctuate while you are resting (internal, or endogenous, changes in the outcome), as well as when you have gone for a jog, or eaten (external, or exogenous, changes in the outcome1). On some days your blood pressure does not reduce as substantially as on other days, and so on those occasions you decide to take more exercise.
The above example can be described as dynamic decision making, in which decisions (i.e., choosing a course of action) are adapted to the ongoing changes in the outcome. More specifically this type of dynamic decision making involves learning about the cue-outcome relations via cue-intervention (control-based decision making). A different approach may involve first monitoring for a period of time the cue-outcome relations by tracking changes in cues (i.e., observing your usual salt intake from day to day) from which one can make predictions about changes to the outcome. This is an example of prediction-based decision making in which cue-outcome relations are acquired via estimates of the expected outcome value. The difference between the two is that in the latter case there is no cue-intervention; instead, changes in cue and outcome values are used to adjust the predictions made.
Both prediction and control are methods of acquiring cue-outcome knowledge, and are examples of dynamic decision making. General models of learning (e.g., Reinforcement learning/reward-based learning, Schultz et al., 1997; Sutton and Barto, 1998; Schultz, 2006) would propose that both prediction and control are comparable ways of acquiring cue-outcome knowledge, because both rely on prediction errors signals arising from a comparison between predicted and actually obtained outcomes. One avenue that this present study explores is to directly compare the accuracy of cue-outcome knowledge when gained via prediction and when gained via control, in order to explore these general claims.
Dynamic decision making (hereafter DDM) is an area of decision making research that is growing in popularity (Brown and Steyvers, 2005; Osman et al., 2008; Lurie and Swaminathan, 2009; Osman, 2010a,b, 2011; Speekenbrink and Shanks, 2010). Typically, tasks designed to examine this type of process involve situations in which the decision maker has a clearly defined goal from the outset. Because the environment is probabilistic and/or dynamic, the desired goal cannot usually be achieved in one step. Therefore the decision maker must plan a series of actions that will help to incrementally move them closer to the goal. Thus, the process of decision making in dynamic environments is often described as goal directed, and the decisions themselves are usually inter-dependent across trials (Brehmer, 1992; Funke, 1992; Osman, 2010a).
Given this type of characterization, planning actions in order to obtain future outcomes is an important component of DDM, and therefore it is likely that some control-based decision are informed by predictions (Osman, 2010a,b). Moreover, the decision maker needs to be sensitive to possible changes in the environment in order to adapt their planned interventions accordingly. For this reason DDM is also referred to as adaptive decision making (Cohen et al., 1996; Klein, 1997; Lipshitz et al., 2001). Typically in DDM contexts accurate estimates of the environment’s future behavior are important for planning the best interventions that would achieve the right outcome. Consider the following engineering example, in which the goal is to maintain a supply of electricity from a power station that meets the consumers’ needs. Since there are obvious changes in the demand according to daily as well as seasonal changes, this enables fairly stable predictions as to consumer use that enables matching the generator’s output to load predictions. However, it is important to estimate future demands in order to adjust the system quickly enough as the changes arise (e.g., sudden unseasonably low temperatures). Predictions regarding fuel consumption are essential to informing the choice of intervention needed to control power supply, and research in the engineering domain supports this (e.g., Leigh, 1992). In fact, optimal control theory (Bryson and Ho, 1975) provides a formal basis for analyzing the changing states of a system in order to provide a complete stochastic description of control under uncertainty. Moreover, the theory has been implemented in psychological research on human motor control (e.g., Körding and Wolpert, 2006).
Many theoretical accounts of DDM (Vancouver and Putka, 2000; Burns and Vollmeyer, 2002; Bandura and Locke, 2003; Goode and Beckmann, 2010; Osman, 2010a,b) and formal descriptions of DDM (Gibson et al., 1997; Sun et al., 2001; Gibson, 2007) claim that controlling outcomes to a target goal involves decisions based on prediction. In their Social-Cognitive theory, Bandura and Locke (2003) refer to prediction as a feedforward process which has a motivational component attached to it. They propose that by estimating future outcomes and future success, when reinforced, successful predictions drive the decision maker to achieve even more accurate or more successful control of the environment. Burns and Vollmeyer (2002) describe DDM within the context of hypothesis testing. They posit that decision makers learn best by exploring the DDM environment. This entails generating expectations about the associations between their actions and the effects they will produce. The effects they achieve through their actions are used as feedback to update hypotheses about the relationship between cues and outcomes in the environment. Gibson’s (Gibson et al., 1997; Gibson, 2007) neural network model also posits that DDM involves the development of hypotheses about cue-outcome associations, from which planned interventions are made. The model includes two submodels: a forward model and an action model. The action submodel decides what action to take based on the current state of the environment and the distance from the target goal. Each action generates an expected outcome which is then compared against the goal; from this the action which is most likely to minimize the distance between the expected state and the goal is chosen. The forward submodel takes as input an action that has been executed and compares its outcome with the goal. It then generates as output an expected outcome which is used to derive an error signal. Back propagation is then used to adjust the connection weights between action and predicted outcome, to improve the ability to predict the effects of actions on the environment.
Osman’s (2010a,b, 2011) Monitoring and Control framework also proposes that there are two different judgments made regarding a DDM environment: its predictability and its controllability. People are sensitive to the endogenous as well as the exogenous changes in the environment. This is because they are repeatedly updating their expectancies of the outcomes that will occur in the environment, and this informs their subjective estimates of confidence in predicting outcomes of events in a dynamic environment (predictability of the environment). As well as developing expectancies about the outcomes that are likely to occur, the actions taken in the environment generate outcomes which can be fed back in order to update one’s expectancies. This informs their subjective estimates of expectancy that an action executed will achieve a specific outcome in a control system (predictability of control).
In sum, the consensus amongst many theorists in the DDM research domain is that prediction forms a strong component of the decision making process needed to plan interventions in order to reliably achieve a target goal (Vollmeyer et al., 1996; Burns and Vollmeyer, 2002; Gibson, 2007; Osman, 2010b). However, there are alternative accounts of DDM that do not assign a role to prediction. For instance, Berry and Broadbent(1984, 1987, 1988) claim that people typically fail to provide a veridical verbal description of their acquired knowledge or to accurately predict different states of the DDM task because the cue-outcome associations are far too complex to learn explicitly. Accurate control of the outcome is achieved through active intervention, from which successful cue-interventions that generate desired outcomes are stored in memory and later recalled when faced with similar task situations. Because there is no need for predictive learning, there is no cue-abstraction, instead successful control performance is based solely on representations of action-outcome associations.
There is little empirical research that has investigated the contribution of prediction (i.e., estimating the outcome that will occur) to control (i.e., planning actions to achieve an outcome) in a dynamic environment. Thus, it is not clear whether controlling a dynamic environment relies on prediction, or for that matter, whether it is possible to learn about a dynamic environment from prediction alone. This is a limitation given the kinds of different theoretical claims made about the relevance of prediction to control. Therefore, the present study aims to separate prediction-based from control-based learning, and directly compare the accuracy of cue-outcome knowledge gained from both forms of learning.
There are two relevant literatures that have considered these issues in isolation, namely, multiple cue probability learning (MCPL) and complex dynamic control (CDC). Research on MCPL examines how we integrate information from different sources in order to learn to predict outcomes in probabilistic environments (Speekenbrink and Shanks, 2010). Typically, MCPL tasks involve presenting people with cues (e.g., symptoms – rash, fever, headaches) which are probabilistically associated with an outcome (e.g., disease – flu, cold). Participants are asked to predict the outcome (e.g., flu) for various cue combinations (e.g., rash, fever), and then receive outcome feedback on their prediction. Research on CDC has investigated the way in which decisions are formed over time in order to reliably control outcomes in dynamic and probabilistic environments (Osman, 2008a). People decide from a set of inputs (cues; e.g., drug A, drug B, drug C) actions that are relevant (e.g., selecting drug A at dosage X) for achieving and maintaining a particular output (outcome; e.g., reduce the spread of disease Y). As with MCPL environments, input–output (hereafter: cue-outcome) associations are probabilistic, and also need to be learned. In addition, the environment can also be dynamic, in the sense that the outcome may change independently of actions made by the individual (e.g., disease Y spreads at a particular rate). In MCPL tasks, learning about the cue-outcome associations is indirect because only observations of the cue patterns are used to predict the events with the aim of reducing the discrepancy between expected and actual outcomes. By contrast, learning about the cue-outcome associations is direct in CDC tasks because the cues are manipulated and the change in outcome that follows serves as feedback which is used to update knowledge of cue-outcome associations.
We briefly review the MCPL and CDC literature in the next section. These research domains have remained relatively separate (Osman, 2010a). A secondary objective of this study, besides comparing prediction-based decision making with control-based decision making in a DDM environment, is to consider the potential common ground shared by the MCPL and CDC research paradigms.
Early MCPL studies were largely concerned with varying different properties of the task environment and examining the effects on predictive accuracy. Properties of the environment that were varied include: the number of cue-outcome associations (Slovic et al., 1971), the combination of continuous cue and binary outcomes (Vlek and van der Heijden, 1970), the presence of irrelevant cues (Castellan, 1973), the type of feedback presented (Björkman, 1971; Hammond et al., 1973; Muchinsky and Dudycha, 1975; Holzworth and Doherty, 1976), time constraints (Rothstein, 1986), and cue validities (Castellan and Edgell, 1973; Edgell, 1974). In the main, the evidence suggests that people show sensitivity to the cue validities and cue probabilities. Moreover, it has been suggested that people update their knowledge of the cue-outcome associations by developing hypothesis testing strategies.
More recently, the weather prediction task (WPT), developed by Knowlton et al. (1994), has become a popular paradigm for studying prediction-based decision making. It was originally designed to study incremental learning processes in clinical populations (e.g., amnesic patients). Knowlton et al. (1994) proposed that amnesics were able to successfully predict outcomes in the task through incidental acquisition of cue-outcome associations (procedurally) rather than explicit cue-abstraction (declaratively). That is to say, accurate cue-outcome knowledge of a probabilistic environment was acquired through processes that did not require deliberate evaluation of expected outcomes and actual outcomes. In support, others (e.g., Knowlton et al., 1996; Poldrack et al., 2001) have since shown that knowledge acquired procedurally is not available to conscious inspection, because of the implicit nature of learning of cue-outcome knowledge. However, critics of this position have investigated these claims in non-clinical (Price, 2009) as well as clinical populations (Speekenbrink et al., 2008) and have found evidence to suggest a correspondence between the accuracy of explicit cue-outcome knowledge and predictive accuracy, suggesting that people do have insight into the cue-outcome knowledge they have acquired. This has been taken to suggest that the strategies people develop to make their predictions are consciously accessible, and that there is an exhaustive evaluative process involved in comparing expected outcomes with actual outcomes on a trial by trial basis.
Research on CDC originated with the work of Dörner (1975), who used control tasks to simulate real world decision making in complex domains (e.g., maintaining ecologies). This line of research is now referred to as complex problem solving (Buchner, 1995). Better known however is Broadbent’s early work on control tasks (Broadbent, 1977; Berry and Broadbent, 1984), which, like MCPL studies, demonstrated that procedural learning is the mechanism that supports control-based decision making. As with the WPT, much of the work that followed from Berry and Broadbent’s (1984) pivotal study has examined the type of knowledge acquired under procedural learning. Broadbent’s Exemplar theory proposes that while interacting with a CDC task, manipulations of specific inputs that lead to successful outcomes are stored as exemplars in a type of “look-up table.” Controlling a CDC task is then based on a process of matching environmental cues to similar stored exemplars, rather than through following the rules acquired in cue-abstraction. In support, some studies have shown that there is limited transfer of control performance to versions that differ from the initial training task, and that people lack insight into the knowledge gained during learning (Dienes and Fahey, 1995, 1998; Gonzales et al., 2003).
In contrast, studies that have encouraged hypothesis testing behavior – either through explicit instruction, or task manipulations such as presenting a task history of action-outcome associations during learning – have shown that rule learning can lead to successful control performance. Moreover, under these conditions cue-outcome knowledge is transferable beyond the trained task environment to other variants as well as other goal criteria, and people show accurate reportable knowledge of cue-outcome associations (Sanderson, 1989; Burns and Vollmeyer, 2002; Osman, 2008a,b,c). In particular, two recent studies (Osman, 2008a,b) examined if actively engaging with a CDC task during learning is necessary for accurate control. Berry (1991) claimed that successful control is dependent on procedural learning, which does not generate cue-outcome knowledge. By extension, learning purely through observation would prevent the uptake of decision-action-outcome associations, and reduce control performance. Osman (2008a,b) used a yoking design to compare the effects of learning through action vs. learning through observation (i.e., simply observing cue changes and tracking their effects on the outcomes). The findings challenged Berry’s original claims by demonstrating that learning through observation and learning through action generate equivalent declarative as well as procedural knowledge. Moreover, the findings demonstrated that rather than independent, accuracy of cue-outcome knowledge was positively associated with control performance. There is an emerging consensus from recent work with CDC tasks that people apply hypothesis testing strategies when planning actions which enables cue-abstraction (e.g., Sun et al., 2001; Burns and Vollmeyer, 2002; Osman, 2010a,b). Much like the MCPL studies, these finding suggest that learning to control outcomes involves a deliberate process of evaluating actions against expected outcomes. Though crucially in CDC tasks there is an additional step which involves selecting actions that are expected to reduce the discrepancy between an achieved and target outcome.
As discussed earlier, MCPL and CDC tasks share many common properties. In particular they are environments in which the decision maker is required to learn probabilistic relationships between cues and outcomes. Moreover, both predicting and controlling an outcome rely on inferring changes in outcome values from patterns of cue/input values. Besides the obvious difference that controlling an outcome involves direct manipulation of the inputs whereas predicting outcomes does not, the other key difference is the way in which the outcome is evaluated (Osman, 2010a). When controlling outcomes, the achieved outcome is evaluated with respect to the target goal. When predicting outcomes, the predicted outcome is evaluated with respect to the achieved outcome. While there are no direct comparisons of prediction- and control-based decision making in dynamic environments, Enkvist et al. (2006) compared the accuracy of cue-outcome knowledge of a group instructed to predict the outcome in a MCPL task with a group instructed to control the outcome to a specific criterion. They found that control-based decision making led to more accurate cue-outcome knowledge. However, this finding was reversed when binary rather than continuous cues were used. Also, as already mentioned, Berry (1991) and Osman (2008a,b,c) yoked active controllers with passive observers and compared both groups on their ability to control an outcome to criterion over successive trials. While Berry found an advantage for active controllers, Osman found no difference between passive and active learners. Osman noted that this divergence can be explained by a critical difference between the studies: in Osman’s study, all participants were encouraged to learn through hypothesis testing, while in Berry’s study participants were explicitly instructed not to engage in hypothesis testing.
We may conclude from these findings that, under certain conditions (i.e., in MCPL tasks when cue-outcome associations involve continuous variables, and in CDC tasks where instructions prevent hypothesis testing), cue-outcome knowledge is more accurate when learning is control-based as compared to prediction-based. However, this conclusion is only tentative, given that to date there have been no studies that compared both forms of learning within the same dynamic decision making task.
In the present study, we sought to induce prediction-based DDM by asking people to first learn to predict the effects of observed actions on the state of the environment. Later on, they were then asked to control the environment. We compared this condition to one in which people were instructed to achieve and maintain a specific target outcome from the outset. The present study used a yoking design such that Controllers and Predictors experienced exactly the same cue-outcome information. To our knowledge, this study is the first to allow such a direct comparison of prediction and control-based learning in a DDM environment. Based on reinforcement learning models, if accurate cue-outcome knowledge is dependent on the generation of prediction errors that are generated either through prediction or control, then performance at test should be equivalent regardless of training condition (Controllers, Predictors). If however, there are fundamental differences between prediction-based and control-based learning, then from previous results in the DDM and MCPL domain, we would expect that at Predictors should show an overall advantage in test of prediction, whereas Controllers should show an advantage on tests of control.
Experiment 1
In Experiment 1, we compared control performance between a group who learnt to control an outcome from the outset (Controllers) and a yoked group who first learnt to predict the outcome from the cue manipulations of those in the first group (Predictors). In addition, we manipulated the level of perturbation (i.e., noise) in the environment. A recent study (Osman and Speekenbrink, 2011) investigated DDM in tasks in which the stability of the environment was varied such that the autonomous changes to the outcome were relatively small (low noise) or large (high noise). The findings revealed that people were sensitive to the different rates at which the outcome fluctuated; accuracy of control performance suffered in high noise environments and more sub-optimal strategies were developed. By manipulating the level of noise in Experiment 1, we examined whether this effect on performance generalizes to prediction as well as control.
Methods
Participants
The 60 graduate and undergraduate students who took part in the study were recruited from the University College London subject pool and were paid £6 for their participation. The assignment of participants to the four conditions was semi-randomized. There were a total of four groups (Control High Noise, Control Low Noise, Prediction High Noise, Prediction Low Noise2), with 15 participants in each. Pairs of participants (controller and yoked predictor) were randomly allocated to one of the two noise conditions3.
Design and Materials
Experiment 1 included two between subject manipulations, namely learning mode (prediction-based vs. control-based) and stability (high noise vs. low noise). Control performance was measured in two control tests. The task environment consisted of three cues and one outcome. One of the cues increased and one of the cues decreased the outcome. The third cue had no effect on the outcome. More formally, the task environment can be described as in the following equation
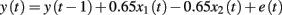
in which y(t) is the outcome on trial t, x1 is the positive cue, x2 is the negative cue, and e a random noise component, normally distributed with a zero mean and SD of 4 (Low Noise) or 16 (High Noise). The null cue x3 is not included in the equation as it had no effect on the outcome.
Procedure
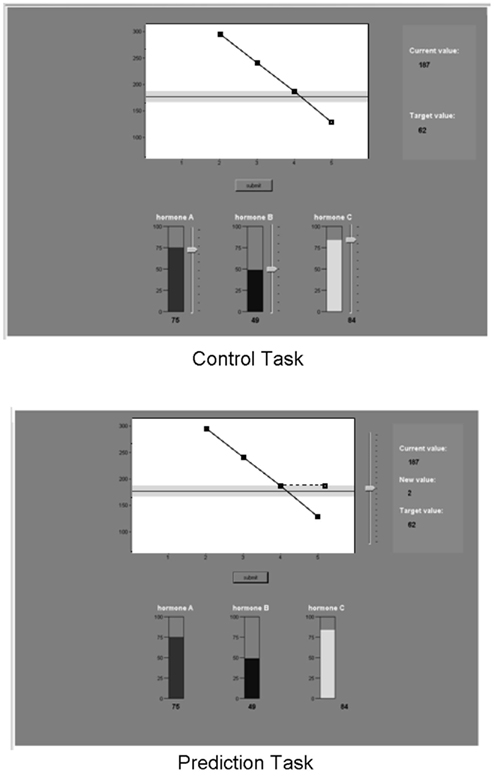
Controllers were informed that as part of a medical research team they would be conducting tests in which they could inject a patient with any combination of three hormones (labeled as hormones A, B, and C), with the aim of maintaining a specific safe level of neurotransmitter release. Predictors were assigned the same role, but were told that they would have to predict the level of neurotransmitter release by observing the level of hormones injected. Figure 1 presents a screen-shot of a learning trial as experienced by Predictors and Controllers in the experiment. The task was performed on a desktop computer, using custom software written in C# for the .NET framework. The task consisted of a total of 80 trials, divided into two phases. The learning phase involved 40 learning trials and the test phase included two tests of 20 trials each.
Learning phase
On each trial, Controllers adjusted a slider to decide how much of each hormone to release (a value between 0 and 100). After confirming their decision, the effect was revealed visually on the outcome graph. On the next trial, the input values were reset to 0, but the outcome value was retained from the previous trial. Predictors were shown the input values chosen on that trial by the Controller they were yoked to. They were asked to predict the resulting outcome value by moving a slider. Once they were satisfied with their prediction, the actual outcome value was revealed alongside their prediction. On a subsequent trial, the previously predicted outcome value was omitted from the outcome graph, but the history of the actual outcome values on the previous five trials remained.
Test phase
The test phase was identical for Controllers and Predictors. Control Test 1 involved the same task as performed by Controllers in the learning phase; this was the first opportunity for Predictors to control the environment. Control Test 2 involved a different desired outcome level in order to examine success in controlling the system to a different criterion4.
Scoring
Prediction performance was measured by a prediction error score Sp(t) calculated as the absolute difference between predicted and expected outcome values:
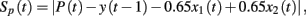
in which P(t) is a participant’s prediction on trial t. We chose to compare predictions to expected rather than actual outcomes as the latter are subject to random noise, resulting in a biased comparison between the High and Low Noise conditions.
Control performance was measured by a control error score Sc(t) calculated as the absolute difference between the expected and best possible outcome:
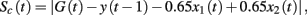
in which G(t) is the goal on trial t: either the target outcome if achievable on that trial, or the closest achievable outcome.
Results and Discussion
Learning phase: controllers
The learning phase was divided into four blocks of 10 trials each. For the following analyses, prediction and control error scores were averaged across each block for each participant; these are presented in Figure 2. A 4 × 2 ANOVA was conducted on the control scores, with Block (learning block 1, 2, 3, 4) as within-subject factor and Noise (high, low) as a between subject factor. As indicated in Figure 2, there was a main effect of Block, F(3,84) = 28.89, p < 0.001, partial η2 = 0.508. To explore the possibility that accuracy of control-based decisions improved over blocks of trials, t-tests revealed that error scores were lower in Blocks 2, 3, and 4 as compare to Block 1 (t = 3.72, p = 0.036, t = 3.76, p = 0.013, t = 3.04, p = 0.013), no other differences reached significance. A main effect of Noise, F(1,28) = 9.48, p = 0.004, partial η2 = 0.253, suggests that control performance was poorer in the High compared to the Low Noise condition. Figure 2 also suggests more pronounced learning in the Low Noise compared to the High Noise condition, which was supported by a significant Noise × Block interaction, F(3,84) = 3.93, p = 0.011, partial η2 = 0.123.
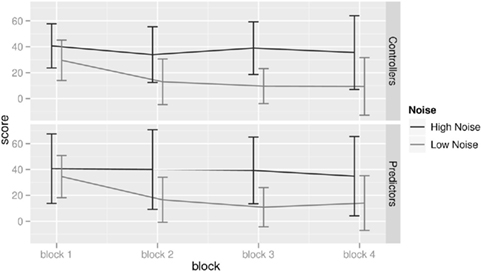
Figure 2. Error scores (± SE) in the learning phase of Experiment 1. For Controllers, these are control error scores, and for Predictors, these are predictive error scores.
Learning phase: predictors
A similar ANOVA on the prediction error scores showed a main effect of Noise, F(1,28) = 6.72, p = 0.015, partial η2 = 0.193, confirming that Predictors in the Low Noise condition outperformed those in the High Noise condition. The main effect of Block, F(3,84) = 2.95, p = 0.037, partial η2 = 0.095. To examine if differences in performance across-blocks reflected learning, t-test comparisons were conducted, and revealed that prediction error scores were lower in Blocks 2, 3, and 4 as compare to Block 1 (t = 2.02, p = 0.036, t = 2.63, p = 0.013, t = 2.63, p = 0.013), no other differences reached significance. To summarize, both Predictors and Controllers showed clear evidence of learning, and performance in both groups was negatively affected by increasing the level of noise in the system.
Test phase
The test phase provided the opportunity to compare the four conditions on an equivalent measure of performance. Each test was divided into two blocks of 10 trials each. The following analyses are based on participants’ average control error scores in each block and test, as presented in Figure 3. Control error scores were first analyzed with a 2 × 2 × 2 × 2 ANOVA with Test (Control Test 1, 2) and Block (block 1, 2) as within-subject factors, and Learning Mode (prediction, control), and Noise (high, low) as between subject factors. The main effect of Test, F(1,56) = 14.94, p < 0.001, partial η2 = 0.211, suggests a general practice effect: even though it included an unfamiliar goal, participants performed better in Control Test 2 than in Control Test 1. There were also practice effects within tests, as shown by a main effect of Block, F(1,56) = 56.99, p < 0.001, partial η2 = 0.504. A significant Test × Learning Mode interaction, F(1,56) = 6.00, p < 0.017, partial η2 = 0.097, indicates that Predictors improved their performance more over tests than Controllers. Controllers performed better than Predictors in Control Test 1, t(58) = 2.11, p = 0.038, but there was no difference in Control Test 2, t(58) = 0.68, p = 0.51. In addition, there was a significant Block × Task × Learning Mode interaction, F(1,56) = 6.38, p = 0.014, partial η2 = 0.102. Follow-up t-tests indicated that Controllers outperformed Predictors only in the first block of Control Test 1, t(58) = 3.14, p < 0.003; there was no significant difference elsewhere (all p’s > 0.29).
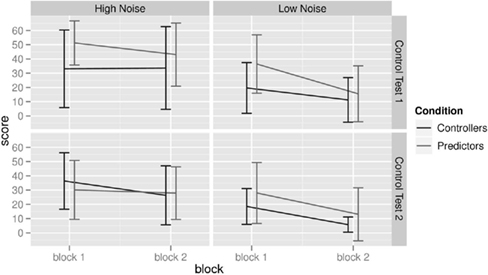
Figure 3. Control error scores (± SE) of predictors and controllers in the test phase of Experiment 1.
There were two significant effects involving noise. Overall, participants in the low noise conditions outperformed those in the high noise conditions, F(1,56) = 14.52, p < 0.001, partial η2 = 0.206. In addition, a Block × Noise interaction, F(1,56) = 13.31, p < 0.001, partial η2 = 0.192, indicates that this difference was particularly strong in the second block. To explore the difference between Controllers and Predictors in the first block of Control Test 1 in more detail, we compared Controllers’ and Predictors’ performance when they were first exposed to the control task. That is, we compared Controllers’ performance in the first block of the learning phase with Predictors’ performance in the first block of Control Test 1. The aim of this across-blocks comparison was to assess the benefit for prediction training prior to encountering the control task. The analysis revealed no significant difference, F(1,28) = 0.44, p = 0.51, partial η2 = 0.016, suggesting that Predictors did not benefit from their four blocks of prediction learning. In contrast, the same analysis comparing Controllers performance in the first block of learning with their performance in the first block of Control Test 1, F(1,28) = 17.38, p = 0.0002, partial η2 = 0.375, suggested that their prior experience was beneficial.
The results from this first experiment can be summarized as follows: given that the accuracy of controlling an environment is dependent to a greater extent on the way the outcome fluctuates (either in a less noisy or more noisy manner) rather than the mode of learning of the environment (either predicting or controlling the outcome), the results are broadly consistent with the view that control and prediction involve similar processes. Moreover, the evidence suggests that Osman and Speekenbrink’s (2011) findings generalize to prediction as well as control. In addition, Predictors required a short period of familiarization with controlling the system in the first 10 trials of Control Test 1, but after that were able to control the environment as well as the Controllers who had been doing so from the outset. However, in this initial first block of testing, Predictors’ performance was no different to Controllers’ performance in the first block of learning, suggesting that prediction-based learning about cue-outcome relations, regardless of environmental stability, was not directly transferable to control. This raises the question whether control-based learning generates flexible cue-outcome knowledge that would facilitate performance on tests of prediction.
Experiment 2
Experiment 1 indicated a small and transient difference in performance between Controllers and Predictors. In Experiment 2 we sought to further examine this by replicating our findings and also examining whether control-based learning generates flexible knowledge which can be used to predict as well as control the outcome.
Method
Participants
The 30 graduate and undergraduate students that took part were recruited from Queen Mary College and were paid £6 for their participation. The assignment of participants to the conditions followed the same yoking design as Experiment 1. There were two conditions (Controllers, Predictors), each with 15 participants.
Design and Procedure
Experiment 2 was identical to Experiment 1 with two exceptions. First, the SD of the noise was kept at a single intermediate value of 8 (between the High and Low conditions of Experiment 1). Second, tests of cue-outcome associations (Insight Tests) were presented directly after Control Test 1 and again after Control Test 2. In the Insight Tests participants were asked to predict the value of the outcome or one of the cues, given the values of the other variables. No feedback was presented in either Insight Test. Each test included 16 trials which were divided into 8 old and 8 new trials, each set containing 2 trials to predict each target (the outcome, positive, negative, and null cue). Old trials were randomly selected from the learning phase (for Controllers these were trials that they had generated themselves, for Predictors these were the same yoked learning trials). The eight new trials were designed prior to the experiment, so neither group had prior experience of them. The presentation of the 16 trials in each Insight Test was randomized for each participant. Performance on the insight tests was measured similarly to the prediction error scores in Experiment 1 as the absolute difference between predicted and expected value.
Results and Discussion
Learning phase
The average control and prediction error scores by block (4 blocks of 10 trials each) in the learning phase are presented in Figure 4. For the Controllers, a one-way ANOVA on control scores showed a significant effect of Block, F(3,42) = 21.93, p < 0.001, partial η2 = 0.610. Further t-test comparisons were conducted and revealed that control error scores were lower in Blocks 2, 3, and 4 as compare to Block 1 (t = 6.67, p < 0.005, t = 5.90, p < 0.005, t = 11.76, p < 0.005). A similar analysis on the prediction scores for Predictors showed no effect of Block, F(3,42) = 0.36, p = 0.78, partial η2 = 0.025. Again, t-tests were conducted to examine if performance improved across-block. Analyses revealed that compared with Block 1, prediction error scores were lower in Block 2, 3, and 4 (t = 2.95, p = 0.011, t = 3.88, p = 0.002, t = 4.18, p = 0.001), no other comparisons were significant.
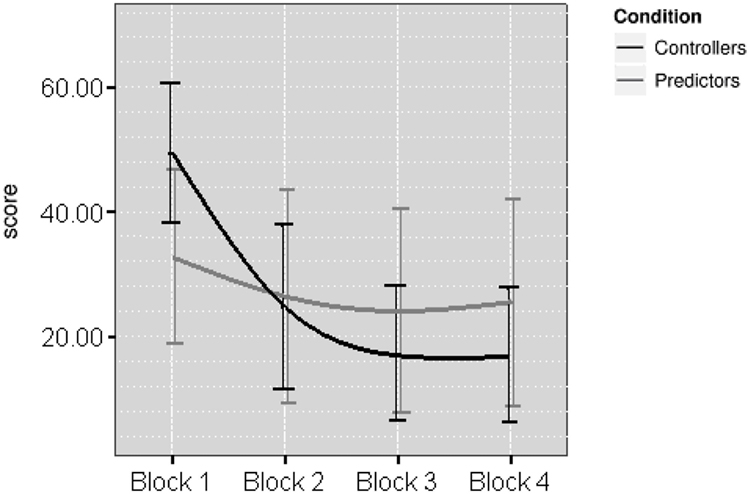
Figure 4. Error scores (± SE) in the learning phase of Experiment 2. For Controllers, these are control error scores, and for Predictors, these are predictive error scores.
Test phase
The following analyses were based on the mean control scores by Block (block, 1, 2) and Test (Control Test 1 and 2) as presented in Figure 5. A 2 × 2 × 2 ANOVA was conducted with Test and Block as within-subject factors, and Learning Mode (prediction, control) as between subject factor. As in Experiment 1, there was a main effect of Block, F(1,28) = 26.01, p < 0.001, partial η2 = 0.482. There was a trend toward an effect of Test, F(1,28) = 3.66, p = 0.066, partial η2 = 0.115; while failing to reach significance, this effect is consistent with Experiment 1. No other main effects were significant. As with Experiment 1, we used an across-blocks comparison to assess the benefit for prediction training prior to encountering the control task. As in Experiment 1, Predictors did not show an advantage when they first came to control the outcome compared to Controllers, F(1,28) = 1.57, p = 0.221, partial η2 = 0.057. However, when comparing Controllers’ performance between block 1 of the learning phase and block 1 of Control Test 1, their prior experience did facilitate control accuracy at test, F(1,28) = 3.73, p = 0.064, partial η2 = 0.152.
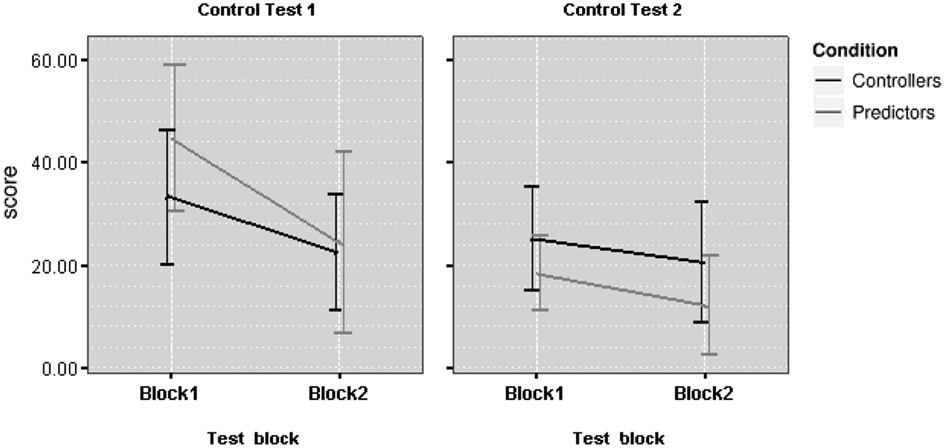
Figure 5. Control error scores (± SE) of predictors and controllers in the test phase of Experiment 2.
Insights tests
Experiment 2 also included tests that enabled comparisons of groups on their ability to accurately predict the states of the system. In all analyses reported below, predictions for the null cue were not taken into account; as this cue had no effect on the outcome, its value was effectively unpredictable (it was only included in the set of questions not to alert participants to this fact). We computed error scores as the absolute difference between participants’ predictions and optimal predictions; these are presented in Figure 6. A 2 × 2 × 3 × 2 ANOVA was conducted with Insight Test (first, second), Trial Type (old, new) and Target (positive cue, negative cue, outcome) as within-subject factors, and Learning Mode (prediction, control) as a between subject factor. This analysis showed only a significant effect of Trial Type, F(1,28) = 14.51, p < 0.001, partial η2 = 0.341, indicating better performance for old than for new items. Other effects were not significant. In particular, there were no effects involving condition (all p’s > 0.10). Comparing the error scores for predictions of the outcome to the prediction error scores of Predictors in the learning phase showed no difference for either Predictors, t(14) = 1.06, p = 0.31 (dependent samples), or Controllers, t(28) = 0.17, p = 0.87 (independent samples). Thus, Controllers were able to predict the outcome with a similar accuracy as Predictors who had learned to do so from the outset.
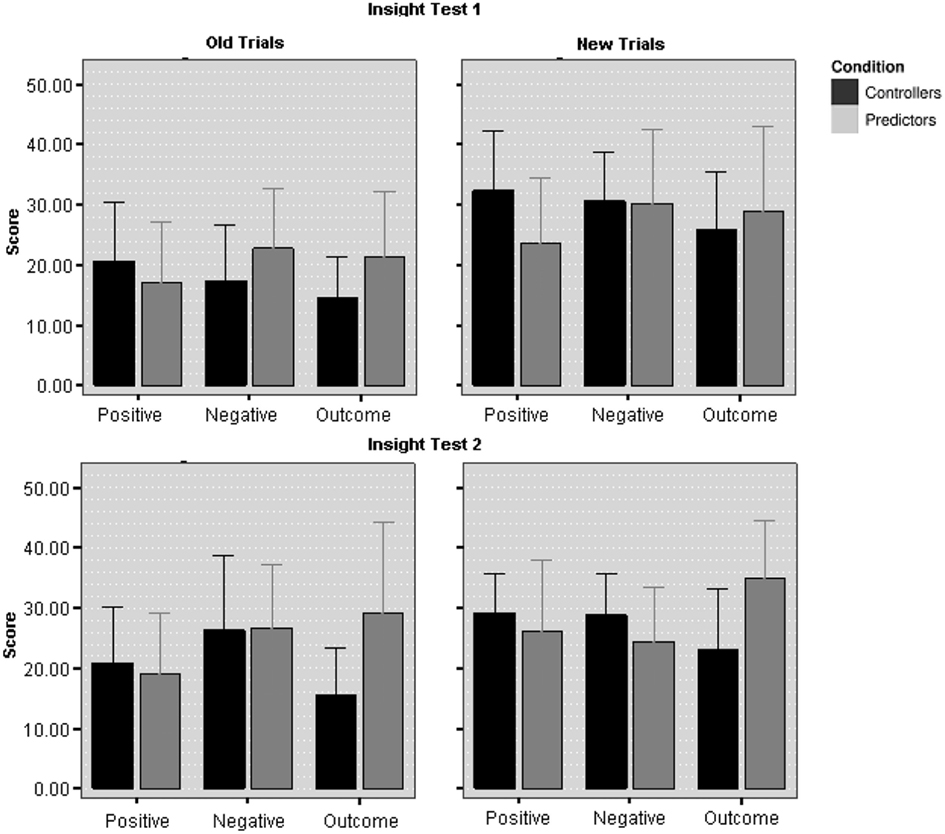
Figure 6. Insight scores (± SE) for predictors and controllers for the insight tests of Experiment 2.
In sum, the findings from Experiment 2 suggest that control-based learning generates cue-outcome knowledge that is sufficiently flexible to enable transfer from control tasks to tests of cue-outcome knowledge. Moreover, the findings indicate that regardless of mode of learning, cue-outcome knowledge is accessible, to the extent that it can be reported in measures of task insight.
General Discussion
Many accounts of DDM have referred to the importance of prediction in processes designed to control outcomes in a dynamic environment (Gibson et al., 1997; Osman, 2010a). In fact cognitive architectures such as ACT-R have been developed to model dynamic decision making, and variants of the framework also include components that assume a prediction-based process (Gonzales et al., 2003). In addition, general models of learning (reinforcement learning models/reward-based learning) claim that prediction-based and control-based decisions generate equivalent knowledge in dynamic learning environment (Schultz et al., 1997; Schultz, 2006). However, to date, there has been little empirical support for this claim in DDM research.
The aim of this investigation was to examine the accuracy of cue-outcome knowledge when applied to tests of control and prediction, by comparing prediction-based learning and control-based learning in the same dynamic environment. We developed a task in which Controllers and Predictors experienced identical cue-outcome information in a dynamic environment. Both Predictors and Controllers were sensitive to the stability of the DDM environment, suggesting that there is greater accuracy in controlling and predicting outcomes in stable than in unstable environments. In both experiments we showed that predictive learning is sufficient to enable accurate control of an outcome in dynamic environments that varied according to stability. After an initial period of familiarization (approximately 10 trials) with the control test, Predictors’ control accuracy was equivalent to that of Controllers. However, in both experiments Predictors’ experience during learning did not generate cue-outcome knowledge that initially facilitated control performance. In contrast, we found that control-based experience during learning enabled successful transfer to predictive tests of cue-outcome associations as well as to tests of control. The discussion focuses on two questions: Did Predictors and Controllers learn in the same way? and How do prediction and control in the present study relate to conceptualizations of prediction and control in other decision making and learning domains?
Did Predictors and Controllers Learn in the Same Way?
We propose that fundamentally prediction and control share basic properties when it comes to evaluating the outcome. In line with Gibson et al.’s (1997) action model, control-based learning involves an online comparison between the expected outcome and achieved outcome, as well as an online comparison between the achieved outcome and the target outcome. Both comparisons are used to form a judgment as to which action to take in order to reach and maintain the target outcome in dynamic tasks with a non-independent trial structure (Gibson et al., 1997; Gibson, 2007). We also propose that, in line with Gibson’s action model, prediction-based learning involves an online comparison between an expected outcome and an achieved outcome, whereas control-based decisions are based on a comparison between the achieved and target outcome. Thus, prediction-based and control-based DDM are similar because both evaluate the achieved outcome according to their expected outcome. Given that in general predictive accuracy was equivalent for Predictors and Controllers, the comparison between actual outcome and expected outcome appears to be sufficient to enable the acquisition of accurate cue-outcome knowledge. However, in both experiments the findings suggest that this comparison is not sufficient to facilitate initial transfer to tests of control, instead training that involves decisions based on comparisons between expected outcome and target outcome is needed. These comparisons are required for planning and our results suggest that such comparisons may need some time to develop, even when cue-outcome knowledge itself is already accurate. Learning cue-outcome relations involves updating expected outcomes in light of achieved outcomes. Learning to control involves updating the expected distance from the goal to the actually achieved distance from the goal.
We have suggested that the critical factor differentiating Predictors from Controllers is related to the type of comparison made (comparing expected to achieved outcomes, and comparing achieved outcomes to the goal outcome). However, there were other factors that may have contributed to the difference between Predictors and Controllers in initial tests of control. In the present study both types of learners could be differentiated in the following three ways. For instance, Controllers intervened on the cues directly, while Predictors could not. Some in the CDC research domain treat this as an important difference given that CDC tasks lend themselves to procedural rather than declarative forms of learning (Berry, 1991; Lee, 1995). In addition, Controllers received different feedback to Predictors. Controllers received feedback with respect to the deviation of their achieved outcome from the target outcome on a trial by trial basis. While this information was also presented to Predictors during learning, it was not directly relevant for their decisions. Only Predictors received direct feedback about the difference between their predicted (expected) outcome and the outcome actually achieved. However, we would argue that Controllers also formed expectations of the outcome value based on their cue-interventions and re-evaluated these predictions in light of to the actual achieved outcome. Finally, Controllers’ actions had direct effects on the outcome in the actual DDM environment, whereas for Predictors an action (prediction) had no consequence on the outcome in the DDM environment. It may be the case that the advantage for Controllers stems from a more thorough evaluation of their decisions because errors not only affect the current outcome, but also future actions and outcomes. For instance, by making a poor cue-intervention which increases the deviation between achieved outcome and target outcome, future actions will have to compensate, and several more actions may be needed to reach the goal. Although Predictors may feel intrinsically motivated to make accurate predictions, and so an error would generate some personal dissonance, predictions do not require the type of planning behaviors needed in control. Further investigation is needed to examine these potential factors, for instance by varying feedback (e.g., positive, negative feedback) and reward (e.g., incentivizing accurate decisions).
How does Prediction and Control in the Present Study Relate to Conceptualizations of Prediction and Control in Other Decision Making and Learning Domains?
MCPL vs. CDC tasks
With respect to the CDC research community the paradigm we used to examine prediction and control relates directly to other dynamic decision making tasks (Berry and Broadbent, 1987; Burns and Vollmeyer, 2002; Gonzales et al., 2003; Osman, 2008a). Crucially, the findings are consistent with the claim that Controllers base their decisions on predictions (Burns and Vollmeyer, 2002; Gibson et al., 1997; Goode and Beckmann, 2010; Osman, 2010a,b; Sun et al., 2001). In the present study the task environment in which prediction was examined involved cumulative changes across trials, whereas in typical MCPL tasks there is no dependency between trials. If prediction and control are determined by the type of environment in which they are tested, it may be that this qualitative difference between MCPL and CDC tasks does not allow one to draw strong conclusions about the similarities between prediction and control, or to generalize our findings to MCPL research. However, if MCPL tasks were designed with a dependent trial structure then our findings suggest that in stable and unstable dynamic environments, cue-outcome knowledge via prediction does not prevent accurate control-based decisions, although it does not facilitate initial transfer of knowledge to control tasks. Further research is required to examine the extent to which these findings generalize to task environments that are traditionally studied in MCPL tasks. If the trial structure makes little difference, then based on the findings from this experiment, we would still predict that overall cue-outcome knowledge for Controllers over Predictors should be equivalent.
Observation vs. intervention
Prediction- and control-based learning can also be viewed within the context of causal reasoning research which contrasts learning via intervention and observation (Meder et al., 2008; Hagmayer et al., 2010). Prediction and observation are both indirect ways of learning about an environment, whereas control and intervention involve direct interaction with the environment while learning (Lagnado and Sloman, 2004; Osman, 2010b). The distinction between these forms of interaction with the environment has been made using formal models (Spirtes et al., 1993; Pearl, 2000) which capture probabilistic dependencies in a given set of data as well as their relationship to the causal structures that could have generated the data. These models provide a strong theoretical basis for arguing that intervention is a crucial component in the acquisition of causal structures.
Studies that examine causal structure learning often require participants to either infer the causal structure from observing causes and effects, or from active learning by manipulating a candidate cause and observing the effects that follow. The evidence suggests that causal knowledge is more accurate when making interventions on causes than when observing causes and their effects (Steyvers et al., 2003; Lagnado and Sloman, 2004). Comparisons between observation and intervention have typically been conducted in static environments (for an exception see Hagmayer et al., 2010), and observation-based learning involves tracking causes and their effects as well as predicting changes in effects given specific causes. Though not commonly referred to, there is a close association between causal reasoning and DDM according to the ways in which prediction (observation) and control (intervention) generate cue-outcome knowledge. Funke and Müller (1988) found that while control performance was marginally impaired when learning was observation-based, causal knowledge of the environment was generally not influenced by mode of learning, and accuracy of casual knowledge predicted control performance. Moreover, recent work that has explored different types of intervention suggests that it is not always the case that intervention is superior to observation. There is converging evidence that atomic interventions (i.e., ones in which acting on the environment will clearly reveal some aspect of the causal structure) lead to superior casual knowledge as compared with uncertain interventions (i.e., ones in which actions may not fix the state of a variable quite so clearly; e.g., Hagmayer et al., 2010; Meder et al., 2008). While interventions are generally helpful in uncovering casual structures, there is evidence to suggest that observation-based learning can generate more accurate causal knowledge than uncertain interventions for particular environments (e.g., Meder et al., 2008). Viewed from this perspective, the findings from the present study suggest that the accuracy of casual knowledge is not impaired when learning is observation-based rather than intervention-based, assuming that parallels can be drawn between observation and prediction. However, again, to forge links between CDC research and causal learning, research is needed to explore the extent to which the types of interventions involved in controlling a dynamic environment are similar to the kinds of interventions used to uncover causal structures, where the latter are typically studied in static environments.
Model-free vs. model-based learning
It is worth examining the possible relationship between prediction and control in the present study with a distinction made in machine learning concerning model-free and model-based reinforcement learning systems (e.g., Sutton and Barto, 1998; Dayan and Daw, 2008; Gläscher et al., 2010). Both model-free and model-based learning involve predictions about the expected reward from future actions, but the mechanism by which this is acquired is different. Model-based learning involves constructing a model of the task environment, which informs the agent about the expected consequences of actions taken in particular situations. Actions can move the environment from one state to another and the agent’s aim is to move the environment to the state with the highest reward. Thus, the agent’s learning involves the full sequence from action to state to reward whereas in model-free learning the agent learns action-reward pairings directly. Model-based methods are more flexible and can more easily accommodate changes in the state-reward pairings. Adaptation to changes in the reward structure is much slower with model-free methods. In our study Predictors were encouraged to learn the cue-outcome associations before being tested on their ability to decide upon actions to move the system to a desired state. In this way, Predictors could be described as model-based learners. The Controllers on the other hand were not explicitly encouraged (though not discouraged) to learn about the structure of the system. But given their performance in tests of prediction, we would speculate that their learning was also model-based. While the initial differences in control performance imply that Predictors and Controllers may have been using different strategies, further research is needed to explore the association between learning strategies (model-free vs. model-based) and modes of learning (prediction vs. control).
Conclusion
While prediction is crucial to control, and both tend to be described as complementary processes, in this article we considered the question whether learning to control a dynamic environment involves decisions based on prediction, and whether learning via prediction is sufficient to enable accurate control. The evidence from two experiments suggests that accurate cue-outcome knowledge is gained via prediction and control, and in general both forms of learning enable transfer to tests of prediction and control. However, Predictors required some familiarization with control whereas Controllers were able to transfer their knowledge to tests of prediction without familiarization to the tests. We propose that Predictors and Controllers evaluated the outcome according to the discrepancy between expected and actual outcomes, whereas Controllers also evaluate the outcome with respect to an intended goal. While there are processes shared by prediction and control, the critical difference between them appears enough to generate more flexible cue-outcome knowledge for Controllers than Predictors.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The support of the ESRC Research Centre for Economic Learning and Human Evolution is gratefully acknowledged. Preparation for this research project was supported by the Economic and Social Research Council, ESRC grant RES-062-23-1511 (Maarten Speekenbrink), and the Engineering and Physical Sciences Research Council, EPSRC grant – EP/F069421/1 (Magda Osman).
Footnotes
- ^“An endogenous variable [that] at time t has an effect of its own state at time t + 1 independent of exogenous influences that might add to the effect” (Funke, 1993, p. 322).
- ^The assignment of noise to the system was first piloted in order to generate High variance (16 SD) and low variance (4 SD).
- ^In order to implement the yoking design in which a participant from each Prediction condition was yoked to a participant from the corresponding control condition, a control participant performed the experiment first in order to generate the learning trials presented to the yoked predictor.
- ^In the learning phase and in Control Test 1, the starting value was 178 and the target value throughout was 62. Participants were instructed to maintain the outcome within a safe range (±10) of the target value. In Control Test 2, the starting value was 156, the target value was 74, and the safe range ±5 from the target value.
References
Bandura, A., and Locke, E. A. (2003). Negative self-efficacy and goal effects revisited. J. Appl. Psychol. 88, 87–99.
Berry, D., and Broadbent, D. E. (1984). On the relationship between task performance and associated verbalizable knowledge. Q. J. Exp. Psychol. 36, 209–231.
Berry, D., and Broadbent, D. E. (1987). The combination of implicit and explicit knowledge in task control. Psychol. Res. 49, 7–15.
Berry, D. C., and Broadbent, D. E. (1988). Interactive tasks and the implicit-explicit distinction. Br. J. Psychol. 79, 251–272.
Björkman, M. (1971). Policy formation as a function of feedback in a non-metric CPL-task. Umeå Psychol. Reports, 49.
Brehmer, B. (1992). Dynamic decision making: human control of complex systems. Acta Psychol. (Amst.) 81, 211–241.
Broadbent, D. E. (1977). Levels, hierarchies and the locus of control. Q. J. Exp. Psychol. 32, 109–118.
Brown, S., and Steyvers, M. (2005). The dynamics of experimentally induced criterion shifts. J. Exp. Psychol. Learn. Mem. Cogn. 31, 587–599.
Buchner, A. (1995). “Basic topics and approaches to the study of complex problem solving,” in Complex Problem Solving: The European Perspective, eds P. A. Frensch and J. Funke (Hillsdale: Lawrence Erlbaum), 27–63.
Burns, B. D., and Vollmeyer, R. (2002). Goal specificity effects on hypothesis testing in problem solving. Q. J. Exp. Psychol. 55, 241–261.
Castellan, N. J. Jr. (1973). Multiple-cue probability learning with irrelevant cues. Organ. Behav. Hum. Perform. 9, 16–29.
Castellan, N. J. Jr., and Edgell, S. E. (1973). An hypothesis generation model for judgment in non-metric multiple-cue probability learning. J. Math. Psychol. 10, 204–222.
Cohen, M. S., Freeman, J. T., and Wolf, S. (1996). Meta-cognition in time stressed decision making: recognizing, critiquing and correcting. Hum. Factors 38, 206–219.
Dayan, P., and Daw, N. (2008). Connections between computational and neurobiological perspectives on decision making. Cogn. Affect. Behav. Neurosci. 4, 429–453.
Dienes, Z., and Fahey, R. (1995). Role of specific instances in controlling a dynamic system. J. Exp. Psychol. Learn. Mem. Cogn. 21, 848–862.
Dienes, Z., and Fahey, R. (1998). The role of implicit memory in controlling a dynamic system. Q. J. Exp. Psychol. 51, 593–614.
Dörner, D. (1975). Wie menschen eine welt verbessern wollten und sie dabei zerstörten [How people wanted to improve the world]. Bild Wiss. 12, 48–53.
Edgell, S. E. (1974). Configural Information Processing in Decision Making. Indiana Mathematical Psychology Program, Report No. 74–4.
Enkvist, T., Newell, B., Juslin, P., and Olsson, H. (2006). On the role of causal intervention in multiple-cue judgment: positive and negative effects on learning. J. Exp. Psychol. Learn. Mem. Cogn. 32, 163–179.
Funke, J. (1992). Dealing with dynamic systems: research strategy, diagnostic approach and experimental results. German J. Psychol. 16, 24–43.
Funke, J. (1993). “Microworlds based on linear equation systems: a new approach to complex problem solving and experimental results,” in The Cognitive Psychology of Knowledge, eds G. Strube and K.-F. Wender (Amsterdam: Elsevier), 313–330.
Funke, J., and Müller, H. (1988). Eingreifen und prognostizieren als determinanten von systemidentifikation und systemsteuerung [Intervention and prediction as determinants of system identfication and system control]. Sprache Kogn. 7, 176–186.
Gibson, F., Fichman, M., and Plaut, D. C. (1997). Learning in dynamic decision tasks: computational model and empirical evidence. Organ. Behav. Hum. Perform. 71, 1–35.
Gibson, F. P. (2007). Learning and transfer in dynamic decision environments. Comput. Math. Organ. Theory 13, 39–61.
Gläscher, J., Daw, N., Dayan, P., and O’Doherty, J. P. (2010). States versus rewards: dissociable neural prediction error signals underlying model-based and model-free reinforcement learning. Neuron 66, 585–595.
Gonzales, C., Lerch, J. F., and Lebiere, C. (2003). Instance-based learning in dynamic decision making. Cogn. Sci. 27, 591–635.
Goode, N., and Beckmann, J. (2010). You need to know: there is a causal relationship between structural knowledge and control performance in complex problem solving tasks. Intelligence 38, 345–352.
Hagmayer, Y., Meder, B., Osman, M., Mangold, S., and Lagnado, D. (2010). Spontaneous causal learning while controlling a dynamic system. Open Psychol. J. 3, 145–162.
Hammond, K. R., Summers, D. A., and Deane, D. H. (1973). Negative effects of outcome feedback in multiple-cue probability learning. Organ. Behav. Hum. Perform. 9, 30–34.
Holzworth, R. J., and Doherty, M. E. (1976). Feedback effects in a metric multiple-cue probability learning task. Bull. Psychon. Soc. 8, 1–3.
Knowlton, B. J., Mangels, J. A., and Squire, L. R. (1996). A neostriatal habit learning system in humans. Science 273, 1399–1402.
Knowlton, B. J., Squires, L. R., and Gluck, M. A. (1994). Probabilistic category learning in amnesia. Learn. Mem. 1, 106–120.
Körding, K., and Wolpert, D. (2006). Bayesian decision theory in sensorimotor control. Trends Cogn. Sci. 7, 319–326.
Lagnado, D., and Sloman, S. A. (2004). The advantage of timely intervention. J. Exp. Psychol. Learn. Mem. Cogn. 30, 856–876.
Lee, Y. (1995). Effects of learning contexts on implicit and explicit learning. Mem. Cogn. 23, 723–734.
Lipshitz, R., Klein, G., Orasanu, J., and Salas, E. (2001). Taking stock of naturalistic decision making. J. Behav. Decis. Mak. 14, 332–351.
Lurie, N. H., and Swaminathan, J. M. (2009). Is timely information always better? The effect of feedback frequency on decision making. Organ. Behav. Hum. Decis. Process 108, 315–329.
Meder, B., Hagmayer, Y., and Waldmann, M. R. (2008). Inferring interventional predictions from observational learning data. Psychon. Bull. Rev. 15, 75–80.
Muchinsky, P. M., and Dudycha, A. L. (1975). Human inference behavior in abstract and meaningful environments. Organ. Behav. Hum. Perform. 13, 377–391.
Osman, M. (2008a). Evidence for positive transfer and negative transfer/anti-learning of problem solving skills. J. Exp. Psychol. Gen. 137, 97–115.
Osman, M. (2008b). Observation can be as effective as action in problem solving. Cogn. Sci. 32, 162–183.
Osman, M. (2010a). Controlling uncertainty: a review of human behavior in complex dynamic environments. Psychol. Bull. 136, 65–86.
Osman, M. (2010b). Controlling Uncertainty: Decision Making and Learning in Complex Worlds. Oxford: Wiley-Blackwell.
Osman, M. (2011). “Monitoring, control and the illusion of control,” in Self Regulation, eds M. Fitzgerald, and T. Jane, Nova Publishers.
Osman, M., and Speekenbrink, M. (2011). Information sampling and strategy development in complex dynamic control environments. Cogn. Syst. Res. 355–364.
Osman, M., Wilkinson, L., Beigi, M., Parvez, C., and Jahanshahi, M. (2008). The striatum and learning to control a complex system? Neuropsychologia 46, 2355–2363.
Pearl, J. (2000). Causality: Models, Reasoning, and Inference. New York: Cambridge University Press.
Poldrack, R., Clark, J., Paré-Blagoev, E. J., Shahomy, D., Creso Moyano, J., Myers, C., and Gluck, M. (2001). Interactive memory systems in the human memory. Nature 414, 546–550.
Price, A. (2009). Distinguishing the contributions of implicit and explicit processes to performance on the weather prediction task. Mem. Cogn. 37, 210–222.
Rothstein, H. G. (1986). The effects of time pressure on judgment in multiple cue probability learning. Organ. Behav. Hum. Decis. Process 37, 83–92.
Sanderson, P. M. (1989). Verbalizable knowledge and skilled task performance: association, dissociation, and mental models. J. Exp. Psychol. Learn. Mem. Cogn. 15, 729–747.
Schultz, W. (2006). Behavioral theories and the neurophysiology of reward. Annu. Rev. Psychol. 57, 87–115.
Schultz, W., Dayan, P., and Montague, R. (1997). A neural substrate of prediction and reward. Science 275, 1593–1599.
Slovic, P., Rorer, L. G., and Hoffman, P. J. (1971). Analyzing use of diagnostic signs. Invest. Radiol. 6, 18–26.
Speekenbrink, M., Channon, S., and Shanks, D. R. (2008). Learning strategies in amnesia. Neurosci. Biobehav. Rev. 32, 292–310.
Speekenbrink, M., and Shanks, D. R. (2010). Learning in a changing environment. J. Exp. Psychol. Gen. 139, 266–298.
Spirtes, P., Glymour, C., and Scheines, P. (1993). Causation, Prediction, and Search. New York: Springer Verlag.
Steyvers, M., Tenenbaum, J. B., Wagenmakers, E. J., and Blum, B. (2003). Inferring causal networks from observations and interventions. Cogn. Sci. 27, 453–489.
Sun, R., Merrill, E., and Peterson, T. (2001). From implicit skills to explicit knowledge: a bottom-up model of skill learning. Cogn. Sci. 25, 203–244.
Vancouver, J. B., and Putka, D. J. (2000). Analyzing goal-striving processes and a test of the generalizability of perceptual control theory. Organ. Behav. Hum. Decis. Process 82, 334–362.
Vlek, C. A. J., and van der Heijden, L. H. C. (1970). Aspects of suboptimality in a mutidimensional probabilistic information processing task. Acta Psychol. 34, 300–310.
Keywords: dynamic, decision making, learning, prediction, control
Citation: Osman M and Speekenbrink M (2012) Prediction and control in a dynamic environment. Front. Psychology 3:68. doi: 10.3389/fpsyg.2012.00068
Received: 06 November 2011; Paper pending published: 22 December 2011;
Accepted: 21 February 2012; Published online: 13 March 2012.
Edited by:
Erica Yu, University of Maryland, USAReviewed by:
Zheng Wang, Ohio State University, USAJoachim Funke, Ruprecht-Karls-Universität Heidelberg, Germany
Copyright: © 2012 Osman and Speekenbrink. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Magda Osman, Biological and Experimental Psychology Centre, School of Biological and Chemical Sciences, Queen Mary College, University of London, Mile End, London E1 4NS, UK. e-mail:bS5vc21hbkBxbXVsLmFjLnVr