- Department of Psychology, Universiteit van Amsterdam, Amsterdam, Netherlands
Classification based on multiple dimensions of stimuli is usually associated with similarity-based representations, whereas uni-dimensional classifications are associated with rule-based representations. This paper studies classification of stimuli and category representations in school-aged children and adults when learning to categorize compound, multi-dimensional stimuli. Stimuli were such that both similarity-based and rule-based representations would lead to correct classification. This allows testing whether children have a bias for formation of similarity-based representations. The results are at odds with this expectation. Children use both uni-dimensional and multi-dimensional classification, and the use of both strategies increases with age. Multi-dimensional classification is best characterized as resulting from an analytic strategy rather than from procedural processing of overall-similarity. The conclusion is that children are capable of using complex rule-based categorization strategies that involve the use of multiple features of the stimuli. The main developmental change concerns the efficiency and consistency of the explicit learning system.
Introduction
The ability to categorize stimuli is central to human cognitive functioning. It is involved in essential processes such as diagnosing diseases, distinguishing cats from lions, and telling the difference between verbs and nouns. As such, categorization has been studied in infants (Mareschal and Quinn, 2001), children (Namy and Gentner, 2002; Sloutsky and Fisher, 2004; Kloos and Sloutsky, 2008; Minda et al., 2008), and adults (for an overview, see Ashby and Maddox, 2005). Understanding the nature of category representations and the learning processes leading to those representations are the core aspects of categorization research. A crucial question in development is whether the dominant form of category representations changes during development (e.g., Sloutsky, 2010), or whether the main developmental change concerns the efficiency of learning category representations.
Category Learning and Representations
In adults, the nature of the category structure determines to a large extent which kind of representation is formed (Ashby and Maddox, 2005). If the category is easy to verbalize by a one-dimensional rule, such as blue objects versus green objects, then human adults typically form rule-based representations. Consequently, in a generalization test that is administered after acquiring such a representation, previously unseen stimuli are classified according to the (one-dimensional) rule. In contrast, if the category structure is more complicated, for example given by a multi-dimensional rule or a rule concerning integrated dimensions (Ashby et al., 1998; Ashby and Ell, 2001), or a rule with multiple exceptions (Medin and Schwanenflugel, 1981), adults do not form rule-based representations. Rather, in the case of a limited number of stimuli, human adults typically form exemplar representations (Nosofsky, 1986). If exemplar representations are formed, categorization of unseen stimuli in a generalization test is based on overall-similarity with previously learned exemplars. In the case of many examples, adults form decision-bound representations (Ashby and Maddox, 2005), in which a (continuous) stimulus space is divided into different sections by the decision-bound. Exemplar representations and decision-bound representations both rely on overall-similarity in judging new stimuli in a generalization test. As the difference between decision-bound and exemplar representations is not pertinent to the current study, we refer to these representations as similarity-based representations.
Recent theories of categorization in adults propose models that form multiple kinds of representations that are related to different modules (Ashby et al., 1998; Erickson and Kruschke, 1998; Nosofsky and Palmeri, 1998). Arguably the most comprehensive neuroscience based multiple systems account of categorization is competition between verbal and implicit systems (COVIS), proposed by Ashby et al. (1998). The COVIS model proposes two competing systems: a verbal learning system and an implicit, or procedural, learning system. The verbal system learns easy to verbalize categories resulting in rule-based representations. COVIS’ implicit learning system implements procedural learning and forms overall-similarity-based representations.
There is ample evidence that both of these learning processes occur in human adults. Rule-based representations are often assumed to result from a process of hypothesis testing applied to series of stimuli. Such learning by hypothesis testing has been studied extensively for decades (going back to, e.g., Bruner et al., 1956). Research into procedural or implicit learning of categories dates back even longer to the classic study by Hull (1920) in which participants were asked to categorize Chinese alphabet characters. Recent advances in neuropsychology relate these (verbal and implicit) learning strategies to the involvement of different brain areas (Ashby et al., 1998; Ashby and Ell, 2001). The verbal (explicit) learning system predominantly involves the anterior cingulate and the prefrontal cortices, whereas the caudate nucleus, and striatal areas, play an essential role in the implicit learning system (Ashby et al., 1998).
Categorization in Children
The issue of rule-based versus similarity-based representations has been the focus of research throughout cognitive science (Hahn and Chater, 1998; Pothos, 2005), in developmental psychology (Gentner and Medina, 1998), and the development of categorization learning in particular (Sloutsky, 2003, 2010). Based on knowledge of different maturational trajectories of prefrontal and striatal areas, the areas involved in verbal versus implicit learning, Ashby et al. (1998) predict that children’s performance on implicit learning tasks is relatively mature; a similar prediction is found in Reber (1992) based on evolutionary considerations. A number of studies indeed found children’s performance in implicit learning to be comparable to adults (e.g., Meulemans et al., 1998; DeGuise and Lassonde, 2001). In contrast, according to COVIS, children’s verbal learning system will be importantly impaired. This is confirmed in a number of studies that find that children are impaired in learning (complex) rule-based categories, whereas they perform similar to adults in similarity-based category learning (Kloos and Sloutsky, 2008; Minda et al., 2008).
Broadly speaking, within multiple systems models of categorization, there are two main possible causes of developmental change: First, the relative dominance of the verbal system increases with age, or second, the efficiency and consistency of the verbal system improves with age. We want to gain insight into these different causes by studying categorization learning in a large sample of children with a large age range and comparing their performance with adults.
In adults, the verbal system certainly is more dominant than the implicit system, meaning that adults typically start by using the verbal system, even when the optimal learning strategy is implicit (Johansen and Palmeri, 2002). Within COVIS, this is modeled as a bias for the verbal system. In developmental research, there is a long tradition of research claiming that the implicit system is dominant in children, for example in free classification (Smith, 1989; see Hanania and Smith, 2010 for a review of similar results). Such claims are, however, not without criticism. At least some developmental studies on free classification show evidence for the formation of rule-based representations during childhood. Both children and adults categorize stimuli that vary on two dimensions, on the basis of a single dimension (Cook and Odom, 1988, 1992; Wilkening and Lange, 1989; Thompson, 1994; Raijmakers et al., 2004). The developmental changes that do occur in those studies mostly concern the consistency of classification (Thompson, 1994), and the relative salience of the stimulus dimensions (cf. Mash, 2006). Hence, one could argue that children tend to use the verbal system if the task permits doing so, albeit less consistently than most adults would do.
To summarize so far, verbal and implicit learning processes result in rule-based and similarity-based representations respectively. To test for the presence of rule-based versus similarity-based representations, generalization trials are administered after the learning phase in a categorization experiment. The default interpretation of such generalization trials is that generalization on the basis of a single-dimension implies rule-based representations. In contrast, generalization on the basis of multiple dimensions to learned examples implies the use of similarity-based representations. However, one could question whether this interpretation applies under all circumstances. If children only attend to a single dimension, did they ever consider using other dimensions? Selective attention to stimulus features plays an important role in categorization learning in children (Kloos and Sloutsky, 2008). Categorization studies in animals show, for example, that pigeons almost never use all available stimulus dimensions in classification (Lea and Wills, 2008). It is typically expected that pigeons’ learning processes are implicit regardless of the task (see Huber, 2001). However, in rule-based categorization tasks in which human adults would form rule-based representations, pigeons do not generalize on the basis of overall-similarity (Lea and Wills, 2008; Lea et al., 2009; Wills et al., 2009). Similar arguments may apply to multi-dimensional categorization. When participants classify stimuli based on multiple dimensions or features, this does not automatically imply that the underlying representations are similarity based. Other sources of information may be necessary to answer this question and we propose to use response times for this purpose, which are further discussed below.
Categorization of Compound Stimuli
To study the relative dominance of the verbal versus the implicit learning system, participants in the current experiment learn to categorize compound stimuli, for which categorization can be successful by using either the verbal or the implicit system. This should bring out any bias that participants have in favor of one the systems. In the current experiment we (1) test which representations are formed of compound (multi-dimensional) stimuli by employing a generalization test with previously unseen stimuli, and (2) study developmental trends in the types of representations that are formed of such stimuli.
If the main driving force of development of categorization concerns the relative dominance of the explicit system, it is hypothesized that (young) children will predominantly form overall-similarity-based representations, and that this predominance decreases with age. However, if the main cause of development of categorization concerns the maturation of the explicit system rather than its dominance, the main age effects should concern consistency, learning ability, and speed of processing. As we use compound, multi-dimensional stimuli, it is expected that rule-based processing of such stimuli using all dimensions is more time-consuming than is rule-based processing using a single dimension or overall-similarity-based processing. Response times may hence be used to discriminate these different representational formats (cf. van der Maas and Jansen, 2003), next to generalization behavior.
The category-learning study presented here largely resembles the comparative study (human adults and pigeons) presented in Lea et al. (2009). The stimulus structures for the compound stimuli are such that both rule-based categorization as well as overall-similarity-based categorization lead to correct classification of stimuli. In the generalization phase of the experiment, different types of trials are used to determine which representations participants have formed. Pre-training on individual dimensions of the stimuli ensures that participants are aware of all the dimensions of the compound stimuli such that limits in selective attention are less likely to determine individual differences in categorization behavior (cf. Kloos and Sloutsky, 2008).
Assuming a multiple systems account of categorization as we do here, important individual differences are expected which need to be accounted for in the analysis of the generalization data (cf. Nosofsky et al., 1994; Erickson and Kruschke, 1998; Johansen and Palmeri, 2002; Visser et al., 2009). The technique of mixture analysis (such as latent class analysis) is a systematic and reliable way of analyzing category-learning data accounting for individual differences, for errors, and for consistency of responding (e.g., Jansen and Van der Maas, 1997, and Bouwmeester et al., 2004; Bouwmeester et al., 2007, for applications in the developmental literature). Since these methods are not standard in the categorization literature, we briefly describe how we intend to apply these techniques.
Statistical Approach
In the present study, a generalization test is used to establish which representations children and adults have formed. Typically, such generalization tests consist of a series of previously unseen items that participants are required to categorize. Subsequently classifying participants as having formed either rule-based or similarity-based representations is hence based on this series of items and is usually done by counting the number of items that deviate from the ideal or expected pattern for both rule-based and similarity-based responding (see, e.g., Johansen and Palmeri, 2002). This way of classifying participants has a number of drawbacks that are briefly discussed in turn.
First, there can be ties for individual participants who then remain unclassified. This can be a serious problem, especially so when the number of items that is used to discriminate strategies is small.
Second, when matching participants’ responses to ideal patterns, it is hard to deal with errors. In particular, participants may not respond consistently according to their strategy, e.g., due to distraction errors. When using the number of responses on which a particular participant deviates from the ideal pattern of responses, it is difficult to judge what an acceptable maximum is for this number of errors. Also related to the quantification of errors in pattern matching, is the question whether an observed pattern of responses is a real pattern, i.e., that should be classified accordingly, or whether it is the result of adding errors (noise) to another, similar pattern. This issue of consistency is particularly relevant with regards to comparing adults and children in their performance in a categorization task because children may be less consistent than adults in applying their strategies (see, e.g., Raijmakers et al., 2004, for an example in the triad classification task).
Third, classifying participants according to an ideal pattern of responses to a set of items precludes the possibility of discovering new or different patterns of responding that were not hypothesized. However, it could very well be the case that participants use strategies that were unforeseen, but that could nevertheless be interesting from a theoretical perspective. Latent class analysis does not suffer from aforementioned drawbacks and has successfully been applied in similar situations when distinct strategies were expected to be found (cf. Jansen and Van der Maas, 1997; Raijmakers et al., 2004). Hence, we propose to apply latent class analysis to model response patterns that result from the generalization task. Below, a brief overview of latent class models is presented to show how it overcomes these drawbacks.
Latent Class Analysis
Latent class models belong to the family of latent structure models (Lazarsfeld and Henry, 1968). The main aim of these types of models is to explain correlations between responses to different items by introducing a latent variable. In our case, the items are generalization items that are administered after learning the categorization. In latent class models, the latent variable is nominal, indicating the existence of a number of different types of people rather than a dimension (such as extraversion) on which people vary continuously.
The interested reader is referred to McLachlan and Peel(2000 Chap. 5) for a general (technical) overview of finite mixture and latent class models. McCutcheon (1987) provides an introduction into latent class models in the social sciences.
In the current application of latent class models, we consider generalization items that participants have to classify as belonging to one of two categories, say, A and B. The latent classes in the proposed model consist of a probability of classifying an item in category A for each of the items. Hence, each latent class consists of a typical pattern of responding to the generalization items. In contrast with the method of counting the number of items that deviate from an ideal pattern of responses, in latent class models, probabilities are estimated for each pattern. Inasmuch as such a probability deviates from 1 or 0, this can be considered as an error rate on that particular item, given a particular class; consequently, the error rates for each of the items provide an estimate of the consistency that participants display in responding to that particular item (see, e.g., McCutcheon, 1987). These item probabilities are usually referred to as the conditional probabilities, as they are estimated conditional on the latent class; that is, each latent class has a particular set of conditional probabilities for all items.
Next to these conditional probabilities, the second set of parameters in a latent class model is the set of unconditional or prior probabilities. These specify the proportions of participants that occupy the latent classes. Based on the estimated conditional, and unconditional probabilities of the best fitting, most parsimonious latent class model, each individual participant can be assigned to a latent class. This is applied below in the results section to separate rule-based classifiers from similarity-based classifiers, such that further analyses can be applied to those data separately, in particular concerning their response times.
Latent class models can be applied in an exploratory fashion so as to allow for the possibility to detect response patterns that were not hypothesized beforehand. By fitting latent class models with an increasing number of latent classes, it is possible to detect unforeseen response patterns. Note that latent class models are not process models of categorization such as the decision-bound or exemplar based models (see, e.g., Ashby and Maddox, 2005, for a description of these). Rather, latent class analysis is used here as a statistical tool to help detect different representations that participants use in categorizing stimuli. In particular, here we apply latent class analysis to cluster patterns of responses to generalization items in order to uncover different representations that participants acquired during learning.
Materials and Methods
The goal of the current experiment is to test which kind of representations children form when learning to categorize multiple-dimensional stimuli. The experiment consisted of three phases: Phase I is a pre-learning phase, Phase II is the learning phase, and Phase III is the generalization phase. To ensure that participants can discriminate the separate dimensions that the compound stimuli consist of, in Phase I of the experiment, the participants are pre-trained on single-dimensional stimuli consisting of the separate dimensions of the compound stimuli used in Phases II and III. In Phase II of the experiment, the participants learn to categorize compound (multi-dimensional) stimuli. In Phase III participants categorize previously unseen stimuli, new compounds of the same dimensions that were learned in Phase I, to test their generalization behavior.
Participants
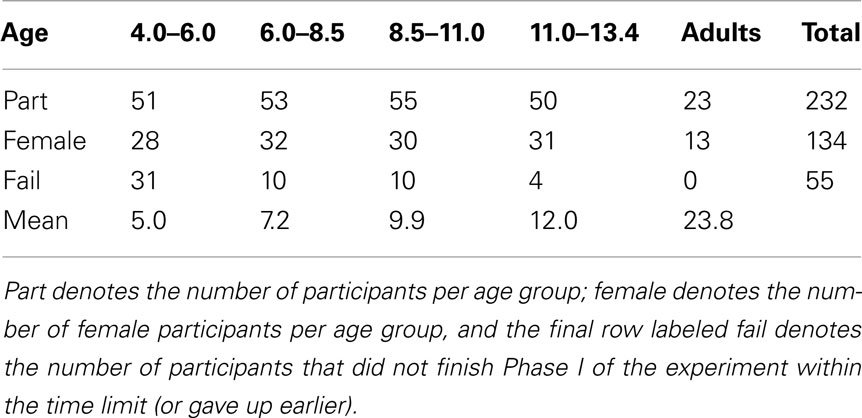
The participant characteristics are listed in Table 1, which contains the total number of participants per age group, their sex, and the number of participants that failed at completing Phase I of the task within the time limit. The age groups of the children were chosen such that they contained approximately equal numbers of participants. Participants stemmed from three groups. The first group of participants consisted of 184 children from a primary school in Amsterdam whose parents consented in their participation in this study. Of these 184 participants, 46 did not finish learning in Phase I in the allotted time of approximately 30 min. Data were incomplete for 14 children, and those were left out of further analyses.
The dropout due to not finishing the task in the first group of participants was concentrated in the 4- to 5-year olds. Hence, to have more participants in this age range, a second group of 4- to 5-year-old participants (whose parents consented in their participation in this study) from a different primary school in Amsterdam were tested. This second group consisted of 40 children, of which 16 finished the task in the first session. Of the remaining children, 11 were re-tested the following day (the other 13 were not re-tested for various reasons), of which only 3 finished the task in a second session. Data of one child was incomplete and was hence left out of further analyses.
The third group of participants consisted of 23 students from the University of Amsterdam who received course credit or a small financial reward (7 Euro) for their participation in the experiment. The mean age of participants in this group was 23.8 (SD = 6). Participants that failed at learning until criterion in Phase I did not proceed to Phases II and III of the experiment. There were 177 participants that finished all three Phases of the experiment; those participants’ data are entered into the strategy analyses below.
Stimuli
In Phase I of the experiment, the pre-training phase, participants learned to categorize the three pairs of stimuli that are depicted in Figure 1. The three dimensions to be learned consist of donut, checkerboard and bar stimuli. Each dimension has two levels, for “donut” stimuli: (level 1) thin and wide versus (level 2) thick and narrow; for checkerboard stimuli: (1) four by four versus (2) eight by eight squares; for bar stimuli: (1) thin and long versus (2) thick and short. All stimuli were 540 × 540 pixels in size (this includes the black background; note that the number of white pixels is identical in all stimulus figures).
In Phase II of the experiment, participants learned to categorize the compound stimuli, see Figure 2. In these stimuli, the dimensions of Phase I are combined in a congruent manner; that is, the level 1 values of each dimension in Phase I were combined, as were the level 2 values. These stimuli can hence be denoted by 111 and 222, indicating the value of the stimulus at each dimension, i.e., the donut, checkerboard, and bar dimensions. Each of these 2 stimuli can be configured into a triangle in six ways, resulting in a total of 12 stimuli that were presented to participants in Phase II1.
In the final Phase III of the experiment, the generalization phase, the set of stimuli is derived from the set of stimuli in Phase II by replacing one of the dimensions by its counterpart; e.g., replacing a wide by a narrow donut. Figure 3 depicts an example; using notation above used for Phase II stimuli, such stimuli can be denoted, e.g., 121 and 112; that is, stimuli in which, respectively, the second or third dimension is altered into its counterpart compared to the Phase II stimuli. This results in a total of 36 stimuli presented in Phase III.
Procedure
Participants were tested individually while seated in front of a 15″ touch screen on which the stimuli were presented one by one on a black background. Two red buttons were drawn to the left and right bottom sides of the screen, respectively, where the participants could touch the screen to classify stimuli as “left” or “right.” Participants were seated such that they could comfortably reach the two red response buttons on the touch screen. Preceding Phase I, participants practiced on two trials, with two stimuli that were different from the stimuli used in the experiment. At each trial, in Phase I–III, participants’ response (“left” or “right”) and the corresponding response time were recorded.
In Phase I, participants learned the correct classification of both levels of all single dimension stimuli (Figure 1) by trial and error. Phase I consisted of one or more blocks of 48 trials in which each of the six stimuli were presented eight times. When, for each dimension, each level was classified correctly for at least six out of eight trials, the participant went on to Phase II. Otherwise, a new block of trials was started. The task was stopped after approximately 30 min if a participant could not finish it because of making too many mistakes or if the participant was becoming frustrated by the task.
Participants had to classify each stimulus by hitting the left (level 1) or right (level 2) response buttons on the touch screen. Showing a smiley face for 0.5 s immediately following a correct response provided positive feedback. The response–stimulus interval (RSI) was 1.3 s after which the next trial was presented. In case of an incorrect response, the stimulus remained on the screen, and the participant had to correct his/her response. Each time the participant touched the screen, a soft sound was to be heard to ensure that participants were aware that they had made a response; this was necessary because on incorrect responses, the layout of the screen did not change in any respect. Suppes and Ginsberg (1962) show that overt correction responses facilitate learning for children, but not for adults.
In Phase II, the same procedure was followed, with blocks of 12 trials. Feedback conditions were identical to Phase I. Participants went on to Phase III of the experiment when in a block of 12 trials no more than two errors were made; otherwise, they were presented with a new block of 12 trials.
In Phase III, the generalization phase, participants were asked to classify the third set of 36 stimuli, which contained incongruent dimensions, as opposed to those in Phase II. The stimuli were presented in random order and once each. The participants received positive feedback for every classification they made, regardless of their answer.
Results
Preliminary Analyses
A binomial regression with age and sex as factors on the combined samples of children and adults, revealed that age was the only significant predictor of finishing Phase I of the experiment, F(1, 232) = 47.9, p < 0.001 (sex had F < 1). The strategy analyses of the generalization performance in Phase III of the Experiments were conducted on all participants who finished the task in one session, which amounts to a total of 177 participants. The average number of blocks needed to complete Phase I learning was 4.2; the average number of blocks needed to complete Phase II learning was 1.3. Age, sex, and the differently configured versions of the stimuli in Phase II did not significantly influence the number of trials needed to reach criterion2.
Strategy Analyses: Model Specification and Selection
The main goal of this study is to classify the representations that participants have formed of the compound stimuli learned in Phase II of the Experiment by means of the generalization trials presented in Phase III. The data in Phase III consists of 36 trials with responses to the stimuli that were incongruent in one of the dimensions (Figure 3). Note that these 36 trials consist of 6 unique combinations of stimulus elements, each presented in 6 different configurations. The responses (left or right) to these stimuli were recoded as zero and one and then summed per stimulus type (i.e., disregarding the different configurations). This results in 6 sum scores that were analyzed; these sum scores ranged from 0 to 6. In the latent class analyses, the sum scores3 were modeled as binomial distributions with n = 6.
Latent class analysis is applied to these 6 sum scores to test whether children had formed different representations that they used in responding to the Phase III stimuli. For example, participants who had formed a (single dimension) rule-based representation were expected to pay attention only to one of the dimensions and choose left or right accordingly. Conversely, children who had formed a similarity-based representation of the stimuli in Phase II were expected to use multiple dimensions in classifying the stimuli in Phase III.
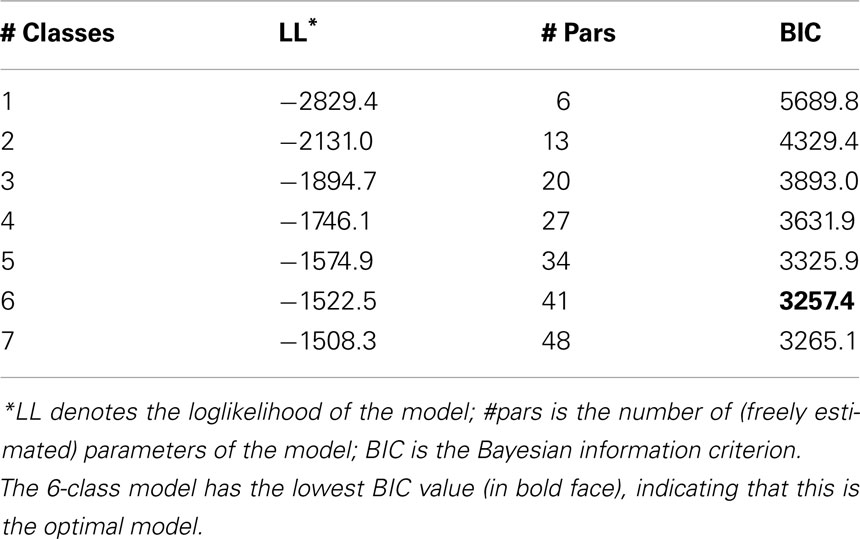
Latent class models with an increasing number of latent classes were fitted to the generalization data. Models were fitted using the flexmix package (Leisch, 2004) for the R statistical programming environment (R Development Core Team, 2009). When fitting a set of models, it is necessary to select which model most adequately describes the data. The Bayesian information criteria (BIC, Schwarz, 1978) is commonly used in comparing non-nested competing models, in this case between models with an increasing number of latent classes (see Lin and Dayton, 1997, for details on the specific use of the BIC, and other information criteria, in latent class models). In the case of non-nested models, traditional tests for comparing models, such as the log likelihood ratio test, are not applicable. The BIC provides a trade-off between goodness-of-fit, the log likelihood, and the number of parameters in the models; note that for each added latent class, a set of conditional probabilities for each of the items needs to be estimated, as well as the class size or prior probability. Lower values of the BIC indicate better models, in which goodness-of-fit and parsimony are balanced. The flexmix package provides the BIC values as output, next to the conditional and unconditional probabilities of the latent classes.
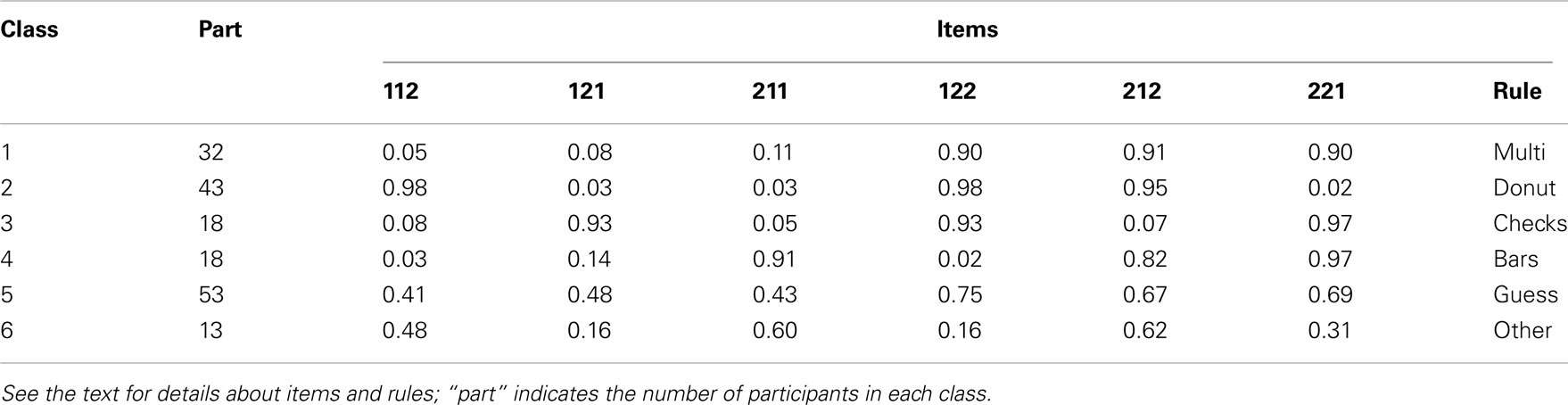
In Table 2, the goodness-of-fit indices for latent class models with one through to seven classes are listed. As can be seen in Table 2, using the BIC, the six-class model is selected as the best fitting, most parsimonious model. In Table 3, the parameter estimates for the six-class model are provided.
The parameter estimates that are given in Table 3 represent the probability of responding with the “right” key on that particular stimulus. Note that the probabilities are the probability of success in a binomial distribution with n = 6 items.
The items in the Table are labeled 112, 121, etc. The first item, for example, refers to the stimulus in which the third dimension has value 2 whereas the other dimensions have value 1; in particular, this is the stimulus that has a thin and wide donut, a four by four checkerboard, and a short and thick bar. The final column of Table 3 gives the interpretations of each of the classes in terms of representational format. These are discussed below.
Single- and Multiple-Dimensional Representations
As can be derived from the probabilities in Table 3, most classes have very clear interpretations. Class 1 in the Table has low probabilities of answering “right” to the items 112, 121, and 211, and high probabilities of answering “right” to the other three items. This is the expected pattern for responding based on multiple dimensions, because the first three items have two dimensions in common with the Phase II stimuli that were categorized “left” (the prototypical stimulus for category “left” has code 111). The second set of three items has two dimensions in common with the Phase II stimuli that were categorized “right” (prototype 222). This class is hence labeled “multi” for multi-dimensional responding.
The pattern of probabilities in Class 2 corresponds to single-dimensional responding, in particular based on the third dimension (“donut”). Participants in Class 2 respond “left” to items 121, 211, and, 221 in which the third dimension has a “1.” In contrast, these participants respond with the “right” key to items 112, 212, and 122. Classes 3 and 4 can be similarly interpreted and are consequently labeled the “checks” and “bars” classes, respectively. Class 5 has probabilities around 0.5 for each of the six items, albeit with quite some variability; that is, participants in Class 5 choose left or right responses approximately equally in response to each of the stimuli and hence do not follow any clear strategy. Consequently, this class is labeled the “guess” class. The pattern of probabilities in Class 6 is hard to interpret with some probabilities around 0.5 but others somewhat below at 0.16. If anything, the pattern tends to the opposite of the “checks” class. Class 6 is labeled “other”4.
From the latent class analysis, it is clear that participants form one of a number of distinct representations in response to the presentation of compound stimuli. The first column in Table 3 provides the number of participants in each class. A number of things are noteworthy about this. First, there are a large number of participants that do not follow any clear strategy, i.e., there are 66 participants in Classes 5 and 6, 37% of the total number of participants. Second, 79 participants (45%) follow a single-dimensional strategy, over half of which use the donut dimension to base their responses on. Third, 32 participants use a multi-dimensional strategy, 18% of the total. Finally, the patterns of probabilities in Classes 1 through 4 are very clear; that is, the probabilities do not differ much from zero or one, indicating a high consistency or stability of these patterns of responding. Together, this pattern of results shows that there are significant individual differences in the preferences of participants to represent the stimuli and to classify new stimuli. In the following section, individual participants are assigned to latent classes to relate these individual differences to age in order to study developmental trends in the formation of different types of representations.
Developmental Trends
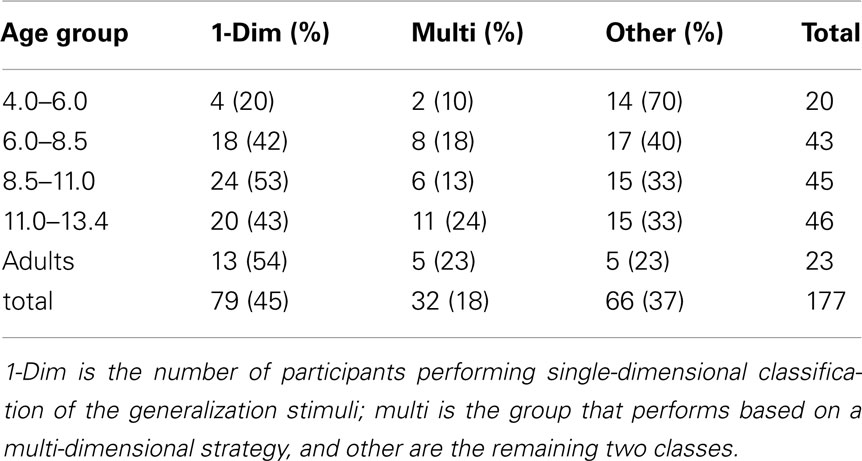
As noted earlier, an important main developmental trend concerns the probability of finishing Phase I of the task, which is related to the efficiency of the verbal learning system because the core task in Phase I is to acquire single dimension rule-based representations. Table 4 lists the numbers of participants that responded using multiple dimensions, a single dimension or otherwise, grouped by age5. The age groups of the children participants are chosen such that these groups contain roughly equal numbers of participants. The single-dimension groups are collapsed here because our main interest is to study whether participants use any single-dimensional rules versus other strategies.
The proportion of participants using the single-dimensional strategies increases with age, from 20% in the youngest age group to 54% of the adult participants. The proportion of participants that have formed a multi-dimensional representation increases slightly with age, from 10% in the youngest children to 23% in the adults. A multinomial logistic regression on class membership with age as (continuous) factor confirms that the overall effect of age on class membership is significant [likelihood ratio χ2(2) = 7.69, p < 0.05]; also the separate effects of age on the probabilities of using a single versus multi-dimensional generalization are both significant (Wald statistics 5.7 and 4.0 respectively, both ps < 0.05). The ratio between single-dimension and multi-dimensional strategies does not show large variability and a Chi-squared test indicates that age does not influence the relative proportion of single- versus multi-dimensional strategy use [χ2(4) = 1.9, p = 0.75]. It is clear from this pattern of results that there is no change with age in preference or bias from similarity-based to rule-based processing as expected. Below, the multi-dimensional group is discussed to more precisely to characterize the underlying representations.
Response Times
To further clarify the interpretation of the multi-dimensional group, the response times of participants in Phase III of the experiment are analyzed. In particular, it was hypothesized that if participants use an overall-similarity representation to base their responses on in Phase III, they should be able to judge items relatively fast. On the other hand, if participants use an analytic strategy, meaning that they take into account each of the dimensions of the compound stimuli in turn to base their decision upon, response times are expected to be relatively slow. The latter would certainly be so when put in contrast with the participants that have formed a single dimensional rule-based representation of those stimuli, as those only need to consider a single dimension instead of all three dimensions. Therefore, in Figure 4, we have plotted the mean response times on trials in Phase III of participants whom were classified into the multi-dimensional class and those who were classified into one of the single-dimensional classes.
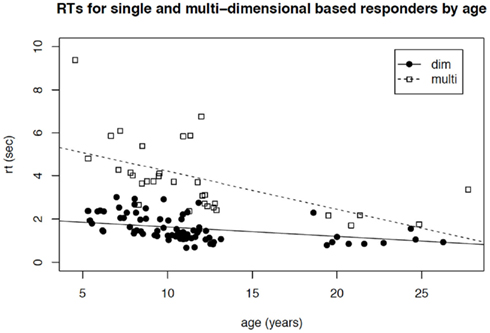
Figure 4. Response times of one-dimensional (dim) responders and multi-dimensional (multi) responders, as a function of age of participants.
Figure 4 reveals that participants in the multi-dimensional group are much slower than are the single-dimensional participants. This is confirmed by a main effect of Class, F(1, 106) = 161.7, p < 0.001, in an ANOVA with Class (multi- versus single dimensional), and age (continuous) as factors. This analysis also reveals that RTs decrease with age, F(1, 106) = 30.2, p < 0.001. Importantly, the interaction between these factors also reaches significance, F(1, 106) = 16.2, p < 0.001. This pattern of results is similar when the adult group is left out of the analyses, and also when the (multi-dimensional strategy) participant with a mean RT of about 9 s is left out (who could be considered an outlier with respect to his/her response times).
The direction of the main effect for Class in the RTs, i.e., multi-dimensional responding is slower than single-dimensional responding, is best interpreted as evidence for the use of an analytic strategy by the participants that use multi-dimensional classification. This conclusion is further supported by the interaction effect with age; it is natural to expect that if participants use an analytic strategy, then it is highly likely that older participants become more efficient at applying such a strategy and that this increase in efficiency is larger when one has to compare three dimensions instead of one dimension. When using an implicit overall-similarity-based representation to classify stimuli, it is not expected that the increase in efficiency with age is larger than for single-dimensional strategies.
This pattern of results indicates that with age children had, when they passed the post of Phase I of the experiment, an increasing probability of learning rule-based representations like adults. We found no evidence of similarity-based representations. Combined with the finding that many of the younger children did not finish Phase I, this indicates a growing efficiency of the verbal learning system as the main factor explaining developmental differences.
Discussion
The present study was designed to characterize patterns of generalization performance that children show in a categorization learning experiment in which both verbal and implicit learning can lead to optimal performance. The results clearly indicate multiple modes of categorization: both single-dimensional and multi-dimensional categorization occur among both children and adults. A third group of participants shows inconsistent generalization performance.
Multi-Dimensional Generalization
The participants that showed single-dimensional generalization were most likely using a rule-based strategy. The pre-training Phase I of the experiment ensured that participants were familiar with the separate dimensions of the compound stimuli and could use them in classification. In addition to the one-dimensional categorizers, we observed a considerable group of participants that showed multi-dimensional categorization in the generalization Phase III. The size of this group increases with age. Following the default interpretation that such multi-dimensional categorization is the result of an overall-similarity representation, this would lead to the counter-intuitive conclusion that human adults show more implicit classification processes than children. The alternative interpretation that the multi-dimensional categorization is an analytical process is hence more likely. This is further supported by the response time analyses.
In such an analytical process, all three dimensions of the stimulus are compared to the learned prototypes and the best match is chosen. This decision process is much more complicated than applying a single-dimensional rule is. This interpretation of multi-dimensional classification is supported by the analysis of the response times. The application of multi-dimensional rules requires more processing time than the application of single-dimensional rules, and the difference decreases with age. This is in contrast with implicit processing which is generally assumed to be faster than processing by the verbal system (Ashby et al., 1998). Moreover, implicit processing is assumed to be relatively stable throughout development (Reber, 1992). If each reasoning step in the categorization process would take a constant amount of time, and if the required time for each step decreases with age, the interaction that we found is typically expected (cf. the analyses of reaction times presented in van der Maas and Jansen, 2003). Hence, the multi-dimensional categorizers are most likely using a multi-dimensional rule-based categorization strategy. Additional experimenting should be used to further confirm this, e.g., by applying a dual task procedure in the generalization phase. This is based on the assumption that implicit or procedural processing of stimuli is not affected by additional working memory load, whereas explicit processing is (Ashby and Maddox, 2011).
Similarity-Based Representations
Our results are partly convergent with those by Minda et al. (2008). Comparable with our results, their results indicate that children and adults perform similarly in categorizing compound stimuli. Minda et al. interpret this finding as evidence that both children and adults use implicit or procedural processing in learning such categories, which fits with the holistic/analytic distinction (e.g., Smith and Shapiro, 1989). In contrast, our strategy analyses and the response time analyses show that behavior is more consistent with rule-based processing. Again, further experimenting should shed light on the differences between these studies. Many factors may explain the differences, such as integrated versus separate dimensions of the stimuli, many or few learning trials (cf. Johansen and Palmeri, 2002), and the separation of learning and generalization phases of the experiments (Minda et al. based their strategy analyses on the learning trials rather than having a separate generalization phase as we did).
Kloos and Sloutsky (2008) conclude that “similarity-based representation is a developmental default, whereas rule-based representations are a product of learning and development” (p. 68). The current results are partly convergent with that conclusion inasmuch as we found that the use of rule-based representations increases with age. In contrast with their results though, we found no evidence of similarity-based representations occurring in children, which Kloos and Sloutsky predicted to be dominant in learning of dense categories (in both children and adults).
This divergence may be due to many differences between these studies. First, our stimulus structures were simpler and had fewer dimensions than those in Kloos and Sloutsky (2008). Second, their training phase consisted of only 16 presentations of the target category, whereas our training phase consisted of training until criterion with stimuli from both categories. The current results further indicate that many children, and even some of the adults, learned to categorize the stimuli but nevertheless did not show consistent generalization behavior.
Our results indicate that children have no problem in processing multi-dimensional stimuli when provided with proper pre-training of the separate stimulus dimensions. Given such pre-training, we found no discernable developmental differences in the dominance of either multi-dimensional or single-dimensional processing. A partly convergent conclusion was recently found in comparing children and adults in information-integration categorization learning (Huang-Pollock et al., 2011). They found that children were less inclined than adults in adopting an implicit processing strategy in learning a category structure that is hard to represent in an explicit manner. If anything, what follows from these results is that children have as strong a preference for explicit processing as do adults, even when this does not lead to optimal performance and learning (Huang-Pollock et al., 2011). The current results extend a similar finding to a much broader age range.
Similarities between child and adult performance has been found in a number of other fields as well (see, e.g., Gopnik et al., 2001, for an example in causal learning; see Wellman and Gelman, 1992, for discussion). Differences between children and adults in this study were related to achieving criterion in pre-training and in the speed of rule execution in the generalization phase of the experiment. From these results it can be concluded that the main cause for developmental differences in categorization is related to the efficiency of the verbal system that learns rule-based representations, rather than an increasing dominance of the verbal system over the implicit system.
Strategy Analyses and Guessing Behavior
As was shown in the strategy analyses, 37% of participants showed unclear patterns of generalization. In particular, 53 participants (30%) were classified as belonging to the “guess” Class of the latent class model. This indicates that these participants have not formed any clear representation of the stimuli, or at least not a representation that could be detected by the items that were used here. It is important to note that with rule-analysis methodologies that match observed response patterns with expected response patterns one cannot reliably detect guessing as a separate strategy (Jansen and Van der Maas, 1997; but see Siegler and Chen, 2008). The “guessers” that we found among the participants are not showing any other strategy6. It is not uncommon, however, that a considerable group of participants does not show systematic categorization behavior in a generalization phase of category-learning studies (e.g., Johansen and Palmeri, 2002). Using latent class analysis, such a group of participants can be separated from other groups of participants showing homogeneous behavior using firm statistical arguments (cf. Raijmakers et al., 2004; van der Maas and Straatemeier, 2008).
In addition to the participants that were included into the strategy analyses, a considerable group of participants did not finish the acquisition Phase I, and consequently also did not enter Phases II and III of the experiment. How could we best characterize these individuals? The largest part of these participants did not learn at all; some of them learned the task partially. Multiple interpretations are consistent with these results. First, children find it difficult to concentrate for the full duration of the task, which was certainly an issue. A second interpretation is that they were learning in some implicit manner, and that they would simply need many more trials to reach criterion. A third interpretation could be that children try to do some explicit learning, but that their memory span and/or abstraction strategies are too limited to memorize the six items simultaneously (cf. Waldron and Ashby, 2001; Zeithamova and Maddox, 2006, for discussion of the role of working memory in categorization). Such different interpretations do not rule each other out and this provides interesting opportunities for future research.
As was shown, the “guess” and “other” class prevalences decrease with age, as the prevalences of the single and multi-dimensional classes increase with age. This can be interpreted as an indication that the younger the children were, the larger the probability that they had an inconsistent response pattern. This could be an indication of a growing ability in rule execution (Crone et al., 2004) as part of the explicit learning system.
Category Learning and Generalization
Characterizing representations is usually done on the basis of generalization data as was done in the current study. Response time data were used to provide additional, and valuable information giving an overall consistent interpretation of the results. Among the children of 4 years of age and older, there are many who form rule-based representations. Some of them even apply multi-dimensional categorization rules. The number of rule users, both one-dimensional and multi-dimensional, increases with age. Nevertheless, we cannot exclude the possibility that some children would eventually come to learn a categorization task with the present complexity with an implicit learning strategy, if they would have been exposed long enough to it.
Next to generalization data and response times, the learning or acquisition curves may provide information about representational formats; studying such curves is common in animal learning (Gallistel et al., 2004), but hardly in humans (see however Schmittmann et al., 2006), and hence provides additional opportunities for studying categorization learning. This may be particularly useful in cases where competition between implicit and explicit learning processes is expected as proposed in the COVIS model of categorization learning (Ashby et al., 1998; Ashby and Maddox, 2011).
Conclusion
We conclude by stressing again that the present research has found ample evidence for the use of both single-dimensional and multi-dimensional rules by school-aged children. Children are able to form complex multi-dimensional representations, and spontaneously do so even when easier options are available. Applying (complex) rules becomes faster as children grow older. The main developmental trend that we found evidence for in this study is the growing efficiency of the verbal system to learn rule-based representations. This is both evident from the decreasing dropout in Phase I as well as the increasing use of consistent representations in Phase III. Important challenges for future research concern the interaction between stimulus structure and representational format in a developmental context. This research illustrates the usefulness of applying latent class analysis to generalization performance in categorization tasks in order to classify participants. Similarly, analyzing response time data in relation to generalization performance has been shown to provide supporting evidence to interpret generalization patterns.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The work of M. E. J. Raijmakers was supported by NWO grant 452-06-008 and by a grant from the priority program Brain & Cognition of the University of Amsterdam.
Footnotes
- ^Phase II of the experiment was further divided into four conditions corresponding to differently configured versions of the stimuli (e.g., the donut could be at the top of the triangle or at one of the bases et cetera). These conditions were added to allow testing whether participants form a representation based on one particular position on the screen when classifying the compound stimuli. Only three participants seemed to be doing so (see the Results for further details).
- ^The characteristics of the children that did not finish the Phase I were as follows. On average, these participants had responded to 4.9 blocks of trials (235 trials) when the experiment was stopped. It should be noted that the distribution of these numbers was quite skewed with 11 participants finishing less than 3 blocks, but also participants that made up to 11 blocks of trials. To gain further insight into how close these participants were to arriving at the criterion, we computed their percentages correct in the final full block of trials that they made. The percentages correct were computed for each pair of stimuli separately. Only 14 participants fulfilled the criterion in this final block on one pair of stimuli, and 9 of those had two pairs above criterion. Note that the criterion for going to Phase two of the experiment was to have six out of eight repetitions correct for each stimulus. Working memory limitations may be the cause of this performance deficit in the youngest children.
- ^Note that analyses are collapsed over differently rotated/configured versions of the stimuli here. Possible effects of the different configurations are discussed later.
- ^One possible type of strategy that is not easily detected using these items is a strategy that we label a “position” strategy. Of each stimulus type, six differently configured versions were presented in Phase III. The latent class analysis above assumes that participants respond to each of those six items identically; however, if they followed a “position” strategy that would not be the case. The position strategy consists in participants choosing a single position from the compound stimuli and base their response on that particular position. For example, a participant could decide to always base a response on the top stimulus in the triangle, whether that is one of the checkerboards or one of the donuts or one of the bar stimuli. We inspected the response patterns of the participants to determine whether they were following such a strategy. For 3 participants this was abundantly clear; these had, 36, 36, and 35 of their responses consistent with a position strategy. Three further participants had 30 responses consistent with a position strategy. Hence, possibly a total of six participants were actually following a “position” strategy.
- ^Note that in Table 4, participants are collapsed over the different configuration conditions of Phase II. It was tested whether the four configuration conditions had any effect on the strategies that participants employed in Phase III of the experiment. This was done by a χ2 test on the cross tabulation of condition and posterior classification, which turned out non-significant, χ2 = 10.5, df = 15, p = 0.79. This indicates that the configuration conditions did not affect the strategies chosen by participants.
- ^Classification on basis of an element that appears in a certain position of the compound stimulus is done by only a few of those participants (see text footnote 4). Hence, this is not a general explanation of the behavior of this group.
References
Ashby, F. G., Alfonso-Reese, L. A., Turken, U., and Waldron, E. M. (1998). A neuropsychological theory of multiple systems in category learning. Psychol. Rev. 105, 442–481.
Ashby, F. G., and Ell, S. W. (2001). The neurobiology of human category learning. Trends Cogn. Sci. (Regul. Ed.) 5, 204–210.
Ashby, F. G., and Maddox, W. T. (2011). Human category learning 2.0. Ann. N. Y. Acad. Sci. 1224, 147–161.
Bouwmeester, S., Sijtsma, K., and Vermunt, J. K. (2004). Latent class regression analysis to describe cognitive developmental phenomena: an application to transitive reasoning. Eur. J. Dev. Psychol. 1, 67–86.
Bouwmeester, S., Vermunt, J. K., and Sijtsma, K. (2007). Development and individual differences in transitive reasoning: a fuzzy trace theory approach. Dev. Rev. 27, 41–74.
Cook, G. L., and Odom, R. D. (1988). Perceptual sensitivity to dimensional and similarity relations in free and rule-governed classification. J. Exp. Child. Psychol. 45, 319–338.
Cook, G. L., and Odom, R. D. (1992). Perception of multidimensional stimuli: a differential-sensitivity account of cognitive processing and development. J. Exp. Child. Psychol. 54, 213–249.
Crone, E. A., Ridderinkhof, K. R., Worm, M., Somsen, R. J., and Van der Molen, M. W. (2004). Switching between spatial stimulus-response mappings: a developmental study of cognitive flexibility. Dev. Sci. 7, 443–455.
DeGuise, E., and Lassonde, M. (2001). Callosal contribution to procedural learning in children. Dev. Neuropsychol. 19, 253–272.
Erickson, M. A., and Kruschke, J. K. (1998). Rules and exemplars in category learning. J. Exp. Psychol. Gen. 127, 107–140.
Gallistel, C. R., Balsam, P. D., and Fairhurst, S. (2004). The learning curve: implications of a quantitative analysis. Proc. Natl. Acad. Sci. U.S.A. 101, 13124–13131.
Gopnik, A., Sobel, D. M., Schulz, L. E., and Glymour, C. (2001). Causal learning mechanisms in very young children: two-, three-, and four-year-olds infer causal relations from patterns of variation and covariation. Dev. Psychol. 37, 620–629.
Hahn, U., and Chater, N. (1998). Similarity and rules: distinct? exhaustive? empirically distinguishable? Cognition 65, 197–230.
Hanania, R., and Smith, L. B. (2010). Selective attention and attention switching: towards a unified developmental approach. Dev. Sci. 13, 622–635.
Huang-Pollock, C. L., Maddox, T. M., and Karalunas, S. L. (2011). Development of implicit and explicit category learning. J. Exp. Child. Psychol. 109, 321–335.
Huber, L. (2001). “Visual categorization in pigeons,” in Avian Visual Cognition, ed. R. G. Cook. Available at: www.pigeon.psy.tufts.edu/avc/huber/
Hull, C. L. (1920). Quantitative aspects of the evolution of concepts. Number 123. Psychol. Monogr. 28, i–86.
Jansen, B. R. J., and Van der Maas, H. L. J. (1997). Statistical test of the rule assessment methodology by latent class analysis. Dev. Rev. 17, 321–357.
Johansen, M. K., and Palmeri, T. J. (2002). Are there representational shifts during category learning? Cogn. Psychol. 45, 482–553.
Kloos, H., and Sloutsky, V. M. (2008). What’s behind different kinds of kinds: effects of statistical density on learning and representation of categories. J. Exp. Psychol. Gen. 137, 52–72.
Lea, S. E. G., and Wills, A. J. (2008). Use of multiple dimensions in learned discriminations. Comp. Cogn. Behav. Rev. 3, 115–133.
Lea, S. E. G., Wills, A. J., Leaver, L. A., Ryan, C. M. E., Bryant, C. M. L., and Millar, L. (2009). A comparative analysis of the categorization of multidimensional stimuli II: strategic information search in humans (Homo sapiens) but not in pigeons (Columba livia). J. Comp. Psychol. 123, 406–420.
Leisch, F. (2004). FlexMix: a general framework for finite mixture models and latent class regression in R. J. Stat. Softw. 11, 1–18.
Lin, T. H., and Dayton, C. M. (1997). Model selection information criteria for non-nested latent class models. J. Educ. Behav. Stat. 22, 249–264.
Mareschal, D., and Quinn, P. C. (2001). Categorization in infancy. Trends Cogn. Sci. (Regul. Ed.) 5, 443–450.
Mash, C. (2006). Multidimensional shape similarity in the development of visual object classification. J. Exp. Child. Psychol. 95, 128–152.
McCutcheon, A. L. (1987). Latent Class Analysis. Number 07-064 in Sage University Paper series on Quantitative Applications in the Social Sciences. Beverly Hills: Sage Publications.
Medin, D. L., and Schwanenflugel, P. J. (1981). Linear separability in classification learning. J. Exp. Psychol. Learn. Mem. Cogn. 7, 355–368.
Meulemans, T., van der Linden, M., and Perruchet, P. (1998). Implicit sequence learning in children. J. Exp. Child. Psychol. 69, 199–221.
Minda, J. P., Desroches, A. S., and Church, B. A. (2008). Learning rule-described and non-rule-described categories: a comparison of children and adults. J. Exp. Psychol. Learn. Mem. Cogn. 34, 1518–1533.
Namy, L., and Gentner, D. (2002). Making a silk purse out of two sow’s ears: young children’s use of comparison in category learning. J. Exp. Psychol. Gen. 131, 5–15.
Nosofsky, R. M. (1986). Attention, similarity, and the identification-categorization relationship. J. Exp. Psychol. Gen. 115, 39–57.
Nosofsky, R. M., and Palmeri, T. J. (1998). A rule-plus-exception model for classifying objects in continuous-dimension spaces. Psychon. Bull. Rev. 5, 345–369.
Nosofsky, R. M., Palmeri, T. J., and McKinley, S. C. (1994). Rule-plus-exception model of classification learning. Psychol. Rev. 101, 53–79.
R Development Core Team. (2009). R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing.
Raijmakers, M. E. J., Jansen, B. R. J., and Van der Maas, H. L. J. (2004). Rules and development in triad classification task performance. Dev. Rev. 24, 289–321.
Reber, A. S. (1992). An evolutionary context for the cognitive unconscious. Philos. Psychol. 5, 33–51.
Schmittmann, V. D., Visser, I., and Raijmakers, M. E. J. (2006). Multiple learning modes in the development of rule-based category-learning task performance. Neuropsychologia 44, 2079–2091.
Siegler, R. S., and Chen, Z. (2008). Differentiation and integration: guiding principles for analyzing cognitive change. Dev. Sci. 11, 433–448.
Sloutsky, V. M. (2003). The role of similarity in the development of categorization. Trends Cogn. Sci. (Regul. Ed.) 7, 246–251.
Sloutsky, V. M. (2010). From perceptual categories to concepts: what develops? Cogn. Sci. 34, 1244–1286.
Sloutsky, V. M., and Fisher, A. (2004). Induction and categorization in young children: a similarity-based model. J. Exp. Psychol. Gen. 133, 166–188.
Smith, J., and Shapiro, J. (1989). The occurrence of holistic categorization. J. Mem. Lang. 28, 386–399.
Smith, L. (1989). A model of perceptual classification in children and adults. Psychol. Rev. 96, 125–144.
Suppes, P., and Ginsberg, R. (1962). Application of a stimulus sampling model to children’s concept formation with and without overt correction responses. J. Exp. Psychol. 63, 330–336.
Thompson, L. A. (1994). Dimensional strategies dominate perceptual classifications. Child Dev. 65, 1627–1645.
van der Maas, H. L. J., and Jansen, B. R. (2003). What response times tell of children’s behavior on the balance scale task. J. Exp. Child. Psychol. 85, 141–177.
van der Maas, H. L. J., and Straatemeier, M. (2008). How to detect cognitive strategies: commentary on “differentiation and integration: guiding principles for analyzing cognitive change.” Dev. Sci. 11, 449–453.
Visser, I., Raijmakers, M. E. J., and Pothos, E. M. (2009). Individual strategies in artificial grammar learning. Am. J. Psychol. 122, 293–307.
Waldron, E., and Ashby, F. (2001). The effects of concurrent task interference on category learning: evidence for multiple category learning systems. Psychon. Bull. Rev. 8, 168–176.
Wellman, H. M., and Gelman, S. A. (1992). Cognitive development: foundational theories of core domains. Annu. Rev. Psychol. 43, 337–375.
Wilkening, F., and Lange, K. (1989). “When is children’s perception holistic? Goals and styles in processing multidimensional stimuli,” in Cognitive Style and Cognitive Development, eds T. Globerson and T. Zelniker (Norwood, NJ: Ablex), 141–171.
Wills, A. J., Lea, S. E. G., Leaver, L. A., Osthaus, B., Ryan, C. M. E., Suret, M. B., Bryant, C. M. L., Chapman, S. J. A., and Millar, L. (2009). A comparative analysis of the categorization of multidimensional stimuli I: unidimensional classification does not necessarily imply analytic processing; evidence from pigeons (Columba livia), squirrels (Sciurus carolinensis), and humans (Homo sapiens). J. Comp. Psychol. 123, 391–405.
Keywords: category learning, multiple systems, rule-based representation, similarity-based representation, strategy analysis
Citation: Visser I and Raijmakers MEJ (2012) Developing representations of compound stimuli. Front. Psychology 3:73. doi: 10.3389/fpsyg.2012.00073
Received: 07 December 2011; Accepted: 27 February 2012;
Published online: 19 March 2012.
Edited by:
Jessica S. Horst, University of Sussex, UKReviewed by:
Yuyan Luo, University of Missouri, USAMoritz Daum, Max Planck Institute for Human Cognitive and Brain Sciences, Germany
Copyright: © 2012 Visser and Raijmakers. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Ingmar Visser, Department of Psychology, Universiteit van Amsterdam, 1018 XA Amsterdam, Netherlands. e-mail:aS52aXNzZXJAdXZhLm5s