The Assumption of a Reliable Instrument and Other Pitfalls to Avoid When Considering the Reliability of Data

Nimon, Kim; Zientek, Linda Reichwein; Henson, Robin K.

doi:10.3389/fpsyg.2012.00102

REVIEW article

Front. Psychol., 12 April 2012

Sec. Quantitative Psychology and Measurement

Volume 3 - 2012 | https://doi.org/10.3389/fpsyg.2012.00102

This article is part of the Research Topic Sweating the Small Stuff: Does data cleaning and testing of assumptions really matter in the 21st century? View all 14 articles

The assumption of a reliable instrument and other pitfalls to avoid when considering the reliability of data

Kim Nimon¹*

Linda Reichwein Zientek²

Robin K. Henson³

¹ Department of Learning Technologies, University of North Texas, Denton, TX, USA
² Department of Mathematics and Statistics, Sam Houston State University, Huntsville, TX, USA
³ Department of Educational Psychology, UNT, University of North Texas, Denton, TX, USA

The purpose of this article is to help researchers avoid common pitfalls associated with reliability including incorrectly assuming that (a) measurement error always attenuates observed score correlations, (b) different sources of measurement error originate from the same source, and (c) reliability is a function of instrumentation. To accomplish our purpose, we first describe what reliability is and why researchers should care about it with focus on its impact on effect sizes. Second, we review how reliability is assessed with comment on the consequences of cumulative measurement error. Third, we consider how researchers can use reliability generalization as a prescriptive method when designing their research studies to form hypotheses about whether or not reliability estimates will be acceptable given their sample and testing conditions. Finally, we discuss options that researchers may consider when faced with analyzing unreliable data.

The vast majority of commonly used parametric statistical procedures assume data are measured without error (Yetkiner and Thompson, 2010). However, research indicates that there are at least three problems concerning application of the statistical assumption of reliable data. First and foremost, researchers frequently neglect to report reliability coefficients for their data (Vacha-Haase et al., 1999, 2002; Zientek et al., 2008). Presumably, these same researchers fail to consider if data are reliable and thus ignore the consequences of results based on data that are confounded with measurement error. Second, researchers often reference reliability coefficients from test manuals or prior research presuming that the same level of reliability applies to their data (Vacha-Haase et al., 2000). Such statements ignore admonitions from Henson (2001), Thompson (2003a), Wilkinson and APA Task Force on Statistical Inference (1999), and others stating that reliability is a property inured to scores not tests. Third, researchers that do consider the reliability of their data may attempt to correct for measurement error by applying Spearman’s (1904) correction formula to sample data without considering how error in one variable relates to observed score components in another variable or the true score component of its own variable (cf. Onwuegbuzie et al., 2004; Lorenzo-Seva et al., 2010). These so-called nuisance correlations, however, can seriously influence the accuracy of the statistics that have been corrected by Spearman’s formula (Wetcher-Hendricks, 2006; Zimmerman, 2007). In fact, as readers will see, the term correction for attenuation may be considered a misnomer as unreliable data do not always produce effects that are smaller than they would have been had data been measured with perfect reliability.

Purpose

The purpose of this article is to help researchers avoid common pitfalls associated with reliability including incorrectly assuming that (a) measurement error always attenuates observed score correlations, (b) different sources of measurement error originate from the same source, and (c) reliability is a function of instrumentation. To accomplish our purpose, the paper is organized as follows.

First, we describe what reliability is and why researchers should care about it. We focus on bivariate correlation (r) and discuss how reliability affects its magnitude. [Although the discussion is limited to r for brevity, the implications would likely extend to many other commonly used parametric statistical procedures (e.g., t-test, analysis of variance, canonical correlation) because many are “correlational in nature” (Zientek and Thompson, 2009, p. 344) and “yield variance-accounted-for effect sizes analogous to r²” (Thompson, 2000, p. 263).] We present empirical evidence that demonstrates why measurement error does not always attenuate observed score correlations and why simple steps that attempt to correct for unreliable data may produce misleading results. Second, we review how reliability is commonly assessed. In addition to describing several techniques, we highlight the cumulative nature of different types of measurement error. Third, we consider how researchers can use reliability generalization (RG) as a prescriptive method when designing their research studies to form hypotheses about whether or not reliability estimates will be acceptable given their sample and testing conditions. In addition to reviewing RG theory and studies that demonstrate that reliability is a function of data and not instrumentation, we review barriers to conducting RG studies and propose a set of metrics to be included in research reports. It is our hope that editors will champion the inclusion of such data and thereby broaden what is known about the reliability of educational and psychological data published in research reports. Finally, we discuss options that researchers may consider when faced with analyzing unreliable data.

Reliability: What is It and Why Do We Care?

The predominant applied use of reliability is framed by classical test theory (CTT, Hogan et al., 2000) which conceptualizes observed scores into two independent additive components: (a) true scores and (b) error scores:

Observed Score (O_{X}) = True Score (T_{X}) + Error Score (E_{X})

(1)

True scores reflect the construct of interest (e.g., depression, intelligence) while error scores reflect error in the measurement of the construct of interest (e.g., misunderstanding of items, chance responses due to guessing). Error scores are referred to as measurement error (Zimmerman and Williams, 1977) and stem from random and systematic occurrences that keep observed data from conveying the “truth” of a situation (Wetcher-Hendricks, 2006, p. 207). Systematic measurement errors are “those which consistently affect an individual’s score because of some particular characteristic of the person or the test that has nothing to do with the construct being measured” (Crocker and Algina, 1986, p. 105). Random errors of measurement are those which “affect an individual’s score because of purely chance happenings” (Crocker and Algina, 1986, p. 106).

The ratio between true score variance and observed score variance is referred to as reliability. In data measured with perfect reliability, the ratio between true score variance and observed score variance is 1 (Crocker and Algina, 1986). However, the nature of educational and psychological research means that most, if not all, variables are difficult to measure and yield reliabilities less than 1 (Osborne and Waters, 2002).

Researchers should care about reliability as the vast majority of parametric statistical procedures assume that sample data are measured without error (cf. Yetkiner and Thompson, 2010). Poor reliability even presents a problem for descriptive statistics such as the mean because part of the average score is actually error. It also causes problems for statistics that consider variable relationships because poor reliability impacts the magnitude of those results. Measurement error is even a problem in structural equation model (SEM) analyses, as poor reliability affects overall fit statistics (Yetkiner and Thompson, 2010). In this article, though, we focus our discussion on statistical analyses based on observed variable analyses because latent variable analyses are reported less frequently in educational and psychological research (cf. Kieffer et al., 2001; Zientek et al., 2008).

Contemporary literature suggests that unreliable data always attenuate observed score variable relationships (e.g., Muchinsky, 1996; Henson, 2001; Onwuegbuzie et al., 2004). Such literature stems from Spearman’s (1904) correction formula that estimates a true score correlation $(r_{T_{X} T_{Y}})$ by dividing an observed score correlation $(r_{O_{X} O_{Y}})$ by the square root of the product of reliabilities (r_XX r_YY):

r_{T_{X} T_{Y}} = \frac{r_{O_{X} O_{Y}}}{\sqrt{r_{XX} r_{YY}}}

(2)

Spearman’s formula suggests that the observed score correlation is solely a function of the true score correlation and the reliability of the measured variables such that the observed correlation between two variables can be no greater than the square root of the product of their reliabilities:

r_{O_{X} O_{Y}} = r_{T_{X} T_{Y}} \sqrt{r_{XX} r_{YY}}

(3)

Using derivatives of Eqs 2 and 3, Henson (2001) claimed, for example, that if one variable was measured with 70% reliability and another variable was measured with 60% reliability, the maximum possible observed score correlation would be 0.65 (i.e., $\sqrt{0.70 \times 0.60}$ ). He similarly indicated that the observed correlation between two variables will only reach its theoretical maximum of 1 when (a) the reliability of the variables are perfect and (b) the correlation between the true score equivalents is equal to 1. (Readers may also consult Trafimow and Rice, 2009 for an interesting application of this correction formula to behavioral task performance via potential performance theory).

The problem with the aforementioned claims is that they do not consider how error in one variable relates to observed score components in another variable or the true score component of its own variable. In fact, Eqs 2 and 3, despite being written for sample data, should only be applied to population data in the case when error does not correlate or share common variance (Zimmerman, 2007), as illustrated in Figure 1. However, in the case of correlated error in the population (see Figure 2) or in the case of sample data, the effect of error on observed score correlation is more complicated than Eqs 2 or 3 suggest. In fact, it is not uncommon for observed score correlations to be greater than the square root of the product of their reliabilities (e.g., see Dozois et al., 1998). In such cases, Spearman’s correction formula (Eq. 2) will result in correlations greater than 1.00. While literature indicates that such correlations should be truncated to unity (e.g., Onwuegbuzie et al., 2004), a truncated correlation of 1.00 may be a less accurate estimate of the true score correlation than its observed score counterpart. As readers will see, observed score correlations may be less than or greater than their true score counterparts and therefore less or more accurate than correlations adjusted by Spearman’s (1904) formula.

FIGURE 1

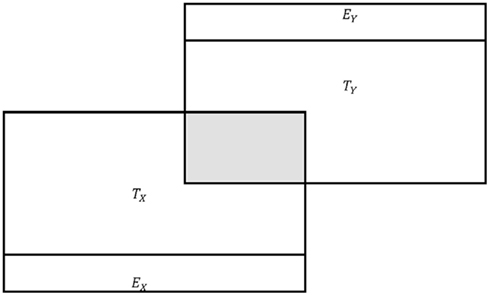
Figure 1. Conceptual representation of observed score variance in the case of no correlated error. T, true scores; E, error scores. Note: shaded area denotes shared variance between T_X and T_Y.

FIGURE 2

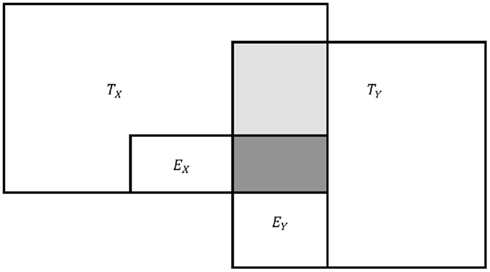
Figure 2. Conceptual representation of observed score variance in the case of correlated error. T, true scores; E, error scores. Note: lighted shaded area denotes shared variance between T_X and T_Y. Dark shaded area denotes shared variance between E_X and E_Y.

To understand why observed score correlations may not always be less than their true score counterparts, we present Charles’s “correction for the full effect of measurement error” (Charles, 2005, p. 226). Although his formula cannot be used when “true scores and error scores are unknown,” the formula clarifies the roles that reliability and error play in the formation of observed score correlation and identifies “the assumptions made in the derivation of the correction for attenuation” formula (Zimmerman, 2007, p. 923). Moreover, in the case when observed scores are available and true and error scores are hypothesized, the quantities in his formula can be given specific values and the full effect of measurement error on sample data can be observed.

Charles’s (2005) formula extends Spearman’s (1904) formula by taking into account correlations between error scores and between true scores and error scores that can occur in sample data:

r_{T_{X} T_{Y}} = \frac{r_{O_{X} O_{Y}}}{\sqrt{r_{XX} r_{YY}}} - \frac{r_{E_{X} E_{Y}} \sqrt{e_{XX}} \sqrt{e_{YY}}}{\sqrt{r_{XX} r_{YY}}} - \frac{r_{T_{X} E_{Y}} \sqrt{e_{YY}}}{\sqrt{r_{YY}}} - \frac{r_{T_{Y} E_{X}} \sqrt{e_{XX}}}{\sqrt{r_{XX}}}

(4)

Although not explicit, Charles’s formula considers the correlations that exist between true scores and error scores of individual measures by defining error (e.g., e_XX, e_YY) as the ratio between error and observed score variance. Although error is traditionally represented as 1 – reliability (e.g., 1 − r_XX), such representation is only appropriate for population data as the correlation between true scores and error scores for a given measure (e.g., $r_{T_{X} E_{X}}$ ) is assumed to be 0 in the population. Just as with $r_{E_{X} E_{Y}}, r_{T_{X} E_{Y}}, r_{T_{Y} E_{X}},$ correlations between true and error scores of individual measures $(r_{T_{X} E_{X}}, r_{T_{Y} E_{Y}})$ are not necessarily 0 in sample data. Positive correlations between true and error scores result in errors (e.g., e_XX) that are less than 1 – reliability (e.g., 1 − r_xx), while negative correlations result in errors that are greater than 1 – reliability, as indicated in the following formula (Charles, 2005):

e_{XX} = (1 - r_{XX} - \frac{{cov}_{T_{X} E_{X}}}{S_{O_{X}}^{2}})

(5)

Through a series of simulation tests, Zimmerman (2007) demonstrated that an equivalent form of Eq. 4 accurately produces true score correlations for sample data and unlike Spearman’s (1904) formula, always yields correlation coefficients between −1.00 and 1.00. From Eq. 4, one sees that Spearman’s formula results in over corrected correlations when $r_{E_{X} E_{Y}}, r_{T_{X} E_{Y}}, and r_{T_{Y} E_{X}}$ are greater than 0, and under-corrected correlations when they are less than 0.

By taking Eq. 4 and solving for $r_{O_{X} O_{Y}},$ one also sees that the effect of unreliable data is more complicated than what is represented in Eq. 3:

\begin{array}{l} r_{O_{X} O_{Y}} & = r_{T_{X} T_{Y}} \sqrt{r_{XX} r_{YY}} + r_{E_{X} E_{Y}} \sqrt{e_{XX}} \sqrt{e_{YY}} + r_{T_{X} E_{Y}} \sqrt{e_{YY}} \sqrt{r_{XX}} \\ + r_{T_{Y} E_{X}} \sqrt{e_{XX}} \sqrt{r_{YY}} & (6) \end{array}

Equation 6 demonstrates why observed score correlations can be greater than the square root of the product of reliabilities and that the full effect of unreliable data on observed score correlation extends beyond true score correlation and includes the correlation between error scores, and correlations between true scores and error scores.

To illustrate the effect of unreliable data on observed score correlation, consider the case where $r_{T_{X} T_{Y}} = 0.50,$ r_XX = r_YY = 0.80, $r_{E_{X} E_{Y}} = 0.50,$ and $r_{T_{X} E_{Y}} = r_{T_{Y} E_{X}} = 0.10 .$ For the sake of parsimony, we assume $r_{T_{X} E_{X}} = r_{T_{Y} E_{Y}} = 0$ and therefore that e_XX = 1 − r_XX and e_YY = 1 − r_YY. Based on Eq. 3, one would expect that the observed score correlation to be 0.40 $(0.50 \sqrt{0.80 \times 0.80}) .$ However, as can be seen via the boxed points in Figure 3, the effect of correlated error, the correlation between T_X and E_Y, and the correlation between T_Y and E_X respectively increase the expected observed score correlation by 0.10, 0.04, and 0.04 resulting in an observed score correlation of 0.58, which is greater than the true score correlation of 0.50, and closer to the true score correlation of 0.50 than the Spearman (1904) correction resulting from Eq. 2 which equals 0.725 (i.e., $0.58 / \sqrt{0.80 \times 0.80}$ . This example shows that the attenuating effect of unreliable data (first term in Eq. 6) is mitigated by the effect of correlated error (second term in Eq. 6) and the effects of correlations between true and error scores (third and forth terms in Eq. 6), assuming that the correlations are in the positive direction. Correlations in the negative direction serve to further attenuate the true score correlation beyond the first term in Eq. 6. This example further shows that observed score correlations are not always attenuated by measurement error and that in some cases an observed score correlation may provide an estimate that is closer to the true score correlation than a correlation that has been corrected by Spearman’s formula.

FIGURE 3

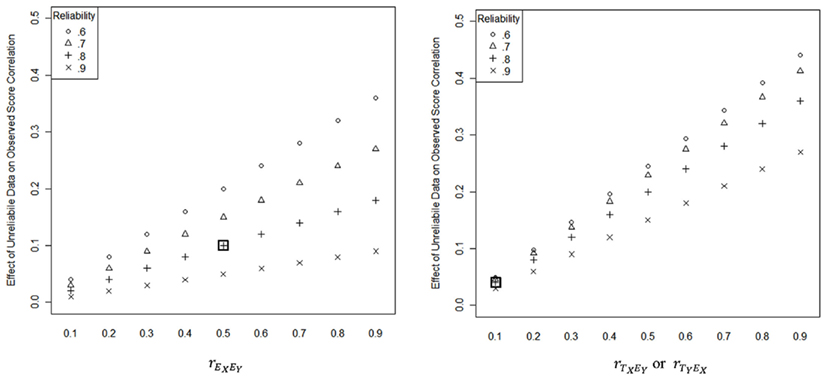
Figure 3. Effect of unreliable data on observed score correlation as a function of reliability, correlated error $(r_{E_{X} E_{Y}}),$ and correlations between true and error scores $(r_{T_{X} E_{Y}}, r_{T_{Y} E_{X}})$ . Note: $r_{T_{X} E_{X}} = r_{T_{Y} E_{Y}} = 0;$ e_XX = e_YY = 1 − reliability. The boxed point on the left-hand panel indicates the effect of correlated error on an observed score correlation when $r_{T_{X} T_{Y}} = 0.50,$ r_XX = r_YY = 0.80, and $r_{E_{X} E_{Y}} = 0.50 .$ The boxed point on the right-hand panel indicates the effect of a correlation between true and error scores (e.g., $r_{T_{Y} E_{X}}$ ) on an observed score correlation when $r_{T_{X} T_{Y}} = 0.50, r_{XX} = r_{YY} = 0.80,$ and $r_{T_{X} E_{Y}} = r_{T_{Y} E_{X}} = 0.10 .$

As illustrated in Figure 3, the effect of correlated error and correlations between true and error scores tend to increase as reliability decreases and the magnitudes of $r_{T_{X} E_{Y}}, r_{T_{Y} E_{X}}$ , and $r_{E_{X} E_{Y}}$ increase. The question, of course, is how big are these so-called “nuisance correlations” in real sample data? One can expect that, on average, repeated samples of scores would yield correlations of 0 for $r_{T_{X} E_{Y}}$ and $r_{T_{Y} E_{X}},$ as these correlations are assumed to be 0 in the population (Zimmerman, 2007). However, correlations between errors scores are not necessarily 0 in the population. Correlation between error scores can arise, for example, whenever tests are administered on the same occasion, consider the same construct, or are based on the same set of items (Zimmerman and Williams, 1977). In such cases, one can expect that, on average, repeated samples of error scores would approximate the level of correlated error in the population (Zimmerman, 2007). One can also expect that the variability of these correlations would increase as the sample size (n) decreases. Indeed, Zimmerman (2007) found that the distributions for $r_{T_{X} E_{Y}}, r_{T_{Y} E_{X}}, and r_{E_{X} E_{Y}}$ yielded SDs of $~ 1 ∕ \sqrt{n - 1} .$ The fact that there is sampling variance in these values makes “dealing with measurement error and sampling error pragmatically inseparable” (Charles, 2005, p. 226).

To empirically illustrate the full effect of unreliable data on observed score correlation, we build on the work of Wetcher-Hendricks (2006) and apply Eq. 6 to education and psychology examples. For education data, we analyzed SAT writing and reading scores (Benefield, 2011; College Board, 2011; Public Agenda, 2011). For psychology data, we analyzed scores from the Beck Depression Inventory-II (BDI-II; Beck, 1996) and Beck Anxiety Inventory (BAI; Beck, 1990). We close this section by contrasting CTT assumptions relating to reliability to population and sample data and summarizing how differences in those assumptions impact the full effect of reliability on observed score correlations.

Education Example

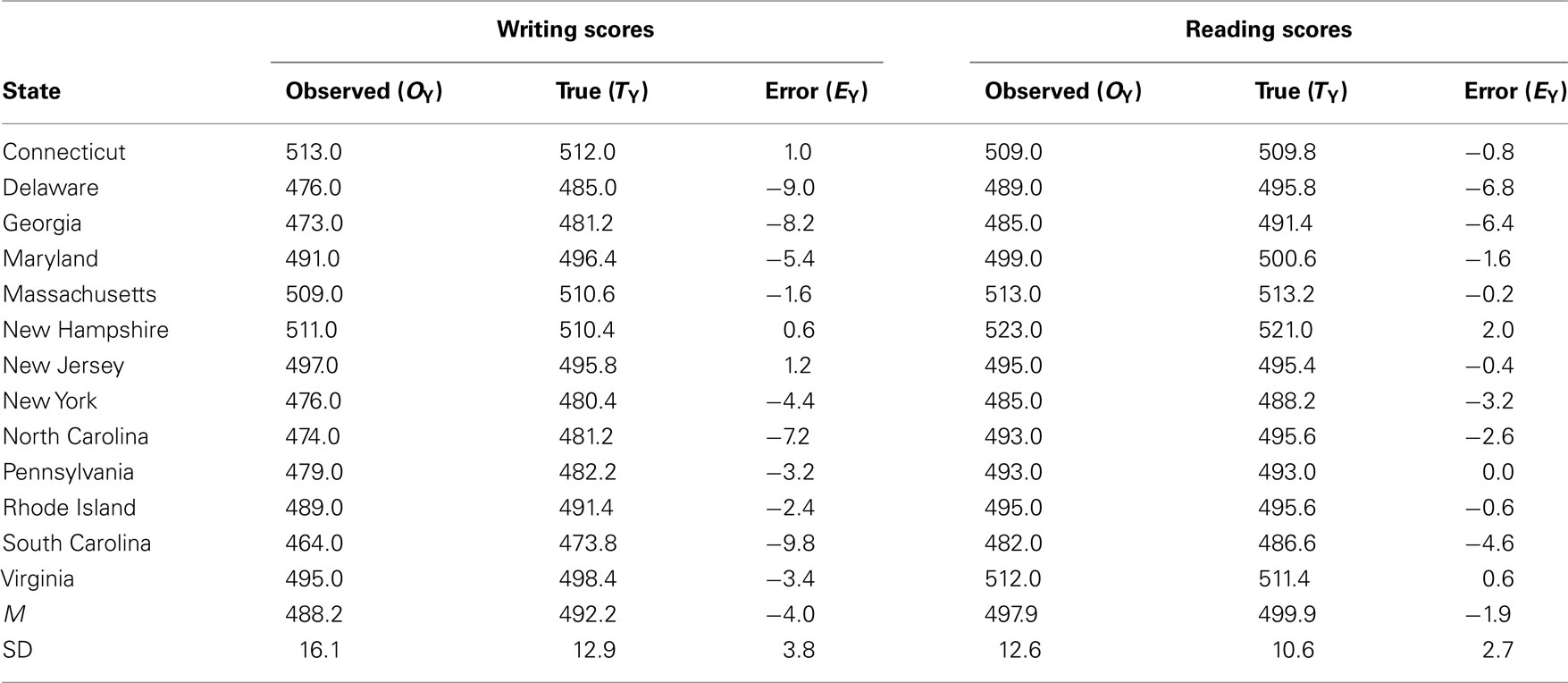
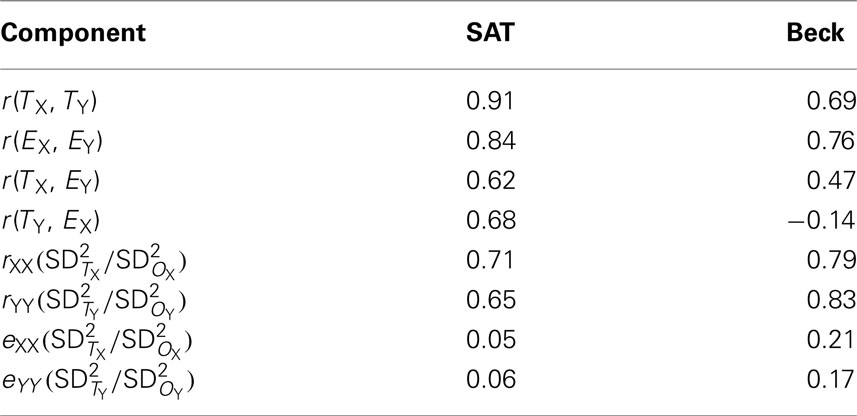
We applied Eq. 6 to average SAT scores from 13 states associated with the original USA colonies (see Table 1). We selected these states as they were a cohesive group and were among the 17 states with the highest participation rates (Benefield, 2011; College Board, 2011; Public Agenda, 2011). We used data reported for 2011 as observed data and the long-run average of SAT scores reported since the new form of the SAT was introduced as true scores, given the psychometric principle from Allen and Yen (1979) that long-run averages equal true score values (cf. Wetcher-Hendricks, 2006). To compute error scores, we subtracted true scores from observed scores. The components of Eq. 6 applied to the SAT data are presented in Table 2 and yield the observed score correlation (0.90), as follows:

\begin{array}{l} r_{O_{X} O_{Y}} = 0.91 \sqrt{0.71 \times 0.65} + 0.84 \sqrt{0.05} \sqrt{0.06} \\ + 0.62 \sqrt{0.06} \sqrt{0.71} + 0.68 \sqrt{0.05} \sqrt{0.65} \\ 0.90 = 0.62 + 0.04 + 0.12 + 0.12 \end{array}

(7)

TABLE 1

Table 1. SAT data observed, error, and true scores.

TABLE 2

Table 2. Values for observed score correlation computation for SAT and beck data.

While the reliability of the SAT data served to attenuate the true score correlation between reading and writing scores (cf. first term in Eq. 7), the correlations between (a) reading error scores and writing errors scores (cf. second term in Eq. 7), (b) reading error scores and writing true scores (cf. third term in Eq. 7), and (c) writing errors scores and reading true scores (cf. forth term in Eq. 7), served to mitigate the effect of that attenuation. Also note that the observed score correlation (0.90) is more in-line with the true score correlation (0.91) than what Spearman’s (1904) correction formula yielded (i.e., $0.90 ∕ \sqrt{0.71 \times 0.65} = 1.33$ ). Given that Spearman’s correction produced a value in excess of 1.00, it would be more accurate to report the observed score correlation, rather than follow conventional guidelines (e.g., Onwuegbuzie et al., 2004) and report 1.00.

Psychology Example

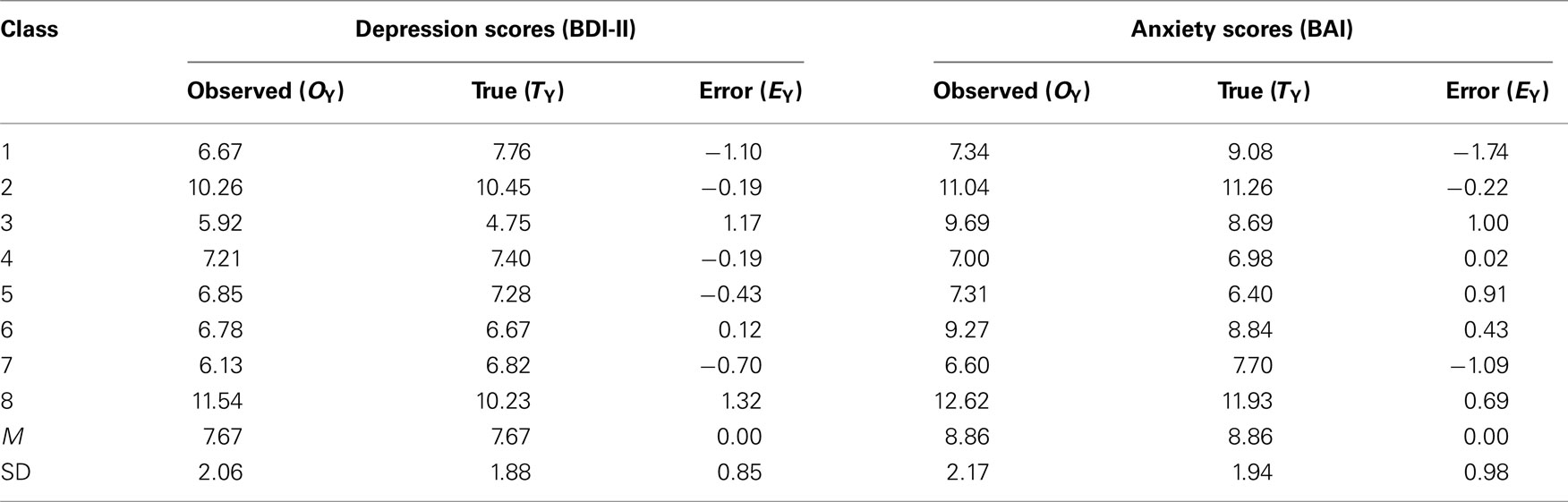
We applied Eq. 6 to average class BDI-II (Beck, 1996) and BAI (Beck, 1990) scores from Nimon and Henson, 2010; see Table 3). In their study, students responded to the BDI-II and BAI at two times within the same semester (i.e., time-1, time-2). Following Wetcher-Hendricks’ (2006) example of using predicted scores as true scores, we used scores for time-1 as observed data and the predicted scores (regressing time-2 on time-1) as true scores. As in the education example, we subtracted true scores from observed scores to compute error scores. The components of Eq. 6 applied to Nimon and Henson’s (2010) data are presented in Table 2 and yield the observed score correlation of 0.81, as follows:

\begin{array}{l} r_{O_{X} O_{Y}} = 0.69 \sqrt{0.79 \times 0.83} + 0.76 \sqrt{0.21} \sqrt{0.17} \\ + 0.47 \sqrt{0.17} \sqrt{0.79} - 0.14 \sqrt{0.21} \sqrt{0.83} \\ 0.81 = 0.56 + 0.14 + 0.17 - 0.06 \end{array}

(8)

TABLE 3

Table 3. Beck data observed, error, and true scores.

In Nimon and Henson’s (2010) data, the true score correlation (0.69) is lower than the observed score correlation (0.81). In this case, the attenuating effect of unreliability in scores was mitigated by other relationships involving error scores which, in the end, served to increase the observed correlation rather than attenuate it. As in the SAT data, Spearman’s (1904) correction $(0.81 ∕ \sqrt{0.79 \times 0.83} = 1.00)$ produced an over corrected correlation coefficient. The over-correction resulting from Spearman’s correction was largely due to the formula not taking into account the correlation between the error scores and the correlation between the true anxiety score and the error depression score.

Summary

Classical test theory can be used to prove that ${ρ_{T_{X}}}_{E_{X}}, {ρ_{T_{Y}}}_{E_{Y}}, {ρ_{T_{X}}}_{E_{Y}}$ , and ${ρ_{T_{Y}}}_{E_{X}}$ all equal to 0 in a given population (Zimmerman, 2007). However, the tenets of CTT do not provide proof that ${ρ_{E_{X}}}_{E_{Y}} = 0 .$ Furthermore, in the case of sample data, $r_{T_{X} E_{X}}, r_{T_{Y} E_{Y}}, r_{T_{X} E_{Y}}, r_{T_{Y} E_{X}}$ , and $r_{E_{X} E_{Y}}$ are not necessarily zero.

Because $r_{T_{X} E_{X}}, r_{T_{Y} E_{Y}}, r_{T_{X} E_{Y}}, r_{T_{Y} E_{X}}, and r_{E_{X} E_{Y}}$ may not be zero in any given sample, researchers cannot assume that poor reliability will always result in lower observed score correlations. As we have demonstrated, observed score correlations may be less than or greater than their true score counterparts and therefore less or more accurate than correlations adjusted by Spearman’s (1904) formula.

Just as reliability affects the magnitude of observed score correlations, it follows that statistical significance tests are also impacted by measurement error. While error that causes observed score correlations to be greater than their true score counterparts increases the power of statistical significance tests, error that causes observed score correlations to be less than their true score counterparts decreases the power of statistical significance tests, with all else being constant. Consider the data from Nimon and Henson (2010) as an example. As computed by G_*Power 3 (Faul et al., 2007), with all other parameters held constant, the power of the observed score correlation ( $r_{O_{X} O_{Y}} = 0.81,$ 1 − β = 0.90) is greater than the power of true score correlation ( $r_{T_{X} T_{Y}} = 0.69$ , 1 − β = 0.62). In this case, error in the data served to decrease the Type II error rate rather than increase it.

As we leave this section, it is important to note that the effect of reliability on observed score correlation decreases as reliability and sample size increase. Consider two research settings reviewed in Zimmerman (2007): In large n studies involving standardized tests, “many educational and psychological tests have generally accepted reliabilities of 0.90 or 0.95, and studies with 500 or 1,000 or more participants are not uncommon” (p. 937). In this research setting, the correction for and the effect of reliability on observed score correlation may be accurately represented by Eqs 2 and 3, respectively, as long as there is not substantial correlated error in the population. However, in studies involving a small number of participants and new instrumentation, reliability may be 0.70, 0.60, or lower. In this research setting, Eq. 2 may not accurately correct and Eq. 3 may not accurately represent the effect of measurement error on an observed score correlation. In general, if the correlation resulting from Eq. 2 is much greater than the observed score correlation, it is probably inaccurate as it does not consider the full effect of measurement error and error score correlations on the observed score correlation (cf. Eq. 4, Zimmerman, 2007).

Reliability: How Do We Assess?

Given that reliability affects the magnitude and statistical significance of sample statistics, it is important for researchers to assess the reliability of their data. The technique to assess reliability depends on the type of measurement error being considered. Under CTT, typical types of reliability assessed in educational and psychological research are test–retest, parallel-form, inter-rater, and internal consistency. After we present the aforementioned techniques to assess reliability, we conclude this section by countering a common myth regarding their collective nature.

Test–Retest

Reliability estimates that consider the consistency of scores across time are referred to as test–retest reliability estimates. Test–retest reliability is assessed by having a set of individuals take the same assessment at different points in time (e.g., week 1, week 2) and correlating the results between the two measurement occasions. For well-developed standardized achievement tests administered reasonably close together, test–retest reliability estimates tend to range between 0.70 and 0.90 (Popham, 2000).

Parallel-Form

Reliability estimates that consider the consistency of scores across multiple forms are referred to as parallel-form reliability estimates. Parallel-form reliability is assessed by having a set of individuals take different forms of an instrument (e.g., short and long; Form A and Form B) and correlating the results. For well-developed standardized achievement tests, parallel-form reliability estimates tend to hover between 0.80 and 0.90 (Popham, 2000).

Inter-Rater

Reliability estimates that consider the consistency of scores across raters are referred to as inter-rater reliability estimates. Inter-rater reliability is assessed by having two (or more) raters assess the same set of individuals (or information) and analyzing the results. Inter-rater reliability may be found by computing consensus estimates, consistency estimates, or measurement estimates (Stemler, 2004):

Consensus

Consensus estimates of inter-rater reliability are based on the assumption that there should be exact agreement between raters. The most popular consensus estimate is simple percent-agreement, which is calculated by dividing the number of cases that received the same rating by the number of cases rated. In general, consensus estimates should be 70% or greater (Stemler, 2004). Cohen’s kappa (κ; Cohen, 1960) is a derivation of simple percent-agreement, which attempts to correct for the amount of agreement that could be expected by chance:

κ = \frac{p_{o} - p_{c}}{1 - p_{c}}

(9)

where p_o is the observed agreement among raters and p_c is the hypothetical probability of chance agreement. Kappa values between 0.40 and 0.75 are considered moderate, and values between 0.75 and 1.00 are considered excellent (Fleiss, 1981).

Consistency

Consistency estimates of inter-rater reliability are based on the assumption that it is unnecessary for raters to yield the same responses as long as their responses are relatively consistent. Inter-rater reliability is typically assessed by correlating rater responses, where correlation coefficients of 0.70 or above are generally considered acceptable (Barrett, 2001).

Measurement

Measurement estimates of inter-rater reliability are based on the assumption that all rater information (including discrepant ratings) should be used in creating a scale score. Principal components analysis is a popular technique to compute the measurement estimate of inter-rater reliability (Harman, 1967). If the amount of shared variance in ratings that is accounted for by the first principal component is greater than 60%, it is assumed that raters are assessing a common construct (Stemler, 2004).

Internal Consistency

Reliability estimates that consider item homogeneity, or the degree to which items on a test are internally consistent, are referred to as internal consistency reliability estimates. Measures of internal consistency are the most commonly reported form of reliability coefficient because they are readily available from a single administration of a test (Hogan et al., 2000; Henson, 2001). Internal consistency reliability is typically assessed by computing coefficient alpha (α; Cronbach, 1951):

α = \frac{k}{(k - 1)} [1 - (\frac{\sum {SD}_{i}^{2}}{{SD}_{Total}^{2}})]

(10)

where k refers to the number of items on the assessment device, i refers to item, and Total refers to the total scale score.

Note that the first part of the formula [k/(k − 1)] attempts to “correct” for potential bias in scales that have a small number of items. The rationale is that the more items in a scale, the less likely items will be biased. As k increases, the correction for bias becomes smaller. For two items, the correction is 2 [2/(2 − 1)]. For 10 items, the correction is 1.1, and for 100 items, the correction is only 1.01.

Due to the impact that internal consistency has on the interpretation of scale scores and variable relationships, researchers typically relate estimates of internal consistency to established benchmarks. Henson (2001) reviewed such benchmarks and cited 0.90 as a minimum internal consistency estimate for standardized test scores used for important educational decisions and 0.80 for scores used for general research purposes. Nunnally (1967) suggested minimum reliabilities of 0.60 or 0.50 for early stages of research, but this was increased to an exploratory standard of 0.70 in his second edition (1978, see also Nunnally and Bernstein, 1994). This change may have resulted in “many researchers citing Nunnally (1978) if they attained this loftier standard and citing the first edition if they did not!” (Henson, 2001, p. 181). In general, internal consistency estimates should be strong for most research purposes, although the exact magnitude of an acceptable coefficient alpha would depend on the purposes of the research.

For example, it is conceivable that coefficient alpha can be too high, which would occur when the items of measurement are highly redundant and measuring the same aspect of a construct. At the extreme of this case, all items would be perfectly correlated and thus alpha would be a perfect 1.00 (see Henson, 2001, for a demonstration). This would reflect poor measurement because of redundancy and, possibly, failure to reflect an appropriate breadth of items from the range of all possible items that could be used to measure the construct (cf. Hulin et al., 2001). Furthermore, a high coefficient alpha is sometimes misinterpreted as an indicator of unidimensionality. This is not the case, and in his summary thoughts on the history of his formula, Cronbach (2004) noted he had “cleared the air by getting rid of the assumption that the items of a test were unidimensional” (p. 397). It is certainly possible to find substantial alpha coefficients even when there are multiple (sometimes subtle) constructs represented in the data.

Conversely, low alphas may indeed reflect a failure to recognize multiple dimensions within a data set, particularly when those dimensions or factors are weakly correlated. In such cases, researchers should first explore the factor structure of their data prior to computation of alpha, and alpha generally should be computed at the subscale (e.g., factor) level rather than on a global test level when there are multiple constructs being assessed. The bottom line is that the interpretation of coefficient alpha when assessing constructs should consider (a) item representativeness and breadth and (b) desired overlap between items.

Multiple Sources of Measurement Error

It is important to note that the sources of measurement error described in this section are separate and cumulative (cf. Anastasi and Urbina, 1997). As noted by Henson (2001),

Too many researchers believe that if they obtain α = 0.90 for their scores, then the same 10% error would be found in a test–retest or inter-rater coefficient. Instead, assuming 10% error for internal consistency, stability, and inter-rater, then the overall measurement error would be 30%, not 10% because these estimates explain different sources of error (p. 182).

The point to be made here is that measurement error can originate from a variety of sources, which can lead to more cumulative measurement error than the researcher might suspect. Of course, this can impact observed relationships, effect sizes, and statistical power.

In order to get a better understanding of the sources of measurement error in scores, generalizability theory (G theory) can be employed which allows researchers to “(a) consider simultaneously multiple sources of measurement error, (b) consider measurement error interaction effects, and (c) estimate reliability coefficients for both “relative” and “absolute” decisions” (Thompson, 2003b, p. 43). As a full discussion of G theory is beyond the scope of this article, readers are directed to Shavelson and Webb (1991) for an accessible treatment. We continue with a discussion of how published reliability estimates can be used to inform research design and RG studies.

How Do We Plan? The Role of RG

As defined by Vacha-Haase (1998), RG is a method that helps characterize the reliability estimates for multiple administrations of a given instrument. Vacha-Haase further described RG as an extension of validity generalization (Schmidt and Hunter, 1977; Hunter and Schmidt, 1990) and stated that RG “characterizes (a) the typical reliability of scores for a given test across studies, (b) the amount of variability in reliability coefficients for given measures, and (c) the sources of variability in reliability coefficients across studies” (p. 6). RG assesses the variability in reliability estimates and helps identify how sample characteristics and sampling design impacts reliability estimates.

In a meta-analysis of 47 RG studies, Vacha-Haase and Thompson (2011) found that the average of the coefficient alpha means from these studies was 0.80 (SD = 0.09) with a range from 0.45 to 0.95. These results illustrate the extent to which reliability estimates can vary across studies, and in this case, across instruments. Because any given RG study quantifies the variation of reliability across studies for a given instrument, the results empirically demonstrate that the phrases “the reliability of the test” and “the test is not reliable” are inappropriate and that reliability is a property inured to data, not instrumentation (Thompson and Vacha-Haase, 2000, p. 175).

Results from RG studies also provide empirical evidence that reliability estimates can vary according to sample characteristics. In their meta-analysis, Vacha-Haase and Thompson (2011) found that “the most commonly used predictor variables included gender (83.3% of the 47 RG studies), sample size (68.8%), age in years (54.2%), and ethnicity (52.1%)” (p. 162). Upon evaluating predictor variables across studies, they found number of items and the sample SD of scale scores to be noteworthy, as well as age and gender. However, as is true with all analyses Vacha-Haase and Thompson’s review was contingent on the independent variables included in the models, as variable omission can impact results (cf. Pedhazur, 1997).

Using RG to Plan

While RG studies demonstrate the importance of assessing reliability estimates for the data in hand, they can also help researchers make educated decisions about the design of future studies. Researchers typically devote considerable energies toward study design because a poorly designed study is likely to produce results that are not useful or do not provide reliable answers to research questions. When data need to be collected from study participants, researchers must determine the most suitable instrument and should consult existing literature to understand the relationship between the reliability of the data to be measured and the population of interest. When available, an RG study can help guide researchers in the instrument selection process. By consulting reliability estimates from published reports, researchers can form hypotheses about whether or not reliability estimates will be acceptable given their sample and testing conditions.

To illustrate how RG studies can improve research design, we provide a hypothetical example. Presume that we want to conduct a study on a sample of fifth-grade students and plan to administer the Self-Description Questionnaire (SDQ; cf. Marsh, 1989). Because we want to conduct a study that will produce useful results, we endeavor to predict if scores from our sample are likely to produce acceptable levels of reliability estimates. Also, presume we are considering modifications such as shortening the 64-item instrument (because of limitations in the available time for administration) and changing the original five-point Likert type scale to a six-point Likert type scale (because of concern about response tendency with a middle option).

Results from Leach et al.’s (2006) RG study of the SDQ may help us decide if the SDQ might be an appropriate instrument to administer to our sample and if our proposed modifications might result in acceptable reliability estimates. For each domain of the SDQ, Leach et al. found that the reliability estimates tended to be within an acceptable range with general self-concept (GSC) scores yielding lower reliability estimates. However, even for GSC scores, the majority of the reliability estimates were within the acceptable range. Furthermore, Leach et al. found that “the most pervasive (predictor of reliability variation) seemed to be the role of the five-point Likert scale and use of the original version (unmodified) of the SDQ I” (p. 300).

The RG study suggests that SDQ I scores for our hypothetical example would likely yield acceptable levels of reliability presuming we did not modify the original instrument by shortening the instrument or changing the five-point Likert scale, and also assuming we employ a sample that is consistent with that for which the instrument was developed. These decisions help us with study design and mitigate our risk of producing results that might not be useful or yield biased effect sizes.

As illustrated, prior to administering an instrument, researchers should consult the existing literature to determine if an RG study has been conducted. RG studies have been published on a variety of measures and in a variety of journals. Researchers might first want to consult Vacha-Haase and Thompson (2011), as the authors provided references to 47 RG studies, including reports from Educational and Psychological Measurement, Journal of Nursing Measurement, Journal of Personality Assessment, Personality and Individual Differences, Personal Relationships, Journal of Marriage and Family, Assessment, Psychological Methods, Journal of Cross-Cultural Psychology, Journal of Managerial Issues, and International Journal of Clinical and Health Psychology. The fundamental message is that RG studies are published, and continue to be published, on a variety of measures in a variety of journals including journals focusing on measurement issues and substantive analyses.

Barriers to Conducting RG Studies

Researchers need to be cognizant of the barriers that impact RG results, as these barriers limit the generalization of results. Insufficient reporting of reliability estimates and sample characteristics are primary difficulties that impact the quality of RG results. When details about measurement and sampling designs are not provided, model misspecifications in RG studies may occur (Vacha-Haase and Thompson, 2011). As Dimitrov (2002) noted, misspecifications may “occur when relevant characteristics of the study samples are not coded as independent variables in RG analysis” (p. 794). When sampling variance is not included, the ability to conduct extensions to Vacha-Haase’s (1998) RG method may also be impeded. For example, Rodriguez and Maeda (2006) noted that some RG studies make direct adjustments of alpha coefficients. However they noted problems with adjusting some but not all alphas in RG studies when researchers fail to publish sample variances.

Reliability estimates

Meticulous RG researchers have been discouraged to find that many of the studies they consult either (a) only report the reliabilities from previous studies (i.e., induct reliability coefficients) and not report reliabilities from their sample at hand or (b) do not report reliabilities at all (cf. Vacha-Haase et al., 2002). Vacha-Haase and Thompson (2011) found that “in an astounding 54.6% of the 12,994 primary reports authors did not even mention reliability!” and that “in 15.7% of the 12,994 primary reports, authors did mention score reliability but merely inducted previously reported values as if they applied to their data” (p. 161).

The file drawer problem of researchers not publishing results that were not statistically significant might be another factor that limits RG results. As discussed above, when reliability estimates are low, the ability to obtain noteworthy effect sizes can be impacted. Rosenthal (1979) noted that the file drawer problem might, in the extreme case, result in journals that “are filled with the 5% of the studies that show Type I errors, while the file drawers back at the lab are filled with the 95% of the studies that show non-significant (e.g., p > 0.05) results” (p. 638). As noted by Rosenthal (1995), when conducting meta-analyses, a solution to the file drawer problem does not exist, “but reasonable boundaries can be established on the problem, and the degree of damage to any research conclusion that could be done by the file drawer problem can be estimated” (Rosenthal, 1995, p. 189). Because RG studies are meta-analyses of reliability estimates, RG studies are not immune to a biased sample of statistically significant studies and reliability estimates that never make it out of the file drawer might be lower than the estimates published in refereed journal publications.

Sample characteristics

Insufficient reporting of sample variance, sample characteristics, and sample design is another barrier impacting RG results. Insufficient reporting practices have been documented by several researchers. Miller et al. (2007) noted “given the archival nature of the analysis, however, selection of predictor variables was also limited to those that were reported in the reviewed articles” (p. 1057). Shields and Caruso (2004) noted limitations on coding variables and stated that “practical considerations and insufficient reporting practices in the literature restrict the number and type of predictor variables that can be coded” (p. 259). Within teacher education research, for example, Zientek et al. (2008) found that only 9% of the articles “included all of the elements necessary to possibly conduct a replication study” (p. 210) and that many studies fail to report both means and SD.

Reporting Recommendations

In order to improve RG studies and remove barriers encountered with insufficient reporting practices, we propose a list of relevant information in Figure 4 to be included in journal articles and research publications. Reporting this information will facilitate RG researchers’ ability to conduct meaningful RG studies. Many of these items are necessary for study replication; hence they adhere to recommendations from the American Educational Research Association (AERA, 2006) and the American Psychological Association (APA, 2009b). We want to emphasize the importance of providing (a) the means and SD for each subscale, (b) the number of items for each subscale, and (c) the technique used to compute scale scores (e.g., sum, average).

FIGURE 4

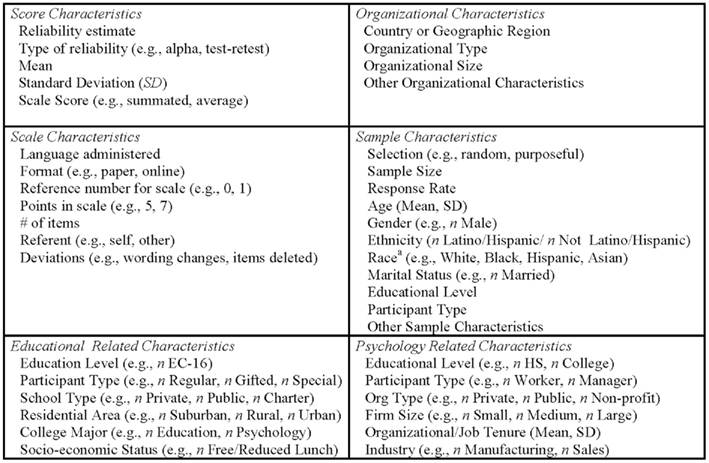
Figure 4. Recommended data to report for each set of scores subjected to an inferential test. Note: Data should be reported for each set of scores analyzed across all measurement occasions (e.g., pre-test, post-test) and groups (e.g., gender, management level). ^aThe Appendix adheres to the APA (2009a) recommendations for reporting race. Reporting of sample characteristics by race should follow APA (2009a) guidelines.

To illustrate how these can be presented succinctly within a journal article format, we present a sample write-up in the Appendix. This narrative can serve as a guide for journal publications and research reports and follows the American Psychological Association (APA, 2009a) guidelines to help reduce bias when reporting sample characteristics. According to APA (2009a),

Human samples should be fully described with respect to gender, age, and, when relevant to the study, race or ethnicity. Where appropriate, additional information should be presented (generation, linguistic background, socioeconomic status, national origin, sexual orientation, special interest group membership, etc.). (p. 4)

In addition to improving the ability to conduct RG studies, providing this information will allow future researchers to replicate studies and compare future findings with previous findings. To address journal space limitations and ease in readability, group means, SD, and reliability estimates may be disaggregated within a table, as illustrated in the Appendix. Readers can also consult Pajares and Graham (1999) as a guide for presenting data.

What Do We Do in the Presence of Unreliable Data?

Despite the best-laid plans and research designs, researchers will at times still find data with poor reliability. In the real-world problem of conducting analyses on unreliable data, researchers are faced with many options which may include: (a) omitting variables from analyses, (b) deleting items from scale scores, (c) conducting “what if” reliability analyses, and (d) correcting effect sizes for reliability.

Omitting Variables from Analyses

Yetkiner and Thompson (2010) suggested that researchers omit variables (e.g., depression, anxiety) that exhibit poor reliability from their analyses. Alternatively, researchers may choose to conduct SEM analyses in the presence of poor reliability whereby latent variables are formed from item scores. The former become the units of analyses and yield statistics as if multiple-item scale scores had been measured without error. However, as noted by Yetkiner and Thompson, reliability is important even when SEM methods are used, as score reliability affects overall fit statistics.

Deleting Items from Scale Scores

Rather than omitting an entire variable (e.g., depression, anxiety) from an analysis, a researcher may choose to omit one or more items (e.g., BDI-1, BAI-2) that are negatively impacting the reliability of the observed score. Dillon and Bearden (2001) suggested that researchers consider deleting items when scores from published instruments suffer from low reliability. Although “extensive revisions to prior scale dimensionality are questionable … one or a few items may well be deleted” in order to increase reliability (Dillon and Bearden, p. 69). Of course, the process of item deletion should be documented in the methods section of the article. In addition, we suggest that researchers report the reliability of the scale with and without the deleted items in order to add to the body of knowledge of the instrument and to facilitate the ability to conduct RG studies.

Conducting “What if” Reliability Analyses

Onwuegbuzie et al. (2004) proposed a “what if reliability” analysis for assessing the statistical significance of bivariate relationships. In their analysis, they suggested researchers use Spearman’s (1904) correction formula and determine the “minimum sample size needed to obtain a statistically significant r based on observed reliability levels for x and y” (p. 236). They suggested, for example, that when $r_{O_{X} O_{Y}} = 0.30,$ r_xx = 0.80, r_yy = 0.80, $r_{T_{X} T_{Y}},$ based on Spearman’s formula, yields $0.38 (0.30 ∕ \sqrt{(0.80 \times 0.80)})$ and “that this corrected correlation would be statistically significant with a sample size as small as 28” (p. 235).

Underlying the Onwuegbuzie et al. (2004) reliability analysis, presumably, is the assumption the error is uncorrelated in the population and sample. However, even in the case that such an assumption in tenable, the problem of “what if reliability” analysis is that the statistical significance of correlation coefficients that have been adjusted by Spearman’s formula cannot be tested for statistical significance (Magnusson, 1967). As noted by Muchinsky (1996):

Suppose an uncorrected validity coefficient of 0.29 is significantly different than zero at p = 0.06. Upon application of the correction for attenuation (Spearman’s formula), the validity coefficient is elevated to 0.36. The inference cannot be drawn that the (corrected) validity coefficient is now significantly different from zero at p < 0.05 (p. 71).

As Spearman’s formula does not fully account for the measurement error in an observed score correlation, correlations based on the formula have a different sampling distribution than correlations based on reliable data (Charles, 2005). Only in the case when the full effect of measurement error on a sample observed score correlation has been calculated (i.e., Eq. 4 or its equivalent) can inferences be drawn about the statistical significance of $r_{T_{X} T_{Y}}$ .

Correcting Effect Sizes for Reliability

In this article we presented empirical evidence that identified limitations associated with reporting correlations based on Spearman’s (1904) correction. Based on our review of the theoretical and empirical literature concerning Spearman’s correction, we offer researchers the following suggestions.

First, consider whether correlated errors exist in the population. If a research setting is consistent with correlated error (e.g., tests are administered on the same occasion, similar constructs, repeated measures), SEM analyses may be more appropriate to conduct where measurement error can be specifically modeled. However, as noted by Yetkiner and Thompson (2010), “score reliability estimates do affect our overall fit statistics, and so the quality of our measurement error estimates is important even in SEM” (p. 9).

Second, if Spearman’s correction is greater than 1.00, do not truncate to unity. Rather consider the role that measurement and sampling error is playing in the corrected estimate. In some cases, the observed score correlation may be closer to the true score correlation than a corrected correlation that has been truncated to unity. Additionally, reporting the actual Spearman’s correction provides more information than a value that has been truncated to unity.

Third, examine the difference between the observed score correlation and Spearman’s correction. Several authors have suggested that a corrected correlation “very much higher than the original correlation” (i.e., 0.85 vs. 0.45) is “probably inaccurate” (Zimmerman, 2007, p. 938). A large difference between an observed correlation and corrected correlation “could be explained by correlated errors in the population, or alternatively because error are correlated with true scores or with each other in an anomalous sample” (Zimmerman, 2007, p. 938).

Fourth, if analyses based on Spearman’s correction are reported, at a minimum also report results based on observed score correlations. Additionally, explicitly report the level of correlation error that is assumed to exist in the population.

Conclusion

In the present article, we sought to help researchers understand that (a) measurement error does not always attenuate observed score correlations in the presence of correlated errors, (b) different sources of measurement error are cumulative, and (c) reliability is a function of data, not instrumentation. We demonstrated that reliability impacts the magnitude and statistical significance tests that consider variable relationships and identified techniques that applied researchers can use to fully understand the impact of measurement error on their data. We synthesized RG literature and proposed a reporting methodology that can improve the quality of future RG studies as well as substantive studies that they may inform.

In a perfect world, data would be perfectly reliable and researchers would not have worry to what degree their analyses were subject to nuisance correlations that exist in sample data. However, in the real-world, measurement error exists, can be systematic, and is unavoidably coupled with sampling error. As such, researchers must be aware of the full impact that measurement error has on their results and do all that they can a priori to select instruments that are likely to yield appropriate levels of reliability for their given sample. If considering these factors, we can better inform our collective research and move the fields of education and psychology forward by meticulously reporting the effects of reliability in our data.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Allen, M. J., and Yen, W. M. (1979). Introduction to Measurement Theory. Monterey, CA: Brooks/Cole.

American Educational Research Association. (2006). Standards for reporting on empirical social science research in AERA publications. Educ. Res. 35, 33–40.