- 1 Rotman Research Institute, Baycrest Centre for Geriatric Care, Toronto, ON, Canada
- 2 Department of Psychology, University of Toronto, Toronto, ON, Canada
Attention and visuospatial working memory (VWM) share very similar characteristics; both have the same upper bound of about four items in capacity and they recruit overlapping brain regions. We examined whether both attention and VWM share the same processing resources using a novel dual-task costs approach based on a load-varying dual-task technique. With sufficiently large loads on attention and VWM, considerable interference between the two processes was observed. A further load increase on either process produced reciprocal increases in interference on both processes, indicating that attention and VWM share common resources. More critically, comparison among four experiments on the reciprocal interference effects, as measured by the dual-task costs, demonstrates no significant contribution from additional processing other than the shared processes. These results support the notion that attention and VWM share the same processing resources.
Introduction
According to Baddeley’s model (Baddeley and Hitch, 1974; Baddeley, 1986, 1992, 2000, 2003; Baddeley and Della Sala, 1996), working memory consists of a central executive and several distinct slave storage systems, including the phonological loop, the visuospatial sketchpad, and the episodic buffer. The central executive oversees working memory; it manages many critical processes, including the direction of attention to relevant information and the suppression of irrelevant information, the supervision of information integration, and the coordination of the slave storage systems. This central executive is thought to depend heavily on the function of selective attention (Engle, 2002) and there is considerable evidence to support this view. For example, attention is important for the process of binding features into a perceptual object representation (Treisman and Gelade, 1980), for maintenance of feature binding and feature values (Wheeler and Treisman, 2002; Fougnie and Marois, 2009; Brown and Brockmole, 2010) in visuospatial working memory (VWM), and for successful change detection (Makovski et al., 2006). Attention also supports the maintenance of these bound representations (Wheeler and Treisman, 2002), and it assists the transfer of perceptual information into working memory (Averbach and Coriell, 1961; Hollingworth and Henderson, 2002; Schmidt et al., 2002).
Attention also plays an important role in the visuospatial sketchpad. Information processing in this system is thought to involve three major processes: encoding, maintenance, and retrieval (e.g., Jonides et al., 2008), with the encoding process modulated by attention which performs the selection of pertinent perceptual items. In fact, attention may have direct and immediate access to the process of encoding (Trick and Pylyshyn, 1994; McElree, 1998; Cowan, 2000), and when new items enter the focus of attention, they displace other items (McElree, 1998; Nairne, 2002). The processing capacities in attention and working memory encoding are managed by common underlying neural mechanisms (Fusser et al., 2011). The maintenance process keeps item representations alive and provides protection against interfering irrelevant stimuli or intruding thoughts (e.g., Funahashi et al., 1989; Pasternak and Greenlee, 2005; Postle, 2006; Ranganath, 2006). Finally, the retrieval process returns items to the focus by switching attention to them (McElree, 2006; Jonides et al., 2008). Thus, attention plays a significant role in the storage of visuospatial information and not just in the various processes of the central executive.
While several stages of processing in working memory where attention plays an important role have been identified, it is still not clear what role – if any – attention plays in determining VWM capacity. Information processing bottlenecks have been observed in both VWM and attentional tasks, and the processing capacities are remarkably similar. In VWM, up to about four items can be stored and manipulated at one time (Luck and Vogel, 1997; Cowan, 2000; Rouder et al., 2008). This “magical number four” has also been cited in attentional tasks. For instance, participants can enumerate up to about four targets in a parallel fashion (Trick and Pylyshyn, 1993, 1994), and they can track about four targets simultaneously (e.g., Pylyshyn and Storm, 1988; Sears and Pylyshyn, 2000; Cavanagh and Alvarez, 2005). However, counting items does not capture all of the various aspects of capacity, and processing capacities are probably more appropriately characterized by considering the information load in addition to the number of items. Indeed, this more nuanced conception of capacity has been proposed for both VWM (Alvarez and Cavanagh, 2004) and attention (Davis et al., 2001).
Since the processing of visuospatial information in working memory seems to depend heavily on attention-based processes, the similarity in the capacities of spatial attention and VWM may be a direct consequence of a limited attentional resource which, in turn, constrains the capacity of VWM (Cowan, 1995, 2000; Awh and Jonides, 2001; Tuholski et al., 2001; Engle, 2002). In Cowan’s (1988, 1995, 2000, 2005a,b) model of VWM capacity, processing of information from long term memory is subject to a limited attentional resource. The constraint on processing ability is observed in working memory tasks and defined as VWM capacity. This attention-based model is supported by evidence from a variety of sources. For example, attention and VWM capacities are highly correlated over individuals (Tuholski et al., 2001; Bleckley et al., 2003). In addition, at the neural level, overlapping brain regions are recruited during attentional and VWM processes (Awh and Jonides, 1998; Mayer et al., 2007), including these regions thought to mediate processing capacities (Xu and Chun, 2006; Fusser et al., 2011). Furthermore, working memory capacity and the ability to control attention have been linked to the same gene (Feng et al., 2005; Söderqvist et al., 2010). These findings, however, along with most other supporting evidence that is correlational, do not provide direct support. While these data indicate that attention and VWM processes involve overlapping underlying mechanisms, they do not demonstrate that the two processes are constrained by access to the same processing resources.
The lack of a definitive demonstration has led various researchers to propose multiple stage interaction models (e.g., Wheeler and Treisman, 2002; Fougnie and Marois, 2006). These models suggest that although the capacity in attention and VWM are largely constrained by shared mechanisms, there is significant contribution from components other than the shared ones (Wheeler and Treisman, 2002; Delvenne and Bruyer, 2004; Fougnie and Marois, 2006). A good example was provided by Fougnie and Marois (2006), who combined a primary VWM task with either an attentional task or a secondary VWM task to form a dual-task. They reasoned that if a limited attentional resource is the only constraint on the capacity of VWM, then both the attentional task and the secondary VWM task, when equally loaded, should produce the same amount of interference on performance in the primary VWM task. However, increasing the load on the attentional task did not produce as much interference as did the secondary VWM task. Fougnie and Marois interpreted this finding as evidence against the shared resource hypothesis.
The dual-task paradigm, such as the one used by Fougnie and Marois (2006), is well-suited for examining the nature of VWM capacity. It is known that attention and VWM interfere with each other, as indicated by slowed responses and increased errors (e.g., Woodman and Luck, 2004). If the loads on the attentional process and the secondary VWM process were equalized, and if each produced comparable interference effects on the primary VWM task, this would suggest that attention and VWM were both constrained by the same processing resources. If the interference effects were not comparable, this would suggest the significant involvement of other processes.
There is, however, a major difficulty with a dual-task approach. Previous studies (e.g., Awh et al., 1998; Oh and Kim, 2004; Woodman and Luck, 2004; Fougnie and Marois, 2006) have focused on comparing task performances which depend critically on the specific tasks and stimuli used. Appropriate load-matching is essential to achieve a fair comparison. Since capacities in both attention and VWM are a function of both the information load and the number of items (Davis et al., 2001; Alvarez and Cavanagh, 2004), non-equivalent interference can occur if the secondary tasks are not equally matched, and simple counting of items is not sufficient to establish comparability. Given the importance of being able to make fair comparisons in the dual-task paradigm (Cowan and Morey, 2007), an accurate match between the secondary attentional and VWM tasks, in terms of the information load, is essential. Achieving such a match is neither simple nor straightforward. Fougnie and Marois (2006) have tackled the problem by equating the number of items and task accuracies on both the attention and working memory tasks. Our approach also uses a dual-task paradigm, but does not rely on load-matching and consequently avoids the potential pitfalls of equating loads.
In our experiments, instead of comparing performance over combinations of tasks and stimuli, we concentrated on the dual-task cost. The dual-task cost is the performance difference between the single-task condition and the dual-task condition. We focused on the pattern of change in dual-task costs, avoiding the tricky problem of matching loads across the primary and secondary tasks. We examined how this cost changes when an attentional task changes from easy (low load) to difficult (high load) and when a working memory task changes from easy (low load) to difficult (high load). The logic of this approach is described below.
A Shared Processing Model
We view capacity as the brain’s ability to manage information. The probability of error when managing increasing amounts of information in either working memory or attention does not increase suddenly at some fixed limit. After a slow initial increase, the error function rises quickly, but not abruptly. Similarly, at very high levels the function decelerates as it approaches asymptote (Bachelder, 2000, p. 116, Figure 1; Vetter et al., 2008, p. 4, Figure 3). When more than one working memory or attentional load is processed at the same time, the notion of shared capacity means that processing or information management of the two loads depends on shared resources in the brain.
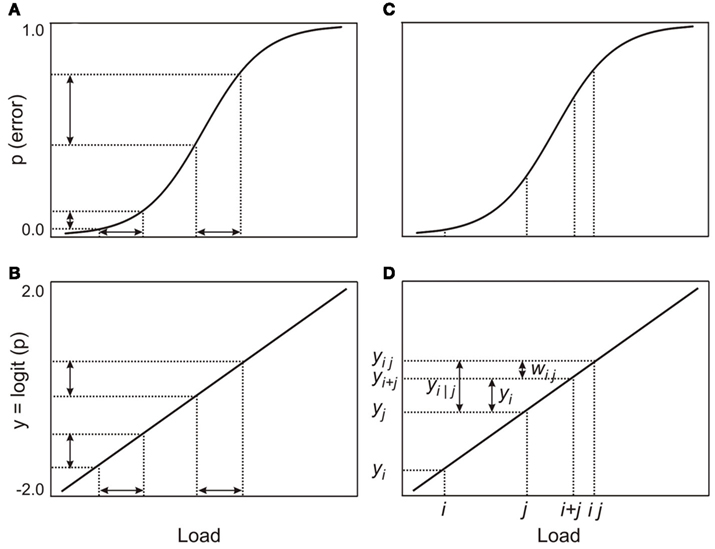
Figure 1. Illustration of the model: (A,B) show the effects of the logit transformation; the transformed differences in probabilities are now proportional to equal differences in loads, (C,D) show the various quantities that are used in the model and how they relate to each other.
Consistent with our belief that the same processing resource supports both working memory and attention, we assume that there is no essential difference between processing a working memory load (mi) and an attentional load (aj). Let the probability of error on a visual working memory task with load mi be pi = P(mi). The analogous probability for an attentional task with load aj is pj = P(aj). The functions for working memory and attentional loads are both approximately ogival and may be linearized (Figures 1A,B) by a logit transformation (Berkson, 1944; Finney, 1947):
In practice, the linearization may not be strictly necessary, since low working memory or attentional loads yield a point on the error function close to the lower bend. Similarly, combinations of high loads are not likely to be far from the upper bend, unless the loads are so high as to make the task impossible for the participant. Between the bends, the function is close to linear. Nonetheless, for completeness, and to make differences in error rates comparable, we assume a logit-linearized error function. After the linearizing transformation, the error probability associated with a load may be considered to be proportional to the magnitude of the load and is thus an indirect measure of the magnitude of the load. This reasoning is similar to the argument used by Fougnie and Marois(2006, p. 529) when they used error rates to establish the equivalence of loads. Since we assume that working memory and attentional loads are processed by the same resource, the term “load” can refer to either function; this, however, does not assume that loads for the two different functions are necessarily equivalent. To avoid repetition in the development below, we omit the qualification “transformed” when we refer to the various probabilities of error.
The dual-task cost, zi|j, of adding a load, i, while a participant is simultaneously processing another load, j, is:
where yi|j is the probability of error for load i on the dual-task while load j is processed simultaneously and yi is the probability of error on the single-task with load i (Figures 1C,D). In the dual-task, load j consumes some of the shared processing resource and, consequently, load i has access to a smaller resource than was available for the single-task. In addition, some overhead is likely charged to the processing resource for managing two loads simultaneously, thus increasing the probability of error for load i in the dual-task.
Since we have assumed that error probabilities are proportional to the magnitudes of loads, we make the further assumption that the overall dual-task probability of error, yij, for loads i and j, is the sum of the single-task probabilities, yi and yj, plus a possible processing overhead, wij, that is also charged to the shared resource; thus yij = yi + yj + wij (Figures 1C,D). The overall error probability, yij, is not directly measurable, but yi|j, the probability of error for load i on the dual-task is observable. Since we have assumed that probabilities are proportional to loads, and that – like the loads – they may be added and subtracted, yi|j = yij − yi. Hence yi|j = yi + wij and thus zi|j = wij. Hence the dual-task costs are identical to the processing overheads, wij. If zi|j − zi|j ′ − zi′|j + zi′|j ′ = 0, for all i, j, i′, and j ′, the dual-task costs will be additive.
Although an infinite number of configurations of the wij (and hence the zi|j) may produce additivity, parsimony suggests that the processing overheads are either constant or related to the magnitudes of the loads. Other than in the trivial case where all wij = 0, the wij will be additive if (a) wij = c, or (b) wij = ci + cj, for all i, j pairs. This implies additivity if (a) the processing overheads, wij, are zero or constant, or (b) the processing overheads are constants proportional to the sizes of the individual loads. While there are other ways of defining the magnitudes of the overheads that could also produce additivity of the wij, such definitions would be increasingly complicated and hence increasingly unlikely.
If zi|j − zi|j ′ − zi′|j + zi′|j ′ = wij − wij′ − wi′j + wi′j ′ ≠ 0, both the dual-task costs and the wij would be non-additive. Non-additivity is inconsistent with a model that assumes a shared processing resource since it would imply that processing of the loads would differ depending on the particular combinations, i and j, of the two loads. In our view, this is only likely to be true if other brain resources, separate and unique to working memory and attention, were involved. If, however, the dual-task costs are additive, this is consistent with a model which assumes that working memory and attentional loads are managed by the same shared processing resource and, furthermore, that some of the same shared resource is allocated to a processing overhead associated with the two loads.
Testing the Model
We further illustrate the shared processing model in Figure 2. In our attention–VWM dual-task paradigm, the response variable of interest is the dual-task cost in either attentional performance (Figure 2A) at low and high attentional loads with low or high VWM loads, or in VWM performance (Figure 2B) at low and high VWM loads with low or high attentional loads. In each panel of Figure 2, two lines connect the dual-task costs in each pair of conditions. If the lines are parallel for the attentional performance cost, increasing the VWM load produces the same effects on the attentional process regardless of the existing attentional load level. If the same pattern is observed for both the attentional and VWM costs (i.e., parallel slopes as in both panels of Figure 2). This suggests that the reciprocal interference effects on the two processes are additive, and thus supports the hypothesis that attention and working memory share the same processing resources. However, if the slopes of the lines in each panel of Figure 2 were to differ, this would imply the involvement of other processes other than shared processes that constrain attentional and VWM capacities.
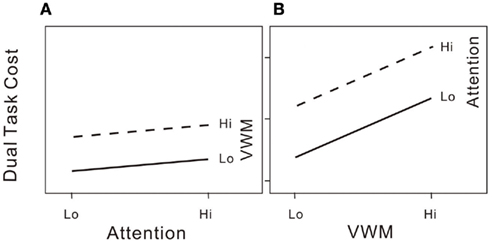
Figure 2. (A) Hypothetical dual-task costs (percentage error) on the attentional task under the 2 × 2 (high/low attentional load × high/low VWM load) conditions if attention is the sole significant limit on VWM capacity. (B) Dual-task costs (percentage error) on the VWM task under the 2 × 2 (high/low attentional load × high/low VWM load) conditions if attention is the sole significant limit on VWM capacity.
Four experiments are required to implement our dual-task costs approach to examining the question of whether attention and VWM share the same processing resources. Each experiment corresponds to one of the four conditions created by combining attentional loads at both low and high levels with VWM loads at low and high levels. First, the baseline dual-task costs incurred are established when both attention and VWM are subject to low loads (Experiment 1). Then the load is increased on either VWM (Experiment 2) or attention (Experiment 3) or both (Experiment 4). In each of the four experiments, we expect some level of interference. If attention and VWM involve common processes – no matter whether partially or completely – we should observe interference between the attentional and VWM processes when both are executed at the same time. Furthermore, the interference should intensify when the load on either process increases. But the critical comparison is the pattern of dual-task costs across the four experiments.
To establish whether attention and VWM completely share the same processing resources, it is necessary to examine how increasing the load on either process contributes to the change in the dual-task cost. If attention and VWM share the same resources, there should be no interaction between the attentional load change and the VWM load change, as illustrated in Figure 2. If, however, the capacities in attention and VWM only partially share common mechanisms, increasing the load on one process should produce differential effects on the other process depending on the existing load on the other process. In statistical terminology, there will be an interaction between attentional load change and VWM load change. In graphs of the changes in the dual-task costs, the cost lines will not be parallel, indicating non-additivity. This may be summarized in the following sub-hypotheses:
1. There will be interference between the attentional and VWM processes;
2. The interference will be reciprocal;
2.1 When the load on either process increases, the reciprocal interference will increase;
2.2 The greatest interference will occur when both processes are subjected to high loads;
2.3 If attention and VWM are supported by completely overlapping mechanisms, the dual-task costs for attention, and VWM will be additive.
If all hypotheses are supported, an additive model would be appropriate and would suggest that attention and VWM share the same processing resources. If, however, 2.1 and 2.2 are supported, but not 2.3, this would suggest that the processing resources are only partially overlapping.
Experiment 1
We examined the interference effects produced when a low-load VWM task (change detection) and a low-load attentional task (enumeration) are performed concurrently (low attentional load + low VWM load). We chose enumeration as the attentional task since: (1) it demonstrates a clear attentional capacity (Trick and Pylyshyn, 1993, 1994); and (2) both the subitizing (within capacity) and counting (beyond capacity) processes rely on attention (Vetter et al., 2008). We chose a change detection task for the VWM task because it is a well established paradigm for investigating working memory capacity (e.g., Luck and Vogel, 1997; Johnson et al., 2008).
Materials and Methods
Participants
Four males and 12 females (aged from 18 to 35) at University of Toronto participated for course credit.
Stimuli
In the attentional task, each trial began with a fixation cross (0.24° × 0.24°) in the center of the screen for 200 ms. A number (one to six) of black squares (each subtending 0.84° × 0.84° with a minimum distance of 0.36° between adjacent pairs) appeared within an invisible square area (light gray, 5.96° × 5.96°) centered on the screen for 50 ms. Participants enumerated the squares and respond by pressing the appropriate number key on the 3 × 3 number keypad. Speed and accuracy were emphasized equally.
A change detection paradigm was used for the VWM task. On each trial, a fixation cross (0.24° × 0.24°) appeared in the center of the screen for 200 ms. A number (one to six) of colored squares (each subtending 0.84° × 0.84° with a minimum distance of 0.36° between adjacent pairs) then appeared at random locations within an invisible square area (light gray, 7.16° × 7.16°) centered on the screen for 50 ms. The colors of the squares were randomly selected from a pool (blue, green, red, violet, white, yellow) with no more than two squares sharing the same color. Participants had to remember the color of each square in the memory array. After a retention interval of 2500 ms, the test array appeared. The two arrays were identical except that on half the trials, one randomly chosen square changed its color subject to the restriction that no more than two squares in the test array could share the same color. Participants reported a color change by pressing the “1” key (change) or the “2” key (no change). Participants pressed the appropriate key on the 3 × 3 number keypad. Speed and accuracy were emphasized equally.
In the dual-task, enumeration (the attentional task) was performed during the retention interval of the change detection task (Figure 3A). Participants enumerated the number of black squares while remembering the memory array of the VWM task. After responding in the attentional task, participants viewed the test array in the VWM task and indicated whether a color change had taken place.
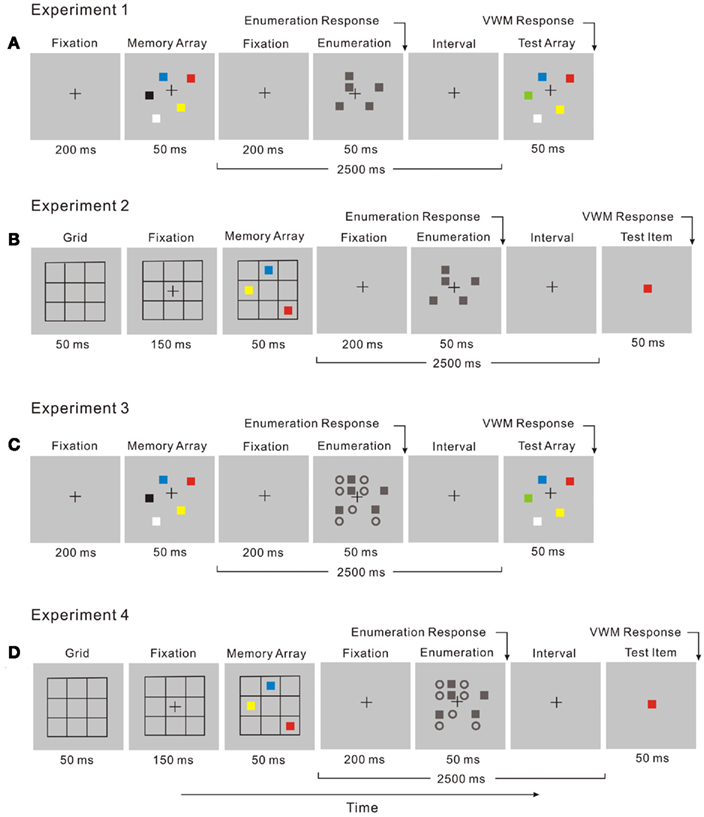
Figure 3. The display sequence for a dual-task trial combines two tasks: (A) in Experiment 1, a change detection task and an enumeration task with no distractors; (B) in Experiment 2, a location recall task and an enumeration task with no distractors; (C) in Experiment 3 a change detection task and an enumeration task with distractors; (D) in Experiment 4, a location recall task and an enumeration task with distractors.
Design and procedure
Both the attentional and VWM single tasks used 96 trials evenly distributed across set sizes varying from one to six, with 16 trials for each set size condition in a single-task. In half the VWM trials, one square changed its color; otherwise the memory and test arrays were identical. There were 216 trials in the dual-task with three trials for each treatment combination (enumeration set size × VWM set size × change/non-change in VWM). Participants maintained fixation on the center of the screen during each trial and they were instructed to devote equal effort to both tasks.
Results
The percentage of errors and log transformed RT in both the attentional and VWM tasks were analyzed in a 6 × 2 (set size × condition) ANOVA. Untransformed percentage of errors were used given the following analyses do not depend on the assumption that requires logit transformation. Performance on enumeration in both the single-task and dual-task conditions clearly revealed (Figure 3A) a subitizing processing (four items or fewer) and a counting process (more than four items; e.g., Trick and Pylyshyn, 1993, 1994): set size effect, F(5, 75) = 16.01, p < 0.01. Participants made more errors when VWM was loaded (upper left panels in Figure 5A): condition effect, F(1, 15) = 6.23, p < 0.05. In the VWM task, performance also depended on the set size in both the single-task and dual-task conditions, revealing a capacity limit pattern, such as that noted by Cowan (2000): set size effect, F(5, 75) = 43.21, p < 0.01. Participants made more errors in the dual-task condition (upper left panel in Figure 5C): condition effect, F(1, 15) = 59.61, p < 0.01. In addition, the capacity breakpoint shifted toward smaller set sizes in the dual-task condition (Figure 4A): set size × condition effect, F(5, 75) = 5.87, p < 0.01. There was no difference in RT in the VWM task (upper left panel in Figure 5D).
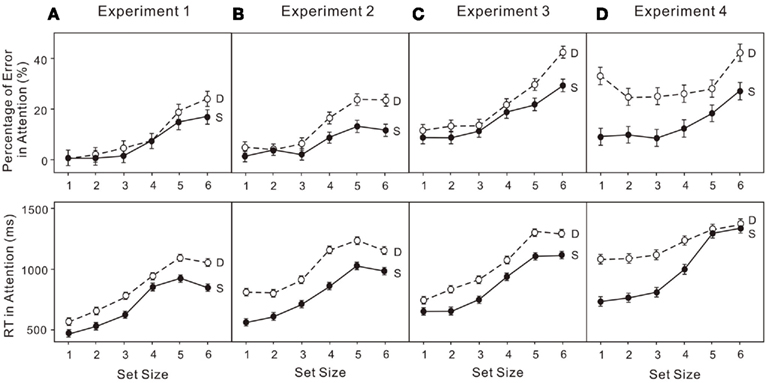
Figure 4. Error rates (upper) and reaction times (RT; lower) for attentional tasks in: (A) experiment 1 (low attentional load); (B) experiment 2 (low attentional load); (C) experiment 3 (high attentional load); (D) Experiment 4 (high attentional load). “S” indicates the enumeration data for single-task trials and “D” indicates the enumeration data for dual-task trials. The error bars represent ± 1 SE computed using Loftus and Masson’s (1994) method for within-subject designs.
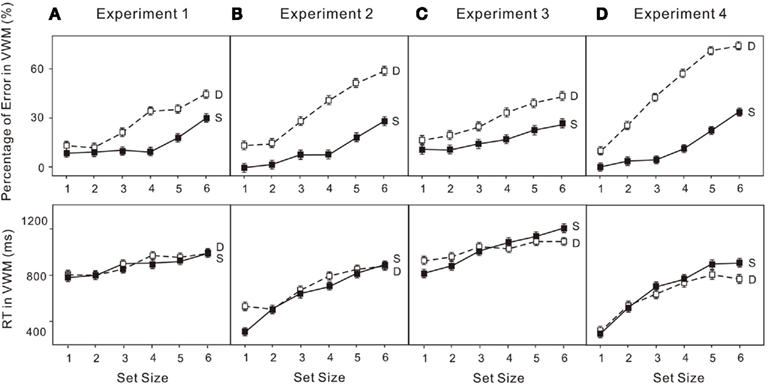
Figure 5. Error rates (upper) and reaction times (RT; lower) for: (A) the VWM task (change detection) in Experiment 1; (B) the VWM task (location recall) in Experiment 2; (C) the VWM task (change detection) in Experiment 3; (D) the VWM task (location recall) in Experiment 4. “S” indicates the VWM single-task trials and “D” indicates the VWM performance in the dual-task trials. The error bars represent ± 1 SE computed using Loftus and Masson’s (1994) method for within-subject designs.
Discussion
The results replicated typical performance patterns in both enumeration (Trick and Pylyshyn, 1993, 1994) and change detection (Luck and Vogel, 1997). Even though the loads for both attention and VWM were low, they were sufficient to produce reciprocal interference in the dual-task condition (Brown, 1997). Participants made more errors in the enumeration task (upper panel in Figure 4B and upper left panel in Figure 6A) and their VWM accuracies were reduced (upper panel in Figure 5A and upper left panel in Figure 6C). These results demonstrate interference between the attentional and VWM processes and are similar to those reported in previous studies (Oh and Kim, 2004; Woodman and Luck, 2004; Fougnie and Marois, 2006).
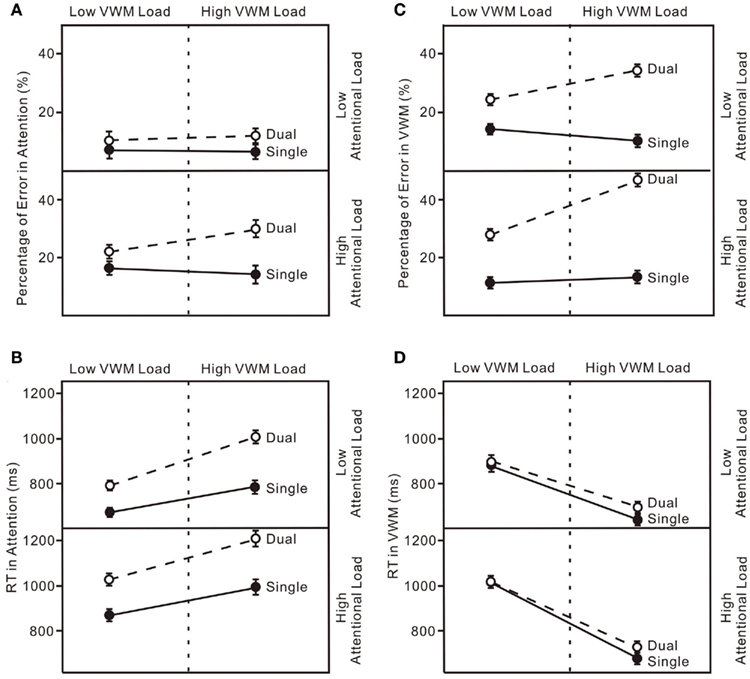
Figure 6. (A) Error rates for the attentional tasks in four experiments (Experiment 1-upper left, Experiment 2-upper right, Experiment 3-lower left, Experiment 4-lower right). “Single” indicates the enumeration data for single-task trials and “Dual” indicates the enumeration data for dual-task trials. (B) Reaction Time (RT) for the attentional tasks in four experiments. (C) Percentage Error for the VWM task in four experiments. (D) Reaction Time (RT) for the VWM task in four experiments. The error bars represent ± 1 SE computed using Loftus and Masson’s (1994) method for within-subject designs.
Experiment 2
The load on attention remained the same as in Experiment 1, while the load on VWM was increased by using a location recall task (low attentional load + high VWM load). The location recall task differs from the change detection task by requiring the participant to recall and report the location of one of the memorized items.
Materials and Methods
Participants
Six males and 10 females (aged from 18 to 24) at the University of Toronto participated for course credit.
Stimuli
All settings remained the same as in Experiment 1 except that a location recall task was used for VWM (Figure 3B). In the VWM task, each trial began with a 3 × 3 grid (1.60° × 1.60°) centered on the screen for 50 ms. A fixation cross (0.24° × 0.24°) then appeared in the center of the grid for 150 ms. A number (one to six) of differently colored squares (0.84° × 0.84°) appeared for 50 ms with each square occupying a unique, random cell in the grid. The colors were randomly selected from a pool (blue, green, red, violet, white, yellow) and each square had a unique color. Participants had to memorize the color and location of each square, a more difficult task than the color-only task in Experiment 1. After a retention interval of 2500 ms, one randomly selected square from the memory array appeared in the center of the screen for 50 ms. Participants indicated its original location by pressing the appropriate key on the 3 × 3 number keypad. Speed and accuracy were emphasized equally.
Design and procedure
These were the same as in Experiment 1.
Results
The untransformed percentage of errors and log transformed RT in both the attentional and VWM tasks were analyzed in a 6 × 2 (set size × condition) ANOVA. The usual indicators of subitizing and counting were observed in both conditions (Figure 3B): set size effect, F(5, 75) = 12.97, p < 0.01. Participants made more errors when VWM was loaded (upper right panels in Figure 5A): condition effect, F(1, 15) = 8.38, p < 0.05. In addition, there was a dual-task cost in RT (upper right panels in Figure 5B): condition effect, F(1, 15) = 15.66, p < 0.01. The error rates were much greater (upper right panels in Figure 5C) for the VWM process, when the attentional process was also active: set size effect, F(5, 75) = 47.52, p < 0.01; condition effect, F(1, 15) = 64.27, p < 0.01. And the capacity breakpoint was no longer apparent (Figure 4B): condition × set size interaction, F(5, 75) = 12.67, p < 0.01. No difference in the RT for VWM was observed (upper right panels in Figure 5D).
Discussion
The combination of low attentional load and high VWM produced considerable interference between the two processes. Even at a great cost in accuracy, participants were much slower in enumeration (Figure 4B). Much higher error rates were also observed at every set size on the VWM process in the dual-task condition, compared to the single-task. And this disparity became greater with the increase in set size.
Experiment 3
The load on attention was increased by introducing distractors in the enumeration task, while the load on VWM remained the same as in Experiment 1 (high attentional load + low VWM load).
Materials and Methods
Participants
Seven males and nine females (aged from 18 to 23) at the University of Toronto participated for course credit.
Stimuli
All settings remained the same as in Experiment 1 except that distractors were added in the enumeration task (Figure 3C). Distractors (black circles, 0.84° × 0.84°) were randomly positioned among the targets (black squares, 0.84° × 0.84°). The total number of items in the stimulus display was always 12 and the number of targets varied from one to six. Participants reported the number of targets. Speed and accuracy were emphasized equally.
Design and procedure
These were the same as in Experiment 1.
Results
The untransformed percentage of errors and log transformed RT in both the attentional and VWM tasks were analyzed in a 6 × 2 (set size × condition) ANOVA. Subitizing and counting processes in enumeration were observed in both the single- and dual-task conditions (Figure 3C): set size effect, F(5, 75) = 15.87, p < 0.01. Participants made more errors when VWM was loaded (lower left panels in Figure 5A): condition effect, F(1, 15) = 5.17, p < 0.05. The dual-task cost in RT was also significant (lower left panels in Figure 5B): condition effect, F(1, 15) = 29.04, p < 0.01. In the VWM task, performance was largely determined by set size (Figure 4C): set size effect, F(5, 75) = 48.70, p < 0.01. The error rate became much greater (lower left panel in Figure 5C) when the attentional process was active: condition effect, F(1, 15) = 110.39, p < 0.01. Moreover, the dual-task cost varied with set size: set size × condition, F(5, 75) = 5.32, p < 0.01. No difference was observed in RT for VWM (low left panel in Figure 5D).
Discussion
In this condition of high attentional load and low VWM load, the dual-task costs on both processes were considerable. Participants performed worse in enumeration in the dual-task condition, particularly at large set sizes (Figure 4C). Their performance in VWM also declined considerably in the dual-task condition (Figure 5C) with bigger discrepancies at larger set sizes.
Experiment 4
The loads on both attention and VWM were increased to high levels (high attentional load + high VWM load).
Materials and Methods
Participants
Five males and 11 females (aged from 18 to 34) at the University of Toronto participated for course credit.
Stimuli
Distractors were added to the enumeration task (as in Experiment 3) and the location recall task was used for VWM (as in Experiment 2; Figure 3D). All other settings remained the same as in Experiment 1.
Design and procedure
These were the same as in Experiment 1.
Results
The untransformed percentage of errors and log transformed RT in both the attentional and VWM tasks were analyzed in a 6 × 2 (set size × condition) ANOVA. The typical pattern associated with subitizing was evident in the single-task condition only (Figure 4D): set size effect, F(5, 75) = 5.90, p < 0.01. With a high VWM load, error rates in enumeration were much higher than in the single enumeration task (lower right panel in Figure 6A): condition effect, F(1, 15) = 16.76, p < 0.01. In addition, participants responded much more slowly (lower right panel in Figure 6B): condition effect, F(1, 15) = 22.83, p < 0.01; condition × set size interaction, F(5, 75) = 8.06, p < 0.01. VWM performance in the dual-task condition was much worse than in the single-task condition (lower right panel in Figure 6C), with no capacity breakpoint apparent in the dual-task condition (Figure 5D): set size effect, F(5, 75) = 71.63, p < 0.01; condition effect, F(1, 15) = 108.07, p < 0.01; condition × set size interaction, F(5, 75) = 22.74, p < 0.01. No difference was observed in RT (lower right panel in Figure 6D).
Discussion
The combination of high attentional load and high VWM load resulted in considerable interference between the two processes. In the dual-task condition, participants responded more slowly and made many more errors in enumeration. This was apparent even at very small set sizes. VWM performance was also much worse in the dual-task condition, and the disparity was greater with increasing set size.
Experiments 1–4
Results
Dual-task costs were calculated by subtracting the logit transformed percentage error in the corresponding single-task conditions from the logit transformed percentage error in the dual-task condition, for both the attentional and VWM processes in each of the four experiments (Figure 7). The dual-task cost to the attentional process increased significantly with an increased load on attention or VWM (Figure 7A): in a 2 × 2 × 6 (attention × memory × set size) repeated measures ANOVA for the dual-task costs on attention, significant main effect of attentional load change, F(1, 60) = 8.57, p < 0.01; significant main effect of VWM load change, F(1, 60) = 6.12, p < 0.05. Moreover, increasing the load on the VWM process did not produce significantly different effects at the two levels of attentional load: no significant attention × VWM interaction, F(1, 60) = 1.10, p = 0.30. Similarly, the dual-task cost to the VWM process increased significantly with an increase in load on either attention or VWM (Figure 7B): in a 2 × 2 × 6 (attention × memory × set size) repeated measures ANOVA for the dual-task costs on memory, significant main effect of attentional load change, F(1, 60) = 7.61, p < 0.01; significant main effect of VWM load change, F(1, 60) = 29.02, p < 0.01. Increasing the load on the attentional process did not produce significantly different effects on VWM performance at the two levels of memory load: no significant VWM × attention interaction, F(1, 60) = 0.12, p = 0.73. Significance tests on the untransformed percentage of errors yielded the same results.
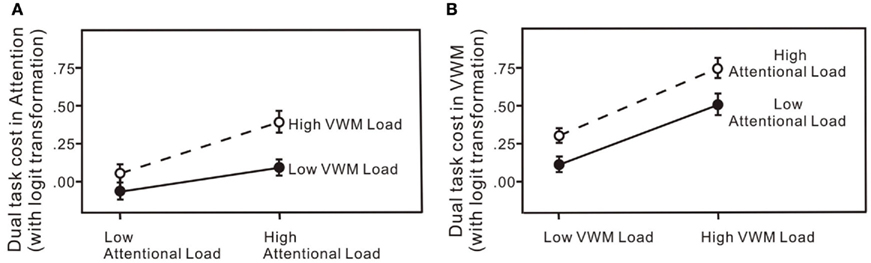
Figure 7. Dual-task costs (percentage error) for: (A) the attentional task across the four experiments; (B) the VWM task across the four experiments. The error bars represent ± 1 SE computed using Loftus and Masson’s (1994) method for within-subject designs.
Discussion
In all four experiments (Figure 6), performance on both the attentional task and the VWM task was worse in the dual-task conditions than in the single-task conditions even with low loads on both attention and working memory (Experiment 1). When the load was increased on one of the processes, accuracies on both declined (Experiments 2 and 3). The greatest interference was observed with high loads on both the attentional and VWM processes (Experiment 4). The critical feature of interest, however, is the pattern of dual-task costs across the four experiments. The patterns of dual-task costs did not yield any significant interaction effects, more consistent with an additive model.
General Discussion
The Dual-Task Costs Approach
Although previous studies have reported interference between attention and VWM in the dual-task paradigm (Awh et al., 1998; Woodman and Luck, 2004), we have introduced a new method of comparing the dual-task costs under both low and high load conditions. The changes in the pattern of dual-task costs showed an increase in interference on both processes when either the attentional or VWM load was increased. More importantly, by independently varying each load, additive reciprocal interference was observed.
Compared to previous load-matching approaches, our dual-task costs approach avoids the difficult issue of how to equalize the loads in different tasks. We focused on how increasing the load on each process in a dual-task influences the dual-task costs, rather than trying to determine whether the costs to one process are comparable to those produced by a different secondary task. Independent loads of increased difficulty on the two processes produced reciprocal, additive interference effects on both processes. Additivity is consistent with a model of shared processing resources. Note that additivity is possible with a partially shared resources model, only under certain restrictive circumstances; that is when an increase in load could produce the same effect (increase) in the partially shared resource and also the separate (unique) processing resources dedicated to the two individual functions (attention and working memory). However, while possible, it seems to us unlikely that the magnitude of the increases in processing in the three separate resources would necessarily be equal.
Varying the set sizes for both tasks from one to six (a greater range than in other studies) also makes it easier to interpret variations in the magnitude of interference. In a dual-task paradigm, if the highest load on one task is lower than the capacity load, part of the load on the other task may be used to occupy most of the processing capacity, resulting in the observed dual-task cost not fully reflecting the real interference. Our VWM–attention dual-task paradigm produced large and easy-to-interpret between-task changes in the dual-task costs incurred by both processes.
Interaction between Attention and Working Memory
In our dual-task paradigm, we positioned the attentional task in the retention interval of the working memory task so that attention had to be diverted to enable the enumeration while simultaneously maintaining the representations of the to-be-remembered objects in memory. A potential criticism is that interference effects could come from any of the sources: (a) the shared processes of attention and working memory encoding (Fusser et al., 2011), (b) the maintenance of feature bindings (Wheeler and Treisman, 2002), (c) the shared mechanisms of attention and “visuospatial rehearsal” (Awh et al., 1998; Awh and Jonides, 2001) in the executive function (Engle, 2002), (d) degraded ability to keep items alive in working memory with a much reduced attentional processing capability (Cowan, 2000). Although our results do not allow us to specify which of these critical shared mechanisms are involved, the increasing, additive interference effects that we observed strongly suggest that attention and VWM share the same processing resources. While it would be premature to rule out categorically the influence of other stage-specific factors, these must play an extremely small role (if any) in constraining the capacities of attention and VWM. Future experimentation would be needed to establish the source(s) of the reciprocal interference. Establishing the overlap between the neural mechanisms of attention and each component of working memory (e.g., Fusser et al., 2011) would be beneficial.
Our data also show the influence of a memory load on subitizing in disjunctive enumeration. Consistent with an attention-demanding mechanism for subitizing (Railo et al., 2008; Vetter et al., 2008, 2011; Burr et al., 2010; Piazza et al., 2011), our result suggests that subitizing accuracy is affected by the amount of attentional resource available. Subitizing was previously thought to reflect a preattentive stage in visual processing (Dehaene and Changeux, 1993), but is now increasingly recognized as an attentional process (Railo et al., 2008; Vetter et al., 2008, 2011). Earlier experiments justified the view that the ability to subitize is not affected by the memory load (Trick and Pylyshyn, 1994), but our new results show that subitizing seems to rely on assistance from working memory. The heavy memory loads in some of our tasks has helped to reveal this phenomenon. It has also been suggested that a sufficiently high load on working memory can result in an increased influence from distractors (Fockert et al., 2001). The evidence that working memory facilitates performance on an attentional task, not only beyond but also within capacity, further strengthens our argument that the capacities in attention and VWM are constrained by the same processing resources.
Conclusion
In sum, the evidence from our examination of performance change using a dual-task paradigm with a load-varying technique supports the shared resource hypothesis. In view of the reciprocal, additive interference observed in the dual-task conditions, it seems very likely that spatial attention and visual working memory are both constrained by the capacity of the same processing resources in the brain.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was supported by Discovery Grants from the Natural Sciences and Engineering Research Council of Canada to Ian Spence and Jay Pratt. This work was completed while Jing Feng was a graduate student in the Department of Psychology, University of Toronto.
References
Alvarez, G. A., and Cavanagh, P. (2004). The capacity of visual short-term memory is set both by visual information load and by number of objects. Psychol. Sci. 15, 106–111.
Averbach, E., and Coriell, A. S. (1961). Short-term memory in vision. Bell Syst. Tech. J. 40, 309–328.
Awh, E., and Jonides, J. (1998). “Spatial selective attention and spatial working memory,” in The Attentive Brain, ed. R. Parasuraman (Cambridge, MA: MIT Press), 353–380.
Awh, E., and Jonides, J. (2001). Overlapping mechanisms of attention and spatial working memory. Trends Cogn. Sci. (Regul. Ed.) 5, 119–126.
Awh, E., Jonides, J., and Reuter Lorenz, P. A. (1998). Rehearsal in spatial working memory. J. Exp. Psychol. Hum. Percept. Perform. 24, 780–790.
Bachelder, B. L. (2000). The magical number 4=7: span theory on capacity limitations. In the Open Peer Commentary section to Cowan, N. (2000). The magical number 4 in short-term memory: a reconsideration of mental storage capacity. Behav. Brain Sci. 24, 87–185.
Baddeley, A. D. (2000). The episodic buffer: a new component of working memory? Trends Cogn. Sci. (Regul. Ed.) 4, 417–423.
Baddeley, A. D. (2003). Working memory: looking back and looking forward. Nat. Rev. Neurosci. 4, 829–839.
Baddeley, A. D., and Della Sala, S. (1996). Working memory and executive control. Philos. Trans. R. Soc. Lond. B Biol. Sci. 351, 1397–1404.
Baddeley, A. D., and Hitch, G. (1974). “Working memory,” in The Psychology of Learning and Motivation, ed. G. A. Bower (New York: Academic Press), 47–89.
Berkson, J. (1944). Application of the logistic function to bio-assay. J. Am. Stat. Assoc. 39, 357–365.
Bleckley, M. K., Durso, F. T., Crutchfield, J. M., Engle, R. W., and Khanna, M. M. (2003). Individual differences in working memory capacity predict visual attention allocation. Psychon. Bull. Rev. 10, 884–889.
Brown, L. A., and Brockmole, J. R. (2010). The role of attention in binding visual features in working memory: evidence from cognitive ageing. Q. J. Exp. Psychol. 63, 2067–2079.
Brown, S. W. (1997). Attentional resources in timing: interference effects in concurrent temporal and nontemporal working memory tasks. Percept. Psychophys. 59, 1118–1140.
Burr, D., Turi, M., and Anobile, G. (2010). Subitizing but not estimation of numerosity requires attentional resources. J. Vis. 10, 1–10.
Cavanagh, P., and Alvarez, G. A. (2005). Tracking multiple targets with multifocal attention. Trends Cogn. Sci. (Regul. Ed.) 9, 349–354.
Cowan, N. (1988). Evolving conceptions of memory storage, selective attention, and their mutual constraints within the human information processing system. Psychol. Bull. 104, 163–191.
Cowan, N. (2000). The magical number 4 in short-term memory: a reconsideration of mental storage capacity. Behav. Brain Sci. 24, 87–185.
Cowan, N. (2005a). On the capacity of attention: its estimation and its role in working memory and cognitive aptitudes. Cogn. Psychol. 51, 42–100.
Cowan, N., and Morey, C. C. (2007). How can dual-task working memory retention limits be investigated? Psychol. Sci. 18, 686–688.
Davis, G., Welch, V. L., Holmes, A., and Shepherd, A. (2001). Can attention select only a fixed number of objects at a time? Perception 30, 1227–1248.
Dehaene, S., and Changeux, J. P. (1993). Development of elementary numerical abilities: a neuronal model. J. Cogn. Neurosci. 5, 390–407.
Delvenne, J. F., and Bruyer, R. (2004). Does visual short-term memory store bound features? Vis. Cogn. 11, 1–27.
Engle, R. W. (2002). Working memory capacity as executive attention. Curr. Dir. Psychol. Sci. 11, 19–23.
Feng, Y., Crosbie, J., Wigg, K., Pathare, T., Ickowicz, A., Schachar, R., Tannock, R., Roberts, W., Malone, M., Swanson, J., Kennedy, J. L., and Barr, C. L. (2005). The SNAP25 gene as a susceptibility gene contributing to attention-deficit hyperactivity disorder. Mol. Psychiatry 10, 998–1005.
Finney, D. J. (1947). Probit Analysis: A Statistical Treatment of the Sigmoid Response Curve. Oxford: Macmillan.
Fockert, J. W., Rees, G., Frith, C. D., and Lavie, N. (2001). The role of working memory in visual selective attention. Science 291, 1803–1806.
Fougnie, D., and Marois, R. (2006). Distinct capacity limits for attention and working memory. Psychol. Sci. 17, 526–534.
Fougnie, D., and Marois, R. (2009). Attentive tracking disrupts feature binding in visual working memory. Vis. Cogn. 17, 48–66.
Funahashi, S., Bruce, C. J., and Goldman-Rakic, P. S. (1989). Mnemonic coding of visual space in the monkey’s dorsolateral prefrontal cortex. J. Neurophysiol. 61, 331–349.
Fusser, F., Linden, D. J., Rahm, B., Hampel, H., Haenschel, C., and Mayer, J. S. (2011). Common capacity-limited neural mechanisms of selective attention and spatial working memory encoding. Eur. J. Neurosci. 34, 827–838.
Hollingworth, A., and Henderson, J. M. (2002). Accurate visual memory for previously attended objects in natural scences. J. Exp. Psychol. Hum. Percept. Perform. 28, 113–136.
Johnson, J. S., Hollingworth, A., and Luck, S. J. (2008). The role of attention in the maintenance of feature bindings in visual short-term memory. J. Exp. Psychol. Hum. Percept. Perform. 34, 41–55.
Jonides, J., Lewis, R. L., Nee, D. E., Lustig, C. A., Berman, M. G., and Moore, K. S. (2008). The mind and brain of short-term memory. Annu. Rev. Psychol. 59, 193–224.
Loftus, G. R., and Masson, M. E. (1994). Using confidence intervals in within-subject designs. Psychon. Bull. Rev. 1, 476–490.
Luck, S. J., and Vogel, E. K. (1997). The capacity of visual working memory for features and conjunctions. Nature 390, 279–281.
Makovski, T., Shim, W. M., and Jiang, Y. V. (2006). Interference from filled delays on visual change detection. J. Vis. 6, 1459–1470.
Mayer, J. S., Bittner, R. A., Nikolic, D., Bledowski, C., Goebel, R., and Linden, D. E. J. (2007). Common neural substrates for visual working memory and attention. Neuroimage 36, 441–453.
McElree, B. (1998). Attended and non-attended states in working memory: accessing categorized structures. J. Mem. Lang. 38, 225–252.
McElree, B. (2006). “Accessing recent events,” in The Psychology of Learning and Motivation, ed. B. H. Ross (San Diego: Academic Press), 155–200.
Nairne, J. S. (2002). Remembering over the short-term: the case against the standard model. Annu. Rev. Psychol. 53, 53–81.
Oh, S.-H., and Kim, M.-S. (2004). The role of spatial working memory in visual search efficiency. Psychon. Bull. Rev. 11, 275–281.
Pasternak, T., and Greenlee, M. W. (2005). Working memory in primate sensory systems. Nat. Rev. Neurosci. 6, 97–107.
Piazza, M., Fumarola, A., Chinello, A., and Melcher, D. (2011). Subitizing reflects visuo-spatial object individuation capacity. Cognition 121, 147–153.
Postle, B. R. (2006). Working memory as an emergent property of the mind and brain. Neuroscience 139, 23–38.
Pylyshyn, Z. W., and Storm, R. W. (1988). Tracking multiple independent targets: evidence for a parallel tracking mechanism. Spat. Vis. 3, 179–197.
Railo, H., Koivisto, M., Revonsuo, A., and Hannula, M. M. (2008). The role of attention in subitizing. Cognition 107, 82–104.
Ranganath, C. (2006). Working memory for visual objects: complementary roles of inferior temporal, medial temporal, and prefrontal cortex. Neuroscience 139, 277–289.
Rouder, J. N., Morey, R. D., Cowan, N., Zwilling, C. E., Morey, C. C., and Pratte, M. S. (2008). An assessment of fixed-capacity models of visual working memory. Proc. Natl. Acad. Sci. U.S.A. 15, 5975–5979.
Schmidt, B. K., Vogel, E. K., Woodman, G. F., and Luck, S. J. (2002). Voluntary and automatic attentional control of visual working memory. Percept. Psychophys. 64, 754–763.
Sears, C. R., and Pylyshyn, Z. W. (2000). Multiple object tracking and attentional processing. Can. J. Exp. Psychol. 54, 1–14.
Söderqvist, S., McNab, F., Peyrard-Janvid, M., Matsson, H., Humphreys, K., Kere, J., and Klingberg, T. (2010). The SNAP25 gene is linked to working memory capacity and maturation of the posterior cingulated cortex during childhood. Biol. Psychiatry 68, 1120–1125.
Treisman, A. M., and Gelade, G. (1980). A feature-intergration theory of attention. Cogn. Psychol. 12, 97–136.
Trick, L. M., and Pylyshyn, Z. W. (1993). What enumeration studies can show us about spatial attention: evidence for limited capacity preattentive processing. J. Exp. Psychol. Hum. Percept. Perform. 19, 331–351.
Trick, L. M., and Pylyshyn, Z. W. (1994). Why are small and large numbers enumerated differently? A limited-capacity preattentive stage in vision. Psychol. Rev. 10, 80–102.
Tuholski, S., Engle, R. W., and Baylis, G. C. (2001). Individual differences in working memory capacity and enumeration. Mem. Cognit. 29, 484–492.
Vetter, P., Butterworth, B., and Bahrami, B. (2008). Modulating attentional load affects numerosity estimation: evidence against a pre-attentive subitizing mechanism. PLoS ONE 3, e3269. doi:10.1371/journal.pone.0003269
Vetter, P., Butterworth, B., and Bahrami, B. (2011). A candidate for the attentional bottleneck: set-size specific modulation of the right TPJ during attentive enumeration. J. Cogn. Neurosci. 23, 728–736.
Wheeler, M. E., and Treisman, A. M. (2002). Binding in short-term visual memory. J. Exp. Psychol. Gen. 131, 48–64.
Woodman, G. F., and Luck, S. J. (2004). Visual search is slowed when visuospatial working memory is occupied. Psychon. Bull. Rev. 11, 269–274.
Keywords: attentional resource, visuospatial working memory, working memory resource, dual-task
Citation: Feng J, Pratt J and Spence I (2012) Attention and visuospatial working memory share the same processing resources. Front. Psychology 3:103. doi: 10.3389/fpsyg.2012.00103
Received: 05 November 2011; Accepted: 20 March 2012;
Published online: 18 April 2012.
Edited by:
Mattie Tops, University of Leiden, NetherlandsCopyright: © 2012 Feng, Pratt and Spence. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Jing Feng, Rotman Research Institute, Baycrest Centre for Geriatric Care, 3560 Bathurst Street, Toronto, ON, Canada M6A 2E1. e-mail:amluZ0Bwc3ljaC51dG9yb250by5jYQ==


