Muscle or motivation? A stop-signal study on the effects of sequential cognitive control

Performance on cognitive control tasks deteriorates when control tasks are performed together with other control tasks, that is, if simultaneous cognitive control is required. Surprisingly, this is also observed if control tasks are preceded by other control tasks, that is, if sequential cognitive control is required. The typical explanation for the latter finding is that previous acts of cognitive control deplete a common resource, just like a muscle becomes fatigued after repeated usage. An alternative explanation, however, is that previous acts of cognitive control reduce motivation to match allocated resources to required resources. In this paper we formalize these muscle and motivation accounts, and show that they yield differential predictions regarding the interaction between simultaneous and sequential cognitive control. These predictions were tested using a paradigm where participants had to perform multiple stop-signal tasks, which varied in their demands on simultaneous and sequential control. Results of two studies supported predictions derived from the motivation account. Therefore, we conclude that the effects of sequential cognitive control are best explained in terms of a reduction of motivation to match allocated to required resources.

Introduction

Cognitive control is essential for optimal everyday functioning. Unfortunately, the capacity for cognitive control is limited, as is evidenced from tasks that require simultaneous use of multiple control functions. For example, stop-signal inhibition deteriorates in tasks that also require inhibition of distracting stimuli (e.g., Verbruggen et al., 2005). Surprisingly, not only simultaneous, but also sequential demands on cognitive control degrade performance (Hagger et al., 2010). For example, stop-signal inhibition deteriorates if a preceding task requires control over food intake (Muraven et al., 2006). The usual account for these effects of sequential cognitive control¹ is that sequential tasks rely on one common resource, just as simultaneous tasks do. This common resource then becomes depleted, as a muscle becomes fatigued after repeated use (Muraven and Baumeister, 2000). However, an alternative account has also been put forward, namely that sequential cognitive control reduces motivation to allocate resources required to meet task demands (Hagger et al., 2010; Robinson et al., 2010).

It is unknown whether the “muscle” or the “motivation” account provides the best explanation for the effects of sequential cognitive control (Baumeister and Vohs, 2007; Hagger et al., 2010; Robinson et al., 2010). In the present paper we therefore aim to test their relative merits. First, we show by means of simple formal modeling, that the muscle and motivation accounts yield differential predictions on the interaction between simultaneous and sequential cognitive control. Second, we test these predictions using a paradigm that varied the demands on both simultaneous and sequential cognitive control. We do this by focusing on a key aspect of cognitive control, namely the ability to inhibit pre-potent motor responses, as assessed in the stop-signal task (Logan and Cowan, 1984; Logan, 1994).

In the stop-signal task, participants are instructed to make a speeded binary response to a go signal, for example participants have to respond left to a left pointing arrow, and right to a right pointing arrow. Shortly after the onset of the go-signal participants occasionally receive a stop signal that requires them to stop the go response. The stop-task yields several informative indices of performance, among which the time required to respond to the go signal (go reaction time, RT), the percentage of choice errors, i.e., responding left if a right-hand response is required and vice versa, and, most importantly, an estimate of the time required to stop the response upon presentation of the stop signal (stop signal reaction time, SSRT, cf. Figure 1). A prolonged SSRT is a reliable index of suboptimal inhibitory performance and thus of impaired cognitive control (Logan and Cowan, 1984; Band et al., 2003).

FIGURE 1

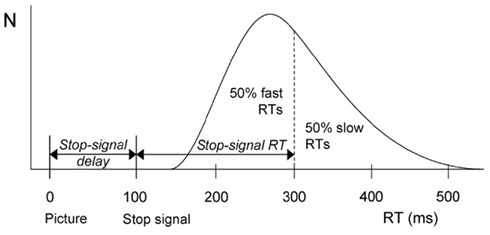
Figure 1. Calculation of stop-signal RT (SSRT) according to the race model (Logan and Cowan, 1984). The black curve depicts the distribution of RTs on go trials (i.e., trials without a stop-change signal) representing the finishing times of the go process. Assuming independence of the go and stop processes, the finishing time of the stop process bisects the go RT distribution. Given that the response could not be stopped on nth percent of all stop-change trials (here at 50%), SSRT (200 ms) is calculated by subtracting the mean stop-change signal delay (100 ms) from the 50th percentile of go RT (300 ms).

The effects of simultaneous demands on cognitive control have been investigated by pairing the stop-signal task with the Eriksen flanker task, the Simon task, and with a spatially incompatible stimulus–response task. In the Eriksen flanker task, a central go stimulus is surrounded by distracting flankers. These flankers can be congruent with the correct response, i.e., both the central target and surrounding flankers indicate the correct response, or they can be incongruent, in which case the incorrect response signaled by the flankers needs to be inhibited (Eriksen and Eriksen, 1974). If the stop task is paired with the Eriksen flanker task, SSRT typically is increased on incongruent trials compared to congruent trials (Kramer et al., 1994; Ridderinkhof et al., 1999). In the Simon task, a go signal is presented at locations that may conflict with the location of the response (Simon, 1969). For example, a left pointing arrow requiring a left hand response is presented at the right side of the screen. If the stop task is paired with the Simon task, SSRT will increase on conflict trials (Verbruggen et al., 2005). On a spatially incompatible stimulus–response task participants have to execute a left hand response to a right pointing arrow and vice versa. Logan and Irwin (2000) observed an increased SSRT for incompatible as compared to compatible responses, but only for eye movements and not for hand movements. van den Wildenberg and van der Molen (2004a,b) also observed a prolonged SSRT for incompatible as compared to compatible responses, but only on a selective stop task, when participants had to inhibit to one stop signal and not to another. Finally, Morein-Zamir et al. (2006) showed, using an alternative paradigm, that inhibition deteriorated if stimulus–response mappings were spatially incompatible. In sum, these studies indicate that SSRT increases if the stop-signal task is paired with another task that also requires cognitive control, although there is mixed evidence for the combined effects of stopping and stimulus–response incompatibility.

The effects of sequential cognitive control are generally investigated by comparing performance under two conditions. In the “depletion” condition participants perform a cognitive control task that is preceded by another cognitive control task. In the “non-depletion” condition participants perform a cognitive control task that is preceded by a task that does not require cognitive control. For example, inhibition of emotional expression is assessed after participants either performed a “depleting” memory updating task or a “non-depleting” memory maintenance task (Schmeichel, 2007). A recent meta-analysis indicated that the effects of sequential cognitive control are very robust: previous acts of cognitive control diminish performance on a variety of subsequently executed cognitive control tasks (Hagger et al., 2010). It is commonly assumed that effects are limited only to subsequent tasks that require cognitive control whereas performance on subsequent tasks that do not require cognitive control is not affected (e.g., Baumeister et al., 1998). Effects are most pronounced for tasks that require “hot” control over emotional responses (Hagger et al., 2010), although a subset of studies also report effects on “cold” control, as is required in the stop-signal task (e.g., Muraven et al., 2006).

While the deleterious effects of sequential tasks requiring cognitive control are quite robust, the underlying mechanism is still unknown. Both a “muscle” and a “motivation” account have been proposed. The standard explanation, the muscle account, states that previous acts of cognitive control deplete a common resource (Muraven and Baumeister, 2000). This account provides a parsimonious explanation for the wealth of studies that find effects of sequential cognitive control. The alternative motivation account states that previous acts of cognitive control reduce motivation to allocate resources to meet current task demands (Hagger et al., 2010; Robinson et al., 2010). Consistent with this interpretation, it has been shown that increasing motivational incentives reduces the detrimental effects of sequential cognitive control (Muraven and Slessareva, 2003). In addition, these effects are reduced if motivation is primed (Martijn et al., 2007) or if the depleting task is intrinsically motivating (Muraven et al., 2008). Thus the motivation account may provide a viable alternative to the muscle account. The aim of the present paper therefore is to test the relative merits of the muscle and motivation account. In order to do so, we first derive simple formal models of these two competing accounts.

Simple Formal Models of Muscle and Motivation Accounts

In this section, we derive simple formal models for the muscle and motivation accounts. We do this by considering the situation in which participants have to perform two versions of the stop-signal task that vary both in their demands on simultaneous control and in their demands on sequential control. We will show that the muscle and motivation accounts yield differential predictions regarding the interaction between simultaneous and sequential cognitive control.

Demands on simultaneous control were manipulated by having participants perform a task using a compatible stimulus–response mapping and a task with an incompatible mapping; the latter task thus requires simultaneous cognitive control (Logan and Irwin, 2000; van den Wildenberg and van der Molen, 2004a,b; Morein-Zamir et al., 2006). Task order was randomized between participants. The factor Task is dummy coded as 0 (compatible task) and 1 (incompatible task). Presentation order is denoted by the factor Order, which is dummy coded as 0 (first task) and 1 (second task)².

A common assumption in resource theory (e.g., Kahneman, 1973; Sarter et al., 2006; Pessoa, 2009) is that cognitive control performance will decrease if allocated resources do not meet required resources. This assumption is supported by studies in which allocated resources were manipulated, for example by requiring simultaneous cognitive control (e.g., Kramer et al., 1994; Ridderinkhof et al., 1999; Logan and Irwin, 2000; van den Wildenberg and van der Molen, 2004a,b; Verbruggen et al., 2005; Morein-Zamir et al., 2006). We therefore assume that SSRT, an index of cognitive control, will increase if allocated resources do not meet required resources:

$\text{SSRT} = \beta 0 + (\text{required resource} - \text{allocated resource),}$(1)

where the constant β0 denotes SSRT if there is a perfect match between required and allocated resources. Note that we assume that SSRT is a linear function of the discrepancy between required and allocated resources. We might have assumed a non-linear function f: SSRT = β0 + f (required resource-allocated resource). However, the functional form of the relationship between resources and performance is difficult to determine. More specifically, there is no evidence to suggest an adequate functional form for the relationship between resources and SSRT (e.g., Norman and Bobrow, 1975; Logan, 1997). Therefore we assume, for reasons of convenience, a linear function.

The required resource in Eq. 1 is a function of task:

$\text{Required resource} = \beta 1 + \beta 2 * \text{Task}.$(2)

Since Task is dummy coded as 0 (compatible) and 1 (incompatible), β1 denotes the resource required for the compatible task and β2 denotes the task effect, which is expected to be positive. That is, incompatible tasks are expected to require more resources than compatible tasks.

Both the muscle and the motivation accounts share the assumptions underlying Eqs 1 and 2, yet they differ in their assumptions concerning allocated resources. The muscle model assumes that either task order or the control demands of the previous task affect allocated resources. The motivation model assumes that task order affects the motivation to match allocated resources to required resources. We will show that these assumptions yield mutually exclusive predictions on the interaction between task and order.

Muscle Model

The meta-analysis by Hagger et al. (2010) indicates that the effects of sequential cognitive control mainly originate in the fact that a cognitive control task is preceded by another cognitive control task, the control demand of this preceding task is of no influence. However, a meta-analysis is necessarily based on a between study comparison of demanding and less demanding depleting tasks. Such a between study comparison may not be very powerful, and therefore we will account for the possibility that control demands of the previous task are of influence. That is, we present two muscle models. In the first muscle model, consistent with Hagger et al., task order affects allocated resources. In the second muscle model, cognitive control demands of previous tasks affect allocated resources.

Muscle model 1: Task order affects allocated resources

In the first muscle model, Order determines the amount of resources allocated to the current task:

$\text{Allocated resource} = \beta 3 + \beta 4 * \text{Order}.$(3)

Since Order is dummy coded as 0 (first task) and 1 (second task), β3 is the allocated resource in the first task and β4 the Order effect, which is expected to be negative; that is, less resources are allocated to the second as compared to the first task. Substitution of Eqs 2 and 3 into (1) yields:

$\text{SSRT} = \left(\beta 0 + \beta 1 - \beta 3\right) + \beta 2 * \text{Task} - \beta 4 * \text{Order}.$(4)

This model thus predicts a main effect of Task, a main effect of Order, yet no interaction. That is, Task effects do not increase or decrease with increasing Order.

Muscle model 2: Control demand preceding task affects allocated resources

In the second muscle model, the control demand of the preceding task determines resources allocated to the current task. By design, a demanding task is necessarily preceded by a less demanding task, and therefore receives relatively high resources, whereas a less demanding task is preceded by a demanding ask, and thus receives relatively low resources. Consequently, this model predicts that task effects decrease with increasing Order.

More specifically, allocated resource is a function of the control demands of the previous task, therefore, we do not only have to include an effect of Order as in Eq. 3, but also an interaction effect of Order and Task:

$\text{Allocated resource} = \beta 5 + \beta 6 * \text{Order} + \beta 7 * \text{Order} * \text{Task}$(5)

Remember, Order is dummy coded as 0 (first task) and 1(second task), Task is dummy coded as 0(compatible) and 1(incompatible). Therefore, β5, denotes resources allocated to the first task, this parameter is expected to be positive. The parameter β6 denotes the order effect (if the current task is compatible), it is expected that less resources are allocated to a second as compared to a first task, therefore this parameter is expected to be negative. The parameter β7 is the additional order effect if the current task is incompatible. Since the incompatible task is preceded by the less demanding compatible task, this parameter is expected to be positive.

Substituting of Eqs 5 and 2 into 1 yields:

$\text{SSRT}=\beta 0+(\beta 1+\beta 2*\text{Task)}-(\beta 5+\beta 6*\text{Order}+\beta 7*\text{Order}*\text{Task)}$

That is:

$\text{SSRT}=\beta 0+\beta 1-\beta 5+\beta 2*\text{Task}-\beta 6*\text{Order}-\beta 7*\text{Order}*\text{Task}$(6)

This model thus predicts main effects of Task and Order and an interaction between Task and Order. Since β2 is expected to be positive and (−β7) is expected to be negative, it is expected that Task effects will decrease with increasing Order.

Motivation Model

Baumeister and Vohs (2007) indicated that motivation is required on cognitive control tasks “to achieve the goal or meet the standard.” We therefore assume that a motivated individual will try to match allocated resources to required resources. More specifically, we assume that allocated resources are a proportion of required resources, and that this proportion increases with increasing motivation.

Robinson et al. (2010) argued that performing one cognitive control task may reduce motivation to allocate resources to a second cognitive control task. This is supported by the observation that the detrimental effects of sequential cognitive control are reduced in the presence of extrinsic or intrinsic motivation (Muraven and Slessareva, 2003; Muraven et al., 2008) or if motivation is primed (Martijn et al., 2007). We therefore assume that motivation to allocate resources decreases with increasing task order.

Given these assumptions, allocated resources are a fraction of required resources, where this fraction decreases with increasing Order. More specifically:

$\begin{array}{llll}\text{Allocated resource}& = \beta 8 * \text{required resource}& & \\ & + \beta 9 * \text{required resource} * \text{Order}& & \text{(7)}\end{array}$

Since Order is dummy coded as 0 (first task) and 1 (second task), β8 denotes the fraction of required resource allocated to the first task, which is between zero and one, and β9 denotes the Order effect on this fraction, which is expected to be between −1 and 0. Required resource is defined in Eq. 2, its substitution into Eq. 7 yields:

$\begin{array}{l}\text{Allocated resource} = \beta 8*(\beta 1 + \beta 2*\text{Task})\\ + \beta 9*(\beta 1 + \beta 2*\text{Task})*\text{Order}\end{array}$(8)

Substitution of Eqs 2 and 8 into 1 yields:

$\begin{array}{l}\text{SSRT}=(\text{β0 + β1 - β8 * β1}) + \text{β2 * (1 - β8) * Task}\\ -\text{β9 * β1 * Order - β9 * β2 * Task * Order}\end{array}$(9)

That is, this model predicts a main effect of Task, a main effect of Order, and an interaction between Task and Order. Since all coefficients are expected to be positive except for β9, which is expected to be negative, Task effects are predicted to be most pronounced for the second task. That is, the motivation model predicts an interaction between Task and Order: Task effects increase with increasing Order.

Study 1

Although all models predict main effects of Task and Order, they differ in their predictions concerning the interaction of Task and Order. The first muscle model predicts that an interaction is absent, the second muscle model predicts that Task effects decrease with increasing Order, whereas the motivation model predicts that Task effects increase with increasing Order.

In study 1 we tested these predictions by having participants perform on three consecutive stop-signal tasks that varied in their demands on simultaneous cognitive control; a compatible stop task, an incompatible stop task, and a stop task in which the mapping between stimulus and response is arbitrary. The latter task was included to increase variation in both task and order and, thus, to increase the power of tests of their main and interaction effects.

Study 1 – Methods

Participants

Thirty-four young healthy adults (23 women and 11 men, M Age = 21.10 SD = 3.78 years) participated in this experiment for course credit or a financial reward. All participants provided informed consent. The study was approved by the local ethics committee.

Stop-signal task

The experimental task was programmed using Presentation® software (Neurobehavioral Systems, www.neurobs.com). Participants were instructed to respond quickly and accurately in response to the identity of white, 8 mm high, go stimuli that were centrally presented against a gray screen background (go trials). Manual responses were made by pressing the “z” or “?” keys of the QWERTY computer keyboard with the left and right index finger, respectively.

Study 1 consisted of a 1-h 30 session in which participants completed three versions of the stop-signal paradigm (Logan and Cowan, 1984; Logan, 1994). Under the compatible and incompatible conditions, the go stimuli consisted of left and right pointing brackets (“<” and “>”), whereas the arbitrary go task incorporated X and O stimuli. Participants were instructed to respond with the hand indicated by the bracket (compatible task), or to respond with the other hand (incompatible task). In the arbitrary task, subjects pressed left to an O and right to an X (or vice versa). Order of the three conditions was counterbalanced between participants.

Go stimuli were presented pseudo-randomly, with the constraint that they signaled left- and right-hand responses equally often. The presentation of go signals was response-terminated or presented with a maximum of 1975 ms. Intervals between subsequent go signals varied randomly but equiprobably, from 1525 to 1975 ms in steps of 50 ms. During these inter-stimulus intervals, a white fixation cross (3 mm in diameter) was presented.

Unpredictably, the white go-signal changed to red on 25% of the trials, upon which the response had to be inhibited (stop trials). A staircase-tracking procedure dynamically adjusted the delay between the onset of the stop signal to control inhibition probability (Levitt, 1971). That is, after a successfully inhibited stop trial, stop-signal delay on the next stop trial increased by 50 ms, whereas the stop-signal delay decreased by 50 ms on the next stop trial when the participant was unable to stop. The initial stop-signal delay was set to 200 ms, the minimum and maximal delay were 50 and 950 ms respectively. This algorithm ensured that responses were successfully inhibited in about half of the stop trials.

Stop signal reaction time was estimated using the integration method (Logan, 1994; Band et al., 2003, p. 215; cf. Figure 1). Estimation of SSRT relies on the race model which assumes independence between going and stopping processes (Logan and Cowan, 1984). If the latency of go-signal processing is affected by stop-signal processing, then the assumption of “functional” or “context” independence is violated (e.g., Logan, 1994; Ridderinkhof et al., 1999; Band et al., 2003). Simulation studies by Band et al. (2003) showed that the race model yields reliable estimates of SSRT despite context dependence between stopping and going (cf., Ridderinkhof et al., 1999). The premise of “stochastic” independence seems more critical (Logan and Cowan, 1984; Logan, 1994). Stochastic independence refers to the condition that stopping and going are not correlated (i.e., go RT and SSRT are independent random variables). Again, extensive simulation studies performed by Band et al. (2003) demonstrated that the race model is quite robust, even against violations of stochastic independence.

Each of the three stop-task versions consisted of five blocks of 96 trials, the first of which served as a practice block to obtain stable performance. This is especially important to avoid negative carry-over effects between compatible and non-compatible tasks. After each block, mean go RT, SD of mean go RT, percentage correct responses and percentage unsuccessful inhibitions were presented on screen. To ensure that the tracking algorithm worked properly, participants were given additional feedback when the percentage of failed inhibition was below 30% or above 70%. In case failed inhibits were below 30% participants were instructed to react as fast as possible to go stimuli. In case of failed inhibits above 70% participants were instructed to keep reacting as fast as possible to the go stimuli, but also to try and withhold their response to the stop stimuli.

Data analysis

The dependent variable of primary interest was SSRT. In addition we analyzed go RT and the percentage of choice errors. The latter two dependent variables were included to test the assumption that effects of order are limited to a decline in cognitive control processes and do not extend to more basic processes like responding to the go stimulus (Baumeister et al., 1998). Task and Order served as independent variables. The design cannot be analyzed using a regular factorial repeated measures ANOVA since each task is only administered once, i.e., there would be many missing values. This design can be analyzed, however, in a straightforward manner by a multilevel analysis (e.g., Snijders and Bosker, 1999) as implemented in SPSS MIXED³. All statistical tests were two-tailed.

Study 1 – Results

No SSRT outliers (below or above 3 SD’s of the mean) were present and therefore all data were analyzed. Analyses included the factors Task and Order and their two-way interaction.

Figure 2, left hand panel, shows SSRT as a function of Task and Order. There was a main effect of Task [F(2, 24.5) = 3.57, p = 0.04]. SSRT was prolonged on arbitrary (p = 0.03) and incompatible tasks (p = 0.02) as compared to the compatible task, with no further differences between tasks. There was a main effect of Order [F(2, 66.34) = 4.36, p = 0.02], SSRT was increased for order 3 (p < 0.01) as compared to order 1, with no further significant differences. The crucial interaction between Task and Order was not significant [F(4, 62.54) = 1.04, p = 0.39]. However, follow-up tests for each level of Order, separately, indicated that a Task effect was only present at order 3 [F(2, 21.24) = 4.87, p = 0.02]⁴. That is, for order 3 SSRT was increased for the incompatible task (p = 0.02) and the arbitrary task (p = 0.04) as compared to the compatible task, with no further differences between tasks (cf. Figure 2). In sum, these results indicate that SSRT lengthened on arbitrary and incompatible tasks (Task effect) and that SSRT was enhanced for the final task relative to the preceding tasks (Order effect). The results indicate that the Task effect was only present for order 3, although the omnibus Task*Order interaction effect was not significant.

FIGURE 2

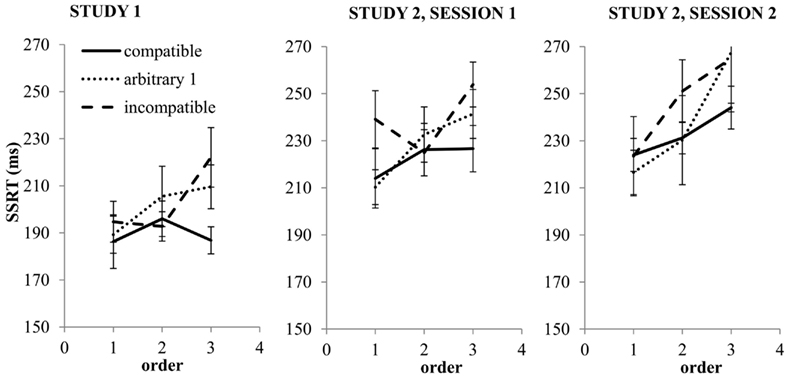
Figure 2. Mean SSRT (error bars denote ± 1 SEM) as a function of Task (compatible, arbitrary 1 or incompatible) and as a function of task order (either first, second, or third task). The left hand panel concerns study 1, the middle panel study 2, session 1 and the right-hand panel study 2, session 2.

There was a main effect of Task on go RT [F(2, 32.59) = 12.11, p < 0.01]. Go RT was longer for the arbitrary task, as compared to the compatible (p < 0.01) and incompatible (p < 0.01) task, with no further differences between tasks. There was a main effect of Order [F(2, 62.26) = 5.69, p < 0.01], Go RT was shorter for order 3, as compared to order 2 (p < 0.01) and order 1 (p = 0.02), while the latter two did not differ. The interaction between Task and Order was not significant [F(4, 56.57) = 1.81, p = 0.14]. Follow-up tests for each level of Order separately, yielded no effects of Task.

There was a main effect of Task on percentage of choice errors [F(2, 33.77) = 6.03, p = 0.01], this percentage was higher for arbitrary (p = 0.01) and incompatible (p < 0.01) tasks as compared to the compatible task, with no further differences between tasks. There was no main effect of Order [F(2, 39.91) = 1.40, p = 0.26], nor an interaction between Task and Order [F(4, 55.71) = 0.07, p = 0.99].

In sum, the results on go RT and percentage of choice errors indicate that the basic go process is not affected by increasing Order. On the contrary, go RT was shortest on the final task while accuracy was maintained.

Study 1 – Discussion

The two muscle models and the motivation model yield differential predictions on the interaction between Task and Order. The first muscle model, assuming that allocated resources depend on task order, does not predict such an interaction. The second muscle model, assuming that allocated resources depend on the cognitive control demands of the previous task, predicts that task effects decrease with increasing order. The motivation model, in which task order determines the motivation to match allocated resources to required resources, predicts that task effects increase with increasing order.

The results of Study 1 do not support the second muscle model. Consistent with the meta-analytic results of Hagger et al. (2010), the effects of sequential cognitive control do not depend on the cognitive control demands of the previous task. The results of Study 1 do not allow for a decisive conclusion regarding the relative merits of the first muscle model and the motivation model. As predicted by the first muscle model, the omnibus interaction between Task and Order was absent. However, as predicted by the motivation model, follow-up analyses did indicate that Task effects on SSRT were most pronounced, and actually were only present, for the third task.

Stop signal reaction time did not only lengthen if the stimulus response mapping was incompatible as compared to compatible, but also when the mapping was arbitrary (i.e., respond left to O and respond right to X). Two explanations have been put forward for the observation that arbitrary mappings are more difficult to inhibit than compatible mappings (Huizenga et al., 2009). First, an arbitrary mapping may initially activate competing responses associated with both hands, responses that need to be inhibited until the appropriate mapping is determined. On stop trials, this inhibitory mechanism then competes with stop-signal inhibition for common resources. Second, maintenance of an arbitrary stimulus–response rule in memory may require cognitive control resources in addition to the resources needed for stopping. Maintenance of an arbitrary rule then competes with inhibitory functioning for common resources. Note however, that maintenance of information in memory is generally not considered as a component of cognitive control, in contrast to the manipulation of information in memory. For example, digit span forward, which only requires maintenance, is not considered as a cognitive control task, whereas digit span backward, which requires manipulation, is considered as a cognitive control task (e.g., Schmeichel, 2007). Therefore the second interpretation offered above is not very plausible. Notwithstanding this theoretical argument, it still is necessary to test these two explanations empirically.

Study 2

The first study did not yield conclusive evidence supporting the first muscle model vs. the motivation model. That is, an omnibus interaction effect of Task and Order was lacking, supporting the first muscle model, whereas follow-up tests did indicate that Task effects were only present for order 3, supporting the motivation model. The absence of an omnibus interaction effect on SSRT might be due to the fact that our compatibility manipulation was not very effective. Participants were required to respond to the direction indicated by centrally presented arrows (i.e., symbolic mapping manipulation) rather than the location of the stimulus itself; e.g., left- vs. right-positioned stimuli requiring a left vs. right response, or vice versa (i.e., spatial mapping manipulation). A spatial mapping manipulation might yield more pronounced differences between compatible and incompatible tasks (cf. Logan and Irwin, 2000, eye movement condition).Therefore, in our second study we used a spatial mapping manipulation. If this stronger manipulation does not yield an interaction between Task and Order, this will provide evidence for the first muscle model. If it does yield an interaction, more specifically, if Task effects increase with increasing Order, this will yield evidence for the motivation model.

The first study indicated that arbitrary stimulus response mappings were more difficult to inhibit than compatible mappings. This might be due to the fact that arbitrary mappings require cognitive control resources to inhibit competing responses until the mapping is determined. Alternatively, it might be due to the fact that cognitive control resources are required to maintain a mapping in memory. In order to further investigate this issue, we employed in our second study an additional manipulation that increased memory load but did not increase response competition. That is, the arbitrary condition was now extended to include three levels in which either one, two, or three characters were mapped to each response hand. If this manipulation does not affect SSRT, it provides evidence for the response competition explanation. If this manipulation would affect SSRT, it provides support for the memory explanation.

Our second study thus featured five stop-signal tasks: a spatial compatible task, a spatial incompatible task and three arbitrary tasks that differed in memory load. These tasks were presented in two sessions on separate days. Inclusion of two sessions allows for an additional test of the muscle vs. motivation models. According to muscle models, resources would be replenished at the beginning of the second session, since people had the opportunity to rest (Tyler and Burns, 2008) and to eat (Gailliot et al., 2007). Therefore a session effect, more specifically, a decrease in cognitive control performance in the second session is inconsistent with a muscle model. Such a finding would, however, not necessarily be inconsistent with the motivation model, since motivation may still decrease between sessions.

In sum, in our second study we addressed three questions. First, we investigated whether task effects on SSRT increase with increasing order. If so, this would provide evidence for the motivation model. Second, we investigated whether arbitrary memory load affects SSRT. If so, this would provide evidence for the memory maintenance, instead of response competition, explanation of difficulties in inhibiting arbitrary mappings. Finally, we determined whether session affects SSRT. If so, this will provide additional evidence for the motivation model.

Study 2 – Methods

Participants

Forty-one young healthy adults (25 women and 16 men, M Age = 22.95 SD = 6.01 years) participated in this experiment for course credit or a financial reward, they did not participate in Study 1. All participants provided informed consent. The study was approved by the local ethics committee.

Stop-signal task

Task characteristics are similar to those of Study 1, except for the following modifications. Participants performed five stop-signal tasks. In the spatially compatible task, go stimuli consisted of a + sign presented either 1.6 cm left or right of fixation point, and participants were instructed to execute a spatially compatible response. The same stimuli were used in the spatially incompatible task but participants were then instructed to execute a spatially incompatible response. In the arbitrary task with a memory load of 1, an X or O was presented, were each character was mapped on one response hand. In the arbitrary task with a memory load of 2, an H and S were mapped on one response hand and a W and T on the other response hand. In the arbitrary task with a memory load of 3 an M, Y, and U were mapped on one response hand and an A, I, and V on the other. All characters were symmetrical along the vertical axis, and thus unrelated to response side.

Stop-task version (compatible, arbitrary 1, arbitrary 2, arbitrary 3 and incompatible) was counterbalanced between subjects. The experiment consisted of two sessions on separate days. Participants were free to choose whether they would perform two or three tasks during the first session.

Data analysis

The data analysis proceeded along the same lines as in Study 1. Again we did not only analyze SSRT, but also go RT and percentage of choice errors, to determine whether effects of sequential cognitive control were confined to cognitive control processes (SSRT) or extended to more primary processes (Go RT and percentage of choice errors).

Study 2 – Results

Data of three participants were removed because SSRT exceeded 3 SD around the mean⁵. The analysis included effects of Task (five levels), Order (three levels), Session (two levels), and their two and three way interactions.

Figure 2, middle and right-hand panel, depicts SSRT as a function of Task, Order, and Session. There was a main effect of Task on SSRT [F(4, 47.69) = 3.91, p < 0.01]. SSRT was longer for the incompatible task, as compared to the compatible task (p < 0.01), the arbitrary 2 task (p = 0.02), and the arbitrary 3 task (p < 0.01). All other differences between tasks were non-significant. More specifically, and important for our second question, the arbitrary tasks did not differ significantly from each other (all p-values >0.1). There was a main effect of Order [F(2, 99.10) = 16.54, p < 0.01]. SSRT tended to be longer for Order 2 than Order 1 (p = 0.09) and was longer for Order 3 as compared to Order 2 (p < 0.01) and Order 1 (p < 0.01). Important for our third question, there was a Session effect; SSRT was longer for the second as compared to the first session [F(1, 119.14) = 26.29, p < 0.01]. Crucially for our first question, there was an interaction effect between Task and Order [F(8, 68.74) = 3.11, p < 0.01]. Follow-up tests for each level of Order, separately, indicated that there was no Task effect associated with Order 1 [F(4, 10.88) = 1.86, p = 0.19] nor for Order 2 [F(4, 10.27) = 2.36, p = 0.12], but there was a nearly significant Task effect for Order 3 [F(4, 14.39) = 2.87, p = 0.06]. Follow-up tests for Order 3 indicated that SSRT associated with the incompatible task was significantly lengthened as compared to the compatible task (p = 0.04) and the arbitrary 2 (p < 0.01) and arbitrary 3 (p = 0.02) tasks. In addition, SSRT on the arbitrary 1 task was significantly longer as compared to the arbitrary 2 task (p = 0.04), with no further differences between tasks. All other interactions were non-significant.

To summarize, these results indicate that Task effects on SSRT increase with increasing Order, yielding support for the motivation model. Second, arbitrary memory load does not affect SSRT, yielding support for the response competition explanation of prolonged SSRT for arbitrary mappings. Third, there was a pronounced session effect, which provides further evidence for the motivation model.

Obviously, there was a main effect of Task on go RT [F(4, 44.22) = 52.80, p < 0.01]. Go RT was longer on the incompatible task than on the compatible task (p < 0.01), and was longer on arbitrary tasks than on the incompatible and compatible tasks (all ps < 0.01). Go RT increased with arbitrary memory load (all ps < 0.01), except for the difference between the arbitrary 2 and arbitrary 3 condition, which was not significant. The main effect of Order did not reach significance [F(2, 105.66) = 2.61, p = 0.08]. Follow-up tests indicated, however, that Go RT was significantly longer on the first as compared to the third task (p < 0.01). Go RT was also significantly longer in the first as compared to the second session [F(1, 113.27) = 8.90, p < 0.01]. All other interactions were not significant.

Obviously, there was a main effect of Task on the percentage of choice errors [F(4, 45.37) = 17.81, p < 0.01]. Percentage of errors was higher on the arbitrary than on the compatible and incompatible tasks (all ps < 0.01) and increased with arbitrary memory load (all ps < 0.05), except for the arbitrary 2 and arbitrary 3 condition, which did not differ significantly. There were no significant main effects of Order nor of Session. There was, however, a significant interaction between Task and Order [F(8, 70.04) = 2.59, p = 0.02]. Follow-up tests for each level of Order, separately, indicated that task effects were present at each level. All other interactions were not significant.

In sum, the results for go RT and percentage of choice errors indicate that repeated sequential control, either within or between sessions, does not degrade Go Task performance. On the contrary, go RT decreased from Order 1 to Order 3, and from Session 1 to Session 2. This speeding of responses was not accompanied by an increase in the percentage of choice errors.

General Discussion

Two explanations have been put forward for the recurrent finding that performance on cognitive control tasks is degraded if such tasks are preceded by other tasks that also require cognitive control. The muscle account states that a common resource is depleted, just as a muscle becomes fatigued, after repeated usage. The motivation account states that repeated acts of cognitive control reduce motivation to match allocated resources to required resources.

The current study demonstrates that these two accounts can be tested using a paradigm where the demands on simultaneous and sequential cognitive control are varied systematically, that is, where both the factor task and the factor order are manipulated. We have formulated two muscle models, one in which allocated resources depend on order and one in which allocated resources depend on the cognitive control demand of previous tasks. In addition we have formulated a motivation model in which the motivation to match allocated resources to required resources is affected by order. We have shown that these three models yield differential predictions on the interaction between task and order. More specifically, the first muscle model does not predict an interaction, the second muscle model predicts that task effects decrease with increasing order, and the motivation model predicts that task effects increase with increasing order. Thus this formalization offered the possibility to test the relative merits of muscle and motivation accounts.

In addition, we have argued that the muscle and motivation account yield different predictions on the effects of cognitive control tasks performed in two separate sessions. A decrease in cognitive control performance over sessions would be inconsistent with the muscle account, whereas it would not necessarily be inconsistent with the motivation account, thus offering an additional test of the relative merits of these two accounts.

These predictions were tested in two studies where participants had to perform a series of stop-signal tasks varying in their demands on simultaneous cognitive control. The advantage of the stop-signal task over other cognitive control tasks is that it does not only yield an index of cognitive control functioning (SSRT), but also yields indices of more basic processes (go RT and percentage of errors). In this manner it is possible to assess whether the effects of sequential cognitive control are confined to control processes or extend also to more basic go processes.

The first study did not yield a significant task by order interaction on SSRT, supporting the muscle account, yet it did indicate that task effects were most pronounced on the final task, supporting the motivation account. The task by order interaction was present in the second study: as predicted by the motivation account, task effects increased with increasing order. In addition, the second study allowed for a test of session effects, which indicated that SSRT was prolonged during the second as compared to the first session, which provides additional evidence for the motivation account.

Collectively, these results suggest that the effects of sequential cognitive control are better explained by the motivation account than by the muscle account. This is in line with studies observing negligible effects of sequential cognitive control under conditions where motivation was enhanced or primed (Muraven and Slessareva, 2003; Martijn et al., 2007; Muraven et al., 2008) see also (Hagger et al., 2010; Robinson et al., 2010). Together these results suggest that it is more likely that the effects of sequential cognitive control originate in a depletion of motivation to match allocated resources to required resources, than in a mere depletion of resources itself.

It might be argued that the effects of order on inhibition are not due to the effects of sequential cognitive control, but rather to carry-over effects between sequential compatible and incompatible tasks. However, this alternative explanation is not very plausible. First, we trained participants before each task, to rule out carry-over effects. Second, if such negative carry-over effects would be present, this should be evidenced by a lengthening of go RT with increasing task order, which was not the case. Third, effects of order were present also for the arbitrary task, which cannot be affected by negative carry-over effects of stimulus–response mapping rules.

It might also be argued that the effects of order on inhibitory performance are related to automatization of primary task performance, as go RT decreased with order. That is, repeated presentation of a stimulus–response mapping can result in automatic associations that may be more difficult to inhibit (Schneider and Shiffrin, 1977). However, it has been shown that automaticity of stimulus–response mappings does not interfere with response inhibition as assessed by SSRT (Logan, 1982; Cohen and Poldrack, 2008). In addition, in our studies, stimulus–response mappings differ between tasks, therefore it is not very likely that associations became automatic. Therefore we do not consider it very likely that this alternative explanation in terms of automaticity holds.

In addition to our main finding, four other findings are worth mentioning. First, the results from both studies indicate that the detrimental effects of order and session on cognitive control performance (SSRT) are not paralleled by effects on more basic processes as indexed by go RT and error proportion. This provides evidence for the common assumption that the effects of sequential cognitive control are confined to cognitive control processes and do not extend to more basic processes (e.g., Baumeister et al., 1998).

Second, we tested two explanations for the Study 1 finding that arbitrary mappings were more difficult to inhibit than compatible mappings. First, an arbitrary mapping may require cognitive control resources to maintain a mapping in memory. Second, an arbitrary mapping may require cognitive control resources to inhibit both response hands until the mapping is determined. The results support the second explanation since SSRT was not affected by a manipulation of memory load. Note, however, that in our second study, employing a spatial instead of a symbolic manipulation of compatibility, arbitrary mappings were not more difficult to inhibit than compatible mappings. This suggests that stopping responses to spatially compatible stimuli takes longer than stopping responses to symbolically compatible stimuli, a suggestion, which should be addressed in future empirical studies.

Third, SSRT was longer on incompatible as compared to compatible tasks. In previous studies, effects of stimulus response compatibility on SSRT were only found in relatively demanding situations, such as for inhibition of eye and not for hand movements (Logan and Irwin, 2000) and for selective and not for non-selective inhibition (van den Wildenberg and van der Molen, 2004a,b). In the present study we only observed significant effects of compatibility in the third task. This finding together with previous findings indicates that effects of stimulus response compatibility on SSRT only become evident in demanding situations.

Fourth, although the task, order, and interaction effects in the first and second study are qualitatively similar, SSRT seems to be prolonged in the second study, even in its first session (cf. Figure 2, compare left and middle panel). Since studies differed in the number of tasks, a potential explanation for this finding is that participants may allocate less resources, yielding a prolonged SSRT, if the number of prospective tasks increases (cf. Muraven et al., 2006; Tyler and Burns, 2009).

The current results have several broader implications. First, the present studies indicate that effects of sequential cognitive control can be found in a relatively “cold” cognitive control task, the stop-signal task. The effects are therefore not limited to tasks that are commonly used in resource depletion studies, i.e., “hot” tasks that require control over emotional responses. Second, the present results indicate that order is an important factor that should be considered in experimental studies that employ a within subjects design. That is, order may introduce variation that, if not accounted for in the analysis, may lower the power of statistical tests. The present study demonstrates that it is very easy to account for order, provided that one is willing to switch from a regular repeated measurements ANOVA to a multilevel analysis. Third, the finding that order has such a profound effect on cognitive control performance, has important implications for neuropsychological assessment, where patients often have to perform a battery of cognitive control tasks. It seems worthwhile to tailor statistical procedures for neuropsychological assessment (i.e. Huizenga et al., 2007) to account for such order effects. Finally, the important role of motivation warrants future experimental studies in which motivation is manipulated and prompts future studies in populations characterized by motivational deficits, for example in children with ADHD (e.g., Slusarek et al., 2001).

To conclude, two explanations have been proposed for the robust finding that repeated acts of cognitive control degrade performance. The muscle account states that repeated acts of cognitive control deplete resources, whereas the motivation account states that repeated acts of cognitive control reduce motivation to match allocated to required resources. Using a simple formal modeling approach, we obtained more evidence for the motivation account than for the muscle account. Therefore, we conclude that it is likely that the effects of sequential cognitive control originate in a reduced motivation to match allocated resources to required resources.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors would like to thank the reviewers and Bernd Figner for their constructive comments.

Footnotes

1. ^Note that in this paper sequential control refers to sequential tasks, and not to sequential trials within a task.
2. ^If the design includes more tasks, for example not only a compatible and an incompatible task but also a task with an arbitrary mapping, two dummy variables are required for Task, and two for Order.
3. ^The error covariance structure was left unspecified, just as in a regular multivariate approach to a repeated measures ANOVA. That is no sphericity or other restrictive assumptions were imposed on the Task covariance structure. Estimates were derived by Maximum Likelihood.
4. ^Analyses at each level of Order separately may yield unstable estimates of the Task covariance structure. Therefore, all such analyses were repeated with a diagonal covariance matrix, which yielded comparable results.
5. ^One participant had short SSRT in the arbitrary 2 task (third task, first session). One participant had long SSRT in compatible (first task first session) and incompatible (second task second session) tasks. One participant had short SSRT in the compatible task (first task first session). In these cases data were removed not only from the SSRT analysis, but also from the Go RT and percentage errors analysis.

References

Band, G. P. H., van der Molen, M. W., and Logan, G. D. (2003). Horse-race model simulations of the stop-signal procedure. Acta Psychol. (Amst.) 112, 105–142.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Baumeister, R. F., Bratslavsky, E., Muraven, M., and Tice, D. M. (1998). Ego depletion: is the active self a limited resource? J. Pers. Soc. Psychol. 74, 1252–1265.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Baumeister, R. F., and Vohs, K. D. (2007). Self-regulation, ego-depletion and motivation. Soc. Personal. Psychol. Compass 1, 115–128.

CrossRef Full Text

Cohen, J. R., and Poldrack, R. A. (2008). Automaticity in motor sequence learning does not impair response inhibition. Psychon. Bull. Rev. 15, 108–115.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Eriksen, B. A., and Eriksen, C. W. (1974). Effects of noise letters upon the identification of target letters in a non-search task. Percept. Psychophys. 16, 143–149.

CrossRef Full Text

Gailliot, M. T., Baumeister, R. F., DeWall, C. N., Maner, J. K., Plant, E. A., Tice, D. M., Brewer, L. E., and Schmeichel, B. J. (2007). Self-control relies on glucose as a limited energy source: willpower is more than a metaphor. J. Pers. Soc. Psychol. 92, 325–336.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hagger, M. S., Wood, C., Stiff, C., and Chatzisarantis, N. L. D. (2010). Ego-depletion and the strength model of self-control: a meta-analysis. Psychol. Bull. 136, 495–525.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Huizenga, H. M., Smeeding, H., Grasman, R. P. P. P., and Schmand, B. (2007). Multivariate normative comparisons. Neuropsychologia 45, 2534–2542.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Huizenga, H. M., van Bers, B. C. W., Plat, J., van den Wildenberg, W. P. M., and van der Molen, M. W. (2009). Task complexity enhances response inhibition deficits in attention deficit hyperactivity disorder (ADHD): a meta regression analysis. Biol. Psychiatry 65, 39–45.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kahneman, D. (1973). Attention and Effort. Englewood Cliffs: Prentice-Hall.

Kramer, A. F., Humphrey, D. G., Larish, J. F., Logan, G. D., and Strayer, D. L. (1994). Aging and inhibition: beyond a unitary view of inhibitory processing in attention. Psychol. Aging 9, 491–512.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Levitt, H. (1971). Transformed up-down methods in psychoacoustics. J. Acoust. Soc. Am. 49, 467–477.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Logan, G. D. (1982). On the ability to inhibit complex movements: a stop-signal study of typewriting. J. Exp. Psychol. Hum. Percept. Perform. 8, 778–792.

CrossRef Full Text

Logan, G. D. (1994). “On the ability to inhibit thought and action: a users guide to the stop signal paradigm,” in Inhibitory Processes in Attention, Memory, and Language, eds D. Dagenbach and T. H. Carr (San Diego: Academic Press), 189–239.

Logan, G. D. (1997). “The automaticity of academic life: unconscious applications of an implicit theory,” in Advances in Social Cognition, ed. R. S. Wyer Vol. 10 (Mahwah: Lawrence Erlbaum), 157–179.

Logan, G. D., and Cowan, W. B. (1984). On the ability to inhibit thought and action: a theory of an act of control. Psychol. Rev. 91, 295–327.

CrossRef Full Text

Logan, G. D., and Irwin, D. E. (2000). Don’t look! don’t touch! inhibitory control of eye and hand movements. Psychon. Bull. Rev. 7, 107–112.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Martijn, C., Alberts, H. J. E. M., Merckelbach, H., Havermans, R., Huijts, A., and de Vries, N. K. (2007). Overcoming ego depletion: the influence of exemplar priming on self-control performance. Eur. J. Soc. Psychol. 37, 231–238.

CrossRef Full Text

Morein-Zamir, P., Nagelkerke, P., Chua, R., and Franks, I. (2006). Compatibility effects in stopping and response initiation in a continuous tracking task. Q. J. Exp. Psychol. 59, 2148–2161.

CrossRef Full Text

Muraven, M., and Baumeister, R. F. (2000). Self-regulation and depletion of limited resources: does self-control resemble a muscle? Psychol. Bull. 126, 247–259.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Muraven, M., Gagné, M., and Rosman, H. (2008). Helpful self-control: autonomy support, vitality, and depletion. J. Exp. Soc. Psychol. 44, 573–585.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Muraven, M., Shmueli, D., and Burkley, E. (2006). Conserving self-control strength. Personal. Process. Individ. Differ. 91, 524–537.

Muraven, M., and Slessareva, E. (2003). Mechanisms of self-control failure: motivation and limited resources. Pers. Soc. Psychol. Bull. 29, 894–906.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Norman, D. A., and Bobrow, D. G. (1975). On data-limited and resource-limited processes. Cogn. Psychol. 7, 44–64.

CrossRef Full Text

Pessoa, L. (2009). How do emotion and motivation direct executive control? Trends Cogn. Sci. (Regul. Ed.) 13, 160–166.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ridderinkhof, K. R., Band, G. P. H., and Logan, G. D. (1999). A study of adaptive behavior: effects of age and irrelevant information on the ability to inhibit one’s actions. Acta Psychol. (Amst.) 101, 315–337.

CrossRef Full Text

Robinson, M. D., Schmeichel, B. J., and Inzlicht, M. (2010). A cognitive control perspective of self-control strength and its depletion. Soc. Personal. Psychol. Compass 4, 189–200.

CrossRef Full Text

Sarter, M., Gehring, W. J., and Kozak, R. (2006). More attention must be paid: the neurobiology of attentional effort. Brain Res. Rev. S1, 145–160.

CrossRef Full Text

Schmeichel, B. J. (2007). Attention, control, memory updating, and emotion regulation temporarily reduce the capacity for executive control. J. Exp. Psychol. Gen. 136, 241–255.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schneider, W., and Shiffrin, R. M. (1977). Controlled and automatic human information processing: I. Detection, search, and attention. Psychol. Rev. 84, 1–66.

CrossRef Full Text

Simon, J. R. (1969). Reactions toward the source of stimulation. J. Exp. Psychol. 81, 174–176.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Slusarek, M., Velling, S., Bunk, D., and Eggers, C. (2001). Motivational effects on inhibitory control in children with ADHD. J. Am. Acad. Child Adolesc. Psychiatry 40, 355–363.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Snijders, T. A. B., and Bosker, R. J. (1999). Multilevel Analysis: An Introduction to Basic and Advanced Multilevel Modeling. Thousand Oaks, CA: Sage.

Tyler, J. M., and Burns, K. C. (2008). After depletion: the replenishment of the self’s regulatory resources. Self Identity 7, 305–321.

CrossRef Full Text

Tyler, J. M., and Burns, K. C. (2009). Triggering conservation of the self’s regulatory resources. Basic Appl. Soc. Psych. 31, 255–266.

CrossRef Full Text

van den Wildenberg, W. P. M., and van der Molen, M. W. (2004a). Developmental trends in simple and selective inhibition of compatible and incompatible responses. J. Exp. Child. Psychol. 87, 201–220.

CrossRef Full Text

van den Wildenberg, W. P. M., and van der Molen, M. W. (2004b). Additive factors analysis of inhibitory processing in the stop-signal paradigm. Brain Cogn. 56, 253–266.

CrossRef Full Text

Verbruggen, F., Liefooghe, B., Notebaert, W., and Vandierendonck, A. (2005). Effects of stimulus-stimulus compatibility and stimulus-response compatibility on response inhibition. Acta Psychol. (Amst.) 120, 307–326.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text