- 1 Faculty of Life Sciences, School of Psychology, London Metropolitan University, London, UK
- 2 Faculty of Psychology, University of Konstanz, Konstanz, Germany
- 3 Laboratory of Neuropsychology, Division of Intramural Research Programs, National Institute of Mental Health/National Institutes of Health, Bethesda, MD, USA
- 4 Institute of Neurology, University College London, London, UK
- 5 University of Klagenfurt, Klagenfurt, Austria
- 6 Hunter College, University of New York, New York, NY, USA
We know that stochastic feedback impairs children’s associative stimulus–response (S–R) learning (Crone et al., 2004a; Eppinger et al., 2009), but the impact of stochastic feedback on sequence learning that involves deductive reasoning has not been not tested so far. In the current study, 8- to 11-year-old children (N = 171) learned a sequence of four left and right button presses, LLRR, RRLL, LRLR, RLRL, LRRL, and RLLR, which needed to be deduced from feedback because no directional cues were given. One group of children experienced consistent feedback only (deterministic feedback, 100% correct). In this condition, green feedback on the screen indicated that the children had been right when they were right, and red feedback indicated that the children had been wrong when they were wrong. Another group of children experienced inconsistent feedback (stochastic feedback, 85% correct, 15% false), where in some trials, green feedback on the screen could signal that children were right when in fact they were wrong, and red feedback could indicate that they were wrong when in fact they had been right. Independently of age, children’s sequence learning in the stochastic condition was initially much lower than in the deterministic condition, but increased gradually and improved with practice. Responses toward positive vs. negative feedback varied with age. Children were increasingly able to understand that they could have been wrong when feedback indicated they were right (self-reflection), but they remained unable to understand that they could have been right when feedback indicated they were wrong (self-assertion).
Sequence Learning Under Uncertainty in Children
Learning under uncertainty is important because persistent yet vague uncertainties provide continuous motivation for further discoveries, growth, and development (Acredolo and O’Connor, 1991). We know, however, that children show impaired performance under stochastic feedback when associating arbitrary stimuli with their responses (S–R learning; Crone et al., 2004a; Eppinger et al., 2009). Here, this approach is extended to another central ability of children, that is sequence learning.
In the Introduction, we first familiarize the reader with the classic conceptual approach of Piaget’s seriation task where children conceptualize sequences with top-down control processes (operations). Thereafter, we elaborate how in more recent approaches, researchers presented bottom-up learning accounts. They either assumed that human sequence learning would occur in an explicit and effortful fashion via discrete steps in an action plan, or that it would occur in both animals and human infants as well as in children and adults of all ages in an implicit fashion via a gradual assembly of a sequence template. The current study tested sequence learning with a four button presses motor task where children had to produce a sequence of left and right button presses.
We presumed that when feedback is correct, children would be able to deduce the correct sequence in the four button press task with relative ease. However, we added to the condition with veridical response feedback (deterministic feedback: 100% correct) a second condition. Children in this second condition experienced response feedback that was mostly correct, but sometimes wrong (stochastic feedback: 85% correct/15% false). Hence, in the second part of the Introduction we give the reader an overview on previous research on children’s development of feedback evaluation. We describe previous research on learning via response feedback, learning under biased (only positive, only negative) feedback, random (unrelated) feedback, and stochastic (proportion of correct and false) feedback.
Sequence Learning in Children
The Classic Conceptual Approach
In Piaget’s (1952) seriation task, children sorted sticks of different length into a sequence according to size. Children’s development of seriation proceeded in stages, from esthetic and idiosyncratic sequences, to alignments along a ground line, to partially and then completely correct sequences. Piaget claimed that children would learn to sequence objects because they would acquire an operational and logical reasoning ability that would develop closely tied to their action schemata. He furthermore assumed that children could only truly understand sequences if they comprehended that seriation involved a concept of dimension and scale. If for instance children would understand that sorting objects on a scale according to size either from small to large, or from large to small, has no impact on the dimension “size” as such (reversibility), and that this could be done independently of the kind of objects, children would have acquired a consolidated and generalizable concept of sequence.
Accounts of Gradual Sequence Learning
Piaget’s seriation/sequencing task later came to the attention of cognitive psychologists (Johnson-Laird, 1988/1993, p. 162; Young, 1976) who agreed that seriation would be brought about by discrete steps in an action plan containing an iterative command structure. It is debated whether this command structure is hierarchically organized, or carried out via accumulated learning that makes associative links between items (e.g., Lashley, 1951). Accumulative learning results in a more gradual acquisition without the need for a genuine hierarchical controller (Rhodes et al., 2004). Single cell response measurements found that sequential action plans were maintained and updated in frontal brain areas (Averbeck and Lee, 2007), showing that sequence learning is an effortful activity that requires mental resources (Zacks et al., 1984) and can be more efficient than predictive learning (Lange-Küttner, 2011).
Mareschal and Shultz, 1999, p. 161) built a neural network architecture for the seriation task where the only instruction was to “move the smallest out-of-order stick.” Interestingly, four types of solutions were found after 150 epochs: sequential groups of pairs and triplets, ascending-then-descending sequences, and correct sequences of sticks. Like young children, only about 55% of the networks could complete the sequence and sort four sticks correctly.
Implicit Sequence Learning
A gradual sequence learning mechanism was shown to exist in 2-year-old (Bremner et al., 2007) and 4-year-old children (Livesey and Little, 1971) as well as in adults (Li et al., 2000). Also monkeys, and to a lesser degree pigeons, were found to gradually build a template of a sequence during training (Terrace, 1993; Terrace and McGonigle, 1994). This suggested that a sequencing is an activity that can be learned via practice, and does not necessarily involve explicit top-down concepts even though these may develop with age enabling increased task control (Maybery and O’Brien-Malone, 1998).
Implicit or incidental learning is mastered early, occurs automatically and without awareness, and usually does not show chronological or mental age differences (Maybery et al., 1995; Reber, 1996; Meulemans and Van der Linden, 1998; Vinter and Perruchet, 2000, 2002; Sloutsky and Fisher, 2008; Weinert, 2009). However, this is not always the case (Thomas et al., 2004). While the type of gradual sequence learning was the same independent of ability, acceleration and error rates could vary significantly (Kelly et al., 2002; Waber et al., 2003). Even for adults with a mature information processing system, implicit sequence learning could be impaired by a concurrent counting task (Shanks et al., 2005). Nevertheless, sequence learning in this dual-task load condition improved so much with practice that it caught up with the performance in the easier single-task load condition. Clearly, these contradictory assumptions and results warrant further research into the underlying factors, such as whether sequence learning would suffer in children when they are uncertain about their success. Even a task that can be solved with deterministic feedback may show decrements under uncertainty, and improvement with practice.
In the current task, children were explicitly asked to discover a sequence of four button presses via a feedback signal. The task involved motor responses only, that is, children had to ascertain a sequence of four left vs. right button presses on a computer laptop without any visible objects that needed to be sorted. Hence, no dimension construction of an object feature such as “size” was necessary. This had the advantage that relatively “pure” deductive reasoning about the exact sequence could be tested, as stimulus properties could not interfere with learning, e.g., stimuli could have potentially been treated as deviants (Ferdinand et al., 2008), or in an idiosyncratic fashion (Kosslyn et al., 1980).
Learning via Feedback
Children’s Need for Deterministic Feedback
Children are used to learning under conditions of certainty and, to a large degree, trust adults’ information and feedback (Goswami, 1992, p. 22). Previous research showed that they prefer to trust information from familiar persons such as their mothers but not strangers (Corriveau et al., 2009a) and from experts like psychologists and priests but not magicians (Chandler and Lalonde, 1994). Accuracy of information and feedback made a difference to 3-year-old children, who distrusted persons who gave them even just one false feedback (Pasquini et al., 2007). From 4 years of age, though, children increasingly assessed reasons for the credibility of an informant before they allowed feedback to have an impact on their perceptions and judgments (e.g., Corriveau et al., 2009b; Nurmsoo and Robinson, 2009a,b; Robinson and Nurmsoo, 2009).
Learning via feedback is often assessed with the Wisconsin Card Sorting test (WCST; e.g., Rosselli and Ardila, 1993; Riccio et al., 1994; Bull et al., 1999; Bull and Scerif, 2001). In the WCST, children sort picture cards of objects into categories according to examiner feedback, usually according to shape, color, or number. The rule itself is not revealed, but must be deduced from the feedback. After a certain number of trials, the examiner changes the sorting criterion without telling the child. Please note that while the experimenter changed mind about the criterion, the feedback itself in the WCST was always true. In computerized versions of the WCST, perseverative errors where children would just continue sorting without paying attention to the feedback decreased between 8 and 12 years, while distraction errors and failure to maintain consistent sorting continued until age 15 (Crone et al., 2004b; Somsen, 2007).
Learning via Stochastic Feedback
Responses toward biased feedback were tested in psychophysiological studies using computerized stimulus–response (S–R) learning with 8- to 12-year-old children and young adults (Crone et al., 2004a; Groen et al., 2007). Pictures of different categories such as vehicles, fruit etc. were coupled with an arbitrary left or right side button response, unrelated to pictures’ categorical membership: pictures acquired a different valence exclusively by the link with the feedback. There was informative and uninformative feedback. Informative feedback had a positive feedback associated with one button press, and a negative feedback associated with the other button. Uninformative feedback, in contrast, was either random, or consistently positive (positive bias) or negative (negative bias) for both button presses. In the Crone et al. study, the dependent measure was heart rate. While the difference between positive or negative feedback did not matter for children when it was random, 8- to 10-year-olds did not distinguish between informative response-dependent negative feedback and uninformative biased negative feedback (Crone et al., 2004a). Children experimented with their responses (frequent key changes) especially after biased negative feedback; this was accompanied by lower frontal activation which reflected decreased attention (Groen et al., 2007).
Bandura (1997, 2007) discussed the fact that theories of self-regulation rely on a negative feedback model that consists of a system with a behavior sensing operation, an inner comparator, and an error correction routine which results in a discrepancy reduction mechanism. Only negative feedback would create individual differences insofar as some may not trust their capability to solve a task and stop trying, while others would not lose faith in their capability and exert more effort to solve the task (see also Dikman and Allen, 2000; Overton and Dick, 2007). In children and adolescents, these individual differences in perseverance occurred dependent on socialization variables such as socioeconomic status, but independently of IQ (Weisz, 1981; Caprara et al., 2008). For example, in another study it was shown that teachers would give negative feedback to both socially adapted and less well adapted pupils, but the latter were exposed to significantly higher levels of repeated commands following compliance (Strain, 1983). Even in an adult work context, negative feedback did not automatically produce the desired effect of improving performance (Ilgen and Davis, 2000). This shows that negative feedback, and particularly a negative feedback bias seems to have a special role in the development of cognition.
In another study on S–R learning in children, Eppinger et al. (2009) required 10- to 12-year-old children to sort objects into two safes in a two-choice computerized decision task. Pictures were consistently linked with the left or right button. A new stochastic condition was introduced when the relation between picture and key held only 80% of the time. The stochastic condition was compared with a 100% correct association and a 100% random association between picture and key. Children performed worse than adults only in the stochastic feedback condition. Importantly, Eppinger et al. (2009) thus showed that in this S–R paradigm, children’s performance suffered only under uncertainty, as both in the entirely consistent, and in the entirely random condition, children learned just as well as adults.
The development of explicit probabilistic concepts of frequency and chance is indeed supposed to continue to develop into adolescence (Piaget and Inhelder, 1975; Byrnes and Overton, 1986; Fischbein et al., 1991). For instance, in the study of Miller et al. (1977) a technically looking feedback machine was used for Piagetian conservation and transitivity problems. The machine was introduced to the children as sometimes making mistakes, although in general feedback would be correct. But in fact, the machine feedback was independent of the 7- and 11-year-old children’s response. Miller et al. (1977) found that children’s confidence level equaled task difficulty when not challenged by random feedback. However, on average 76% of the children surrendered to false negative machine feedback, without a significant age difference, in Piagetian sequencing tasks according to size or weight. With age, though, children did raise their game toward challenges when they were reasonably confident, such as judgment of the mass of objects whose shape had changed (conservation task).
The Current Study
In the current study, there were no images of objects present. Instead, children were explicitly instructed to learn sequences of left–right button presses that formed a motor sequence. The sequence of button presses needed to be deducted from a red/green feedback signal that was displayed on the computer screen. Children learned sequences of four left–right (L–R) button presses. The sequences were LLRR, RRLL, LRLR, RLRL, LRRL, and RLLR.
One group of children experienced consistent feedback only (deterministic feedback, 100% correct). In this condition, green feedback on the screen indicated that the children had been right when they were right, and red feedback indicated that the children had been wrong when they were wrong. Another group of children experienced inconsistent feedback (stochastic feedback, 85% correct, 15% false). In this condition, green feedback on the screen could signal that children were right when in fact they were wrong, and red feedback could indicate that they were wrong when in fact they had been right. Children were informed beforehand about the experimental condition, that is, whether feedback would be always right, or mostly right and sometimes wrong.
Children needed to deduce the correct sequence from these feedback signals on the screen. For example, if in the first block children were certain that the first two button presses were LL, they could predict that the subsequent button presses were RR. Hence, a clear-cut top-down if-then deductive reasoning process was required. However, the evidence for a prediction of RR was equivocal in the stochastic feedback condition because the on-screen feedback was programmed to be only correct in 85% of the trials, but false in 15% of the trials. Thus, children needed to monitor the veridicality of feedback and their success rate more closely, and there was a strong interactive bottom-up learning process involved.
We investigated whether children would be able to solve the four button sequencing task when receiving accurate feedback. We furthermore investigated whether children’s motor response sequence learning would be better or worse when feedback was stochastic. Given the results from previous research using biased and stochastic response feedback methodology in contingency learning, no age differences for this effect were predicted. We also analyzed whether positive or negative feedback had a more conducive effect on learning, and expected that especially false negative feedback in the stochastic feedback condition would cause performance deterioration.
Method
Participants
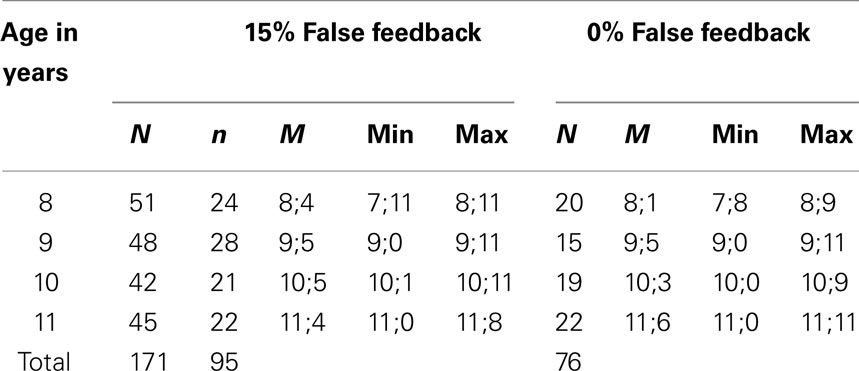
Overall, N = 186 participants were tested. All children had normal or corrected-to-normal vision, and none was reported as color-blind. For all children, parental consent was obtained. In the stochastic condition, six 8-year-olds, three 9-year-olds, and five 10-year-olds did not complete the last two response sets. In the control condition, this was the case for only one 11-year-old participant. These 15 data sets were excluded from analyses. Mean ages (years; months) of the remaining sample (N = 171) are listed in Table 1. In the experimental condition there were n = 95 children (54 girls), and in the control condition n = 76 children (35 girls).
Apparatus and Material
A computer task was developed using MATLAB (Mathworks) that randomized the six sequences LLRR, RRLL, LRLR, RLRL, LRRL, and RLLR with a random number generator. Children responded with their left and right index finger on the keyboard of a Windows laptop computer. They pressed the button “Z” on the left side of the keyboard and the “-” button on the right side of the keyboard (UK keyboard layout), both were marked with colored varnish. They kept their index fingers on these buttons throughout the experiment.
There was no stimulus material in the form of object pictures presented on the screen. Children only saw a feedback signal on the screen following each button press, see Figure 1. Each button press on the keyboard was followed by either a green (signal for correct button press) or a red (signal for incorrect button press) feedback signal on the screen. In the experimental condition, stochastic feedback was 85% correct and 15% false, while in the deterministic control condition, feedback was 100% correct. Also the stochastic feedback trials were randomized by the experimental program on each session, per participant.
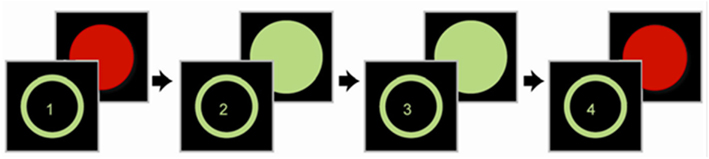
Figure 1. Sequence learning task. The task was self-paced and there were no stimuli to look at; only the color-coded feedback signal to the button presses appeared on the screen. The lower row in the figure represents the four button presses that children would carry out on the computer keyboard. The upper row shows the feedback signal, with red indicating negative feedback (wrong button) and green indicating positive feedback (correct button) after each button press. Figure adapted from Seo et al. (2010).
The correct feedback allowed an immediate deduction of a sequence from the feedback. An example: The first four left–right button presses (R = right, L = left) trigger the following color feedback: R-red, R-green, L-green, L-red (red–green–green–red, 50% correct, see Figure 1). The first and last button presses that had triggered the red feedback then had to be corrected in the second run of this sequence to L-green, R-green, L-green, R-green (green–green–green–green, 100% correct). In contrast, the stochastic feedback for a button press did not allow the participants to correct their mistakes in such a straightforward manner, but an integration of feedback from multiple response sets was required to determine the correct sequence of the four button presses.
Responses were self-paced without time constraints. Response times were not measured, only accuracy was recorded by the computer program. In the control condition, children had to execute the sequence correctly eight times, and in the more challenging stochastic feedback condition they had to execute the sequence correctly six times, before the program moved on to the next sequence. If participants did not learn the sequence after twenty sets of key presses, the block was aborted and they were advanced to the next sequence. When the learning and repetition of a sequence was completed, the sentence “You have a new sequence to learn” appeared on the screen.
In order to test whether positive and negative feedback trials had a differential effect especially in the stochastic feedback condition, a learning model was fit that estimated how much participants learned from feedback on each trial. The positive learning parameter that we computed was a variable that measured how likely the children were to repeat the same button press at a particular position in the sequence, in the next trial, if they had received green feedback. The negative learning parameter tested the complement. Please see the Appendix for the computational details.
Procedure and Instruction
Children were tested individually, or in pairs, with a laptop for each child. Children’s test session lasted about 30 min. After the completion of the six sequences LLRR, RRLL, LRLR, RLRL, LRRL, and RLLR, the entire test was repeated. The order of presentation of the sequence blocks was randomized for each child by the experimental program, within each round. At the beginning of the experiment, the experimenter read the standardized instructions from the computer screen aloud to each child. The instruction was not given in one go, but sentences were presented in several screenshots.
Experimental condition (with stochastic feedback)
Welcome to “Learn the 4 Button Presses task.” You are given a left and a right button to press. You need to learn these 4 buttons in a particular sequence, e.g., Left, Right, Left, Right. Each time you press a button, a green circle will appear to show that you pressed the correct button in the sequence. A red circle will appear like a streetlight, if you pressed a wrong button in the sequence. However, the computer will also give you wrong feedback 15% of the time. Even if you pressed the correct button, it may appear as false with a red circle. Even if you pressed the wrong button, it may appear as correct with a green circle. Therefore, even if you think you know the sequence, sometimes you may have to ignore the feedback. After learning the correct “4 Button Presses” repeat the same sequence six times and you will proceed to learn another new sequence.
Control condition (with 100% correct feedback)
Welcome to “Learn the 4 Button Presses task.” You are given a left and a right button to press. You need to learn these 4 buttons in a particular sequence, e.g., Left, Right, Left, Right. Each time you press a button, a red or a green circle will appear. The circle is like a streetlight to show whether you pressed the correct or wrong button. The computer always gives you correct feedback. If you press the correct button, a green circle appears; if you press the wrong button, a red circle appears. After learning the correct “4 Button Presses” repeat the same sequence eight times and you will proceed to learn another new sequence.
Results
For analysis, data were averaged across the six sequences and two runs. Accurate responses from the first six repeated sequence response sets were analyzed, for group means per age and condition (see Table 2).
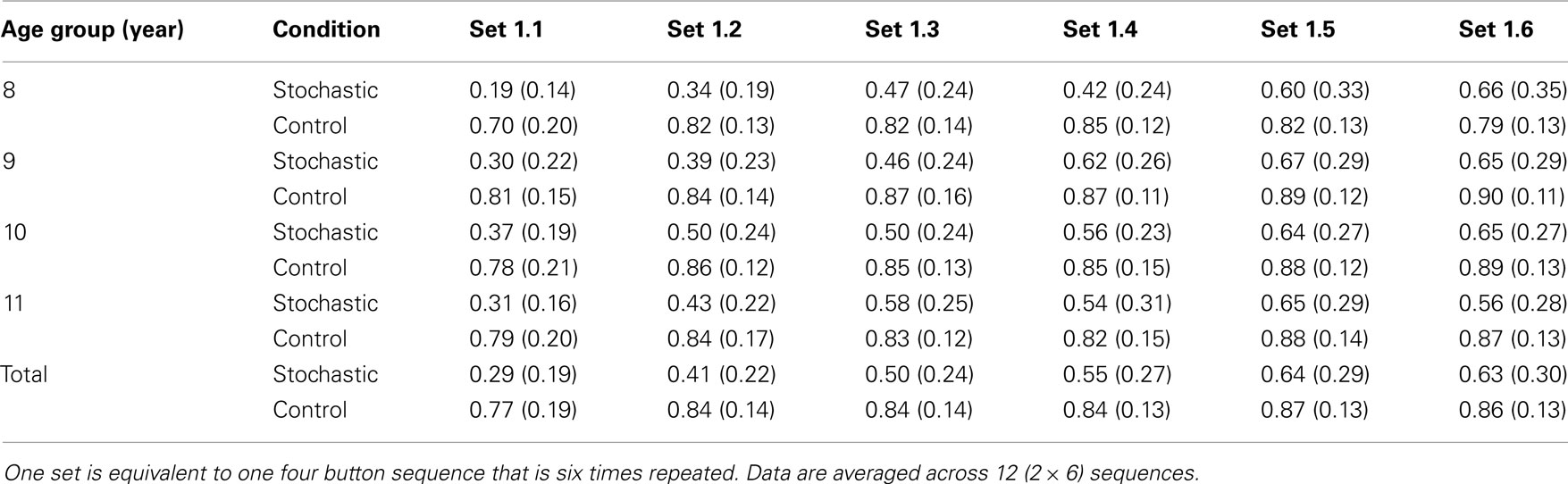
Table 2. Performance percent correct in the 4 button press task (N = 171; group means per age group per condition, SD in brackets).
A 6 (sets) by 2 (condition) by 4 (age groups) by 2 (gender) mixed ANOVA with repeated measures of the first factor showed that there was a significant main effect of age, F(3, 171) = 2.80, p < 0.05, η2 = 0.05. Success in the deduction of the four button press sequence from feedback increased between 8 and 9 years and stayed the same thereafter (8 years M = 0.62, 9 years M = 0.69, 10 years M = 0.69, 11 years = 0.68). Interaction effects with age were not significant, ps > 0.40.
Because the Mauchly test for sphericity was significant for the effect of response sets, degrees of freedom were corrected according to Greenhouse–Geisser. There were significant effects of sets, F(4.52, 171) = 35.02, p < 0.001, η2 = 0.18, condition, F(1, 171) = 263.14, p < 0.001, η2 = 0.63, and a significant two-way interaction of sets by condition, F(4.52, 171) = 12.88, p < 0.001, η2 = 0.08. Children in the control condition with deterministic correct feedback had learned the task with relative ease after the first block, while children in the experimental condition who had experienced stochastic feedback started at a lower level, showed only gradual learning, and caught up, but did not close the gap completely, see Figure 2. Post hoc tests (independent samples t-tests, two-tailed, Bonferroni adjustment of confidence levels to 99%) showed that the performance difference between experimental conditions was significant in all sets, ps < 0.001, see Table 3. The T-values of the mean difference between stochastic and control condition diminished, but the performance difference remained significant.
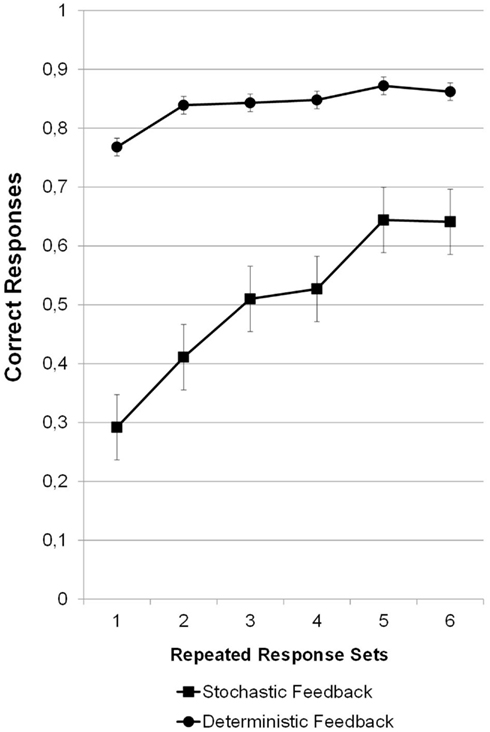
Figure 2. Sequence learning. The graph shows the first six response sets of four sequential button presses averaged across the sequences LLRR, RRLL, LRLR, RLRL, LRRL, and RLLR which were tested twice in random order. Learning with stochastic feedback started at a significantly lower level, but showed considerable and significant improvement during the repetitions. Bars denote the SE.
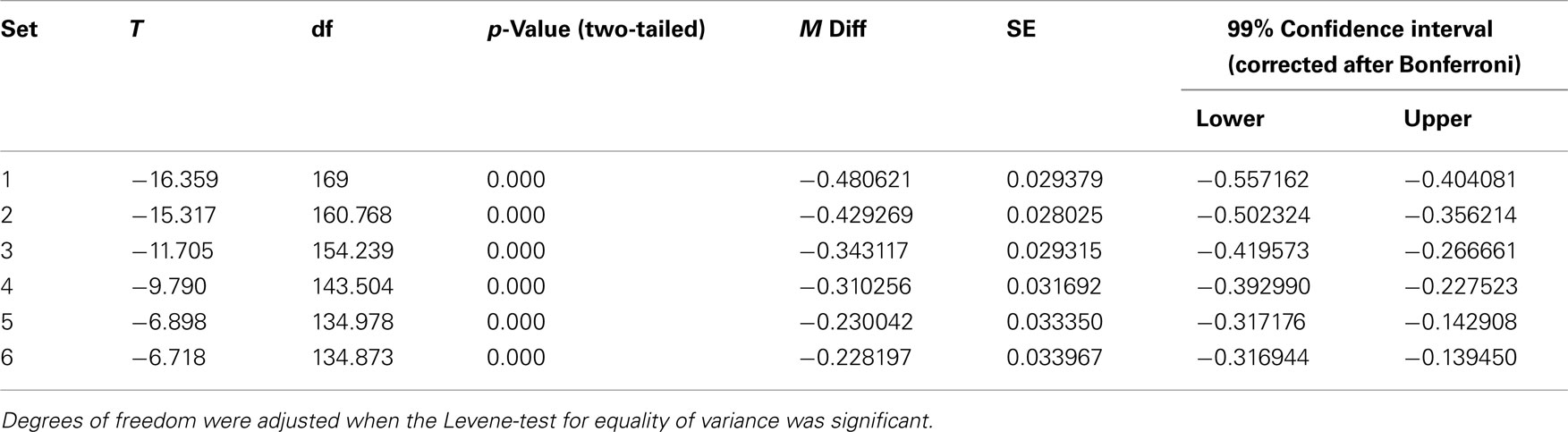
Table 3. Post ho c tests of the interaction of sets by condition (t-tests for independent samples) in order to compare performance of the stochastic and control samples per set.
There was no significant main effect of gender (82 boys, 89 girls), F(1, 171) = 0.09, ns, showing that boys and girls performed at the same overall level. However, there was a small, but significant gender by sets effect, F(4.52, 171) = 2.39, p < 0.05, η2 = 0.02. Post hoc tests (pairwise samples t-tests, two-tailed, Bonferroni adjustment of confidence levels to 99%) showed that boys (n = 82) kept improving their performance during the task, trial 1 M = 0.52, trial 2 M = 0.60, trial 3 M = 0.66, trial 4 M = 0.67, trial 5 M = 0.79, trial 6 M = 0.76, see Table 4, while girls (n = 89) significantly improved their performance only from the first to the second trial, with much smaller increments thereafter, trial 1 M = 0.49, trial 2 M = 0.60, trial 3 M = 0.64, trial 4 M = 0.68, trial 5 M = 0.70, trial 6 M = 0.71. Other interactions with gender did not reach significance, ps > 0.06.
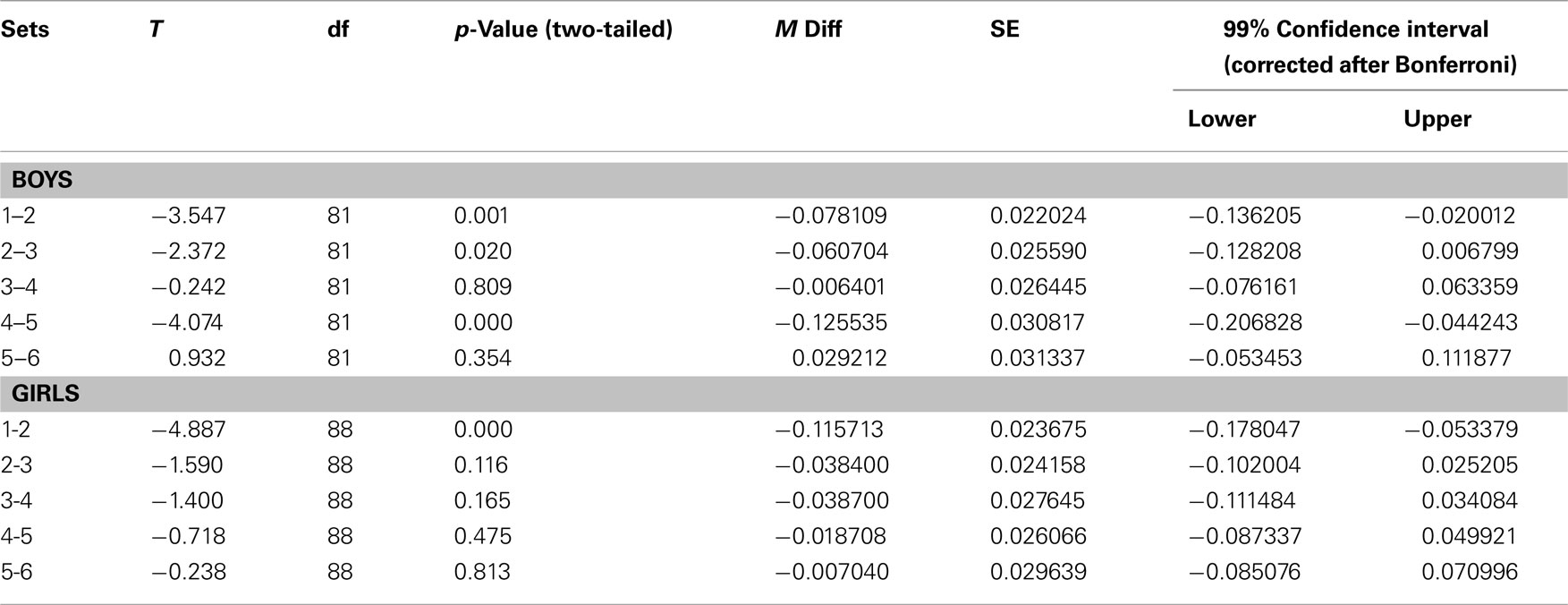
Table 4. Post hoc tests of the interaction of sets by gender (paired t-tests, gender split-sample) testing learning effects in consecutive trials for boys vs. girls.
Statistical Comparison of Learning from Positive and Negative Feedback
The amount of learning after positive and negative feedback was analyzed in a 2 (feedback type) by 2 (condition) by 4 (age groups) by 2 (gender) mixed ANOVA with repeated measures of the first factor. Gender did not reach significance as a main effect, p > 0.06, nor in interactions, p > 0.10. The three main effects of feedback type, condition, and age were highly significant. Positive feedback increased the probability of learning (M = 0.20) more than negative feedback (M = 0.04) as there was next to no learning from negative feedback as the mean approached zero, F(1, 171) = 218.02, p < 0.001, η2 = 0.58.
Not surprisingly, children learned more from correct feedback (M = 0.19) than from stochastic feedback (M = 0.04), F(1, 171) = 79.85, p < 0.001, η2 = 0.34.
It is important to note, though, that both learning from stochastic feedback and learning from correct negative feedback was approaching zero (M = 0.04). Thus children might have perceived both types of feedback, one vague and probabilistic, and one telling them they were wrong, as equally hostile, preventing learning.
However, a main effect of age, F(3, 171) = 5.73, p < 0.001, η2 = 0.10, and a significant three-way interaction of age with feedback and condition, F(3, 171) = 4.32, p < 0.01, η2 = 0.08 showed that this was dependent on age. Figure 3 illustrates the three-way interaction of age, feedback and condition. Learning in the deterministic feedback condition (100% correct; see Figure 3B) increased with age with both positive and negative feedback, but learning after true positive feedback was always more pronounced, while learning from true negative feedback only started at age 9.
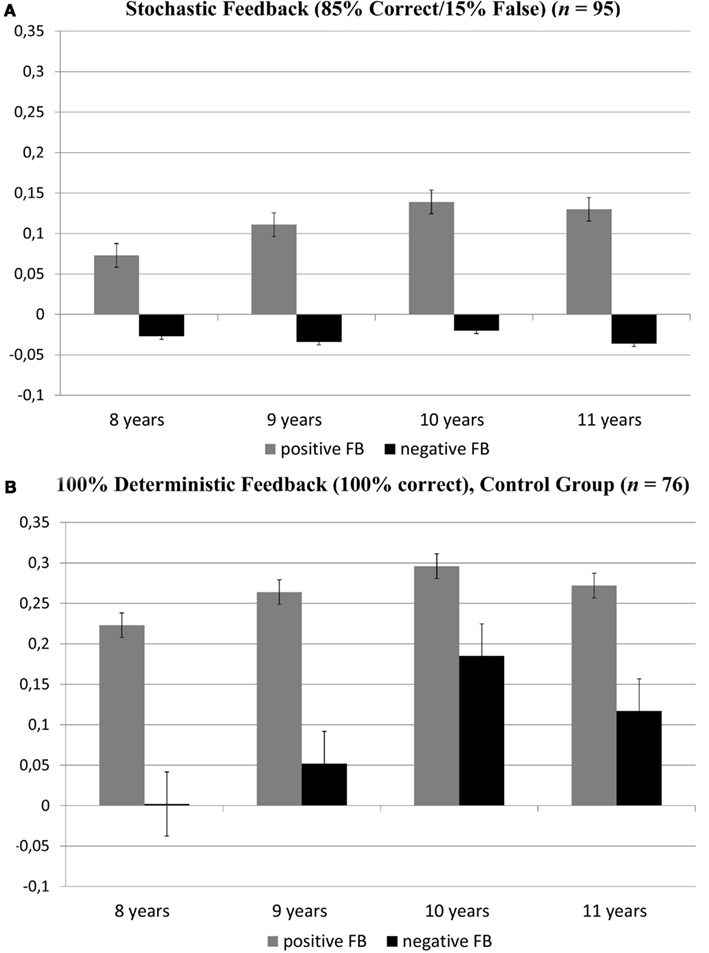
Figure 3. Amount of learning after positive and negative feedback. A value of 0.5 on the y-axis indicates perfect learning. Learning after stochastic feedback was reduced after negative feedback in all age groups, but increased with age for positive feedback (A). Learning after deterministic, correct feedback increased with age for both positive and negative feedback, but stayed more pronounced for positive feedback (B). Bars denote the SE.
In contrast, in the stochastic feedback condition (see Figure 3A), learning increased only in trials with positive feedback (containing 15% false positive feedback), while it stayed at floor level in trials with negative feedback (containing 15% false negative feedback) in all age groups. Even more striking, the negative values for stochastic negative feedback indicated that learning was actually impaired.
Discussion
We used a sequence learning task which required children to select sequences of four button presses. On-screen feedback was used to investigate for the first time whether children’s motor response sequence learning would be better or worse when feedback was stochastic. The 8- to 11-year-old children showed quick deductive reasoning about sequences with correct feedback. Hence, this would qualify as an efficient top-down reasoning approach. However, it became clear that children needed to learn to cope with the stochastic feedback, as their task performance was much lower. Recovery was shown to be dependent on positive feedback, but was not supported by false negative feedback demonstrating a strong interactive aspect of cognition (Averbeck and Duchaine, 2009). For children, especially negative feedback seems to be an external force that can impinge on a consolidated cognitive conceptual structure and thwarts performance.
That children started at a significantly lower level in the stochastic compared to deterministic feedback condition occurred independently of their age. This result was in line with previous S–R research using biased and stochastic feedback (Crone and Van der Molen, 2007; Eppinger et al., 2009; Van den Bos et al., 2009) and Piagetian seriation tasks with random feedback (Miller et al., 1977). However, children successfully improved accuracy of the four button press sequence in the stochastic condition, even though their performance increased only gradually and did not reach the same level as in the control condition with deterministic feedback.
Furthermore, an age difference was found in children’s responses toward positive vs. negative feedback. They learned more from positive than from negative feedback. In fact, children began to learn from negative feedback only from age 9, and this increased thereafter. With regards to the stochastic feedback, children were increasingly capable to understand that they could have been wrong even if the feedback indicated they were right (false positive feedback), but they remained unable to understand that they could have been right when the feedback indicated they were incorrect (false negative feedback). This suggested that self-reflective abilities did develop with age, while cognitive self-assertiveness remained low. These findings of the current study are discussed in the following two sections.
Sequence Learning Under Uncertainty
The performance reduction effect caused by the uncertainty of feedback had a large effect size that showed that this result was not only statistically reliable, but also powerful and replicable. With on average 48% performance decrement in comparison to the control condition at the beginning and still about 23% in the sixth repetition, the extent of performance reduction in this sequence learning task was much larger than for instance in S–R learning in the Eppinger et al. (2009) study, where stochastic feedback lead to a decrement of about 10% in adults and 15% in children. However, it was comparable to the only other developmental study using a reasoning task (Miller et al., 1977).
With informative feedback, some gradual performance improvement can occur in S–R learning (Groen et al., 2007). Performance improved also with stochastic feedback, but the performance gap between informative and stochastic feedback stayed about the same in both children and adults (Eppinger et al., 2009). This may have occurred because children would improve via some trial-and-error key switches independently of the feedback condition (Groen et al., 2007). In the current study, more correct sequencing of the four button presses emerged via practice in the stochastic condition, and the initially larger performance gap to the control condition narrowed. True improvements in feedback processing may have been possible during repetitions because long-term event memory for correct and false feedback trials across repeated blocks of a specific sequence set could aid performance. In another study that used stochastic feedback, excellent adult learners were comparably more likely to use their long-term memory to avoid stimuli that had received negative stochastic feedback (Klein et al., 2007).
In short, motor sequence learning that requires some deductive reasoning may be both more vulnerable to interference than S–R learning, but also more amenable to improvement than S–R learning. Sequence learning is a higher order cognitive process that is also easily interfered with in adults (Shanks et al., 2005). Stochastic feedback may represent a higher cognitive load on a deductive process in comparison to arbitrary S–R associations. The subsequent performance increment would reflect that stochastic feedback represents more of a jeopardy than a hazard, but this was very much dependent on the type of feedback.
Age Differences in Positive and Negative Stochastic Feedback
Like in previous research using paired force-choice tasks (Crone and Van der Molen, 2007; Van den Bos et al., 2009), age differences were found once the effects of positive or negative feedback on the amount of learning were considered.
The current study did not just use negative feedback that indicated that children’s responses were at fault, but also unjustified positive and negative feedback. In this way, not just the processing of an error signal was investigated (e.g., Falkenstein et al., 2000; Hajcak et al., 2005), but processing of a potentially untrustworthy and unreliable error signal. Furthermore, children in the experimental group faced some proportion of unjustified negative feedback during repeated trials where they had to maintain their response; hence, the feedback could not only undermine the learning process, but also achieved results. However, this did not happen, as performance continuously increased. Significant setbacks could be observed neither in boys, nor in girls. However, in the present relatively large sample, boys kept improving their performance throughout the task, while girls did not.
Feedback bias is clearly an important issue for learning research (Dai and Sternberg, 2004). Feedback is usually differentiated between social feedback vs. performance feedback (Zimmerman and Schunk, 2004). In the current study, the deterministic condition would amount to performance-related feedback, while children may have experienced the dose of false positive and negative feedback like in the stochastic condition in their social context.
However, 8-year-old children appeared to have perceived both types of negative feedback as equally hostile, one vague and probabilistic, and one telling them they were wrong, and both were not supporting, or even prevented learning. This suggested that 8-year-old children did not differentiate between performance-related and social feedback. But 9-year-old children and the older age groups began to consider negative feedback when it was veridical.
In contrast, positive feedback facilitated sequence learning in all age groups. The support of positive feedback increased with age, and this occurred even if it included some stochastic false positive feedback. But the same amount of false negative feedback in the stochastic feedback condition actually prevented learning, and there was no development with age. While straightforward conditioning with punishment helped children to make advantageous choices (Crone et al., 2005), stochastic negative feedback remained a challenge for children’s deduction of a sequence. Children of all age groups appeared to find it difficult to think that they were right when the feedback signaled that they may have been wrong. To maintain to be right in the face of an opposing false signal is quite different to understanding another person’s perspective which develops much earlier (Lange-Küttner, 2009, 2012). That cognitive self-assertiveness remained low, while self-reflective abilities developed with age, is a new finding that revealed that there are two types of cognitive incongruity reduction.
We could find only one single study on false positive feedback given to children as an intervention. Heath and Glen (2005) demonstrated a fascinating paradox: children with average IQ but academic difficulties in subjects such as written language and math overestimated their performance, but when given a standardized false positive feedback, they revised their positive bias and could predict their actual performance precisely. Heath and Glen had a self-protective bias hypothesis, where persistent unjustified positive feedback made it unnecessary for the children to deny their difficulties.
Selective sensitivity toward positive feedback when reasoning under uncertainty is seen as adaptive in the developmental literature (Bjorklund and Green, 1992; Bjorklund et al., 2009, pp. 128). A question for future research is whether children’s reasoning under uncertainty actually needs a positive feedback loop, either self-induced, or via an experimenter, or via a computer program as in the current study, and whether it actually needs to be true. Thus, a positive feedback bias may yield uninformative feedback as it is unrelated to the actual performance, but it nevertheless seems highly conducive for learning in children.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank teaching staff and children from the following schools: Church of England Sir John Cass Primary School, London, UK, International School Kreuzlingen, Switzerland, St. Konrad Realschule, Ravensburg, Germany and the following institutions in Konstanz, Germany: Grundschule Haidelmoos, Geschwister-Scholl-Schule, Kinderhort Albert Schweizer, Kinderhort Konradihaus (Caritas), Kinderhort Edith Stein, and Kinderhort Rappelkiste.
References
Acredolo, C., and O’Connor, J. (1991). On the difficulty of detecting cognitive uncertainty. Hum. Dev. 34, 204–223.
Averbeck, B. B., and Duchaine, B. (2009). Integration of social and utilitarian factors in decision making. Emotion 9, 599–608.
Averbeck, B. B., and Lee, D. (2007). Prefrontal neural correlates of memory for sequences. J. Neurosci. 27, 2204–2211.
Bandura, A. (2007). Much ado over a faulty conception of perceived self-efficacy grounded in faulty experimentation. J. Soc. Clin. Psychol. 26, 641–658.
Bjorklund, D. F., and Green, B. L. (1992). The adaptive nature of cognitive immaturity. Am. Psychol. 47, 46–54.
Bjorklund, D. F., Periss, V., and Causey, K. (2009). The benefits of youth. Eur. J. Dev. Psychol. 6, 120–137.
Bremner, A. J., Mareschal, D., Destrebecqz, A., and Cleeremans, A. (2007). Cognitive control of sequential knowledge in 2-year-olds. Psychol. Sci. 18, 261–266.
Bull, R., Johnston, R. S., and Roy, J. A. (1999). Exploring the roles of the visual-spatial sketch pad and central executive in children’s arithmetical skills: views from cognition and developmental neuropsychology. Dev. Neuropsychol. 15, 421–442.
Bull, R., and Scerif, G. (2001). Executive functioning as a predictor of children’s mathematics ability: inhibition, switching, and working memory. Dev. Neuropsychol. 19, 273–293.
Byrnes, J. P., and Overton, W. F. (1986). Reasoning about certainty and uncertainty in concrete, causal, and propositional contexts. Dev. Psychol. 22, 793–799.
Caprara, G. V., Fida, R., Vecchione, M., Del Bove, G., Vecchio, G. M., Barbaranelli, C., and Bandura, A. (2008). Longitudinal analysis of the role of perceived self-efficacy for self-regulated learning in academic continuance and achievement. J. Educ. Psychol. 100, 525–534.
Chandler, M. J., and Lalonde, C. E. (1994). Surprising, magical and miraculous turns of events: children’s reactions to violations of their early theories of mind and matter. Br. J. Dev. Psychol. 12, 83–95.
Corriveau, K. H., Harris, P. L., Meins, E., Fernyhough, C., Arnott, B., Elliott, L., Liddle, B., Hearn, A., Vittorini, L., and de Rosnay, M. (2009a). Young children’s trust in their mother’s claims: Longitudinal links with attachment security in infancy. Child Dev. 80, 750–761.
Corriveau, K. H., Meints, K., and Harris, P. L. (2009b). Early tracking of informant accuracy and inaccuracy. Br. J. Dev. Psychol. 27, 331–342.
Crone, E. A., Bunge, S. A., Latenstein, H., and Van der Molen, M. W. (2005). Characterization of children’s decision making: sensitivity to punishment frequency, not task complexity. Child Neuropsychol. 11, 245–263.
Crone, E. A., Jennigs, J. R., and Van der Molen, M. W. (2004a). Developmental change in feedback processing as reflected by phasic heart rate changes. Dev. Psychol. 40, 1228–1238.
Crone, E. A., Ridderinkhof, R. K., Worm, M., Somsen, R. J., and Van Der Molen, M. W. (2004b). Switching between spatial stimulus–response mappings: a developmental study of cognitive flexibility. Dev. Sci. 7, 443–455.
Crone, E. A., and Van der Molen, M. W. (2007). Development of decision making in school-aged children and adolescents: evidence from heart rate and skin conductance analysis. Child Dev. 78, 1288–1301.
Dai, D. Y., and Sternberg, R. J. (eds). (2004). Motivation, Emotion and Cognition: Integrative Perspectives on Intellectual Functioning and Development. Mahwah, NJ: Erlbaum.
Dikman, Z. V., and Allen, J. J. B. (2000). Error monitoring during reward and avoidance learning in high- and low-socialized individuals. Psychophysiology 37, 43–54.
Eppinger, B., Mock, B., and Kray, J. (2009). Developmental differences in learning and error processing: evidence from ERPs. Psychophysiology 46, 1043–1053.
Falkenstein, M., Hoormann, J., Christ, S., and Hohnsbein, J. (2000). ERP components on reaction errors and their functional significance. Biol. Psychol. 51, 87–107.
Ferdinand, N. K., Mecklinger, A., and Kray, J. (2008). Error and deviance processing in implicit and explicit sequence learning. J. Cogn. Neurosci. 20, 629–642.
Fischbein, E., Sainati Nello, M., and Sciolis Marino, M. (1991). Factors affecting probabilistic judgements in children and adolescents. Educ. Studies Math. 22, 523–549.
Groen, Y., Wijers, A. A., Mulder, L. J. M., Minderaa, R. B., and Althaus, M. (2007). Physiological correlates of learning by performance feedback in children: a study of EEG event-related potentials and evoked heart rate. Biol. Psychol. 76, 174–187.
Hajcak, G., Moser, J. S., Yeung, N., and Simons, R. F. (2005). On the ERN and the significance of errors. Psychophysiology 42, 151–160.
Heath, N. L., and Glen, T. (2005). Positive illusory bias and the self-protective hypothesis in children with learning disabilities. J. Clin. Child Adolesc. Psychol. 34, 272–281.
Ilgen, D., and Davis, C. (2000). Bearing bad news: reactions to negative performance feedback. Appl. Psychol. 49, 550–565.
Johnson-Laird, P. (1988/1993). The Computer and the Mind. An Introduction to Cognitive Science, 2nd Edn. London: Fontana Press.
Kelly, S. W., Griffiths, S., and Frith, U. (2002). Evidence for implicit sequence learning in dyslexia. Dyslexia 8, 43–52.
Klein, T. A., Neumann, J., Reuter, M., Hennig, J., von Cramon, D. Y., and Ullsperger, M. (2007). Genetically determined differences in learning from errors. Science 318, 1642–1645.
Kosslyn, S. M., Heldmeyer, K. H., and Glass, A. L. (1980). “Where does one part end and another begin?” in Information Integration by Children, eds F. Wilkening, J. Becker, and T. Trabassso (Hillsdale, NJ: Erlbaum), 147–168.
Lange-Küttner, C. (2009). Invited commentary: viewing and attention in children. Acta Paediatr. 98, 1553–1555.
Lange-Küttner, C. (2012). Invited inaugural article: the importance of reaction times for developmental science: what a difference milliseconds make. Int. J. Dev. Sci. 6.
Lashley, K. (1951). “The problem of serial order in behavior,” in Cerebral Mechanisms in Behaviour, ed. L. A. Jeffries (New York: Wiley), 112–136.
Li, K. Z. H., Lindenberger, U., Rünger, D., and Frensch, P. A. (2000). The role of inhibition in the regulation of sequential action. Psychol. Sci. 11, 343–347.
Livesey, P. J., and Little, A. (1971). Sequential learning by children. J. Genet. Psychol. 118, 33–38.
Mareschal, D., and Shultz, T. R. (1999). Development of children’s seriation: a connectionist approach. Connect. Sci. 11, 149–186.
Maybery, M., and O’Brien-Malone, A. (1998). “Implicit and automatic processes in cognitive development,” in Implicit and Explicit Mental Processes, eds K. Kirsner, C. Speelman, M. Maybery, A. O’Brien-Malone, M. Anderson, and C. MacLeod (Mahwah, NJ: Lawrence Erlbaum Associates Publishers), 149–170.
Maybery, M., Taylor, M., and O’Brien-Malone, A. (1995). Implicit learning: sensitive to age but not IQ. Aust. J. Psychol. 47, 8–17.
Meulemans, T., and Van der Linden, M. (1998). Implicit sequence learning in children. J. Exp. Child. Psychol. 69, 199–221.
Miller, S. A., Brownell, C. A., and Zukier, H. (1977). Cognitive certainty in children: effects of concept, developmental level, and method of assessment. Dev. Psychol. 13, 236–245.
Nurmsoo, E., and Robinson, E. J. (2009a). Children’s trust in previously inaccurate informants who were well or poorly informed: when past errors can be excused. Child Dev. 80, 23–27.
Nurmsoo, E., and Robinson, E. J. (2009b). Identifying unreliable informants: do children excuse past inaccuracy? Dev. Sci. 12, 41–47.
Overton, W. F., and Dick, S. (2007). “A competence-procedural and developmental approach to logical reasoning,” in Integrating the Mind. Domain General Versus Domain Specific Processes in Higher Cognition, ed. M. J. Roberts (Hove: Psychology Press), 233–256.
Pasquini, E. S., Corriveau, K. H., Koenig, M., and Harris, P. L. (2007). Preschoolers monitor the relative accuracy of informants. Dev. Psychol. 43, 1216–1226.
Piaget, J. (1952). The Origins of Intelligence in Children. New York, NY: International Universities Press.
Piaget, J., and Inhelder, B. (1975). The Origins of the Idea of Chance in the Child. London: Routledge and Kegan Paul.
Rhodes, B. J., Bullock, D., Verwey, W. B., Averbeck, B. B., and Page, M. P. A. (2004). Learning and production of movement sequences: behavioral, neurophysiological, and modeling perspectives. Hum. Mov. Sci. 23, 699–746.
Riccio, C. A., Hall, J., Morgan, A., and Hynd, G. W. (1994). Executive function and the Wisconsin Card Sorting Test: relationship with behavioral ratings and cognitive ability. Dev. Neuropsychol. 10, 215–229.
Robinson, E. J., and Nurmsoo, E. (2009). When do children learn from unreliable speakers? Cogn. Dev. 24, 16–22.
Rosselli, M., and Ardila, A. (1993). Developmental norms for the Wisconsin Card Sorting Test in 5- to 12-year-old children. Clin. Neuropsychol. 7, 145–154.
Seo, M., Beigi, M., Jahanshahi, M., and Averbeck, B. (2010). Effects of dopamine medication on sequence learning with stochastic feedback in Parkinson’s disease. Front. Syst. Neurosci. 4:36. doi: 10.3389/fnsys.2010.00036
Shanks, D. R., Rowland, L. A., and Ranger, M. S. (2005). Attentional load and implicit sequence learning. Psychol. Res. 69, 369–382.
Sloutsky, V. M., and Fisher, A. V. (2008). Attentional learning and flexible induction: how mundane mechanisms give rise to smart behaviors. Child Dev. 79, 639–651.
Somsen, R. J. M. (2007). The development of attention regulation in the Wisconsin Card Sorting Task. Dev. Sci. 10, 664–680.
Strain, P. S. (1983). Naturalistic assessment of children’s compliance to teachers’ requests and consequences for compliance. J. Appl. Behav. Anal. 16, 243–249.
Terrace, H. S. (1993). The phylogeny and ontogeny of serial memory: list learning by pigeons and monkeys. Psychol. Sci. 4, 162–169.
Terrace, H. S., and McGonigle, B. (1994). Memory and representation of serial order by children, monkeys, and pigeons. Curr. Dir. Psychol. Sci. 3, 180–189.
Thomas, K. M., Hunt, R. H., Vizueta, N., Sommer, T., Durston, S., Yang, Y., and Worden, M. S. (2004). Evidence of developmental differences in implicit sequence learning: an fMRI study of children and adults. J. Cogn. Neurosci. 16, 1339–1351.
Van den Bos, W., Güroglu, B., Van den Bulk, B. G., Rombouts, S. A. R. B., and Crone, E. A. (2009). Better than expected or as bad as you thought? The neurocognitive development of probabilistic feedback processing. Front. Hum. Neurosci. 3:55. doi: 10.3389/neuro.09.052.20091–11
Vinter, A., and Perruchet, P. (2000). Implicit learning in children is not related to age: evidence from drawing behavior. Child Dev. 71, 1223–1240.
Vinter, A., and Perruchet, P. (2002). Implicit motor learning through observational training in adults and children. Mem. Cognit. 30, 256–261.
Waber, D. P., Marcus, D. J., Forbes, P. W., Bellinger, D. C., Weiler, M. D., Sorensen, L. G., and Curran, T. (2003). Motor sequence learning and reading ability: is poor reading associated with sequencing deficits? J. Exp. Child Psychol. 84, 338–354.
Weinert, S. (2009). Implicit and explicit modes of learning: similarities and differences from a developmental perspective. Linguistics 47, 241–271.
Weisz, J. R. (1981). Learned helplessness in Black and White children identified by their schools as retarded and nonretarded: performance deterioration in response to failure. Dev. Psychol. 17, 499–508.
Young, R. (1976). Seriation by Children: An Artificial Intelligence Analysis of a Piagetian Task. Basel: Birkhauser.
Zacks, R. T., Hasher, L., Alba, J., Sanft, H., and Rose, K. C. (1984). Is temporal order encoded automatically? Mem. Cognit. 12, 387–394.
Zimmerman, B. J., and Schunk, D. H. (2004). “Self-regulating intellectual processes and outcomes: a social cognitive perspective,” in Motivation, Emotion and Cognition: Integrating Perspectives on Intellectual Functioning and Development, eds D. Y. Dai, and R. J. Sternberg (Mahwah, NJ: Erlbaum), 312–349.
Appendix
Parameter Fitting of Learning after Positive and Negative Feedback
We fit Bayesian statistical models to the behavior of individual participants. The models allowed us to quantify how much the participants had learned about which sequence or which button was correct in the current block. The Bayesian model allows us to estimate how much positive feedback for a given button press (i.e., a green circle) increased the probability that subjects would press the same button in future trials, as well as how much negative feedback (i.e., a red circle) decreased the probability that subjects would press the same button in future trials. Thus, the model gives us a tool to estimate overall learning rates parametrically, because learning can be equated to the effect of feedback on future button presses. It also gives us the ability to split learning into the effects of positive and negative feedback.
The participants could press either the left or right button at each point in the sequence and therefore they had a binary decision. The model assumed that the participants were trying to optimize the number of times green feedback was received. This can be accomplished by remembering how often green feedback was given for the left (or right) button at each point in the sequence across multiple trials. For example, if green feedback was given more often for the left button for the first movement, then the left button should be pressed. Thus, the model accumulates information about red vs. green feedback given for left and right button presses individually for each of the four button presses in the sequence. The model was based on a binomial likelihood function for each movement of the sequence, given by:
Where θi, j is the probability that pressing button i (i ∈ {left, right}) on movement j (j ∈ {1,‥, 4}) would be followed by green feedback. The variable ri,j, defined below, is the number of times reward (green feedback) was given when button i was pressed on movement j (or red feedback was given when the other button was pressed), and Nj is the number of trials. The vector DT represents the data collected up to trial T for the current block, which in this case are the values of r and N. This was the only data relevant to inferring the correct sequence of button presses.
The probability that the left button should be pressed for movement j after T trials (i.e., that it is more likely to be the correct button) is given by:
We have written the posterior here (i.e., ). Button probabilities were equally likely in the experiment so the prior was flat and the posterior is just the normalized likelihood for this estimate.
In order to better predict participant behavior we added two parameters to the basic model that allowed for differential weighting of positive and negative feedback. The differential weighting was implemented by using the following equation for the feedback:
The subscripts positive and negative indicate whether the feedback was positive (green) or negative (red). The total reward (feedback), in Eq. 1 was then given by:
The parameter u(t) takes a value of one if green feedback was given and zero if red feedback was given on trial t. Thus, α and β scale the amount that is learned from positive and negative feedback. For an ideal observer both parameters would be 0.5. The parameters, α and β were fit to individual participant decision data by maximizing the likelihood of the participant’s sequence of decisions, given the model parameters. Thus, we maximized:
where Ct is the choice that the participant made for each movement at time t (Ct = 1 for left, Ct = 0 for right) and D* indicates the vector of decision data with elements Ct. Here t iterates over the data without explicitly showing sequence boundaries, as this is how the data is analyzed. This function was maximized using non-linear function maximization techniques in Matlab. We also utilized multiple starting values for the parameters (−0.1, 0, 0.1) to minimize the effects of local minima.
Keywords: sequence learning, learning under uncertainty, stochastic feedback, positive and negative feedback
Citation: Lange-Küttner C, Averbeck BB, Hirsch SV, Wießner I and Lamba N (2012) Sequence learning under uncertainty in children: self-reflection vs. self-assertion. Front. Psychology 3:127. doi: 10.3389/fpsyg.2012.00127
Received: 21 February 2012; Accepted: 11 April 2012;
Published online: 03 May 2012.
Edited by:
Jessica S. Horst, University of Sussex, UKReviewed by:
Evan Kidd, Australian National University, AustraliaSarah Creel, University of California at San Diego, USA
Copyright: © 2012 Lange-Küttner, Averbeck, Hirsch, Wießner and Lamba. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Christiane Lange-Küttner, Faculty of Life Sciences, School of Psychology, London Metropolitan University, Room CS2-13, 1 Old Castle Street, E1 7NT, London, UK. e-mail:Yy5sYW5nZWt1ZXR0bmVyQGxvbmRvbm1ldC5hYy51aw==


 Silvia V. Hirsch5
Silvia V. Hirsch5