- Division of Psychology, Nottingham Trent University, Nottingham, UK
The chunking hypothesis suggests that during the repeated exposure of stimulus material, information is organized into increasingly larger chunks. Many researchers have not considered the full power of the chunking hypothesis as both a learning mechanism and as an explanation of human behavior. Indeed, in developmental psychology there is relatively little mention of chunking and yet it can be the underlying cause of some of the mechanisms of development that have been proposed. This paper illustrates the chunking hypothesis in the domain of non-word repetition, a task that is a strong predictor of a child’s language learning. A computer simulation of non-word repetition that instantiates the chunking mechanism shows that: (1) chunking causes task behavior to improve over time, consistent with children’s performance; and (2) chunking causes perceived changes in areas such as short-term memory capacity and processing speed that are often cited as mechanisms of child development. Researchers should be cautious when considering explanations of developmental data, since chunking may be able to explain differences in performance without the need for additional mechanisms of development.
Introduction
The chunking hypothesis (Miller, 1956) suggests that repeated exposure to a stimulus set will lead to the stimuli being represented using larger and larger chunks. That is, when first encountering a stimulus set each item may be coded as an individual chunk, but after repeated exposure several items may be coded as one chunk. The chunking hypothesis is therefore a powerful learning mechanism that suggests that we are constantly monitoring patterns in stimuli and in our environment and are coding the patterns as increasingly larger chunks of knowledge.
The benefit of a chunking mechanism is that it mediates the amount of knowledge that one can process at any one time (Miller, 1956). Information that we use for processing is stored temporarily in short-term memory (Baddeley and Hitch, 1974), often perceived as a bottleneck to our learning (Crain et al., 1990). If the capacity of short-term memory is limited to a finite number of chunks (Miller, 1956; Cowan, 2000; Gobet and Clarkson, 2004) then when the chunks are small, only a small amount of information can be represented in short-term memory; when the chunks are large, a large amount of information can be represented in short-term memory.
Take as an example the learning of new words. The sounds of our language are represented by phonemes, the smallest unit of speech. For the very young child, only a limited amount of spoken information will be stored in short-term memory. Relative to older children, very young children have had little exposure to their native language and therefore they will have little opportunity to chunk phoneme sequences into large chunks. This means children’s early vocabulary acquisition will proceed slowly, because they will find it difficult to represent in short-term memory all of the necessary phoneme sequences that constitute a word. Over time, however, children store increasingly larger chunks of phoneme sequences, meaning that over time, children are able to store all of the necessary phonemes for words, phrases, and even whole utterances within their short-term memory, all because they have chunked the constituent phonemes. There is likely to be a “tipping point” during this developmental trajectory whereby the child has now learned enough chunked phoneme sequences to suddenly be able to store and subsequently learn the phoneme sequences for many new words – predicting the so-called vocabulary spurt that we see in children’s vocabulary acquisition (Gopnik and Meltzoff, 1986; Dromi, 1987; Goldfield and Reznick, 1990).
Although the chunking hypothesis seems to be able to predict phenomena such as the vocabulary spurt, its use in developmental psychology is not extensive. While it is rare to see any criticism of chunking, it is equally rare for chunking to be mentioned at the forefront of any theoretical literature, including developmental theories. This is something of a surprise because Miller himself suggested that a lot more research needed to be done to explore chunking since he believed it to be “the very lifeblood of the thought processes” (Miller, 1956, p. 95).
Obviously no serious researcher would argue against new knowledge being created throughout development. However, while various developmental theories describe different methods of knowledge acquisition (e.g., Piaget’s, 1950, 1952 schemas; Case’s, 1985 automatization), as far as I am aware there is no developmental theory that explicitly references the learning and organization of knowledge that chunking provides. This paper seeks to address this by not only advocating chunking as a mechanism of development but also illustrating why chunking should be considered as an explanation of age-related changes in performance before any other mechanisms of development.
Outside of knowledge, the two most prominent mechanisms of development are probably short-term memory capacity (Case, 1985; Pascual-Leone, 1987; Halford, 1993; Passolunghi and Siegel, 2001) and processing speed (Kail, 1988, 1991). Proponents of short-term memory capacity as a mechanism of development argue that as a child develops, their capacity to temporarily store information increases. A direct consequence of an increase in capacity is that more information can be held and processed at any one time, leading to improved performance. A similar argument is made for processing speed. As children develop, it is proposed that their processing speed increases. The result of an increase in processing speed is that information can now be processed more quickly, leading to improved performance.
Chunking and capacity have a long history within developmental psychology focused mainly in the 1970s and early 1980s, when researchers attempted to establish the extent to which each mechanism could explain developmental change. Proponents of chunking – based on the developmental literature available at the time – concluded that there was insufficient evidence for changes in capacity with age (Chi, 1976). Subsequent work (e.g., Chi, 1977, 1978; Dempster, 1978) seemed to show that chunking could explain age differences in performance without the need for developmental increases in capacity. For example, Dempster (1978) showed that recall of items was strongly influenced by how well the items could be chunked. Stimuli such as digit sequences – being relatively simple to chunk together – had a greater span than stimuli such as non-words that are relatively difficult to chunk together. However, other research argued for developmental changes in capacity based on findings that showed age-related increases in children’s performance when chunking was controlled for (e.g., Huttenlocher and Burke, 1976; Burtis, 1982). To further complicate matters, Case et al. (1982) showed that processing speed was highly correlated with capacity, with any differences in capacity being removed when processing speed was controlled for. Further research has also supported processing speed as a mechanism of development (e.g., Kail, 1988, 1991). One might think that arguments for and against different mechanisms of development may have been reconciled in the last three decades. Unfortunately not – there is still no consensus regarding the extent to which developmental changes in task performance are caused by capacity, processing speed, and changes to knowledge via chunking (e.g., Halford et al., 2007; Jones et al., 2008).
There are arguably two problems with past research examining chunking, capacity, and processing speed. First, there is sometimes little thought as to how these mechanisms interact with one another. For example, if we can process information more quickly then it stands to reason that we would be able to maintain more information within a limited short-term memory capacity – but how much more, and is it a linear increase or an exponential one? Second, although some of the studies try and hold one mechanism constant across ages, it is unlikely that this has been accomplished. For example, some studies attempt to ensure that children of all ages have learnt the same chunks on a task by either training all children on particular aspects of the task (e.g., Huttenlocher and Burke, 1976) or selecting materials that would be expected to be chunked by all children (e.g., Burtis, 1982). However, this does not mean that children are equated for the chunks they use when performing a task. Older children are likely to use a broader range of chunks to complete a task than younger children because older children have learnt a greater number of chunks than younger children, owing to their greater real-world experience. Even if young and old children were matched for chunked knowledge, the use of those chunks is likely to be more efficient for older children (e.g., Servan-Schreiber and Anderson, 1990).
Computational modeling is an approach whereby all mechanisms have to be fully specified because the aim of a computational model is to simulate human behavior. A computational model of a developmental task may therefore have to specify capacity limitations, how chunks are learnt, and how quickly information is processed. The beauty of this approach is that some aspects of the model can be held constant in order to investigate how performance changes for those processes that were allowed to vary. I will therefore examine a computational model that incorporates plausible accounts of chunking, processing speed, and capacity in order to examine whether an increase in the number of chunks that are known by the model can account for age-related increases in task performance that are seen in children.
The developmental task that will be used to demonstrate the chunking hypothesis explanation of developmental change is non-word repetition. This task involves accurately repeating a nonsense word (non-word) after it has been spoken aloud by the experimenter. Non-word repetition is an ideal task for a chunking hypothesis to simulate because it consistently shows developmental change, with older children reliably out-performing younger children (Gathercole and Baddeley, 1989; Jones et al., 2007).
This paper will show how the chunking hypothesis not only demonstrates developmental change in non-word repetition, but also how chunking causes perceived changes in short-term memory capacity and perceived changes in processing speed – even though both of these will be fixed within the simulations. I first describe a computational model of non-word repetition that instantiates the chunking hypothesis. Second, I illustrate how the results of the model show developmental change and how the chunking hypothesis explains other developmental mechanisms such as processing speed. Finally, I conclude by detailing the implications of the results presented.
Chunking Hypothesis Model of Non-Word Repetition
The computational instantiation of the chunking hypothesis (Jones et al., 2007, 2008; Jones, 2011) is based in Elementary Perceiver and Memorizer (EPAM, Feigenbaum and Simon, 1984). A fuller description of the model can be found in the Appendix. However, the modeling environment is not overly important since the method of chunking is very straightforward, as is the method by which capacity constrains the amount of information that is heard by the model and how new chunks are learnt by the model. Let me consider each in turn, before I describe how the model performs the non-word repetition test.
Method of Chunking
Input to the model consists of any word or utterance in its phonemic form (e.g., 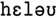 ([“hello”],
([“hello”], 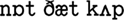 [“not that cup”]). For any given phonemic input, the model encodes the input in as few chunks as possible, based on its existing knowledge of chunked phoneme sequences. For example, if the model has already learnt as chunks the phoneme sequences “
[“not that cup”]). For any given phonemic input, the model encodes the input in as few chunks as possible, based on its existing knowledge of chunked phoneme sequences. For example, if the model has already learnt as chunks the phoneme sequences “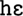 ” and “
” and “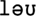 ,” then “hello” could be encoded using two chunks; similarly if the words “
,” then “hello” could be encoded using two chunks; similarly if the words “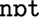 ,” “
,” “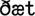 ,” and “
,” and “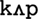 ” existed as chunks, then the phrase “not that cup” could be encoded as three chunks, even though it is nine phonemes in length.
” existed as chunks, then the phrase “not that cup” could be encoded as three chunks, even though it is nine phonemes in length.
Method of Limiting Short-Term Capacity
In line with the working memory model (Baddeley and Hitch, 1974), a highly influential model of short-term memory, the capacity for verbal information is set at 2,000 ms. Information that requires less time than 2,000 ms can be reliably stored, albeit temporarily, in working memory. Once this capacity is exceeded however, then the temporary storage of auditory information becomes unreliable.
The EPAM model of phoneme chunk learning assigns a time to encode each chunk that varies depending on the size of the chunk. The allocation of a time to encode a chunk stems from a reconciliation of the chunking account of short-term memory (e.g., Simon, 1974) and the time-based account of short-term memory (e.g., Baddeley, 1981). Based on a series of studies involving span and reading measures for Chinese and English words and characters, Zhang and Simon (1985) found that the time to encode a chunk was roughly 400 ms and the time to encode each phoneme in a chunk was roughly 30 ms, excluding the first phoneme1.
Note that there is no limit to the size of a chunk and any given input is represented by as few chunks as possible. There are other more complex views of chunk learning and chunk matching. For example, Servan-Schreiber and Anderson (1990) suggest that chunks compete with one another for representing a given input, with the winning chunk(s) being selected based on the usage of each chunk and its sub-chunks. A usage-based account is also used in part by Pothos (2010) when explaining how entropy can be used to account for artificial grammar learning. Pothos suggests that bigrams and trigrams (i.e., chunks of two or three items) that are encountered in the learning phase of the artificial grammar are used to compare to novel test strings in order to determine whether the novel strings are grammatical or not. This previous research could have been used to include a selection process for chunks that are in competition with one another and a parameter could have been set to limit chunk length to a particular number of elements (e.g., Dirlam, 1972, suggests that chunk sizes of 3 or 4 are the most efficient). However, my goal is to provide the most parsimonious explanation of the effects seen. I therefore minimize the number of parameters in the model and when I am forced into using a parameter, its value is set based on previous literature rather than any of my own research. The model therefore uses the timing estimates of Zhang and Simon (1985) without additional mechanisms relating to the encoding of chunks. The chunks “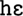 ” and “
” and “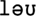 ” would therefore each be assigned a time of 430 ms to be encoded irrespective of how often each chunk had been used previously. The 430 ms is calculated from 400 ms to encode the chunk and an additional 30 ms to encode the “
” would therefore each be assigned a time of 430 ms to be encoded irrespective of how often each chunk had been used previously. The 430 ms is calculated from 400 ms to encode the chunk and an additional 30 ms to encode the “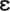 ” and the “
” and the “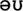 ” in each chunk (note: “
” in each chunk (note: “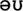 ” is a diphthong and is classed as one phoneme). Similarly, each of the chunked words in “not that cup” [
” is a diphthong and is classed as one phoneme). Similarly, each of the chunked words in “not that cup” [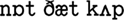 ] would take 460 ms to encode, since each chunk has two additional phonemes.
] would take 460 ms to encode, since each chunk has two additional phonemes.
The benefit of chunking one’s knowledge should be clear when one considers capacity limitations. Take for example the utterance “not that cup.” When each of the words are chunked, then the utterance can be reliably encoded (3 × 460 ms = 1,380 ms). However, before any chunking of phoneme sequences takes place, each phoneme would need to be encoded as a single chunk and therefore the utterance would require 9 × 400 ms = 3,600 ms to be encoded. Since the capacity for verbal information is 2,000 ms, the utterance would fail to be reliably encoded. When this occurs, the encoding of each chunk is probabilistic, based on the capacity available (2,000 ms) and the length of time it will take to encode the whole sequence (3,600 ms): the probability of encoding each chunk would therefore be 2,000/3,600 = 0.56. This provides a simple illustration of how, when capacity is exceeded, the information in short-term memory is compromised.
Method of Learning New Chunks
Once an input has been encoded as chunks, the model can learn new chunks. The method for learning a new chunk is very simple: two chunks that are adjacent in the encoded list of chunks, provided both have been reliably encoded, can be chunked together to become one chunk. For example, the word “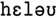 ,” if no phoneme sequences had been chunked in the model, would be encoded as four single phoneme chunks “
,” if no phoneme sequences had been chunked in the model, would be encoded as four single phoneme chunks “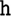 ,” “
,” “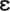 ,” “
,” “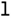 ,” and “
,” and “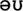 .” Since the four chunks can be encoded reliably (4 × 400 ms = 1,600 ms) then a new chunk can be learned for each set of adjacent chunks: that is, a new chunk for each of the following phoneme sequences: “
.” Since the four chunks can be encoded reliably (4 × 400 ms = 1,600 ms) then a new chunk can be learned for each set of adjacent chunks: that is, a new chunk for each of the following phoneme sequences: “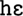 ,” “
,” “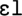 ,” and “
,” and “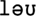 .” If “hello” was presented to the model again, it could now be encoded using two chunks (“
.” If “hello” was presented to the model again, it could now be encoded using two chunks (“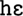 ” and “
” and “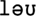 ”) and subsequent learning would create a new chunk that joined these two phoneme sequences together.
”) and subsequent learning would create a new chunk that joined these two phoneme sequences together.
When an utterance can only be encoded in a time that exceeds the 2,000 ms capacity limit, then each chunk cannot be encoded reliably. As shown earlier, when capacity is exceeded, the reliable encoding of chunks becomes probabilistic. Learning will only proceed for adjacent chunks that have been reliably encoded, thus reducing the amount of learning that can take place when short-term memory capacity is compromised.
Performing the Non-Word Repetition Test
In order to learn chunked phoneme sequences, the model is trained on a linguistic input that mirrors the style of input that children receive. At the beginning of training therefore, the model is presented with mother’s utterances from interactions with 2- to 3-year-old children from the Manchester corpus (Theakston et al., 2001) on CHILDES (MacWhinney, 2000). There are an average of 25,519 mother’s utterances per child (range 17,474–33,452), each of which is converted to phonemes. Later on in the model’s training, sentences from books aimed at 4- to 5-year-old children (converted to phonemes) are included as part of the training regime in order to approximate the increased diversity in young children’s language input. The inclusion of the sentences gradually increases as more input is presented to the model and replaces mother utterances. For example, Anne’s mother produces 31,393 utterances2. The model is presented with 31,393 lines of input but sentences from books form an increasingly larger proportion of the input over time. Figure 1 illustrates the relative proportion of mother’s utterances and sentences from books that are seen over time for the “Anne” dataset. The model is able to perform a non-word repetition test early on in its training (to compare performance against 2- to 3-year-old children) and later on in its training (to compare performance against 4- to 5-year-old children).
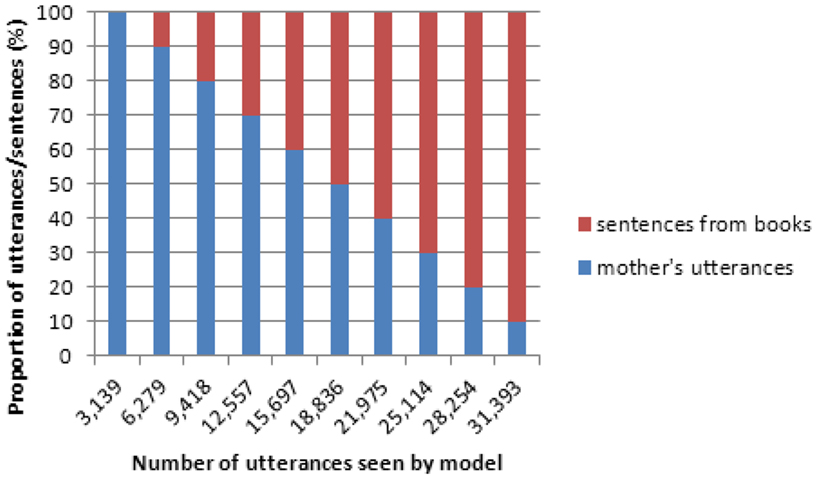
Figure 1. Proportion of mother’s utterances and sentences from books that are used as input at each stage of the model’s learning, for the “Anne” dataset.
For each presentation of an input utterance or sentence, the processes described in the above sections are carried out – that is, encoding the input into as few chunks as possible, attempting to reliably store the encoded chunks in short-term memory, and learning new chunks from the stored input. It has probably not gone unnoticed that the learning of new chunks occurs rapidly – but given that the language input that the model receives is but a tiny fraction of the language that children hear, it makes sense to have learning occur whenever possible. However, reducing the learning rate has been successful for other variants of EPAM models (e.g., Croker et al., 2003).
Non-word repetition tests are relatively straightforward in the model – the non-word must first be reliably encoded and then it must be articulated correctly. Each non-word is presented to the model in the same way that an input utterance is presented. If the non-word can be encoded reliably within short-term memory capacity, then the model attempts to articulate it correctly. Correct articulation is based on both the number of chunks that are required to represent the non-word together with the frequency of those chunks. Put simply, if one can encode a non-word using very few chunks, it stands to reason that the probability of correctly articulating the constituent phonemes within the chunks should be greater than that for non-words that are encoded using a large number of chunks. Similarly, it stands to reason that the frequency with which a chunk is encoded when parsing the native language will influence one’s ability to correctly articulate the phonemes within the chunk. Note that when a non-word fails to be reliably encoded, the non-word is said to be repeated incorrectly.
Simulation
The model is compared to the children’s non-word repetition results of Jones et al. (2007). As Figures 2 and 3 show, the model provides a good fit to the data3: correlations are 0.99 between the early model and the 2- to 3-year-old data and 0.96 between the late model and the 4- to 5-year-old data; RMSE scores are 4.55 when comparing the early model with the 2- to 3-year-old children and 3.87 when comparing the late model with the 4- to 5-year-old children. The RMSE scores indicate the percentage discrepancy between the NWR performance of the model and the NWR performance of the children. Developmental research involving children’s problem solving suggests that an RMSE of approximately 5% would indicate a very good fit between data and model (Jones et al., 2000). The RMSE scores in the current research indicate that across non-word lengths, the NWR score of the early model averages to be within 4.55% of the 2- to 3-year-old children. The late model averages a NWR score that is within 3.87% of the 4- to 5-year-old children. The model not only closely matches the trends in the child data but it also matches closely the actual repetition performance of the children.
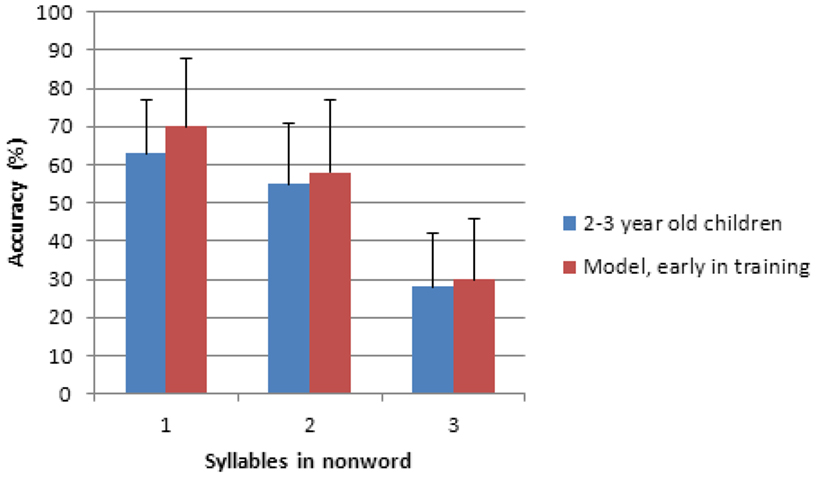
Figure 2. Two- to three-year-old children’s non-word repetition performance together with the model’s performance early in its training. Error bars indicate standard deviation.
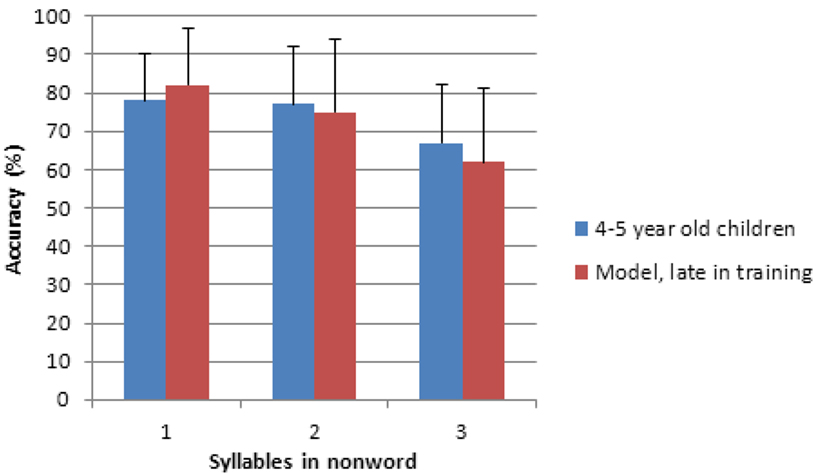
Figure 3. Four- to five-year-old children’s non-word repetition performance together with the model’s performance late in its training. Error bars indicate standard deviation.
While the fit to the child data is undoubtedly of importance it is a secondary concern for the current paper, since my aim is to show how the chunking hypothesis is able to cause perceived changes in mechanisms that have been suggested to underlie developmental change. Let us summarize, therefore, how the chunking hypothesis model captures the child data: (1) over time, the model learns chunks of phoneme sequences; (2) by chunking the linguistic input into increasingly larger chunks of phoneme sequences, the model is able to store larger and larger amounts of information within a fixed short-term memory capacity; and (3) the combination of (1) and (2) mean that the model is more able to repeat non-words correctly when there are a large amount of chunked sequences within the model rather than a small amount of chunked sequences – therefore developmental differences in non-word repetition arise purely from children accruing a greater amount of phonological knowledge.
Table 1 shows how the chunks involved in three different non-words change over time in the model. If we consider only the three example non-words shown, two of the three would fail to be reliably encoded early on in the model’s training (i.e., after the model has only been subjected to a small amount of the linguistic input). However, all three are reliably encoded after the model has processed a large amount of the linguistic input. That is, early on in training there is the appearance that long non-words (e.g., three syllable non-words) are difficult for the child to store in short-term memory whereas later in training there is the appearance that long non-words are relatively easy for the child to store in short-term memory. Note how short-term memory capacity has not changed – it is fixed at 2,000 ms of auditory information – but through chunking, the amount of information that can fit into the 2,000 ms increases over time. Therefore chunking can give the perception that short-term memory capacity increases with age.
Table 1 also shows the time taken to encode each of the non-words. It is clear that as the model is subjected to larger and larger amounts of the linguistic input, the time taken to encode a non-word declines. That is, there is a perception that processing speed has increased because the same amount of information is now being processed (encoded) in a reduced length of time. Therefore chunking can give the perception that processing speed increases with age.
Discussion
A computational model has been presented that incorporates plausible accounts of chunking, short-term memory capacity, and processing speed. The model was presented with naturalistic phonemic input and gradually learnt increasingly larger chunks of phonemic knowledge. By holding capacity and processing speed constant and only allowing the number of chunks to vary, it was shown that when the model had been presented with only a small amount of linguistic input it was able to match the NWR performance of 2- to 3-year-old children; when the model had been presented with a large amount of linguistic input, it was able to match the NWR performance of 4- to 5-year-old children. That is, developmental changes in NWR performance were accounted for solely by increases in the amount of chunked linguistic knowledge. The model shows that changes to developmental mechanisms such as capacity and processing speed may not be necessary to explain age-related changes in some developmental tasks.
The results support other developmental literature that has shown how chunking is able to show developmental differences in task performance without the need for additional mechanisms of development. For example, Freudenthal et al. (2007) have shown how optional infinitive errors in children’s speech across four different languages can primarily be explained by the chunking of phrases and utterances based on their statistical properties within the input across each of the languages. Chi (1978) has shown how child chess experts have smaller memory spans than adult chess novices for remembering digit sequences; yet child chess experts have significantly larger memory spans than adult chess novices for remembering pieces from familiar chess positions. The explanation for these effects is that child chess experts have a larger array of chunked knowledge for chess positions than adult chess novices but the reverse is true for digit sequences. Arguably there are also connectionist models that learn in a way that is somewhat analogous to chunking. For example, Plunkett and Marchman (1993) show how gradually increasing the number of utterances that are presented as training results in a developmental profile for past-tense verb inflections that is similar to young children. In particular, the network undergoes reorganizations that enable shifts in performance. Reorganizing knowledge is exactly the type of function that chunking performs.
I do not deny that age differences in NWR can also be accounted for by increases in short-term memory capacity and by increases in processing speed. If children’s capacity for temporarily storing information increased with age, then older children would be able to store more linguistic information in short-term memory than their younger counterparts. This would enable older children to out-perform younger children on tests of non-word repetition. Similarly, if the speed by which children process information increased with age, then it stands to reason that at any one time older children will be able to process more information than younger children – leading to improved NWR performance for older children over younger children.
However, the one aspect of child development that all researchers should agree upon is that the child’s knowledge base increases with age – which is exactly what occurs with the chunking hypothesis. The simplicity of chunking hides the fact that it is a very powerful learning mechanism. Coupled with a plausible account of short-term memory, I have shown how chunking can cause developmental changes that had previously been assumed to require mechanisms over and above simple increases in accrued knowledge, such as increases in short-term memory capacity or processing speed. Moreover, the computational model of the chunking hypothesis shows how chunking can cause perceived changes in capacity and perceived changes in processing speed – even though these were both held constant.
The purpose of this paper is not to dismiss the potential roles of capacity and processing speed in children’s development. Rather, the purpose is to highlight that capacity and processing speed should not be considered as the causes of developmental change on a task before changes to the child’s knowledge base have been considered as an explanation. If changes to knowledge are found to play a primary role in explaining developmental changes in task performance, then one needs to ask whether matters should be complicated by adding developmental mechanisms that may not be necessary to explain the data at hand.
This paper has asked whether the most agreed upon mechanism of development – changes to knowledge – is sufficient to explain a range of developmental phenomena. The research shows that since there are no serious arguments against the chunking hypothesis; since it is a very simple yet powerful learning mechanism; and since it is able to explain developmental differences in task behavior, it makes sense for developmental researchers to see whether chunking can provide an explanation for any age effects that are seen in developmental tasks before considering explanations such as capacity and processing speed.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Footnotes
- ^Zhang and Simon (1985) based their estimates on syllables; since our model is based on phonemes we convert the syllable matching time of 90 ms to a time of 30 ms to match a phoneme, since the majority of English monosyllables are three phonemes in length.
- ^To give an idea of type/token ratios, Anne’s mother’s utterances consisted of 8,257 utterance types and 17,967 utterance tokens. It is interesting to note, however, that on average, the maternal utterances only contain 3,046 unique words.
- ^To give an idea of the learning that took place in the model, on average 25,698 chunks were created during the learning phase.
References
Baddeley, A. D. (1981). The concept of working memory: a view of its current state and probable future development. Cognition 10, 17–23.
Baddeley, A. D., and Hitch, G. J. (1974). “Working memory,” in The Psychology of Learning and Motivation: Advances in Research and Theory, ed. G. Bower (New York, NY: Academic Press), 47–90.
Baddeley, A. D., Thompson, N., and Buchanan, M. (1975). Word length and the structure of short-term memory. J. Verbal Learn. Verbal Behav. 14, 575–589.
Burtis, P. J. (1982). Capacity increase and chunking in the development of short-term memory. J. Exp. Child. Psychol. 34, 387–413.
Case, R., Kurland, D. M., and Goldberg, J. (1982). Operational efficiency and the growth of short-term memory span. J. Exp. Child. Psychol. 33, 386–404.
Chi, M. T. H. (1976). Short-term memory limitations in children: capacity or processing deficits? Mem. Cognit. 4, 559–572.
Chi, M. T. H. (1978). “Knowledge structures and memory development,” in Children’s Thinking: What Develops? ed. R. S. Siegler (Hillsdale, NJ: LEA), 73–96.
Cowan, N. (2000). The magical number 4 in short-term memory: a reconsideration of mental storage capacity. Behav. Brain Sci. 24, 87–185.
Crain, S., Shankweiler, D., Macaruso, P., and Bar-Shalom, E. (1990). “Working memory and sentence comprehension: investigations of children with reading disorders,” in Impairments of Short-Term Memory, eds G. Vallar and T. Shallice (Cambridge: Cambridge University Press), 539–552.
Croker, S., Pine, J. M., and Gobet, F. (2003). “Modelling children’s negation errors using probabilistic learning in MOSAIC,” in Proceedings of the Fifth International Conference on Cognitive Modeling, eds F. Detje D. Dörner, and H. Schaub (Bamberg: Universitäts-Verlag), 69–74.
Daehler, M. W., Horowitz, A. B., Wynns, F. C., and Flavell, J. H. (1969). Verbal and non-verbal rehearsal in children’s recall. Child Dev. 40, 443–452.
Dempster, F. N. (1978). Memory span and short-term memory capacity: a developmental study. J. Exp. Child. Psychol. 26, 419–431.
Feigenbaum, E. A., and Simon, H. A. (1984). EPAM-like models of recognition and learning. Cogn. Sci. 8, 305–336.
Freudenthal, D., Pine, J. M., Aguado-Orea, J., and Gobet, F. (2007). Modelling the developmental patterning of finiteness marking in English, Dutch, German and Spanish using MOSAIC. Cogn. Sci. 31, 311–341.
Gathercole, S. E., and Baddeley, A. D. (1989). Evaluation of the role of phonological STM in the development of vocabulary in children: a longitudinal study. J. Mem. Lang. 28, 200–213.
Gobet, F., and Clarkson, G. (2004). Chunks in expert memory: evidence for the magical number four … or is it two? Memory 12, 732–747.
Goldfield, B. A., and Reznick, J. S. (1990). Early lexical acquisition: rate, content, and the vocabulary spurt. J. Child Lang. 17, 171–184.
Gopnik, A., and Meltzoff, A. (1986). Relations between semantic and cognitive development in the oneword stage – the specificity hypothesis. Child Dev. 57, 1040–1053.
Halford, G. S. (1993). Children’s Understanding: The Development of Mental Models. Hillsdale, NJ: Lawrence Erlbaum Associates.
Halford, G. S., Cowan, N., and Andrews, G. (2007). Separating cognitive capacity from knowledge: a new hypothesis. Trends Cogn. Sci. 11, 236–242.
Huttenlocher, J., and Burke, D. (1976). Why does memory span increase with age? Cogn. Psychol. 8, 1–31.
Jones, G. (2011). A computational simulation of children’s performance across three nonword repetition tests. Cogn. Syst. Res. 12, 113–121.
Jones, G., Gobet, F., and Pine, J. M. (2007). Linking working memory and long-term memory: a computational model of the learning of new words. Dev. Sci. 10, 853–873.
Jones, G., Gobet, F., and Pine, J. M. (2008). Computer simulations of developmental change: the capacity and long-term knowledge. Cogn. Sci. 32, 1148–1176.
Jones, G., Ritter, F. E., Wood D. J. (2000). Using a cognitive architecture to examine what develops. Psychol. Sci. 11, 93–100.
Kail, R. (1988). Developmental functions for speeds of cognitive processes. J. Exp. Child. Psychol. 45, 339–364.
Kail, R. (1991). Developmental change in speed of processing during childhood and adolescence. Psychol. Bull. 109, 490–501.
MacWhinney, B. (2000). The CHILDES Project: Tools for Analyzing Talk, 3rd Edn. Mahwah, NJ: Lawrence Erlbaum Associates.
Miller, G. A. (1956). The magical number seven, plus or minus two: some limits on our capacity for processing information. Psychol. Rev. 63, 81–97.
Pascual-Leone, J. (1987). Organismic processes for neo-Piagetian theories: a dialectical causal account of cognitive development. Int. J. Psychol. 22, 531–570.
Passolunghi, M. C., and Siegel, L. S. (2001). Short-term memory, working memory and inhibitory control in children with difficulties in arithmetic problem solving. J. Exp. Child. Psychol. 80, 44–57.
Piaget, J. (1952). The Origins of Intelligence in Children. New York, NY: International Universities Press.
Plunkett, K., and Marchman, V. (1993). From rote learning to system building: acquiring verb morphology in children and connectionist nets. Cognition 48, 21–69.
Pothos, E. M. (2010). An entropy model for artificial grammar learning. Front. Psychology 1:16. doi:10.3389/fpsyg.2010.00016
Servan-Schreiber, E., and Anderson, J. R. (1990). Learning artificial grammars with competitive chunking. J. Exp. Psychol. Learn. Mem. Cogn. 16, 592–608.
Theakston, A. L., Lieven, E. V. M., Pine, J. M., and Rowland, C. F. (2001). The role of performance limitations in the acquisition of verb-argument structure: an alternative account. J. Child Lang. 28, 127–152.
Zhang, G., and Simon, H. A. (1985). STM capacity for Chinese words and idioms: chunking and acoustical loop hypothesis. Mem. Cognit. 13, 193–201.
Appendix
Model Details
This section provides additional information regarding the model. In particular, it details how chunks are represented in the model and how capacity and processing speed are specified.
Representing Chunks
Chunks within the model are hierarchical and contain sequences of one phoneme or more. As one proceeds further down the chunk hierarchy, chunks get progressively larger – thus the chunked knowledge is represented as a tree-like structure. For example, the word “cup” might have been progressively chunked, with “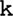 ” having the chunk “
” having the chunk “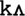 ” below it, which in turn is above the chunk “
” below it, which in turn is above the chunk “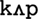 .” The hierarchical structure means that the temporal sequence of phonemes is maintained – therefore chunks further down the hierarchy contain the phoneme sequence of their parent chunk plus additional phoneme(s) that occurred after the parent phoneme sequence in the input. The link between each parent and child chunk contains the additional phoneme(s). An example hierarchy of chunks is given in Figure A1. Here it can be seen that the model has chunked each of the words “Cup,” “Can,” and “Cap.”
.” The hierarchical structure means that the temporal sequence of phonemes is maintained – therefore chunks further down the hierarchy contain the phoneme sequence of their parent chunk plus additional phoneme(s) that occurred after the parent phoneme sequence in the input. The link between each parent and child chunk contains the additional phoneme(s). An example hierarchy of chunks is given in Figure A1. Here it can be seen that the model has chunked each of the words “Cup,” “Can,” and “Cap.”
Representing Capacity and Processing Speed
Following from the work of Zhang and Simon (1985), capacity is time-based in order to incorporate both a capacity mechanism and a method by which processing speed can be represented. Information in short-term memory has a temporal duration of 2,000 ms unless rehearsed (e.g., Baddeley et al., 1975). Since the results of the model are compared to 2- to 5-year-old children who show little sign of rehearsal (e.g., Daehler et al., 1969), the model does not include a method by which items in short-term memory can be rehearsed.
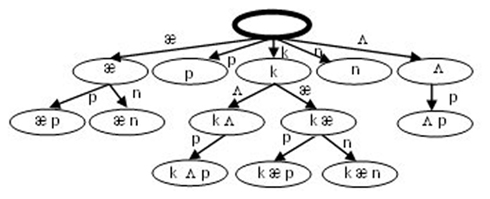
Figure A1. An example of a chunk hierarchy within the model. In this instance, the chunks for “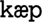 ,” “
,” “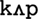 ,” and “
,” and “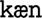 ” have each been learnt incrementally. Each chunk is represented by an ellipse. The topmost chunk (the “root”) is always empty.
” have each been learnt incrementally. Each chunk is represented by an ellipse. The topmost chunk (the “root”) is always empty.
Based on the work of Zhang and Simon (1985), a time is allocated to access/encode a chunk and its constituent phonemes. It takes 400 ms to access and encode a chunk plus an additional 30 ms for each phoneme in the chunk except the first phoneme. These timings are used when the model is presented with an input utterance. For example, let us assume that the input utterance “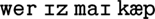 ” (“where’s my cap?”) can be encoded using four chunks, one for each word. The time to represent this input would therefore be 400 + (2 × 30) + 400 + (1 × 30) + 400 + (1 × 30) + 400 + (2 × 30) = 1,780 ms (noting that
” (“where’s my cap?”) can be encoded using four chunks, one for each word. The time to represent this input would therefore be 400 + (2 × 30) + 400 + (1 × 30) + 400 + (1 × 30) + 400 + (2 × 30) = 1,780 ms (noting that 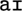 is a diphthong and is therefore one phoneme only).
is a diphthong and is therefore one phoneme only).
Note how chunking is critical in determining the time to access a given input. If the model had not yet learnt the chunk for “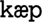 ” and (for example) required the two chunks “
” and (for example) required the two chunks “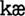 ” and “
” and “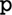 ” to represent it, then the encoding time would be 2,150 ms and therefore capacity would be compromised.
” to represent it, then the encoding time would be 2,150 ms and therefore capacity would be compromised.
Keywords: chunking, computational modeling, cognitive development, developmental change, non-word repetition, short-term memory capacity, processing speed
Citation: Jones G (2012) Why chunking should be considered as an explanation for developmental change before short-term memory capacity and processing speed. Front. Psychology 3:167. doi: 10.3389/fpsyg.2012.00167
Received: 14 December 2011; Accepted: 10 May 2012;
Published online: 15 June 2012.
Edited by:
Emmanuel Pothos, Swansea University, UKCopyright: © 2012 Jones. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Gary Jones, Division of Psychology, Nottingham Trent University, Chaucer Building, Nottingham NG1 5LT, UK. e-mail:Z2FyeS5qb25lc0BudHUuYWMudWs=.