Evidence Accumulator or Decision Threshold – Which Cortical Mechanism are We Observing?

Most psychological models of perceptual decision making are of the accumulation-to-threshold variety. The neural basis of accumulation in parietal and prefrontal cortex is therefore a topic of great interest in neuroscience. In contrast, threshold mechanisms have received less attention, and their neural basis has usually been sought in subcortical structures. Here I analyze a model of a decision threshold that can be implemented in the same cortical areas as evidence accumulators, and whose behavior bears on two open questions in decision neuroscience: (1) When ramping activity is observed in a brain region during decision making, does it reflect evidence accumulation? (2) Are changes in speed-accuracy tradeoffs and response biases more likely to be achieved by changes in thresholds, or in accumulation rates and starting points? The analysis suggests that task-modulated ramping activity, by itself, is weak evidence that a brain area mediates evidence accumulation as opposed to threshold readout; and that signs of modulated accumulation are as likely to indicate threshold adaptation as adaptation of starting points and accumulation rates. These conclusions imply that how thresholds are modeled can dramatically impact accumulator-based interpretations of this data.

1. The Threshold Concept in Abstract Decision-Making Models

Simple perceptual decision-making is typically thought to involve some kind of weighing of evidence. According to this story, sensory data is repeatedly sampled in order to build confidence that one decision option is correct, and the others incorrect.

Accumulating evidence is only half the battle when making a decision, however. The other half requires that a subject have a physically implemented policy governing the termination of evidence collection and the transition into action. Indeed, many of the most important results in decision theory consist of carefully designed stopping rules that terminate decisions. These policies result in hypothesis-testing procedures that are optimal or near-optimal according to some objective function. Psychological modelers are therefore naturally guided to focus on decision rules as an important source of performance adaptation in humans and other animals.

A common view in neuroscience, in contrast, is premised on the routine finding that firing rates of suspected accumulator-neurons reach a fixed threshold near the time of a behavioral response, suggesting that the critical level that causes responding or decision commitment (in monkeys at least) is close to the peak firing rate. Performance by these animals (their response times and accuracy) is therefore thought to be adapted by changing the rate, starting point, or starting time of evidence accumulation.

Once constraints on how networks of neurons can compute are taken into consideration, pressing theoretical questions arise for both views of performance adaptation. First, how can accumulating evidence produce a behavioral response when it exceeds a critical level by some small value, but not when it is just slightly below that level? Further, once a model of a threshold mechanism is proposed that answers this question, how can physiological signs of its operation be discriminated from signs of evidence accumulation? Finally, is behavioral performance adapted by modulating the activity of accumulators, thresholds, or both?

Here I formally define some basic, unavoidable physical assumptions about decision-threshold mechanisms, and I consider how these must affect interpretations of neural data. I argue that firing-rate data commonly thought to be observations of accumulators in action may instead be observations of threshold mechanisms, and that mistaken identities of this sort may be the source of an apparent conflict between findings in neuroscience (fixed thresholds) and findings in psychology (strategically controlled thresholds).

I show that this conflict eases if neural accumulators have sometimes been confused with neural threshold mechanisms. As I demonstrate with a simple decision-making model, the final-firing-rate-premise of the fixed-threshold account actually implies very little, if we allow for threshold mechanisms to send positive feedback to accumulators – a concept consistent with anatomical patterns of connectivity in parietal and prefrontal cortex. With this addition to an otherwise purely feedforward model, threshold mechanisms can serve to lift accumulators to a common final level of activation near the time of responding, even when different levels actually trigger decision commitment under different task conditions. These theoretical considerations suggest that physiological data is frequently ambiguous regarding the locus of decision-circuit control.

2. Implications for Mapping Decision-Making Processes onto Brain Activity

In this section, I present a generic model of a neural threshold mechanism inspired by the individual neuron’s action potential threshold. I then discuss what its implementation at the cortical population level would predict in terms of a firing-rate profile during threshold-crossing (while acknowledging that this threshold model could in fact be implemented subcortically). If the model is correct, these predictions imply that some current interpretations of single-unit recordings from monkeys performing perceptual decision-making and visual search tasks may need to be revised.

2.1. Neural Implementations of Abstract Decision-making Models Require Physical Threshold Mechanisms

Decision thresholds traditionally play an important role in psychology in explaining one of the most salient features of human perceptual categorization. This is that spending more time observing a stimulus tends to increase decision accuracy regarding which category the stimulus belongs to. Such speed-accuracy tradeoffs are easily explained as a process of accumulation to threshold: to make a decision, evidence must accumulate to a point that a decision-threshold is crossed and an action is triggered. Higher thresholds imply greater accuracy (less chance of crossing the wrong threshold), but longer response times (the decision variable has a greater distance to travel). Furthermore, just as incentives are hypothesized to change category boundaries in signal detection theory (Green and Swets, 1966), top-down control strategies have been hypothesized to adapt decision thresholds in response-time tasks in order to modify speed-accuracy tradeoff functions (see Luce, 1986)¹.

This basic scheme of accumulation-to-threshold is implemented by most decision models, although even simpler, non-evidence-accumulating models can account for speed-accuracy tradeoffs (e.g., the “urgency-gating” model of Cisek et al., 2009, which responds whenever an unusually favorable sample of evidence arrives and weights evidence by a ramping urgency signal; or purely ballistic models that sample evidence only at one instant, such as the ballistic accumulator model of Brown and Heathcote, 2005, and the LATER model of saccade response times, Reddi and Carpenter, 2000). In addition, recent accumulation-based modeling approaches attempt to account for physiological evidence of fixed thresholds by adapting baseline levels of activity in competing response channels. Adapting baseline activity results in an effective change of threshold height without any change in the level of channel-activation necessary to make a response (Bogacz et al., 2010b; see also van Ravenzwaaij et al., 2011). This approach is similar but not identical to decision-threshold adaptation. Activating a response channel in these models must initiate a decision process based on accumulated noise that will ultimately culminate in a decision, even if no stimulus is present. Actual decision-threshold adaptation, in contrast, can be achieved without producing any response until a stimulus is present, allowing for top-down control to be exerted over arbitrarily long delays prior to stimulus onset.

In all cases, however, decisions must not be initiated before some critical level of evidence or some other quantity either accumulates or is momentarily sampled. Before committing to a particular decision – a period that may theoretically last an arbitrarily long time – the motor system is often assumed to receive no input from the evidence-weighing process. Thus a physical barrier must be assumed, which, once exceeded, leads inexorably to a particular outcome, but below which no response is possible. What sort of non-linear transformation of the net evidence or the “urgency to respond” can meet this specification and be implemented physically?

The simplest answer is: the same sort of transformation implemented by threshold-crossing detectors in human-engineered systems, namely switches. Physically implemented switches nearly always have two, related, dynamical properties – bistability and hysteresis – that define them specifically to be latches in engineering terminology. Bistability means that these systems are attracted to one of two stable states that are separated by an unstable equilibrium point; hysteresis means that the response of such a system to a given input depends heavily on its past output (loosely speaking, hysteresis means “stickiness” and involves a basic form of persisting memory of the past; in contrast, linear systems are non-sticky and respond to constant inputs in such a way that the system’s initial conditions are forgotten at an exponential rate over time). Energy functions can be defined for such systems, consisting of two wells separated by a hump (see Figure 1). Any such system can then be accurately visualized as a particle bouncing around inside one or the other well under the influence of gravity, and occasionally escaping over the hump into the other well. Each “escape” is analogous to the flipping of the switch. The importance of the double-well design is that it reduces chatter, or bouncing of the switch between states as a result of noise (it “latches” into one or the other state), imposing a repulsive force away from the undefined region between ON and OFF.

FIGURE 1

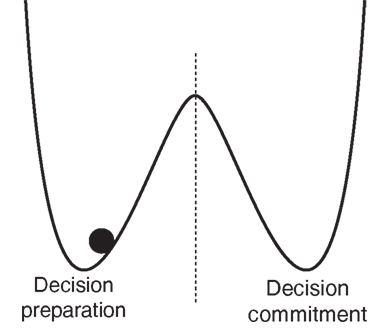
Figure 1. Double-well energy potential function, with system trapped in left well. Transitions to the right well (“escapes”) maybe considered transitions from an OFF state to an ON state, or a decision-preparation to a decision-committed state.

It is important to note that such devices do not implement a simple step-function applied to their inputs, as suggested by a common, simplified representation of switching behavior in the form of a step-function (or “Heaviside function”). Instead, their input-output relationships are not strictly functions at all: a given input level maps to more than one output level. Step-functions are nonetheless frequently used to formalize the ideal of an abstract decision threshold. This idealization is frequently very useful in both psychology and neuroscience, but it has the potential to bias the interpretation of various kinds of physiological recordings, since these are usually easier to map onto the gradual accumulation of evidence than onto the sudden, quantum leap represented by a step-function.

An analogous problem holds in the design of digital electronics: logic engineers who use idealized switch representations must factor in lower limits on the switching-speed of their basic components in their circuit designs. If they violate these constraints on assumed switching speeds, then their assumptions that a particular component will output a 1 or 0 at a given time may in turn be violated (the output may not yet have changed from its previous value, or it may be in an indeterminate level representing neither 1 nor 0). The end result is unpredictable circuit behavior (Hayes, 1993). This analogy suggests that when it comes to interpreting, for example, single-unit firing-rate data in decision-making, we may be in the position of the physicists and engineers who design the transistors, rather than those who compose switching devices into large circuits. Using idealized models of switching at the sub-digital scale leads to substantial errors of prediction in electronics; making the same sort of mistake in psychology and neuroscience may lead to substantial errors of interpretation.

2.2. The Axonal Membrane Implements a Physical Threshold

Another constructive analogy for modeling decision-making circuits comes from a well known physical threshold device even more familiar to neuroscientists: the axonal membrane of an individual neuron. In central nervous system neurons, a high density of voltage-gated sodium-channels in the axon imparts bistability to the voltage across its membrane. This channel-density is typically highest at the axon hillock, where the axon leaves the soma, so that most action potentials are generated in this area, known as the “trigger zone” (Kandel et al., 2000). In contrast, the soma itself typically has a much higher (possibly non-existent) action potential threshold, and is classically thought to function more as a spatiotemporal integrator than as a switch.

According to the deterministic Hodgkin-Huxley equations, raising the membrane to nearly its threshold potential and then shutting off input current leads to a return to the negative resting potential – the axon-potential’s low stable value – without an action potential. Physically, this corresponds to a failure to trigger a chain reaction of voltage-gated sodium-channel openings. Injecting a current that is slightly larger instead triggers this chain reaction with high probability, producing an action potential that is stereotyped in magnitude and duration under fixed conditions of temperature and chemical concentration. During the action potential, the membrane traverses a no-man’s-land of positive voltages, reaches its stereotyped peak – its high stable value – and then resets to its low stable value as voltage-gated potassium channels open up. These are hallmarks of a double-well system.

The primary player in this all-or-none process is a voltage-amplifying mechanism with strong positive feedback – the voltage-gated sodium-channel population – which ranges between two stable, attracting values: all-open (1), and all-closed (0). A time-delayed version of these activation dynamics is then employed by a voltage-gated potassium-channel population to produce a shutoff switch. A central claim of this paper is that these roles may easily be played by any neural population conforming to certain assumptions, and that some cortical populations may indeed conform to them.

This important feature of individual membrane potential dynamics does more than provide a useful analogy for modeling decision-making circuits. It suggests that a simple mathematical model may be usefully employed to describe both the dynamics of the individual neuron and the dynamics of interconnected neural populations. The generation of an individual action potential in a neuron, after all, qualitatively fits the description of a typical decision process: sub-threshold, leaky integration of post-synaptic potentials in a neural soma is analogous to evidence accumulation in a decision circuit; action potential generation in the trigger zone is analogous to crossing a decision threshold.

The other major claim of this paper regards interpretation of behavioral and physiological data collected during decision making. Many researchers (e.g., Shadlen and Newsome, 2001; Purcell et al., 2010) describe their findings in ways that suggest they are observing the population-analog of a neuron’s somatic membrane potential, when a better analogy in some cases may be that they are observing the analog of an axon’s membrane potential.

2.3. “Turtles all the Way Down”: Neurons and Neural Populations as Thresholded Leaky Integrators

Since so much inspiration for the present model of decision-making circuits comes from the individual neuron, I now show briefly how the dynamics of the individual neuron can, in principle, be reproduced by whole populations. Figure 2 depicts how a population of leaky-integrate-and-fire (LIF) neurons can collectively implement a single leaky integrator whose output is the population’s spike train. Suppose that many neurons project to a given receiving population and have uncorrelated spike times; that the resulting post-synaptic potentials are small due to weak synaptic connections; and that excitation is balanced by some level of inhibition. In that case, each unit in the receiving population can be modeled as a leaky integrator (Figure 3), whose sub-threshold membrane potential approaches some asymptotic level (see Smith, 2010). A similar model of sub-threshold membrane dynamics as a drift-diffusion process (without leak) was given in Gerstein and Mandelbrot (1964).

FIGURE 2

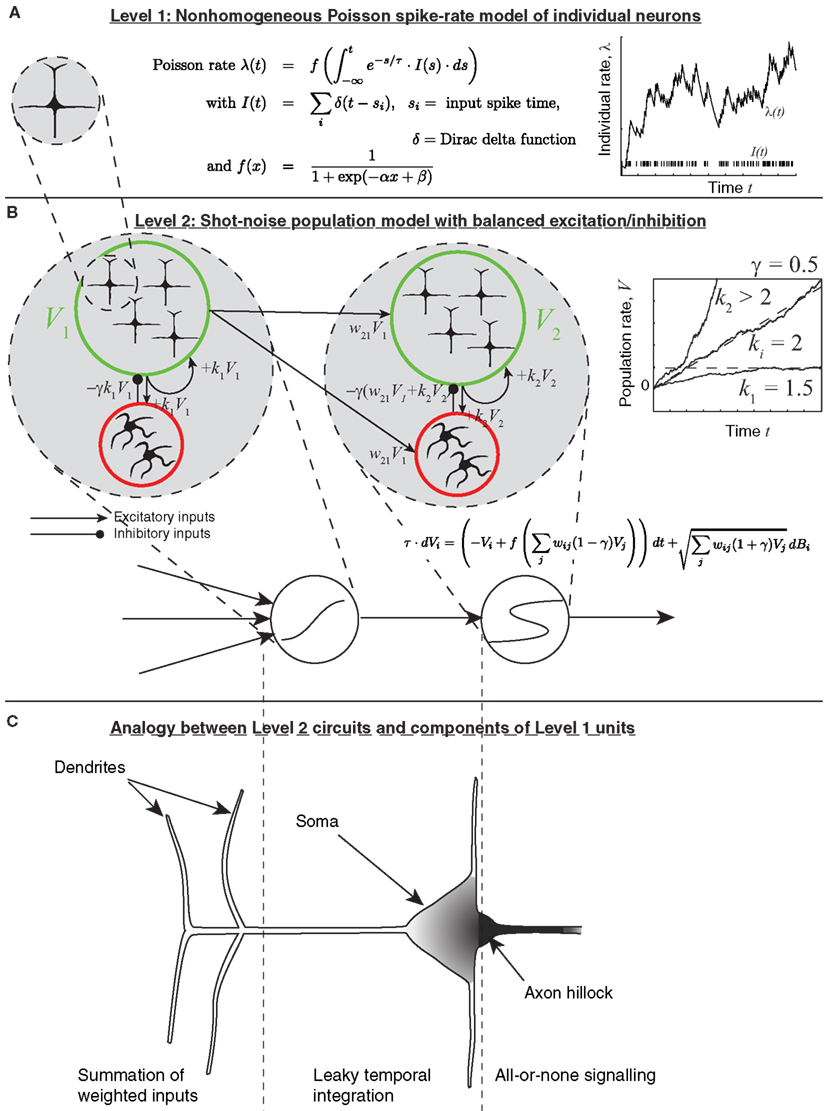
Figure 2. The multiple spatial-scale modeling approach. (A) For simplicity, an individual neuron is modeled as a Poisson spike generator, with rate parameter determined by the leaky integral of weighted inputs from other units. (B) The population model, which allows for chaining a leaky integrator and a latch. (C) Correspondence of each circuit component to parts of a more classical model of a neuron. The axon hillock corresponds to a latch; the soma corresponds to a leaky integrator; shading indicates density of voltage-gated sodium-channels.

FIGURE 3

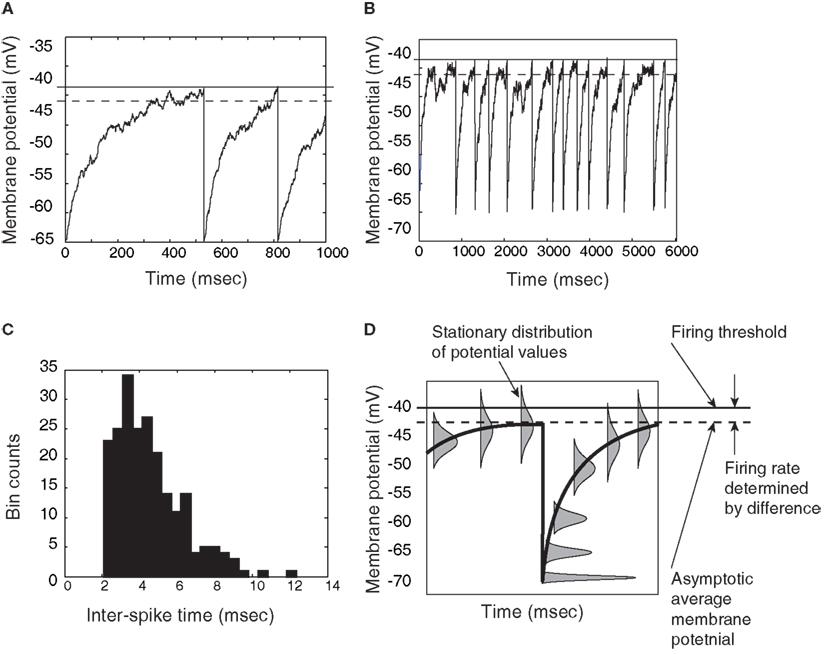
Figure 3. Demonstration that a thresholded Ornstein-Uhlenbeck (OU) process, or leaky integrator, can give approximately exponential inter-spike times if the asymptotic level of the integrator is below threshold. (A) Close-up view of an OU process rising to a threshold, then resetting and rising again. (B) A longer time-course of the same process; inter-spike times are the times between resets (downward jumps). (C) Histogram of threshold-OU model’s inter-spike intervals. The main deviation from true Poisson statistics is the lack of inter-spike intervals below a 2 ms limit – in other words, a refractory period. (D) Distributions of trajectories relative to spike time, showing that aside from the brief refractory period when the system has not reached asymptote (on average), the model is essentially a white noise process positioned just under the action potential threshold, leading to memoryless inter-spike times. The rate of those spikes depends on the distance between the threshold and the sub-threshold asymptote (Gardiner, 2004).

If the receiving population is large enough, then the receiving population’s spiking output represents what the population’s average membrane potential would be if its units lacked voltage-gated sodium-channels and therefore generated no action potentials. An asymptotic potential would be reached, with the level depending on the input strength and the leak. (Action potentials naturally tend to erase the record of previous potential levels in each unit after resetting.)

If this asymptotic level is below the action potential threshold, however, then the inter-spike times of the model will be largely memoryless. The hazard rate of a new spike is almost flat, meaning that if a spike has not occurred at some time t following the previous spike, then it has a constant probability of occurring in the next small time window, for all t > 0. This occurs because threshold-crossings will be due only to momentary noise. Formally, this is once again a problem of escape from an energy well. Note, here, however, that an idealized step-function threshold is employed for its simplicity. For the purpose of modeling population activity over the course of a perceptual decision as an emergent property of collective spiking, the assumption here is that the biophysical details of action potential generation make no difference.

The first-passage time distribution of this system would be approximately exponential (Gardiner, 2004), deviating from the exponential mainly by lacking a high probability of very short inter-spike times: the resetting of the membrane to its resting potential, followed by increase toward asymptote, must produce a refractory period that would prevent truly exponential inter-spike time distributions (see Figure 3C). The model’s average inter-spike interval is an exponential function of the distance between the firing threshold and the asymptotic average potential (Gardiner, 2004): stronger inputs to a unit lead to a higher asymptote and higher firing rate. If inputs lift the asymptote above the firing threshold, the model breaks down, and inter-spike time distributions approach the Wald distribution (Gerstein and Mandelbrot, 1964).

Thus we can recreate the dynamics of the individual neuron at the population level by building a circuit consisting of a leaky integrator population feeding into a switch population (see the mapping from Figures 2B,C).

2.4. The Formal Model of Population Activity

The model is based on the assumptions outlined above and in more detail in Simen and Cohen (2009); Simen et al. (2011b), most of which are common in neural network models of decision making. It is assumed that neural population activity (firing rate) can be represented approximately as a non-homogeneous Poisson spike train (equation 1). Its rate parameter λ is governed by an ordinary differential equation with a leak term and a sigmoidal activation function f. The input I to the activation function is a shot-noise process, equal to the weighted sum of input spikes received from other populations, convolved with an exponential decay term (see Figure 2A):

$\begin{array}{c}\text{Poisson}\text{rate}\lambda \left(t\right)=f\left({\int }_{-\text{inf}}^t{e}^{-s∕\tau }\cdot I\left(s\right)\cdot ds\right)\\ \text{with}{I}_i\left(t\right)=\sum _j{w}_{ij}\cdot \delta \left(t-s_j\right),\\ \text{and}f\left(y\right)=\frac{1}{1+exp\left(-\alpha y+\beta \right)}\end{array}$ (1)

Here, w_ij = connection strength between input j and unit i, s_j = input spike time, δ = Dirac delta function.

The resulting population model approximates a leaky integrator, or stable Ornstein-Uhlenbeck (OU) process x(t) (defined by equation (2)), as long as the input I(t) is positive, and as long as inputs remain in the linear region of the sigmoidal activation function f:

$\begin{array}{c}\tau \cdot d{x}_i=\left(-x_i+f\left(I_i\right)\right)\cdot dt+c\cdot d{W}_i,\\ I_i=\sum _j{w}_{ij}{x}_j.\end{array}$ (2)

Unlike a true OU process, when the population’s net input I is negative, its output goes to 0, but not below it.

For readers not familiar with stochastic differential equations, the following discrete time approximation to equation (2) may be easier to understand:

$\tau \cdot x_i\left(t+\Delta t\right)=x_i\left(t\right)+\left[-x_i\left(t\right)+f\left(I_i\left(t\right)\right)\right]\cdot \Delta t+c\sqrt{\Delta t}\cdot 𝒩\left(0,1\right).$ (3)

Here, a normal random variable is added to the deterministic system at each time step, with magnitude weighted by the square root of the time step size. Equation (3) also defines the “Euler method” by which simulations of the system in equation (2) are carried out (Gardiner, 2004).

When recurrent self-excitation, k ≡ w_ii, is included in the input term I, the population’s intrinsic leak parameter can be reduced or, at a higher level of precisely tuned positive feedback, completely canceled (Seung, 1996). Exact cancelation gives rise to perfect (leakless) temporal integration, which is critical for implementing decision-making algorithms that are optimal in certain contexts (Gold and Shadlen, 2002). Such exact cancelation requires more precise tuning for larger leak terms (Simen et al., 2011a). At still higher levels of positive feedback, bistability results (see Figure 4). The likely consequence for an explicit, purely excitatory, spiking LIF model of populations in the case of stronger self-excitation would be synchronization of spiking, since stronger excitatory connectivity in a population would make any given spike more likely to produce another spike in another cell at nearly the same time. However, we assume further that a form of balanced inhibition can cancel spike-time correlations (Simen et al., 2011b). Under this assumption, any excitatory input of magnitude M to a population would be balanced by inhibitory input of magnitude γM, with γ defining the excitatory-inhibitory ratio. That is, if every excitatory spike received by a population produces an excitatory post-synaptic potential of magnitude 1 in one of its cells, then that population also receives an inhibitory post-synaptic potential of magnitude γ in one of its cells, on average.

FIGURE 4

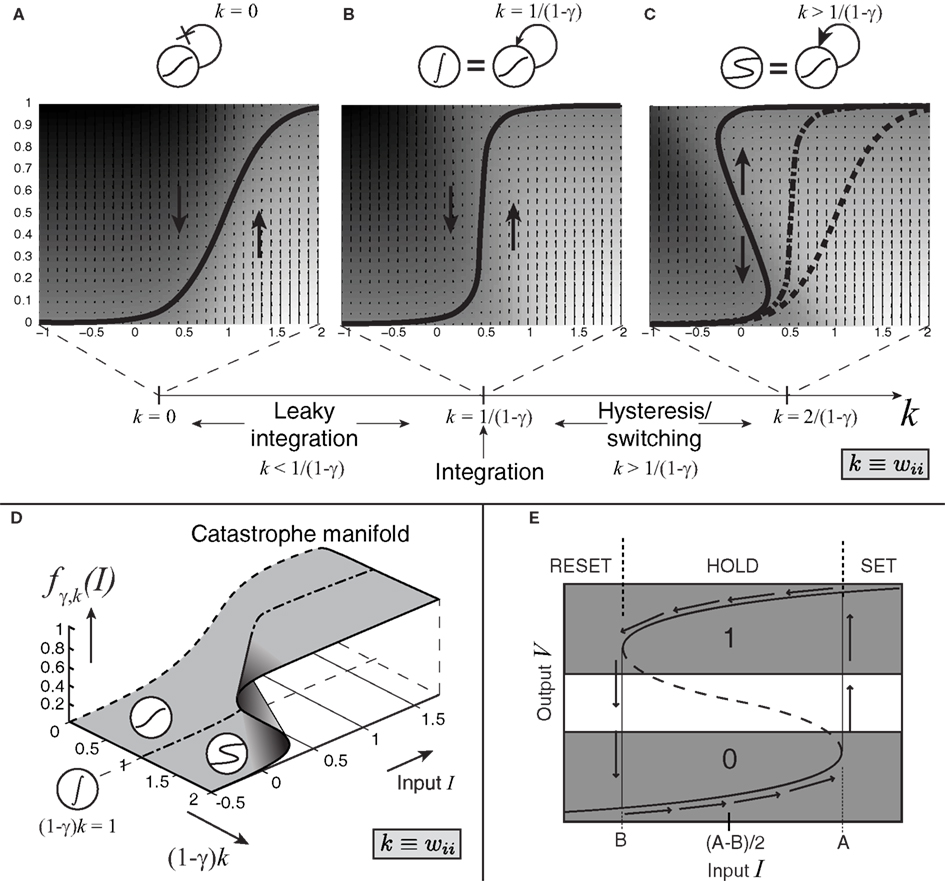
Figure 4. Effect of self-excitation on the sigmoidal activation unit defined by equation 2. (A) The input-output equilibrium function f_γ,k of the system (thick black curve) for the sigmoidal unit with self-excitation k = 0 and noise coefficient c set to 0; when c > 0, this function still describes the average behavior of the system. Upward and downward arrows and shading indicate system velocity at different input-output combinations (dark = negative; light = positive). (B) Self-excitation k = 1/(1 − γ) cancels leak and produces a vertical effective activation function and leakless temporal integration [k < 1/(1 − γ) produces leaky integration]. (C) Latching/switching behavior occurs for all k > 1/(1 − γ); here k = 2/(1 − γ). (D) A section of the complete catastrophe manifold defined over the space of input and self-excitation pairs. (E) Binarization diagram demonstrating separated ON (1) and OFF (0) areas of output activation and hysteresis. Dashed section of S-curve denotes unstable equilibria; solid sections denote stable equilibria.

These changes in self-excitation strength can be depicted in the form of an “effective” activation function, f_γ,k, specifying the output level of firing-rate for a given level of net weighted input strength, parameterized by the level of positive, recurrent feedback, k, and the inhibitory balance, γ. As the model transitions from leaky (Figure 4A) to bistable (Figure 4C) behavior through the bifurcation point at which perfect integration occurs (Figure 4B), this effective activation folds back on itself (Figure 4D). This folding is known as a “cusp catastrophe” in the terminology of non-linear dynamical systems.

The bistable behavior demonstrated in Figures 4C,E now serves to establish a threshold level of input values: beginning with an output level on the bottom stable attracting arm of the folded sigmoid, inputs that exceed a critical level (the horizontal coordinate of the bottom fold) trigger a transition toward the upper stable attracting arm. Two key dynamical features now result. The first is a clearly defined quantization – in fact, binarization – of output levels. The upper stable arm of the folded sigmoid now represents an ON state (Figure 4E); the lower stable arm represents an OFF state; and potential confusion about which state the system is in is reduced by a large no-man’s land of unstable activation levels. Hysteresis also results: a dip in the input below the threshold level does not now reduce the output to its OFF state; instead, it remains ON until input dips below the horizontal coordinate of the upper fold.

Figure 5 demonstrates an extremely simple circuit composed of an integrator sandwiched between two latches, along with their corresponding, predicted activation levels over time.

FIGURE 5

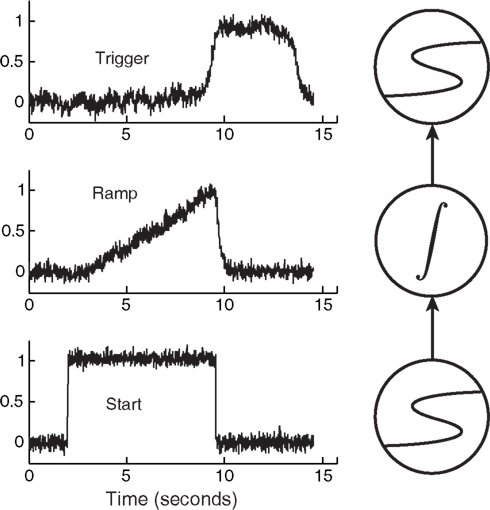
Figure 5. A simple circuit composed of latches and an integrator. This particular circuit can be used for interval timing by tuning the slope of the ramp, which reduces to tuning how hard the Start unit drives the integrator (Simen et al., 2011b). Here the Start unit is clamped to an output of 1 at 2 s, then is clamped to 0 when the threshold-unit exceeds an output of 0.8.

2.5. Behavior of the Threshold Mechanism, and Comparison to Firing-Rate Data

Since we are concerned with discriminating between accumulators and threshold mechanisms in perceptual decision-making, a critical question is the following: what should we expect the population activity corresponding to each mechanism to look like? Previous work (e.g., Lo and Wang, 2006; Boucher et al., 2007) has suggested that, in the case of eye movements, a successive sharpening of bursting activity occurs as activity propagates from cortical circuits to the basal ganglia, and thereafter to the superior colliculus. That is, bursting activity begins more abruptly, with less gradual ramping, and also ends more abruptly, at later stages of processing.

The model shown in Figure 6 illustrates similar progressive sharpening as signals progress from the accumulator to the threshold latch². Figure 6 also clearly shows, however, that the threshold mechanism’s activation (in red) qualitatively matches the description of an accumulator, in that the level of activation rises throughout the stimulus presentation to a maximum that is time-locked to the response. Compared to the accumulator in this trace (green), the threshold is very distinct, since its activation accelerates during the stimulus into a final ballistic component. However, without the green trace for comparison, the red threshold trace would be difficult to rule out as the signature of an evidence accumulator. Furthermore, as shown later, task variables that modulate the ramping activity of putative neural accumulators should also be expected to modulate threshold-unit activity, compounding the difficulty of discriminating between accumulator and threshold mechanisms.

FIGURE 6

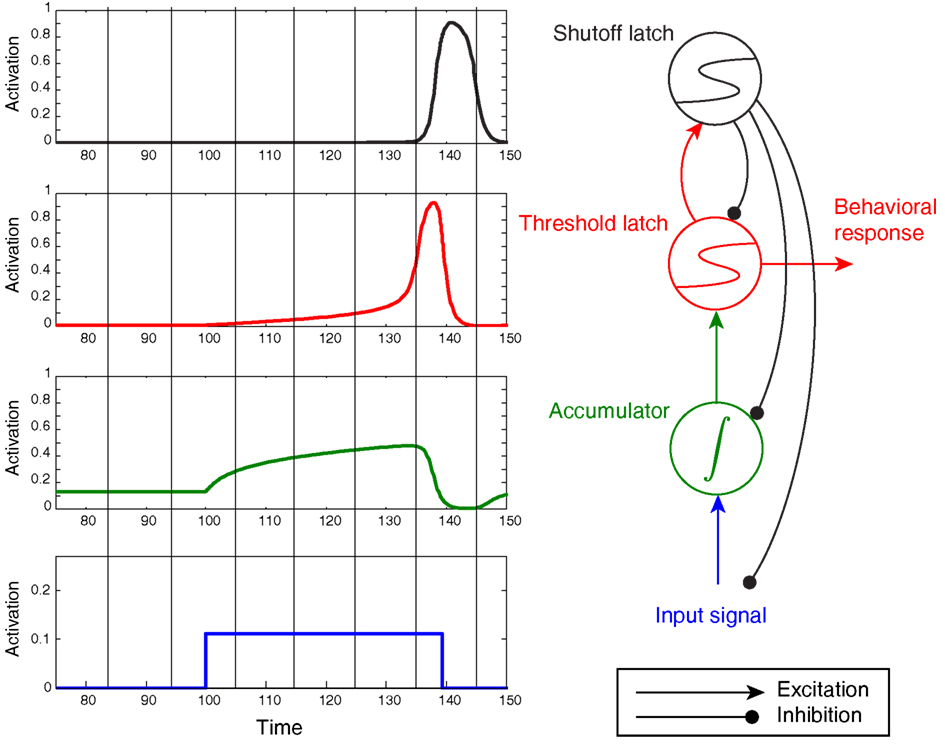
Figure 6. Noiseless activation traces of a complete circuit comprising an accumulator/integrator, threshold latch, and shutoff latch, but lacking positive feedback from threshold-to-accumulator. Blue: input signal; green: accumulator; red: threshold latch; black: shutoff latch. Here the stimulus was arbitrarily terminated when the threshold latch exceeded 0.8 activation. Note the post-response dip below baseline in the accumulator.

One additional feature of the model in Figure 6 – the “shutoff latch” component (black) – is worth mentioning at this point, since without it, connection weights in the circuit can easily be tuned to preserve a decision commitment over a delay period (note how long the threshold mechanism is active in Figure 5, for example). Without a shutoff signal, the circuit could make a decision commitment and maintain it indefinitely (the red threshold latch could latch into the ON state). Such behavior would be required in working memory tasks, and may occur even in tasks for which such behavior would seem to be suboptimal (e.g., Kiani et al., 2008). For tasks that require immediate responding and resetting for future decisions, however, adding a shutoff latch increases reset speed and can prevent undesired latching of the threshold-unit.

Examining traces of FEF activity during visual search tasks for neurons that have been interpreted as accumulators (reprinted in Figure 7) shows how similar their average activation pattern is to the pattern produced by the threshold model in Figure 6 (red trace). Much the same is true for FEF recordings collected during dot-motion discrimination tasks, as shown, for example, in Figure 2 of Ding and Gold(2012, reprinted here as Figure 8). In the model, furthermore, differences in evidence-accumulation rates lead to corresponding differences in the ramp-up rate of the threshold mechanism (see Figure 9C). Stochastic model simulations in Figure 9C show that changes in the threshold mechanism activation naturally mimic changes in the neural firing-rate data in Figure 7 across fast/slow response-time conditions, as well as the firing-rate changes in Figure 8 across motion coherence-level conditions.

FIGURE 7

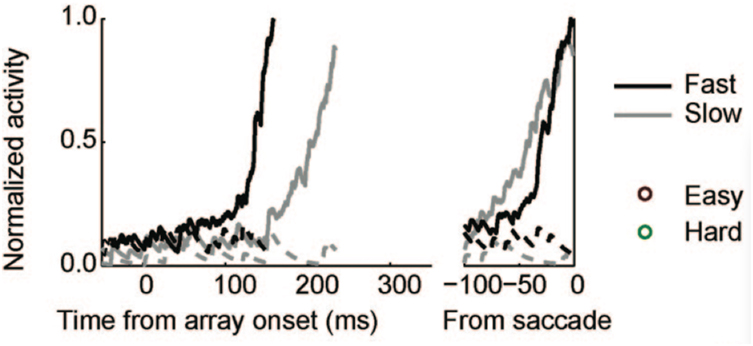
Figure 7. Reprint of Figure 10A, from Purcell et al. (2010), showing movement neurons in monkey FEF whose activation profiles correlate with reaction-time in a visual search task.

FIGURE 8

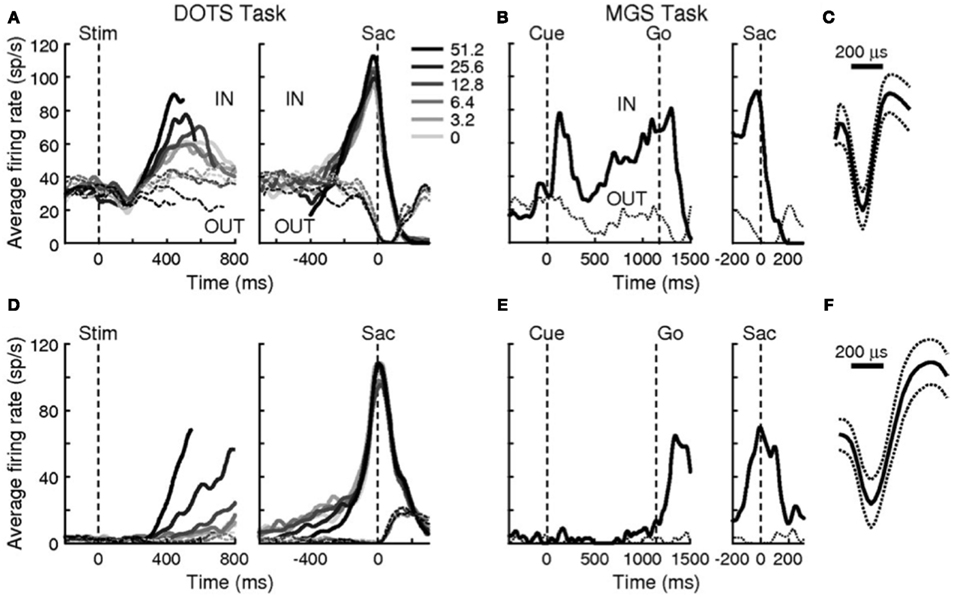
Figure 8. Reprint of Figure 2, Ding and Gold (2012), showing accumulator-dynamics in FEF neurons likely to be inhibitory (top row) and excitatory (bottom row). Data were obtained during a reaction-time version of a dot-motion discrimination task (A,D) and a memory-guided saccade task (B,E). (C) The narrow action potential profile of the presumably inhibitory interneuron in (A,B). (F) The broader action potential profile of the presumably excitatory pyramidal cell in (D,E).

FIGURE 9

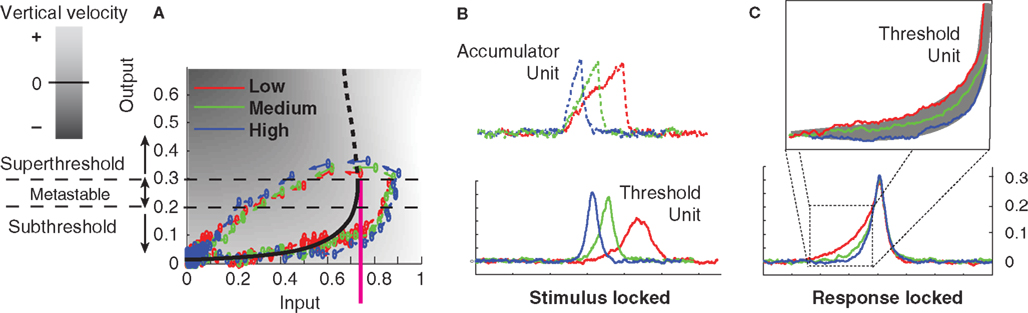
Figure 9. Dynamics of a threshold latch in response to three different signal strengths, with non-zero noise. Blue: strong signal; green: medium signal; red: weak signal. (A) Input-output evolution of the threshold-unit’s dynamics, starting at the origin and moving rightward, and upward along the bottom branch of the folded, effective activation function. Note the failure of the system’s output value to exceed 0.4 before the shutoff inhibition drives the system down and to the left well before the system’s output reaches its stable attracting value just below 1. (B) Stimulus-locked averages of activation (dashed: accumulator; solid: threshold-unit). (C) Response-locked averages of the threshold-unit activations, showing a common final level of activation, but differences in buildup rate for different signal qualities defining the gray area in the magnified inset (compare to Figures 7 and 8).

The pattern of activity shown in Figure 7 also motivates a theoretical alternative to the threshold-interpretation proposed in this paper. This alternative is known as the “gated accumulation” theory of FEF movement neuron activity (Purcell et al., 2010). According to this theory (at least as applied to monkey eye movements during visual search tasks), evidence accumulation is a process that may happen close to the time of the response, after a kind of initial quality check determines whether stimulus information should pass through a gate into the accumulator. Changes in the rate of this accumulation determine response time.

“Gate” is another word for threshold. Thus the gated accumulation theory incorporates a threshold mechanism between the retina and the accumulator that is not directly observed in the recordings of Figure 7. What seems more parsimonious and consistent with the predictions of the model presented here, however, is that gated accumulators are themselves the gates. The rise-time of any physical switching mechanism must be non-zero, so ramping, or accumulation, is probably a necessary feature of gate dynamics. Figures 9B,C show an example in which stronger, faster, negative feedback is applied to the threshold latch by the shutoff latch, as compared to the system in Figure 6 (to reduce the height of the peak response). When noise is added to the processing, the stimulus-locked and response-locked averages of the threshold mechanism’s activation in this case look remarkably like the gated-accumulator in Figure 7. In Figure 9, three different levels of input signal were applied to the model in Figure 6 while keeping the noise level constant.

One objection to this characterization of the (Purcell et al., 2010) data might be based on the relatively long switching time of such FEF switches, which according to Figure 7 could exceed 100 ms. Neural populations in the brain are clearly capable of transitioning much more quickly from low firing rates to high firing rates, after all. For example, Figure 3 of Boucher et al. (2007) shows a much more rapid transition from low to high firing rates, over the course of only a few msec, in bursting neurons in the brainstem. This extremely rapid switching behavior contrasts with hypothesized switch dynamics in FEF that take 100 ms to complete a transition from low to high firing-rates. Such extended switch-on times might therefore reasonably be taken to support accumulator dynamics that do not involve bistability. However, it is important to note that any bistable positive feedback system can be made to linger at its inflection point of activation (the lower fold of the cusp catastrophe manifold) for arbitrarily long times, if the inputs to it are tuned precisely enough. The first gates/thresholds in the processing cascade, when faced with weak signals, may be expected therefore to ramp-up very gradually in some task conditions. Furthermore, time-locked averaging of abrupt activation-increases across trials can in any case smear out the abrupt onsets into a gradual ramp if the onset-times are not perfectly locked to the average-triggering event. Figure 9 demonstrates similar smearing in panel b, in which Threshold Layer activation seems to rise to a different average level in the “Low” vs. the “High” condition, whereas response-locking as in panel c shows that activation rises to the same level in all conditions, and ramping is less gradual than in panel b.

Given these considerations, what phenomena would clearly distinguish threshold mechanisms from accumulator mechanisms? So far, the green accumulator component of the model in Figure 6 lacks the red threshold trace’s late, ballistic component, and the upward inflection point that initiates that component. This difference might seem to be a useful feature for distinguishing between accumulator and threshold activations. Unfortunately, there is good reason to suspect that the lack of feedback connections from the threshold mechanism to the accumulator in the model in Figure 6 is unrealistic. There are known to be connections from FEF back to parietal cortex and extrastriate visual cortex that can conduct spatial attentional signals, for example (Moore and Fallah, 2001; Moore and Armstrong, 2003). When such feedback connections are included, as in Figure 10, the ballistic component produced in the threshold mechanism is transferred backward to the accumulator as well. Under this plausible scenario, the activation profiles of evidence accumulators and threshold mechanisms become qualitatively indistinguishable.

FIGURE 10

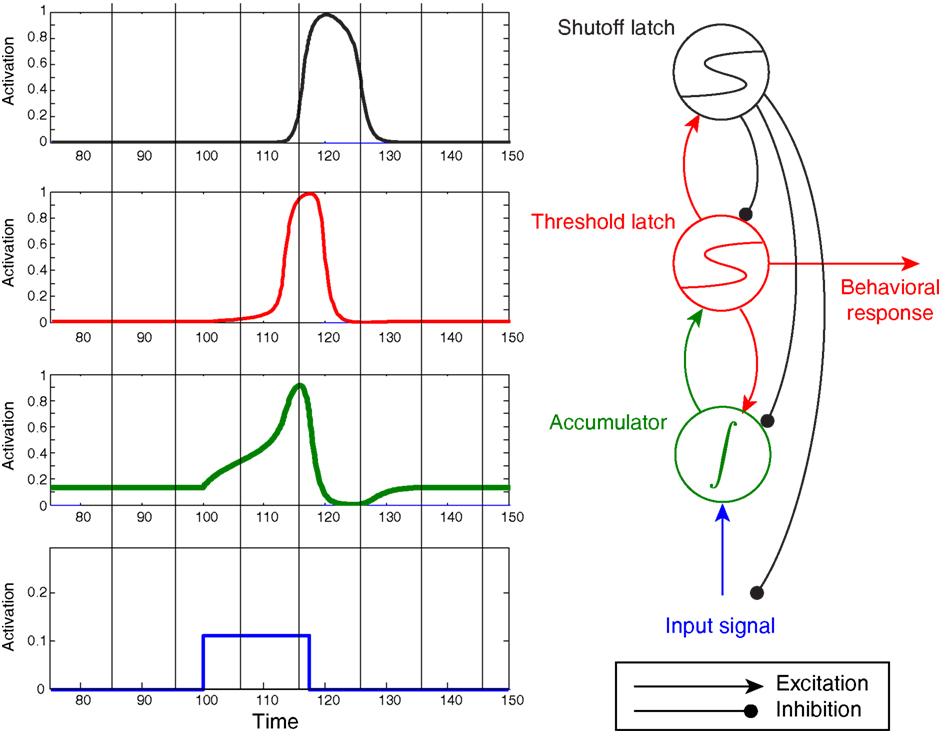
Figure 10. Same circuit as in Figure 6, except that excitatory threshold-to-accumulator feedback is included. The green trace now has a late ballistic component, reflecting the ballistic activation of the threshold latch. Positive feedback also shortens the decision time considerably relative to the same model without threshold-to-accumulator feedback.

According to the model in Figure 10, activation in both components should ramp up during the course of a decision, then finish with a ballistic jump near the time of the decision commitment. As Figure 11 shows, activation in both components of this model should be modulated by the stimulus presented and the choice ultimately made – two criteria commonly used to associate firing-rate data with accumulators. Furthermore, activation should be modulated by the incentives offered, regardless of where in the circuit any incentive-induced control signals are actually applied. Applying a continuous, constant, additive biasing signal, either to the accumulator (Figure 11A) or to the threshold (Figure 11B), has qualitatively similar effects on the pre-ballistic components of ramping activation in both mechanisms.

FIGURE 11

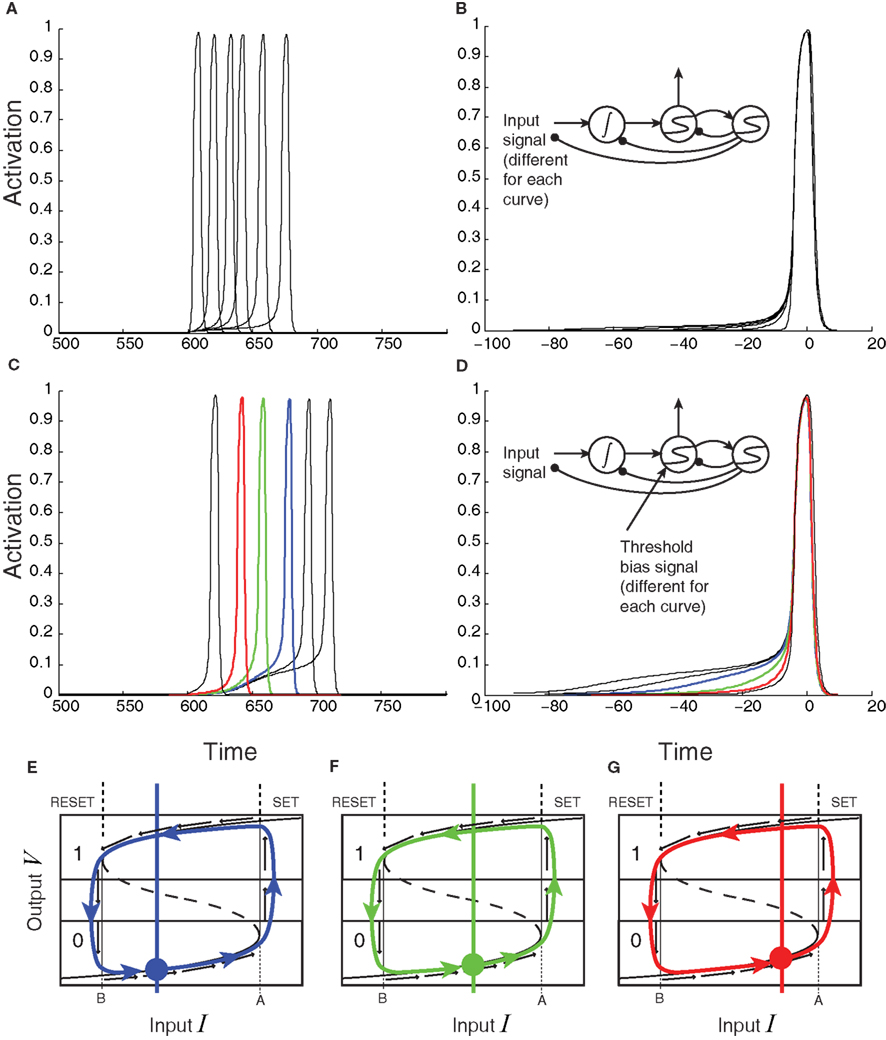
Figure 11. Effects of biasing on the threshold-unit’s activation. (A,B) Constant additive biasing of the accumulator can dramatically decrease response times for a fixed level of stimulus strength [offsets of stimulus-locked traces, (A)] and slightly modulates the initial rise period of the activation [slight changes in response-locked traces (B)]. (C–G) Constant additive biasing of the threshold-unit also affects stimulus-locked response times (C) and dramatically modulates the duration of the initial rise in response-locked averages (D). (E–G) Three different levels of biasing (shifts of the initial input level denoted by the colored circle) with colors corresponding to the traces in (C) and (D) blue = low bias; green = medium bias; red = high bias.

One possibility for discriminating between two candidates for an accumulator/threshold pair would be to microstimulate one area while inactivating the other, e.g., with muscimol. A threshold mechanism should continue to display bistability in response to increasing current injections when accumulators are inactivated, whereas an accumulator should lack bistability and hysteresis – its response to increasing currents should be a monotonic function of that current when the feedback excitation from the corresponding threshold mechanism is disabled.

Of course, it is quite possible that accumulator and threshold mechanisms consist of networks of neurons distributed widely across the brain. In that case, it would be difficult to cleanly inactivate one component without affecting the other. If clean, independent inactivation could be achieved, however, then clear behavioral distinctions should emerge: knocking out integrators should spare the ability to respond, while performance accuracy should approach chance; knocking out threshold mechanisms, in contrast, would abolish responding altogether. A more graded impairment could emerge from less potent inactivation: by inhibiting a threshold mechanism, more evidence would be required to accumulate to produce a decision, leading to improved accuracy, and increased response time; inhibiting an accumulator, in contrast, would presumably both increase response times and decrease accuracy.

Yet another possibility is that ramping activity in an area during decision making might be more or less epiphenomenal – relating neither to evidence accumulation nor threshold readout, per se, but instead to some sort of performance monitoring, or even simply to spreading correlations of activity that play no functional role. In this case, the inactivation tests proposed here would fail to produce the intended effects, but this outcome would at least suggest that a given area is not functionally relevant to the decision-making task at hand.

3. Concluding Remarks

Here I have assembled a list of reasons to consider a two-layer neural model, much like others discussed in neuroscience and psychology that are either explicitly composed of two layers, or that combine an evidence-accumulation process with an idealized decision threshold (e.g., Usher and McClelland, 2001; Corrado et al., 2005; Diederich and Busemeyer, 2006; Lo and Wang, 2006; Boucher et al., 2007; Ratcliff and McKoon, 2008; Gao et al., 2011). Like those models, the model proposed here splits different functions across different layers, rather than lumping them into a single layer (e.g., Wang, 2002). It thereby sacrifices parsimony for potentially better, more rewarding performance.

Unlike most multi-layer models, however, a model previously proposed by my colleagues and me (Simen et al., 2006) sends continuous, additive biasing signals to control the second layer (the threshold layer) rather than the first (the accumulator layer). Other models that we have proposed (Simen and Cohen, 2009; McMillen et al., 2011) tune multiplicative weights applied to the accumulated evidence before it is fed into the threshold mechanism. Increasing these weights amounts to reducing thresholds divisively. In certain tasks (e.g., Bogacz et al., 2006), such approaches are both approximately optimal and mechanistically feasible.

Optimal biasing of accumulators rather than thresholds, in contrast, requires the biasing signals to be punctate rather than continuous, and I have raised doubts here about the physiological plausibility of punctate signals. These doubts are premised on the idea that any switch-like process in the brain must have a non-negligible rise-time and thus a non-zero, minimal duration – a duration that might plausibly take up a substantial proportion of a typical response time in perceptual decision making. Human and non-human primate behavior is frequently suboptimal, however, so considerations of optimality do not rule out accumulator-biasing. Behavioral data, nonetheless often appear to support the notion that thresholds are strategically controlled, sometimes optimally (Simen et al., 2009; Bogacz et al., 2010a; Balci et al., 2011; Starns and Ratcliff, 2012). Furthermore, Ferrera et al. (2009) observed FEF activity that is consistent with a role for FEF as a tunable threshold mechanism, and (Ding and Gold, 2012) found a multitude of different functions expressed in FEF after previously finding much the same in the caudate nucleus (Ding and Gold, 2010). An inelegant but likely hypothesis supported by these and similar findings is that the separate functions of decision-making models are implemented by neural populations that are themselves distributed widely across the brain. What seems unquestionable, in any case, is that bistable switch mechanisms in either a one- or two-layer model would appear to play a necessary role in any full account of the data reviewed here.

It is also noteworthy that adaptive properties of the individual neuron’s inter-spike time behavior have been explained by a form of threshold adaptation that is analogous to the population level threshold adaptation proposed here. As with neural population models, different models of the individual neuron can frequently mimic each other, whether they adapt action potential thresholds (Kobayashi et al., 2009) or the resting membrane potential after firing (Brette and Gerstner, 2005). In an international competition to model spike-time data, however, a relatively simple model with adjustable action potential thresholds (Kobayashi et al., 2009) defeated all other modeling approaches (Gerstner and Naud, 2009). Consistent with this evidence for adjustable action potential thresholds, recent findings suggest that sophisticated signal processing can occur at the axon’s initial segment (Kole and Stuart, 2012). The same principles of accumulation, bistable readout, and threshold adaptation may therefore play out at multiple levels of neural organization.

I have argued that population threshold mechanisms are sufficiently non-ideal in their physical implementation that they should often be modeled explicitly rather than abstractly. What are the risks of getting this modeling choice wrong? Erring on the side of abstractness and simplicity risks:

1. misplacing the locus of evidence accumulation in the brain;

2. amplifying a disconnect between psychology and neuroscience in terms of which model-parameter or neural mechanism is modulated when speed-accuracy tradeoffs are adapted;

3. missing the possibility that cortical switch mechanisms might allow the cerebral cortex to implement a complex, sequential system (see Simen and Polk, 2010) without always requiring the involvement of structures such as the basal ganglia.

Conversely, insisting on an overly elaborate model of thresholds risks raising counterproductive doubts about neural data that is in fact tied to evidence accumulation. It also risks unnecessary inelegance and lack of parsimony. The optimal tradeoff between such risks is rarely obvious, and this article has not derived one. Its primary intent is to guard against the first kind of risk, since much of the decision neuroscience community currently seems safe from the second type.

A final, important point that should be kept in mind when neural evidence is brought to bear on psychological models (made elsewhere – e.g., Cohen et al., 2009 – but worth repeating) is that apparently slight changes in tasks may have dramatic consequences on the firing-rate patterns subserving performance of the tasks. Thus, although the conventional wisdom appears to be that there has been little electrophysiological evidence of threshold adaptation as a mechanism underlying behavioral performance adaptation, this lack probably depends heavily on the types of tasks that neuroscientists have examined. Fairly strong behavioral support (Simen et al., 2009; Bogacz et al., 2010a; Balci et al., 2011; Starns and Ratcliff, 2012) has been gathered for models of threshold adaptation in tasks for which such adaptation tends to maximize rewards (e.g., Bogacz et al., 2006). The tasks proposed in Bogacz et al. (2006) hold signal-to-noise ratios at a constant level across trials within any block of trials, whereas most physiological research with monkeys involves varying levels of signal-to-noise ratio from trial to trial. It therefore appears that valuable information could be gained about the neural mechanisms of economic influence on decision making if the exact task described in, for example, Bogacz et al. (2006), were tested directly in awake, behaving monkeys.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Thanks to Michael Loose for comments on the manuscript.

Footnotes

1. ^Note that the use of the term “threshold” here is equivalent to that term’s use in neurophysiology. It is distinct from its common use in psychology as the name of an arbitrary accuracy criterion for characterizing perceptual acuity.
2. ^Matlab code for this model is available at: www.oberlin.edu/faculty/psimen/ThresholdModelCode.m

References

Balci, F., Simen, P., Niyogi, R., Saxe, A., Hughes, J., Holmes, P., and Cohen, J. D. (2011). Acquisition of decision making criteria: reward rate ultimately beats accuracy. Atten. Percept. Psychophys. 73, 640–657.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bogacz, R., Brown, E., Moehlis, J., Holmes, P., and Cohen, J. D. (2006). The physics of optimal decision making: a formal analysis of models of performance in two-alternative forced choice tasks. Psychol. Rev. 113, 700–765.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bogacz, R., Hu, P., Holmes, P., and Cohen, J. D. (2010a). Do humans select the speed-accuracy tradeoff that maximizes reward rate? Q. J. Exp. Psychol. 63, 863–891.

CrossRef Full Text

Bogacz, R., Wagenmakers, E.-J., Forstmann, B. U., and Nieuwenhuis, S. (2010b). The neural basis of the speed-accuracy tradeoff. Trends Neurosci. 33, 10–16.

CrossRef Full Text

Boucher, L., Palmeri, T. J., Logan, G. D., and Schall, J. D. (2007). Inhibitory control in mind and brain: an interactive race model of countermanding saccades. Psychol. Rev. 114, 376–397.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Brette, R., and Gerstner, W. (2005). Adaptive exponential integrate-and-fire model as an effective description of neuronal activity. J. Neurophysiol. 94, 3637–3642.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Brown, S., and Heathcote, A. (2005). A ballistic model of choice response time. Psychol. Rev. 112, 117–128.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cisek, P., Puskas, G. A., and El-Murr, S. (2009). Decisions in changing conditions: the urgency-gating model. J. Neurosci. 29, 11560–11571.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cohen, J. Y., Heitz, R. P., Woodman, G. F., and Schall, J. D. (2009). Letter to the editor: reply to Balan and Gottlieb. J. Neurophysiol. 102, 1342–1343.

CrossRef Full Text

Corrado, G. S., Sugrue, L. P., Seung, H. S., and Newsome, W. T. (2005). Linear-nonlinear-poisson models of primate choice dynamics. J. Exp. Anal. Behav. 84, 581–617.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Diederich, A., and Busemeyer, J. R. (2006). Modeling the effects of payoff on response bias in a perceptual discrimination task: bound-change, drift-rate-change, or two-stage-processing hypothesis. Percept. Psychophys. 68, 194–207.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ding, L., and Gold, J. I. (2010). Caudate encodes multiple computations for perceptual decisions. J. Neurosci. 30, 15747–15759.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ding, L., and Gold, J. I. (2012). Neural correlates of perceptual decision making before, during, and after decision commitment in monkey frontal eye field. Cereb. Cortex. 22, 1052–1067.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ferrera, V. P., Yanike, M., and Cassanello, C. (2009). Frontal eye field neurons signal changes in decision criteria. Nat. Neurosci. 12, 1454–1458.

CrossRef Full Text

Gao, J., Tortell, R., and McClelland, J. L. (2011). Dynamic integration of reward and stimulus information in perceptual decision making. PLoS ONE 6:e16479. doi:10.1371/journal.pone.0016749

CrossRef Full Text

Gardiner, C. W. (2004). Handbook of Stochastic Methods, 3rd Edn. New York, NY: Springer-Verlag.

Gerstein, G. L., and Mandelbrot, B. (1964). Random walk models for the spike activity of a single neuron. Biophys. J. 4, 41–68.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gerstner, W., and Naud, R. (2009). How good are neuron models? Science 326, 379–380.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gold, J. I., and Shadlen, M. N. (2002). Banburismus and the brain: decoding the relationship between sensory stimuli, decisions, and reward. Neuron 36, 299–308.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Green, D. M., and Swets, J. A. (1966). Signal Detection Theory and Psychophysics. New York: Wiley.

Hayes, J. (1993). Introduction to Digital Logic Design. New York, NJ: Addison-Wesley.

Kandel, E. R., Schwartz, J. H., and Jessell, T. M. (eds). (2000). Principles of Neural Science. Norwalk, CT: Appleton and Lange.

Kiani, R., Hanks, T., and Shadlen, M. N. (2008). Bounded integration in parietal cortex underlies decisions even when viewing duration is dictated by the environment. J. Neurosci. 28, 3017–3029.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kobayashi, R., Tsubo, Y., and Shinomoto, S. (2009). Made-to-order spiking neuron model equipped with a multi-timescale adaptive threshold. Front. Comput. Neurosci. 3:9. doi:10.3389/neuro.10.009.2009

CrossRef Full Text

Kole, M. H. P., and Stuart, G. J. (2012). Signal processing in the axon initial segment. Neuron 73, 235–247.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lo, C.-C., and Wang, X.-J. (2006). Cortico-basal ganglia circuit mechanism for a decision threshold in reaction time tasks. Nat. Neurosci. 9, 956–963.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Luce, R. D. (1986). Response Times: Their Role in Inferring Elementary Mental Organization. New York, NY: Oxford University Press.

McMillen, T., Simen, P., and Behseta, S. (2011). Hebbian learning in linear-nonlinear networks with tuning curves leads to near-optimal, multi-alternative decision making. Neural Netw. 24, 417–426.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Moore, T., and Armstrong, K. M. (2003). Selective gating of visual signals by microstimulation of frontal cortex. Nature 421, 370–373.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Moore, T., and Fallah, M. (2001). Control of eye movements and spatial attention. Proc. Natl. Acad. Sci. U.S.A. 98, 1273–1276.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Purcell, B. A., Heitz, R. P., Cohen, J. Y., Schall, J. D., Logan, G. D., and Palmeri, T. J. (2010). Neurally constrained modeling of perceptual decision making. Psychol. Rev. 117, 1113–1143.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ratcliff, R., and McKoon, G. (2008). The diffusion decision model: theory and data for two-choice decision tasks. Neural. Comput. 20, 873–922.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Reddi, B. A. J., and Carpenter, R. H. S. (2000). The influence of urgency on decision time. Nature 3, 827–830.

Seung, H. S. (1996). How the brain keeps the eyes still. Proc. Natl. Acad. Sci. U.S.A. 93, 13339–13344.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Shadlen, M. N., and Newsome, W. T. (2001). Neural basis of a perceptual decision in the parietal cortex (area LIP) of the rhesus monkey. J. Neurophysiol. 86, 1916–1936.

Pubmed Abstract | Pubmed Full Text

Simen, P., Balci, F., deSouza, L., Cohen, J. D., and Holmes, P. (2011a). Interval timing by long-range temporal integration. Front. Integr. Neurosci. 5:28. doi:10.3389/fnint.2011.00028.

CrossRef Full Text

Simen, P., Balci, F., deSouza, L., Cohen, J. D., and Holmes, P. (2011b). A model of interval timing by neural integration. J. Neurosci. 31, 9238–9253.

CrossRef Full Text

Simen, P., and Cohen, J. D. (2009). Explicit melioration by a neural diffusion model. Brain Res. 1299, 95–117.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Simen, P., Cohen, J. D., and Holmes, P. (2006). Rapid decision threshold modulation by reward rate in a neural network. Neural Netw. 19, 1013–1026.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Simen, P., Contreras, D., Buck, C., Hu, P., Holmes, P., and Cohen, J. D. (2009). Reward rate optimization in two-alternative decision making: empirical tests of theoretical predictions. J. Exp. Psychol. Hum. Percept. Perform. 35, 1865–1897.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Simen, P., and Polk, T. A. (2010). A symbolic/subsymbolic interface protocol for cognitive modeling. Log. J. IGPL 18, 705–761.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Smith, P. L. (2010). From Poisson shot noise to the integrated Ornstein-Uhlenbeck process: neurally principled models of information accumulation in decision-making and response time. J. Math. Psychol. 54, 266–283.

CrossRef Full Text

Starns, J., and Ratcliff, R. (2012). Age-related differences in diffusion model boundary optimality with both trial-limited and time-limited tasks. Psychon. Bull. Rev. 19, 139–145.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Usher, M., and McClelland, J. L. (2001). The time course of perceptual choice: the leaky, competing accumulator model. Psychol. Rev. 108, 550–592.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

van Ravenzwaaij, D., van der Maas, H., and Wagenmakers, E.-J. (2011). Optimal decision making in neural inhibition models. Psychol. Rev. 119, 201–215.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wang, X. J. (2002). Probabilistic decision making by slow reverberation in cortical circuits. Neuron 36, 955–968.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text