- 1 Knowledge Media Research Center, Tuebingen, Germany
- 2 Department of Psychology, Eberhard Karls University, Tuebingen, Germany
- 3 Section Neuropsychology, Department of Neurology, University Hospital, RWTH Aachen University, Aachen, Germany
- 4 Department of Experimental Psychology, University of Oxford, Oxford, UK
Currently, there is a controversial debate on whether there is an abstract representation of number magnitude, multiple different ones, or multiple different ones that project onto a unitary representation. The current study aimed at evaluating this issue by means of a magnitude comparison task involving Arabic numbers and structured as well as unstructured non-symbolic patterns of squares. In particular, we were interested whether a specific numerical effect, the unit-decade compatibility effect reflecting decomposed processing of tens and units complying with the place-value structure of the Arabic number system, is affected by input notation. Indeed, a reliable unit-decade compatibility effect was observed in the symbolic-digital notation condition but was absent for unstructured non-symbolic notation. However, for structured non-symbolic notation a – albeit negative – compatibility effect was observed as well. Theses results are hard to reconcile with the notion of an abstract representation of number magnitude. Instead, our data support the existence of multiple representations of numerical magnitude. In addition, the current data indicate that it may not be a question of symbolic vs. non-symbolic notation only but also an issue of the structuring of the input notation. While unstructured non-symbolic quantities seemed to be processed holistically we found evidence suggesting at least partially decomposed processing not only for symbolic Arabic numbers but also for structured non-symbolic quantities.
Introduction
The most evident and important semantic information conveyed by a number is its magnitude (e.g., Miller and Gelman, 1983). As a consequence, all theoretical models, which have been proposed for the cognitive mechanisms underlying numerical cognition, include a representation for number magnitude as a central aspect (e.g., McCloskey, 1992). This is also the case for the currently most influential model in numerical cognition, the so-called Triple-Code Model by Dehaene and colleagues (Dehaene et al., 2003; Dehaene and Cohen, 1995, 1997). The Triple-Code Model posits numerical information to be processed in three different codes – a numerical (amodal) magnitude representation, a verbal representation referring to number words but also arithmetic facts, as well as a visual number form representation assumed to be relevant to identify our Arabic number symbols as meaningful items. However, since number magnitude represents the most important characteristic of numbers, the present study aimed at investigating specific representational characteristics of the number magnitude representation.
As regards the representation of number magnitude, the dominant view claims that “robust evidence demonstrates that with or without language, number is represented abstractly – independently of perceptual features, dimensions, modality, and notation. In fact, this is the very definition of ‘number”’ (Cantlon et al., 2009a, p. 331). However, in recent years there is accumulating evidence questioning the general validity of this notion and suggesting different representations of numerical magnitude (see Cohen Kadosh and Walsh, 2009a for a review and commentaries).
A Unitary vs. Multiple Representations of Number Magnitude
Generally, numerical magnitude can be conveyed by different notations such as non-symbolic set size of, for instance, dot patterns (e.g., •••••), symbolic digits (e.g., 5), number words (e.g., five), or even Roman numerals (e.g., V). As a consequence it is of interest whether all possible notations activate a unitary magnitude representation. In line with this, some researchers suggested that “adults can be said to rely on an abstract representation of number if their behavior depends only on the size of the numbers involved, not on the specific verbal or non-verbal means of denoting them” (Dehaene et al., 1998, p. 356, see also McCloskey, 1992, for a similar definition, but see Pesenti and Andres, 2009). Empirical evidence supporting this notion comes from behavioral (e.g., Reynvoet and Brysbaert, 1999), but also neuro-cognitive studies (e.g., Pinel et al., 2001; Eger et al., 2003; Libertus et al., 2007; Piazza et al., 2007). Behavioral studies have shown that numerical notation does not influence numerical effects assumed to stem from the magnitude representation. Additionally, fMRI studies indicated common neural activation for different numerical notations (e.g., Pinel et al., 2001; Piazza et al., 2007; Cohen Kadosh et al., 2011) or input modalities (e.g., Eger et al., 2003). The location of this activation around the intraparietal sulcus (IPS) is in line with other studies suggesting a crucial role of intraparietal areas for the representation of number magnitude (see Cohen Kadosh et al., 2008 for a review and meta-analysis).
Nevertheless, the notion of a unitary representation of number magnitude was questioned in recent years. Evidence against this notion also comes from both behavioral (e.g., Campbell and Epp, 2004) as well as neuro-cognitive studies (e.g., Cohen Kadosh et al., 2007, 2010, 2011; Cao et al., 2010; Santens et al., 2010). For instance, in an fMRI adaptation study Cohen Kadosh et al. (2007) observed an interaction between input notation and neural activity in the right IPS suggesting that at least parts of the neuronal substrates for numerical representation are notation-dependent. Similarly, Cohen Kadosh et al. (2011) showed that while brain activation in the bilateral IPS can be independent of the input notation, the functional connectivity between these brain regions is affected by the type of notation. Taken together, these results suggest multiple different representations of numerical magnitude instead of a unitary magnitude representation.
However, there is also a third hybrid account on the nature of number magnitude representation. Based on a series of computational modeling simulations Verguts and Fias, 2004, see also Verguts et al., 2005; Verguts and Fias 2008) proposed a number-selective coding system, which represents quantity regardless of the input format, similar to the Triple-Code model. However, this number-selective coding system is accessed through different pathways for non-symbolic and symbolic input. Thus, the authors assume a notation-specific representation of non-symbolic quantity that needs to be preprocessed in some way and then project onto the general number representation system. This notion was corroborated by recent fMRI data (Santens et al., 2010). The preferred pathway for processing non-symbolic quantities is supposed to include an area in the superior parietal cortex, whereas the pathway for processing symbolic quantities is assumed to directly access the number magnitude representation in the IPS (see also Cohen Kadosh and Walsh, 2009a for a similar account discussed below).
Taken together, this indicates that there is an ongoing debate on the nature of the representation of number magnitude with recent evidence suggesting multiple different representations of numerical magnitude which may converge on a unitary magnitude representation (see also Kucian and Kaufmann, 2009 for the notion of overlapping notation-dependent representations).
While this controversy has been addressed extensively with single-digit numbers, and mostly within symbolic notations, fewer studies have examined the issue of a unitary vs. multiple different magnitude representations with larger numbers and/or symbolic and non-symbolic notations (Reynvoet and Brysbaert, 1999; Ansari et al., 2007; Libertus et al., 2007; Piazza et al., 2007; Roggemann et al., 2007; Cantlon et al., 2009b; Eger et al., 2009; Knops et al., 2009). For instance, in the fMRI study of Ansari et al. (2007) the data revealed common clusters of IPS activation for both symbolic and non-symbolic conditions irrespective of whether the display involved a single- or a two-digit number. Thereby, the results of Ansari et al. (2007) suggest that even for quantities in the two-digit number range evidence for a unitary representation exists (see also Libertus et al., 2007; Piazza et al., 2007; Cantlon et al., 2009b; Knops et al., 2009 for similar conclusions). This is particularly interesting as there is an important structural difference between symbolic and non-symbolic notations for two-digit numbers. Symbolic numbers are usually presented as Arabic numbers, reflecting a positional numerical notation system organized in a place-value structure. This means that the value of the single digits is determined by their position within the digit string, (see Chrisomalis, 2004 for a taxonomy of numerical notation systems). Thereby, the overall magnitude of a two-digit number can only be derived by integrating the single digits’ magnitudes of tens and units. Thus, for symbolic magnitudes consideration of the place-value structure of the Arabic number system seems crucial and there is accumulating evidence that the place-value structure exerts considerable influence on the processing of multi-digit number magnitude (e.g., Nuerk et al., 2001; Macizo and Herrera, 2010; see Nuerk et al., 2011 for a review).
Holistic vs. Decomposed Processing of Multi-Digit Numbers
As regards the nature of the mental representation of number magnitude the Triple-Code Model (Dehaene and Cohen, 1995, 1997; Dehaene et al., 2003) proposes a holistic representation of numerical magnitude (e.g., Moyer and Landauer, 1967; Restle, 1970; Hinrichs et al., 1981; Dehaene et al., 1990; Zhang and Wang, 2005). In this context holistic means that each individual number (e.g., 38) is assumed to be represented as an integrated entity. As a consequence, speed and accuracy of discriminating between two numbers generally increase with the overall numerical distance between them (i.e., the distance effect, e.g., Dehaene et al., 1990; see also Pinel et al., 2001; Wood et al., 2006 for neural correlates). It has to be acknowledged that in a holistic representation no specific place-value information is retained. Instead, units, tens, hundreds, etc., are merged into one holistic magnitude representation and, thus, are not considered separately. Nevertheless, the notion of a purely holistic representation of number magnitude has been questioned in recent years.
Nuerk et al. (2001, 2004, 2005; see also Ratinckx et al., 2006; Ganor-Stern et al., 2007; Moeller et al., 2009a,b; Macizo and Herrera, 2010) observed differences in reaction time (RT) and error rates for the comparison of two two-digit numbers even though overall numerical distance was held constant. When comparing two-digit numbers the number pairs can be either unit-decade compatible (i.e., separate comparisons of tens and units bias the same decision, e.g., 42_57 → 4 < 5 and 2 < 7) or unit-decade incompatible (i.e., comparing tens and units separately yields opposed decision biases, e.g., 47_62 → 4 < 6 but 7 > 2) although overall numerical distance is identical (15 for both examples). Usually, decisions for compatible number pairs are faster and less error prone. Thereby, the unit-decade compatibility effect indicates that tens and units are processed separately in a decomposed fashion (see Nuerk and Willmes, 2005; Nuerk et al., 2011, for reviews). On a broader level, these findings suggest influences of the place-value structure of the Arabic number system on the processing of multi-digit number magnitude (see also Korvorst and Damian, 2008 for a compatibility effect for three-digit numbers). And indeed computational modeling simulations revealed that an explicit differentiation between place-value stack information is a necessary prerequisite for the compatibility effect (cf. Moeller et al., 2011)1.
However, the question of holistic vs. decomposed processing can also be seen in terms of the dual code theory suggested by Cohen Kadosh and Walsh (2009a). The dual code theory is based on the assumption that different codes are active during numerical representation. In particular, at the first stage an automatic activation of the numerical quantity in the IPS is assumed that is modality- and notation-specific. This representation is suggested to be only a rough estimation of numerical magnitude (Banks et al., 1976; Tzelgov et al., 1992; Cohen Kadosh and Walsh, 2009b). In other words, not only that number magnitude is activated in an automatic, rough, modality-, and notation-dependent manner in a first stage, this initial processing may be specific for each individual feature of the input format. In the second stage, the representation of numerical information in the IPS becomes intentional and more fine-grained. The transition from automatic to intentional representation is subserved by the PFC neural circuitry reflecting learned associations and rules (e.g., Duncan, 2001). Importantly, this refinement depends on task demands and is resource-dependent.
For instance, in two-digit numbers the digits at the tens and unit position may be processed individually first. Only later, when synced with the structural information of the place-value structure during the intentional processing stage the overall magnitude of the number may be constructed. This means that numerical information in multi-digit numbers is processed in a decomposed fashion. As such decomposed processing requires a strong structuring of the input such as the place-value structure of the Arabic number system it is only possible when there is a clear structure logically relating the specific features to each other. In the place-value system this structure is the place coding of units, tens, hundreds, etc. This decomposed input is then combined into the shared information of the number’s holistic magnitude. However, assuming that our hypothesis is correct proposing that the grade of structure present in the input determines whether the input is processed in a decomposed fashion or not, we should be able to observe evidence for decomposed processing for non-symbolic stimuli as well – given that it is structured in an appropriate way.
Considering the debate whether or not numerical representations are notation-specific, such an explicit reference to place-value information should be present in digital symbolic notation but not in unstructured non-symbolic notations such as, e.g., random square patterns. However, when the structure of the non-symbolic input allows any kind of decomposition, an influence of this structure should be observed. Thus, evaluating the compatibility effect for digital symbolic as well as structured and unstructured non-symbolic magnitudes might be a valuable approach to gain further evidence regarding the debate whether numerical magnitudes are represented in a unitary or rather differentiated way.
The Present Study
Considering above introduced argument on unitary vs. multiple different representations of number magnitude and the influence of the place-value structure of the Arabic number system, the aim of the current study was straightforward. We aimed at pursuing the question whether the human magnitude representation of two-digit numbers is (i) unitary, notation-specific or a rather hybrid combination of both and (ii) in what way the external structure of the input influences magnitude processing. Therefore, we conducted two experiments. In Experiment 1, participants had to compare the quantities of two stimuli in the two-digit number range presented as either two Arabic numbers or two arrays of unstructured randomly distributed squares. Contrarily, in Experiment 2, we contrasted the comparison of two Arabic numbers and two non-symbolic magnitudes presented in arrays of squares structured in a 10 × 10 grid. We were interested in whether or not the explicit identification of external structuring (i.e., place-value information for Arabic numbers and/or 10 × 10 structure of non-symbolic quantities) modulated task performance and in particular the unit-decade compatibility effect. Our specific hypotheses were as follows:
(i) A unitary magnitude representation would be indicated by a consistent observation of either no compatibility effects or significant compatibility effects in all three presentation conditions. However, when an explicit external structuring is necessary to observe the compatibility effect, we should find a reliable compatibility effect in the symbolic but not in the non-symbolic presentation conditions. As a consequence, the absence of the compatibility effect in the non-symbolic stimuli conditions would provide further evidence for multiple but different magnitude representations.
(ii) On the other hand, notation-specific representations may only reflect the initial stage of magnitude processing and converge onto an abstract representation of number magnitude in later stages. In this case external structuring of the non-symbolic input allowing for decomposition similar to that observed for Arabic numbers should reduce the differences between symbolic and non-symbolic notations as indicated by influences of unit-decade compatibility. Assuming that participants considered the structural information of the 10 × 10 grid (i.e., filled rows and/or columns as tens) influences of unit-decade compatibility should be detectable: as the decade distance of incompatible number pairs is necessarily larger than that of compatible pairs when overall distance is matched, this means that on average the number of completely filled rows or columns is larger for incompatible than for compatible number pairs (see Nuerk et al., 2004 for a more detailed discussion). In turn, we should observe faster responses for incompatible pairs in the structured non-symbolic condition due to the larger decade distance in this condition. Thereby, the debate on a unitary vs. multiple different representations of number magnitude may be moderated by the question of input structuring.
As the results of both experiments need to be evaluated in an integrated manner, they will be discussed jointly.
Experiment 1: Unstructured Non-Symbolic Input Method
Participants
Twenty-four students (17 female; 7 male) of the University of Tuebingen participated in the study as partial fulfillment of course requirements. Mean age was 24.5 years (SD = 5.2 years, range: 20–42 years). All participants reported normal or corrected-to-normal vision and all but three were right-handed. All participants gave their written informed consent prior to the experiment.
Task, Stimuli, and Design
Participants were to solve a magnitude comparison task by singling out the larger of two quantities. These were either presented symbolically in digital notation as two-digit numbers or non-symbolically as pseudo-random patterns of squares. The 240 between-decade number pairs (e.g., 32_57) as introduced by Nuerk et al. (2001) were used in the current study. These between-decade stimuli reflected a 2 × 2 × 2 design with the factors unit-decade compatibility (compatible: e.g., 32_57 vs. incompatible: e.g., 37_62), decade distance (small: i.e., 1–3 vs. large: i.e., 4–7), and unit distance (small: i.e., 1–3 vs. large: i.e., 4–8) manipulated orthogonally. Additionally, a set of 240 within-decade stimuli (e.g., 64_69) was used to balance between- and within-decade comparisons. Thus, the critical stimulus set of 480 items (240 between- and 240 within-decade comparisons) was presented twice, once in symbolic-digital and once in non-symbolic notation. Both, symbolic-digital and non-symbolic stimuli were presented in a blocked design. Block order (i.e., symbolic-digital – non-symbolic vs. non-symbolic – symbolic-digital) was counterbalanced across participants with trial order being pseudo-randomized under each condition separately. Stimuli were displayed as white digits against a black background or patterns of black squares within a circular white background (see Figure 1). Digits were presented in font Arial size 50 besides each other at x/y locations 280/0 and −280/0 of a 16′ screen driven with a resolution of 1024 × 768 pixel. The distance between the two numbers was ∼13 cm. Non-symbolic quantities were presented as pictures with the center of the two pictures located at the same x/y coordinates as the symbolic stimuli. For the non-symbolic stimuli we varied the position of the squares randomly for each numerosity and trial as well as the sizes of the square coding either numerosity. Thereby, overall area occupied by the rectangles as well as overall luminance, total circumference, density, exact appearance, and linear span between the rectangles were controlled for (see Dehaene et al., 2005 for further details). The two white circles in that the randomly distributed squares were presented had a diameter of ∼10 cm.
Figure 1. Schematic illustration of two example stimuli. (A) depicts a symbolic-digital pair of to be compared numbers, whereas (B) reflects the corresponding pair of non-symbolic quantities. Participants had to indicate the larger number/numerosity.
Procedure
Participants were seated ∼50 cm from the screen and had to decide which one of the two presented numbers/numerosities was the numerically larger one by pressing a corresponding response button. When the left number/numerosity was the larger one than the “arrow key left” of a standard German QWERTZ keyboard had to be pressed, whereas the “arrow key right” had to be pressed when the right number/numerosity was the larger one. Instructions focused on both speed and accuracy. Prior to the experiment participants performed 10 practice trials in each of the two notation conditions to become familiar with display layouts and task requirements. In each trial a fixation cross was displayed in the center of the screen for 500 ms followed by the two numbers/numerosities which were presented until one of the response buttons was pressed or the time limit of 3000 ms was reached. Altogether, the experiment took about 35–45 min.
Analysis
The data were analyzed by conducting a repeated-measures ANOVA discerning the within-subject factors notation condition (symbolic-digital vs. non-symbolic), compatibility (compatible vs. incompatible), decade distance (small vs. large), and unit distance (small vs. large).
Results
Generally, error rates for the relevant between-decade comparisons were very low and did not differ between symbolic and non-symbolic conditions [symbolic: M = 3.7%, SD = 2.2%; non-symbolic: M = 4.7%, SD = 2.7%, t(23) = 1.51, p = 0.14]. We excluded all participants from further analyzes with an error rate of ≥30% (50% was guessing rate) in any one of the critical conditions. This affected two participants. Furthermore, as there were even conditions in which participants did not commit a single error (presenting a harsh violation of ANOVA preconditions), we focused our analyses on response latencies. Yet, the mean correlation of RT and error rates over participants was r = 0.42 (SEM = 0.06) which is reliably larger than 0 [t(21) = 7.23; p < 0.001] and thus indicated corresponding result patterns for RT and errors and no speed accuracy trade-off. Only RT followed by a correct response were submitted to further analyzes. Moreover, a two-step trimming procedure was applied: first, all latencies shorter than 200 ms and longer than 2,000 ms were eliminated, second, all RT falling outside the interval ±3 SD around an individual’s mean RT were excluded. Overall trimming resulted in an additional loss of 0.8% of the data.
In the following, the description of the results will be separated into two paragraphs. In the first paragraph we will focus on the results, which directly test our hypotheses. For the sake of lucidity the remaining more or less unspecific ANOVA results will be presented in a second paragraph to complete the statistical evaluation of the data.
Results Primarily Relevant for the Notation-specific vs. -independent Debate
The ANOVA revealed a reliable main effect of compatibility [F(1, 21) = 46.14, p < 0.001, ] with compatible number pairs being responded to faster as compared to incompatible number pairs (626 vs. 656 ms, respectively). Crucially, this main effect was modulated significantly by notation condition [F(1, 21) = 57.79, p < 0.001, ]. The interaction indicated a compatibility effect (i.e., RT incompatible – RT compatible) in the symbolic-digital notation condition, but no effect in the non-symbolic condition (60 vs. 1 ms, respectively, see Figure 2). Moreover, as previously observed compatibility interacted reliably with unit distance [F(1, 21) = 16.12, p < 0.001, ]: the compatibility effect was more pronounced for large unit distances than for small (41 vs. 18 ms, respectively). This interaction was further specified by the significant three-way interaction of compatibility, unit distance, and notation condition [F(1, 21) = 17.80, p < 0.001, ]. Breaking down this three-way interaction into its constituting two-way interactions revealed that the interaction of compatibility and unit distance was only reliable for the symbolic-digital condition [F(1, 21) = 28.51, p < 0.001, : compatibility effect more pronounced for large unit distances than for small 80 vs. 38 ms, respectively] but not for the non-symbolic notation condition [F(1, 21) < 1: compatibility effect 2 and 0 ms for large and small unit distances, respectively].
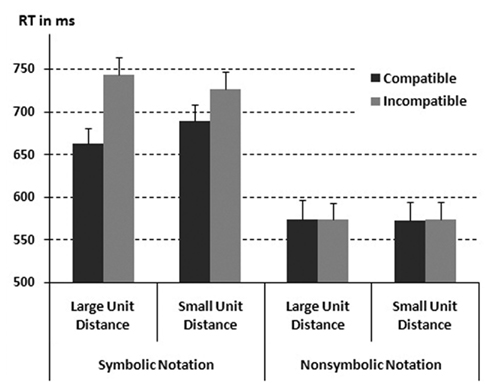
Figure 2. Response latencies for compatible and incompatible comparisons separated for symbolic and unstructured non-symbolic notation and large vs. small unit distance. Error bars indicate 1 standard error of the mean (SEM).
Further ANOVA Results
Apart from these results that directly tested our hypotheses, the results were as follows. The main effect of decade distance turned out to be significant [F(1, 21) = 163.15, p < 0.001, ] with responses being faster for number pairs with a large as compared to pairs with a small decade distance (590 vs. 693 ms, respectively). Furthermore, a significant main effect of notation condition was observed [F(1, 21) = 46.79, p < 0.001, ]. Response latencies were shorter in the non-symbolic compared to the symbolic-digital condition (568 vs. 714 ms, respectively). Moreover, the interaction of decade distance and notation condition was reliable [F(1, 21) = 17.02, p < 0.001, ]: the decade distance effect was smaller in the symbolic-digital than in the non-symbolic notation condition (75 vs. 130 ms, respectively). Additionally, this two-way interaction was further specified by the reliable three-way interaction of compatibility, decade distance and notation condition format [F(1, 21) = 7.71, p < 0.05, ]. Breaking down this three-way interaction into its constituting two-way interactions revealed that the interaction of decade distance and notation condition was significant for both compatible [F(1, 21) = 20.51, p < 0.001, ] and incompatible comparisons [F(1, 21) = 9.28, p < 0.01, ]. However, inspection of the marginal means indicated that for compatible comparisons the difference between the decade distance effects for symbolic-digital and non-symbolic notation was reliably larger than the difference between the symbolic-digital and non-symbolic decade distance effects for incompatible number pairs [68 vs. 40 ms, respectively; t(21) = 2.78, p < 05]. Most likely, the reason for this data pattern may be the fact that decade distance is inevitably larger for incompatible as compared to compatible comparisons (e.g., incompatible 37_52: decade distance 2; compatible 32_47: decade distance 1, with an overall distance of 15 in both cases). As this larger decade distance leads to a larger decade distance effect for RT in the symbolic-digital notation condition, the difference in decade distance effects between the symbolic-digital and non-symbolic notation condition should be reduced for incompatible number pairs. Finally, this interrelation was further specified by the four-way interaction of compatibility, unit distance, decade distance, and notation condition format [F(1, 21) = 14.83, p < 0.01, ]. This interaction indicated that above described reduced difference in decade distance effects between symbolic-digital and non-symbolic notation for incompatible number pairs was primarily driven by pairs with a small unit distance. This may indicate that the higher decade distance for incompatible comparisons seems to be especially relevant when both decade and unit distances are small and thus comparable. It has to be noted that the latter effects were clearly driven by properties of the current stimulus set. Nevertheless, the higher decade distance effects for incompatible number pairs should only influence processing of symbolic-digital number as for non-symbolic numerosities no explicit distinction between tens and units is evident. Thus, this pattern of results further corroborated our interpretation that the nature of the underlying representations of symbolic-digital and non-symbolic magnitudes may indeed differ. All other main effects and interactions were not statistically reliable (all F < 2.42, all p > 0.14).
Experiment 2: Structured Non-Symbolic Input Method
Experimental details were very similar to those of Experiment 1. Therefore, only aspects differing from the method of Experiment 1 will be described in the following.
Participants
Twenty-six students (two male) of the University of Tuebingen participated in the study. Mean age was 20.8 years (SD = 2.4 years, range: 19–29 years). All participants reported normal or corrected-to-normal vision and all but two were right-handed. Written informed consent was obtained from all participants prior to the experiment.
Task, Stimuli, and Design
Instead of dots distributed randomly within a circle the dots were presented as black squares arranged in a 10 × 10 grid within a white square. Arabic numbers were displayed as white digits against a black background or patterns of black squares within two larger white squares with an edge length of ∼10 cm (see Figure 3). Otherwise the presentation scheme was identical to that of Experiment 1. For the non-symbolic stimuli we varied the position of the squares randomly for each numerosity and trial as well as the sizes of the squares coding either numerosity.

Figure 3. Schematic illustration of an example stimulus of the structured non-symbolic number pair. Participants had to indicate the larger numerosity.
Results
Again, overall error rates for the relevant between-decade comparisons were very low and did not differ between symbolic and non-symbolic conditions [symbolic: M = 3.4%, SD = 2.9%; non-symbolic: M = 3.2%, SD = 2.5%, t(23) = 0.57, p = 0.58]. Nevertheless, we excluded all participants from further analyzes whose error rate was ≥30% (50% was guessing rate) in any one condition. This affected two participants. As for Experiment 1 we focused our analyzes on response latencies. The mean correlation of RT and error rates over participants was r = 0.55 (SEM = 0.06) which is reliably larger than 0 [t(23) = 9.71; p < 0.001] and thus indicated corresponding results pattern for RT and errors and no speed accuracy trade-off. A trimming procedure identical to that applied to the data of Experiment 1 resulted in an additional loss of 1% of the data.
Results Primarily Relevant for the Notation-Specific vs. -Independent Debate
The ANOVA discerning the within-subject factors notation condition (symbolic-digital vs. non-symbolic), compatibility (compatible vs. incompatible), decade distance (small vs. large), and unit distance (small vs. large) revealed a reliable main effect of compatibility [F(1, 23) = 12.19, p < 0.01, ] with compatible number pairs being responded to faster as compared to incompatible number pairs (729 vs. 744 ms, respectively, see Figure 4). Crucially, this main effect was modulated significantly by notation condition [F(1, 23) = 44.06, p < 0.001, ]. The interaction indicated a standard compatibility effect in the symbolic-digital presentation condition, but a reversed effect in the non-symbolic condition (+37 vs. −12 ms, respectively, see Figure 4). Importantly, testing our hypothesis of a reversed compatibility effect directly revealed that RT for incompatible number pairs was indeed faster than that for compatible pairs in this condition [t(23) = 1.67, p = 0.05, tested one-sided]. Moreover, as previously observed compatibility interacted marginally reliably with unit distance [F(1, 23) = 3.96, p = 0.06, ]: the compatibility effect tended to be more pronounced for large unit distances than for small (23 vs. 6 ms, respectively).
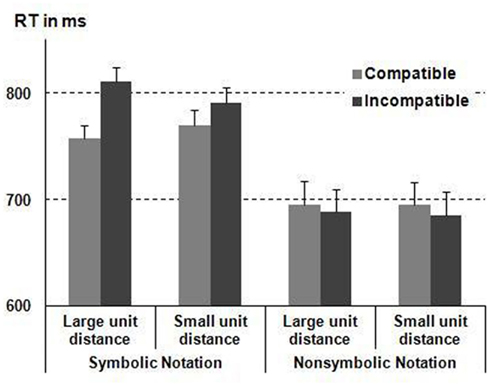
Figure 4. Response latencies for compatible and incompatible comparisons separated for symbolic and structured non-symbolic notation and large vs. small unit distance. Error bars reflect 1 SEM.
Further ANOVA Results
Apart from these results that directly tested our hypotheses, the results were as follows. The main effect of decade distance turned out to be significant [F(1, 23) = 151.36, p < 0.001, ] with responses being faster for number pairs with a large as compared to pairs with a small decade distance (673 vs. 800 ms, respectively). Furthermore, a significant main effect of notation condition was observed [F(1, 23) = 8.73, p < 0.01, ]. Response latencies were shorter in the non-symbolic compared to the symbolic-digital condition (691 vs. 782 ms, respectively). Moreover, the interaction of decade distance and notation condition was reliable [F(1, 21) = 42.19, p < 0.001, ]: the decade distance effect was smaller in the symbolic-digital than in the non-symbolic notation condition (77 vs. 178 ms, respectively). Additionally, the two-way interaction of compatibility and decade distance was reliable [F(1, 23) = 15.55, p < 0.01, ] indicating that the compatibility effect was more pronounced for large than for small decade distances (28 vs. 0 ms, respectively). Finally, the four-way interaction of compatibility, unit distance, decade distance, and notation condition format was significant again [F(1, 23) = 7.25, p < 0.05, ]. Comparable to the results of Experiment 1 this interaction indicated that a difference in decade distance effects between symbolic-digital and non-symbolic notation was observed for incompatible number pairs with a small unit distance in particular. Again, we wish to emphasize that the latter effect was probably driven by properties of the current stimulus set. All other main effects and interactions were not statistically reliable (all F < 2.19, all p > 0.15).
Discussion
The current study pursued the question whether the human representation of two-digit number magnitude is unitary, notation-dependent or a specific combination of both. In particular, we were interested whether the unit-decade compatibility effect is modulated by numerical input notation and, for the case of non-symbolic input, by its external structure. Therefore, we evaluated participants’ performance when comparing the quantities of two stimuli in the two-digit number range presented as Arabic numbers or arrays of either randomly or regularly distributed squares. We hypothesized that (i) a single unitary magnitude representation should be indicated by the presence of the compatibility effect irrespective of notation condition. (ii) We assumed external structure to be essential for decomposed processing of specific stimulus features. As a consequence we expected to observe reliable indices of decomposed processing for non-symbolic input when structured accordingly, if the processing of structural information is a prerequisite step toward an integrated and abstract representation of number magnitude.
A Unitary Representation of Number Magnitude?
The significant interaction between compatibility and notation condition in Experiment 1 was due to a compatibility effect for symbolic Arabic numbers only. This means that the presence of the compatibility effect was limited to the case that place-value information was explicitly conveyed by the notation condition. This importance of structuring information is further corroborated by the results of Experiment 2 in which we also observed evidence for influences of unit-decade compatibility when non-symbolic quantities are structured in an according manner. Critically, the compatibility effect for structured non-symbolic quantities was reversed (i.e., faster responses to incompatible pairs). Importantly, this can be accounted for by properties of the stimulus set and the presentation in the 10 × 10 grid. The decade distance of incompatible number pairs is necessarily larger than that of compatible pairs when overall distance is matched (cf. Nuerk et al., 2001, 2004 for a discussion of this point). Taking into account the presentation in the 10 × 10 grid in Experiment 2 this means that on average the number of completely filled rows or columns was larger for incompatible than for compatible number pairs. Assuming that participants considered the structural information of the 10 × 10 grid, this should result in faster responses for incompatible pairs in the structured non-symbolic condition due to the larger decade distance in this condition.
Thus, the current results strongly suggests that the human number magnitude representation cannot be exclusively unitary as in such a case we should have observed consistent results for both symbolic-digital and both non-symbolic notation conditions. The current results add to previous studies showing quantitative differences in the effects underlying numerical representations (e.g., Ito and Hatta, 2003; Cohen Kadosh, 2008; Cohen Kadosh et al., 2008; Droit-Volet et al., 2008), by providing evidence for a qualitative differences between the notations and extending the results to multi-digit number processing. Taken together, such a differential pattern of results is in line with the argument of Cohen Kadosh and Walsh (2009a) challenging a unitary representation of numerical magnitude.
Number Magnitude Representation and Input Structure
The representation for structured input notations (i.e., symbolic-digital Arabic and structured non-symbolic) is characterized by decomposed processing of tens and units, whereas the representation of unstructured non-symbolic quantities is characterized by rather holistic processing. Synced with previous findings of quantitative differences between the notations, some of them also present in the current study (e.g., the interaction between decade distance and notation, see below for a discussion), the current data provide strong support for at least initially separate representations for unstructured non-symbolic and symbolic-digital numerical notations. Importantly, it has to be noted that the stimulus sets for the two presentation conditions were identical regarding the numerical magnitudes involved. Exactly the same number pairs had to be compared with the only difference that the two-digit numbers involved were presented as either Arabic numerals or random square patterns. Thereby, these results corroborate the proposition of Moeller et al. (2011) on the influence of place-value information. In a computational modeling study on two-digit number magnitude comparison Moeller et al. (2011) only found indications for decomposed processing of tens and units for simulations incorporating an explicit distinction between representations of tens and units. From this finding the authors concluded that such an explicit representation of place-value stack information is a necessary prerequisite for decomposed processing of tens and units. In turn, this assumption implies that there should be no empirical indicators for decomposed processing of tens and units for numerical notations that do not allow for a clear identification of tens and units, such as dot or square patterns.
While this seems trivial at a first glance, the results of Experiment 2 indicate that the question of symbolic vs. non-symbolic may only be part of the story. It was suggested that there may be initial notation-dependent representations of magnitude that later on converge onto a unitary representation of magnitude. In their dual code theory Cohen Kadosh and Walsh (2009a) suggested that this convergence is due to the application of known associations and/or rules. In Experiment 2 we observed evidence suggesting that this may fit nicely to the processing of two-digit number quantity. At the first processing step a modality- and notation-specific activation of numerical quantity information is supposed to be activated automatically. The compatibility effect suggests that in the case of two-digit numbers this is the magnitude of the single digits of tens and units. To move on to a unitary magnitude representation the single digits’ magnitudes need to be integrated. Our results suggest that one important mechanism modulating this integration of input features is the external structure of the input. The fact that the notation-specific differences between input notations (symbolic vs. randomly displayed non-symbolic input) diminishes when the non-symbolic input is presented in a regularly structured way, clearly suggests that structural integration seems to be a crucial step toward a unitary numerical representation.
This notion can also be transferred to the neuro-functional results by Santens et al. (2010). When we assume that more or less structural information is inherent to all kind of combined (visual) input, then this structural information has to be processed and integrated in a specific cortical area. For the case of symbolic processing, Santens et al. (2010) employed single-digit numbers which are highly overlearned and do not require the integration of components. Therefore, apart from IPS activation associated with magnitude information no further activation spots indicating integration processes were observed for symbolic stimuli by Santens et al. (2010). When our account is valid, the processing of two-digit numbers should require the processing of external structure information, that is, the place-value structure of the Arabic number system. This hypothesis is corroborated by recent fMRI data indicating the integration of place-value information to be subserved by the posterior part of the IPS, anatomically distinct from the number magnitude representation situated in the hIPS (e.g., Wood et al., 2006; Klein et al., 2010). It is important to note that the activation observed in the Santens et al. (2009) study for the, in our notion, integration of non-symbolic quantity was observed in the direct vicinity of the activation reported in the studies of Klein et al. (2010) and Wood et al. (2006) for the case of place-value integration: namely medial, superior, and posterior to the hIPS in the posterior extension of the IPS. In summary, our account suggests structural information to be an important parameter influencing the converging of initial notation-dependent representations of number magnitude onto a unitary one. However, it might well be that while they converge in a single brain region, as in Santens et al.’s (2010) study, the numerical representation is still notation-dependent, and is subserved by different neuronal subpopulations that overlap in the same anatomical location (for experimental evidence for such possibility see Cohen Kadosh et al., 2011). The dissociation between a negative compatibility for non-symbolic structured presentation, and a positive compatibility for a symbolic-digit numbers observed in the current study lend further support to this view.
Further Differences between Processing Symbolic and Non-Symbolic Magnitudes
At this point it is important to note that in light of to date literature the current results are not trivial. As argued above there is considerable evidence suggesting a unitary representation of number magnitude for quantities in the two-digit range neglecting structural differences in (re)presentational format (e.g., Libertus et al., 2007; Piazza et al., 2007; Cantlon et al., 2009b; Knops et al., 2009). Interestingly, the finding that notation condition modulated numerical effects not only quantitatively, but also qualitatively, applied also to the case of the (decade) distance effect. On the one hand, we observed the decade distance effect to be consistently smaller in the symbolic-digital than in the non-symbolic notation condition reflecting a quantitative difference in the processing of (decade) distance between notation conditions. On the other hand, there were even qualitative differences for the case of the distance effect. Running separate stepwise multiple regression analyzes for symbolic-digital and unstructured non-symbolic presentation incorporating the predictors linear and logarithmic overall distance as well as unit distance as a measure of unit-decade compatibility (see Nuerk et al., 2001 for a discussion of this proceeding) yielded the following results. We found that for symbolic-digital notation linear overall distance [b = −0.63, t(239) = 15.75, p < 0.001] and unit distance [b = −0.47, t(239) = 11.70, p < 0.001] were the only significant predictors of overall RT [R = 0.79, adj. R2 = 0.62, F(2, 237) = 195.27, p < 0.001]. In contrast, for the non-symbolic notation logarithmic overall distance [b = −0.77, t(239) = 18.47, p < 0.001] was the only reliable predictor of RT [R = 0.77, adj. R2 = 0.59, F(1, 238) = 340.99, p < 0.001]. The observed differential influence of linear and logarithmic distance on overall RT provides additional support for the idea that the magnitude representations underlying the distance effect in the symbolic-digital and at least the unstructured non-symbolic condition may not be identical. Taken together, these additional analyzes provide further evidence for a not only quantitative but also qualitative difference of the initial magnitude representation recruited when comparing either symbolic Arabic numbers or unstructured non-symbolic patterns of squares. Moreover, the fact that this dissociation was not observed for the case of structured non-symbolic quantities again corroborates our interpretation that the processing of additional structural information may lead to an integration and transformation on the representational level as well.
Conclusion
The current study set off to evaluate the nature of the human number magnitude representation (unitary vs. multiple notation-dependent vs. hybrid) in a magnitude comparison task involving symbolic Arabic numbers as well as structured and unstructured non-symbolic patterns of squares. Thereby, the current data were informative as regards the ongoing debate on whether there is a unitary human number magnitude representation or rather multiple ones. In line with the latter multiple representations view, a regular unit-decade compatibility effect was only observed in the symbolic-digital notation condition. However, we also found reliable influences of compatibility in the structured non-symbolic condition indicating that the differentiation of number magnitude representations into symbolic vs. non-symbolic may only part of the story. On the one hand, the dissociation of the compatibility effect is hard to reconcile with the notion of a single unitary representation of number magnitude. However, the influence of structural information may indicate in what way the initially notation-dependent representations of number magnitude may converge onto a unitary and abstract one: by being integrated into a superordinate structure such as the place-value structure of the Arabic number system. From a theoretical point of view, the current study follows a new approach as it addressed the questions at hand by evaluating the presence of a specific multi-digit number processing effect. Thereby, we not only considered numerical magnitude per se (as indicated by the distance effect) but also its organizing principle as informative.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research was funded in part by the German Research Foundation (DFG) by means of a project within the Research Group (Forschergruppe) Analyse und Förderung effektiver Lehr-Lern-Prozesse (FOR 738/2/TP02) granted to Ulrike Cress and Hans-Christoph Nuerk supporting Korbinian Moeller. Additionally, part of this research was supported by a project in the ScienceCampus (WissenschaftsCampus) Tuebingen (Cluster 1/TP 1). Roi Cohen Kadosh is supported by the Wellcome Trust (WT88378).
Footnote
- ^At this point it is important to note that the unit-decade compatibility effect is not a purely perceptual congruity effect. Rather, its interaction with unit distance (i.e., the compatibility is more pronounced for large as compared to small unit distances) indicates that it is indeed based on the processing of semantic internal number magnitude information (Moeller et al., 2009b).
References
Ansari, D., Lyons, I., van Eimeren, L., and Xu, F. (2007). Linking visual attention and number processing in the brain: the role of the temporo-parietal junction in small, and large non-symbolic number comparison. J. Cogn. Neurosci. 19, 1845–1853.
Banks, W. P., Fujii, M., and Kayra-Stuart, F. (1976). Semantic congruity effects in comparative judgments of magnitudes of digits. J. Exp. Psychol. Hum. Percept. Perform. 2, 435–447.
Campbell, J. I. D., and Epp, L. J. (2004). An encoding-complex approach to numerical cognition in Chinese-English bilinguals. Can. J. Exp. Psychol. 58, 229–244.
Cantlon, J. F., Cordes, S., Libertus, M. E., and Brannon, E. M. (2009a). Numerical abstraction: it ain’t broke. Behav. Brain Sci. 32, 331–332.
Cantlon, J. F., Libertus, M. E., Pinel, P., Dehaene, S., Brannon, E. M., and Pelphrey, K. A. (2009b). The neural development of an abstract concept of number. J. Cogn. Neurosci. 21, 2217–2229.
Cao, B. H., Li, F. H., and Li, H. (2010). Notation-dependent processing of numerical magnitude: electrophysiological evidence from Chinese numerals. Biol. Psychol. 83, 47–55.
Chrisomalis, S. (2004). A cognitive typology for numerical notation. Cambridge Archaeol. J. 14, 37–52.
Cohen Kadosh, R. (2008). Numerical representation: abstract or nonabstract? Q. J. Exp. Psychol. (Hove) 61, 1160–1168.
Cohen Kadosh, R., Bahrami, B., Walsh, V., Butterworth, B., Popescu, T., and Price, C. J. (2011). Specialisation in the human brain: the case of numbers. Front. Hum. Neurosci. 5:62. doi: 10.3389/fnhum.2011.00062
Cohen Kadosh, R., Cohen Kadosh, K., Kaas, A., Henik, A., and Goebel, R. (2007). Notation-dependent and -independent representations of numbers in the parietal lobes. Neuron 53, 307–314.
Cohen Kadosh, R., Henik, A., and Rubinsten, O. (2008). Are Arabic and verbal numbers processed in different ways? J. Exp. Psychol. Learn. Mem. Cogn. 34, 1377–1391.
Cohen Kadosh, R., Muggleton, N., Silvanto, J., and Walsh, V. (2010). Double dissociation of format-dependent and number-specific neurons in human parietal cortex. Cereb. Cortex 20, 2166–2171.
Cohen Kadosh, R., and Walsh, V. (2009a). Numerical representations in the parietal lobes: abstract or not abstract? Behav. Brain Sci. 32, 313–328.
Cohen Kadosh, R., and Walsh, V. (2009b). Non-abstract numerical representations in the IPS: further support, challenges, and clarifications. Behav. Brain Sci. 32, 356–373.
Dehaene, S., and Cohen, L. (1995). Towards an anatomical and functional model of number processing. Math. Cogn. 1, 83–120.
Dehaene, S., and Cohen, L. (1997). Cerebral pathways for calculation: double dissociation between rote verbal and quantitative knowledge of arithmetic. Cortex 33, 219–250.
Dehaene, S., Dehaene-Lambertz, G., and Cohen, L. (1998). Abstract representations of numbers in the animal and human brain. Trends Neurosci. 21, 355–361.
Dehaene, S., Dupoux, E., and Mehler, J. (1990). Is numerical comparison digital? Analogical and symbolic effects in two-digit number comparison. J. Exp. Psychol. Hum. Percept. Perform. 16, 626–641.
Dehaene, S., Izard, V., and Piazza, M. (2005). Control Over Non-Numerical Parameters in Numerosity Experiments. Available at: www.unicog.org
Dehaene, S., Piazza, M., Pinel, P., and Cohen, L. (2003). Three parietal circuits for number processing. Cogn. Neuropsychol. 20, 487–506.
Droit-Volet, S., Clément, A., and Fayol, M. (2008). Time, number and length: similarities and differences in discrimination in adults and children. Q. J. Exp. Psychol. 61, 1827–1846.
Duncan, J. (2001). An adaptive coding model of neural function in prefrontal cortex. Nat. Rev. Neurosci. 2, 820–829.
Eger, E., Michel, V., Thirion, B., Amadon, A., Dehaene, S., and Kleinschmidt, A. (2009). Deciphering cortical number coding from human brain activity patterns. Curr. Biol. 19, 1608–1615.
Eger, E., Sterzer, P., Russ, M. O., Giraud, A.-L., and Kleinschmidt, A. (2003). A supramodal number representation in human intraparietal cortex. Neuron 37, 719–725.
Ganor-Stern, D., Tzelgov, J., and Ellenbogen, R. (2007). Automaticity of two-digit numbers. J. Exp. Psychol. Hum. Percept. Perform. 33, 483–496.
Hinrichs, J. V., Yurko, D. S., and Hu, J.-M. (1981). Two-digit number comparison: use of place information. J. Exp. Psychol. Hum. Percept. Perform. 7, 890–901.
Ito, Y., and Hatta, T. (2003). Semantic processing of Arabic, Kanji, and Kana numbers: evidence from interference in physical and numerical size judgments. Mem. Cognit. 31, 360–368.
Klein, E., Willmes, K., Dressel, K., Domahs, F., Wood, G., Nuerk, H.-C., and Moeller, K. (2010). Categorical and continuous - Disentangling the neural correlates of the carry effect in multi-digit addition. Behav. Brain Funct. 6, 70.
Knops, A., Thirion, B., Hubbard, E. M., Michel, V., and Dehaene, S. (2009). Recruitment of an area involved in eye movements during mental arithmetic. Science 324, 1583–1585.
Korvorst, M., and Damian, M. F. (2008). The differential influence of decades and units on multi-digit number comparison. Q. J. Exp. Psychol. 61, 1250–1264.
Kucian, K., and Kaufmann, L. (2009). A developmental model of number representations. Behav. Brain Sci. 32, 340–341.
Libertus, M. E., Woldorff, M. G., and Brannon, E. M. (2007). Electrophysiological evidence for notation independence in numerical processing. Behav. Brain Funct. 3, 1–15.
Macizo, P., and Herrera, A. (2010). Two-digit number comparison: decade-unit and unit-decade produce the same compatibility effect with number words. Can. J. Exp. Psychol. 64, 17–24.
McCloskey, M. (1992). Cognitive mechanisms in numerical processing: evidence from acquired dyscalculia. Cognition 44, 107–157.
Miller, K. F., and Gelman, R. (1983). The child’s representation of number: a multidimensional scaling analysis. Child Dev. 54, 1470–1479.
Moeller, K., Fischer, M. H., Nuerk, H.-C., and Willmes, K. (2009a). Sequential or parallel decomposed processing of two-digit numbers? Evidence from eye-tracking. Q. J. Exp. Psychol. 62, 323–334.
Moeller, K., Nuerk, H.-C., and Willmes, K. (2009b). Internal number magnitude representation is not holistic, either. Eur. J. Cogn. Psychol. 21, 672–685.
Moeller, K., Huber, S., Nuerk, H.-C., and Willmes, K. (2011). Two-digit number processing – holistic, decomposed or hybrid? A computational modelling approach. Psychol. Res. 75, 290–306.
Moyer, R. S., and Landauer, T. K. (1967). The time required for judgments of numerical inequality. Nature 215, 1519–1520.
Nuerk, H.-C., Moeller, K., Klein, E., Willmes, K., and Fischer, M. H. (2011). Extending the mental number line: a review of multi-digit number processing. Z. Psychol. 219, 3–22.
Nuerk, H.-C., Weger, U., and Willmes, K. (2001). Decade breaks in the mental number line? Putting the tens and units back in different bins. Cognition 82, B25–B33.
Nuerk, H.-C., Weger, U., and Willmes, K. (2004). On the perceptual generality of the unit-decade-compatibility effect. Exp. Psychol. 51, 72–79.
Nuerk, H.-C., Weger, U., and Willmes, K. (2005). Language effects in magnitude comparison: small, but not irrelevant. Brain Lang. 92, 262–277.
Nuerk, H.-C., and Willmes, K. (2005). On the magnitude representation of two-digit numbers. Psychol. Sci. 47, 52–72.
Pesenti, M., and Andres, M. (2009). Common mistakes about numerical representations. Behav. Brain Sci. 32, 346–347.
Piazza, M., Pinel, P., Le Bihan, D., and Dehaene, S. (2007). A magnitude code common to numerosities and number symbols in human intraparietal cortex. Neuron 53, 293–305.
Pinel, P., Dehaene, S., Riviére, D., and LeBihan, D. (2001). Modulation of parietal activation by magnitude distance in a number comparison task. Neuroimage 14, 1013–1026.
Ratinckx, E., Nuerk, H.-C., van Dijk, J.-P., and Willmes, K. (2006). Effects of interhemispheric communication on two-digit number processing. Cortex 42, 1128–1137.
Reynvoet, B., and Brysbaert, M. (1999). Single-digit and two-digit Arabic numerals address the same semantic number line. Cognition 72, 191–201.
Roggeman, C., Verguts, T., and Fias, W. (2007). Priming reveals differential coding of symbolic and non-symbolic quantities. Cognition, 105, 380–394.
Santens, S., Fias, W., and Verguts, T. (2009). Abstract representations of number: what interactions with number form do not prove and priming effects do. Behav. Brain Sci. 32, 351–352.
Santens, S., Roggeman, C., Fias, W., and Verguts, T. (2010). Number processing pathways in human parietal cortex. Cereb. Cortex 20, 77–88.
Tzelgov, J., Meyer, J., and Henik, A. (1992). Automatic and intentional processing of numerical information. J. Exp. Psychol. Learn. Mem. Cogn. 18, 166–179.
Verguts, T., and Fias, W. (2004). Representation of number in animals and humans: a neural model. J. Cogn. Neurosci. 16, 1493–1504.
Verguts, T., and Fias, W. (2008) Symbolic and nonsymbolic pathways of number processing. Phil. Psychol. 21, 539–554.
Verguts, T., Fias, W., and Stevens, M. (2005). A model of exact small-number representation. Psychonomic Bull. Rev. 12, 66–80.
Keywords: number magnitude representation, symbolic/non-symbolic, abstract/notation-dependent
Citation: Moeller K, Klein E, Nuerk H and Cohen Kadosh R (2012) A unitary or multiple representations of numerical magnitude? – the case of structure in symbolic and non-symbolic quantities. Front. Psychology 3:191. doi: 10.3389/fpsyg.2012.00191
Received: 10 May 2011; Accepted: 24 May 2012;
Published online: 14 June 2012.
Edited by:
Anna M. Borghi, University of Bologna and Institute of Cognitive Sciences and Technologies, ItalyReviewed by:
Oliver Lindemann, Donders Institute for Brain, NetherlandsArnaud Badets, Centra National de la Recherche Scientifique, France
Copyright: © 2012 Moeller, Klein, Nuerk and Cohen Kadosh. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited
*Correspondence: Korbinian Moeller, Knowledge Media Research Center, Schleichstrasse 6, 72076 Tuebingen, Germany. e-mail:a29yYmluaWFuLm1vZWxsZXJAdW5pLXR1ZWJpbmdlbi5kZQ==



