- 1Department of Cell and Developmental Biology, Vanderbilt University Medical School, Nashville, TN, USA
- 2Departments of Psychology and Ophthalmalogy and Visual Sciences, Vanderbilt University, Nashville, TN, USA
We show that many ideal observer models used to decode neural activity can be generalized to a conceptually and analytically simple form. This enables us to study the statistical properties of this class of ideal observer models in a unified manner. We consider in detail the problem of estimating the performance of this class of models. We formulate the problem de novo by deriving two equivalent expressions for the performance and introducing the corresponding estimators. We obtain a lower bound on the number of observations (N) required for the estimate of the model performance to lie within a specified confidence interval at a specified confidence level. We show that these estimators are unbiased and consistent, with variance approaching zero at the rate of 1/N. We find that the maximum likelihood estimator for the model performance is not guaranteed to be the minimum variance estimator even for some simple parametric forms (e.g., exponential) of the underlying probability distributions. We discuss the application of these results for designing and interpreting neurophysiological experiments that employ specific instances of this ideal observer model.
Introduction
Ideal observer models are an important tool in the effort to understand the neural bases of perception and behavior (FitzHugh, 1957; Ratliff, 1962; De Valois et al., 1967; Ratliff et al., 1968; Talbot et al., 1968; Barlow and Levick, 1969; Barlow et al., 1971; Mountcastle et al., 1972; Johansson and Vallbo, 1979; Bradley et al., 1987; Newsome et al., 1989; Vogels and Orban, 1990; Geisler, 2001). Ideal observer analysis can be applied to the organism as a whole, as in psychophysical studies, or to a specific stage of information processing within the visual system of the organism, as is often done in neurophysiological studies (sometimes referred to as “sequential ideal observer analysis,” see Geisler, 1989). Here we focus exclusively on ideal observer models that arise in the analysis and interpretation of neurophysiological data. In this context, we define an ideal “observer” model as a set of operations and processes by which the experimenter optimally decodes stimuli, perceptual decisions, or behavioral outcomes from sensory neural activity (Green and Swets, 1966; Geisler, 1989, 2001, 2004). In the early stages of a sensory system, such an ideal “observer” model can be used to study the efficiency of a neuron. For example, Barlow et al. (1971) used an ideal detector model to compute detection probability from the number of photons absorbed by photoreceptors and related the results to retinal ganglion cell responses. In this manner, they were able to estimate the average number of impulses emitted by a retinal ganglion cell per quantum of light absorbed by photoreceptors. They concluded ganglion cells are efficient and sensitive. In the intermediate stages of sensorimotor transformation, ideal observer models are often used to optimally decode behavioral choice related information from the responses of a single sensory neuron (Celebrini and Newsome, 1994; Britten et al., 1996). Such analyses associate neural responses with perceptual decisions (rev. Parker and Newsome, 1998). Ideal observer analysis can also be applied to optically imaged cortical signals to assess neural population sensitivity for detection or discrimination (Chen et al., 2006, 2008; Purushothaman et al., 2009; see also rev: Cohen et al., 2011).
The statistical properties of an ideal observer model impact the results. For example, an ideal observer typically yields an unbiased estimate of performance and increasing the number of trials will decrease the variance of this estimate. These assumptions are generally valid when the underlying probability distributions take certain parametric forms but deviations from these assumptions can influence the results. Furthermore, it is not always straightforward to take into account confidence intervals for model performance in interpreting the results. Statistically valid methods of computing confidence intervals are known for some applications (e.g., Agarwal et al., 2005; Sarma et al., 2011) but this is not true in general. Therefore, heuristic or Monte-Carlo simulations are used to compute confidence intervals of ideal observer performance where necessary (e.g., Purushothaman et al., 2009). The main goal of this paper is to investigate the statistical properties and limitations of ideal observer models commonly used in the analyses of neurophysiological data. To achieve this goal, we first generalize four common forms of such ideal observer models.
The first of these was used in studies of the absolute visual detection threshold (Hecht et al., 1942; Hartline et al., 1947; Ratliff, 1962). Hecht et al. (1942) showed that the probability with which human observers detected flashes of light, that presumably delivered a certain average number of quanta of energy (a) to the retina, closely followed the probability of drawing a “threshold” number of n or more quanta from a Poisson distribution with mean arrival rate a. Analysis of the electrophysiological data of Hartline et al. (1947) from the Limulus eye showed that the frequency with which a neuron emitted at least a criterion number (NC) of impulses also closely followed the probability of drawing NC or more impulses from the Poisson distribution with arrival rate equal to a (Ratliff, 1962). Implicit in this analysis is the linking hypothesis that the neuron signals to the animal the presence of an external stimulus whenever the number of impulses emitted by the neuron is greater than or equal to NC (Teller, 1984). Given this hypothesis, the ideal observer model estimates the maximum detection probability for a set of neural responses. It can be said that the criterion NC is chosen in this model to fit detection probabilities but without regard to the false alarm rate. Since the “maintained” or “background” discharge rate of the neuron also fluctuates (Ratliff et al., 1968; Barlow and Levick, 1969), in some trials, the number of impulses emitted by the neuron will equal or exceed NC simply due to this random fluctuation and the ideal observer will falsely signal the presence of a stimulus. This false alarm rate is not incorporated into this model.
The second ideal observer model we consider takes the false alarm rate into account [e.g., Barlow and Levick, 1969; rev. Green and Swets, 1966]. Typically, the probability distribution of the number of impulses in the maintained discharge is used to determine NC so that the probability of false alarm is less than or equal to a predetermined value [e.g., 0.2% in Barlow and Levick (1969)]. The probability distribution for the stimulus-induced response will then determine the detection rate for this criterion. The ideal observer in this analysis performs essentially the same operation as the one above, signaling the presence of a stimulus whenever the number of impulses emitted by the neuron exceeds NC. But this criterion value is chosen based on a constraint on the false alarm rate.
The third model arises in Two-Alternative Forced-Choice (2-AFC) paradigms employed in detection and discrimination studies (Green and Swets, 1966). Typically, a reference and a test stimuli are presented either at two spatial locations (simultaneously) or in two temporal intervals (sequentially). The task of the observer is to indicate the location or the interval in which the test stimulus occurred. Because decisions are based on the comparison of two stimuli or neural responses to two stimuli, there is no need in this case to set a fixed criterion level. For example, the ideal observer can consistently associate the larger response with the test stimulus (e.g., Barlow et al., 1971). Computationally, the experimenter builds two histograms of neural responses, one each for the reference and test stimuli. The correct detection or discrimination probability for the ideal observer in the 2-AFC task is then the average rate at which the observer can correctly identify which sample belongs to which distribution when presented with two random samples, one drawn from the reference distribution and the other from the test distribution (Green and Swets, 1966). This probability can be estimated as the area under the receiver operating characteristic (ROC) curve for the pair of histograms (Green and Swets, 1966).
The fourth model we consider is computationally similar to the third model but has an important conceptual difference in that it is used to predict the choices made by a subject in a 2-AFC task based on the neural responses for near-threshold stimuli (Johansson and Vallbo, 1979; Celebrini and Newsome, 1994; Britten et al., 1996). This analysis can be used to link subjective perceptual decisions to single neuron responses (rev. Parker and Newsome, 1998; Romo, 2001; see also Vallbo and Johansson, 1980). As a consequence, this ideal observer model has found wide application recently (Dodd et al., 2001; Cook and Maunsell, 2002; Romo et al., 2002; Williams et al., 2003; Stoet and Snyder, 2004; Uka and DeAngelis, 2004; Williams et al., 2004; Purushothaman and Bradley, 2005; Pessoa and Padmala, 2005; Gu et al., 2007, 2008; Cohen and Newsome, 2009; Bosking and Maunsell, 2011).
The main difference between the first two ideal observer models and the last two is that the latter models are presented with two observations instead of one, making it possible to render decisions based on a direct comparison of the given observations, independent of a free parameter in the form of a constant criterion number. While this makes the two types of ideal observers different from functional point of view, it is possible to have a single mathematical framework within which the performance of both types of models can be quantitatively described. Consider an ideal observer with two inputs r0 and r1 and two outputs C0 and C1. Let P(r0) and P(r1) be the probability distributions of the two input variables. In the following, we show that with appropriate choices for C0, C1 and P(r0), P(r1), this ideal observer can be used for absolute sensory detection tasks (first two categories described above) as well as for 2-AFC tasks (last two categories). In this framework, the performance (i.e., true positive, false positive, true negative, and false negative rates) of all four types of ideal observers can be described using the same closed-form expression. We then address the following questions: 1) How does the performance of the generalized ideal observer compare to the area under the ROC curve? 2) Is it possible to determine a priori the number of input samples required so that the estimated value of the observer's performance will lie within a specified confidence interval at a specified confidence level? 3) Are these estimates unbiased and consistent, i.e., does estimation error decrease with increasing number of observations and at what rate? 4) Do efficient (minimum variance) estimators exist for the performance of these ideal observers? 5) Is the standard method of estimating performance (area under the ROC curve) efficient? Answers to these questions will facilitate a more efficient design of neurophysiological experiments for ideal observer analysis.
Results
Generalized Ideal Observer Equations
In the notation introduced above, consider an ideal observer model with inputs r0 and r1. Let S0 and S1 be the two experimental conditions associated with r0 and r1, respectively. The probability distributions P0(r0) and P1(r1) are given by the conditional distributions P0(r0) = P0(r0|S0) and P1(r1) = P1(r1|S1). The ideal observer, who has no a priori knowledge of which input sample comes from which condition, makes a prediction to that effect using a “decision rule”. If the observer predicts that r0 comes from the condition S0 (or, equivalently, from the distribution P0(r0|S0)) and that r1 comes from S1 (i.e., from P1(r1|S1)), then the observer will be correct. The opposite association will be incorrect. The variables r0 and r1 may represent the frequency of impulses emitted by the neuron. Without loss of generality, assume that the values of r0 and r1 lie within the upper right quadrant of the real plane, i.e., the sample space consists of all points = (r0, r1) ∈ ℜ+ × ℜ+. The decision region 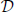 ⊂ ℜ+ × ℜ+ consists of all values of r0 and r1 for which the ideal observer makes a correct prediction. Then the probability of correct prediction for this ideal observer is given by
⊂ ℜ+ × ℜ+ consists of all values of r0 and r1 for which the ideal observer makes a correct prediction. Then the probability of correct prediction for this ideal observer is given by
where p(r0, r1) is the joint probability density function corresponding to the joint probability distribution P(r0, r1). In many experiments, the responses to the two conditions are independent random variables. Hence P(r0, r1) = P0(r0|S0)P1(r1|S1). Furthermore, the optimal decision variable (e.g., the likelihood ratio) or its sufficient statistic, involve monotone functions of the two variables r0 and r1 thereby resulting in a partition of the sample space ℜ+ × ℜ+ into a decision region of the form 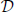 = {(r0, r1) ∈ ℜ+ × ℜ+|r1 ≥ r0}. Substituting this integration region into Equation (1) and choosing the summation of the elemental areas along the two possible directions yields two equivalent expressions for the performance of the ideal observer as
= {(r0, r1) ∈ ℜ+ × ℜ+|r1 ≥ r0}. Substituting this integration region into Equation (1) and choosing the summation of the elemental areas along the two possible directions yields two equivalent expressions for the performance of the ideal observer as
and
where Ef(x)[G(x)] = ∫G(x)f(x)dx denotes the expectation of the function G with respect to the probability density function f, and pi(ri), i = 0,1 are the marginal probability density functions. It is important to note that P(p0(r0), p1(r1)) = 1 − P(p1(r1), p0(r0)) and therefore the order of the two distribution in the argument of P(.,.) cannot be exchanged.
This general ideal observer gives rise to the four specific ideal observers described above. In simple detection tasks, the two stimulus conditions are typically S1 = “Stimulus present” and S0 = “Stimulus absent.” Choose p0(r0) = δ(r0 − NC) where δ(x) is the Dirac delta function such that ∫∞− ∞δ(x) = 1 and δ(x) = 0 ∀x ≠ 0. Then Equation (2) simplifies to
which is the probability P1(r1 > NC), the hit rate in the detection task. Thus, for the choice of p0(r0) = δ(r0 − NC), the general ideal observer model simplifies to the first category of ideal observers that signal the presence of a stimulus whenever the response of the neuron under consideration equals or exceeds the fixed criterion number NC. The second category of ideal observers used in detection tasks differs from the first only in the choice of the criterion number NC. Therefore these models can be derived using p0(r0) = δ(r0 − NC) where NC is now determined using the inequality ∫∞NC p0(r0)dr0 ≤ α. It is also clear that the general observer fully describes the third category of ideal observers used to quantify neural detection and discrimination performance in 2-AFC tasks. Finally, for the fourth category of ideal observers, the two “stimulus” conditions need to be replaced with the two “choices” available to the subject. Thus, this general ideal observer provides a complete description of the four types of ideal observers considered above. We should note that this generalization does not imply that all four categories of ideal observers are functionally or physiologically equivalent. This generalization is just mathematical and provides a unified framework for the following analyses.
Estimators for the Performance of the Ideal Observer
Suppose R1 = [r11r12 … r1i … r1N] and R0 = [r01r02 … r0k … r0N] are two sets of N samples each obtained in the experiment from the conditions S1 and S0, respectively. In the above notation, the elements of R1 are independent and identically distributed as P1 and those of R0 are similarly drawn from P0. I[0, x](y) is the indicator function of y on the closed interval [0, x] such that I[0, x](y) = 1 iff y ∈ [0, x] and 0 otherwise. Then, based on Equation (2), an estimator of the performance of the generalized ideal observer as a function of the samples R0 for given a value of r1i can be proposed as
This provides an estimate for the inner integral in Equation (2), given a value of r1. Using all 2N samples of both R1 and R0, P can be estimated as
The estimator based on Equation (3) can be similarly obtained as
Equation (4) provides one simple way to estimate the performance of the generalized ideal observer. We pick one sample from R1, say r1i, and count the number of samples of R0 that are less than or equal to r1i. We repeat this for all samples in R1 and divide the result by N2. Equation (5) provides a similar method. Computationally, this sequence of operations can be rearranged to resemble the operations involved in computing the area under the ROC curve for the normalized frequency histograms constructed from R0 and R1. Thus, there are at least 3 different methods to estimate the performance of this ideal observer. We show below that all three methods compute the area under the ROC curve, empirically constructed from R0 and R1.
Relationship to the Area Under the ROC Curve
For a fixed criterion T, the hit rate (β) and false alarm rate (α) are
and
Using Equation (6), we can rewrite the expression for the performance of the ideal observer in Equation (3) as
Using Equation (7) in the above, we have the performance of the ideal observer as
Since the ROC curve is the plot of β against α as the criterion varies from 0 to ∞, the quantity ∫ βdα is the area under the ROC curve (Figure 1A). Therefore, estimates of the quantities in Equations (2) and (3) are also estimators of the area under the ROC curve.
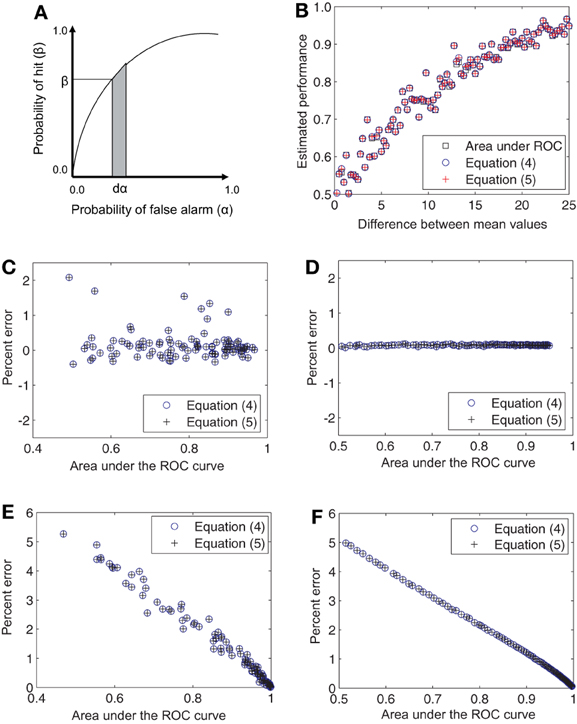
Figure 1. Relationship of the derived estimators to the area under the ROC curve. (A) Area under the ROC curve ∫βdα has the equivalent definitions given Equations (2) and (3) and admits the estimators given in Equations (4) and (5). (B) Single estimates of the area under the ROC curve and Equations (4) and (5) are shown comparatively for a progressively increasing difference in the mean firing rates for Gaussian distributions. The points are predominantly coincident. (C) The percent error for single estimates lies within 2%. (D) When 100 such trial estimates are averaged together, the percent error falls close to 0%. These differences in the estimates are not systematic and are entirely due to numerical errors. (E,F) Same as (C,D) but for Poisson distributions. In this case the errors decrease monotonically from about 5 to close to 0%.
Figures 1, 2 numerically illustrate the fact that estimators (4) and (5) are equivalent to the conventional estimate of performance as the area under the ROC curve. For Figure 1, we assumed Gaussian distributions for P0 and P1 with the mean of P1 greater than that for P0. A random set of 100 samples were drawn from each distribution and the area under the ROC curve was estimated. Performance was also estimated using Equations (4) and (5). The difference between the mean values of Gaussian distributions was then increased in the range [0.5, 25] in steps of 0.5. The variances were set to 1.28 × mean1.2 to mimic the firing rate statistics of MT neurons (Britten et al., 1992; Purushothaman and Bradley, 2005). The estimates were computed for this entire range of mean values (Figure 1B). The deviation of the estimators (4) and (5) from the area under the ROC curve (computed in the traditional manner), was evaluated as Percent error = 100 × (Area under ROC − estimate)/estimate. The three estimates differed by less than 1.5% from each other (Figure 1C). When the estimates were averaged over 100 repetitions, the errors became negligible (Figure 1D). Simulations with Poisson distributions showed errors in the range of 0 − 5% (Figures 1E,F). For Figure 2, we again assumed Gaussian distributions for P0 and P1 with the mean of P1 greater than that for P0. However, in these simulations, the difference between the mean values were held constant while the ratio of the variance of P1 to that of P0 was increased in the range [1, 25]. The percent error was computed as above. These simulations also showed that the estimates averaged over 100 repetitions had negligible error (Figure 2C).
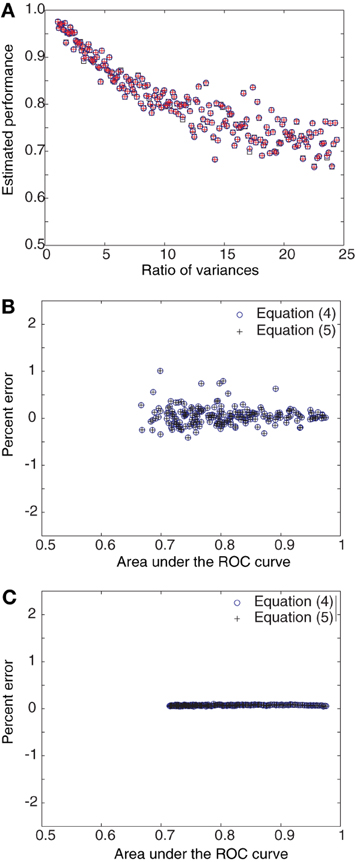
Figure 2. Derived estimators and area under ROC curve as a function of variances. (A) Single estimates of the area under the ROC curve and Equations (4) and (5) are compared for progressively increasing ratio of variances for Gaussian distributions. The points are predominantly coincident. (B) The percent error for single estimates lies within 2%. (C) When 100 such trial estimates are averaged together, the percent error falls close to 0%.
Unbiased Estimation of the Ideal Observer Performance
It is easy to verify that the estimators given in Equations (4) and (5) are unbiased, i.e., their expected values are equal to the true value to be estimated (Van Trees, 1966, pp. 65–73). We note that (R0, R1) is a joint transformation of the independent random variables r0k and r1i, i, k = 1, 2, …, N and that rik, k = 1, 2, …, N are identically distributed for each i. Therefore the expected value of the estimator in Equation (4) can be computed as
Substituting Equation (4) into the above equation, we get
Therefore, in Equation (4) is an unbiased estimator of P. Similarly, it can be shown that the estimator of Equation (5) is also unbiased.
Variance of the Estimator
The variances of the estimators in Equations (4) and (5) can be computed by first subtracting P from both sides of Equation (4) and squaring them :
Expanding the summand of S1 as (I[0, r1i](r0k) − P)2 = I[0, r1i](r0k) + P2 − 2 P I[0, r1i](r0k) and noting that E[I[0, r1i](r0k)] = P, we obtain for the expectation of the first term, E[S1] = N2P(1 − P). Next, we rewrite the second sum as
Consider the first sum on the right side of Equation (11) above. We compute the expectation of the product I[0, r1i](r0k)I[0, r1j](r0k) for j ≠ i as
Since min(r1i, r1j) ≤ r1i, we get the following bound:
Therefore, we have for the expectation of the first term on the right side of Equation (11) the bound E[S21] ≤ N2(N − 1)[P(1 − P)]. Now consider the second sum. The expectation of the product I[0, r1i](r0k) I[0, r1i](r0m) for m ≠ k is given by
where we used the bound ∫r1i0(r0m) p0(r0m)dr0m ≤ 1 in Equation (14). Therefore, we have for the expectation of S22 the bound E[S22] ≤ N2(N − 1)[P(1 − P)]. Finally, we note that in the last term S23, the summand (I[0, r1i](r0k) − P)(I[0, r1l](r0m) − P) is the product of two independent and zero-mean random variables for (i, k) ≠ (l, m). Hence the variance of the estimator in Equation (4) has the bound
Similar calculations yield the same bound for the variance of the estimator in Equation (5).
Consistency of the Estimator
Next, we verify if the estimators are consistent, i.e., if the estimates progressively converge to the true value as the number of observations is increased (Van Trees, 1966, pp. 65–73). To do so, we first apply the Tchebycheff-Bienayme inequality to . For any ε > 0, we have
Thus converges to P in probability as N → ∞ and is a consistent estimator of P.
Deviation of an Estimate from the True Value
The above analyses showed that the proposed estimators give an unbiased estimate of the performance of the ideal observer and that as the number of observations increases, the error of estimation (i.e., the variance of the estimator) decreases at the rate of 1/N. In addition to establishing these properties, the above analyses also give us tools for designing the ideal observer model. Suppose the experiment has been performed and an estimate of the performance of the ideal observer has been obtained for a neuron. It is desirable to determine the likelihood that the true value of the performance lies within a known range of the estimate obtained, i.e., we would like to state a confidence interval for the estimate at a given significance level. Currently, this confidence interval, when reported, is obtained using bootstrapping or other empirical methods. The above analyses provides a tool for quantifying the deviation of a performance estimate from its true value in a simpler and more rigorous manner. Equation (16) can be used for this purpose. Suppose we require the percent error in the estimate, 100 × |P − |/, to be less than 5%. This gives ε = 0.05 × , from which the probability that the true value lies outside this error range can be computed as
Thus, the quantity gives the significance level for the desired confidence interval. We note that since |P − | ≥ ε, α does not necessarily depend upon the unknown P. For large N, 2N >> 1. Hence α ≈ 2P(1 − P)/N(0.05 × )2.
We investigated the tightness of this bound using a series of simulations (Figure 3). We simulated N trials by drawing N samples of R0 and R1, each, from Gaussian distributions whose mean values differed by progressively increasing amounts so that the true value of the ideal observer performance varied from 0.5 to 1.0. For each set (R0, R1), we obtained one estimate of P. We performed this simulation 1000 times and computed the maximum deviation of the estimate from the true value, the average deviation and the minimum deviation for the 1000 estimates. We repeated all of these simulations for Gamma distributions. The results are shown superimposed on the corresponding values of ε for α values of 0.01 and 0.05 (Figure 3). The same pattern of results were obtained for Poisson and scaled Poisson distributions. These simulations show that for small values of N (≤ 100) and α(= 0.01), the actual difference between the true and estimated values is much smaller than the theoretical bound ϵ. At α = 0.05 and for higher values of N, the theoretical deviation approaches the maximum empirical deviation obtained in the simulations. The implications of the varying tightness of the theoretical bound for experimental design are discussed below.
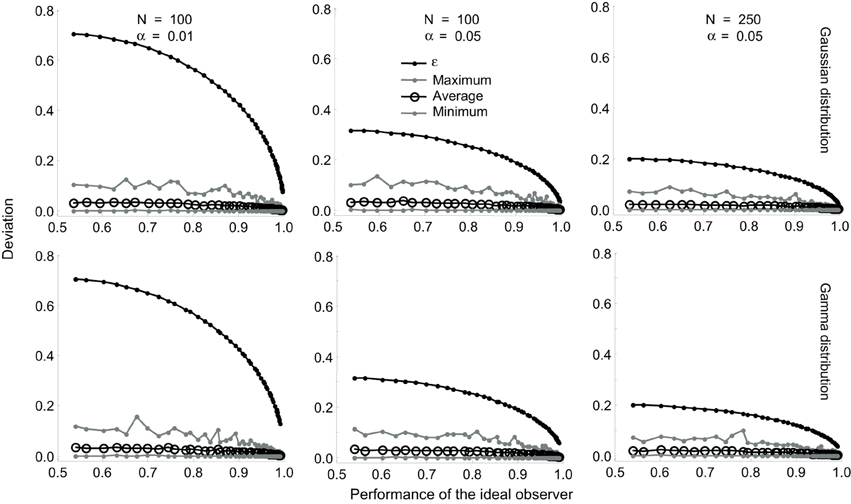
Figure 3. Tightness of the bound in Equation (17). Results are shown for Gaussian (top row) and Gamma (bottom row) distributions. The difference between the mean values were progressively increased so that the true value of the ideal observer performance varied from 0.5 to 1.0. This performance is plotted on the X-axis. The performance was estimated 1000 times and the maximum deviation of the estimate from the true value, the average deviation, and the minimum deviation were computed. The corresponding values of e are also plotted on all the graphs. The effect of varying (α = 0.01 and 0.05) for a fixed (N = 100) is shown in the left and middle columns. The effect of varying (N = 100 and 250) for a fixed (α = 0.05) is shown in the middle and right columns.
Designing Experiments for Reliable Estimation of Ideal Observer Performance
Some previous studies have empirically investigated the number of trials required to obtain a reliable estimate of the ideal observer's performance. For example, Britten et al. (1996) computed “choice probability” separately for odd and even numbered trials. This allowed them to compute a measure of the random dispersion of the probability values. One goal of that investigation was to test whether or not the population average choice probability was significantly different from chance. For the population average choice probability of 0.55, at least 100 trials were required for the odd and even estimates to differ by less than 0.05 (i.e., 0.55–0.5). A different empirical approach was required to estimate the number of trials required to significantly reduce estimation errors in the ROC analysis of optically imaged intrinsic signals (Purushothaman et al., 2009).
From the results obtained in the previous section, we can arrive at a general formula for systematically determining the number trials required for the estimate of the performance of the generalized ideal observer to reach a desired confidence interval. From Equation (16) above, we have, ∀ε > 0,
First, as an example, we consider the Britten et al. (1996) study. Assume that the true value of choice probability in that study was 0.55. Suppose we require that the estimate should lie within ± 0.05 of the true value at an alpha (or significance) level of 0.05, i.e., we require P{| − P| ≥ 0.05} ≤ 0.05 so that, in concordance with the empirical test performed by Britten et al. (1996), the dispersion in the choice probability estimate reliably excludes the chance value of 0.5. Then the number of trials N should be at least . The empirical test by Britten et al. (1996) yielded N ≈ 100, quite close to this value. However, the above formula also allows us to determine N at other significance levels. At a significance level of 0.01, we get N ≥ 198.
While many studies that followed Britten et al. (1996) have used this “100 trials” rule to determine N, our analysis shows that fewer trials suffice when higher values are expected for the performance of the ideal observer. For example, multistable percepts are linked to fluctuations in neural activity quite strongly (Dodd et al., 2002) and neurons in higher brain areas also show a strong link between their activity and perceptual decisions (Shadlen and Newsome, 2001). Using Table 1 and Equation (18), it is possible to estimate the required value of N during experimental design. It is also possible to estimate confidence intervals (i.e., ε) for a given value of N during data analysis without resorting to numerical simulations. Table 1 provides a look-up of ε and N for various values of P. As mentioned above, our simulations showed that at a given value of N and α, the actual deviation between the true and estimated values was much smaller than the theoretical bound set at ϵ (Figure 1). Therefore, the values of N shown in Table 1 are likely to be overestimates, i.e., fewer trials might suffice to reach the desired confidence interval in some cases.
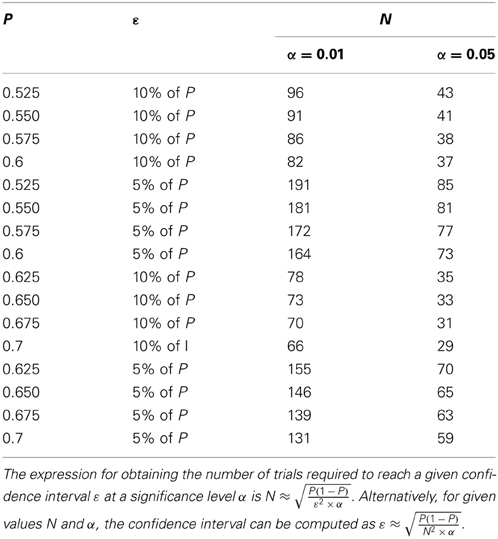
Table 1. The confidence interval (ε) and the number of trials (N) are shown for various true values of P.
Efficient Estimators of Ideal Observer Performance May not Exist
Since the performance of the ideal observer can be estimated in more than one way, it is natural to ask if some of these methods are “better” than others. In addition to requiring that estimators be unbiased and consistent, it is also required that estimators should be “efficient” when possible (Van Trees, 1966, pp. 66–73). An efficient estimator has the minimum possible variance among all unbiased estimators for a quantity and therefore will yield the lowest possible error for a given number of observations, on average. Under some conditions, maximum likelihood (ML) estimators are minimum variance estimators. Therefore, it is natural to seek for ML estimators for the performance of the ideal observer model. In this section, we first show that (R0, R1) is “efficient” in a limited sense. We then present a counter-example to show that the maximum-likelihood (ML) estimator for the performance of an ideal observer is not guaranteed to be minimum variance.
We will first describe a limited sense in which is efficient. Let M(R0, R1) = ∑Ni = 1 ∑Nk = 1 I[0, r1i](r0k) so that (R0, R1) = M(R0, R1)/N2. Then, for a given value of P, the probability distribution function for M is simply the binomial distribution
Therefore it can be verified that the calculation
gives the ML estimator as
We note also that
i.e., ml(m) satisfies the sufficient condition to be an efficient estimator (Van Trees, 1966, pp. 66–73). In addition, EM(ml(m)) = P. Therefore, ml(m) = m/N2 is an unbiased and efficient estimator of P. However, it is important to note that ml(m) is an estimator of P as a function of the transformed random variable M(R0, R1) and not as a function of R0 and R1. The following counter-example shows that it is not possible to guarantee that ML estimators of P are minimum variance.
Let the two conditional distributions be exponential, with p0(r0) = α0 exp(−α0 r0) and p1(r1) = α1 exp(−α1 r1). We can calculate P for this case using Equation (2) as P(P0, P1) = α0/(α1 + α0). Let us note that
- if α1 = α0, then P = 0.5,
- P → 1 as α0 → ∞ for a given α1 < ∞ (i.e., as the mass in the tail of the distribution P0 accumulates while that of P1 remains constant), and
- P → 0 as α0 → 0 for a given α1 < ∞.
Thus the conditional density of the observed variables for a given value of P can be written as
which gives
Equating the right hand side to 0, we obtain the ML estimator for P in this case as
We now note that equation (21) cannot be put in the form
where T(P) is a function of P alone. Therefore, the sufficient condition for ml(r0, r1) to be efficient is not satisfied (e.g., Van Trees, 1966, pp. 66–73). Further, it is also clear that (r0, r1) is a biased estimator. Hence the ML estimator of P for this case cannot be guaranteed to be minimum variance.
Discussion
We proposed a general form of an ideal observer for decoding stimulus information and perceptual decisions from neural responses. We showed that several ideal observer models used in previous studies are special cases of this general form. We investigated the statistical properties of this general ideal observer model. These analyses provide various tools for designing experiments with the goal of using an ideal observer analysis on neural data. We have provided a lower bound on the number of observations required for the estimate to lie within a pre-specified range of its true value (“confidence interval”), within a specified confidence level.
We also showed that there is not a uniformly “best” (i.e., minimum variance) estimator for the performance of the ideal observer since the existence of such an estimator depends on the parametric forms of the underlying probability distributions. It is sometimes argued that computing the area under the ROC curve offers a non-parametric way of estimating ideal observer performance. While it is true that this estimation procedure does not depend on the parametric forms of the underlying probability distributions, it is important to note that the resulting estimate will be invariably influenced by the underlying parametric forms. Therefore, for some parametric forms and under some conditions, neither the estimators provided in Equations (4) and (5) nor the area under the ROC curve will be efficient. However, regardless of which estimator is chosen, the relationship between the number of trials, the confidence interval and the confidence level derived in this paper can be used to design the experiment and validate the results.
It is worth noting that the number of trials required for the estimate to lie within a confidence interval at a given confidence level is not the optimum number of trials required for reaching the decision. Therefore in certain applications other methods, such as sequential probablity ratio tests, may be more appropriate (Wald, 1945).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was supported by National Institutes of Health Grants R01-EY001778, R21-EY019232, P30-EY008126, P30-HD15052.
References
Agarwal, S., Graepel, T., Herbrich, R., Har-Peled, S., and Roth, D. (2005). Generalization error bounds for the area under the roc curve. J. Mach. Learn. Res. 6, 393–425.
Barlow, H. B., and Levick, W. R. (1969). Three factors limiting the reliable detection of light by retinal ganglion cells of the cat. J. Physiol. 200:124.
Barlow, H. B., Levick, W. R., and Yoon, M. (1971). Responses to single quanta of light in retinal ganglion cells of the cat. Vision Res. 3, 87–101. doi: 10.1016/0042-6989(71)90033-2
Bosking, W. H., and Maunsell, J. H. R. (2011). Effects of stimulus direction on the correlation between behavior and single units in MT during a motion detection task. J. Neurosci. 31, 8230–8238. doi: 10.1523/JNEUROSCI.0126-11.2011
Bradley, A., Skottun, B. C., Ohzawa, I., Sclar, G., and Freeman, R. D. (1987). Visual orientation and spatial frequency discrimination: a comparison of single cells and behavior. J. Neurophysiol. 57:75572.
Britten, K. H., Newsome, W. T., Shadlen, M. N., Celebrini, S., and Movshon, J. A. (1996). A relationship between behavioral choice and the visual responses of neurons in macaque. Vis. Neurosci. 13, 87–100. doi: 10.1017/S095252380000715X
Britten, K. H., Shadlen, M. N., Newsome, W. T., and Movshon, J. A. (1992). The analysis of visual motion: a comparison of neuronal and psychophysical performance. J. Neurosci. 12, 4745–4765.
Celebrini, S., and Newsome, W. T. (1994). Neuronal and psychophysical sensitivity to motion signals in extrastriate area MST of the macaque monkey. J. Neurosci. 14, 4109–4124.
Chen, Y., Geisler, W. S., and Seidemann, E. (2006). Optimal decoding of correlated neural population responses in the primate visual cortex. Nat. Neurosci. 9, 1412–1420. doi: 10.1038/nn1792
Chen, Y., Geisler, W. S., and Seidemann, E. (2008). Optimal temporal decoding of V1 population responses reaction-time detection task. J. Neurophysiol. 99, 1366–1379. doi: 10.1152/jn.00698.2007
Cohen, J. R., Asarnow, R. F., Sabb, F. W., Bilder, R. M., Bookheimer, S. Y., Knowlton, B. J., et al. (2011). Decoding continuous variables from neuroimaging data: basic and clinical applications. Front. Neurosci. 5:75.
Cohen, M. R., and Newsome, W. T. (2009). Estimates of the contribution of single neurons to perception depend on timescale and noise correlation. J. Neurosci. 29, 6635–6648. doi: 10.1523/JNEUROSCI.5179-08.2009
Cook, E. P., and Maunsell, J. H. R. (2002). Dynamics of neuronal responses in macaque MT and VIP during motion detection. Nat. Neurosci. 5, 985–994. doi: 10.1038/nn924
De Valois, R. L., Abramov, I., and Mead, W. R. (1967). Single cell analysis of wavelength discrimination at the lateral geniculate nucleus in the macaque J. Neurophysiol. 30, 415–433.
Dodd, J. V., Krug, K., Cumming, B. G., and Parker, A. J. (2001). Perceptually bistable three-dimensional figures evoke high choice probabilities in cortical area MT J. Neurosci. 21, 4809–4821.
FitzHugh, R. (1957). The statistical detection of threshold signals in the retina. J. Gen. Physiol. 40, 925–948. doi: 10.1085/jgp.40.6.925
Geisler, W. S. (1989). Ideal-observer theory in psychophysics and physiology. Phys. Scripta 39, 153–160. doi: 10.1088/0031-8949/39/1/025
Geisler, W. S. (2001). Contributions of ideal observer theory to vision research. Vis. Res. 51, 771–781. doi: 10.1016/j.visres.2010.09.027
Geisler, W. S. (2004). “Ideal Observer analysis,” in Visual Neurosciences, eds L. Chalupa and J. Werner (Boston, MA: MIT press), 825–837.
Green, D. M., and Swets, J. A. (1966). Signal Detection Theory and Psychophysics. New York, NY:Wiley.
Gu, Y., Angelak, D. E., and DeAngelis, G. C. (2008). Neural correlates of multisensory cue integration in macaque MSTd. Nat. Neurosci. 11, 1201–1210. doi: 10.1038/nn.2191
Gu, Y., DeAngelis, G. C., and Angelaki, D. E. (2007). A functional link between area MSTd and heading perception based on vestibular signals. Nat. Neurosci. 10, 1038–1047. doi: 10.1038/nn1935
Hartline, H. K., Milne, L. J., and Wagman, I. H. (1947). Fluctuation of response of single visual sense cells. Fed. Proc. 6:124.
Hecht, S., Shlaer, S., and Pirenne, M. H. (1942). Energy, quanta and vision. J. Gen. Physiol. 25:81940.
Johansson, R. S., and Vallbo, Å. B. (1979). Tactile sensibility in the human hand: relative and absolute densities of four types of mechanoreceptive units in glabrous skin. J. Phys. Lond. 297, 405–422.
Mountcastle, V. B., LaMotte, R. H., and Carli, G. (1972). Detection thresholds for stimuli in humans and monkeys: comparison with threshold events in mechanoreceptive afferent nerve fibers innervating the monkey hand. J. Neurophysiol. 35:12236.
Newsome, W. T., Britten, K. H., and Movshon, J. A. (1989). Neuronal correlates of a perceptual decision. Nature 341:5254.
Parker, A. J., and Newsome, W. T. (1998). Sense and the single neuron: probing the physiology of perception. Annu. Rev. Neurosci. 21, 227–277. doi: 10.1146/annurev.neuro.21.1.227
Pessoa, L., and Padmala, S. (2005). Quantitative prediction of perceptual decisions during near-threshold fear detection. Proc. Natl. Acad. Sci. U.S.A. 102, 5612–5617. doi: 10.1073/pnas.0500566102
Purushothaman, G., and Bradley, D. C. (2005). Neural population code for fine perceptual decisions in area MT. Nat. Neurosci. 8, 99–106. doi: 10.1038/nn1373
Purushothaman, G., Khaytin, I., and Casagrande, V. A. (2009). Quantification of optical images of cortical responses for inferring functional maps. J. Neurophysiol. 101, 2708–2724. doi: 10.1152/jn.90696.2008
Ratliff, F. (1962). “Some interrelations among physics, physiology, and psychology in the study of vision,” in Psychology: A Study of a Science, Biologically Oriented Fields, their Place in Psychology and the Biological Sciences, Vol. 4, ed S. Koch (New York, NY: McGraw-Hill), 417–482.
Ratliff, F., Hartline, H. K., and Lange, D. (1968). Variability of interspike intervals in optic nerve fibers of limulus: effect of light and dark adaptation Proc. Natl. Acad. Sci. U.S.A. 60, 464–469. doi: 10.1073/pnas.60.2.464
Romo, R. (2001). Touch and go: decision-making mechanisms in somatosensation Annu. Rev. Neurosci. 24, 107–137. doi: 10.1146/annurev.neuro.24.1.107
Romo, R., Hernandez, A., Zainos, A., Lemus, L., and Brody, C. D. (2002). Neuronal correlates of decision-making in secondary somatosensory cortex. Nat. Neurosci. 5, 1217–1225. doi: 10.1038/nn950
Sarma, S. V., Nguyen, D. P., Czanner, G., Wirth, S., Wilson, M. A., Suzuki, W., et al. (2011). Computing confidence intervals for point process models Neural Comput. 23, 2731–2745.
Shadlen, M. N., and Newsome, W. T. (2001). Neural basis of a perceptual decision in the parietal cortex (Area LIP) of the rhesus monkey. J. Neurophysiol. 86, 1916–1936.
Stoet, G., and Snyder, L. H. (2004). Single neurons in posterior parietal cortex of monkeys encode cognitive set. Neuron 42, 1003–1012. doi: 10.1016/j.neuron.2004.06.003
Teller, D. Y. (1984). Linking propositions. Vision Res. 24, 1233–1246. doi: 10.1016/0042-6989(84)90178-0
Uka, T., and DeAngelis, G. C. (2004). Contribution of area MT to stereoscopic depth perception: choice-related response modulations reflect task strategy. Neuron 42, 297–310.
Talbot, W. H., Darian-Smith, I., Kornhuber, H. H., and Mountcastle, V. B. (1968). The sense of fluttervibration: comparison of the human capacity with response patterns of mechanoreceptive afferents from the monkey hand. J. Neurophysiol. 31:30134.
Vallbo, Å. B., and Johansson, R. S. (1980). “Coincidence and cause: a discussion on correlations between activity in primary afferents and perceptive experiences in cutaneous sensibility,” in Sensory Functions of the Skin of Humans, ed D. R. Kenshalo (New York, NY: Plenum Press), 299–310.
Vogels, R., and Orban, G. A. (1990). How well do response changes of striate neurons signal differences in orientation: a study in the discriminating monkey. J. Neurosci. 10, 3543–3558.
Wald, A. (1945). Sequential tests of statistical hypotheses. Ann. Math. Stat. 16, 117–186. doi: 10.1214/aoms/1177731118
Williams, Z. M., Bush, G., Rauch, S. L., Cosgrove, G. R., and Eskandar, E. N. (2004). Human anterior cingulate neurons and the integration of monetary reward with motor responses. Nat. Neurosci. 7, 1370–1375. doi: 10.1038/nn1354
Keywords: ideal observer model, signal detection theory, neural decoding, receiver operating characteristic, maximum likelihood estimation
Citation: Purushothaman G and Casagrande VA (2013) A Generalized ideal observer model for decoding sensory neural responses. Front. Psychol. 4:617. doi: 10.3389/fpsyg.2013.00617
Received: 07 August 2012; Accepted: 04 February 2013;
Published online: 20 September 2013.
Edited by:
Prathiba Natesan, University North Texas, USAReviewed by:
Martin Lages, University of Glasgow, UKErik P. Cook, McGill University, Canada
Prathiba Natesan, University North Texas, USA
Copyright © 2013 Purushothaman and Casagrande. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Gopathy Purushothaman, Department of Cell and Developmental Biology, Vanderbilt University Medical School, T2304, Medical Center North, 1161 21st Avenue South, Nashville, TN 37232, USA e-mail:Z29wYXRoeS5wdXJ1c2hvdGhhbWFuQHZhbmRlcmJpbHQuZWR1

