- Department of Education, Center for Educational Science and Psychology, Eberhard Karls Universität Tübingen, Tübingen, Germany
In the past 2 decades latent variable modeling has become a standard tool in the social sciences. In the same time period, traditional linear structural equation models have been extended to include non-linear interaction and quadratic effects (e.g., Klein and Moosbrugger, 2000), and multilevel modeling (Rabe-Hesketh et al., 2004). We present a general non-linear multilevel structural equation mixture model (GNM-SEMM) that combines recent semiparametric non-linear structural equation models (Kelava and Nagengast, 2012; Kelava et al., 2014) with multilevel structural equation mixture models (Muthén and Asparouhov, 2009) for clustered and non-normally distributed data. The proposed approach allows for semiparametric relationships at the within and at the between levels. We present examples from the educational science to illustrate different submodels from the general framework.
In the past 2 decades latent variable modeling has become a standard tool in the social sciences. Linear structural equation models have been extended to include non-linear interaction and quadratic effects (for a review see Schumacker and Marcoulides, 1998; Algina and Moulder, 2001; Marsh et al., 2004, 2006), and for the capability to model multilevel data structures (e.g., Rabe-Hesketh et al., 2004; Muthén and Asparouhov, 2009). However, a systematic combination of both non-linear structural equation modeling and multilevel modeling has not been implemented in a more general framework. In this article, we present a GNM-SEMM that combines recent semiparametric non-linear structural equation models (Kelava and Nagengast, 2012; Kelava et al., 2014) with multilevel structural equation mixture models (Muthén and Asparouhov, 2009) for clustered and non-Gaussian data. The proposed framework is capable of modeling non-linear parametric and semiparametric relationships at the within and at the between levels, and it allows non-normally distributed data to be considered. We will provide an empirical example from educational sciences to illustrate the applicability of the proposed framework. We will begin by providing an overview of current approaches for estimating non-linear structural equation models and current frameworks for multilevel structural equation (mixture) models.
1. Non-Linear Structural Equation Models
Numerous parametric approaches for the estimation of non-linear effects have been developed (for a review, see Schumacker and Marcoulides, 1998; Algina and Moulder, 2001; Marsh et al., 2004, 2006), including product indicator approaches (e.g., Kenny and Judd, 1984; Bollen, 1995; Jaccard and Wan, 1995; Ping, 1995; Jöreskog and Yang, 1996; Algina and Moulder, 2001; Marsh et al., 2004, 2006; Little et al., 2006; Kelava and Brandt, 2009), distribution analytic approaches (Klein and Moosbrugger, 2000; Klein and Muthén, 2007), Bayesian approaches (e.g., Arminger and Muthén, 1998; Lee et al., 2007), and method of moments based approaches (Wall and Amemiya, 2003; Mooijaart and Bentler, 2010). Whereas most product indicator approaches have been ad-hoc methods for the specification of non-linear interaction effects and have thus suffered from requiring complicated measurement models, recent distribution analytic and Bayesian approaches have tried to overcome the need for non-linear measurement models. Method-of-moments-based approaches (Wall and Amemiya, 2003; Mooijaart and Bentler, 2010) and some indicator approaches (Bollen, 1995; Jöreskog and Yang, 1996) have been proposed as methods that do not rely as heavily on the normality assumption of the latent variables as other approaches (e.g., the distribution analytic approaches). The relaxation of distributional assumptions may lead to a reduction in the threat of biased estimates for non-linear effects in situations in which data are non-normally distributed, but for most of these approaches, relaxing these assumptions is associated with a low power for detecting the effects (Schermelleh-Engel et al., 1998; Brandt et al., 2014).
A different approach for modeling non-linear relations between latent variables is the use of semiparametric structural equation mixture models (SEMM; Arminger and Stein, 1997; Jedidi et al., 1997a,b; Dolan and van der Maas, 1998; Arminger et al., 1999; Muthén, 2001; Bauer and Curran, 2004; Bauer, 2005; Pek et al., 2009, 2011). Finite mixtures of linear structural equation models are used to approximate the unknown functional form of the non-linear relationship of the latent variables1. Furthermore, by assuming mixtures, the SEMM approach relaxes the assumption of normally distributed latent variables and disturbances necessary in conventional structural equation models. Therefore, the SEMM approach is a flexible tool for predicting latent dependent variables when data are not normal, and when obtaining a strict parametric representation of the functional relation does not have the highest priority (for a discussion see Bauer, 2005). However, one drawback is that the linearity assumption of latent relationships and the normality assumption of the latent variables are relaxed simultaneously. This drawback can be manifested in the problem that observed non-normality in the data cannot be attributed to either non-normality of the latent variables or non-linearity between the latent variables. A way to overcome this problem is the specification of non-linear structural equation mixture models (NSEMM; Kelava et al., 2014) that allow distributional and linearity assumptions to be relaxed separately for the latent variables and their relationships.
Although, the use of mixtures for modeling non-linear latent variable relationships (e.g., Curran et al., 1996; Dolan and van der Maas, 1998; Bauer and Curran, 2004; Bauer, 2005) or the non-normality of latent variables in the context of non-linear structural equation models (Lubke and Muthén, 2005; Lee et al., 2008; Yang and Dunson, 2010; Kelava and Nagengast, 2012; Brandt et al., 2014; Kelava et al., 2014) have received increased attention in recent years, systematic evaluations have been rare. As an additional limitation, all approaches presented so far have been strictly limited to single-level models and have not accounted for nested data structures.
2. Multilevel Structural Equation Modeling
Nested data structures have been addressed with multilevel models for relationships between manifest variables (for an introduction see Snijders and Bosker, 1999; Hox, 2010). In the past 2 decades, researchers have proposed frameworks that are capable of modeling nested data structures in latent variable models (e.g., Muthén, 1994; Rabe-Hesketh et al., 2004; Muthén and Asparouhov, 2009). For example, these frameworks have included models that account for random effects on the within-level, multilevel path analysis (Heck and Thomas, 2000), or multilevel confirmatory factor analysis (Muthén, 1994). Furthermore, mixtures of distributions have been applied in latent growth curve modeling (Muthén and Asparouhov, 2009).
So far, very limited psychometric developments have been proposed in the context of non-linear multilevel structural equation models that incorporate latent interaction effects. Leite and Zuo (2011) presented a product-indicator-based approach that allows for a specification of latent interactions on the between-level (e.g., at the school level). Their approach was a first attempt to extend the product-indicator approach for non-linear interaction effects in latent multilevel models. Products of between-level indicators are used for the specification of a measurement model of the between-level latent product variable.
Focusing more generally on within-person processes in psychology (Molenaar, 2004; Molenaar and Campbell, 2009), Nagengast et al. (2013) adapted the unconstrained product indicator approach to account for latent interactions on the within-level. In predicting homework motivation, they found support for the latent interaction between homework expectancy and homework value at the within-student level.
Despite these first successful adaptations, several problems that are associated with single-level non-linear structural equation modeling remain unsolved. First, the hitherto applied constrained and unconstrained product-indicator approaches for multilevel models are vulnerable to violations of distributional assumptions (normal distributions are typically assumed; for a discussion see Kelava et al., 2011). The specification of constrained and unconstrained product-indicator approaches strongly depends on the distributions involved (Kelava and Brandt, 2009), and biased estimates of the parameters and standard errors can be expected when specification errors occur (Kelava et al., 2008) or distributional assumptions are not met (Kelava and Nagengast, 2012). Hence, product-indicator approaches that are extended for multilevel data structures are even more vulnerable because more distributional assumptions on different levels have to be met.
Second, the proposed extensions of single-level non-linear structural equation models specify a parametric non-linearity (by involving products of latent variables). Recently, a strong emphasis has been placed on the relaxation of this simple functional relationship, including mixtures of latent variables that also allow for non-normally distributed variables (e.g., Bauer, 2005; Kelava et al., 2014). Therefore, on the one hand there is a need for an optional specification of a semiparametric relationship of the latent variables (at the within and between levels) to better approximate the non-linear reality. On the other hand, there is a need for an optional specification of mixtures that can account for non-normality or heterogeneity across subpopulations.
Third, the application of single-level non-linear structural equation modeling in substantive research has suffered from too many approaches that use the same distributional assumptions (see paragraphs above) and too few simulation studies that offer clear recommendations for the application of specific approaches (for an overview, see Kelava et al., 2011). Approaches that agree with regard to distributional assumptions may lead to contradictory results; that is, some approaches might suggest significant non-linear effects, whereas others might not. Substantive researchers cannot solve this kind of problem by referring to empirical data. Further information that is based on simulation studies (for single-level non-linear models see e.g., Brandt et al., 2014) is needed here.
In total, there is a need for a framework that incorporates several special cases of multilevel modeling and that offers general as well as specific solutions for both substantive and methodological research in non-linear latent variable modeling. From a substantive standpoint, non-linear hypotheses (e.g., interactions) can be examined in more detail. From a methodological standpoint, the framework will foster the comparison of different kinds of estimators (e.g., MCMC, ML, or moment methods) in the context of different distributions.
As a result of these considerations, in the next section, we will present a general non-linear multilevel structural equation mixture modeling (GNM-SEMM)framework that allows for the separate relaxation of distributional and linearity assumptions of the latent variables and their relationships on different levels of a nested data structure. We will provide several theoretical and practical examples to illustrate what is possible within the framework. In general, within this framework, it is possible to derive specific submodels that include crucial parts of the model as well as a combination of several aspects that have not been combined before.
3. A General Non-Linear Multilevel Structural Equation Mixture Model
In this section, we will present a GNM-SEMM framework that allows for semiparametric latent non-linear effects on the within and the between levels. The framework presented here is similar to the general multilevel mixture model and notation presented by Muthén and Asparouhov (2009). Whereas Muthén and Asparouhov's (2009) model focuses only on linear relationships, the GNM-SEMM framework accounts for non-linear semiparametric relationships of the manifest and latent variables involved. This allows for a more precise modeling of latent variable relationships at different data levels while relaxing the linearity assumptions of standard latent multilevel frameworks (e.g., Rabe-Hesketh et al., 2004).
3.1. Observed and Mixture Variables
3.1.1. Definition
Let yjik be the score of the j-th (j = 1, …, J) observed (indicator) variable for individual i (i = 1, …, Nk) in a cluster k (k = 1, …, K). Note that the individual index i is cluster-specific. Its range depends on the cluster size Nk (e.g., the number of pupils in a given school k is denoted as Nk). Let zlk be the score of the l-th (l = 1, …, L) observed (indicator) variable for cluster k. The observed scores yjik and zlk could be realizations of dichotomous, ordered categorical, continuous normally distributed, or count variables.
Categorical (mixture) variables are used for the definition of mixtures on the individual (within) and cluster (between) levels. Let Cik be an within-level latent categorical variable for individual i in cluster k, which takes values 1, …, C*d. Let Dk be a between-level latent categorical variable for cluster k, which takes values 1, …, D*. Note that the number of latent classes on the within-level may be different across the latent classes on the between-level.
Analogous to Rabe-Hesketh et al. (2004), Muthén (1984), and Muthén and Asparouhov (2009), for observed dichotomous and ordered categorical variables, the underlying normally distributed latent variables y*jik and z*lk are defined such that for a set of threshold parameters τjscd and τls′d, and categories s and s′, respectively, the following equations hold for each subject i in cluster k:
where the vertical bar ·|· indicates a “conditional on” statement, and ↔ indicates an equivalence. For continuous normally distributed variables, y*jik = yjik and z*lk = zlk are assumed, and for count variables, y*jik = log(λjik) and z*lk = log(λlk) hold, where λjik and λlk are the expectations of the Poisson distribution. Additional assumptions regarding the mean and covariance structure will be made in the following subsections, which will specify the measurement and structural models on the within and between levels.
3.1.2. Example
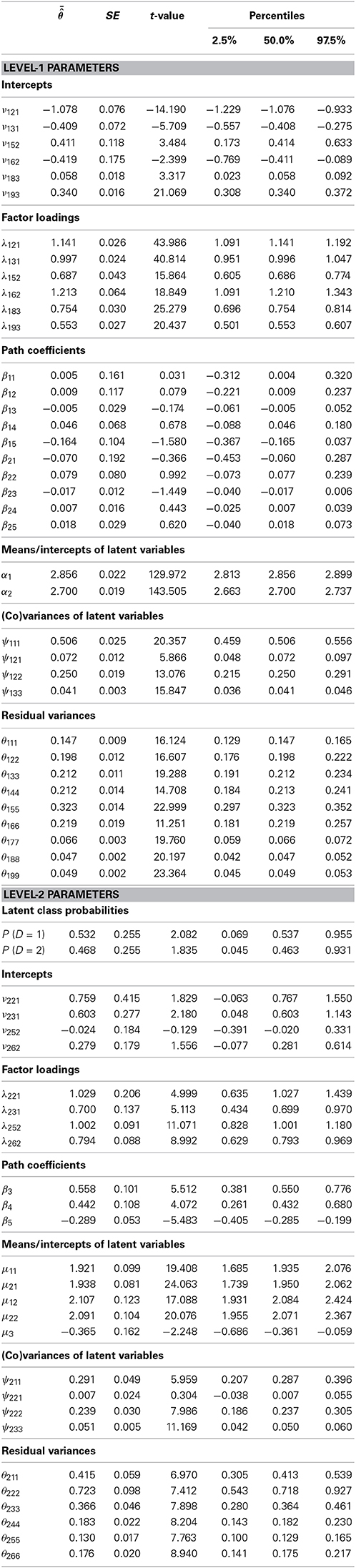
Suppose that pupils from several schools take part in a math test. For a given pupil i from school k the score on a sub-task j from the math test is given by yjik. In addition, for school k, there is a score zlk that indicates the school's social problems (e.g., the degree of bullying reported by the principal). In Figure 1, two latent categorical variables Cik and Dk on the within-level (Level 1) and the between-level (Level 2), respectively, are introduced. These variables may account for heterogeneity that occurs in the scores on both levels. On Level 1, heterogeneity in the distribution of the math test may occur due to additional private lessons in math that some pupils received. On Level 2, heterogeneity may occur in the distribution of the school's social problems, for example, due to the general (unobserved) socioeconomic status of the neighborhood where the school is located. Furthermore, school k might belong to an unobserved group of schools Dk = d that explicitly prepared for the math test. This may then influence the distribution of the math scores.
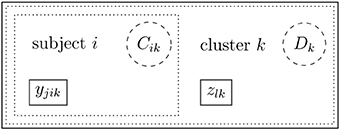
Figure 1. Observed variable scores yjik (within-level) and zlk (between-level) as well as mixtures Cik (within-level) and Dk (between-level).
Figure 1 shows a diagram with the observed and mixture variables. At this stage, there is no model that can explain the relationship between the scores yjik and zlk and no measurement model that can describe the realizations of the scores. The mixtures are indicated by Cik and Dk.
3.2. Level 1 – Within Level
3.2.1. Measurement model
3.2.1.1. Definition. Let y*ik be the J-dimensional vector for individual i in cluster k that includes scores for all dependent observed within variables. The measurement model is defined by a mixture distribution model
where ν1kcd is a J-dimensional vector of latent intercepts, Λ1kcd is a J × m(f1) loading matrix. η1ikcd = (η11ikcd, …, η1ikmcd)′ is an m-dimensional vector of variables including all latent exogenous and endogenous variables. f1(·) is a smooth polynomial function mapping the m-dimensional variable vector η1ikcd to an m(f1)-dimensional vector f1(η1ikcd). f1(η1ikcd) could be a vector that includes product variables [e.g., (η11ikcd, η12ikcd, η11ikcd η12ikcd)′ or (η11ikcd, (η11ikcd)2, η12ikcd, (η12ikcd)2)′] (e.g., Schumacker and Marcoulides, 1998; Kelava et al., 2011) or splines (Freund and Hoppe, 2007). K1kcd is a J × Q(g1) matrix with regression coefficients. x1ik is a Q-dimensional vector of all observed unexplained (within) covariates that may have an additional influence on the indicator variables y*ik. g1(·) is a smooth polynomial function mapping the Q-dimensional vector of covariates to a Q(g1)-dimensional vector g1(x1ik), and ϵ1ikcd is a J-dimensional vector of residual variables with a zero mean vector and covariance matrix Θ1kcd.
For observed categorical variables yik, a normality assumption for ϵ1ikcd is equivalent to a probit regression for yik on η1ikcd and x1ik. Alternatively, for dichotomous variables yik, ϵ1ikcd can have a logistic distribution, resulting in a logistic regression. For count variables yik, the residual ϵ1ikcd is assumed to be zero. For normally distributed continuous variables yik, the residual variable ϵ1ikcd is assumed to be normally distributed.
3.2.1.2. Example. Suppose that in the above-mentioned math test example, data for two additional constructs (attitude toward reading and the teaching strategies experienced by the student) were collected with three items for each construct. The measurement model [cp. Equation (3)] is illustrated in Figure 2, and accordingly, it assumes two latent factors η11ikc (attitude toward reading) and η12ikc (experienced teaching strategies). For didactical purposes, all schools here belong to one class D = 1, so that the index d can be omitted, and there is no between-level model. Furthermore, heterogeneity is assumed on the within-level such that each pupil i belongs to an unobserved class (mixture) Cik = c. The example measurement model derived from the framework above is a confirmatory factor mixture model that is given by yik|Cik = c = ν1kc + Λ1kcη1ikc + ϵ1ikc. The heterogeneity, which is implied by the mixture c, can be accounted for differently by the (statistical) model depending on the hypothesized population model: First, a non-normal distribution of the latent variables can be modeled as a mixture distribution. For example, attitude toward reading might not be normally distributed. A mixture distribution of η11ikc (with varying expectations and covariance structure for each mixture component c) could represent the non-normality (see Kelava et al., 2014). Second, the measurement model might be completely different for each unobserved subgroup (with varying factor loadings etc.). For example, some pupils might have poor reading skills, and hence, do not understand the items well enough. As a consequence, factor loadings in this subgroup may be lower (or residual variances may be larger) compared with other subgroups. and such differences may lead in turn to an observed heterogeneity.
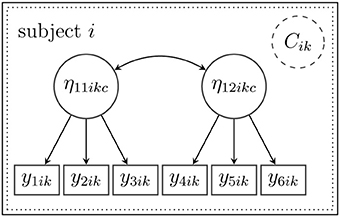
Figure 2. A measurement model for subject i for two latent variables with a mixture distribution on the within-level (the between-level ith not included in this example). The mixture distribution is symbolized by the frame with dashed lines. It was assumed that all subjects belonged to one latent class D = 1 on the between-level so that the index d could be omitted.
3.2.2. Structural model
The structural model for the latent variable vector η1ikcd is given for each subject i in cluster k by
where αkcd is an m-dimensional vector of intercepts, B1kcd is an m × m(F1) loading matrix. F1(·) is a smooth polynomial function mapping the m-dimensional vector of latent variables η1ikcd to an m(F1)-dimensional vector F1(η1ikcd). Γ1kcd is an m × Q(G1) matrix with regression coefficients. G1(·) is a smooth polynomial function mapping the Q-dimensional vector of covariates x1ik to a Q(G1)-dimensional vector G1(x1ik). Note that for identification purposes, vector G1(x1ik) has to be completely different from vector g1(x1ik). ζ1ikcd is an m-dimensional vector of residual variables with zero mean vector and covariance matrix Ψ1kcd.
3.2.3. Mixture part
The model for the latent categorical variable Cik is a multinomial logit model
where a1kcd and b1kcd are regression coefficients, and h1(·) is again a smooth (e.g., polynomial) function.
3.2.3.1. Example. In the following illustrative example, the math skills of pupil i from school k (η13ikc) are predicted by the attitude toward reading (η11ikc) and by experienced teaching abilities (η12ikc; see also the example above). All three constructs are modeled as latent variables, which are measured with three indicator variables each. In addition, we assume that math skills can be predicted by gender, which is introduced into the model as an observed covariate (x11ik). For simplicity, the model is restricted to the within-level. Furthermore, it is assumed that there is unobserved heterogeneity due to a latent class Cik. Membership in one of the latent classes is predicted by a second observed covariate x12ik (e.g., additional private math lessons). In contrast to an ordinary linear approximation of the relationship between the latent variables, the unknown and potentially curvilinear relationship is approximated by a latent spline model. Figure 3 illustrates the proposed model; the semiparametric spline model is indicated by the snake-type arrow.
Figure 3. Structural model for subject i in latent class Cik with a nonlinear spline relationship between the latent variables (indicated by the snake-type arrow). Note that this figure shows only a single-level model; the index d is therefore omitted.
3.3. Level 2 – Between (Cluster) Level
The multilevel (between) part of the model is conceptualized as follows. Each of the intercepts (ν1kcd, αkcd, a1kcd) and slopes or loading parameters (Λ1kcd, K1kcd, B1kcd, Γ1kcd, b1kcd) in Equations (3), (4), and (5) can be either a fixed coefficient or a random effect that varies across the observed clusters k.
3.3.1. Structural model
Let η2kd be the U-dimensional vector of all such random effect variables and any additional between-level latent exogenous variables that explain these random effects and vary across the clusters. Note that η2kd is different from η1ikcd which is the individual-level latent variable vector. For a given cluster k, the between-level structural model for η2kd is defined as
where μd is a U-dimensional vector of intercepts, and B2d is a U × U(F2) loading matrix. F2(·) is a smooth polynomial function mapping the U-dimensional vector of variables η2kd to a U(F2)-dimensional vector F2(η2kd). Γ2d is a U × V(G2) matrix with regression coefficients. x2k is a V-dimensional vector of all observed unexplained between-level covariates that may have an additional influence on the variables in vector η2kd. Note that x2k is different from x1ik. G2(·) is a smooth polynomial function mapping the V-dimensional vector of between-level covariates x2k to a V(G2)-dimensional vector G2(x2k). ζ2kd is a U-dimensional vector of residual variables with a zero mean vector and covariance matrix Ψ2d. μd, B2d, and Γ2d are fixed parameters.
3.3.1.1. Example. Suppose that the model in Figure 3 is extended to allow for multilevel effects on the between-level (Level 2). In Figure 4 depicts a latent random intercept model that implies a school-specific intercept (α3kd) for school k when the math skills (η13ikd) of a given pupil i are examined. In order to approximate a potentially non-normal distribution of the school-specific intercepts or to reveal a certain heterogeneity in the latent intercepts (i.e., average math skills), a latent mixture model with the latent categorical variable Dk is applied. This mixture reflects Level-2 heterogeneity that may stem from (unobserved) sources, for example, certain school characteristics that influence the average math skills in school k.
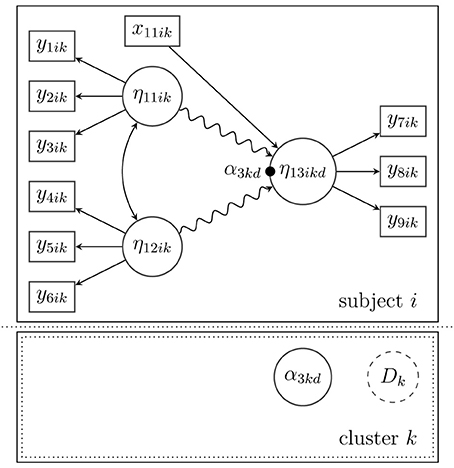
Figure 4. Structural model for subject i in cluster k with a nonlinear spline relationship between the latent variables on the within-level (indicated by the snake-type arrow) and a random intercept (α3kd) that is modeled as a mixture of normal distributions on the between-level.
3.3.2. Measurement model
Let z*k be the L-dimensional vector for cluster k that includes scores on all observed between-level variables that are indicators of the latent variables in vector η2kd. For a given cluster k, the measurement model is defined by
where ν2d is an L-dimensional vector of intercepts, Λ2d is an L × U(f2) loading matrix. f2(·) is a smooth polynomial function mapping the U-dimensional vector of variables η2kd to a U(f2)-dimensional vector f2(η2kd). K2d is an L × V(g2) matrix with regression coefficients. x2k is the V-dimensional vector of all observed unexplained between-level covariates that may have an additional influence on the indicator variables z*k. g2(·) is a smooth polynomial function mapping the V-dimensional vector of between-level covariates x2k to a V(g2)-dimensional vector g2(x2k). Note that for identification purposes g2(x2k) has to be completely different from G2(x2k). ϵ2kd is a L-dimensional vector of residual (mixture) variables with a zero mean vector and covariance matrix Θ2d. ν2d, Λ2d, and K2d are fixed parameters.
3.3.3. Mixture part
The model for the between-level categorical variable Dk is also a multinomial logit regression
where a2d and b2d are regression coefficients, and h2(·) is again a smooth (e.g., polynomial) function.
3.3.3.1. Example. In this last example (see Figure 5, the random intercept model in Figure 4 has been expanded by adding two latent Level-2 predictor variables (η21kd and η22kd) that may influence the average math-skill level, for example, structural problems and social problems in school. Besides the linear effects of the latent predictors, there is an interaction effect that models the hypothesis that high scores on both between-level predictors may lead to a particularly low (or high) average math-skill level. A potential heterogeneity of the latent predictors (e.g., a non-normal distribution) is taken into account by introducing a latent categorical variable Dk. In addition, a manifest predictor variable x21k, for example, school size or school type (private or public), is included in the model to predict the latent class probability of Dk as described more generally in Equation (8).
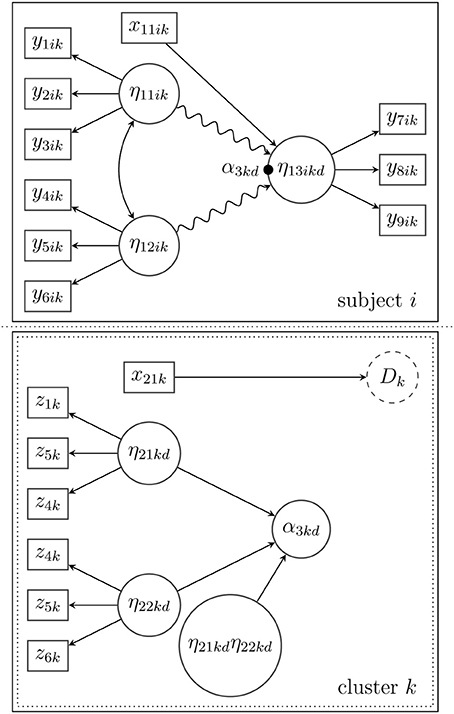
Figure 5. Structural model for subject i in cluster k with a spline relationship between the latent variables on the within-level (indicated by the snake-type arrow), and a random intercept (α3kd) that is predicted by an interaction model on the between-level. The distribution of the between-level's predictors is approximated by a mixture of normal distributions. The latent categorical variable Dk is predicted by a between-level covariate x21k.
3.4. Summary
In the model described by Equations (3) to (8), the latent variables on Level 1 (η1ikcd, ϵ1ikcd, and ζ1ikcd) and on Level 2 (η2kd, ϵ2kd, and ζ2kd) are conceptualized as variables stemming from mixtures on level 1 and level 2, respectively. The possibility of specifying within- and between-level mixture components is a result of introducing the latent categorical variables Cik and Dk on the individual and cluster levels, respectively. On the within-level, unobserved latent classes may refer to different subpopulations (within each cluster), for example, pupils with different socioeconomic backgrounds in a given school. On the between-level, latent mixtures additionally allow for a specification of heterogeneity across/between observed clusters, for example, heterogeneity that is caused by certain characteristics of the schools. Furthermore, due to the conceptualization of mixture variables, a semiparametric modeling of non-normally distributed latent variables is available (e.g., Yang and Dunson, 2010; Kelava and Nagengast, 2012; Kelava et al., 2014), or a simple semiparametric formulation of the latent relationships (e.g., Bauer, 2005) is possible. Finally, the implementation of general polynomial functions F1(·), f1(·), G1(·), and g1(·) allows for a flexible inclusion of different parametric or semiparametric relationships (e.g., interaction effects or splines; Hastie et al., 2009), which extends the opportunities to model non-linear effects (e.g., Guo et al., 2012; Song et al., 2013).
4. Model Identification
As in any other latent variable framework, within the GNM-SEMM framework, the user must ensure that the specified model is identified. In this section, we will summarize important aspects that need to be considered even though model identification is not straightforward (cf. San Martín et al., 2011; Song et al., 2013). For the identification of the proposed model, four separate aspects need to be taken into account. However, the actual identification of a specific model needs to be examined individually.
First, within each mixture component standard assumptions for non-linear structural equation models need to be met. This mainly implies that restrictions be placed on manifest scaling variables or latent exogenous variables (e.g., a necessary condition for the identification is to set one factor loading for each latent predictor variable or the latent predictors' variance to one). In addition, either the latent intercepts of the indicator variables or the latent intercepts of the latent variables may be estimated in a model. Note that when latent exogenous variables (e.g., η11ikcd, η12ikcd) are identified, their latent product terms (e.g., η11ikcd η12ikcd) do not need product indicators for identification (cf. Klein and Moosbrugger, 2000).
Second, regarding the inclusion of polynomial functions for the observed covariates, it is necessary that the vectors g1(x1ik) and G1(x1ik) on Level 1 and, respectively, the vectors g2(x2k) and G2(x2k) on Level 2 are completely different from each other. For example, a model including g1(x1ik) = G1(x1ik) = (x11ik, x211ik)' would not be identified because x11ik would be a predictor in the measurement and structural models [see Equations (3) and (4)]. In this case, two effects of x11ik would be estimated simultaneously on the right side of one regression equation, which would not be identified. The same holds for the polynomial functions of the latent variables. Again, f1(η1ikcd) and F1(η1ikcd) on Level 1 as well as f2(η2kd) and F2(η2kd) on Level 2 have to be unequal [see Equations (7) and (6)]2. Otherwise, perfect collinearity would be the result, meaning that the covariates and latent variables, respectively, would have the same influence on the measurement and the structural models. Their impacts would not be separable. Furthermore, polynomial (semiparametric) functions should not include constants. Otherwise, latent intercepts in the measurement and structural models would not be identified.
Third, on the between (cluster) level the inclusion of latent exogenous variables, which explain the variability in the random coefficients, requires measurement models (see Figure 5). The exogenous latent variables at Level 2 need to be identified as well according to identification rules, which are the same as in single-level structural equation models.
Fourth, additional assumptions concerning the latent classes of the mixture components are required. For the identification of the discrete latent variables, (a) the unconditional probabilities in Equations (5) and (8) need to sum up to one. and (b), the ambiguity of mixture components due to the so-called label switching problem makes it necessary to impose additional (artificial) constraints or relabeling strategies e.g., restrictions on the mean structure or ordinality of mixture proportions (see Equations 15–19; Redner and Walker, 1984; Stephens, 2000; Kelava and Nagengast, 2012).
Note that the identification of separate parts of a model (e.g., the measurement model and the structural model) does not automatically imply that the whole model is identified. General necessary and sufficient conditions to guarantee the identifiability of a latent variable model are difficult to establish. Hence, we focus primarily on the necessary identification conditions in this article.
5. Model Estimation
Generally speaking, latent variable modeling offers a large variety of methods for the estimation of specified models. The choice of the best estimation method strongly depends on the distributional assumptions of the observed and latent variables, the given sample size, the type of specified model, potential confounders, and many more aspects. Just to mention a few large classes, these methods comprise maximum likelihood estimators (e.g., Jöreskog, 1973; Rabe-Hesketh et al., 2005; Muthén and Asparouhov, 2009), least squares methods (e.g., Joreskog and Goldberger, 1972; Browne, 1974, 1984), and methods of moments (e.g., Bentler, 1983), among others. For example, when applying a maximum likelihood estimator, in the well-known EM algorithm (Dempster et al., 1977), which treats latent variables as missing data, the likelihood L of the observed indicator vector y is given as:
where f1ikcd(·), ψ1ikcd(·), and ψ2kd(·) are probability density functions for the observed variables y, and the latent variables η1ikcd and η2kd, respectively (cf. Muthén and Asparouhov, 2009). Because the likelihood function L of the observed indicator vector yik is not given in closed form in general, numerical integration can be utilized in the evaluation of the likelihood using both adaptive and non-adaptive quadrature. As an alternative, the likelihood could be directly optimized by applying a quasi-Newton algorithm. Both approaches of estimating parameters are very complex due to the non-linearity (for a discussion of latent interaction effects, see Klein and Moosbrugger, 2000).
However, in recent years, the Bayesian framework has become very popular in latent variable modeling (e.g., Lee et al., 2004; Lee, 2007; Lee et al., 2007; Song et al., 2009). The main reason is that it provides flexible options for specifying and estimating models. Bayesian estimation methods and algorithms (e.g., Markov Chain Monte Carlo: MCMC) can handle numerous complex parametric, semiparametric, and non-parametric relationships and distributions, for example, latent mixture distributions (e.g., Yang and Dunson, 2010; Kelava and Nagengast, 2012), non-linear models (e.g., Lee et al., 2007; Guo et al., 2012; Song et al., 2013), and multilevel structures (e.g., Fox and Glas, 2001; Song and Lee, 2004). Referring to the proposed GNM-SEMM framework with its semiparametric functional forms and its capability of considering non-normally distributed variables, a Bayesian approach seems to be a viable way to estimate models. In this sense, we will provide general descriptions of the specifications of the variables' distributions and the selection of prior distributions.
Parameter vectors are defined as follows: For the Level-1 parameters, let θM1kcd = (ν′1kcd, vec(Λ1kcd)′, vec(K1kcd)′, vec(Θ1kcd)′)′ for the measurement model, where vec(·) vectorizes all elements of a given matrix. For the structural model, let θS1kcd = (α′kcd, vec(B1kcd)′, vec(Γ1kcd)′, vec(Ψ1kcd)′)′, and for the mixture model part let θm1kcd = (a1kcd, b′1kcd)′. Analogously, for the Level-2 parameters, let θM2d = (ν′2d, vec(Λ2d)′, vec(K2d)′, vec(Θ2d)′)′ for the measurement model. For the structural model, let θS2d = (μ′d, vec(B2d)′, vec(Γ2d)′, vec(Ψ2d)′)′, and for the mixture model part let θm2d = (a2d, b′2d)′. Finally, let θM1, θS1, θm1, θM2, θS2, and θm2 be the vectors that include all parameters from the defined model parts across all latent classes c = 1, …, C*d, d = 1, …, D*, and observed clusters k = 1, …, K.
5.1. Specification of the Variables' Distribution
5.1.1. Level 1
For the Bayesian analysis, the j = 1, …, J indicator variables on Level 1 are specified as a cluster-specific mixture distribution. The single mixture is given as
where μy*(θM1kcd, θS1kcd, x1ik) is the vector of conditional expectations of y*ik, which are specified in Equation (3) and depend on the parameter vectors θM1kcd and θS1kcd, and on the covariate vector x1ik. Θ−11kcd is the precision matrix of the multivariate normal distribution of the measurement error variables (i.e., the inverse of the covariance matrix). The model implies a specific mean vector and covariance matrix for subjects stemming from a certain latent class c on Level 1 that is clustered in a latent class d on Level 2, which in turn is given for an observed cluster k. Within each cluster k, y*ik is a mixture of D* components, which model heterogenity in the observed clusters. Further, within in each mixture component d, y*ik is a mixture of C*d components, which induce heterogenity on the individual level (C*d may change across different latent classes on Level 2).
The latent variables η1ikcd on Level 1 are specified as
with the vector μη1(θS1kcd, x1ik) of conditional expectations for η1ikcd that depend on the parameter vector θS1kcd and covariate vector x1ik as specified in Equation (4) as well as in the precision matrix Ψ−11kcd.
5.1.2. Level 2
Analogous to the specification of the variables' distributions on Level 1, the indicator vector z*k is modeled as
with the vector μz*(θM2d, θS2d, x2d) of conditional expectations for z*k as specified in Equation (7) and precision matrix Θ−12d. The unconditional indicator vector z*k is composed of D* mixture components. Finally, the distribution of the latent variable vector η2kd, is given as
with the vector of conditional expectations μη2(θS2d, x2k) specified in Equation (6) and precision matrix Ψ−12d.
5.2. Specification of Prior Distributions
For the prior specification, informative or non-informative priors can be selected (Gelman et al., 2004). This selection is primarily based on the availability of prior knowledge. Because the application of non-informative priors may lead to suboptimal solutions (e.g., Lee et al., 2007), it may be necessary to analyze parts of the model (e.g., a confirmatory factor analysis for the Level-2 predictors) to obtain information about the parameters. Here, a very general description of the proposed model is provided. For a detailed description of priors see Gelman et al. (2004).
The class probabilities Pr(Cik = c|Dk = d, x1ik) and Pr(Dk = d|x2k) depend on the multinomial logit models given in Equations (5) and (8) and thus depend on the parameters in θm1 and θm2. For these parameters, uninformative priors are suggested unless information about heterogeneity is available (see also Kelava and Nagengast, 2012).
For each precision matrix of the mixture distributions defined above, that is for Θ−11kcd, Θ−12d for the indicator variables, and for Ψ−11kcd, Ψ−12d for the latent variables, a multivariate normal distribution is assumed within each component. Conjugate priors are then given for c = 1, …, C*d, d = 1, …, D* as
The hyperparameters ρ and the (positive definite) matrices Θ01kcd, Θ02d, Ψ01kcd, and Ψ02d of the Wishart distribution include parameter information that may stem from previous studies or knowledge about the parameters. For example, Ψ02d includes information about the variances and covariances of the random coefficients, and about the latent endogenous and exogenous variables on Level 2. This information may refer to estimates of the (co)variances for the latent exogenous variables retrieved from a separately estimated confirmatory factor analysis.
The conjugate priors can be modified, for example, if the residual covariance matrix Θ2d on Level 2 is assumed to be diagonal, then each diagonal element Θj2d (j = 1, …, J) can be assumed to be inverse Gamma distributed, that is (Θj2d)−1 ~ Gamma(αΘj2d, βΘj2d) (with hyperparameters α, β) (Kelava and Nagengast, 2012). Further information about the selection of priors for count or ordinal data can be found in Song et al. (2013).
For the other parameters in θM1, θS1, θM2, and θS2, normally distributed priors are used within each mixture component. Though, the definition of some priors needs to be formulated recursively (cf. Kelava and Nagengast, 2012). For example, let νj1kcd be the j-th element of the vector ν1kcd (which specifies the intercept of the j-th variable in y*ik|Cik = c, Dk = d), and let Θj1kcd be the j-th diagonal element in the matrix Θ1kcd. Then for the latent classes c = 1, d = 1, the conjugate (normal) prior for νj1k11 is specified as
with hyperparameters H0 and νj01k11 that include information about νj1k11. For all other latent classes, that is c > 1 or d > 1, the following prior is selected:
with
If parameters are constrained to be the same across mixture components (e.g., ν1kcd = ν1k and Θ1kcd = Θ1k), Equations (15) to (19) simplify to
For the other parameter matrices, that is for Λ1kcd, K1kcd, αkcd, B1kcd, Γ1kcd and so forth on Level 1 and ν2d, Λ2d, K2d, μd, B2d, Γ2d and so forth on Level 2, a specification corresponding to the formulation above given is straightforward when the appropriate precision matrices are used. In order to avoid the label-switching problem in a mixture distribution, only one of the parameter matrices needs to be formulated recursively.
6. Empirical Example
In this section, we will provide an extensive illustration of the GNM-SEMM with an example that is based on data from the Program for International Student Assessment 2009 (PISA; Organisation for Economic Co-Operation and Development, 2010), which is publicly available under http://pisa2009.acer.edu.au/downloads.php. The sample was a German subsample of N = 1, 474 pupils from 226 schools who took a math test. Additional covariate information were available on the individual level as well as on the school level.
As before, we predicted pupil's math skills (Math) with their general attitude toward reading (Att) and the teaching strategies they experienced (Strat). We further expected that pupil's average math skills (latent intercept of Math) would vary systematically across schools3, and that this variation could be (partly) accounted for by Level-2 predictors with measurement errors, here, structural problems in school (Prob) and the schools's social environment (Soc).
We will report the results for a model that accounted for different aspects of the general model. The example is not exhaustive with regard to all potential parameters within the GNM-SEMM framework, but it provides an indication of the flexibility of the proposed framework in accommodating different aspects of the data: A spline model on Level 1 described a semiparametric flexible relationship between Att, Strat, and Math. A random intercept for Math was explained by the Level-2 predictors Prob and Soc, and the interaction effect between them. Furthermore, a mixture model accounted for the non-normality of the latent predictors on Level 2 (heterogeneity).
6.1. Model Formulation
In the following, we will provide the specified measurement and structural equations for the model. For reasons of clarity, we restricted the subscripts (k, c or d) in the model formulation to those model parameters that actually depended on the latent classes or the Level-2 model. Figure 6 presents a diagram of the model and its parameters.
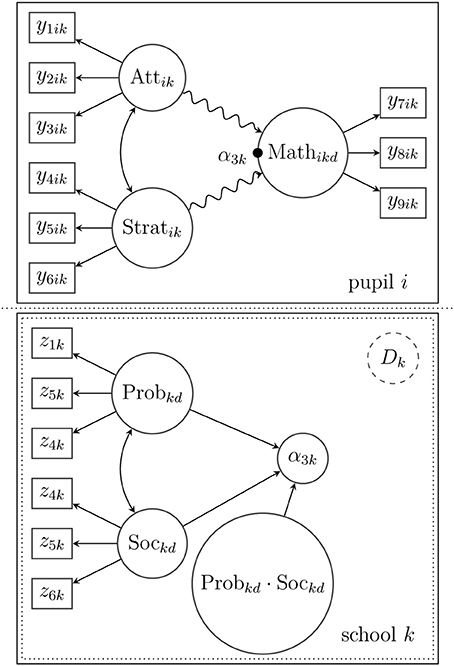
Figure 6. Structural models and measurement models on the within-level (Level 1) and between-level (Level 2). On Level 1, the math skill (Math) of a pupil i is predicted by his/her general attitude toward reading (Att) and his/her experienced teaching strategies (Strat). The snake-type arrows indicate a flexible spline approximation of the latent variable relationship. On Level 2, the average math skills of pupils (latent intercept α3k) in school k are explained by a nonlinear interaction between structural problems in the school (Prob) and the school's social environment (Soc). The non-normality of the latent predictors is approximated by a mixture distribution.
6.1.1. Structural models
The Level-1 structural model [cf. Equation (4)] for the i-th pupil in school k was given by
where F11 and F22 both defined a latent cubic spline model with two knots at ξ1 = 2, ξ2 = 3 that approximated the (curvilinear) relationships between the variables (e.g., Hastie et al., 2009):
Only the latent intercept α3k was assumed to vary across schools. The Level-2 structural model [cf. Equation (6)] for school k was given by
with η2kd = (Probkd, Sockd, α3k)′ and F2(η2kd) = (Probkd, Sockd, Probkd · Sockd)′. The product term Probkd · Sockd implemented the interaction effect of the structural problems in school and the social environment. Because the non-normal distributions of the latent predictors were approximated by a mixture distribution, their expectations μ1d and μ2d were assumed to vary across the unobserved mixtures (Kelava and Nagengast, 2012).
6.1.2. Measurement models
For each of the latent variables between nine and 13 items were available; they were aggregated to three indicator variables for each latent variable (item parcels) for didactic purposes. It was assumed that the indicator variables were continuously distributed, resulting in an identity link function in the measurement model (y*ik = yik and z*k = zk, respectively).
On Level 1, the measurement model for pupil i in the k-th school [cf. Equation (3)] was given by
where f1(η1ik) = (Attik, Stratik, Mathik)′.
On Level 2, the measurement model [cf. Equation (7)] was given by
where f2(η2kd) = (Probkd, Sockd)′. The factor loading matrices Λ1 and Λ2 were formulated with a simple structure (i.e., each item loaded on only one latent variable). The residual variables ϵ1ik and ϵ2ik were assumed to be mutually uncorrelated and normally distributed with zero mean vectors and (diagonal) covariance matrices Θ1 and Θ2, respectively.
6.1.3. Parameter constraints and identification
Besides employing the standard identification constraints for structural equation models, we restricted the measurement model parameters and the structural model parameters to be the same across schools except for the latent intercept α3k. Due to the invariance of the measurement models for the latent predictors on Levels 1 and 2, in Equations (24) and (25) the non-linear effects in the polynomial spline model and the interaction effect in Equations (22) and (23) were identified. For the mixture model, we fit two latent classes (Dk = 1, 2).
6.2. Model Estimation
To keep this example as simple as possible, missing data were assumed to be missing at random, and this was accounted for directly in the analysis by applying the Gibbs sampler (Gelman et al., 2004). The analysis of the latent multilevel model was implemented by using the R-project software (R Core Team, 2013) and the OpenBugs package (Lunn et al., 2009). Syntax for the empirical example can be obtained upon request from the authors.
6.2.1. Starting values and prior selection
Starting values for the measurement model parameters were based on the prior analyses conducted in Mplus Muthén and Muthén (1998–2010) for separate parts of the model. Informative priors were then selected in accordance with recommendations by Gelman et al. (2004) as well as Kelava and Nagengast (2012).
6.2.2. Bayesian analysis
For the analysis, three chains with 100,000 iterations each were generated. The first 75,000 iterations (burn in) were then discarded. As proposed by Gelman (1996), convergence of the estimation procedure was achieved when all (EPSR Estimated Potential Scale Reduction; Gelman, 1996) values were below 1.2, which occurred after about 60,000 iterations (see the Supplementary Material, Figure S1). Trace plots also indicated good convergence (see the Supplementary Material, Figure S2). Means, standard errors, t-values, and percentiles of the posterior distributions of the parameter estimates based on the last 25,000 iterations are reported in the next subsection.
6.3. Results
We will summarize the main results in this subsection. Detailed results for the estimated multilevel model are presented in Table 1. In the measurement models, the factor loadings were all significant and positive, thus indicating that the latent constructs were measured reliably.
The results for the semiparametric approximation of the true relationships between the Level-1 latent variables Att, Strat, and Math are illustrated in Figure 7. The relationship between Math and Att resembled a cubic relationship; the subjects' Math scores slowly increased with increasing Att scores, whereby a stronger increase was found for Att scores greater than 3 and a slight decrease for Att scores greater than 4. The relationship between Strat and Math seemed to be slightly quadratic with the highest Math scores for medium Strat scores.
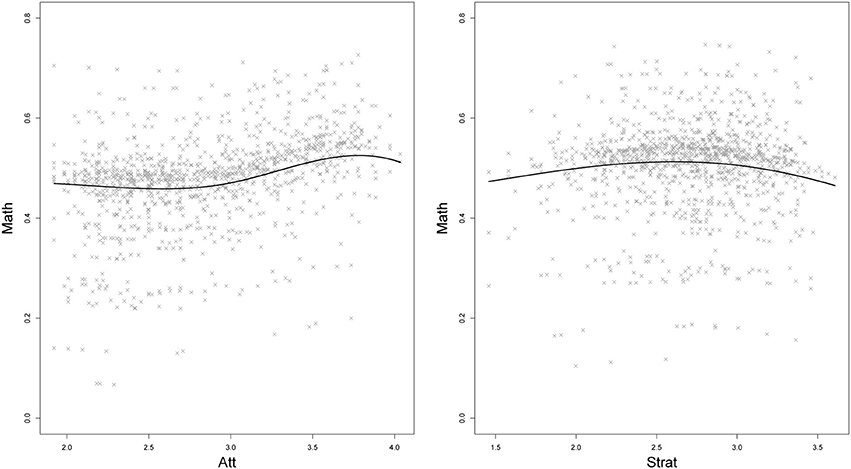
Figure 7. Semiparametric Level-1 relationships between pupils' math skills (Math) and their general attitude toward reading (Att; left), and Math and experienced teaching strategies (Strat; right). The gray crosses indicate the predicted slope with a predicted school-specific random intercept; the black line indicates the predicted Math score for the mean random intercept.
In order to test the hypotheses on the cubic relationship for Att and the quadratic relationship for Strat4, we estimated a model that changed Equation (22) to β1F(Attik) = β11Attik + β12Att2ik + β13Att3ik and β2F12(Stratik) = β21 Stratik + β22Strat2ik. Results for the structural parameters on the within-level can be found in Table 2. The parametric cubic relationship for Att was not significant (13 = 0.003, p = 0.745 for the cubic effect and 11 = − 0.045, p = 0.723 for the linear effect). The attitude toward reading did not significantly predict the math ability. The parametric model for Strat indicated a significant negative quadratic relationship (22 = −0.034, p = 0.037). This indicated that pupils' math skills were highest for those subjects who rated the experienced teaching strategies as average.
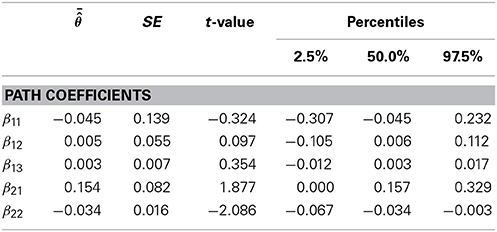
Table 2. Mean parameter estimates, standard errors, t-values, and 2.5, 50.0, and 97.5% percentiles for the parametric model (cubic relationship for Att and quadratic relationship for Strat) on Level 1.
On Level 2, the random intercept factor α3k had a significant negative intercept (3 = −0.365, p = 0.024) and an unexplained variance across schools of 233 = 0.051. The linear effects of the predictors were significant with 3 = 0.558 (p < 0.001) for school problems (Prob) and 4 = 0.442 (p < 0.001) for social problems (Soc). The interaction effect was significant and negative with 5 = −0.289 (p < 0.001). Figure 8 illustrates the complex non-linear association between Prob, Soc, and the random intercept α3k. The expected math level of a school with an average score on school and social problems was about 0.5 (E[α3|Prob = Prob, Soc = Soc] = 0.461); the expected math level was higher in schools for which one of the problems was above average and the other was below average; and the math level decreased rapidly when both problems increased together.
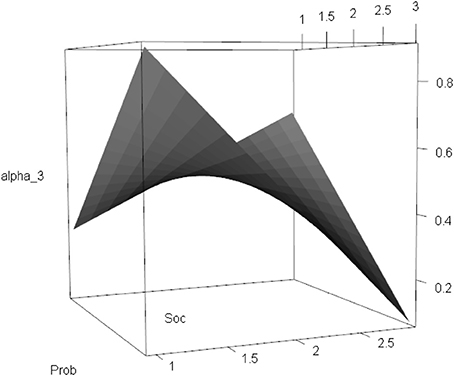
Figure 8. Between-level: Three-dimensional illustration of the relationship between school problems (Prob), social problems (Soc), and the random intercept α3k of Math.
Finally, the results of the mixture model for the Level-2 predictors are illustrated in Figure 9. As can be inferred from Figure 9, the distribution of the latent variables was slightly non-normal. In this empirical example, the means of the latent variables in the two classes were marginally different (with means of about 11 ≈ 21 ≈ 1.9 in Class 1 and 12 ≈ 22 ≈ 2.1 in Class 2). Additional analyses may reveal the necessity to increase or decrease the number of latent classes (e.g., using the DIC). Here, the DIC was 14,780 for a model including the mixtures and 14,770 for a model without the mixture distribution. This indicates that a mixture may not have been necessary in this case.
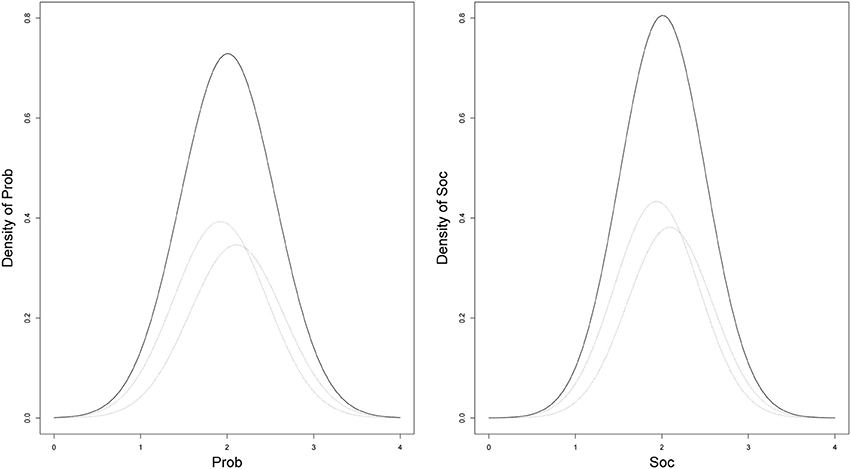
Figure 9. Predicted slightly non-normal densities of the Level-2 predictors Prob and Soc obtained from a two-class solution.
7. Discussion
In this article, we presented a generalized non-linear multilevel structural equation mixture model (GNM-SEMM) framework. A key characteristic its ability to specify non-linear functional relationships between outcome variables on one side and latent predictors or manifest covariates on the other side by using semiparametric regression functions (e.g., splines; Freund and Hoppe, 2007; Hastie et al., 2009). This feature is given for both levels, the within and between (cluster) levels of nested data structures. Given that (multilevel) latent variable modeling frameworks are typically linear (Bollen, 1989; van der Linden and Hambleton, 1997; Rabe-Hesketh et al., 2004; Muthén and Asparouhov, 2011), the relaxation of the linearity assumption is a step forward toward a more realistic approximation of a non-linear world. It thus extends the hitherto available multilevel modeling frameworks.
A second key characteristic is the ability to specify latent mixture distributions on both levels. As in recent semiparametric latent variables approaches (e.g., Bauer and Curran, 2004; Bauer, 2005; Kelava et al., 2014), this allows for an approximation of non-normally distributed latent predictor variables for a thorough introduction with regard to manifest variables, see McLachlan and Peel (2000). Again, the relaxation of a typical assumption that can be found in most applications of latent variable modeling allows for a more precise modeling of relationships for heterogeneous populations or distributions.
A third key characteristic of the proposed approach is that it is flexible enough to specify a large number of special cases. For example, it offers the ability to approximate a non-normal distribution using mixture modeling and provides an easy way to interpret the parametric functional form of the latent variable relationship. As another example, it is possible to specify a non-linear latent variable relationship in one subpopulation but not in the other. The same is true for different levels. If functional forms of the relationships are unknown, semiparametric approximations of these relationships are also possible using mixtures.
Taken together, these properties are desirable. Nevertheless, the identification and estimation of the models is a general issue. Additional assumptions have to be introduced as was exemplified in the sections before (see Level-1 section on the measurement model). Fortunately, these assumptions are standard identification assumptions in latent mixture, latent (non)linear, and (semi)parametric modeling, but researchers should be careful when specifying models. For example, multiple intercepts in spline models might lead to identification issues. However, the wide range of specifiable models offers a variety of adaptable estimators that could be applied from a theoretical standpoint. Bayesian MCMC, Newton-type algorithms, and adapted EM-Algorithms are just a few examples.
In this paper, we also used a substantive example from educational science. A complex model was applied to data from the large-scale PISA study (Organisation for Economic Co-Operation and Development, 2010) illustrating several conditions that may occur in empirical data. First, an a priori unknown curvilinear relationship between the latent variables was identified on Level 1 using a semiparametric latent spline model. Second, the proposed mixture part on Level 2 could be used to control for the potential non-normality of the latent Level-2 predictors. In this example, only a slight indication of non-normality was visible. The model may have also been extended to include a mixture model on Level 1. Third, on Level 2 a latent random intercept modeled a school-dependent math skill, which allowed us to account for the clustering of the data. The random intercept was predicted by a latent non-linear interaction model. The model may be extended further, for example, to test the linearity assumption on Level 2 of the relationship between the latent variables apart from the interaction effect. Other random effects could also be included. In any case, the specification of these effects should be theory-driven.
Finally, we want to mention two important considerations. The proposed model should be viewed as a general framework that includes a variety of different possible models. A model that includes all aspects as presented in the model section would be highly parameterized and may overfit the data. In each empirical situation, we recommend that the actual applied model be restricted to a simpler model that allows for an adequate but parsimonious representation of the data. A decision concerning the necessity to include different parts of the model depends on the hypothesized model (e.g., random factor loadings in a confirmatory factor model or a latent spline to predict a latent slope in the structural model) and on model comparisons. In the Bayesian framework, Bayesian indices/information criteria for model selection (e.g., the deviance information criterion, DIC: Spiegelhalter et al., 2002; Celeux et al., 2006; or the Bayes factor, Bernardo and Smith, 1994) are the primary model fit indices, although they only allow only for a model comparison to be made, and they are not absolute fit indices. In general, for (both frequentist and Bayesian) non-linear models there are no absolute fit indices (Klein and Schermelleh-Engel, 2010). Hence, a top-down (or bottom-up) strategy using information criteria may be a viable way to improve the model (i.e., to restrict the model to its necessary parts). An illustration of such a strategy for multilevel models in general can be found, for example, in West et al. (2007).
Furthermore, we did not show how to implement the presented framework with statistical software. In this article, a Bayesian estimator was applied and implemented in OpenBugs, thus allowing us to analyze a complete but specific semiparametric non-linear multilevel model. Future research should improve this implementation so that it will be feasibly available within standard statistical latent variable software (e.g., Mplus) that can be directly applied to different models by the substantive researcher.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgment
This work was supported by the Deutsche Forschungsgemeinschaft (DFG; Grants No. KE 1664/1-1).
Supplementary Material
The Supplementary Material for this article can be found online at: http://www.frontiersin.org/journal/10.3389/fpsyg.2014.00748/abstract
Footnotes
1. ^In SEMM linear models are estimated within several latent classes. Non-linear relationships between two variables are modeled by the parameter estimates for the linear effects that change in size across the (finite number of) latent classes.
2. ^An exception is the special case in which the coefficient matrix B = 0: that is, for confirmatory factor models.
3. ^The ICC was 0.407 for the manifest variable, which was the sum of all Math items.
4. ^A direct inference with regard to a parametric relationships, including a linear relationship, based on the parameter estimates for the spline model (e.g., β11) is not straightforward (Cox et al., 1988; Cox and Koh, 1989; Zhang and Lin, 2003; Liu and Wang, 2004). In general, an additional model that can actually test a parametric hypothesis seems to be a viable procedure (Azzalini and Bowman, 1993).
References
Algina, J., and Moulder, B. C. (2001). A note on estimating the Jöreskog-Yang model for latent variable interaction using LISREL 8.3. Struct. Equ. Model. 8, 40–52. doi: 10.1207/S15328007SEM0801_3
Arminger, G., and Muthén, B. O. (1998). A Bayesian approach to nonlinear latent variable models using the Gibbs sampler and the Metropolis-Hastings algorithm. Psychometrika 63, 271–300. doi: 10.1007/BF02294856
Arminger, G., and Stein, P. (1997). Finite mixtures of covariance structure models with regressors. Sociol. Methods Res. 26, 148–182. doi: 10.1177/0049124197026002002
Arminger, G., Stein, P., and Wittenberg, J. (1999). Mixtures of conditional mean- and covariance-structure models. Psychometrika 64, 475–494. doi: 10.1007/BF02294568
Azzalini, A., and Bowman, A. (1993). On the use of nonparametric regression for checking linear relationships. J. R. Stat. Soc. B 55, 549–557.
Bauer, D. J. (2005). A semiparametric approach to modeling nonlinear relations among latent variables. Struct. Equat. Model. 12, 513–535. doi: 10.1207/s15328007sem1204_1
Bauer, D. J., and Curran, P. J. (2004). The integration of continous and discrete latent variable models: potential problems and promising opportunities. Psychol. Methods 9, 3–29. doi: 10.1037/1082-989X.9.1.3
Bentler, P. M. (1983). Simultaneous equations systems as moment structure models. J. Econom., 22, 13–42. doi: 10.1016/0304-4076(83)90092-1
Bernardo, J., and Smith, A. F. M. (1994). Bayesian Theory. New York, NY: Wiley. doi: 10.1002/9780470316870
Bollen, K. A. (1995). Structural equation models that are nonlinear in latent variables: a least squares estimator. Soc. Method. 1995, 223–251. doi: 10.2307/271068
Brandt, H., Kelava, A., and Klein, A. G. (2014). A simulation study comparing recent approaches for the estimation of nonlinear effects in SEM under the condition of non-normality. Struct. Equ. Model. 21, 181–195. doi: 10.1080/10705511.2014.882660
Browne, M. W. (1974). Generalized least-squares estimatators in the analysis of covariance structures. S. Afr. Satist. J. 8, 1–24.
Browne, M. W. (1984). Asymptotic distribution free methods in the analysis of covariance structures. Br. J. Math. Stat. Psychol. 37, 62–83. doi: 10.1111/j.2044-8317.1984.tb00789.x
Celeux, G., Forbes, F., Robert, C. P., and Titterington, D. M. (2006). Deviance information criteria for missing data models. Bayesian Anal. 1, 651–674. doi: 10.1214/06-BA122
Cox, D. D., and Koh, E. (1989). A smoothing spline based test of model adequacy in polynomial regression. Ann. Inst. Stat. Math. 41, 383–400. doi: 10.1007/BF00049403
Cox, D. D., Koh, E., Wahba, G., and Yandell, B. (1988). Testing the (parametric) null model hypothesis in (semiparametric) partial and generalized spline models. Ann. Stat. 16, 113–119. doi: 10.1214/aos/1176350693
Curran, P. J., West, S. G., and Finch, J. F. (1996). The robustness of test statistics to nonnormality and specification error in confirmatory factor analysis. Psychol. Methods 1, 16–29. doi: 10.1037/1082-989X.1.1.16
Dempster, A. P., Laird, N. M., and Rubin, D. B. (1977). Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. B 39, 1–38.
Dolan, C. V., and van der Maas, H. L. J. (1998). Fitting multivariate normal finite mixtures subject to structural equation modeling. Psychometrika 63, 227–253. doi: 10.1007/BF02294853
Fox, J. P., and Glas, C. A. W. (2001). Bayesian estimation of a multilevel IRT model using Gibbs sampling. Psychometrika 66, 271–288. doi: 10.1007/BF02294839
Freund, R. W., and Hoppe, R. H. W. (2007). Stoer/Bulirsch: Numerische Mathematik 1 [Numerical Mathematics 1], Vol. 1. Heidelberg: Springer.
Gelman, A. (1996). “Inference and monitoring convergence,” in Markov Chain Monte Carlo in Practice, eds W. R. Gilks, S. Richardson, and D. J. Spiegelhalter (Boca Raton, FL: Chapman & Hall/CRC), 131–143. doi: 10.1007/978-1-4899-4485-6_8
Gelman, A., Carlin, J. B., Stern, H. S., and Rubin, D. B. (2004). Bayesian Data Analysis. Boca Raton, FL: Chapman & Hall/CRC.
Guo, R., Zhu, H., Chow, S.-M., and Ibrahim, J. G. (2012). Bayesian lasso for semiparametric structural equation models. Biometrics 68, 567–577. doi: 10.1111/j.1541-0420.2012.01751.x
Hastie, T., Tibshirani, R., and Friedman, J. (2009). The Elements of Statistical Learning, 2nd Edn. New York, NY: Springer.
Heck, R., and Thomas, S. (2000). An introduction to Multilevel Modeling Techniques. Mahwah, NJ: Lawrence Erlbaum Associates.
Jaccard, J., and Wan, C. (1995). Measurement error in the analysis of interaction effects between continuous predictors using multiple regression: multiple indicator indicator and structural equation approaches. Psychol. Bull. 117, 348–357. doi: 10.1037/0033-2909.117.2.348
Jedidi, K., Jagpal, H. S., and DeSarbo, W. S. (1997a). Finite-mixture structural equation models for response based segmentation and unobserved heterogeneity. Market. Sci. 16, 39–59. doi: 10.1287/mksc.16.1.39
Jedidi, K., Jagpal, H. S., and DeSarbo, W. S. (1997b). STEMM: a general finite mixture structural equation model. J. Class. 14, 23–50. doi: 10.1007/s003579900002
Joreskog, K., and Goldberger, A. (1972). Factor analysis by generalized least squares. Psychometrika 37, 243–260. doi: 10.1007/BF02306782
Jöreskog, K. G. (1973). “A general method for estimating a linear structural equation system,” in Structural Equation Models in the Social Sciences, eds A. S. Goldberger and O. D. Duncan (New York, NY: Seminar), 85–112.
Jöreskog, K. G., and Yang, F. (1996). “Nonlinear structural equation models: the Kenny-Judd model with interaction effects,” in Advanced Structural Equation Modeling: Issues and Techniques, eds G. A. Marcoulides and R. E. Schumacker, (Mahwah, NJ: Lawrence Erlbaum Associates), 57–87.
Kelava, A., and Brandt, H. (2009). Estimation of nonlinear latent structural equation models using the extended unconstrained approach. Rev. Psychol. 16, 123–131.
Kelava, A., Moosbrugger, H., Dimitruk, P., and Schermelleh-Engel, K. (2008). Multicollinearity and missing constraints: a comparison of three approaches for the analysis of latent nonlinear effects. Methodology 4, 51–66. doi: 10.1027/1614-2241.4.2.51
Kelava, A., and Nagengast, B. (2012). A bayesian model for the estimation of latent interaction and quadratic effects when latent variables are non-normally distributed. Multivar. Behav. Res. 47, 717–742. doi: 10.1080/00273171.2012.715560
Kelava, A., Nagengast, B., and Brandt, H. (2014). A nonlinear structural equation mixture modeling approach for nonnormally distributed latent predictor variables. Struct. Equ. Model. 21, 468–481. doi: 10.1080/10705511.2014.915379
Kelava, A., Werner, C., Schermelleh-Engel, K., Moosbrugger, H., Zapf, D., Ma, Y., et al. (2011). Advanced nonlinear structural equation modeling: theoretical properties and empirical application of the distribution-analytic LMS and QML estimators. Struct. Equat. Model. 18, 465–491. doi: 10.1080/10705511.2011.582408
Kenny, D., and Judd, C. M. (1984). Estimating the nonlinear and interactive effects of latent variables. Psychol. Bull. 96, 201–210. doi: 10.1037/0033-2909.96.1.201
Klein, A. G., and Moosbrugger, H. (2000). Maximum likelihood estimation of latent interaction effects with the LMS method. Psychometrika 65, 457–474. doi: 10.1007/BF02296338
Klein, A. G., and Muthén, B. O. (2007). Quasi maximum likelihood estimation of structural equation models with multiple interaction and quadratic effects. Multivar. Behav. Res. 42, 647–674. doi: 10.1080/00273170701710205
Klein, A. G., and Schermelleh-Engel, K. (2010). Introduction of a new measure for detecting poor fit due to omitted nonlinear terms in SEM. ASTA Adv. Stat. Anal. 94, 157–166. doi: 10.1007/s10182-010-0130-5
Lee, S.-Y. (2007). Structural Equation Modeling: A Bayesian Approach. New York, NY: Wiley. doi: 10.1002/9780470024737
Lee, S.-Y., Lu, B., and Song, X.-Y. (2008). Semiparametric bayesian analysis of structural equation models with fixed covariates. Stat. Med. 27, 2341–2360. doi: 10.1002/sim.3098
Lee, S.-Y., Song, X.-Y., and Poon, W. Y. (2004). Comparison of approaches in estimating interaction and quadratic effects of latent variables. Multivar. Behav. Res. 39, 37–67. doi: 10.1207/s15327906mbr3901_2
Lee, S.-Y., Song, X.-Y., and Tang, N. S. (2007). Bayesian methods for analyzing structural equation models with covariates, interaction, and quadratic latent variables. Struct. Equ. Model. 14, 404–434. doi: 10.1080/10705510701301511
Leite, W., and Zuo, Y. (2011). Modeling latent interactions at level 2 in multilevel structural equation models: an evaluation of mean-centered and residual-centered approaches. Struct. Equ. Model. 18, 449–464. doi: 10.1080/10705511.2011.582400
Little, T. D., Bovaird, J. A., and Widaman, K. F. (2006). On the merits of orthogonalizing powered and interaction terms: Implications for modeling interactions among latent variables. Struct. Equat. Model. 13, 497–519. doi: 10.1207/s15328007sem1304_1
Liu, A., and Wang, Y. (2004). Hypothesis testing in smoothing spline models. J. Stat. Comput. Simul. 74, 581–597. doi: 10.1080/00949650310001623416
Lubke, G. H., and Muthén, B. O. (2005). Investigating population heterogeneity with factor mixture models. Psychol. Methods 10, 21–39. doi: 10.1037/1082-989X.10.1.21
Lunn, D., Spiegelhalter, D., Thomas, A., and Best, N. (2009). The BUGS project: evolution, critique, and future directions. Stat. Med. 28, 3049–3067. doi: 10.1002/sim.3680
Marsh, H. W., Wen, Z., and Hau, K.-T. (2004). Structural equation models of latent interactions: evaluation of alternative estimation strategies and indicator construction. Psychol. Methods 9, 275–300. doi: 10.1037/1082-989X.9.3.275
Marsh, H. W., Wen, Z., and Hau, K.-T. (2006). “Structural equation models of latent interaction and quadratic effects,” in Structural equation modeling: A second course, eds G. R. Hancock and R. O. Mueller (Greenwich, CT: Information Age Publishing), 225–265.
McLachlan, G. J., and Peel, D. (2000). Finite Mixture Models. New York, NY: Wiley. doi: 10.1002/0471721182
Molenaar, P. (2004). A manifesto on psychology as idiographic science: bringing the person back into scientific psychology, this time forever. Meas. Interdiscip. Res. Perspect. 2, 201–218. doi: 10.1207/s15366359mea0204_1
Molenaar, P., and Campbell, C. (2009). The new person-specific paradigm in psychology. Curr. Direct. Psychol. Sci. 18, 112–117. doi: 10.1111/j.1467-8721.2009.01619.x
Mooijaart, A., and Bentler, P. M. (2010). An alternative approach for nonlinear latent variable models. Struct. Equ. Model. 17, 357–373. doi: 10.1080/10705511.2010.488997
Muthén, B. O. (1984). A general structural equation model with dichotomous, ordered categorical, and continuous latent variable indicators. Psychometrika 49, 115–132. doi: 10.1007/BF02294210
Muthén, B. O. (1994). Multilevel covariance structure analysis. Soc. Methods Res. 22, 376–399. doi: 10.1177/0049124194022003006
Muthén, B. O. (2001). “Second-generation structural equation modeling with a combination of categorical and continuous latent variables: New opportunities for latent class/latent growth modeling,” in New Methods for The Analysis of Change, eds A. Sayer and L. Collins (Washington, DC: American Psychological Association), 291–322.
Muthén, B. O., and Asparouhov, T. (2009). “Growth mixture modeling: analysis with non-Gaussian random effects,” in Longitudinal Data Analysis, eds G. Fitzmaurice, M. Davidian, G. Verbeke, and G. Molenberghs (Boca Raton, FL: Chapman & Hall/CRC), 143–165.
Muthén, B., and Asparouhov, T. (2011). “Beyond multilevel regression modeling: multilevel analysis in a general latent variable framework,” in Handbook of Advanced Multilevel Analysis, eds J. Hox and J. K. Roberts (New York, NY: Taylor and Francis), 15–40.
Muthén, L. K., and Muthén, B. O. (1998–2010). Mplus User's Guide. 6th Edn. Los Angeles, CA: Muthén & Muthén.
Nagengast, B., Trautwein, U., Kelava, A., and Lüdtke, O. (2013). Synergistic effects of expectancy and value on homework engagement: the case for a within-person perspective. Multivar. Behav. Res. 48, 428–460. doi: 10.1080/00273171.2013.775060
Organisation for Economic Co-Operation and Development (2010). PISA 2009 Results: What Students Know and Can Do – Student Performance in Reading, Mathematics and Science, Vol. 1. Paris: OECD.
Pek, J., Losardo, D., and Bauer, D. J. (2011). Confidence intervals for a semiparametric approach to modeling nonlinear relations among latent variables. Struct. Equ. Model. 18, 537–553. doi: 10.1080/10705511.2011.607072
Pek, J., Sterba, S. K., Kok, B. E., and Bauer, D. J. (2009). Estimating and visualizing nonlinear relations among latent variables: a semiparametric approach. Multivar. Behav. Res. 44, 407–436. doi: 10.1080/00273170903103290
Ping, R. A. (1995). A parsimonious estimating technique for interaction and quadratic latent variables. J. Market. Res. 32, 336–347. doi: 10.2307/3151985
Rabe-Hesketh, S., Skrondal, A., and Pickles, A. (2004). Generalized multilevel structural equation modeling. Psychometrika 69, 167–190. doi: 10.1007/BF02295939
Rabe-Hesketh, S., Skrondal, A., and Pickles, A. (2005). Maximum likelihood estimation of limited and discrete dependent variable models with nested random effects. J. Econom. 128, 301–323. doi: 10.1016/j.jeconom.2004.08.017
R Core Team (2013). R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing.
Redner, R. A., and Walker, H. F. (1984). Mixture densities, maximum likelihood and the EM algorithm. Soc. Ind. Appl. Math. Rev. 26, 195–239.
San Martín, E., Jara, A., Rolin, J. M., and Mouchart, M. (2011). On the Bayesian nonparametric generalization of IRT-type models. Psychometrika 76, 385–409. doi: 10.1007/s11336-011-9213-9
Schermelleh-Engel, K., Klein, A., and Moosbrugger, H. (1998). “Estimating nonlinear effects using a Latent Moderated Structural Equations Approach,” in Interaction and nonlinear effects in structural equation modeling, eds R. E. Schumacker and G. A. Marcoulides (Mahwah, NJ: Lawrence Erlbaum Associates), 203–238.
Schumacker, R., and Marcoulides, G. (1998). Interaction and Nonlinear Effects in Structural Equation Modeling. Mahwah, NJ: Lawrence Erlbaum Associates.
Snijders, T., and Bosker, R. (1999). Multilevel Analysis: An Introduction to Basic and Advanced Multilevel Modeling. London: Sage.
Song, X. Y., and Lee, S. Y. (2004). Bayesian analysis of two-level nonlinear structural equation models with continuous and polytomous data. Br. J. Math. Stat. Psychol. 57, 29–52. doi: 10.1348/000711004849259
Song, X.-Y., Li, Z.-H., Cai, J.-H., and Ip, E. H.-S. (2013). A Bayesian approach for generalized semiparametric structural equation models. Psychometrika 78, 624–647. doi: 10.1007/s11336-013-9323-7
Song, X.-Y., Xia, Y.-M., and Lee, S.-Y. (2009). Bayesian semiparametric analysis of structural equation models with mixed continuous and unordered categorical variables. Stat. Med. 28, 2253–2276. doi: 10.1002/sim.3612
Spiegelhalter, D. J., Best, N. G., Carlin, B. P., and van der Linde, A. (2002). Bayesian measures of model complexity and fit (with discussion). J. R. Stat. Soc. B 64, 583–616. doi: 10.1111/1467-9868.00353
Stephens, M. (2000). Dealing with label switching in mixture models. J. R. Stat. Soc. B 62, 795–809. doi: 10.1111/1467-9868.00265
van der Linden, W., and Hambleton, R. (eds.). (1997). Handbook of Modern Item Response Theory. New York, NY: Springer. doi: 10.1007/978-1-4757-2691-6
Wall, M. M., and Amemiya, Y. (2003). A method of moments technique for fitting interaction effects in structural equation models. Br. J. Math. Stat. Psychol. 56, 47–64. doi: 10.1348/000711003321645331
West, B. T., Welch, K. U., and Galecki, A. T. (2007). Linear Mixed Models: A Practical Guide Using Statistical Software. Boca Raton, FL: Chapman & Hall/CRC.
Yang, M., and Dunson, D. B. (2010). Bayesian semiparametric structural equation models with latent variables. Psychometrika 75, 675–693. doi: 10.1007/s11336-010-9174-4
Keywords: latent variables, semiparametric, non-linear, mixture distribution, structural equation modeling, multilevel
Citation: Kelava A and Brandt H (2014) A general non-linear multilevel structural equation mixture model. Front. Psychol. 5:748. doi: 10.3389/fpsyg.2014.00748
Received: 15 November 2013; Accepted: 26 June 2014;
Published online: 18 July 2014.
Edited by:
Tobias Koch, Freie Universität Berlin, GermanyCopyright © 2014 Kelava and Brandt. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Augustin Kelava, Department of Education, Center for Educational Science and Psychology, Eberhard Karls Universität Tübingen, Europastr. 6, 72072 Tübingen, Germany e-mail:YXVndXN0aW4ua2VsYXZhQHVuaS10dWViaW5nZW4uZGU=
 Augustin Kelava
Augustin Kelava Holger Brandt
Holger Brandt