- 1Learning Disabilities Studies and Haddad Center for Dyslexia and Learning Disabilities, School of Education, Bar-Ilan University, Ramat-Gan, Israel
- 2Learning Disabilities Studies, School of Education, Bar-Ilan University, Ramat-Gan, Israel
Complexity has been shown to affect performance on artificial grammar learning (AGL) tasks (categorization of test items as grammatical/ungrammatical according to the implicitly trained grammar rules). However, previously published AGL experiments did not utilize consistent measures to investigate the comprehensive effect of grammar complexity on task performance. The present study focused on computerizing Bollt and Jones's (2000) technique of calculating topological entropy (TE), a quantitative measure of AGL charts' complexity, with the aim of examining associations between grammar systems' TE and learners' AGL task performance. We surveyed the literature and identified 56 previous AGL experiments based on 10 different grammars that met the sampling criteria. Using the automated matrix-lift-action method, we assigned a TE value for each of these 10 previously used AGL systems and examined its correlation with learners' task performance. The meta-regression analysis showed a significant correlation, demonstrating that the complexity effect transcended the different settings and conditions in which the categorization task was performed. The results reinforced the importance of using this new automated tool to uniformly measure grammar systems' complexity when experimenting with and evaluating the findings of AGL studies.
Introduction
Artificial grammar learning (AGL) refers to an experimental approach that explores pattern recognition in a set of structured sequences, typically comprising strings of alphabetical letters. Such experiments include a training phase and a testing phase (Reber, 1967, 1969). Studies on AGL have demonstrated that participants are able to acquire the abstract representation or rule underlying an artificial grammar system.
Researchers have utilized AGL tasks to explore the distinction between explicit and implicit learning, to identify the representations acquired through learning, and as a model for the process of language acquisition. AGL studies can be carried out either explicitly, where the participant is informed during the training phase that the stimuli were constructed according to a set of rules, or implicitly, where the participant is unaware of the fact that certain rules underlie the stimuli (Reber, 1967; Lorsbach and Worman, 1989; Gebauer and Mackintosh, 2007). Various theories have been debated to explain what characterizes the learning process and what is acquired during AGL training sessions, including the probabilistic learning approach (Reber, 1967), the exemplar-based learning approach (Brooks and Vokey, 1991), and a third approach suggesting that learners' acquisition of abstract rules during the training phase enables them to judge the sequences at the testing phase (Redington and Chater, 1996; Pothos, 2010). The AGL paradigm has also been proposed as a model for language or syntax acquisition, but questions remain as to how broadly it applies to the tasks faced by language learners (Marcus et al., 1995; Pena et al., 2002; Endress and Bonatti, 2007; Aslin and Newport, 2008).
AGL experiments typically involve letter strings that are generated based on a grammar system and then are shown to the learner during a training session. In studies of implicit learning, learners are asked to memorize stimulus strings during this training phase (Dienes et al., 1991; Pavlidou et al., 2009), whereas in explicit AGL tasks, learners are informed during training that the stimuli were constructed according to a complex set of rules, and they are asked to look for those rules (Kirkhart, 2001; Gebauer and Mackintosh, 2007). In the testing phase, two types of strings, grammatical and ungrammatical, are shown to learners. Learners are asked to decide whether or not the strings are grammatical, namely, whether they were constructed using the same set of rules used to construct the strings shown in the training session (Reber, 1967). Participants consistently score above chance on such AGL tasks, even when they are unable to specifically extract the underlying rule and regardless of whether learners were initially informed explicitly about strings' rule-based construction (Dulany et al., 1984; Dienes et al., 1991). This consistent finding in the literature indicates that individuals are able to acquire some awareness of the rule even without explicit exposure to the rule's existence (Servan-Schreiber and Anderson, 1990; Gebauer and Mackintosh, 2007).
The standard AGL experiment is based on a grammar system, with sequences of symbols presented as letter strings such as TTS or VXVPS (Reber, 1967). For example, when using Reber's (1967) grammar chart (see Grammar C in Figure 1), all sequences must begin at the IN arrow and end at the OUT arrow. The path from the IN arrow can be either from State 0 (S0) to State 1 (S1) or from S0 to State 3 (S3). Therefore, the first symbol can only be a T or a V. Moving on, if a sequence begins with a V, then the only possible transitions are from S3 to itself (see curved arrow in the figure), thereby adding an X, or else from S3 to S4, thereby adding a V. If a second V is added after the X by moving to S4, then we can next move in one of two directions: from S4 to S2, adding a P, or from S4 to S5, adding an S and ending the sequence. In contrast, from S4 the move back to S3 is illegal (ungrammatical); therefore, adding a consecutive V is not an option. Thus, using this chart, a sequence such as VXVS is grammatical, but creating a sequence such as VXVV is ungrammatical (Pothos and Kirk, 2004).
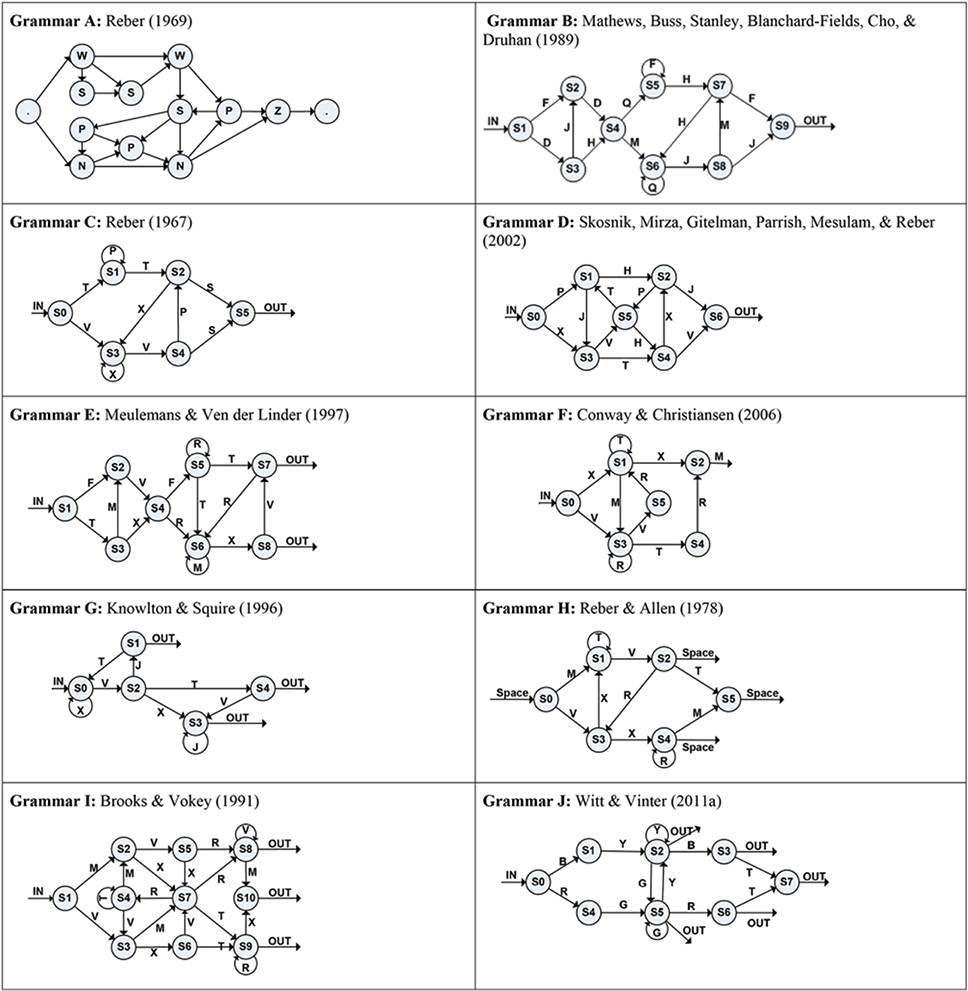
Figure 1. Charts of the 10 artificial grammars appearing in Table 1.
Previous AGL studies have come under heavy criticism for the effect of grammar system complexity on learners' performance (Reber, 1967; Perruchet et al., 1998; Van den Bos and Poletiek, 2008), claiming that when the grammar system includes more rules (arrows), uncertainty increases, and the grammar is harder to acquire, and vice versa (Ziegler and Goswami, 2005). However, complexity has not always been systematically defined by AGL researchers, who have employed different ways to measure the complexity of AGL stimuli's structure.
Johnstone and Shanks (2001) suggested one method for measuring complexity of a testing item, by calculating its “transition rule strength” (TRS), which refers to the number of rules constituting the grammar system. These rules are defined as (a) the number of letters that can be added to a string at each node of the grammar chart and (b) the number of letters that can terminate a string. For example, using Brooks and Vokey's (1991) chart (see Grammar I in Figure 1), Johnstone and Shanks calculated a total of 17 transitions (arrows), including 3 nodes where the same letter could be used more than once (S2, S3, S4) and 3 nodes where the string could end (S8, S9, S10). Johnstone and Shanks (1999) asserted that more repetitions of a specific transition from one node to another (e.g., the transition from S7 to S8, adding the letter R, in Grammar I) during the entire training phase would lower that particular rule's complexity. To calculate this complexity measure for a particular item on a testing task (where participants were asked to indicate if a given string was grammatical), these researchers summed the number of times each transition in the testing string had appeared across all of the trained strings, and then they divided that sum by the number of letters forming that specific testing string. For example, using Brooks and Vokey's grammar (see Grammar I in Figure 1), the testing string VXVRM contained the following six transitions: V was selected at the transition from S1 to S3, X at the transition from S3 to S6, V at the transition from S6 to S7, R at the transition from S7 to S8, M at the transition from S8 to S10, and the ending transition was at S10. In Johnstone and Shanks' (1999) training phase, these six transitions had appeared 64, 33, 17, 45, 19, and 39 times respectively, across 125 training strings. The calculation of complexity for VXVRM was therefore (64 + 33 + 17 + 45 + 19 + 39) divided by 5 letters, totaling 43.4. They concluded that increasing the number of transitions increased the string's complexity (Johnstone and Shanks, 1999, 2001).
A second way to measure the complexity of a test item was proposed by Perruchet et al. (1998), who noted that learning, may be influenced by the number of “segments” to be acquired. In other words, when presented with information that contains multiple elements, segmentation into smaller units leaves larger but fewer units or “chunks” to remember (e.g., 2-letter bigram chunks or 3-letter trigram chunks). Moreover, a bigram that repeats itself in the stimuli creates a simpler structure than one composed of many unique bigrams (Van den Bos and Poletiek, 2008). For each test item (string), a “global chunk strength” value can be calculated, comprising the average frequency at which all of its bigrams and trigrams appeared during the training phase (Knowlton and Squire, 1994, 1996). For example, in computing the chunk strength of testing string MSXVVR, one must calculate how frequently each of the following chunks appeared in training—MS, SX, XV, VV, VR, MSX, SXV, XVV, and VVR—and calculate their average (Pothos, 2010).
A third means of measuring the complexity of AGL stimuli, the “exemplar” view, derives from information theory. Jamieson and Mewhort (2005) proposed that intact stimuli are stored in memory, and that classification or recognition is determined by the degree of similarity between a stimulus and the stored exemplars. They explored the effect of redundancy on implicit learning, Jamieson and Mewhort quantified the structure in individual stimuli (local redundancy) as well as the structure in the grammatical rules from which the exemplars were derived (grammatical redundancy). The two kinds of redundancy were found to be correlated, where local redundancy increased with grammatical redundancy. However, when separated experimentally, performance was predicted by local redundancy but not by grammatical redundancy.
We assert that these varying measures of complexity adopted by prior researchers may preclude reliable comparison and interpretation of the mixed findings yielded by previous AGL research. In the current article, we propose Bollt and Jones's (2000) topological entropy (TE) measure of complexity as the tool of choice to enable quantitative standardization of the different grammatical charts on which all AGL system stimuli are based. Each AGL chart consists of nodes (states) and arrows showing the transitions' directional flow. Bollt and Jones (2000) developed the concept of TE by showing that each chart can be represented by a transition matrix (also known as Markov matrix), which is a mathematical way of representing all possible transitions in a given chart. Raising the number of transitions (arrows) increases TE, thus increasing uncertainty, and vice versa. The TE measure is also sensitive to the size of the matrix that represents a given chart and to the presence of short- and long-distance dependencies, and it is also correlated with the number of elements required to determine the current state in the chart. The formal calculation of TE as presented in definition eight in Bollt and Jones (2000) is described below:
In this formula, h(∑M), which is the TE of ∑M, is defined to be the limit of the logarithm of the number of words of length n, divided by n, as n goes to infinity. More specifically, M is a transition matrix of a Markov representation (defined by the AGL chart), and ∑M is the set of all possible sequences defined by M. Also, wn(∑M) is the number of sub-sequences of length n that are contained in ∑M, and n is the length of a single sequence. Note that although the length of a single sequence is one of the parameters in the formula, the TE formula has no dependency on length. The formula is not meant to calculate the results for a specific sequence, but rather to give a global index that measures the complexity of the chart. Bollt and Jones (2000) also presented a useful technique for calculating the TE of a given transition matrix of a Markov representation. Theorem 6 in Bollt and Jones (2000) states that if ρ(M) is the largest non-negative eigenvalue of the matrix M, then h(∑M) = ln ρ(M).
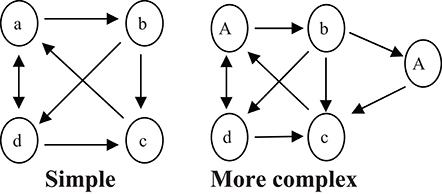
Computing TE directly from the formula can be very difficult. Bollt and Jones (2000) explained that in complex cases when an element appears more than once, a simple matrix cannot represent the chart. Figure 2 presents examples of a simple and a complex chart. When constructing the complex chart, knowing which letter in the sequence precedes A is the key to identifying at which A we are positioned. Bollt and Jones (2000) defined this as a system with memory (of the previous element or elements). However, a Markov matrix representation is restricted because the system it represents must be memoryless; that is, the transition to the next element must depend only on the current element without needing any reference to prior or ensuing transitions. For that reason, Bollt and Jones (2000) developed the concept of “lift action,” defined as a change in the dimension of the matrix required to build a memoryless system. Bollt and Jones presented a calculation of the lift action for the complex chart in Figure 2. They used the letter m to define the basic number of elements (excluding repeated elements), which in the case of Figure 2's complex chart would be m = 4 (a, b, c, and d). They used the letter k to define the minimum number of elements required in order to know one's present position in the chart. In the complex chart (Figure 2), k would equal 2, indicating that at least two transitions are required to know at which A in the chart we are positioned. In order to make a lift, Bollt and Jones defined mk new elements based on the original elements. The new elements will be all the possible sequences in length k of the m original elements. In the present example, the minimum number of transitions required to identify at which A we are located is two (i.e., the number of basic elements that every new element will contain after the lift action is k = 2). The number of new elements will be mk, namely 16: aa = 1, ab = 2, ac = 3, ad = 4, ba = 5… The matrix will now be at size mk × mk (16 = 42 in the current example, i.e., the matrix will have 16 × 16 options), which will include all possible transitions according to the chart's arrows, where each transition is represented by two elements.
In general, when elements in the chart are repeated more often, a larger sequence of elements needs to be remembered in order to determine one's current state in the chart, thereby increasing memory load. Hence, these types of charts cannot be represented in a simple way. Bollt and Jones (2000) demonstrated that a chart's TE is easily extracted as the natural logarithm of the largest positive real eigenvalue of the matrix; however, in a large matrix the eigenvalue must be calculated by a computer. Thus, Bollt and Jones's method for calculating TE is much more practical than computing TE directly from the formula, as explained in Appendix A in Supplementary Material.
In the current article, we expanded on Bollt and Jones's (2000) matrix-lift-action method by suggesting a novel technique for automating the full process of determining a specific grammar's complexity level. As explained in detail in Appendix B in Supplementary Material, we extended the code used in Bailey and Pothos's (2008) StimSelect software to uniformly calculate grammatical complexity for various AGL charts used in many prior research studies, thus enabling meta-analysis of learner performance in previous investigations of artificial grammar tasks based on different grammars. Once the level of complexity of each prior grammar chart was assessed, the following question was addressed: Did ____er TE values correlate with greater learner success (identifying grammatical/ungrammatical strings above chance level—over 50%) in AGL studies? We also examined the effect of age in AGL task performance, to determine if age differences between children and adults would transcend the effects of grammatical complexity.
Materials and Methods
Meta-Analysis Literature Survey
To systematically locate the maximum possible number of charts representing AGL systems that appeared in previously published experimental research, we conducted a comprehensive review of the AGL empirical literature. We used different databases to find the articles: Google, Google Scholar, ProQuest, PubMed, and APA PsycNET. The keywords selected for the literature review were: artificial grammar learning, topological entropy, and explicit and implicit learning. We looked only for studies written in English or translated into English. We searched for articles written after 1967 (following Reber's first article from that year). We included mostly journal articles but also a few book chapters. Inclusion criteria for the literature we identified were as follows:
1. Articles that did not include an experiment, such as review articles, were excluded. Review articles usually present other researchers' studies or do not present experiments at all (e.g., Reber, 1989; Cleeremans et al., 1998).
2. We excluded studies that did not include and describe a visual chart of the finite state grammar used (e.g., Saffran et al., 1996, 1997). Thus, auditory-based AGL studies (e.g., Andrade and Baddeley, 2011; Rohrmeier et al., 2011) were not included because many did not include a chart, and their findings were inconclusive as to associations between the visual and auditory paradigms.
3. Studies that developed stimuli from a combination of two or more different finite state grammars were also excluded, as we were unable to determine to which of the charts the results could be attributed (e.g., Knowlton and Squire, 1994; Reber and Squire, 1999; Van den Bos and Poletiek, 2008).
4. In articles including more than one experiment, one of which was the classic version of the AGL task and the other a manipulation of the stimuli, only the classic version was included. For example, we excluded Jamieson and Mewhort's (2010) manipulated version, which included blanks between the letters which the participants were requested to fill. In Evans et al. (2009), we excluded the second version of the experiment that required participants to choose an ice cream flavor according to the sequences they learned in the training phase. We only used the version that implemented the classic AGL task to avoid confounding variables related to changes in procedures.
5. In articles examining special populations, for example persons with dyslexia (Rüsseler et al., 2006), Williams' Syndrome (Don et al., 2003), or other atypically developing individuals, we included only the results of the control group because the present study explored typical populations only.
6. In multisession AGL articles (e.g., Reber, 1967; de Vries et al., 2010), only the results of the first session were included to avoid confounding variables related to multisession procedures.
7. With respect to articles that utilized both explicit and implicit instructions (Gebauer and Mackintosh, 2007; Scott and Dienes, 2008), only the results of the implicit stimuli were used to avoid inconsistencies between the results of these two methods. Furthermore, as relatively fewer studies involved explicit learning, comparison was impossible.
8. For a few AGL charts (e.g., Gebauer and Mackintosh, 2007), calculating the TE according to Bollt and Jones's (2000) matrix-lift-action technique was beyond our ability, because we could not find a memoryless system for these charts, even after doing a lift with k = 10. We do not know the implications of excluding these extremely complex charts from our meta-analysis. Inasmuch as we could not evaluate them according to the currently proposed theory, we could not draw conclusions about how such complexity levels may influence participants' task performance.
9. Articles with different kinds of visual stimuli (e.g., letters, shapes, colors) were included in the analysis because Pothos et al. (2006) showed that the type of visual stimuli presented to participants demonstrated no significant effects on performance.
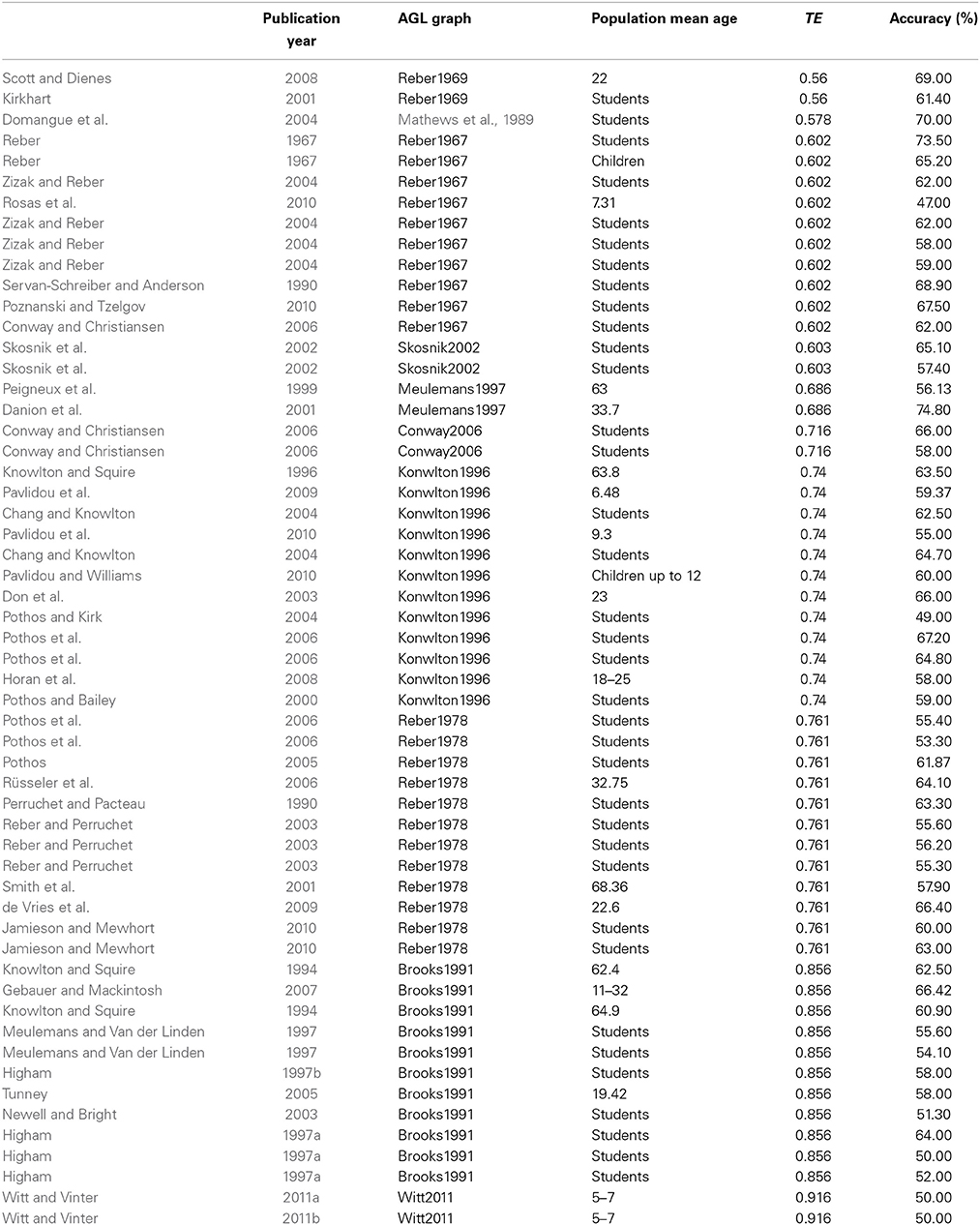
Based on these inclusion criteria, we located 56 experiments deriving from 38 publications as presented in Table 1, referring to 10 different grammatical charts (see Figure 1).
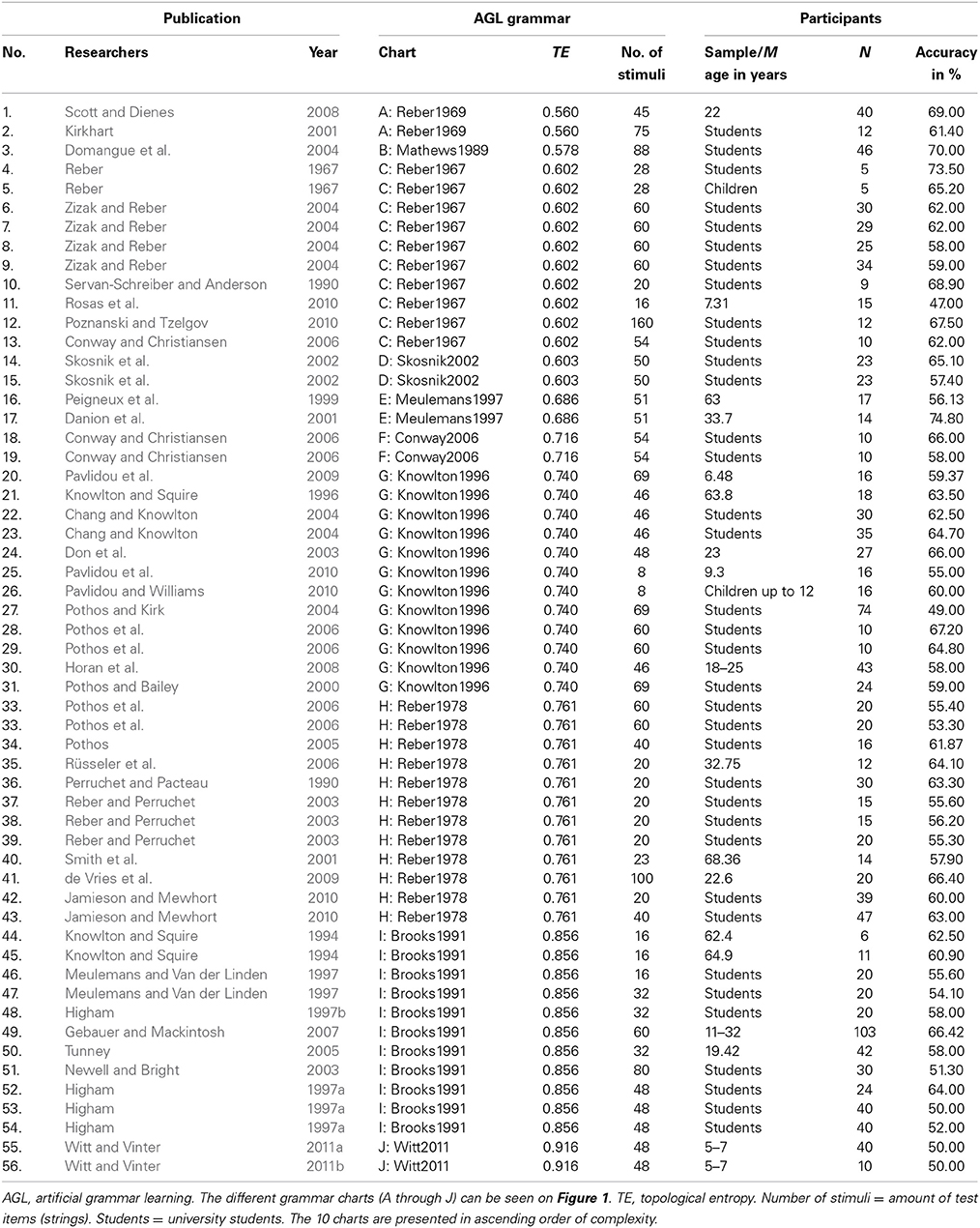
Table 1. Experimental AGL studies by grammar's chart, TE value, and No. of stimuli and participants' number, age, and task performance accuracy.
Procedure
As described in detail in Appendix B in Supplementary Material, we selected and developed software to fully automate TE calculation from a given AGL chart. We selected Bailey and Pothos's (2008) StimSelect software package to provide a fast, easy way for presenting AGL charts in a computerized manner and to provide commands for extracting grammatical sequences out of charts. Bollt and Jones (2000) claimed that if there is a transition matrix representing an AGL chart, then the chart's TE will be the natural logarithm of that matrix's largest non-negative eigenvalue. As detailed in Appendix B in Supplementary Material, we next wrote code extension to recover the Markov transition matrix representing the chart with the correct lift size; thus, after easily finding the eigenvalue we calculated the TE value. Appendix C in Supplementary Material presents an illustration of calculating TE for Reber's (1967) grammatical chart, according to Bollt and Jones's (2000) matrix-lift-action method using Bailey and Pothos's (2008) StimSelect software and our code extension.
Data Analysis
To examine the hypothesis that learners' accuracy of test performance in each experiment would be associated with the complexity level of that study's AGL chart, we first calculated the TE for each of the 10 grammar charts and then we arranged all the publications into Table 1 by grouping them according to chart. To compare learners' performance to each chart's TE values, we performed two Pearson correlations. One correlation was at the chart level: For each of the 10 AGL charts, we computed the correlation between TE and the mean accuracy level obtained by participants for all experiments based on that particular chart. The other correlation was at the study level, using accuracy data from the separate studies. In addition, we conducted a meta regression analysis of effect sizes, to examine whether sample size and percentage of success would predict the chart's complexity level and the participants' mean performance accuracy. In this regression, the weight of each study equaled the inverse of the variance (i.e., high variance received low weight, and vice versa). Finally, to examine age effects, we conducted analysis of variance (ANOVA) with age as an independent variable and then conducted the same analysis with TE entered as a covariate to determine whether age effects would be evident beyond the effects of grammatical complexity.
Results
The findings of the present meta-analysis demonstrate, for the first time, that the complexity effect remains across the different settings and conditions in which the categorization task takes place. The descriptive statistics in Table 1 reveal that the TE value has a short range from 0.56 (low complexity) to 0.916 (high complexity), with learners' performance accuracy ranging from 47 to 75%. Yet, there is a highly significant negative Pearson correlation between the TE values and performance on AGL tasks. Specific examples of experiments' outcomes seem to suggest that the complexity of the AGL system as measured by TE may be related to participants' performance on the categorization task (into grammatical vs. ungrammatical categories) at the testing phase, indicating that learners may have been affected by the grammar system's difficulty. For example, in the experiments described in Witt and Vinter (2011a) and Newell and Bright (2003), the TE values were very high (0.916 for Grammar J and 0.856 for Grammar I, respectively, as seen on Table 1), indicating exceedingly complex grammars, and participants' task performance was only at or slightly above chance level (50 and 53.1% accuracy, respectively). In contrast, in studies with low TE values, the high percentage of participants' correct responses may be explained by the grammar's simplicity. To illustrate, the TEs of the grammar systems were only 0.56 in Scott and Dienes (2008; Grammar A) and 0.578 in Domangue et al. (2004; Grammar B), and participants in these studies achieved impressively high percentages of accurate responses: 69 and 70%, respectively.
In addition, highly significant negative Pearson correlations emerged between TE values and performance on AGL tasks, both at the chart level using the averaged accuracies for all experiments using a particular chart (r = −0.40, N = 56, p = 0.002), and at the study level, using accuracy data from the separate studies (r = −0.85, N = 10, p = 0.002). However, the outcomes of the meta regression analysis yielded a much lower, albeit significant, correlation between the grammatical complexity level and participants' mean performance accuracy in past studies: The Pearson correlation for accuracy vs. TE on corrected data was R = −0.316, N = 56, p = 0.013. In addition, the meta regression performed for performance accuracy included two independent variables: TE values, and number of stimuli (the amount of test items or strings). The general model was significant, R = 0.327, N = 56, p = 0.0001, and a significant negative effect of TE emerged on accuracy, p = 0.0001, whereas no significant effect emerged for number of stimuli on accuracy, p > 0.05.
With regard to the issue of age, we first grouped the surveyed studies according to child vs. adult participants in the different experiments, and we examined the TE values and performance levels (Table 2). Descriptive findings for children may add data about this pattern of relations between task performance and grammar complexity. To illustrate, Witt and Vinter (2011a,b) found that 5- to 7-year-olds were not successful AGL learners inasmuch as their performance rates were at guessing level (50% and less); however, these children were using the chart with the highest complexity that we measured (Grammar J: TE = 0.916). Conversely, Reber (1967) reported a higher percentage of correct responses in children (65.2%) when using one of the least complex charts that we measured (Grammar C: TE = 0.602). These discrepancies indicate that part of the reason why children score lower than adults on AGL tasks may be linked to the complexity level of the tested AGL system. We next conducted an ANOVA for performance accuracy, with age (children vs. adults) as the independent variable, and a significant age effect emerged, F(1, 36) = 4.01, p = 0.05. However, when the grammatical chart's TE value study was entered as a covariate in an ANCOVA, the age effect was no longer significant, F(1, 35) = 2.5, p = 0.12, indicating that the complexity of the AGL charts used in experimental studies might be a confounding variable with participants' age. Thus, although it was reasonable to assume that children's lower accuracy in AGL tasks compared to adults should be attributed to their younger age, the ANCOVA suggests that charts' complexity is a better predictor of accuracy than age.
Discussion
The present study has enhanced the usefulness and practicality of TE, the AGL complexity measure introduced by Bollt and Jones (2000), by automating the process of obtaining TE values from memoryless charts. This new matrix-lift-action method enables uniform comparisons among different experimental research publications that previously utilized varying charts for AGL testing. By reviewing previously published AGL experiments, this study redefines the significance of TE as a measure of grammar complexity and provides researchers with an efficient means for calculating the complexity of a given AGL system. Furthermore, the current meta-analysis documenting diverse charts' range of TE values pinpoints complexity level as an important measurement to be taken into account by future researchers when designing and selecting their experimental AGL stimuli.
The current findings validate and extend the existing literature investigating learners' performance on tasks of varying complexity. Evidence is available demonstrating that higher TE values coincide with poorer ability to categorize test items as grammatical or ungrammatical, and vice versa (e.g., Van den Bos and Poletiek, 2008); however, such research tested the same group of participants on AGL systems of different levels of difficulty. The current study adopted a broader approach by systematically surveying the literature to locate previous AGL experiments that were carried out under different conditions, and by using meta-regression analysis to establish that the TE measure significantly correlates with performance across AGL tasks. Future researchers use the matrix-lift-action method to compare implicit vs. explicit learning conditions as well as different complexity levels in studies with children. Other complexity measures (such as the redundancy method, TRS, and the bigram/ trigram method) which refer to the other components of the AGL task might also play a role. It is recommended that future studies examine the correlation of these metrics with respect to the performance data, comparing TE with them.
Concluding Remarks
Complexity has been previously shown to affect performance on artificial grammar learning (AGL) tasks. Yet, past AGL studies did not employ consistent measures to examine the comprehensive effect of grammar complexity on task performance. In the present study we computerized Bollt and Jones's (2000) technique of calculating topological entropy (TE), a quantitative measure of AGL charts' complexity, with the aim of examining associations between grammar systems' TE and learners' AGL task performance. The results of the meta-regression analysis indicate that the complexity effect transcended the different settings and conditions in which the categorization task was performed. The results reinforced the significance of utilizing this new automated tool to uniformly measure grammar systems' complexity when experimenting with and evaluating the findings of AGL studies.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgment
This study was part of Pesia Katan's doctoral research conducted at Bar Ilan University.
Supplementary Material
The Supplementary Material for this article can be found online at: http://www.frontiersin.org/journal/10.3389/fpsyg.2014.01084/abstract
References
Andrade, J., and Baddeley, A. (2011). The contribution of phonological short-term memory to artificial grammar learning. Q. J. Exp. Psychol. 64, 960–974. doi: 10.1080/17470218.2010.533440
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Aslin, R. N., and Newport, E. L. (2008). “What statistical learning can and can't tell us about language acquisition,” in Infant Pathways to Language: Methods, Models, and Research Directions, eds J. Colombo, P. McCardle, and L. Freund (Mahwah, NJ: Erlbaum), 15–29.
Bailey, T. M., and Pothos, E. M. (2008). AGL StimSelect: Software for automated selection of stimuli for artificial grammar learning. Behav. Res. Methods 40, 164–176. doi: 10.3758/BRM.40.1.164
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Bollt, E. M., and Jones, M. A. (2000). The complexity of artificial grammars. Nonlin. Dyn. Psychol. Life Sci. 4, 153–168. doi: 10.1023/A:1009524428448
Brooks, L. R., and Vokey, J. R. (1991). Abstract analogies and abstracted grammars: Comments on Reber (1989). J. Exp. Psychol. 120, 316–323. doi: 10.1037/0096-3445.120.3.316
Chang, G. Y., and Knowlton, B. J. (2004). Visual feature learning in artificial grammar classification. J. Exp. Psychol. 30, 714–722. doi: 10.1037/0278-7393.30.3.714
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Cleeremans, A., Destrebecqz, A., and Boyer, M. (1998). Implicit learning: news from the front. Trends Cogn. Sci. 2, 406–416. doi: 10.1016/S1364-6613(98)01232-7
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Conway, C. M., and Christiansen, M. H. (2006). Statistical learning within and between modalities pitting abstract against stimulus-specific representations. Psychol. Sci. 17, 905–912. doi: 10.1111/j.1467-9280.2006.01801.x
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Danion, J. M., Meulemans, T., Kauffmann-Muller, F., and Vermaat, H. (2001). Intact implicit learning in schizophrenia. Am. J. Psychiatry 158, 944–948. doi: 10.1176/appi.ajp.158.6.944
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
de Vries, M. H., Barth, A. C. R., Maiworm, S., Knecht, S., Zwitserlood, P., and Flöel, A. (2009). Electrical stimulation of Broca's area enhances implicit learning of an artificial grammar. J. Cogn. Neurosci. 22, 2427–2436. doi: 10.1162/jocn.2009.21385
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
de Vries, M. H., Ulte, C., Zwitserlood, P., Szymanski, B., and Knecht, S. (2010). Increasing dopamine levels in the brain improves feedback-based procedural learning in healthy participants: an artificial-grammar-learning experiment. Neuropsychologia 48, 3193–3197. doi: 10.1016/j.neuropsychologia.2010.06.024
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Dienes, Z., Broadbent, D., and Berry, D. (1991). Implicit and explicit knowledge bases in artificial grammar learning. J. Exp. Psychol. 17, 875–887. doi: 10.1037/0278-7393.17.5.875
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Domangue, T. J., Mathews, R. C., Sun, R., Roussel, L. G., and Guidry, C. E. (2004). Effects of model-based and memory-based processing on speed and accuracy of grammar string generation. J. Exp. Psychol. 30, 1002–1011. doi: 10.1037/0278-7393.30.5.1002
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Don, A. J., Schellenberg, E. G., Reber, A. S., DiGirolamo, M. K., and Wang, P. P. (2003). Implicit learning in children and adults with Williams Syndrome. Dev. Neuropsychol. 23, 201–225. doi: 10.1080/87565641.2003.9651892
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Dulany, D. E., Carlson, R. A., and Dewey, G. I. (1984). A case of syntactical learning and judgment: how conscious and how abstract? J. Exp. Psychol. 113, 541–555. doi: 10.1037/0096-3445.113.4.541
Endress, A. D., and Bonatti, L. L. (2007). Rapid learning of syllable classes from a perceptually continuous speech stream. Cognition 105, 247–299. doi: 10.1016/j.cognition.2006.09.010
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Evans, J. L., Saffran, J. R., and Robe-Torres, K. (2009). Statistical learning in children with specific language impairment. J. Speech Lang. Hear. Res. 52, 321–335. doi: 10.1044/1092-4388(2009/07-0189)
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Gebauer, G. F., and Mackintosh, N. J. (2007). Psychometric intelligence dissociates implicit and explicit learning. J. Exp. Psychol. 33, 34–54. doi: 10.1037/0278-7393.33.1.34
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Higham, P. A. (1997a). Chunks are not enough: the insufficiency of feature frequency-based explanations of artificial grammar learning. Can. J. Exp. Psychol. 51, 126–137. doi: 10.1037/1196-1961.51.2.126
Higham, P. A. (1997b). Dissociations of grammaticality and specific similarity effects in artificial grammar learning. J. Exp. Psychol. 23, 1029–1045. doi: 10.1037/0278-7393.23.4.1029
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Horan, W. P., Green, F. M., Knowlton, B. J., Wynn, J. K., Mintz, J., and Nuechterlein, K. H. (2008). Impaired implicit learning in Schizophrenia. Neuropsychology 22, 606–617. doi: 10.1037/a0012602
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Jamieson, R. K., and Mewhort, D. J. K. (2005). The influence of grammatical, local, and organizational redundancy on implicit learning: an analysis using information theory. J. Exp. Psychol. 31, 9–23. doi: 10.1037/0278-7393.31.1.9
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Jamieson, R. K., and Mewhort, D. J. K. (2010). Applying an exemplar model to the artificial-grammar task: string completion and performance on individual items. Q. J. Exp. Psychol. 63, 1014–1039. doi: 10.1080/17470210903267417
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Johnstone, T., and Shanks, D. R. (1999). Two mechanisms in implicit artificial grammar learning? Comment on Meulemans and Van der Linden (1997). J. Exp. Psychol. 25, 524–531. doi: 10.1037/0278-7393.25.2.524
Johnstone, T., and Shanks, D. R. (2001). Abstractionist and processing accounts of implicit learning. Cogn. Psychol. 42, 61–112. doi: 10.1006/cogp.2000.0743
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Kirkhart, M. W. (2001). The nature of declarative and nondeclarative knowledge for implicit and explicit learning. J. Gen. Psychol. 128, 447–461. doi: 10.1080/00221300109598921
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Knowlton, B. J., and Squire, L. R. (1994). The information acquired during artificial grammar learning. J. Exp. Psychol. 20, 79–91. doi: 10.1037/0278-7393.20.1.79
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Knowlton, B. J., and Squire, L. R. (1996). Artificial grammar learning depends on implicit acquisition of both abstract and exemplar-specific information. J. Exp. Psychol. Learn. Mem. Cogn. 22, 169–181. doi: 10.1037/0278-7393.22.1.169
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Lorsbach, T., and Worman, L. J. (1989). The development of explicit and implicit forms of memory in learning disabled children. Contemp. Educ. Psychol. 14, 67–76. doi: 10.1016/0361-476X(89)90006-4
Marcus, G. F., Brinkmann, U., Clahsen, H., Wiese, R., and Pinker, S. (1995). German inflection: the exception that proves the rule. Cogn. Psychol. 29, 189–256 doi: 10.1006/cogp.1995.1015
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Mathews, R. C., Buss, R. R., Stanley, W. B., Blanchard-Fields, F., Cho, J. R., and Druhan, B. (1989). Role of implicit and explicit processes in learning from examples: a synergistic effect. J. Exp. Psychol. 15, 1083–1110. doi: 10.1037/0278-7393.15.6.1083
Meulemans, T., and Van der Linden, M. (1997). Associative chunk strength in artificial grammar learning. J. Exp. Psychol. 23, 1007–1028. doi: 10.1037/0278-7393.23.4.1007
Newell, B. R., and Bright, J. E. H. (2003). The subliminal mere exposure effect does not generalize to structurally related stimuli. Can. J. Exp. Psychol. 57, 61–68. doi: 10.1037/h0087413
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Pavlidou, E. V., Kelly, L. M., and Williams, J. M. (2010). Do children with developmental dyslexia have impairments in implicit learning? Dyslexia 16, 143–161. doi: 10.1002/dys.400
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Pavlidou, E. V., and Williams, J. M. (2010). Developmental dyslexia and implicit learning: evidence from an AGL transfer study. Procedia Soc. Behav. Sci. 2, 3289–3296. doi: 10.1016/j.sbspro.2010.03.503
Pavlidou, E. V., Williams, J. M., and Kelly, L. M. (2009). Artificial grammar learning in primary school children with and without developmental dyslexia. Ann. Dyslexia 59, 55–77. doi: 10.1007/s11881-009-0023-z
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Peigneux, P., Meulemans, T., Ven der Linden, M., Salmon, E., and Petit, H. (1999). Exploration of implicit artificial grammar learning in Parkinson's disease. Acta Neurol. Belg. 99, 107–117.
Pena, M., Bonatti, L. L., Nespor, M., and Mehler, J. (2002). Signal-driven computations in speech processing. Science 298, 604–607. doi: 10.1126/science.1072901
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Perruchet, P., and Pacteau, C. (1990). Synthetic grammar learning: Implicit rule abstraction or explicit fragmentary knowledge? J. Exp. Psychol. 119, 264–275. doi: 10.1037/0096-3445.119.3.264
Perruchet, P., Vinter, A. S., and Michael, A. (1998). “Learning and development: the implicit knowledge assumption reconsidered,” in Handbook of implicit learning, ed P. A. Frensch (Thousand Oaks, CA: Sage), 495–531.
Pothos, E. M. (2005). Expectations about stimulus structure in implicit learning. Mem. Cogn. 33, 171–181. doi: 10.3758/BF03195306
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Pothos, E. M. (2010). An entropy model for artificial grammar learning. Front. Psychol. 1:16. doi: 10.3389/fpsyg.2010.00016
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Pothos, E. M., and Bailey, T. M. (2000). The importance of similarity in artificial grammar learning. J. Exp. Psychol. Learn. Mem. Cogn. 26, 847–862. doi: 10.1037/0278-7393.26.4.847
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Pothos, E. M., Chater, N., and Ziori, E. (2006). Does stimulus appearance affect learning? Am. J. Psychol. 119, 277–301. doi: 10.2307/20445339
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Pothos, E. M., and Kirk, J. (2004). Investigating learning deficits associated with dyslexia. Dyslexia 10, 61–76. doi: 10.1002/dys.266
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Poznanski, Y., and Tzelgov, J. (2010). Modes of knowledge acquisition and retrieval in artificial grammar learning. Q. J. Exp. Psychol. 63, 1495–1515. doi: 10.1080/17470210903398121
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Reber, A. S. (1967). Implicit learning of artificial grammars. J. Verbal Learn. Verbal Behav. 6, 855–863. doi: 10.1016/S0022-5371(67)80149-X
Reber, A. S. (1969). Transfer of syntactic structure in synthetic languages. J. Exp. Psychol. 81, 115–119. doi: 10.1037/h0027454
Reber, A. S. (1989). Implicit learning and tacit knowledge. J. Exp. Psychol. 118, 219–235. doi: 10.1037/0096-3445.118.3.219
Reber, P. J., and Squire, L. R. (1999). Intact learning of artificial grammars and intact category learning by patients with Parkinson's disease. Behav. Neurosci. 113, 235–242. doi: 10.1037/0735-7044.113.2.235
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Reber, R., and Perruchet, P. (2003). The use of control groups in artificial grammar learning. Q. J. Exp. Psychol. 56A, 97–115. doi: 10.1080/02724980244000297
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Redington, M., and Chater, N. (1996). Transfer in artificial grammar learning: a reevaluation. J. Exp. Psychol. 125, 123–138. doi: 10.1037/0096-3445.125.2.123
Rohrmeier, M., Rebuschat, P., and Cross, I. (2011). Incidental and online learning of melodic structure. Conscious. Cogn. 20, 214–222. doi: 10.1016/j.concog.2010.07.004
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Rosas, R., Ceric, F., Tenorio, M., Mourgues, C., Thibaut, C., Hurtado, E., et al. (2010). ADHD children outperform normal children in an artificial grammar implicit learning task: ERP and RT evidence. Conscious. Cogn. 19, 341–351. doi: 10.1016/j.concog.2009.09.006
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Rüsseler, J.Gerth, I., and Münte, M. F. (2006). Implicit learning is intact in adult developmental dyslexic readers: evidence from serial reaction time task and artificial grammar learning. J. Clin. Exp. Neuropsychol. 28, 808–827. doi: 10.1080/13803390591001007
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Saffran, J. R., Aslin, R. N., and Newport, E. L. (1996). Statistical learning by 8-month-old infants. Science 274, 1926–1928. doi: 10.1126/science.274.5294.1926
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Saffran, J. R., Newport, E. L., Aslin, R. N., Tunick, R. A., and Barrueco, S. (1997). Incidental language learning: listening (and learning) out of the corner of your ear. Psychol. Sci. 8, 101–105. doi: 10.1111/j.1467-9280.1997.tb00690.x
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Scott, R. B., and Dienes, Z. (2008). The conscious, the unconscious, and familiarity. J. Exp. Psychol. 34, 1264–1288. doi: 10.1037/a0012943
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Servan-Schreiber, E., and Anderson, J. R. (1990). Learning artificial grammars with competitive chunking. J. Exp. Psychol. 16, 592–608. doi: 10.1037/0278-7393.16.4.592
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Skosnik, P. D., Mirza, F., Gitelman, D. R., Parrish, T. B., Mesulam, M.-M., and Reber, P. J. (2002). Neural correlates of artificial grammar learning. Neuroimage 17, 1306–1314. doi: 10.1006/nimg.2002.1291
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Smith, J. G., Siegert, R. J., McDowall, J., and Abernethy, D. (2001). Preserved implicit learning on both the serial reaction time task and artificial grammar in patients with Parkinson's disease. Brain Cogn. 45, 378–391. doi: 10.1006/brcg.2001.1286
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Tunney, R. J. (2005). Sources of confidence judgments in implicit cognition. Psychon. Bull. Rev. 12, 367–373. doi: 10.3758/BF03196386
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Van den Bos, E., and Poletiek, F. H. (2008). Effects of grammar complexity on artificial grammar learning. Mem. Cogn. 36, 1122–1131. doi: 10.3758/MC.36.6.1122
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Witt, A., and Vinter, A. (2011a). Artificial grammar learning in children: abstraction of rules or sensitivity to perceptual features? Psychol. Res. 76, 97–110. doi: 10.1007/s00426-011-0328-5
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Witt, A., and Vinter, A. (2011b). Learning implicitly to produce avoided behaviors. Q. J. Exp. Psychol. 1–14. doi: 10.1080/17470218.2010.543283
Ziegler, J. C., and Goswami, U. (2005). Reading acquisition, developmental dyslexia, and skilled reading across languages: a psycholinguistic grain size theory. Psychol. Bull. 131, 3–29. doi: 10.1037/0033-2909.131.1.3
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Zizak, D. M., and Reber, A. S. (2004). Implicit preferences: the role(s) of familiarity in the structural mere exposure effect. Conscious. Cogn. 13, 336–362. doi: 10.1016/j.concog.2003.12.003
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Keywords: artificial grammar learning, topological entropy, complexity, grammar system
Citation: Schiff R and Katan P (2014) Does complexity matter? Meta-analysis of learner performance in artificial grammar tasks. Front. Psychol. 5:1084. doi: 10.3389/fpsyg.2014.01084
Received: 26 May 2014; Accepted: 08 September 2014;
Published online: 25 September 2014.
Edited by:
Andrea Moro, Institute for Advanced Study IUSS Pavia, ItalyReviewed by:
Hua Shu, Beijing Normal University, ChinaCristiano Chesi, Institute for Advanced Study IUSS Pavia, Italy
Copyright © 2014 Schiff and Katan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Rachel Schiff, Learning Disabilities Studies and Haddad Center for Dyslexia and Learning Disabilities, School of Education, Bar-Ilan University, Building 905, 52900 Ramat-Gan, Israel e-mail:cmFjaGVsLnNjaGlmZkBiaXUuYWMuaWw=
 Rachel Schiff
Rachel Schiff Pesia Katan
Pesia Katan