- 1Laboratory CHArt (PARIS), Université Paris 8, Paris, France
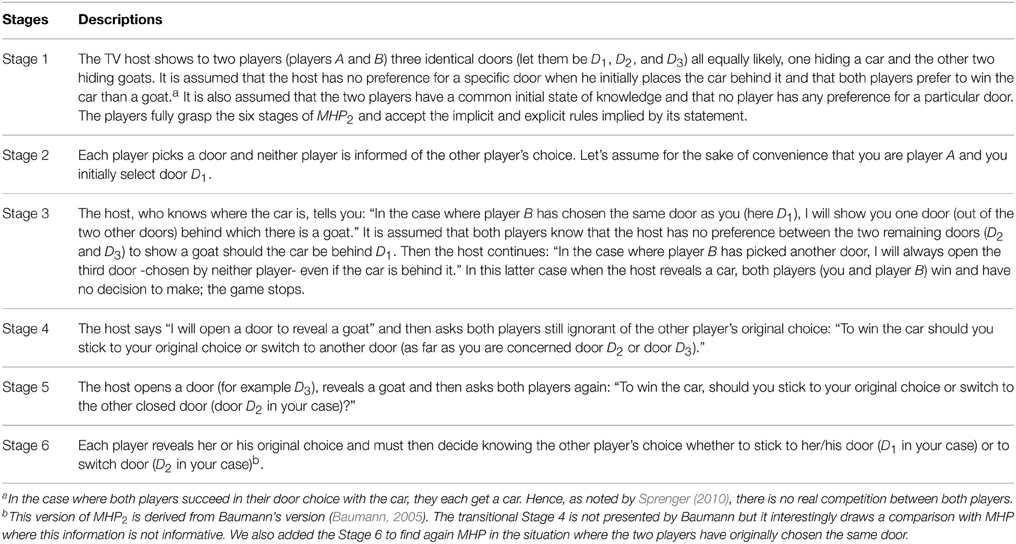
- 2Institut Jean Nicod, Paris, France
The Monty-Hall Problem (MHP) has been used to argue against a subjectivist view of Bayesianism in two ways. First, psychologists have used it to illustrate that people do not revise their degrees of belief in line with experimenters' application of Bayes' rule. Second, philosophers view MHP and its two-player extension (MHP2) as evidence that probabilities cannot be applied to single cases. Both arguments neglect the Bayesian standpoint, which requires that MHP2 (studied here) be described in different terms than usually applied and that the initial set of possibilities be stable (i.e., a focusing situation). This article corrects these errors and reasserts the Bayesian standpoint; namely, that the subjective probability of an event is always conditional on a belief reviser's specific current state of knowledge.
1. Introduction
In the Monty Hall Problem (MHP), you know that the car you want is behind one of three closed doors and a goat behind the other two doors. You choose a door and Monty (the host who knows where the car is) opens another door with a goat behind (as you know he can neither open your door nor a door with the car behind). After the host's action, would you rather stick to your original choice or switch to the remaining door?
MHP is a much-studied experimental paradigm investigating the inability of (naive and expert) people to revise their degrees of belief in a Bayesian manner (for a recent review see Tubau et al., 2015). Specific reformulations of format (natural frequencies, nested sets, visual representation, etc.) improving Bayesian performance have triggered some psychological debates on the underlying cognitive processes at play (for a recent analysis see Brase and Hill, 2015). Baratgin (2009) argues that these different formats facilitating Bayesian performance actually enhance the correct representation of the situation of revision in a stable universe, called the situation of focusing (Dubois and Prade, 1992, 1997) for which only Bayes' rule applies. The standard formulation of MHP prompts participants to form different representations of the situation of revision. However, when participants perceive the situation of focusing (for instance in a disambiguated version of MHP as in Baratgin and Politzer, 2010), they produce the Bayesian answer. Hence, participants cannot be considered as incoherent but only prone to an error induced by experimenters' presentation (Baratgin, 2009; Baratgin and Politzer, 2010).
MHP is also used as an argument against the notion of single-case probabilities. Moser and Mulder (1994) argued that there existed two opposite rational solutions: “sticking” for a MHP proposed as a one-shot problem and “switching” for a MHP cast in a frequentist context (i.e., when imagining a sufficiently large number of games). Horgan (1995) opposed this view making explicit the correct solution for the one shot MHP and showing that switching is the only correct solution to both formulations. Baumann (2005, 2008) produced a new argument based on a generalization of MHP: the Monty Hall Problem with two players (MHP2, see Table 1). In his view, although the two players share the same initial state of knowledge, they eventually form two different probability distributions. This point of view is opposed by Levy (2007) and by Sprenger (2010) who rightly argue that the two players do not necessarily share the same state of knowledge throughout the game in particular when their original choices differ. However, these authors do not explain the rationale of Baumann's mistake and do not explicitly define the causal structure of MHP21.
This paper will address these questions. First, the solution to MHP2 proposed as a one shot and its causal structure will be detailed. Then, explanations for the failure of researchers investigating MHP2 will be advanced and related to the “bias” that conducts psychologists to wrongly conclude that participants' responses to MHP are of a non-Bayesian nature, that is, the neglect of the Bayesian standpoint (de Finetti, 1974).
2. Solving the Monty Hall Problem with Two Players
Let's consider the following variables that define the properties of the possible doors (D1,D2,D3) in MHP2: The three variables C (The host's original choice of the door in which to place the car), Y (Your original choice of door) and B (Player B's original choice of door). C, Y, and B can take any of the three values Di (with i ∈ {1, 2, 3}), respectively noted from now on ci, yi, and bi. The variable H (the host's choice when opening a door) is composed of the two complementary sub variables ‘G’ (the host's revealing a goat) and ‘C’ (the host's revealing a car). The sub variables ‘G’ and ‘C’ can take the three values Di (with i ∈ {1, 2, 3}), respectively noted from now on ‘gi’ and ‘ci’2.
Following Walliser and Zwirn (2011), your beliefs before learning message ‘g3’ assuming your initial choice is D1 (Stage 2) can be represented as a hierarchical dynamic probabilistic structure (see Figure 1). The layer 0 depicts the four possible strategies of the host, i.e., showing a goat behind D2 or D3 (‘g2’ or ‘g3’) or showing a car when the two players have originally chosen two different doors with goats behind (‘c2’ or ‘c3’). Layer 1 corresponds to the three possible original choices of player B (b1, b2 or b3). Layer 2 represents the original car placement choice of the host (c1, c2, or c3). Layer 3 is your original choice (y1). The probability distributions of the variables at the different layers are defined by the statement of MHP2 with implicit and explicit hypotheses about the host's action and the players' preferences.
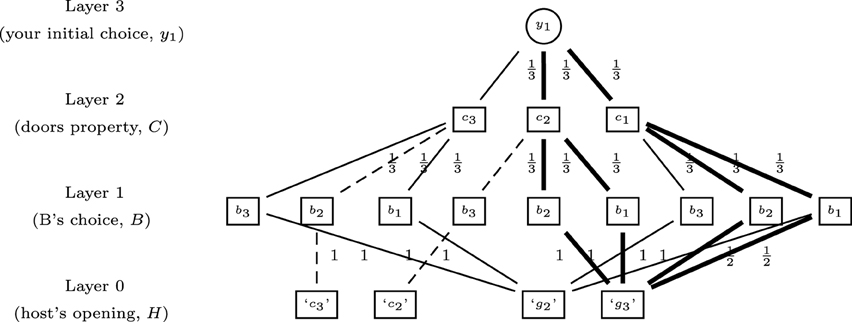
Figure 1. The general tri-probabilistic structure of MHP2 before learning message ‘g3’ assuming your initial choice is D1 (Y = y1). The continuous lines correspond to the subset left after compiling information at Stage 4 and the bold lines to the subset left after compiling the information at Stage 5. Conversely the dashed lines represent the initial structure dropped out at Stage 4.
At Stage 4 you learn that the host will open a door with a goat behind. You know that (i) this door is either door D2 or D3 and (ii) the car is either behind your door D1 or player B's originally chosen door. Hence you focus on the subset where ‘g2’ or ‘g3’ is true (the continuous lines in Figure 1). You are better off sticking to your initial choice D1.
Second at Stage 5 the host opens door D3 and reveals a goat behind. You focus on the subset where ‘g3’ is true (the bold lines in Figure 1). This information combined with your original choice of door provides information about the door behind which Monty placed the car. You are better off switching to door D2.
Finally at Stage 6 you learn what was player B's original choice. On the one hand, it can coincide with yours (b1). Both players are then exactly in the same situation with the same common knowledge. MHP2 amounts to MHP. Hence, you know that C is twice as likely to have the value c2 as to have the value c1. The best strategy is to switch from your original choice to the other closed door D2.
On the other hand you may learn that player B's original choice is different from yours (b2). In this case there is no best strategy and you are indifferent to sticking or switching.
3. The Collider Principle
Glymour (2001) was the first to identify the causal structure in MHP as a situation where two independent variables that mutually influence another variable are dependent conditional on the value of the variable they both affect. In MHP2, the three independent variables Y, B, and C symmetrically influencing (colliding with) another variable H (common effect) actually appear dependent conditionally on the values of the variable H. Hence observing the value of H provides some information on the possible values of Y, B or C. In the same way, knowing the values of any couple of variables (C, H), (B, H), and (Y, H) provides some information about the values of couples (Y, B), (Y, C), and (B, C), respectively. Finally observing the values of triples (Y, C, H), (B, C, H), (Y, B, H), respectively determines the values of variables B, Y, and C. Solving MHP2 as a one shot game relies on the latter triple (Y, B, H). It is easy when two variables are fixed to derive some qualitative predictions (Wellman and Henrion, 1993). For instance, MHP2's solution supports a phenomenon of reversal decision resulting from this collider principle. On learning H = ‘g3’ given your original choice (Y = y1) the likelihoods that B and C equal b2 and c2, respectively, are higher than the likelihoods that B and C equal b1 and c1, respectively. However, if in addition you learn that B equals b1 then the outcome c2 seems the more likely. However, if you learn that B equals b2 then the probabilities for the car being behind either D1 or D2 are even.
Recent studies have provided some evidence that “naive” adults and also children make correct qualitative predictions in collider principle situations when pairs of causal conditionals are explicitly presented (Ali et al., 2010, 2011). Precisely in MHP, participants perform better when the relation between the player's original choice and the host's strategy is explicit in conditional form (Macchi and Girotto, 1994, cited in Johnson-Laird et al., 1999). In the same way, when participants can construct a representation analogous to Figure 1 for MHP using a graph or by means of physical handling, participants' performance improves significantly (Yamagishi, 2003; Baratgin and Politzer, 2010). Thus, it seems that when participants can infer the causal structure of MHP by physical or explanatory cues, they are able to solve MHP (Burns and Wieth, 2004; Chater and Oaksford, 2006).
4. The Neglect of the Bayesian Standpoint
De Finetti's subjective Bayesian standpoint proposes that individuals form two levels of knowledge (de Finetti, 1980; Baratgin and Politzer, in press):
• An elementary level of knowledge of an event E that is always conditioned on an individual's specific state of knowledge {H0} at this time. Furthermore, any event is actually a tri-event (the third value representing ignorance between true event and false event).
• A meta-level of knowledge concerning the degrees of belief of an individual. Here ignorance is specified, and refined, into degrees of belief. From an inferential point of view, your subjective probability of this event E at time t0 is always conditional on your current state of knowledge {H0} [and should be written P(E|H0)]. It is coherent if (i) it follows the axiom of additive probabilities3 and (ii) when acquiring a new knowledge H, your probability also depends on this new knowledge {H0H} [and should be written P(E|H0H)].
A person dismissing the Bayesian standpoint considers the probability of a single event as questionable as compared to a “frequentist” conception of probability. She takes the frequentist conception to be the “correct” comparative representation, and confines Bayesianism to just a set of Bayesian techniques (de Finetti, 1974). In the psychological literature this “bias” leads to two significant mistakes: (i) to the neglect of pragmatic constraints on the methodology (to understand H0 and H); (ii) to the conclusion that people's behavior is “non-Bayesian,” even when the behavior does not violate Bayesian coherence (Baratgin, 2002; Mandel, 2014a). In the analysis of MHP2, this bias is characterized by inadequate terminology and interpretation of the revision situation.
4.1. The Use of an “Ambiguous Terminology”
For a subjective Bayesian, an event E always refers to a certain outcome in a single well-defined case (a unit in which the definition is unambiguous and complete) and cannot be used in a generic sense (such as a collection of “identical events”). There is no repetition of the same event but a succession of many distinct events, which can be different illustrations of the same phenomenon. In Moser and Mulder (1994), Baumann (2005), Levy (2007), and Baumann (2008), MHP2 is presented in an ambiguously termed way (de Finetti, 1977/1981, p. 357). The variables are considered as trials of the same phenomenon without completely specifying them and their possible values. Every specific door corresponds to a generic door D that is characterized by two properties: having a car (C) or a goat (G) behind it. Every player's original door choice is analyzed by its correspondence with C and G. The host's door opening ‘H’ is characterized by the two sub-classes ‘G’ and ‘C’. The players' final decisions to win the car are commingled and considered to pertain to the same classes of events “to stick,” “to switch” or “nothing.”
Following this frequentist “jargon” (de Finetti, 1979a,b), MHP2 is analyzed as an observation of a repetitive problem where the different variables are interchangeable in function of the host's car placement. Instead of considering each player with specific states of knowledge relative to each stage of MHP2 both players are assumed to have a common knowledge at each stage of the game. Their probabilities that there is a car behind one of the two remaining doors (after the door with a goat behind was opened) is 3∕7 for the door originally chosen and 4∕7 for the other door. Thus, imagining they made a different original choice, each door can be associated with two different probabilities (3∕7 and 4∕7) illustrating Bauman's paradox. Now, if we consider the specific knowledge of each player, the paradox disappears. In Stages 4 and 5, player B's probabilities on c1 and c2 are identical to your probabilities (relations 1–3) when his/her specific initial state knowledge is identical to yours (his/her original choice is b1). Conversely when his/her original choice is b2, his/her state of knowledge is different from yours and his/her probabilities correspond to different probabilities (relations 5 and 6):
However, player B's decisions are identical: sticking at Stage 4 and switching at Stage 5. At Stage 6, both players have an identical state of knowledge and probabilities (relation 4).
4.2. Neglect of the Situation of Focusing
MHP2 illustrates that the situation of revision implied by the Bayesian standpoint is a process of focusing on a subset of the initial state of knowledge {H0} (de Finetti, 1957; Dubois and Prade, 1992, 1997). It is assumed that one object is selected from the universe and that a message releases information about it. A reference class different from the initial one is consequently considered by focusing attention on a given subset of the original set that complies with the information about the selected object. This is not a temporal revision process because the information ‘g3’ just focuses on the selection of a particular posterior probability that was virtually available (among others) (see the bold lines of Figure 1). Yet participants in MHP seem to adopt (for pragmatic reasons) another representation of the revision situation, known as updating (Katsuno and Mendelzon, 1992; Walliser and Zwirn, 2002) in which, they infer from the message ‘g3’ the information as “door D3 have been removed,” and conceive a new probability distribution consistent with this new problem (Baratgin and Politzer, 2007, 2010; Baratgin, 2009). In this representation there is obviously no collider effect because, in this new problem with two doors, the variables Y and H always remain independent after the information is provided by the host. Participants form a new distribution of probability P′ for this new game4. Two typical analyses are consistent with this interpretation:
The stick or switch response: if you originally chose door D1 and the host opens door D3 with a goat behind, the worlds c1 and c2 are evenly close (in fact proportionally to their prior probabilities) to the invalidated world c3. The weight of c3 is redistributed proportionally on c1 and c2. This is MHP's solution in the updating context proposed by Dubois and Prade (1992).
It corresponds to the “equiprobability” solution given by nearly all participants to MHP but also by some experts in their analysis of MHP in a single isolated situation (Moser and Mulder, 1994) and of MHP2 (Levy, 2007).
The switch response: The worlds c3 and c2 (the two doors not originally chosen by the player) are considered closer. The probability of the invalidated world c3 is transferred to c2 alone. This is MHP's solution in the updating context proposed by Cross (2000).
This response is given by only few participants to MHP (see for review Baratgin, 2009). It corresponds to Moser and Mulder's explanation for MHP's solution in a suitable long run of relevantly similar situations. To explain the “causal structure” of MHP, Levy (2007) proposed also a process in line with this updating interpretation. However, it is difficult here to support the “switch” response to MHP2 with the symmetric role of the two players (Levy, 2007). Thus, the “stick or switch response” should be privileged to solve MHP2 in an updating representation.
5. Conclusion
This paper describes the supposedly paradoxical solutions attributed to MHP2 from the perspective of a thorough Bayesian standpoint perspective. It outlines the methodological care that one should take to comprehend the problem in relation to the single case terminology and the focusing context of revision. Not taking into account these features prevents one from fully grasping the probabilistic temporal dynamics of the problem and consequently the corresponding causal collider structure.
Psychologists who study subjective Bayesian reasoning should carefully formulate the statement without ambiguity and respect the Bayesian standpoint. This is also true especially for complex problems (such as the Sleeping Beauty problem Baratgin and Walliser, 2010; Mandel, 2014b) in which different solutions can be envisaged depending on the interpretations made by participants.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Financial support for this work was provided by a grant from the ANR Chorus 2011 (project BTAFDOC). The author thanks N. Cruz, G. Politzer, and B. Walliser for very helpful comments on a previous draft of this manuscript.
Footnotes
1. ^The term “causal” is missing in Baumann (2005). We find Horgan's terminology of “causal structure” in Levy (2007) with the vague definition of: “the set of conditions that ultimately explains why sticking and switching have the probabilities that they do” (Levy, 2007, p. 146). Finally, Sprenger (2010, p. 337) admits that “the place of causality in the ‘causal structure’ of a Monty Hall game remains obscure.”
2. ^We use here quotes for all sub-variables related to the host's actions during the game.
3. ^See for example on this special research topic (Cruz et al., 2015; Evans et al., 2015; Mandel, 2015) and also (Politzer and Baratgin, in press).
4. ^P′ along the following process: (i) The worlds ‘c3’ and ‘g2’ are canceled and a simpler probabilistic structure composed of the two worlds (c1, c2) is obtained, (ii) The new distribution P′ stems from a redistribution of the weights (the probabilities) of the removed worlds on the two remaining worlds.
References
Ali, N., Chater, N., and Oaksford, M. (2011). The mental representation of causal conditional reasoning: mental models or causal models. Cognition 119, 403–418. doi: 10.1016/j.cognition.2011.02.005
Ali, N., Schlottmann, A., Shaw, A., Chater, N., and Oaksford, M. (2010). “Causal discounting and conditional reasoning in children,” in Cognition and Conditionals. Probability and Logic in Human Thinking, eds M. Oaksford and N. Chater (New York, NY: Oxford University Press), 117–134.
Baratgin, J. (2002). Is the human mind definitely not bayesian? A review of the various arguments. Curr. Psychol. Cogn. 21, 653–682.
Baratgin, J. (2009). Updating our beliefs about inconsistency: the Monty-Hall case. Math. Soc. Sci. 57, 67–95. doi: 10.1016/j.mathsocsci.2008.08.006
Baratgin, J., and Politzer, G. (2007). The psychology of dynamic probability judgment: order effect, normative theories and experimental methodology. Mind Soc. 6, 53–66. doi: 10.1007/s11299-006-0025-z
Baratgin, J., and Politzer, G. (2010). Updating: a psychologically basic situation of probability revision. Think. Reason. 16, 253–287. doi: 10.1080/13546783.2010.519564
Baratgin, J., and Politzer, G. (in press). “Logic, probability inference: a methodology for a new paradigm,” in Cognitive Unconscious Human Rationality, eds L. Macchi, M. Bagassi, R. Viale (Cambridge, MA: MIT Press).
Baratgin, J., and Walliser, B. (2010). Sleeping beauty and the absent-minded driver. Theory Decis. 69, 489–496. doi: 10.1007/s11238-010-9215-6
Baumann, P. (2005). Three doors, two players, and single-case probabilities. Am. Philos. Q. 42, 71–79. Available online at: http://www.jstor.org/stable/20010183?seq=1#page_scan_tab_contents
Baumann, P. (2008). Single-case probabilities and the case of Monty Hall: Levy's view. Synthese 162, 265–273. doi: 10.1007/s11229-007-9185-6
Brase, G. L., and Hill, W. T. (2015). Good fences make for good neighbors but bad science: a review of what improves bayesian reasoning and why. Front. Psychol. 6:340. doi: 10.3389/fpsyg.2015.00340
Burns, B., and Wieth, M. (2004). The collider principle in causal reasoning: why the Monty Hall dilemma is so hard. J. Exp. Psychol. 133, 434–449. doi: 10.1037/0096-3445.133.3.434
Chater, N., and Oaksford, M. (2006). “Information sampling and adaptive cognition,” in Mental Mechanisms. Speculations on Human Causal Learning and Reasoning, eds K. Fiedler and P. Juslin (Cambridge: Cambridge University Press), 210–236.
Cross, C. B. (2000). A characterization of imaging in terms of Popper functions. Philos. Sci. 67, 316–338. doi: 10.1086/392778
Cruz, N., Baratgin, J., Oaksford, M., and Over, D. E. (2015). Bayesian reasoning with ifs and ands and ors. Front. Psychol. 6:192. doi: 10.3389/fpsyg.2015.00192
de Finetti, B. (1957). L'informazione, il ragionamento, l'inconscio nei rapporti con la previsione. L'industria 2, 3–27.
de Finetti, B. (1974). Bayesianism: its unifying role for both the foundations and applications of statistics. Int. Stat. Rev. 42, 117–130.
de Finetti, B. (1979a). Jargon-derived and underlying ambiguity in the field of probability. Scientia 114, 713–716.
de Finetti, B. (1979b). Probability and exchangeability from a subjective point of view. Int. Stat. Rev. 47, 129–135.
Dubois, D., and Prade, H. (1992). Evidence, knowledge, and belief functions. Int. J. Approx. Reason. 6, 295–319. doi: 10.1016/0888-613X(92)90027-W
Dubois, D., and Prade, H. (1997). “Focusing vs. belief revision: a fundamental distinction when dealing with generic knowledge,” in Qualitative and Quantitative Practical Reasoning, Vol. 1244 of Lecture Notes in Computer Science, eds D. Gabbay, R. Kruse, A. Nonnengart, and H. Ohlbach (Berlin; Heidelberg: Springer), 96–107.
Evans, J. S. Thompson, V. A., and Over, D. E. (2015). Uncertain deduction and conditional reasoning. Front. Psychol. 6:398. doi: 10.3389/fpsyg.2015.00398
Glymour, C. (2001). The Mind's Arrows: Bayes Nets and Graphical Causal Models in Psychology. Cambridge, MA: The MIT Press.
Johnson-Laird, P. N, Legrenzi, P., Girotto, V., and Sonino-Legrenzi, M. S. (1999). Naive probability: a mental model theory of extensional reasoning. Psychol. Rev. 106, 62–88. doi: 10.1037/0033-295X.106.1.62
Katsuno, A., and Mendelzon, A. (1992). “On the difference between updating a knowledge base and revising it,” in Belief Revision, ed P. Gärdenfors (Cambridge: Cambridge University Press), 183–203.
Levy, K. (2007). Baumann on the Monty Hall problem and single-case probabilities. Synthese 158, 139–151. doi: 10.1007/s11229-006-9065-5
Macchi, L., and Girotto, V. (1994). “Probabilistic reasoning with conditional probabilities: the three boxes paradox,” in Paper presented at the Annual Meeting of the Society for Judgement and Decision Making. (St. Louis, MO)
Mandel, D. R. (2014a). The psychology of bayesian reasoning. Front. Psychol. 5:1144. doi: 10.3389/fpsyg.2014.01144
Mandel, D. R. (2014b). Visual representation of rational belief revision: another look at the sleeping beauty problem. Front. Psychol. 5:1232. doi: 10.3389/fpsyg.2014.01232
Mandel, D. R. (2015). Instruction in information structuring improves bayesian judgment in intelligence analysts. Front. Psychol. 6:387. doi: 10.3389/fpsyg.2015.00387
Moser, P. K., and Mulder, D. H. (1994). Probability in rational decision-making. Philos. Pap. 23, 109–128. doi: 10.1080/05568649409506416
Politzer, G., and Baratgin, J. (in press). Deductive schemas with uncertain premises using qualitative probability expressions. Think. Reason. doi: 10.1080/13546783.2015.1052561
Sprenger, J. (2010). Probability, rational single-case decisions and the Monty Hall problem. Synthese 174, 331–340. doi: 10.1007/s11229-008-9455-y
Tubau, E., Aguilar-Lleyda, D., and Johnson, E. D. (2015). Reasoning and choice in the monty hall dilemma (mhd): implications for improving bayesian reasoning. Front. Psychol. 6:353. doi: 10.3389/fpsyg.2015.00353
Walliser, B., and Zwirn, D. (2002). Can Bayes rule be justified by cognitive rationality principles? Theory Decis. 53, 95–135. doi: 10.1023/A:1021227106744
Walliser, B., and Zwirn, D. (2011). Change rules for hierarchical beliefs. Int. J. Approx. Reason. 52, 166–183. doi: 10.1016/j.ijar.2009.11.005
Wellman, M., and Henrion, M. (1993). Explaining ‘explaining away’. IEEE Trans. Pattern Anal. Mach. Intell. 15, 287–292.
Keywords: Bayesian standpoint, Monty-Hall problem with two players, probability revision, collider principle, single case probability
Citation: Baratgin J (2015) Rationality, the Bayesian standpoint, and the Monty-Hall problem. Front. Psychol. 6:1168. doi: 10.3389/fpsyg.2015.01168
Received: 30 March 2015; Accepted: 24 July 2015;
Published: 11 August 2015.
Edited by:
David R. Mandel, Defence Research and Development Canada, CanadaCopyright © 2015 Baratgin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jean Baratgin, Laboratory CHArt, Université Paris 8, Site Paris-EPHE: 4–14 rue Ferrus, 75014 Paris, France,amVhbi5iYXJhdGdpbkB1bml2LXBhcmlzOC5mcg==
 Jean Baratgin
Jean Baratgin