- 1Lucertis Kinder- en Jeugdpsychiatrie, Rotterdam, Netherlands
- 2Department of Special Education, Utrecht University, Utrecht, Netherlands
The goal of this randomized controlled trial was to investigate whether Jungle Memory working memory training (JM) affects performance on working memory tasks, performance in mathematics and gains made on a mathematics training (MT) in school aged children between 9–12 years old (N = 64) with both difficulties in mathematics, as well as attention and working memory. Children were randomly assigned to three groups and were trained in two periods: (1) JM first, followed by MT, (2) MT first, followed by JM, and (3) a control group that received MT only. Bayesian analyses showed possible short term effects of JM on near transfer measures of verbal working memory, but none on visual working memory. Furthermore, support was found for the hypothesis that children that received JM first, performed better after MT than children who did not follow JM first or did not train with JM at all. However, these effects could be explained at least partly by frequency of training effects, possibly due to motivational issues, and training-specific factors. Furthermore, it remains unclear whether the effects found on improving mathematics were actually mediated by gains in working memory. It is argued that JM might not train the components of working memory involved in mathematics sufficiently. Another possible explanation can be found in the training’s lack of adaptivity, therefore failing to provide the children with tailored instruction and feedback. Finally, it was hypothesized that, since effect sizes are generally small, training effects are bound to a critical period in development.
Introduction
Studies have shown that persistent difficulties in mathematics develop in approximately 5% of school-aged children. An even larger number of children struggle with math on a day-to-day basis, without meeting the criteria for developmental dyscalculia. The underpinnings for math difficulties are manifold, with both cognitive as well as emotional factors contributing to its manifestation and maintenance over time. Recent literature can be divided in multiple foci of interest. Attentional resources (Marzocchi et al., 2002; Dormal et al., 2014), memory processes (Perna et al., 2015), basic number sense (Piazza, 2010; Brankaer et al., 2014; Vanbinst et al., 2015), as well as math anxiety (i.e., Maloney and Beilock, 2012) hold their own in what seems to be a still unintegrated field of research. Mathematics disabilities are recognized as complex neuro-psychological syndromes related to many distinct neurocognitive constructs (Perna et al., 2015) and underlying brain activation (Arsalidou and Taylor, 2011; Metcalfe et al., 2013; Demir et al., 2014). However, relationships between these constructs remain largely unclear.
A large body of research, however, has been conducted in the field of executive functions and their relationship to mathematics. Predominantly, the role of working memory has been a topic of interest. Following the most influential model proposed by Baddeley and Hitch (1977), elaborated upon by Miyake et al. (2000), working memory can be viewed as a cognitive buffer system that allows the temporary storage and manipulation of incoming information necessary for complex tasks. The model describes two slave systems: a visuo-spatial sketchpad and an auditory-verbal component, called the phonological loop. Both slave systems are supervised by a flexible control system, the Central Executive (CE), that is thought to monitor and update information as well as inhibit incoming irrelevant information.
A slightly different approach to working memory has been advocated by Cowan (1988). In this model, working memory is conceptualized as a memory storage in the center of attention, that is limited in both duration and load, so that its contents can be operated on and be integrated with information in long-term memory. Compared to the model of the Baddeley and Hitch model, emphasis is placed on awareness and both voluntary as well as involuntary attentional processes. In this view, not only processing errors of updating can lead to mathematical difficulties. Problems with activating previously learned information or attentional problems would lead to the same behavioral results. This approach is relevant for the present study, as it incorporates attentional processes.
Regarding the role of working memory in the development of mathematical competency the updating component of working memory plays an important part (Lee et al., 2012; Van der Ven et al., 2012; Kolkman et al., 2013a). Updating represents the ability to update relevant information in working memory and the concurrent ability to inhibit irrelevant information. The construct is part of the CE component of working memory in the Baddeley and Hitch model. Updating seems to be the process involved in keeping track of intermediate outcomes of mental arithmetic and problem solving (Passolunghi and Pazzaglia, 2004, 2005). Involvement of working memory in mental arithmetic in children might follow a developmental path, with the contribution of verbal working memory increasing with age, while that of visuospatial working memory decreases (Van de Weijer-Bergsma et al., 2015c). Children with less working memory capacity tend to perform worse on general mathematical tasks than typically developing peers (Friso-van den Bos et al., 2013).
Despite the fact that most recent contemporary reviews consider working memory to be a relevant factor in mathematics learning and development, contrasting views are advocated by different authors. Considering different aspects of working memory, some authors have found deficits in visual working memory, but no apparent problems in verbal working memory (McLean and Hitch, 1999). Furthermore, Landerl et al. (2004) describe a group of children with mathematics learning disorder in the absence of difficulties in working memory. In this same vein, Temple and Sherwood (2002) found no relationship between working memory and number sense, or working memory and arithmetic capabilities. Working memory is considered by these authors to be neither a necessary, nor a sufficient factor in explaining mathematical difficulties. They advocate a standpoint in which number sense abilities play the most prominent role in a developmental model of mathematical difficulties. Other authors, however, propose a double deficit model: Number sense and working memory both lead to weaker performance in tasks involving mathematical problem solving. Children that exhibit both number sense as well as working memory difficulties, obtain lowest results (Östergren and Träff, 2013; Kroesbergen and van Dijk, 2015). In addition to contrasting research findings, variation in research design, usage of working memory tasks involving counting and covariance of working memory with other domain-general factors, like processing speed, make interpreting results quite difficult (Cowan and Powell, 2014).
Relationship between Attention Problems and Mathematics
Both clinical observations as well as scientific research have pointed out a high incidence of comorbidity between attention problems and learning disorders. Estimations currently revolve around 30% (DuPaul and Volpe, 2009). Recent evidence from twin-studies suggests a genetic link between symptoms of ADHD, primarily the inattentive symptoms, and mathematic disabilities (Greven et al., 2014). Inattentive children tend to make more mistakes when calculating than attentive children, quite possibly due to working memory deficits frequently found in groups of children with both ADHD and persistent math disabilities. Both working memory and attention are neurocognitive traits that can be viewed as dimensional constructs, with - at the lower end of the continuum- the deficits common in children with ADHD (e.g., Larsson et al., 2012; Martin et al., 2015) and developmental dyscalculia. Based on the above, it could be concluded that a group of children with mild or moderate problems in attention or working memory, in the presence of normal general intelligence, is struggling with mathematics, but doesn’t meet the formal criteria for ADHD or developmental dyscalculia. This is, however, a highly interesting group that is often overlooked and that is -at least in the Netherlands- not eligible for specialized treatment. Teachers could benefit from knowledge on this subject, as well as methods describing how to remediate difficulties with mathematics. However, scientific knowledge about cognitive underpinnings of learning problems is not frequently transferred to the classroom or remediation programs in school.
Working Memory Training and Mathematics
One of the possible training programs that could possibly find, and has found, its way into the schools is working memory training. Some research suggests beneficial effects of working memory training on mathematics (Bergman-Nutley and Klingberg, 2014; Söderqvist and Bergman Nutley, 2015), but effect sizes are generally small and studies have their methodological limitations, mostly because of a small sample size. The largest sample size to date can be found in a study by Holmes and Gathercole (2013). These authors used Cogmed Working Memory Training in a classroom setting and found considerable long term effects on both working memory as well as mathematics. There is, however, debate in the literature on transfer of working memory training in general. Meta-analyses carried out recently point out effects of training on both verbal and non-verbal working memory, but authors disagree on the matter of far transfer. Melby-Lervåg and Hulme (2013) conclude that at follow-up limited near transfer effects could be measured and there is no clear evidence of generalization of training to other skills. Specifically, for arithmetic, effect sizes are generally low and non-significant. On the other hand, two recent meta-analyses showed long term effects of working memory training on measures of attention in everyday functioning (Shinaver et al., 2014; Spencer-Smith and Klingberg, 2015), which should be beneficial for learning behavior and for outcomes of academic performance, including mathematics. Possibly, effects of working memory training on mathematics are indirect and depend on instructions and training of mathematical skills after gains in working memory have been made. The present study elaborates existing literature by addressing this issue. The questions raised by existing literature are whether children with attentional problems and problems in working memory (a) profit from training working memory and (b) show more gain in a training of mathematical abilities than their untrained peers.
To address these two questions, we trained working memory in a sample of children in primary schools using Jungle Memory training (JM) for 8 weeks, before training basic arithmetic abilities (addition, subtraction, multiplication, and dividing) using a Dutch computer based adaptive arithmetic training (Math Garden) for 8 weeks and compared this group to two control groups. We measured transfer to both verbal and non-verbal working memory tasks and a speeded arithmetic task. Based on some previous studies, we expected a limited transfer to mathematical abilities directly after working memory training but a larger training effect of the arithmetic training compared to our control groups. Current literature, however, is not clear about this issue and the direction this hypothesis is leading, giving us other concurring hypotheses to consider. Based on the meta-analysis by Melby-Lervåg and Hulme (2013) one could hypothesize that all groups would profit equally from the mathematics training. A third possibility would be that performance in mathematics depends on working memory as a base engine, in which case both groups training working memory would perform equally well and better than the group training mathematics only.
Materials and Methods
Participants
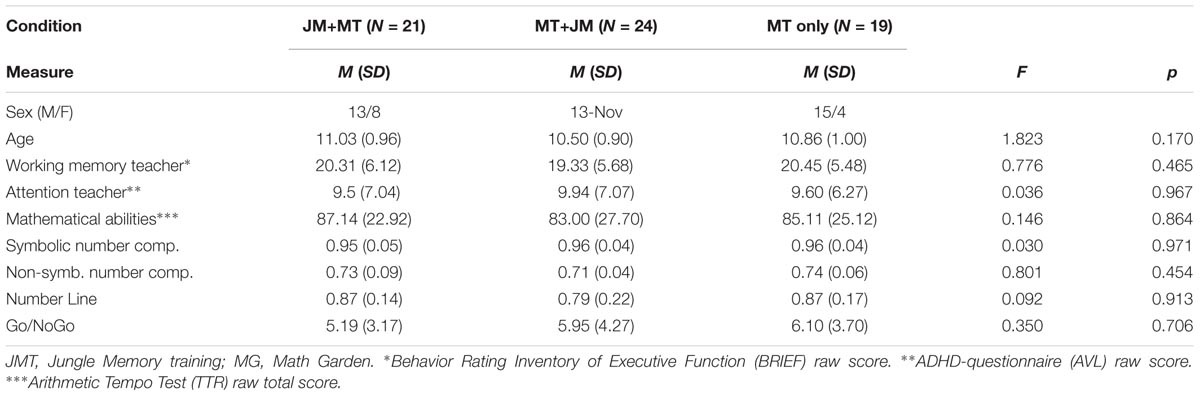
Children (N = 64) were recruited from regular elementary schools in The Netherlands, primarily in the Rotterdam area. Teachers of different schools were asked to participate and they selected the children based on the inclusion criteria provided to them. Children were eligible to participate if they were 9–12 years old when training started (Grades 4–6), had difficulties in mathematics (scores on standardized school based tests below or far below average), and were observed to have attentional difficulties (above average scores on a standardized rating scale – Scholte and van der Ploeg, 2005) as rated by their teachers. Working memory was evaluated by the teachers as well. They were asked to fill out the BRIEF (Behavior Rating Inventory of Executive Function), a rating scale measuring a variety of executive functions, including working memory (Huizinga and Smidts, 2010). Children were, however, not excluded when they did not exhibit specific working memory problems as rated by their teachers. Descriptive statistics can be found in Table 1. Children with below average scores on reading or reading comprehension or known psychiatric disorders other than ADHD were excluded from participation.
Parents received written information on the study and we obtained their written consent, in accordance with the Declaration of Helsinki, before starting the assessments and training. The study was approved by the ethics committee of the Faculty of Social and Behavioral science, Utrecht University (FETC14-022).
Tests
There were three main variables of interest in this study: verbal and spatial working memory and mathematical ability. The tests that were used for measuring working memory were (1) a visuospatial working memory task called ‘Lion Game,’ and (2) a verbal working memory task called ‘Monkey Game’ (Van de Weijer-Bergsma et al., 2015b,c). Tasks were administered on a computer with headphones in the school setting, supervised by a student who was present the whole time.
The Lion Game is a visual-spatial complex span task, in which children have to search for colored lions. Children are presented with a 4×4 matrix containing 16 cells. In each trial, eight lions of different colors (red, blue, green, yellow, and purple) are consecutively presented at different locations for 2000 ms. Children have to remember the last location where a lion of a certain color has appeared and use the mouse to click on that location after the sequence has ended. The tasks consist of five levels each of four items, in which working memory load is manipulated by the number of colors children have to remember and update. No cut-off rules are applied (Van de Weijer-Bergsma et al., 2015b). Proportion correct responses were collected. Reliability and validity of The Lion Game have been studied recently (Van de Weijer-Bergsma et al., 2015b). Good internal consistency reliability (Cronbach’s α = 0.87), satisfactory test–retest reliability (α = 0.71) and good concurrent (α = 0.51) and predictive validity have been found. Scores on The Lion Game appear to be a significant predictor of math ability.
The Monkey Game is a verbal span-backward task, in which children have to remember and recall different words backward. Children hear spoken words (i.e., moon, fish, rose, eye, house, ice, fire, cat, and coat). In Dutch, these words are some of the words first learned in reading by children in first grade. Children have to remember the words and recall them backward, by clicking on the written words presented visually in a 3×3 matrix. The task consists of five levels each of four items, in which working memory load is manipulated by the number of words children have to remember and recall backward, ranging from two words in level 1 to six words in level 5. No cut-off rules were applied (Van de Weijer-Bergsma et al., 2015c). Proportion correct responses were collected. The Monkey Game has good internal consistency (Cronbach’s α ranging from 0.78–0.89) and shows good concurrent and predictive validity (Van de Weijer-Bergsma et al., 2015a).
The test used to measure mathematical abilities was the Arithmetic Tempo Test (Tempo Toets Rekenen, de Vos, 1992), a fast paper-and-pencil screening instrument. Five columns are presented, each with 40 arithmetic exercises: addition, subtraction, multiplication, division, and mixed, slowly increasing in difficulty. All problems consist of two-operant equations with outcomes smaller than 100. Pupils are instructed to solve as many problems as they can within a 1-min limit per column. Test–retest reliability was computed in a study by Van de Weijer-Bergsma et al. (2015c) and ranged from α = 0.84–0.87 after 4 months and from α = 0.82–0.86 after 8 months. Combined number of correct answers in the five columns was used as an outcome measure in this study.
To check whether there were group differences in number sense abilities or inhibition, four tasks were administered during the first assessment only. Children were given (1) a symbolic number task that asked them to evaluate which of two numbers was greatest, (2) a non-symbolic number task on which they were asked to evaluate the number of dots presented on either end of the screen. (3) A number line task was presented on which participants had to place a given number on a line that ranged from 0 to 100. A further description of these tasks, as well as information on reliability and validity can be found in an article by Kolkman et al. (2013b). (4) An inhibition task following a Go–NoGo paradigm (De Weerdt et al., 2013) concluded the assessment. Speed and accuracy were measured in these tasks. These tasks were administered individually. As can be seen in Table 1, groups did not differ meaningfully in performance on these tasks.
Intervention
Jungle MemoryTM (2008) is a web-based memory training program aimed at 7–16 year-old children. In comprises of three interactive computer games with up to 30 levels of difficulty in each game to train working memory. Each game trains different aspects of working memory and provides the student with regular feedback of progress, both during training and in the back-end of the program. Game 1 (Quicksand) involves memory for and later use of word endings, Game 2 (Code Breaker) features mental rotation of letters, and Game 3 (River Crossing) involves sequential memory of mathematical solutions. Motivational features in the program included positive verbal feedback, a display of the user’s best scores, percentile rankings, and the number of ‘super monkeys’ collected as a result of successfully completing training levels (Alloway et al., 2013). Completion of all three tasks can be obtained in 20–25 min. The program can be found on a website by Memosyne Ltd (2011) – http://lb.junglememory.com.
The Math Garden (Van der Maas et al., 2009) is an adaptive web-based game in which children are able to train their math skills. It comprises of different games of which five calculation-based games (addition, subtraction, multiplication, division, and speed) were used during this study. Children are presented with 10 math problems per game during which they received direct feedback on their answers. To encourage motivation, children are presented with a virtual garden that grows and blooms depending on the effort and progress. The website for Math Garden can be found on Memosyne Ltd (2011) – http://www.rekentuin.nl.
Procedure
First, children were randomly assigned to three groups. These groups were given three different treatment procedures: (1) the experimental group received Jungle Memory Training (JM) first (8 weeks), before starting mathematics training [MT (mathematics training), 8 weeks]; (2) one control group that received the mathematics training first, before commencing JM, and (3) a second control group that received education as usual in the first period and MT the second period. Assessment occurred three times: prior to training, after 8 weeks and post training. This was done in a group setting on individual computers with headphones. The assessment and treatment procedures are depicted schematically in Figure 1.
During training periods, progress and effort was monitored by trained undergraduate students visiting schools. In the back-end of both training programs, number of times trained as well as quality of the training can be easily monitored. Undergraduate students visited schools at least once every 2 weeks, giving children feedback on the obtained results, showing their progress and thereby trying to motivate the children. Both children training with JM as well as those training with MT were encouraged to complete four sessions a week by their teachers, as well as the undergraduate students. They were provided training time and a quiet place to train by their teacher during school days. Furthermore, they were provided with training schedules stating the days and the time on which they were supposed to train. Children were given no further rewards or incentives. Both teachers and undergraduate students looked for motivational or technical problems occurring during training. These problems were reported to the corresponding author who attempted to solve the issues. Motivational issues most commonly arose when training or assessment times were planned during a specific activity that was liked by the pupil. These were easily adjusted and no children dropped out. The most common technical issue was a temporary problem with the server of the web-based training programs or the working memory tasks. Sometimes appointments for assessment or training times had to be rescheduled. Children training with JM received feedback and were provided with strategies by the undergraduate students to improve their skills on the training tasks when they failed to pass the task three times in a row. This feedback was based on a protocol that was provided to us by LerendBrein, an organization based in The Netherlands, specializing in training professionals in healthcare and education. Children training with MT received no further feedback; The training program provided all the necessary feedback.
Data Screening
Missing data showed a number of missing data points, most probably due to server problems during the administration of one the working memory tasks. Missing value counts ranged from 3.1 to 10.1% in one instance, randomly distributed (χ2 = 6.011, σ = 1.00). Since the software for the data analysis does not allow for missing data, single imputation based on the series mean was used to replace missing values. The data contained no significant outliers.
Main Analyses
First, to examine the relationship between progress during JM and gains on the external working memory tasks, Pearson’s r correlations were calculated between the working memory pre-test and the reported improvement within the game. Correlations were calculated both for the first and for the second training period, as we were interested in both short and long term effects of JM.
To be able to test the multiple hypothesis formulated without the loss of power, Bayesian evaluation of informative hypotheses was used to examine the relationship between working memory and mathematical abilities. For a detailed introduction to Bayesian statistics, one is directed to Klugkist et al. (2005) and Van de Schoot et al. (2011). This type of analysis is confirmative and provides a quantification of support in the data for each hypothesis discussed and is therefore especially useful in studies with smaller sample sizes. The posterior model probability (PMP) is computed for each hypothesis to quantify the support in the data. If the PMP of one hypothesis is larger than the PMP of the unconstrained hypothesis (Hu), the constraints used to describe the hypotheses are supported by the data. If the PMP of a first hypothesis is larger than the PMP of a second hypothesis, the support in the data is largest for the first. Mark that the sum of the PMPs for a given set of competitive hypothesis is always one.
Next, the Bayes-factor was computed. This is a measure for the degree of support for each hypothesis compared to a hypothesis without constraints. This Bayes-factor was computed by dividing the PMP-value of a hypothesis by the PMP-value of the unconstrained hypothesis, which results in a value showing the evidence in favor of one hypothesis compared with the unconstrained hypothesis.
For effect of JM on gains in working memory we considered two competing hypotheses, for both short and long term effects. All four hypotheses were translated into statistical hypotheses with (in)equality constrained parameters (Klugkist et al., 2005). In this case, the parameters were group means on a verbal and a visual working memory task. For the first training period, the first hypothesis stated that the children that received the JM first would outperform other groups on the working memory tasks, i.e., μ1 > μ2 = μ3 (Model 1). The second hypothesis was that all groups would perform equally well μ1 = μ2 = μ3 (Model 2). For the second training period, the second group -now receiving JM- would have gained more at the working memory measures: μ2 > μ1 = μ3. The alternative hypothesis we formulated was μ1 = μ2 = μ3, stating that all groups would perform equally well.
For effect of JM on gains made in the MT, three hypotheses were formulated for both the first and second training period. During the first training period, the group receiving MT was thought to perform best, with the group receiving JM performing better than the group receiving no training at all: μ2 > μ1 > μ3 (Model 1). Alternative hypotheses were as follows: μ2 > μ1 = μ3 (Model 2, no direct effect of JM on mathematical abilities), and μ1 = μ2 = μ3 (Model 3, no effect of both trainings). During the second period, the formulated hypotheses were the following: μ1 > μ3 > μ2 (Model 1, stating that the experimental group would outperform the other groups, with the third group -now receiving MT- would gain more than the second group), μ1 = μ3 > μ2 (Model 2, no added effect of JM on MT), and μ1 = μ2 = μ3 (Model 3, suggesting no effects of both MT and JM).
The main question of this study was assessed by examining the total gains on the mathematical abilities outcome measure over both training periods. The first hypothesis stated that children that received the JM first, before the MT, would outperform the groups that either received the JM after the MT or received the MT only, i.e., μ1 > μ2 > μ3 (Model 1). The second hypothesis stated that both groups that trained their working memory would outperform the third group training mathematical abilities only μ1 = μ2 > μ3 (Model 2). The last hypothesis stated that all groups would perform equally well on the last test for mathematical abilities μ1 = μ2 = μ3 (Model 3). All informative hypotheses stated in the section above were compared to the alternative empty hypothesis: μ1, μ2, μ3 (Model 0), to protect against incorrectly choosing the hypotheses.
Results
Descriptive Statistics
Table 2 shows the descriptive statistics considering the outcome measures of mathematical abilities, visual, and verbal working memory of our three groups.
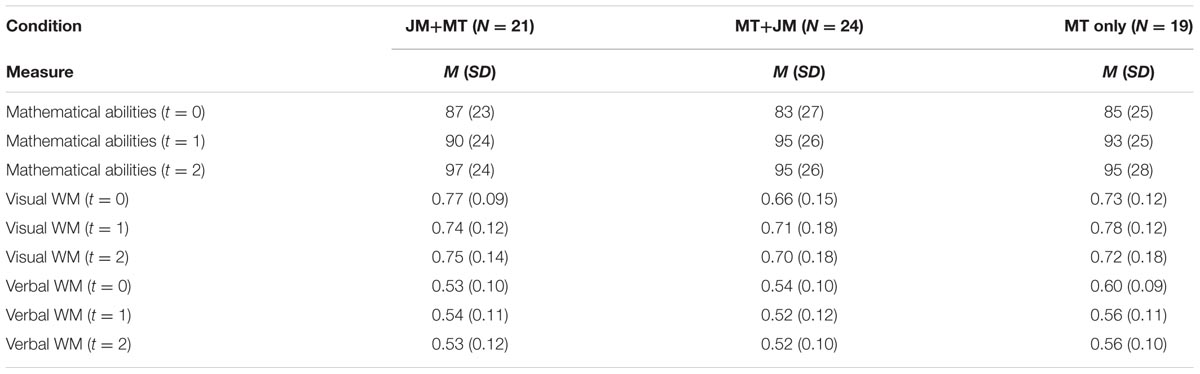
TABLE 2. Means and standard deviations on pre-, between and post-tests of mathematical abilities and visual and verbal working memory.
Table 3 shows the descriptive statistics considering the training periods.

TABLE 3. Means and standard deviations of total training intensity of both JM and MT in three groups.
Relationship between Gains Made in JM and Generalization to Non-trained Tasks
Table 4 shows the Pearson’s r correlations between gains obtained in JM by the experimental group, as shown in the stats tab provided by the program, and scores on the non-trained working memory tasks, both after the first (short term) and after the second (long term) period of training. No significant correlations could be obtained. Generalization of the training thus seemed negligible.
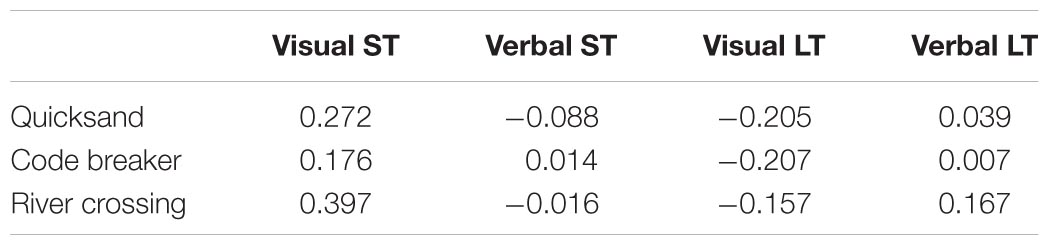
TABLE 4. Progression during JM on the three trained tasks in the JM+MG condition and correlations with both short and long term scores on non-trained working memory tasks (visual and verbal WM).
Working Memory Training and Gains in Working Memory
Table 5 depicts the results of Bayesian analysis of the group effects on the working memory outcome measures, BFs (Bayes Factors) and PMPs are presented. It was expected that during the first training period (t = 1), the experimental group would gain most on working memory outcome measures, μ1 > μ2 = μ3 (Model 1). Model 2 stated that all groups would perform equally well, μ1 = μ2 = μ3 (Model 2). These were compared to the empty Model 0 (μ1, μ2, μ3). For visual working memory, no support was found for our first hypothesis. For verbal working memory, however, the data showed some support for effects of JM. Both the first and the second model received substantial support by our data, but the first model was more likely.
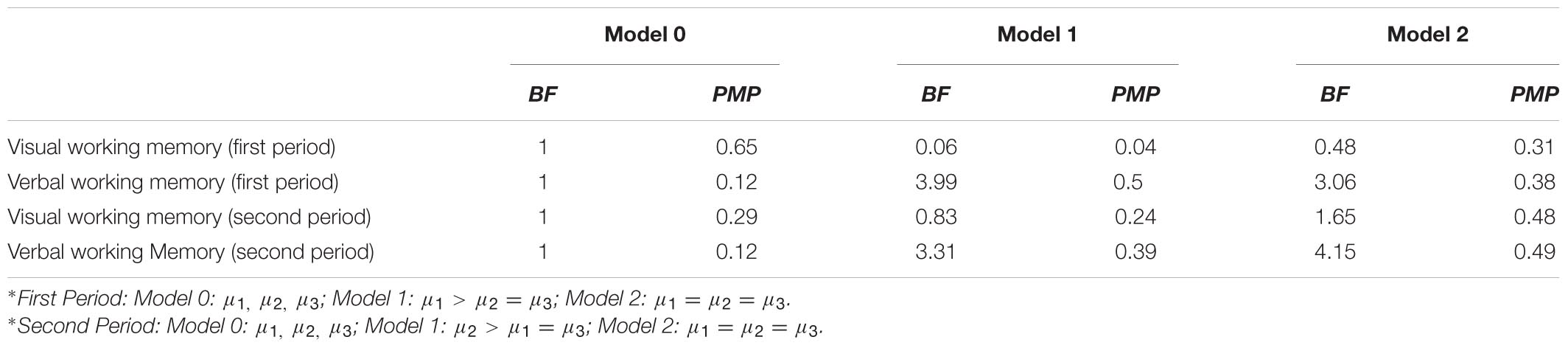
TABLE 5. Bayes Factors (BF) and Posterior Model Probabilities (PMP) of the three models and the visual and verbal working memory outcome measures (t = 1 and t = 2).
During the second period (t2), it was expected that our second group, training with JM, would show more gains in working memory: μ2 > μ1 = μ3 (Model 1), while the alternative hypothesis was that all groups would gain equally well: μ1 = μ2 = μ3 (Model 2). Both for visual and for verbal working memory, most support was found for the second hypothesis, respectively, receiving weak and substantial support by our data.
Working Memory Training and Mathematical Abilities
Table 6 shows the results of Bayesian analysis for the mathematics training. During the first training period it was hypothesized that the group training with MT would perform best on the mathematical abilities outcome measure and a smaller training effect could be found for the JM as well (μ2 > μ1 > μ3,Model 1). Alternative hypotheses were formulated: μ2 > μ1 = μ3 (Model 2) and μ1 = μ2 = μ3 (Model 3). Most, but only weak support was found for the second hypothesis, indicating a training effect for MT and not for JM on mathematical abilities.

TABLE 6. Bayes Factors and Posterior Model Probabilities of the four models and gains on mathematics outcome measure (t1–t0 and t2–t1).
During the second period, the experimental group trained with the MT. It was hypothesized that this group would show most gains in mathematical abilities after this period, followed by the third group, also training with MT: μ1 > μ3 > μ2 (Model 1). Alternative hypotheses were formulated: μ1 = μ3 > μ2 (Model 2) indicating no added effect of JM, and μ1 = μ2 = μ3 (Model 3) suggesting no effect of both JM and MT during the second period. Our data provided most and substantial support for the first model.
Table 7 shows the results of the analysis on group differences on the mathematical abilities outcome measure, to examine which group benefited most from both trainings, regarding mathematical abilities: BFs and PMPs are presented. Recall that Model 0 represents the alternative (empty) hypothesis (μ1, μ2, μ3). Model 1 stated that the children training with JM first would benefit most from the MT: μ1 > μ2 > μ3. Model 2 stated both groups training with JM would show most improvement on the MT: μ1 = μ2 > μ3, while Model 3 stated that all three groups would perform equally and profit equally from training mathematics. Model 1 received most support from the data, indicating an effect of the working memory training, although the effect seems small and weak compared to the empty Model 0.

TABLE 7. Bayes Factors and Posterior Model Probabilities of the four models and improvement after mathematics training.
Discussion
This intervention study compared three groups of children with math difficulties and attentional problems on effects of both a working memory training (Jungle Memory) and a math training (Math Garden). To our knowledge this is the first attempt to combine both training procedures to investigate the effects of working memory training on both measures of working memory and learning mathematics. Prior research has been inconsistent regarding the effects of working memory training and low effect sizes are reported, especially on mathematical abilities, so multiple hypotheses were tested in this study, using Bayesian statistics.
Regarding the immediate and long term effects of working memory training on closely related working memory tasks, mathematical abilities and learning mathematics, results were discouraging. Gains made in JM showed little or no relationship with gains on non-trained working memory tasks. Some support was found for short term gains in verbal working memory only, but long-term retention was not supported by our data. Children generally trained less during the second training period, most likely due to holiday periods and extracurricular activities that occurred during this period or motivational issues. The experimental group, however, trained relatively often, compared to the control groups. It was observed that individual children that trained most, gained most in both verbal working memory and mathematical abilities, but on a group level this could not be confirmed.
Support was found for an effect of MT on gains in speeded mathematics, as was expected. Also, an added effect of JM was found. Children training with JM improved their mathematical abilities directly after training. After completing both JM and MT, the group training with JM first, showed most improvement. The effects, however, are small and were possibly mediated by the amount of training (our experimental group trained more frequently than our control groups that did not train with JM first). Furthermore, it could be argued that JM contains a task in which pupils are required to solve (and retain and update) mathematical problems. Therefore, these children had more practice time, solved more problems, than children that did not train with JM. This fact confounded the results obtained by this study.
Theoretically, working memory is a considerable factor in predicting math problems. However, training working memory with Jungle Memory does not seem to have a profound effect on mathematical abilities, requires supervised practice, and has to be accompanied by specific feedback by a trainer. Several explanations, both theoretical and practical, could be given for these results. It could be argued that Jungle Memory does not specifically train the aspects of working memory relevant to mathematics. Since Jungle Memory does train the updating component of working memory and has a processing speed component, it could be argued that attentional focus and activation of long-term memory, not directly trained by Jungle Memory, would play a crucial role in mathematics. This would give indirect support for the model proposed by Cowan (1988), that emphasized these components of working memory. Another explanation, and one that fits the Baddeley model of working memory, would be that Jungle Memory does not provide the trainee with the adequate components necessary for training working memory efficiently. Regarding this issue, lack of the program’s ability to adapt efficiently to the level of the trainee -as has been proposed by Klingberg et al. (2002, 2005)- could be an explanation for the results obtained by this study.
In studies that found transfer effects of working memory training in mathematical abilities, authors generally describe a small effect. In these studies, speeded arithmetic tasks were used (St Clair-Thompson et al., 2010; Bergman-Nutley and Klingberg, 2014), just like in the present study, but only addition and subtraction problems were administered. It could be argued that other operations of calculation, specifically division, could load on working memory more heavily, because of the fact that most pupils are less familiar with dividing. The effect of training could therefore be somewhat larger than has yet been shown. However, although this study used a composite score of four basic operations, it is not likely that this kind of effect would have been found, given the small and noisy effects that were obtained. A study by Alloway and Alloway (2009), that did administer a division task, has shown effects on mathematical ability, using the same working memory training as in the present study. This study, however, was underpowered and effects on improvement in mathematics were small. Another study (Holmes et al., 2009) only found long term effects (6 months) of WMT on mathematics and used a mathematical reasoning task that measures number sense, in contrast to basic calculating operations. This finding could be similar to the effect that was found in this study, whereas children that trained with JM first, performed slightly better during the second period than their peers. A last study (Kroesbergen et al., 2012) also found effects of working memory training on early numeracy, but was conducted with pupils in kindergarten. This leads to the hypothesis that there might be a sensitive period for working memory training, during earlier development, and that no great effects of working memory training are to be expected when pupils are trained during later classes of primary school.
Limitations
The present findings are to be viewed in light of several shortcomings. It proved to be very difficult to plan the intervention periods within a school setting. Training periods were interrupted frequently by vacations, sports activities, preparations for end-of-year activities, and other extracurricular enterprises. After the month of May, training compliance dropped both with pupils as well as teachers. Both lack of continuity as well as decreasing training compliance will have influenced our results in several ways. First, training compliance might have caused gains to be less than they could have been. Second, some children expressed their boredom with the tasks that were used during the assessments. This might have led to less effort on the part of the pupils during the last measurement especially.
Another hazard was the fact that pupils were selected from several different schools, which might have had consequences for standardization of child-teacher relationships and teaching material. Different schools use different methods of teaching mathematics, all with slightly different contents and possible effects on outcome measures. The study design doesn’t allow to control for this effect.
The sample size was lower than expected, due to a lower number of eligible children in the different classes, and due to time restrictions. Bayesian analysis was used to control for this issue. Even though the sample size was small, the feedback system provided to us by LerendBrein was quite difficult to carry out, because schools were far apart and only few pupils per school were eligible to participate in this study due to strict inclusion criteria. Feedback provided to the pupils therefore might have been less than optimal during this study. This might have negatively affected both the intensity and efficacy of the training and therefore the obtained results regarding working memory gains and possibly mathematical abilities.
Conclusion
In sum, this study provides a limited contribution to the literature of working memory training and its near and far transfer effects, by directly examining the effects on mathematics training. On the positive side, computerized mathematics training has a desirable effect on mathematical abilities in children, in higher grades of elementary school, with difficulties in mathematics and attentional problems. Working memory training, specifically Jungle Memory, did seem to have a positive and added effect on outcomes, but it is still unclear if these effects are mediated by improvement of verbal and/or visual working memory. Unfortunately, this could not be confirmed by our study. These findings are in concordance with existing literature. Based on observations during the study, increasing the amount of effort in working memory training might improve the outcomes in working memory and ultimately mathematics. More research would be needed on this matter. The role of working memory and its mechanisms in mathematical abilities remain unclear. Due to its limitations, the results of this study must be considered with caution. Further research has to account for the precise planning of the intervention program, proper support of the children during their training periods and probably a reward system encouraging the children to do their best during measurements. Furthermore, it is recommended that other outcome measures of mathematical abilities are used concurring with the speeded tests used in most studies. More theoretically, training of attention and strategies aiding retrieval from long term memory might be beneficial for children with mathematical difficulties and attentional problems in higher grades of elementary school. Further research is needed to test these hypotheses.
Author Contributions
All authors listed have made substantial, direct, and intellectual contributions to the work, and approved for publication. EK and MN construed the study together, EK provided the master students that gathered the data. Analyses were carried out by MN while receiving feedback from EK. MN wrote the paper and EK gave constructive feedback an suggestions on improving the paper.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors would like to thank all pupils, parents, and schools that participated in this study. Furthermore, the authors acknowledge the contribution of LerendBrein, providing us with necessary training and the feedback protocol used in the study. Parts of the results in this paper have been presented at the 2016 International Neuropsychological Society Mid-Year Meeting on the eight of July 2016.
References
Alloway, T. P., and Alloway, R. G. (2009). The efficacy of working memory training in improving crystallized intelligence. Nat. Proc. doi: 10.1038/npre.2009.3697.1
Alloway, T. P., Bibile, V., and Lau, G. (2013). Computerized working memory training: can it lead to gains in cognitive skills in students? Comput. Hum. Behav. 29, 632–638. doi: 10.1016/j.chb.2012.10.023
Arsalidou, M., and Taylor, M. J. (2011). Is 2+2 = 4? Meta-analyses of brain areas needed for numbers and calculations. NeuroImage 54, 2382–2393. doi: 10.1016/j.neuroimage.2010.10.009
Baddeley, A. D., and Hitch, G. (1977). “Commentary on working memory,” in Human Memory: Basic Processes, ed. G. D. Bower (New York, NY: Academic Press), 191–241.
Bergman-Nutley, S., and Klingberg, T. (2014). Effect of working memory training on working memory, arithmetic and following instructions. Psychol. Res. 78, 869–877. doi: 10.1007/s00426-014-0614-0
Brankaer, C., Ghesquière, P., and De Smedt, B. (2014). Numerical magnitude processing deficits in children with mathematical difficulties are independent of intelligence. Res. Dev. Disabil. 35, 2603–2613. doi: 10.1016/j.ridd.2014.06.022
Cowan, N. (1988). Evolving conceptions of memory storage, selective attention, and their mutual constraints within the human information-processing system. Psychol. Bull. 104, 163–191. doi: 10.1037/0033-2909.104.2.163
Cowan, R., and Powell, D. (2014). The contributions of domain-general and numerical factors to third-grade arithmetic skills and mathematical learning disability. J. Educ. Psychol. 106, 214–229. doi: 10.1037/a0034097
Demir,Ö. E., Prado, J., and Booth, J. R. (2014). The differential role of verbal and spatial working memory in the neural basis of arithmetic. Dev. Neuropsychol. 39, 440–458. doi: 10.1080/87565641.2014.939182
De Weerdt, F., Desoete, A., and Roeyers, H. (2013). Behavioral inhibition in children with learning disabilities. Res. Dev. Disabil. 34, 1998–2007. doi: 10.1016/j.ridd.2013.02.020
Dormal, V., Schuller, A. M., Nihoul, J., Pesenti, M., and Andres, M. (2014). Causal role of spatial attention in arithmetic problem solving: evidence from left unilateral neglect. Neuropsychologia 60, 1–9. doi: 10.1016/j.neuropsychologia.2014.05.007
DuPaul, G. J., and Volpe, R. J. (2009). ADHD and learning disabilities: research findings and clinical implications. Curr. Atten. Disord. Rep. 1, 152–155. doi: 10.1007/s12618-009-0021-4
Friso-van den Bos, I., van der Ven, S. H. G., Kroesbergen, E. H., and van Luit, J. E. H. (2013). Working memory and mathematics in primary school children: a meta-analysis. Educ. Res. Rev. 10, 29–44. doi: 10.1016/j.edurev.2013.05.003
Greven, C. U., Kovas, Y., Willcutt, E. G., Petrill, S. A., and Plomin, R. (2014). Evidence for shared genetic risk between ADHD symptoms and reduced mathematics ability: a twin study. J. Child Psychol. Psychiatry Allied Disciplines 55, 39–48. doi: 10.1111/jcpp.12090
Holmes, J., and Gathercole, S. E. (2013). Taking working memory training from the laboratory into schools. Educ. Psychol. 34, 440–450. doi: 10.1080/01443410.2013.797338
Holmes, J., Gathercole, S. E., and Dunning, D. L. (2009). Adaptive training leads to sustained enhancement of poor working memory in children. Dev. Sci. 12, 9–16. doi: 10.1111/j.1467-7687.2009.00848.x
Huizinga, M., and Smidts, D. P. (2010). Age-related changes in executive function: a normative study with the dutch version of the Behavior Rating Inventory of Executive Function (BRIEF). Child Neuropsychol. 17, 51–66. doi: 10.1080/09297049.2010.509715
Klingberg, T., Fernell, E., Olesen, P. J., Johnson, M., Dahlstr, K., Om, €, et al. (2005). Computerized training of working memory in children with ADHD—a randomized, controlled trial. J. Am. Acad. Child Adolesc. Psychiatry 44, 177–186. doi: 10.1097/00004583-200502000-00010
Klingberg, T., Forssberg, H., and Westerberg, H. (2002). Training of working memory in children with ADHD. J. Clin. Exp. Neuropsychol. 24, 781–791. doi: 10.1076/jcen.24.6.781.8395
Klugkist, I., Laudy, O., and Hoijtink, H. (2005). Inequality constrained analysis of variance: a Bayesian approach. Psychol. Methods 10, 477–493. doi: 10.1037/1082-989X.10.4.477
Kolkman, M. E., Hoijtink, H. J. A., Kroesbergen, E. H., and Leseman, P. P. M. (2013a). The role of executive functions in numerical magnitude skills. Learn. Individ. Differ. 24, 145–151. doi: 10.1016/j.lindif.2013.01.004
Kolkman, M. E., Kroesbergen, E. H., and Leseman, P. P. M. (2013b). Early numerical development and the role of non-symbolic and symbolic skills. Learn. Instr. 25, 95–103. doi: 10.1016/j.learninstruc.2012.12.001
Kroesbergen, E. H., and van Dijk, M. (2015). Working memory and number sense as predictors of mathematical (dis-)ability. Z. Psychol. 223, 102–109. doi: 10.1027/2151-2604/a000208
Kroesbergen, E. H., van ’t Noordende, J. E., and Kolkman, M. E. (2012). Training working memory in kindergarten children: effects on working memory and early numeracy. Child Neuropsychol. 20, 23–37. doi: 10.1080/09297049.2012.736483
Landerl, K., Bevan, A., and Butterworth, B. (2004). Developmental dyscalculia and basic numerical capacities: a study of 8 – 9-year-old students. Cognition 93, 99–125. doi: 10.1016/j.cognition.2003.11.004
Larsson, H., Anckarsater, H., Råstam, M., Chang, Z., and Lichtenstein, P. (2012). Childhood attention-deficit hyperactivity disorder as an extreme of a continuous trait: a quantitative genetic study of 8,500 twin pairs. J. Child Psychol. Psychiatry Allied Disciplines 53, 73–80. doi: 10.1111/j.1469-7610.2011.02467.x
Lee, K., Ng, S. F., Pe, M. L., Ang, S. Y., Hasshim, M. N. A. M., and Bull, R. (2012). The cognitive underpinnings of emerging mathematical skills: executive functioning, patterns, numeracy, and arithmetic. Br. J. Educ. Psychol. 82, 82–99. doi: 10.1111/j.2044-8279.2010.02016.x
Maloney, E. A., and Beilock, S. L. (2012). Math anxiety: who has it, why it develops, and how to guard against it. Trends Cogn. Sci. 16, 404–406. doi: 10.1016/j.tics.2012.06.008
Martin, J., Hamshere, M. L., Stergiakouli, E., O’Donovan, M. C., and Thapar, A. (2015). Neurocognitive abilities in the general population and composite genetic risk scores for attention-deficit hyperactivity disorder. J. Child Psychol. Psychiatry 56, 648–656. doi: 10.1111/jcpp.12336
Marzocchi, G. M., Lucangeli, D., De Meo, T., Fini, F., and Comoldi, C. (2002). The disturbing effect of irrelevant information on arithmetic problem solving in inattentive children. Dev. Neuropsychol. 21, 73–92. doi: 10.1207/S15326942DN2101_4
McLean, J. F., and Hitch, G. J. (1999). Working memory impairments in children with specific arithmetic learning difficulties. J. Exp. Child Psychol. 74, 240–260. doi: 10.1006/jecp.1999.2516
Melby-Lervåg, M., and Hulme, C. (2013). Is working memory training effective? A meta-analytic review. Dev. Psychol. 49, 270–291. doi: 10.1037/a0028228
Memosyne Ltd (2011). Jungle Memory. Retrieved from http://lb.junglememory.com
Metcalfe, A. W. S., Ashkenazi, S., Rosenberg-Lee, M., and Menon, V. (2013). Fractionating the neural correlates of individual working memory components underlying arithmetic problem solving skills in children. Dev. Cogn. Neurosci. 6, 162–175. doi: 10.1016/j.dcn.2013.10.001
Miyake, A., Friedman, N. P., Emerson, M. J., Witzki, A. H., Howerter, A., and Wager, T. D. (2000). The unity and diversity of executive functions and their contributions to complex “Frontal Lobe” tasks: a latent variable analysis. Cogn. Psychol. 41, 49–100. doi: 10.1006/cogp.1999.0734
Östergren, R., and Träff, U. (2013). Early number knowledge and cognitive ability affect early arithmetic ability. J. Exp. Child Psychol. 115, 405–421. doi: 10.1016/j.jecp.2013.03.007
Passolunghi, M. C., and Pazzaglia, F. (2004). Individual differences in memory updating in relation to arithmetic problem solving. Learn. Individ. Differ. 14, 219–230. doi: 10.1016/j.lindif.2004.03.001
Passolunghi, M. C., and Pazzaglia, F. (2005). A comparison of updating processes in children good or poor in arithmetic word problem-solving. . Learn. Individ. Differ. 15, 257–269. doi: 10.1016/j.lindif.2005.03.001
Perna, R., Loughan, A. R., Le, J., Hertza, J., and Cohen, M. J. (2015). Spectrum of mathematical weaknesses: related neuropsychological correlates. Appl. Neuropsychol. Child 4, 157–165. doi: 10.1080/21622965.2013.827573
Piazza, M. (2010). Neurocognitive start-up tools for symbolic number representations. Trends Cogn. Sci. 14, 542–551. doi: 10.1016/j.tics.2010.09.008
Scholte, E. M., and van der Ploeg, J. D. (2005). Handleiding ADHD-Vragenlijst (Avl). Houten: Bohn Stafleu van Loghum.
Shinaver, C. S., Entwistle, P. C., and Söderqvist, S. (2014). Cogmed WM training: reviewing the reviews. Appl. Neuropsychol. Child 3, 163–172. doi: 10.1080/21622965.2013.875314
Söderqvist, S., and Bergman Nutley, S. (2015). Working memory training is associated with long term attainments in math and reading. Front. Psychol. 6:1711. doi: 10.3389/fpsyg.2015.01711
Spencer-Smith, M., and Klingberg, T. (2015). Benefits of a working memory training program for inattention in daily life: a systematic review and meta-analysis. PLoS ONE 10:e0119522. doi: 10.1371/journal.pone.0119522
St Clair-Thompson, H., Stevens, R., Hunt, A., and Bolder, E. (2010). Improving children’s working memory and classroom performance. Educ. Psychol. 30, 203–219. doi: 10.1080/01443410903509259
Temple, C. M., and Sherwood, S. (2002). Representation and retrieval of arithmetical facts: developmental difficulties. Q. J. Exp. Psychol. A 55, 733–752. doi: 10.1080/02724980143000550
Van de Schoot, R., Hoijtink, H., and Jan-Willem, R. (2011). Moving beyond traditional null hypothesis testing: evaluating expectations directly. Front. Psychol. 2:24. doi: 10.3389/fpsyg.2011.00024
Van de Weijer-Bergsma, E., Kroesbergen, E. H., Jolani, S., and Van Luit, J. E. H. (2015a). The monkey game: a computerized verbal working memory task for self-reliant administration in primary school children. Behav. Res. Methods 48, 756–771. doi: 10.3758/s13428-015-0607-y
Van de Weijer-Bergsma, E., Kroesbergen, E. H., Prast, E. J., and Van Luit, J. E. H. (2015b). Validity and reliability of an online visual–spatial working memory task for self-reliant administration in school-aged children. Behav. Res. Methods 47, 708–719. doi: 10.3758/s13428-014-0469-8
Van de Weijer-Bergsma, E., Kroesbergen, E. H., and Van Luit, J. E. H. (2015c). Verbal and visual-spatial working memory and mathematical ability in different domains throughout primary school. Mem. Cogn. 43, 367–378. doi: 10.3758/s13421-014-0480-4
Van der Maas, H., Straatemeijer, M., and Klinkenberg, S. (2009). Rekenen in rekentuin: ook voor zwakke rekenaars? Tijdschr. voor Remedial Teach. 3, 18–21.
Van der Ven, S. H. G., Kroesbergen, E. H., Boom, J., and Leseman, P. P. M. (2012). The development of executive functions and early mathematics: a dynamic relationship. Br. J. Educ. Psychol. 82, 100–119. doi: 10.1111/j.2044-8279.2011.02035.x
Keywords: working memory, training, mathematics, attention deficits, ADHD, dyscalculia
Citation: Nelwan M and Kroesbergen EH (2016) Limited Near and Far Transfer Effects of Jungle Memory Working Memory Training on Learning Mathematics in Children with Attentional and Mathematical Difficulties. Front. Psychol. 7:1384. doi: 10.3389/fpsyg.2016.01384
Received: 02 June 2016; Accepted: 30 August 2016;
Published: 21 September 2016.
Edited by:
José Jesús Gázquez, University of Almería, SpainReviewed by:
Thomas James Lundy, virtuallaboratory.net, inc., USALudmila Nunes, Purdue University, USA
Copyright © 2016 Nelwan and Kroesbergen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Michel Nelwan, bS5uZWx3YW5AbHVjZXJ0aXMubmw=
 Michel Nelwan
Michel Nelwan Evelyn H. Kroesbergen
Evelyn H. Kroesbergen